Cohesive Fracture Study of a Bonded Coarse Silica Sand Aggregate Bond Interface Subjected to Mixed-Mode Bending Conditions
Abstract
:1. Introduction
2. Research Significance
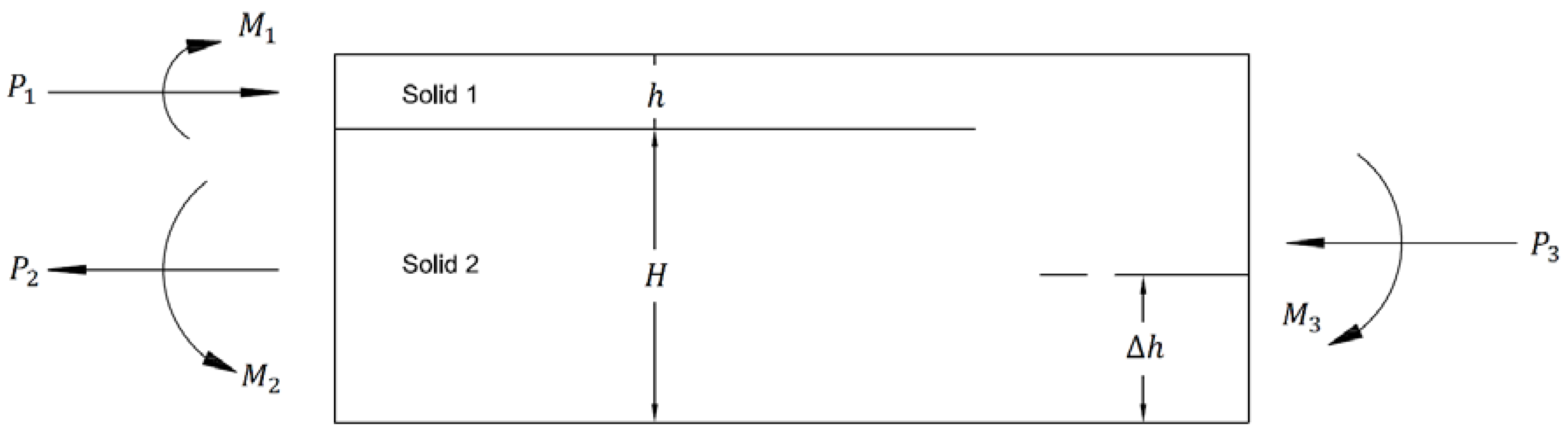
3. Experimental Testing of Mixed-Mode Bending Specimens
3.1. Introduction
3.2. Design and Construction of Specimens
3.3. Material Properties
3.4. Testing Set-Up and Instrumentation
| Specimen ID | Initial crack length (a) (mm) | Moment arm (c) (mm) |
|---|---|---|
| S-a80-c250 | 80 | 250 |
| S-a100-c250 | 100 | 250 |
| S-a120-c100 | 120 | 100 |
| S-a120-c175 | 120 | 175 |
| S-a120-c250 | 120 | 250 |
| S-a120-c325 | 120 | 325 |
| S-a120-c400 | 120 | 400 |
| S-a140-c250 | 140 | 250 |
| S-a160-c250 | 160 | 250 |

3.5. Experimental Results
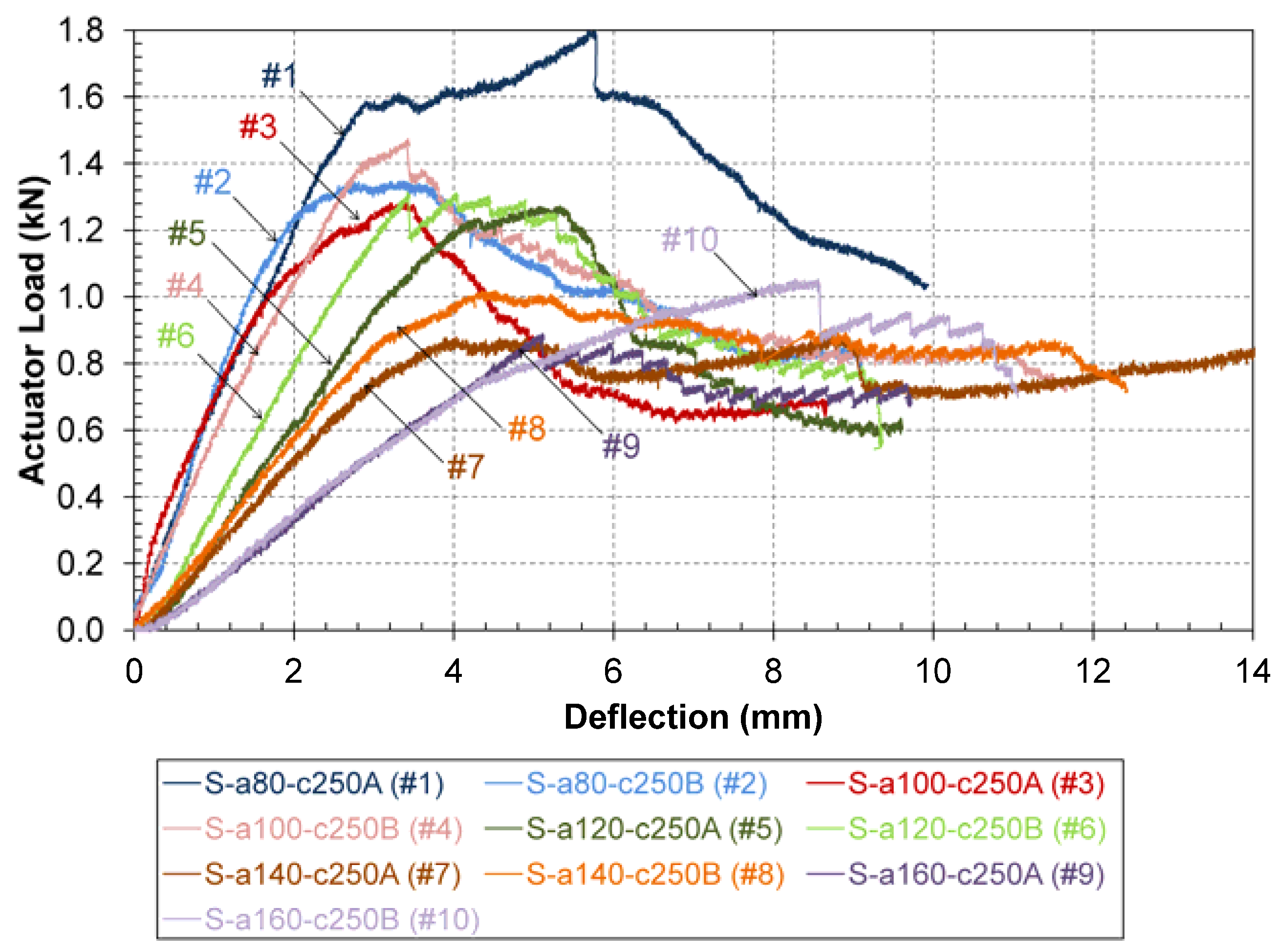
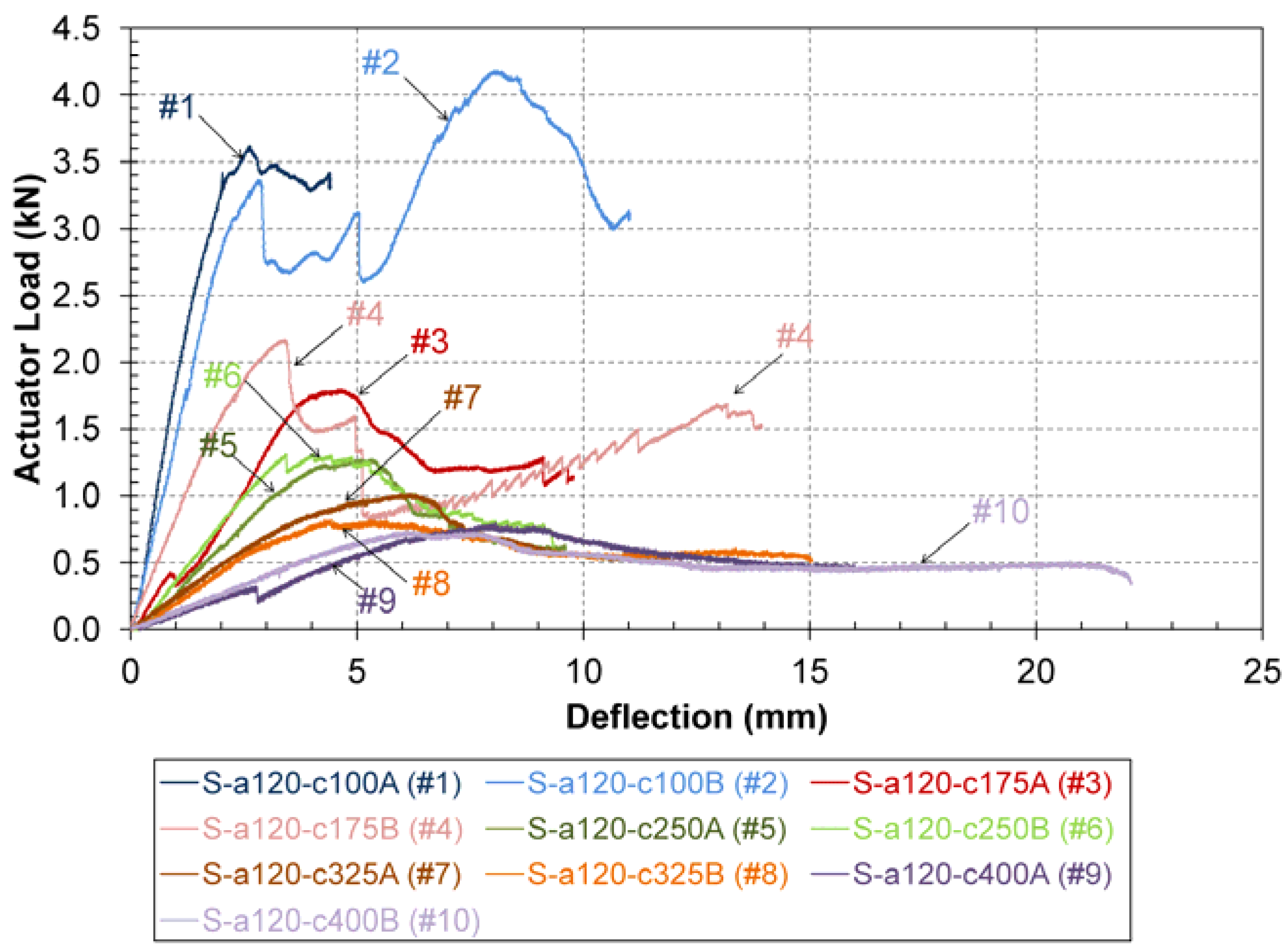

4. Numerical Analysis for Cohesive Parameters
4.1. Introduction
4.2. Derived Relationships for Fracture Energy
4.2.1. Global Method
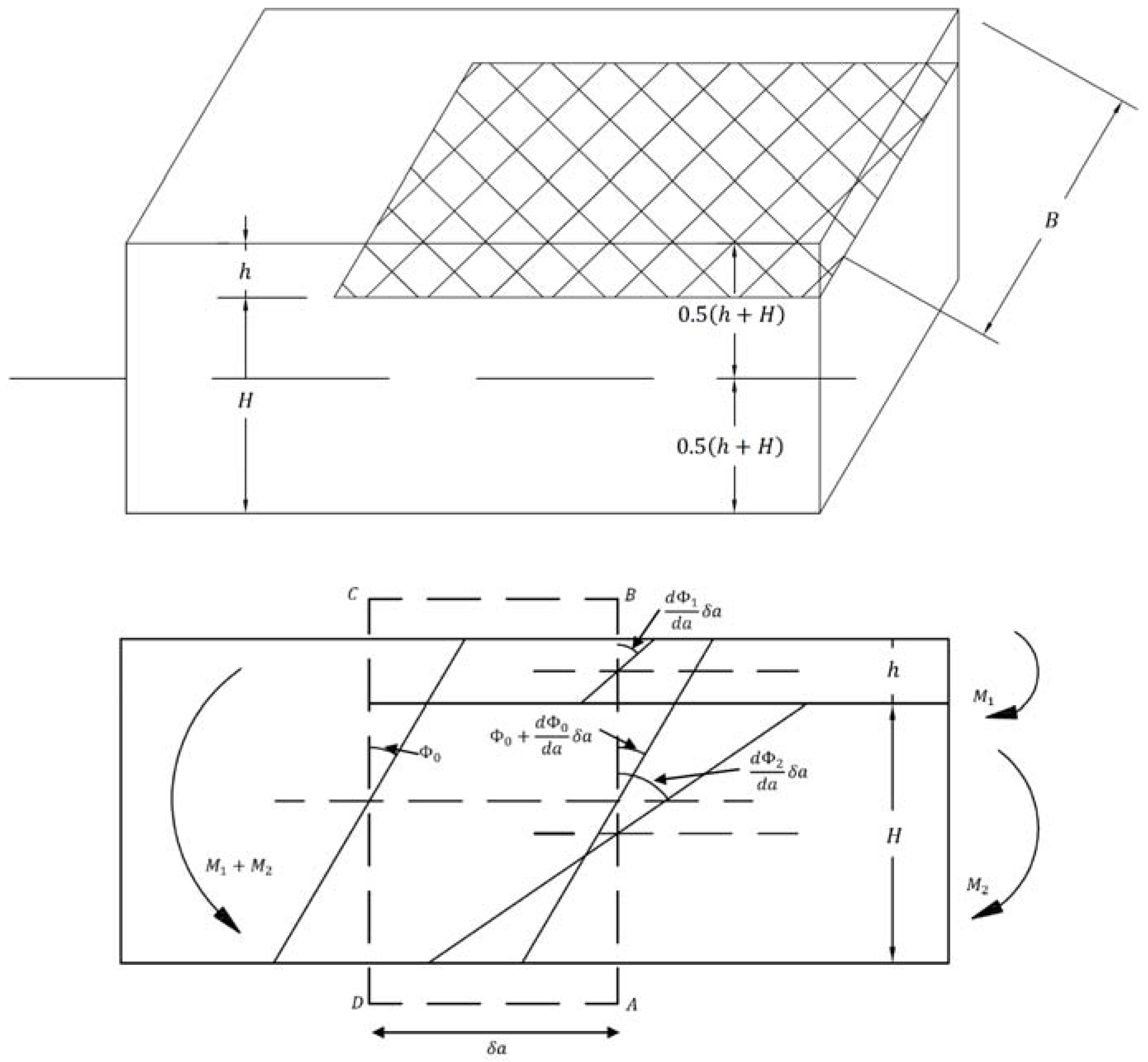
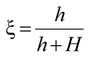
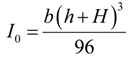
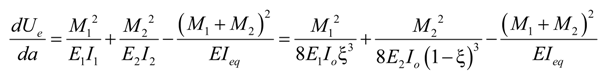
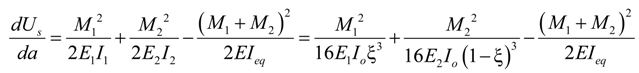
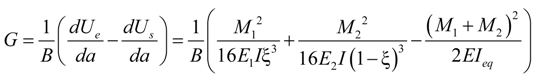
- 1.
- Under pure Mode II loading,
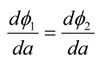
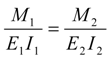
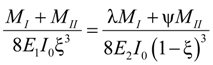
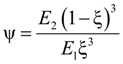
- 2.
- Under pure Mode I loading,
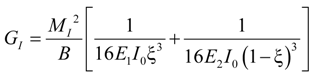
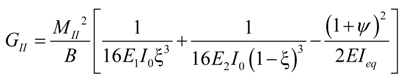
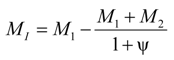

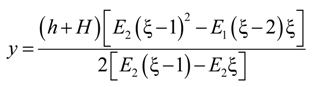
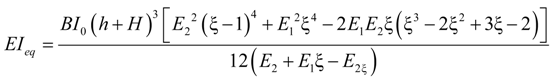
4.2.2. Local Method
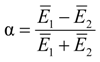

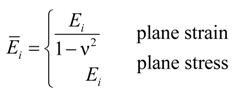
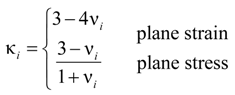

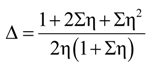
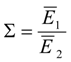
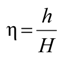
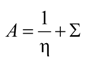
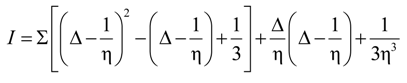
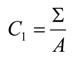
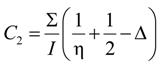
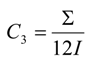
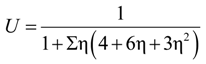
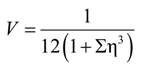
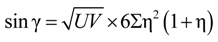
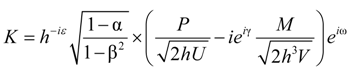
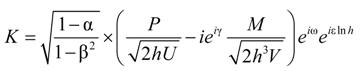
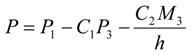
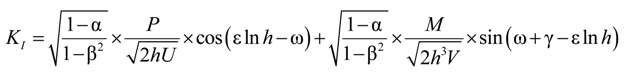
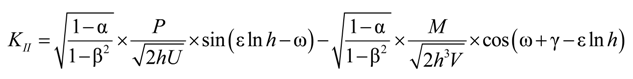
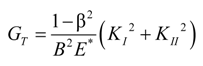
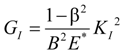
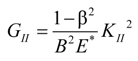
4.3. Considerations for Correction Factors and Non-Linearity Effects
| Specimen ID | Angle of rotation (degrees) | Horizontal Force (kN) | Moment (kNm) | Nonlinearity due to horizontal force (%) | |
|---|---|---|---|---|---|
| Horizontal Force | Vertical Force | ||||
| S-a80-c250A | 0.66 | 0.018 | 0.003 | 0.394 | 1 |
| S-a80-c250B | 0.64 | 0.015 | 0.002 | 0.336 | 1 |
| S-a100-c250A | 0.77 | 0.017 | 0.003 | 0.317 | 1 |
| S-a100-c250B | 0.65 | 0.016 | 0.002 | 0.351 | 1 |
| S-a120-c100A | 1.56 | 0.097 | 0.015 | 0.362 | 4 |
| S-a120-c100B | 1.69 | 0.10 | 0.015 | 0.336 | 4 |
| S-a120-c175A | 1.50 | 0.047 | 0.007 | 0.314 | 2 |
| S-a120-c175B | 1.10 | 0.042 | 0.006 | 0.379 | 2 |
| S-a120-c250A | 0.93 | 0.020 | 0.003 | 0.301 | 1 |
| S-a120-c250B | 0.78 | 0.018 | 0.003 | 0.325 | 1 |
| S-a120-c325A | 1.0 | 0.017 | 0.003 | 0.315 | 1 |
| S-a120-c325B | 0.76 | 0.011 | 0.002 | 0.261 | 1 |
| S-a120-c400A | 1.03 | 0.014 | 0.002 | 0.300 | 1 |
| S-a120-c400B | 1.09 | 0.014 | 0.002 | 0.291 | 1 |
| S-a140-c250A | 0.93 | 0.014 | 0.002 | 0.218 | 1 |
| S-a140-c250B | 0.97 | 0.017 | 0.003 | 0.250 | 1 |
| S-a160-c250A | 1.17 | 0.018 | 0.003 | 0.222 | 1 |
| S-a160-c250B | 1.54 | 0.026 | 0.004 | 0.240 | 2 |
4.4. Application of Derived Relationships to Experimental Data
| Specimen ID | Global Method [7] | Local Method (plane stress) [8] | Local Method (plane strain) [8] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GT | GI | GII | GI/GII | GT | GI | GII | GI/GII | GT | GI | GII | GI/GII | |
| S-a80-c250 | 0.443 | 0.443 | 0.0002 | 2138 | 0.443 | 0.196 | 0.247 | 0.792 | 0.421 | 0.186 | 0.235 | 0.792 |
| S-a100-c250 | 0.335 | 0.335 | 0.0002 | 2138 | 0.335 | 0.148 | 0.187 | 0.792 | 0.319 | 0.141 | 0.178 | 0.792 |
| S-a120-c100 | 0.966 | 0.965 | 0.0013 | 721 | 0.966 | 0.412 | 0.554 | 0.743 | 0.919 | 0.392 | 0.527 | 0.743 |
| S-a120-c175 | 0.769 | 0.769 | 0.0005 | 1470 | 0.769 | 0.336 | 0.433 | 0.777 | 0.732 | 0.320 | 0.412 | 0.777 |
| S-a120-c250 | 0.662 | 0.662 | 0.0003 | 2138 | 0.662 | 0.292 | 0.370 | 0.792 | 0.370 | 0.278 | 0.352 | 0.792 |
| S-a120-c325 | 0.572 | 0.572 | 0.0002 | 2704 | 0.572 | 0.254 | 0.318 | 0.799 | 0.544 | 0.242 | 0.302 | 0.799 |
| S-a120-c400 | 0.597 | 0.596 | 0.0002 | 3179 | 0.597 | 0.266 | 0.331 | 0.804 | 0.568 | 0.252 | 0.315 | 0.804 |
| S-a140-c250 | 0.491 | 0.491 | 0.0002 | 2138 | 0.491 | 0.217 | 0.274 | 0.792 | 0.467 | 0.206 | 0.261 | 0.792 |
| S-a160-c250 | 0.668 | 0.668 | 0.0003 | 2138 | 0.668 | 0.295 | 0.373 | 0.792 | 0.636 | 0.281 | 0.355 | 0.792 |
4.5. Trends of Partitioned Fracture Energy to Crack Length and Mode-Mixity
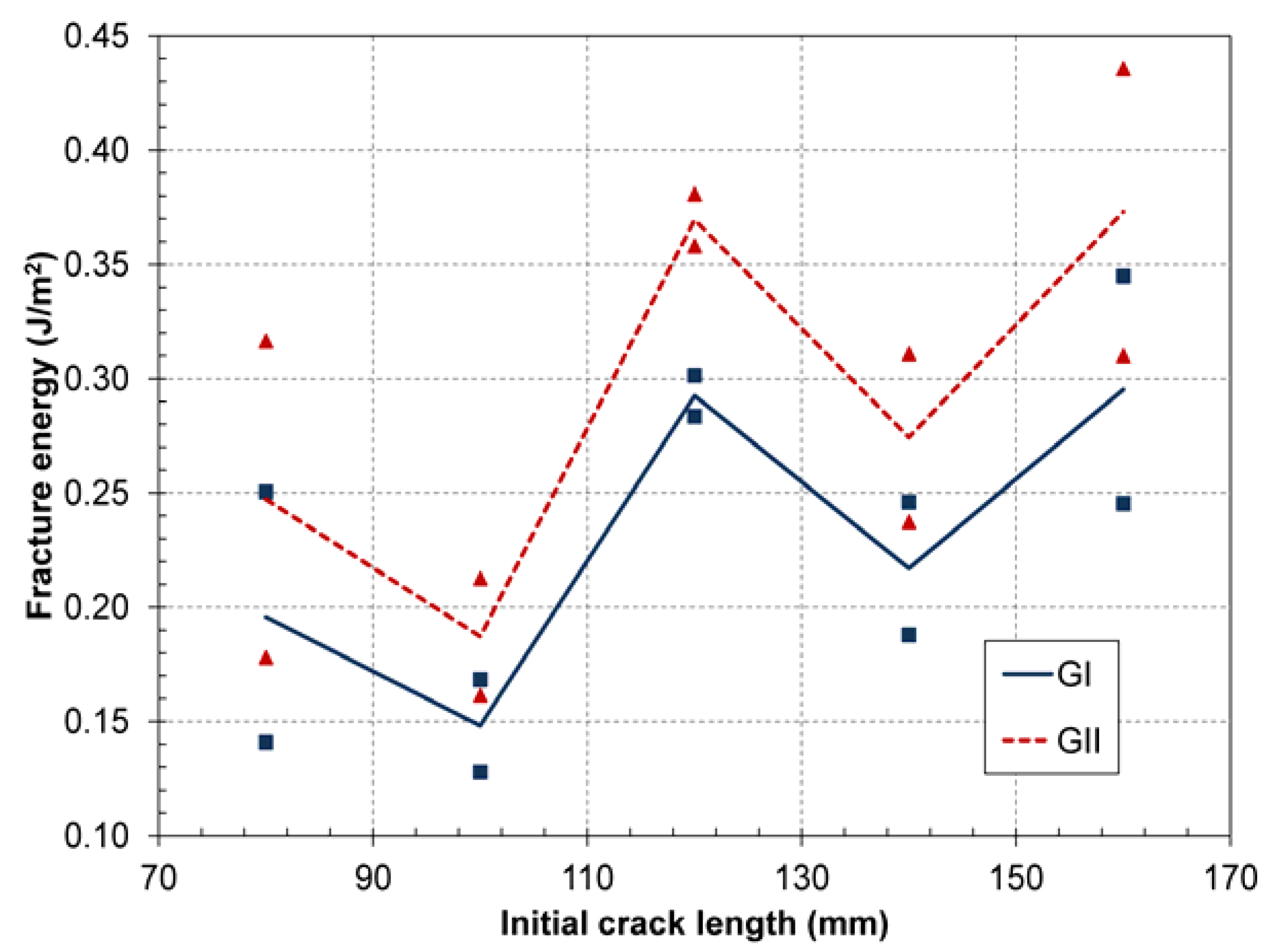

4.6. Applicability of Derived Partitioned Critical Fracture Energy
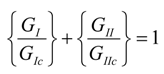
5. Finite Element Analysis: Validation and Consistent Parameters
5.1. Composition of Traction-Separation Model

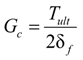
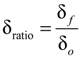
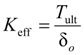
5.2. FE Model Development
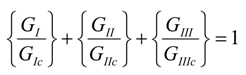
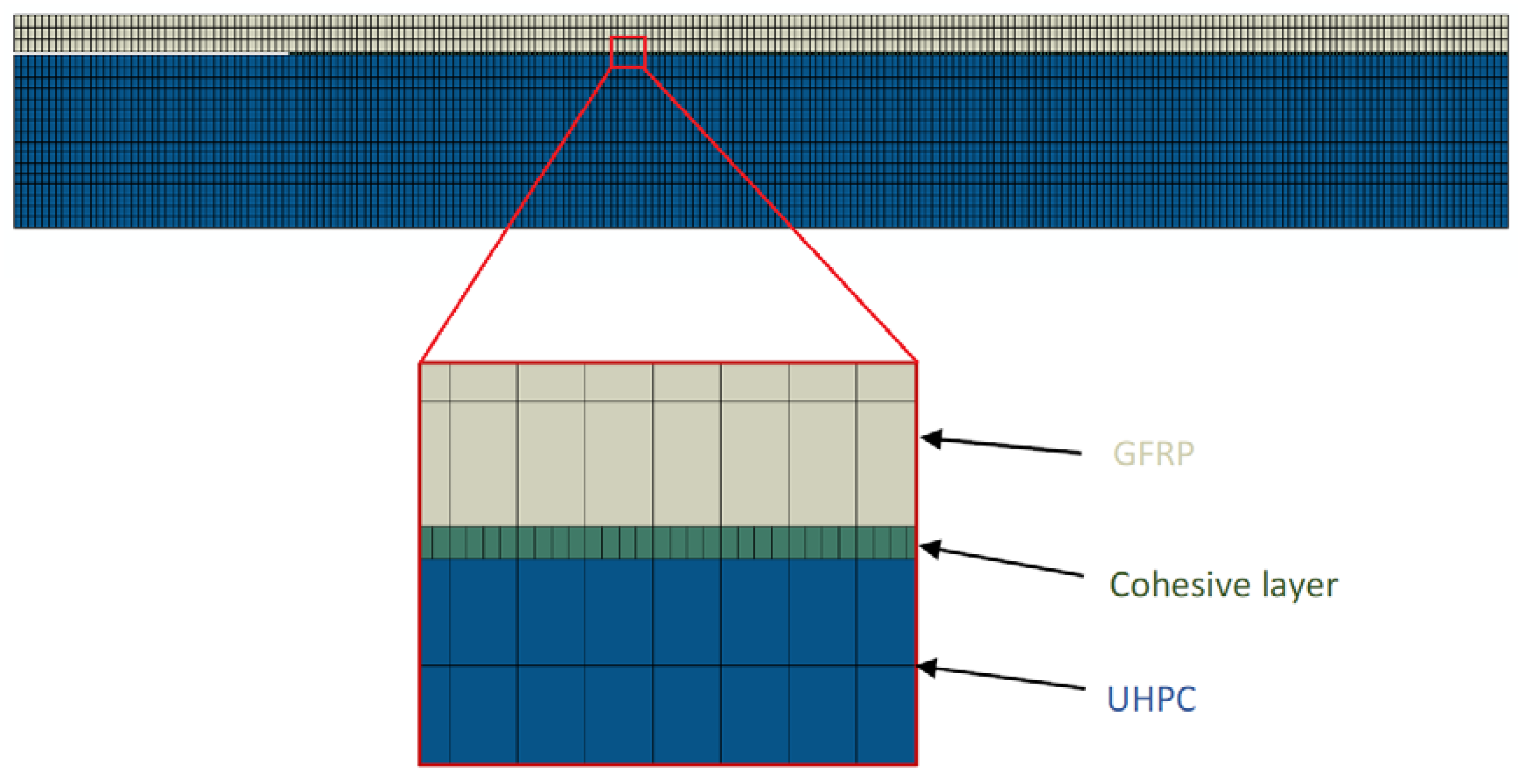
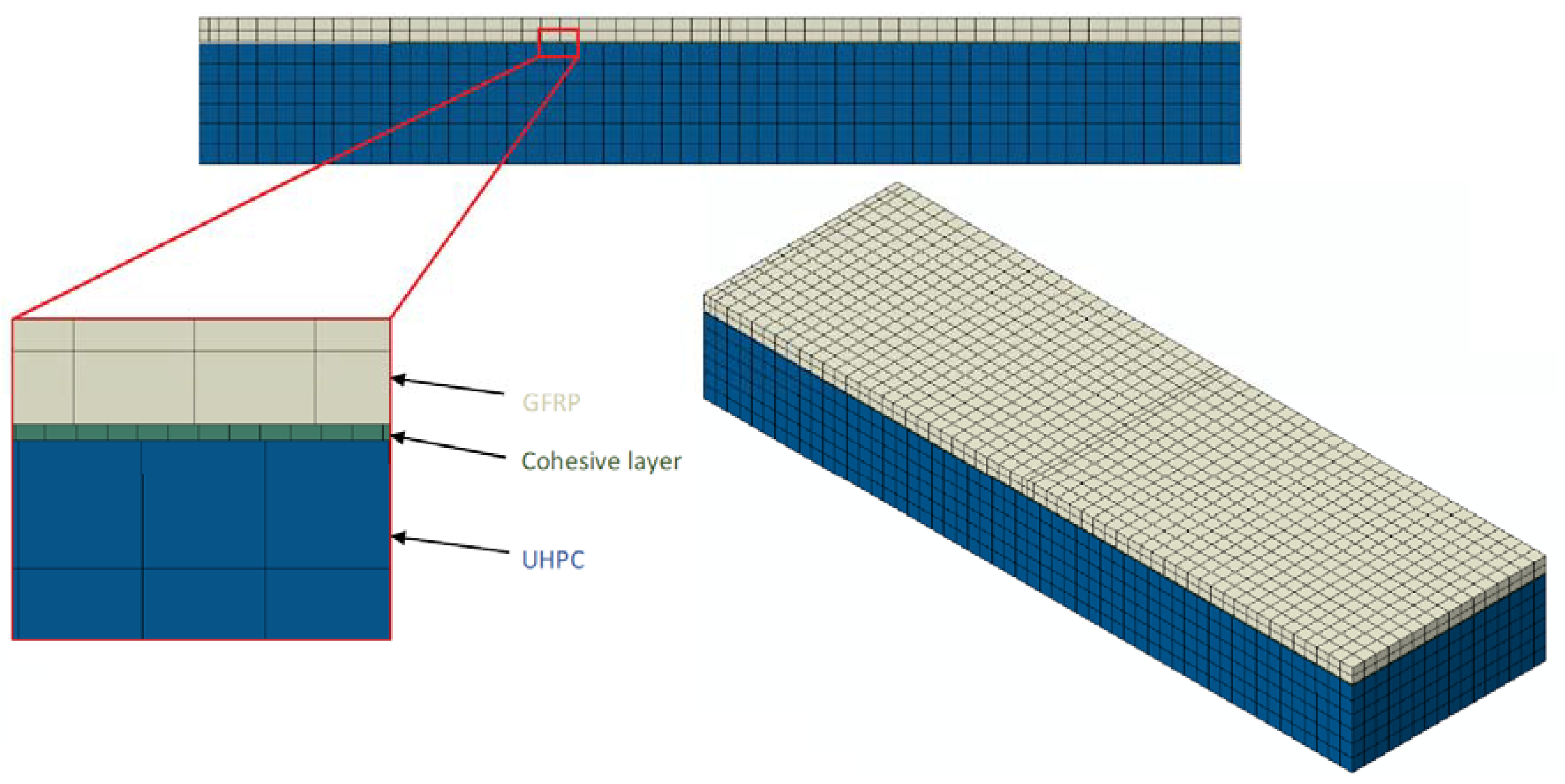
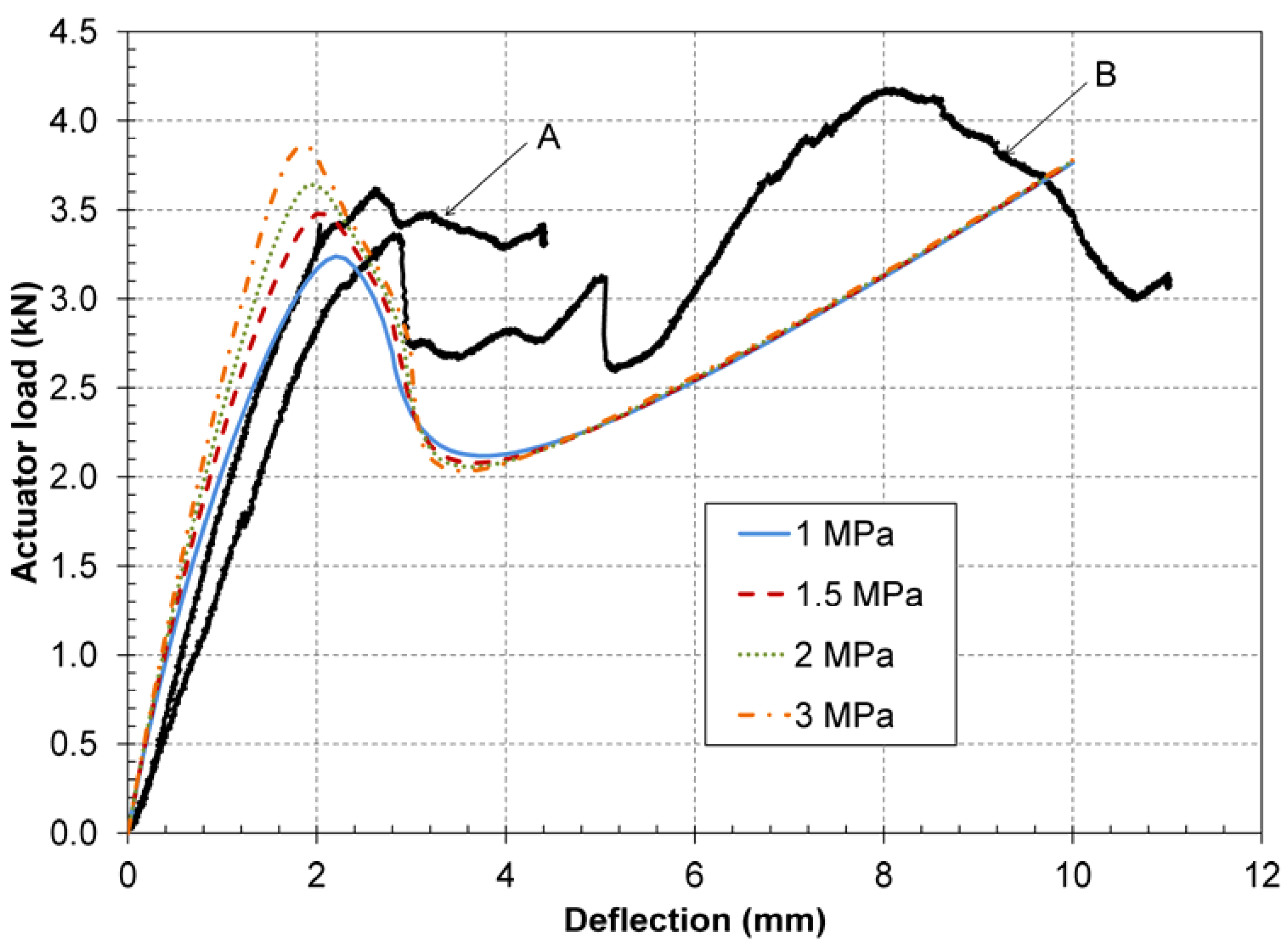
5.3. Two-Dimensional FE Model: Parametric Study and Model Validation
| Model ID | Fracture energy (G) (kJ/m2) | Effective nominal stress (Tult) (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| Per unit width (mm) | Per 130 mm width | Per unit width (mm) | Per 130 mm width | |||||
| GI | GII | GI | GII | (Tult)I | (Tult)II | (Tult)I | (Tult)II | |
| S-a120-c100-1MPa-v 2D | 0.412 | 0.554 | 53.55 | 72.05 | 1.0 | 1.35 | 130 | 174.90 |
| S-a120-c100-1.5MPa-v 2D | 0.412 | 0.554 | 53.55 | 72.05 | 1.5 | 2.02 | 195 | 262.36 |
| S-a120-c100-2MPa-v 2D | 0.412 | 0.554 | 53.55 | 72.05 | 2.0 | 2.69 | 260 | 349.81 |
| S-a120-c100-3MPa-v 2D | 0.412 | 0.554 | 53.55 | 72.05 | 3.0 | 4.04 | 390 | 524.71 |
| Model ID | Fracture energy (G) (kJ/m2) | Effective nominal stress (Tult) (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| Per unit width (mm) | Per 130 mm width | Per unit width (mm) | Per 130 mm width | |||||
| GI | GII | GI | GII | (Tult)I | (Tult)II | (Tult)I | (Tult)II | |
| S-a80-c250-2MPa-v 2D | 0.196 | 0.247 | 25.44 | 32 | 2 | 2.53 | 260 | 328 |
| S-a100-c250-2MPa-v 2D | 0.148 | 0.187 | 19.25 | 24 | 2 | 2.53 | 260 | 328 |
| S-a120-c100-2MPa-v 2D | 0.412 | 0.554 | 53.55 | 72 | 2 | 2.69 | 260 | 350 |
| S-a120-c175-2MPa-v 2D | 0.336 | 0.433 | 43.73 | 56 | 2 | 2.57 | 260 | 334 |
| S-a120-c250-2MPa-v 2D | 0.292 | 0.370 | 38.02 | 48 | 2 | 2.53 | 260 | 328 |
| S-a120-c325-2MPa-v 2D | 0.254 | 0.318 | 33.01 | 41 | 2 | 2.50 | 260 | 325 |
| S-a120-c400-2MPa-v 2D | 0.266 | 0.331 | 34.56 | 43 | 2 | 2.49 | 260 | 323 |
| S-a140-c250-2MPa-v 2D | 0.217 | 0.274 | 28.21 | 36 | 2 | 2.53 | 260 | 328 |
| S-a160-c250-2MPa-v 2D | 0.295 | 0.373 | 38.38 | 48 | 2 | 2.53 | 260 | 328 |
5.4. Determination of Consistent Parameters of Traction-Separation Model
| Parameter | Mode I | Mode II |
|---|---|---|
| Damage initiation ratio (δratio) | 5 | |
| Critical partitioned fracture energy ratio (GIC/GIIC) | 0.33 | |
| Fracture energy (Gi) (kJ/m2) | 0.3 | 0.9 |
| Effective nominal stress (Tult) (MPa) | 2 | 6 |
| Initial material stiffness (K) (MPa/mm) | 33.33 | 100 |
5.5. Validation and Discussion of Consistent Cohesive Parameters

6. Conclusions
Nomenclature
| A | Dimensionless cross-section |
| a | Crack length |
| B | Section width |
| C1, C2, C3, U, V, γ | Geometric factors |
| E* | Complex interface equivalent modulus of elasticity |
| E1, E2 | Modulus of elasticity of upper arm, and lower arm |
| Ē1, Ē2 | Modulus of elasticity in upper arm, and lower arm, accounting for plane stress and plane strain effects |
| EIeq | Equivalent flexural stiffness of uncracked section |
| F-ratio | Ratio of the mean square between the groups to the mean square within the group as defined in the Single Factor ANOVA test |
| GI, GII | Mode I, and Mode II fracture energy |
| GC | Critical fracture energy |
| h, H | Height of upper arm, and lower arm |
| I | Dimensionless moment of inertia |
| I0 | Moment of inertia of equivalent section with one material |
| I1, I2 | Moment of inertia of upper arm, and lower arm |
| K | Initial material stiffness |
| KI, KII | Complex stress intensity factor associated with Mode I, and Mode II |
| L | Length of MMB specimen |
| M | Linear combination of edge moments |
| MI, MII | Bending moment contribution from Mode I, and Mode II |
| M1, M2 | Bending moment applied to upper arm, and lower arm |
| P | Linear combination of edge loads |
| Tult | Effective nominal stress |
| Ue | External work performed |
| Us | Potential strain energy |
| y | Location neutral axis in uncracked section |
| Δ, Σ, η | Neutral axis parameters |
| α, β | Dundurs’ elastic mismatch parameters |
| δo, δf | Separation at damage initiation, and failure |
| δratio | Damage initiation ratio |
| ε | Oscillation index |
| κ1, κ2 | In-plane bulk modulus in upper arm, and lower arm |
| λ | Partitioning coefficient associated with Mode I |
| μ1, μ2 | Poisson’s ratio in upper arm, and lower arm |
| ξ | Height factor |
| ϕ1, ϕ2 | Curvature in upper arm, and lower arm |
| ψ | Partitioning coefficient associated with Mode II |
| ω | Angle shift due to elastic mismatch |
Acknowledgments
Conflicts of Interest
References
- Inglis, G.R. Analysis of stresses and strains near the end of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar]
- Griffith, A.A. The phenomenon of rupture and flow in solids. Philos. Trans. R. Soc. Lond. 1920, A221, 163–198. [Google Scholar]
- Dugdale, D.S. Yielding of sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Parmigiani, J.P.; Thouless, M.D. The effects of cohesive strength and toughness on mixed-mode delamination of beam-like geometries. Eng. Fract. Mech. 2007, 74, 2675–2699. [Google Scholar] [CrossRef]
- Hashemi, S.; Kinloch, A.J.; Williams, J.G. Corrections needed in double-cantilever beam tests for assessing the interlaminar failure of fibre-composites. J. Mater. Sci. Lett. 1989, 8, 125–129. [Google Scholar] [CrossRef]
- Williams, J.G. End corrections for orthotropic DCB specimens. Compos. Sci. Technol. 1989, 35, 367–376. [Google Scholar] [CrossRef]
- Williams, J.G. On the calculation of energy release rates for cracked laminates. Int. J. Fract. 1988, 36, 101–119. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Suo, Z. Mixed mode cracking in layered materials. Adv. Appl. Mech. 1992, 29, 63–191. [Google Scholar] [CrossRef]
- El-Hacha, R.; Chen, D. Behaviour of hybrid FRP-UHPC beams subjected to static flexural loading. Compos. Part B 2011, 43, 582–593. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Jacobsen, T.K. Determination of cohesive laws by the J integral approach. Eng. Fract. Mech. 2003, 70, 1841–1858. [Google Scholar] [CrossRef]
- ASTM Standard D6671. Standard Test Method for Mixed Mode I-Mode II Interlaminar Fracture Toughness of Unidirectional Fiber Reinforced Polymer Matrix Composites. In ASTM International; American Society for Testing and Materials: Philadelphia, PA, USA, 2006.
- Sika Canada. Sikadur® 330 Product Data Sheet; Sika Canada Inc.: Pointe-Claire, Canada, 2007. [Google Scholar]
- St-Cyr, D. Director of Research and Development. In Personal Communication; Pultrall Inc.: Thetford Mines, QC, Canada, 2013. [Google Scholar]
- Graybeal, B.A. Material Property Characterization of Ultra-High Performance Concrete; Report No. FHWA-HRT-06–103; Federal Highway Administration: Washington, DC, USA, August; 2006. [Google Scholar]
- Quispitupa, A.; Berggreen, C.; Carlsson, L.A. On the analysis of a mixed-mode bending sandwich specimen for debond fracture characteristics. Eng. Fract. Mech. 2009, 76, 597–613. [Google Scholar]
- Da Silva, L.F.M.; Esteves, V.H.C.; Chaves, F.J.P. Fracture toughness of a structural adhesive under mixed mode loadings. Mater. Werkst. 2011, 42, 460–470. [Google Scholar] [CrossRef]
- Bui, Q.V. A modified Benzeggagh-Kenane fracture criterion for mixed-mode delamination. J. Compos. Mater. 2011, 45, 389–413. [Google Scholar] [CrossRef]
- Harvey, C.M.; Wang, S. Experimental assessment of mixed-mode partition theories. Compos. Struct. 2012, 94, 2057–2067. [Google Scholar] [CrossRef]
- Bennati, S.; Fisicaro, P.; Valvo, P.S. An enhanced beam-theory model of the mixed-mode bending (MMB) test—Part I: Literature review and mechanical model. Meccanica 2013, 48, 443–462. [Google Scholar] [CrossRef]
- Wang, S.; Harvey, C.M.; Guan, L. Partition of mixed modes in layered isotropic double cantilever beams with non-rigid cohesive interfaces. Eng. Fract. Mech. 2013, 111, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Dharamawan, F.; Simpson, G.; Herszberg, I.; John, S. Mixed mode fracture toughness of GFRP composites. Compos. Struct. 2006, 75, 328–338. [Google Scholar] [CrossRef]
- Reeder, J.R.; Crews, J.R., Jr. Nonlinear analysis and redesign of the mixed-mode bending delamination test. NASA Tech. Memo. 1991, 14. [Google Scholar] [CrossRef]
- Ducept, F.; Gamby, D.; Davies, P. A mixed-mode failure criterion derived from tests on symmetric and asymmetric specimens. Compos. Sci. Technol. 1999, 59, 609–619. [Google Scholar] [CrossRef]
- Kinloch, A.J.; Wang, Y.; William, J.G.; Yayla, P. The mixed-mode delamination of fibre composite materials. Compos. Sci. Technol. 1993, 47, 225–237. [Google Scholar] [CrossRef]
- Schapery, R.A.; Davidson, B.D. Prediction of energy release rate for mixed-mode delamination using classical plate theory. Appl. Mech. Rev. 1990, 43, S281–S287. [Google Scholar] [CrossRef]
- Reeder, J.R.; Crew, J.R., Jr. Mixed-mode bending methods for delamination testing. Am. Inst. Aeronaut. Astronaut. 1990, 28, 1270–1276. [Google Scholar] [CrossRef]
- De Moura, M.F.S.F.; Campilho, R.D.S.G.; Gonçalves, J.P.M. Pure mode II fracture characterization of composite bonded joints. Int. J. Adhes. Adhes. 2009, 46, 1589–1595. [Google Scholar]
- Hashemi, S.; Kinloch, A.J.; Williams, J.G. The analysis of interlaminar fracture in uniaxial fibre-polymer composites. Proc. R. Soc. Lond. Ser. A 1990, 427, 173–199. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of uni-directional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Kanninen, M.F.; Popelar, C.H. Advanced Fracture Mechanics; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
- Sills, R.B.; Thouless, M.D. The effect of cohesive-law parameters on mixed-mode fracture. Eng. Fract. Mech. 2012, 109, 353–368. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. The influence of plasticity of mixed mode interface toughness. J. Mech. Phys. Solid 1993, 41, 110–135. [Google Scholar]
- Tvergaard, V.; Hutchinson, J.W. On the toughness of ductile adhesive joints. J. Mech. Phys. Solid 1996, 44, 789–800. [Google Scholar] [CrossRef]
- Campilho, R.D.S.G.; Banea, M.D.; Neto, J.A.B.P.; da Silva, L.F.M. Modelling adhesive joints with cohesive zone models: Effect of the cohesive law shape of the adhesive layer. Int. J. Adhes. Adhes. 2013, 44, 48–56. [Google Scholar]
- Diehl, T. On using a penalty-based cohesive-zone finite element approach. Part I: Elastic solution benchmarks. Int. J. Adhes. Adhes. 2008, 28, 237–255. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia Corp. Abaqus Analysis User’s Manual; Version 6.9; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2009. [Google Scholar]
- Blackman, B.R.K.; Hadavinia, H.; Kinloch, A.J.; Williams, J.G. The use of a cohesive zone model to study the fracture of fibre composites and adhesively-bonded joints. Int. J. Fract. 2003, 119, 25–46. [Google Scholar] [CrossRef]
- Chen, D.; El-Hacha, R. Bond strength between cast-in-place ultra-high-performance-concrete and glass fibre reinforced polymer plates using epoxy bonded coarse silica sand. J. ASTM Int. 2012, 9. [Google Scholar] [CrossRef]
- Chen, D.; El-Hacha, R. Characterization of Cohesive Bond Interfaces under Mode II Loading Using Finite Element Methods. In Proceedings of 4th Asia-Pacific Conference on FRP in Structures (APFIS 2013), Melbourne, Australia, 11–13 December 2013; p. 6.
- Högberg, J.L. Mixed mode cohesive law. Int. J. Fract. 2006, 141, 549–559. [Google Scholar] [CrossRef]
- Camanho, P.P.; Dávila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; NASA/TM-2002-211737; National Aeronautics and Space Administration: Hampton, Virginia, USA.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, D.; El-Hacha, R. Cohesive Fracture Study of a Bonded Coarse Silica Sand Aggregate Bond Interface Subjected to Mixed-Mode Bending Conditions. Polymers 2014, 6, 12-38. https://doi.org/10.3390/polym6010012
Chen D, El-Hacha R. Cohesive Fracture Study of a Bonded Coarse Silica Sand Aggregate Bond Interface Subjected to Mixed-Mode Bending Conditions. Polymers. 2014; 6(1):12-38. https://doi.org/10.3390/polym6010012
Chicago/Turabian StyleChen, Donna, and Raafat El-Hacha. 2014. "Cohesive Fracture Study of a Bonded Coarse Silica Sand Aggregate Bond Interface Subjected to Mixed-Mode Bending Conditions" Polymers 6, no. 1: 12-38. https://doi.org/10.3390/polym6010012




