Fluctuating Entanglements in Single-Chain Mean-Field Models
Abstract
:1. Introduction
- Consistency with multi-chain models. The single-chain model should predict the same magnitude for the elastic modulus as multi-chain models and therefore estimate the same entanglement density when comparing with rheological data. Cross-linked network calculations have already established the importance of node fluctuations for this agreement [30,31,32,33,34]. In the present paper, we verify only qualitatively whether the effect of ESFs on the plateau modulus in single-chain mean-field models is consistent with that observed in multi-chain models. Specifically, the plateau modulus should decrease when the size of ESFs increases.
- Consistency with nonequilibrium thermodynamics. Equilibrium thermodynamics and statistical mechanics can be applied in a straightforward way to cross-linked systems [52]. Similarly one can apply nonequilibrium thermodynamics to entangled melts, using either GENERIC or a simple virtual-work argument to derive the stress tensor. For cross-linked systems we simply require that the entropy of the universe not decrease when reversibly deforming a network.
- Consistency with the stress-optic rule (for moderate deformations). It is well established experimentally [38] that polymer melts show a linear relationship between the stress tensor and the refractive index tensor when the chains are Gaussian [53,54]. The dependence of the refractive index tensor on chain conformations has a straightforward derivation [55], so we assume that it is correct. The refractive index tensor should be compared to the stress tensor from criterion 2.
- Consistency between Green–Kubo predictions and the relaxation modulus predicted for infinitesimal deformations. Linear response theory requires that the relaxation of stress from small external perturbations should be the same as relaxation from small fluctuations that arise at equilibrium [56]. Both expressions require as input an expression for the stress tensor, and this expression should come from criterion 2.
2. Existing Entangled Melt Models and the Four Criteria
2.1. Doi–Edwards Model and Öttinger’s Generalization
| Model ↓ | Criterion → | 1: ESFs | 2: NETD | 3: SOR/OC | 4: GKR |
|---|---|---|---|---|---|
| Doi–Edwards model [1,2,3,4,5] | ✕ | ✓ | ✓ | ✓ | |
| Öttinger model [63] | ✓ | ✓ | ? | ✓ | |
| Associating polymer model I [41] | ✕ | ✓ | ✕ | ✓ | |
| Associating polymer model II [41] | ✓ | ✕ | ✓ | ✓ | |
| Slip-link model [10,64] | ✕ | ✓ | ✓ | ✓ | |
| Slip-spring simulation (2005) [65] | ✓ | ✕ | ✓ | ✕ | |
| Slip-spring simulation (2007) [39] | ✓ | ✕ | ✓ | ✓ | |
| PCN simulation [66] | ✓ | ✕ | ✓ | ✓ | |
| Heinrich–Straube–Helmis model [57] | ✓ | ✓ | ✓ | NA | |
| Rubinstein–Panyukov model [58,59] | ✓ | ✓ | ✓ | NA | |
| Everaers model [60] | ✓ | ✓ | ✓ | NA | |
2.2. Associating Polymers
2.3. Slip-Link Model
2.4. Slip-Spring Simulation
2.5. PCN Simulation
3. Proposed Virtual-Spring Dynamics of Ronca and Allegra
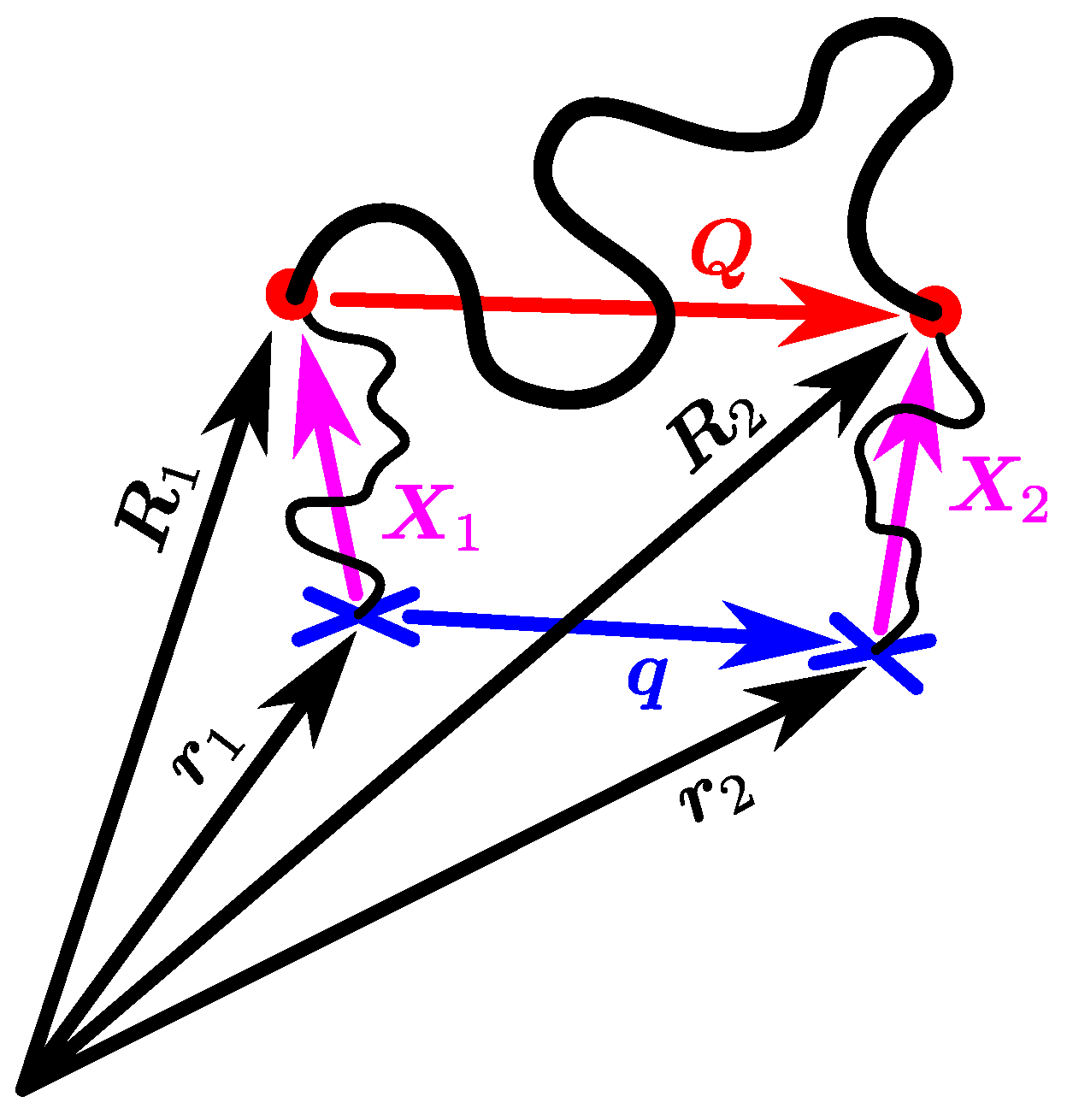
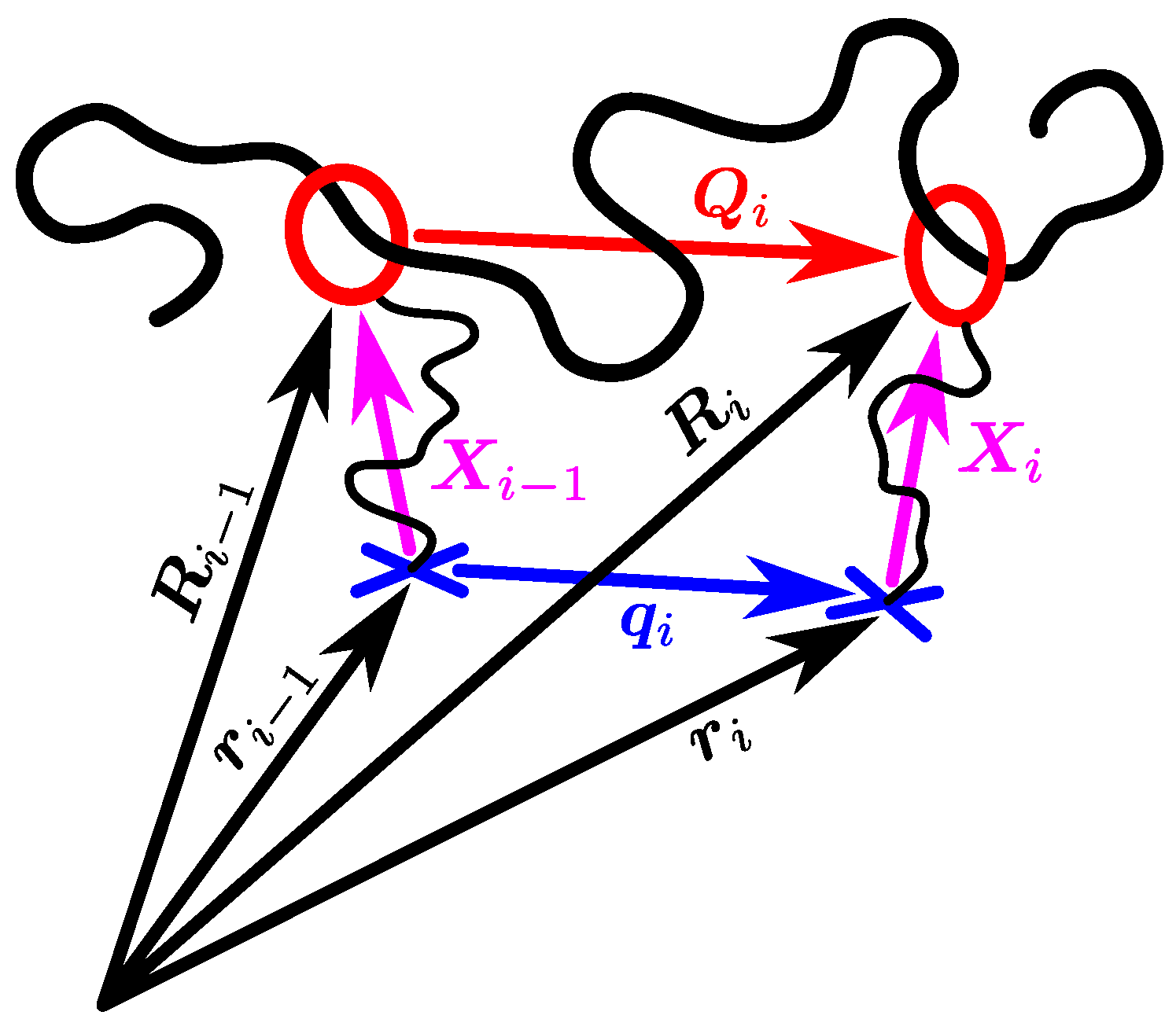
4. Examples: Single-Strand Mean-Field Unentangled Network Models
4.1. Detailed Single-Strand Unentangled Network Model
4.1.1. Stress Tensor and Stress-Optic Rule
4.1.2. Green–Kubo Relation and Infinitesimal Deformations
4.2. Coarse-Grained Single-Strand Unentangled Network Model
4.2.1. Stress Tensor and Stress-Optic Rule
4.2.2. Green–Kubo Relation and Infinitesimal Deformations
4.2.3. Consistency with the Multi-Strand Front Factor
5. Proposed Slip-Link Models
5.1. Detailed Mobile Slip-Link Model
5.2. Coarse-Grained Mobile Slip-Link Model
6. Conclusions
Acknowledgements
Appendix
A. Differential Formulation of the Molecular Stress Function Model
B. Details of the Single-Strand Mean-Field Unentangled Network Models
B.1. Derivation of the Mean Strand Conformation
B.2. Coarse-Graining
B.3. Change of Free Energy and Mean Path Under Infinitesimal Deformation
C. Coarse-Graining of the Detailed Mobile Slip-Link Model
References
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 1. Brownian motion in the equilibrium state. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 2. Molecular motion under flow. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1802–1817. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 3. The constitutive equation. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1818–1832. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 4. Rheological properties. J. Chem. Soc. Faraday Trans. 2 1979, 75, 38–54. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics. Volume 73, In International Series of Monographs on Physics; Clarendon Press: Oxford, NY, USA, 1986. [Google Scholar]
- Milner, S.T.; McLeish, T.C.B. Parameter-free theory for stress relaxation in star polymer melts. Macromolecules 1997, 30, 2159–2166. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C.B. Quantitative theory for linear dynamics of linear entangled polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- Graham, R.S.; Likhtman, A.E.; McLeish, T.C.B.; Milner, S.T. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J. Rheol. 2003, 47, 1171–1200. [Google Scholar] [CrossRef]
- Schieber, J.D.; Nair, D.; Kitkrailard, T. Comprehensive comparisons with nonlinear flow data of a consistently unconstrained Brownian slip-link model. J. Rheol. 2007, 51, 1111–1141. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Self-consistent modeling of constraint release in a single-chain mean-field slip-link model. Macromolecules 2009, 42, 7504–7517. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Application of the slip-link model to bidisperse systems. Macromolecules 2010, 43, 6202–6212. [Google Scholar] [CrossRef]
- Pilyugina, E.; Andreev, M.; Schieber, J.D. Dielectric relaxation as an independent examination of relaxation mechanisms in entangled polymers using the discrete slip-link model. Macromolecules 2012, 45, 5728–5743. [Google Scholar] [CrossRef]
- Andreev, M.; Khaliullin, R.N.; Steenbakkers, R.J.A.; Schieber, J.D. Approximations of the discrete slip-link model and their effect on nonlinear rheology predictions. J. Rheol. 2013, 57, 535–557. [Google Scholar] [CrossRef]
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and microscopic topology of entangled polymeric liquids. Science 2004, 303, 823–826. [Google Scholar] [CrossRef] [PubMed]
- Svaneborg, C.; Grest, G.G.; Everaers, R. Strain-dependent localization, microscopic deformations, and macroscopic normal tensions in model polymer networks. Phys. Rev. Lett. 2004, 93, 257801:1–257801:4. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems. Comput. Phys. Commun. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Mavrantzas, V.G.; Kröger, M. Primitive path identification and entanglement statistics in polymer melts: Results from direct topological analysis on atomistic polyethylene models. Macromolecules 2006, 39, 4207–4216. [Google Scholar] [CrossRef]
- Tzoumanekas, C.; Theodorou, D.N. Topological analysis of linear polymer melts: A statistical approach. Macromolecules 2006, 39, 4592–4604. [Google Scholar] [CrossRef]
- Kamio, K.; Moorthi, K.; Theodorou, D.N. Coarse grained end bridging Monte Carlo simulations of poly(ethylene terephthalate) melt. Macromolecules 2007, 40, 710–722. [Google Scholar] [CrossRef]
- Spyriouni, T.; Tzoumanekas, C.; Theodorou, D.; Müller-Plathe, F.; Milano, G. Coarse-grained and reverse-mapped united-atom simulations of long-chain atactic polystyrene melts: Structure, thermodynamic properties, chain conformation, and entanglements. Macromolecules 2007, 40, 3876–3885. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Analytic expressions for the statistics of the primitive-path length in entangled polymers. Phys. Rev. Lett. 2008, 100, 188302:1–188302:4. [Google Scholar] [CrossRef] [PubMed]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M.; Kröger, M.; Mansfield, M.L. Universal scaling, entanglements, and knots of model chain molecules. Phys. Rev. Lett. 2008, 101, 265702:1–265702:4. [Google Scholar] [CrossRef] [PubMed]
- Harmandaris, V.A.; Kremer, K. Dynamics of polystyrene melts through hierarchical multiscale simulations. Macromolecules 2009, 42, 791–802. [Google Scholar] [CrossRef]
- Hoy, R.S.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803:1–031803:13. [Google Scholar] [CrossRef] [PubMed]
- Toepperwein, G.N.; Karayiannis, N.C.; Riggleman, R.A.; Kröger, M.; de Pablo, J.J. Influence of nanorod inclusions on structure and primitive path network of polymer nanocomposites at equilibrium and under deformation. Macromolecules 2011, 44, 1034–1045. [Google Scholar] [CrossRef]
- Li, Y.; Kröger, M.; Liu, W.K. Primitive chain network study on uncrosslinked and crosslinked cis-polyisoprene polymers. Polymer 2011, 52, 5867–5878. [Google Scholar] [CrossRef]
- Zhou, Q.; Larson, R.G. Primitive path identification and statistics in molecular dynamics simulations of entangled polymer melts. Macromolecules 2005, 38, 5761–5765. [Google Scholar] [CrossRef]
- Shanbhag, S.; Kröger, M. Primitive path networks generated by annealing and geometrical methods: insights into differences. Macromolecules 2007, 40, 2897–2903. [Google Scholar] [CrossRef]
- Hill, T.L. Thermodynamics of Small Systems, Part I and Part II; Dover: Mineola, NY, USA, 2002. [Google Scholar]
- Duiser, J.A. Het Visco-Elastische Gedrag van Twee Polycarbonzuren in Water. Ph.D. Thesis, Rijksuniversiteit Leiden, Leiden, The Netherlands, 1965. [Google Scholar]
- Graessley, W.W. Statistical mechanics of random coil networks. Macromolecules 1975, 8, 186–190. [Google Scholar] [CrossRef]
- Graessley, W.W. Elasticity and chain dimensions in Gaussian networks. Macromolecules 1975, 8, 865–868. [Google Scholar] [CrossRef]
- Flory, P.J.; Gordon, M.; McCrum, N.G. Statistical thermodynamics of random networks [and discussion]. Proc. R. Soc. Lond. A 1976, 351, 351–380. [Google Scholar] [CrossRef]
- Staverman, A.J. Properties of phantom networks and real networks. Adv. Polym. Sci. 1982, 44, 73–101. [Google Scholar]
- Larson, R.G.; Sridhar, T.; Leal, L.G.; McKinley, G.H.; Likhtman, A.E.; McLeish, T.C.B. Definitions of entanglement spacing and time constants in the tube model. J. Rheol. 2003, 47, 809–818. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Ianniruberto, G.; Greco, F.; Marrucci, G. Entanglement molecular weight and frequency response of sliplink networks. J. Chem. Phys. 2003, 119, 6925–6930. [Google Scholar] [CrossRef]
- Everaers, R. Topological versus rheological entanglement length in primitive-path analysis protocols, tube models, and slip-link models. Phys. Rev. E 2012, 86, 022801:1–022801:5. [Google Scholar] [CrossRef] [PubMed]
- Janeschitz-Kriegl, H. Polymer Melt Rheology and Flow Birefringence; Springer-Verlag: Berlin, Germany, 1983. [Google Scholar]
- Ramírez, J.; Sukumaran, S.K.; Likhtman, A.E. Significance of cross correlations in the stress relaxation of polymer melts. J. Chem. Phys. 2007, 126, 244904:1–244904:6. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: New York, NY, USA, 1987; Chapter 8. [Google Scholar]
- Indei, T.; Schieber, J.D.; Takimoto, J. Effects of fluctuations of cross-linking points on viscoelastic properties of associating polymer networks. Rheol. Acta 2012, 51, 1021–1039. [Google Scholar] [CrossRef]
- Biot, M.A. Variational principles in irreversible thermodynamics with application to viscoelasticity. Phys. Rev. 1955, 97, 1463–1469. [Google Scholar] [CrossRef]
- Marrucci, G. The free energy constitutive equation for polymer solutions from the dumbbell model. Trans. Soc. Rheol. 1972, 16, 321–330. [Google Scholar] [CrossRef]
- Doi, M. Variational principle for the Kirkwood theory for the dynamics of polymer solutions and suspensions. J. Chem. Phys. 1983, 79, 5080–5087. [Google Scholar] [CrossRef]
- Schieber, J.D.; Öttinger, H.C. On consistency criteria for stress tensors in kinetic theory models. J. Rheol. 1994, 38, 1909–1924. [Google Scholar] [CrossRef]
- Kaufman, A.N. Dissipative Hamiltonian systems: A unifying principle. Phys. Lett. A 1984, 100, 419–422. [Google Scholar] [CrossRef]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Öttinger, H.C.; Grmela, M. Dynamics and thermodynamics of complex fluids. II. Illustrations of a general formalism. Phys. Rev. E 1997, 56, 6633–6655. [Google Scholar] [CrossRef]
- Öttinger, H.C. General projection operator formalism for the dynamics and thermodynamics of complex fluids. Phys. Rev. E 1998, 57, 1416–1420. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ronca, G.; Allegra, G. An approach to rubber elasticity with internal constraints. J. Chem. Phys. 1975, 63, 4990–4997. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 2nd ed.; Clarendon Press: Oxford, NY, USA, 1958. [Google Scholar]
- Mead, D.W.; Leal, L.G. The reptation model with segmental stretch I. Basic equations and general properties. Rheol. Acta 1995, 34, 339–359. [Google Scholar] [CrossRef]
- Luap, C.; Karlina, M.; Schweizer, T.; Venerus, D.C. Limit of validity of the stress-optical rule for polystyrene melts: Influence of polydispersity. J. Non-Newtonian Fluid Mech. 2006, 138, 197–203. [Google Scholar] [CrossRef]
- Fuller, G.G. Optical Rheometry of Complex Fluids; Topics in Chemical Engineering, Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Kubo, R.; Toda, M.; Hashitsume, N. Statistical Physics II: Nonequilibrium Statistical Mechanics; Springer-Verlag: Berlin, Germany, 1985. [Google Scholar]
- Heinrich, G.; Straube, E.; Helmis, G. Rubber elasticity of polymer networks: Theories. Adv. Polym. Sci. 1988, 85, 33–87. [Google Scholar]
- Rubinstein, M.; Panyukov, S. Nonaffine deformation and elasticity of polymer networks. Macromolecules 1997, 30, 8036–8044. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Elasticity of polymer networks. Macromolecules 2002, 35, 6670–6686. [Google Scholar] [CrossRef]
- Everaers, R. Constrained fluctuation theories of rubber elasticity: General results and an exactly solvable model. Eur. Phys. J. B 1998, 4, 341–350. [Google Scholar] [CrossRef]
- Steenbakkers, R.J.A.; Tzoumanekas, C.; Li, Y.; Liu, W.K.; Kröger, M.; Schieber, J.D. Primitive-path statistics of entangled polymers: Mapping multi-chain simulations onto single-chain mean-field models. 2013. to be submitted for publication. [Google Scholar] [CrossRef]
- Basu, A.; Wen, Q.; Mao, X.; Lubensky, T.C.; Janmey, P.A.; Yodh, A.G. Nonaffine displacements in flexible polymer networks. Macromolecules 2011, 44, 1671–1679. [Google Scholar] [CrossRef]
- Öttinger, H.C. Thermodynamically admissible reptation models with anisotropic tube cross sections and convective constraint release. J. Non-Newtonian Fluid Mech. 2000, 89, 165–185. [Google Scholar] [CrossRef]
- Schieber, J.D.; Neergaard, J.; Gupta, S. A full-chain, temporary network model with sliplinks, chain-length fluctuations, chain connectivity and chain stretching. J. Rheol. 2003, 47, 213–233. [Google Scholar] [CrossRef]
- Likhtman, A.E. Single-chain slip-link model of entangled polymers: Simultaneous description of neutron spin-echo, rheology, and diffusion. Macromolecules 2005, 38, 6128–6139. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Takimoto, J.; Koyama, K.; Ianniruberto, G.; Marrucci, G.; Greco, F. Brownian simulations of a network of reptating primitive chains. J. Chem. Phys. 2001, 115, 4387–4394. [Google Scholar] [CrossRef]
- Ianniruberto, G.; Marrucci, G. Stress tensor and stress-optical law in entangled polymers. J. Non-Newtonian Fluid Mech. 1998, 79, 225–234. [Google Scholar] [CrossRef]
- Öttinger, H.C.; Beris, A.N. Thermodynamically consistent reptation model without independent alignment. J. Chem. Phys. 1999, 110, 6593–6596. [Google Scholar] [CrossRef]
- Milner, S.T. Thermodynamic admissibility of the reptation model. J. Rheol. 2004, 48, 53–67. [Google Scholar] [CrossRef]
- Edwards, B.J. Letter to the editor: Comments on “Thermodynamic admissibility of the reptation model” [J. Rheol. 48, 53 (2004)]. J. Rheol. 2004, 48, 705–708. [Google Scholar] [CrossRef]
- Wagner, M.H.; Rubio, P.; Bastian, H. The molecular stress function model for polydisperse polymer melts with dissipative convective constraint release. J. Rheol. 2001, 45, 1387–1412. [Google Scholar] [CrossRef]
- Wagner, M.H. The effect of dynamic tube dilation on chain stretch in nonlinear polymer melt rheology. J. Non-Newtonian Fluid Mech. 2011, 166, 915–924. [Google Scholar] [CrossRef]
- Marrucci, G.; Ianniruberto, G. Interchain pressure effect in extensional flows of entangled polymer melts. Macromolecules 2004, 37, 3934–3942. [Google Scholar] [CrossRef]
- Leygue, A.; Bailly, C.; Keunings, R. A tube-based constitutive equation for polydisperse entangled linear polymers. J. Non-Newtonian Fluid Mech. 2006, 136, 1–16. [Google Scholar] [CrossRef]
- Winnik, M.A.; Yekta, A. Associative polymers in aqueous solution. Curr. Opin. Colloid Interface Sci. 1997, 2, 424–436. [Google Scholar] [CrossRef]
- Chassenieux, C.; Nicolai, T.; Benyahia, L. Rheology of associative polymer solutions. Curr. Opin. Colloid Interface Sci. 2011, 16, 18–26. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically crosslinked networks. 1. Transient network theory. Macromolecules 1992, 25, 1516–1523. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically crosslinked networks. Part 1. Non-linear stationary viscoelasticity. J. Non-Newtonian Fluid Mech. 1992, 43, 247–271. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically crosslinked networks. Part 2. Dynamic mechanical moduli. J. Non-Newtonian Fluid Mech. 1992, 43, 273–288. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically crosslinked networks. Part 3. Time-dependent phenomena. J. Non-Newtonian Fluid Mech. 1992, 43, 289–309. [Google Scholar] [CrossRef]
- Green, M.S.; Tobolsky, A.V. A new approach to the theory of relaxing polymeric media. J. Chem. Phys. 1946, 14, 80–92. [Google Scholar] [CrossRef]
- Lodge, A.S. A network theory of flow birefringence and stress in concentrated polymer solutions. Trans. Faraday Soc. 1956, 52, 120–130. [Google Scholar] [CrossRef]
- Yamamoto, M. The visco-elastic properties of network structure I. General formalism. J. Phys. Soc. Jpn. 1956, 11, 413–421. [Google Scholar] [CrossRef]
- Yamamoto, M. The visco-elastic properties of network structure II. Structural viscosity. J. Phys. Soc. Jpn. 1957, 12, 1148–1158. [Google Scholar] [CrossRef]
- Yamamoto, M. The visco-elastic properties of network structure III. Normal stress effect (Weissenberg effect). J. Phys. Soc. Jpn. 1958, 13, 1200–1211. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids Volume II: Kinetic Theory; Wiley-Interscience: New York, NY, USA, 1987; Chapter 20. [Google Scholar]
- Wang, S.Q. Transient network theory for shear-thickening fluids and physically crosslinked networks. Macromolecules 1992, 25, 7003–7010. [Google Scholar] [CrossRef]
- Vaccaro, A.; Marrucci, G. A model for the nonlinear rheology of associating polymers. J. Non-Newtonian Fluid Mech. 2000, 92, 261–273. [Google Scholar] [CrossRef]
- Tripathi, A.; Tam, K.C.; McKinley, G.H. Rheology and dynamics of associative polymers in shear and extension: theory and experiments. Macromolecules 2006, 39, 1981–1999. [Google Scholar] [CrossRef]
- Indei, T.; Koga, T.; Tanaka, F. Theory of shear-thickening in transient networks of associating polymers. Macromol. Rapid Commun. 2005, 26, 701–706. [Google Scholar] [CrossRef]
- Cifre, J.G.H.; Barenbrug, T.M.A.O.M.; Schieber, J.D.; van den Brule, B.H.A.A. Brownian dynamics simulation of reversible polymer networks under shear using a non-interacting dumbbell model. J. Non-Newtonian Fluid Mech. 2003, 113, 73–96. [Google Scholar] [CrossRef]
- Schieber, J.D.; Horio, K. Fluctuation in entanglement positions via elastic slip-links. J. Chem. Phys. 2010, 132, 074905:1–074905:11. [Google Scholar] [CrossRef] [PubMed]
- Indei, T.; Takimoto, J. Linear viscoelastic properties of transient networks formed by associating polymers with multiple stickers. J. Chem. Phys. 2010, 133, 194902:1–194902:13. [Google Scholar] [CrossRef] [PubMed]
- Jongschaap, R.J.J.; Wientjes, R.H.W.; Duits, M.H.G.; Mellema, J. A generalized transient network model for associative polymer networks. Macromolecules 2001, 34, 1031–1038. [Google Scholar] [CrossRef]
- Rubinstein, M.; Semenov, A.N. Thermoreversible gelation in solutions of associating polymers. 2. Linear dynamics. Macromolecules 1998, 31, 1386–1397. [Google Scholar] [CrossRef]
- Indei, T.; Schieber, J.D. Correction of Doi–Edwards’ Green function for a chain in a harmonic potential and its implication for the stress-optical rule. Available online: http://arxiv.org/abs/1302.5151 (accessed on 28 May 2013).
- Chassenieux, C.; Tassin, J.F.; Gohy, J.F.; Jérôme, R. Elongation of telechelic ionomers under shear: A rheological and rheo-optical study. Macromolecules 2000, 33, 1796–1800. [Google Scholar] [CrossRef]
- Pellens, L.; Vermant, J.; Mewis, J. Deviations from the stress-optical rule in telechelic associative polymer solutions. Macromolecules 2005, 38, 1911–1918. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. I. Theory and single-step strain predictions. J. Chem. Phys. 1998, 109, 10018–10027. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D.; Venerus, D.C. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. II. Double-step strain predictions. J. Chem. Phys. 1998, 109, 10028–10032. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D.; Venerus, D.C. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. III. Shear flows. J. Rheol. 1999, 43, 701–717. [Google Scholar] [CrossRef]
- Schieber, J.D. GENERIC compliance of a temporary network model with sliplinks, chain-length fluctuations, segment-connectivity and constraint release. J. Non-Equilib. Thermodyn. 2003, 28, 179–188. [Google Scholar] [CrossRef]
- Schieber, J.D. Fluctuations in entanglements of polymer liquids. J. Chem. Phys. 2003, 118, 5162–5166. [Google Scholar] [CrossRef]
- Nair, D.; Schieber, J.D. Linear viscoelastic predictions of a consistently unconstrained Brownian slip-link model. Macromolecules 2006, 39, 3386–3397. [Google Scholar] [CrossRef]
- Chappa, V.C.; Morse, D.C.; Zippelius, A.; Müller, M. Translationally invariant slip-spring model for entangled polymer dynamics. Phys. Rev. Lett. 2012, 109, 148302. [Google Scholar] [CrossRef] [PubMed]
- Uneyama, T.; Masubuchi, Y. Multi-chain slip-spring model for entangled polymer dynamics. J. Chem. Phys. 2012, 137, 154902:1–154902:13. [Google Scholar] [CrossRef] [PubMed]
- Uneyama, T.; Masubuchi, Y. Detailed balance condition and effective free energy in the primitive chain network model. J. Chem. Phys. 2011, 135, 184904:1–184904:17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- James, H.M.; Guth, E. Theory of the elastic properties of rubber. J. Chem. Phys. 1943, 11, 455–481. [Google Scholar] [CrossRef]
- James, H.M. Statistical properties of networks of flexible chains. J. Chem. Phys. 1947, 15, 651–668. [Google Scholar] [CrossRef]
- James, H.M.; Guth, E. Simple presentation of network theory of rubber, with a discussion of other theories. J. Polym. Sci. B Polym. Phys. 1949, 4, 153–182. [Google Scholar] [CrossRef]
- Edwards, S.F. The statistical mechanics of polymerized material. Proc. Phys. Soc. 1967, 92, 9–16. [Google Scholar] [CrossRef]
- Steenbakkers, R.J.A.; Schieber, J.D. Derivation of free energy expressions for tube models from coarse-grained slip-link models. J. Chem. Phys. 2012, 137, 034901:1–034901:19. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.K.; Khaliullin, R.; Schieber, J.D. Self-consistent modeling of entangled network strands and linear dangling structures in a single-strand mean-field slip-link model. Rheol. Acta 2012, 51, 21–35. [Google Scholar] [CrossRef]
- Steenbakkers, R.J.A.; Schieber, J.D. Thermodynamically consistent incorporation of entanglement spatial fluctuations in the slip-link model. 2013. to be submitted for publication. [Google Scholar]
- Van Heel, A.P.G.; Hulsen, M.A.; van den Brule, B.H.A.A. Simulation of the Doi–Edwards model in complex flow. J. Rheol. 1999, 43, 1239–1260. [Google Scholar] [CrossRef]
- Peters, E.A.J.F.; van Heel, A.P.G.; Hulsen, M.A.; van den Brule, B.H.A.A. Generalization of the deformation field method to simulate advanced reptation models in complex flows. J. Rheol. 2000, 44, 811–829. [Google Scholar] [CrossRef]
- Read, D.J.; Jagannathan, K.; Likhtman, A.E. Entangled polymers: Constraint release, mean paths, and tube bending energy. Macromolecules 2008, 41, 6843–6853. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Schieber, J.D.; Indei, T.; Steenbakkers, R.J.A. Fluctuating Entanglements in Single-Chain Mean-Field Models. Polymers 2013, 5, 643-678. https://doi.org/10.3390/polym5020643
Schieber JD, Indei T, Steenbakkers RJA. Fluctuating Entanglements in Single-Chain Mean-Field Models. Polymers. 2013; 5(2):643-678. https://doi.org/10.3390/polym5020643
Chicago/Turabian StyleSchieber, Jay D., Tsutomu Indei, and Rudi J. A. Steenbakkers. 2013. "Fluctuating Entanglements in Single-Chain Mean-Field Models" Polymers 5, no. 2: 643-678. https://doi.org/10.3390/polym5020643





