Spontaneous Enhancement of Packing Regularity of Spherical Microdomains in the Body-Centered Cubic Lattice upon Uniaxial Stretching of Elastomeric Triblock Copolymers
Abstract
: Block copolymers forming glassy spheres in the matrix of rubbery chains can exhibit elastomeric properties. It is well known that the spherical microdomains are arranged in the body-center cubic (bcc) lattice. However, recently, we have found packing in the face-centered cubic (fcc) lattice, which is easily transformed into the bcc lattice upon uniaxial stretching. In the same time, the packing regularity of the spheres in the bcc lattice was found to be enhanced for samples completely recovered from the stretched state. This reminds us that a cycle of stretching-and-releasing plays an important role from analogy of densification of the packing in granules upon shaking. In the current paper, we quantify the enhancement of packing regularity of spherical microdomains in the bcc lattice upon uniaxial stretching of the same elastomeric triblock copolymer as used in our previous work by conducting small-angle X-ray scattering (SAXS) measurements using high brilliant synchrotron radiation. Isotropically circular rings of the lattice peaks observed for the unstretched sample turned into deformed ellipsoidal rings upon the uniaxial stretching, with sharpening of the peaks in the direction parallel to the stretching direction and almost disappearing of the peaks in the perpendicular direction. By quantitatively analyzing the SAXS results, it was found that the packing regularity of the spherical microdomains was enhanced in the parallel direction while it was spoiled in the perpendicular direction under the stretched state. The enhanced regularity of packing was unchanged even if the stretching load was completely removed.1. Introduction
In block copolymers comprising rubbery and glassy chains with the glassy minor component, spherical microdomains are formed due to microphase separation, which are dispersed in the rubbery matrix. Such a microphase-separated structure imparts elastomeric properties to the material since the glassy spherical microdomains play the role of a crosslinker. Meanwhile, they can be melt-processed above the glass transition temperature of the glassy component. Thus, they are referred to as a thermoplastic elastomer [1]. The microphase-separated structures in block copolymers have been studied for many decades and much has been uncovered [2–10], such as that spherical microdomains regularly order in the body-centered cubic (bcc) lattice [6]. We also have studied why the block copolymers favor the bcc over the face-centered cubic (fcc) lattice, and have been able to demonstrate a very rare case of spherical microdomains exhibiting the fcc lattice [9]. In the course of the study, we have accidentally discovered the transition from fcc to bcc upon uniaxial stretching of the block copolymer sample. Furthermore, it seems that the resultant bcc lattice (after releasing the tensile force from the stretched state) achieved enhanced packing regularity in the direction parallel to the uniaxial stretching. This fact seems to imply that mechanical stretching can play the role of an external field. However, the ability to enhance the packing regularity of spherical microdomains is exclusive to the mechanical stretching, bearing in mind that other external fields are generally effective for alignment or orientation of microdomains [7,8,10]. It should be further mentioned that a cycle of stretching-and-releasing plays an important role from analogy of densification of packing in granules upon shaking. In the current paper, we quantify the enhancement of packing regularity of spherical microdomains in the bcc lattice upon uniaxial stretching of the same elastomeric triblock copolymer as used in our previous work [9] by conducting small-angle X-ray scattering (SAXS) measurements using high brilliant synchrotron radiation.
2. Experimental Section
The material used is a poly(1,3-cyclohexadiene)-block-poly(ethylene-co-but-1-ene)-block-poly(1,3-cyclohexadiene) (PCHD-PEB-PCHD) triblock copolymer, having the volume fraction of PCHD (ϕPCHD) of 0.293 (determined by 1H-NMR), Mn = 5.73 × 104, and Mw/Mn = 1.09 (determined by gel permeation chromatography, GPC) where Mn and Mw are the number- and weight-average molecular weight, respectively. Note here that the GPC column was calibrated with the polystyrene standard (Polymer Laboratories, Inc.) so that the molecular weight is polystyrene equivalent. It should be also noted that the glass transition temperatures (Tg), which were determined from peak positions of the mechanical tan δ for PCHD and PEB are 150 °C and −58 °C, respectively, indicating that the PCHD domains play a role of physical crosslinking points in the rubbery PEB matrix. We prepared a film of this sample by compression molding at 230 °C (as-mold sample).
The SAXS measurements were performed at SAXS beamlines BL-10C and BL-15A in the Photon Factory of the High Energy Accelerator Research Organization, Tsukuba, Japan [11,12], and at SAXS beamline BL45XU of SPring-8 in the Japan Synchrotron Radiation Research Institute [13]. The wavelength of the X-rays was tuned to λ = 0.149 nm for BL-10C, λ = 0.150 nm for BL-15A, and λ = 0.099 nm for BL45XU. Imaging plates of 250 × 200 mm size and 100 × 100 μm resolution were used as detectors at BL-10C and BL-15A. The measured two-dimensional SAXS pattern was converted to the one-dimensional profile by conducting sector averaging in the direction where diffraction peaks were most prominent. The annealed film was trimmed into a rectangular shape (5 mm wide, 20 mm long with a thickness of 0.5 mm) and it was cramped with a pair of jaws on the homemade stretching device (see Figure 1 of [14] for the schematic illustration of the stretching device) with the gauge length of 15 mm, which enabled 2d-SAXS measurements under the stretched state at room temperature [14].
Transmission electron microscopy (TEM) was performed for ultrathin sections, each with a thickness of ca. 80 nm. The sample was sliced at 183 K using a Reichert-Jung Ultracut T with a cryo-sectioning system (Reichert-Nissei FC-S). The thin section was picked up on 400-mesh copper grids and exposed to ruthenium tetraoxide (RuO4) vapor for about 12 h to stain selectively the PCHD domain. TEM was performed at 100 kV on a JEM-2010 instrument (Nippon Denshi Co., Ltd.).
3. Results and Discussion
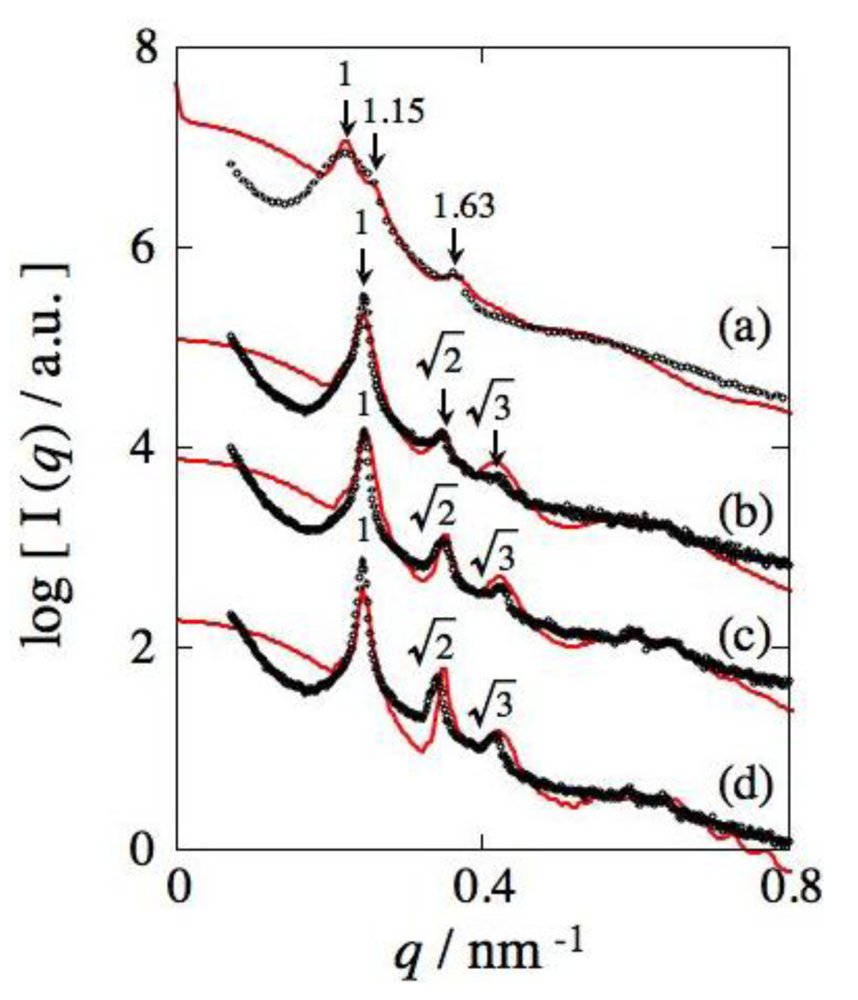
Before going into the details, we will mention our previous SAXS results, shown in Figure 1, where the logarithm of the scattering intensity, I(q), is plotted as a function of the magnitude of the scattering vector, q = (4π/λ) sin (θ/2), with λ and θ being the wavelength of X-ray and the scattering angle, respectively [9]. Here, the sample subjected to the measurement was prepared as follows. The as-mold sample was further treated by imposing the planar shear flow (flow-imposed sample) at 220 °C for two hours, followed by further annealing at 210 °C for two hours without the flow in order to eliminate any effects of the flow. The 1d-SAXS profiles shown in Figure 1 were obtained by conducting sector average in the direction parallel to the original stretching direction (μ = 0° ± 5° where μ is the azimuthal angle defined as increasing clockwise with respect to the meridional direction pointing upward (φ = 0°; parallel to the stretching direction). For the as-annealed sample, prior to being subjected to the uniaxial stretching, the scattering peaks were observed at the relative q-positions of 1:1.15 (√(4/3):1.63 (√(8/3)). This fact reminds us that the scattering originates from the fcc lattice [(111) and (200) reflections, respectively]. Therefore, we conducted the fcc model calculation of the scattering curve based on the same procedure [9]. See the Appendix for details of the formulation. The solid curve is the result of the model calculation, which shows a good agreement with the experimental result (open circles), although we found here that better fitting was attained with a new set of structural parameters as compared to those reported before [9]. The structural parameters include d, the Bragg spacing of the (111) plane giving rise to the first-order peak, the g-factor, the so-called paracrystalline distortion factor, R, the average radius of spherical microdomains, σR the standard deviation in R, and tI, the characteristic thickness of the interfacial region of the spherical microdomains. The values of the structural parameters used for the model calculation are summarized in Table 1. Here, the values of the average radius of spheres R are considerably larger than observed by TEM (Figure 2), except for the values listed in Table 1(b) under the stretched state in the perpendicular direction, which are around 4.2 ∼ 5 nm, showing good agreement with the TEM results. The fact that the radius is larger in the parallel direction than in the perpendicular direction does not represent deformation of the spheres, because the spheres are composed of PCHD, such that they were in the glassy state at room temperature where the in situ SAXS experiments were conducted. The overestimation of the radius might be an artifact, though the reason is not clear at present. There may be limitation of the applicability of the model calculation based on the isotropic orientation (random orientation) of the cubic lattice to the deformed cubic lattice, as well. For the purpose of the current work, we just recognize the structural values evaluated from the model calculation for the case of the in situ SAXS profiles as values equivalent to the undeformed cubic lattice.
Figure 1 also contains the SAXS results of the samples suffering the uniaxial stretching at room temperature up to the stretching ratio of (b) α = 4.0, (c) α = 7.5, and (d) α = 8.0. The stretching ratio α is defined by α = ℓ/ ℓ0 with ℓ0 and ℓ being the original length of the sample before stretching and the length of the sample at the stretched state, respectively. Note that these SAXS profiles were obtained for the samples after complete removal of the mechanical stretching, i.e., under the state being relaxed from the stretched state. It was found that all SAXS profiles other than that for the unstretched sample show the scattering peaks at the relative q-positions of 1:√2:√3 which are ascribed to the bcc lattice, clearly demonstrating that the mechanical stretching induces transformation of the packing manner from fcc to bcc. It can be further recognized that the peaks are sharper for the sample suffering the higher extent of uniaxial stretching. The peak sharpness correlates with regularity of the packing of spherical microdomains. To quantify the degree of the packing regularity, we calculated the model scattering function based on the bcc lattice by following a similar procedure [6,15,16]. The solid curves are the results of the calculation by appropriately adjusting the structural parameters as mentioned above where d denotes, in this particular case for the bcc lattice, the Bragg spacing of the (110) plane giving rise to the first-order peak of the bcc lattice. Among them, the g-factor rationalizes the degree of the packing regularity as g = Δa/a where Δa and a denote, respectively, the standard deviation in a due to the paracrystalline distortion and the edge length of the unit cell. Note that the smaller value of the g-factor indicates better packing regularity. As expected, the g-factor exhibits decreasing tendency (i.e., the packing regularity is being enhanced) as a function α of the sample suffering prior to the SAXS measurement (see Figure 3). Thus, it is quantitatively confirmed that the regularity of the bcc lattice is better when the sample suffers a higher extent of uniaxial stretching. This result, furthermore, reminds us that a cycle of stretching-and-releasing plays an important role from analogy of densification of packing in granules upon shaking.
Now, we confirm whether the enhancement of packing regularity of spherical microdomains in the bcc lattice takes place in the sample under the stretched state or not. For this purpose, we conducted in situ 2d-SAXS measurements of the sample under the uniaxial stretching using the homemade stretching device [14] with the initial gauge length of 15 mm and the initial thickness and width of the film being 0.5 mm and 5 mm, respectively. Here, the sample subjected to the measurement was prepared as follows. The as-mold sample was further annealed at 210 °C for one hour, without imposing the planar shear flow. Figure 2 shows TEM photographs for the as-mold sample and the sample further annealed at 210 °C for one hour. The PCHD phase is selectively stained with RuO4 and appears dark. Although for both samples, PCHD spheres were identified, the packing regularity is very different; the regularity is much better for the annealed sample. This annealed sample was used for the in situ 2d-SAXS measurements. It is noticed here that the average radius was found to be approximately 5 nm from the TEM photos for both samples.
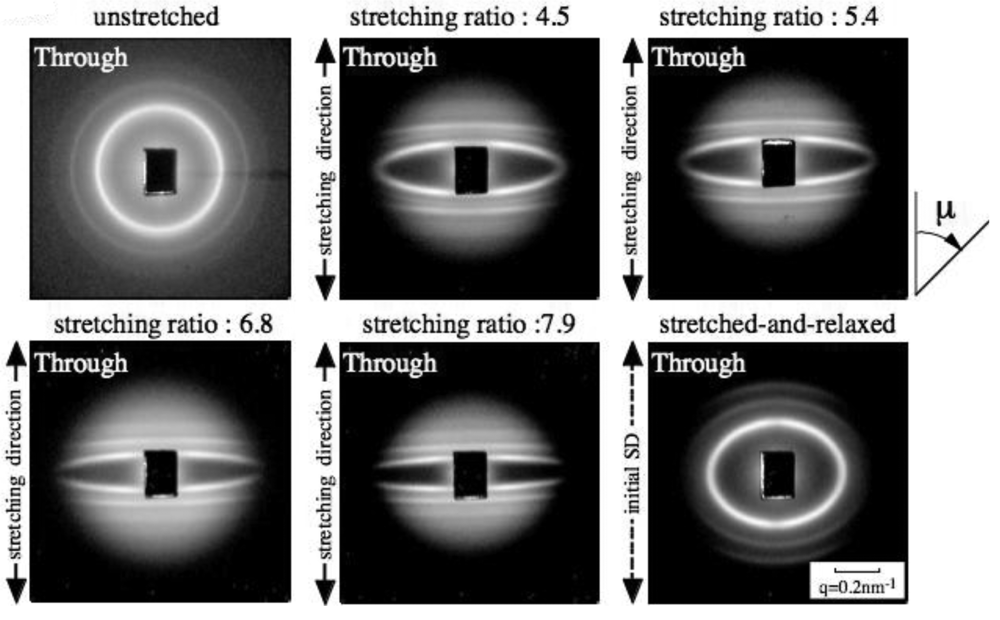
Figure 4 displays 2d-SAXS patterns as a function of the stretching ratio. From the isotropic circular peaks observed for the unstretched state to the elliptic patterns under stretched states, the 2d-SAXS pattern changed. In the direction parallel to the stretching direction, the peaks moved towards the smaller q-position while the peaks moved towards the higher q-positions in the direction perpendicular to the stretching direction, both of which give rise qualitatively to the elliptic shape of the 2d-SAXS pattern. Furthermore, the scattering peaks appeared much clearer for the samples under higher stretching in the direction parallel to the stretching direction. These results qualitatively remind us that the bcc regularity already becomes better even in the samples under the stretched state. To quantify the enhancement of the packing regularity, the model SAXS function was calculated and was fitted to the experimental results in the direction parallel to the stretching direction.
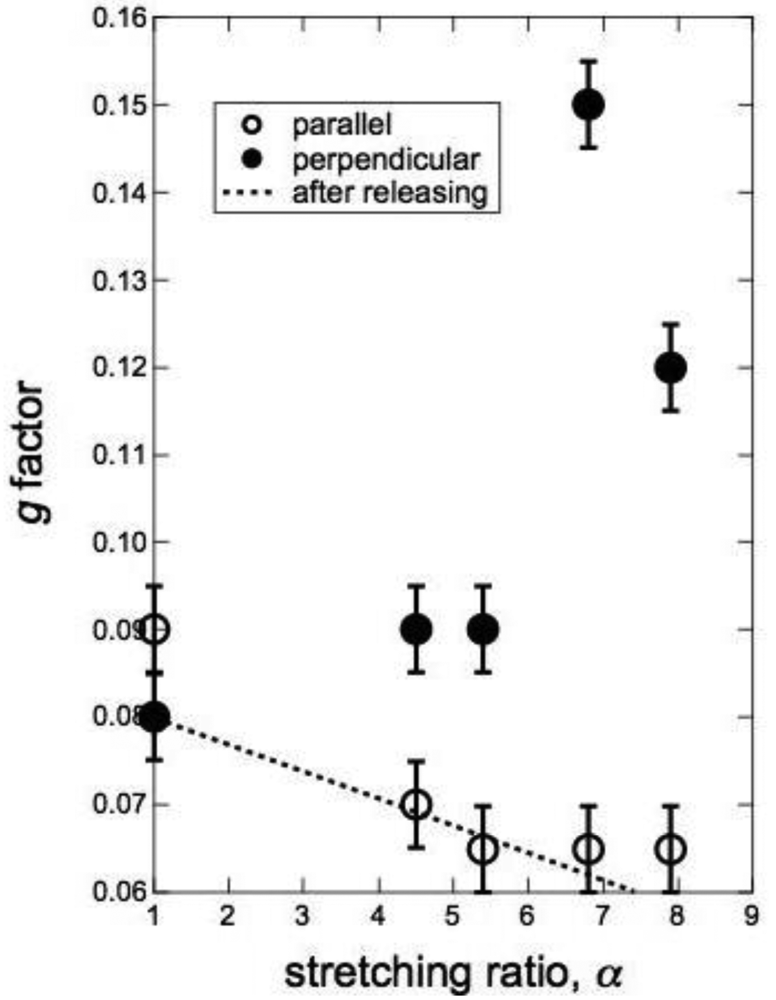
Figure 5 displays the fitting, where the open circles denote the experimental result and the solid curve the result of the model calculation. Meanwhile, for the direction perpendicular to the stretching direction, similar plots are shown in Figure 6. The evaluated g-factor is shown in Figure 7 as a function of α. It is clearly found that the plots exhibit a monotonic decrease in the g-factor with an increase in α. To compare with the previous results plotted in Figure 3, the approximated line for these data is included in Figure 7. The fact that the line expresses firmly the tendency of data points indicates definitely that the enhancement of the packing regularity is already attained in the course of the uniaxial stretching and the better regularity attained is not spoiled in the following releasing process. In other words, the releasing process after the stretching is not necessarily required for the enhancement of the packing regularity. As for the g-factor in the direction perpendicular to the stretching direction, the results are shown together in Figure 7, and the g-factor is observed to considerably increase with an increase in α. Thus, in the perpendicular direction, the packing regularity becomes worse in the course of the uniaxial stretching. Although this result seems to be reasonable because it compensates the enhancement of the regularity in the parallel direction, the regularity in the perpendicular direction is much worse! In other words, the better regularity in the parallel direction is a bit independent. Another important aspect is that the enhanced regularity in the parallel direction attained in the course of the uniaxial stretching was able to be maintained after releasing of the tensile load, as shown in Figure 7.
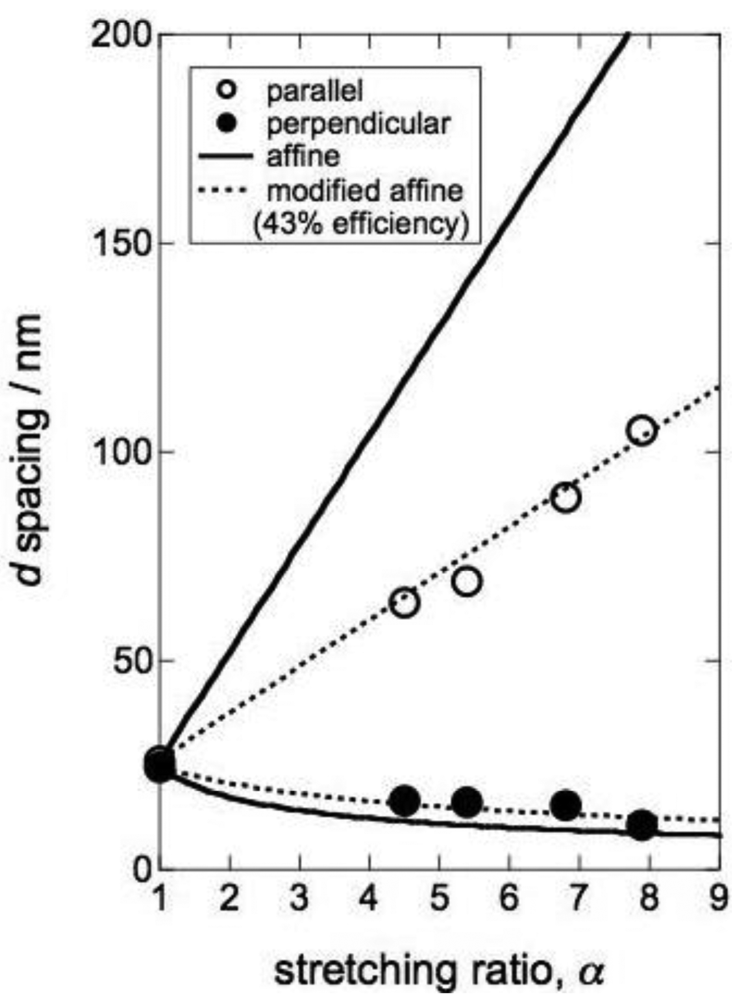
These two facts imply there is a special mechanism behind. To uncover the mechanism, it is worthwhile examining the change in the domain spacing d along with the uniaxial stretching as shown in Figure 8. The solid curves indicate behaviors when assuming that the affine deformation takes place. Note that the affine deformation stands for the fact that macroscopic deformation can be transmitted to the microscopic level, and for the particular case of the block copolymers the degree of deformation in the microdomain repeating distance can be identical to the macroscopic deformation ratio. The solid curves shown in Figure 8 are based on the following equations:
As clearly seen in Figure 8, the data points do not follow the affine deformation, which suggests slip during the stretching. To quantify the apparent efficiency of the stretching, the above equation is modified by introducing a parameter k in the degree of elongation (α−1), giving the modified affine deformation as:
By adjusting the parameter k, good agreement between the data points and the modified affine behaviors can be confirmed in Figure 8, where the broken curves in Figure 8 show the modified affine with k = 0.43. Macroscopic slippage of the film sample at the jaws of the stretching device cannot explain such a tremendous deficiency of the mechanical stretching.
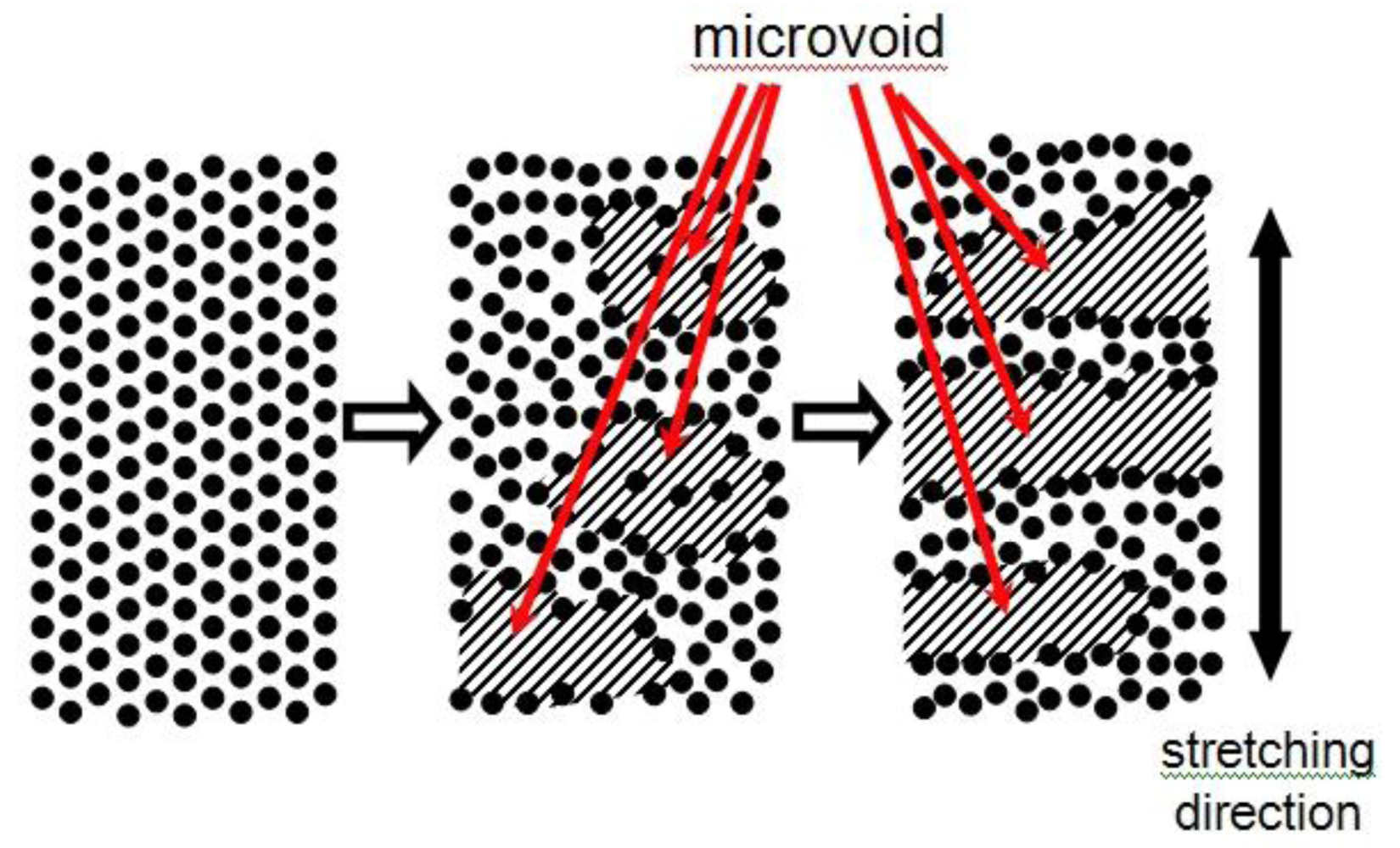
Then the possible explanation for the deviation from the affine deformation exists in the sample, which is referred to as inner slippage, and void formation during the stretching may be responsible. Inoue et al. reported a peculiar light scattering pattern (so-called butterfly pattern) for sphere-forming elastomeric block copolymer samples (comprising polystyrene and polyisoprene blocks) under stretched state at room temperature [17]. They ascribed the results to microvoid formation for which such a mechanism as that shown schematically in Figure 9 was also incorporated [17]. This model can be explained as follows: In the initial stage before stretching, there is some extent of number density fluctuation of the hard spheres, which might be due to paracrystalline distortion, and the fluctuation is enhanced upon the stretching. The resultant regions where the number density is lower turn into microvoids due to stress concentration. Interestingly, such microvoid regions are elongated in the direction perpendicular to the stretching direction. This two-region model can explain the failure of the affine deformation. Namely, the microvoid regions are heavily deformed while the other (microdomain) regions are less deformed than the macroscopic deformation. It is needless to note that the microdomain regions are also deformed, but what we like to say here is that the degree of the deformation is less than the macroscopic one. Due to the heavy deformation in the microvoid regions, the effective strain in the microdomain regions is 43% of the macroscopic one, considering k = 0.43 evaluated above.
The microvoid formation results in non-recovery eternal strain after releasing the tensile load, which is so-called remaining strain. Using the values of the d spacing, the remaining strain can be estimated.
At a first glance, the two-region model proposed in Figure 9 cannot explain our result of the small remaining strain. However, if we consider that the microvoid region does not really contain voids but is filled with heavily stretched rubbery chains, then this region also can exhibit complete recovery upon removal of the stretching load. Therefore, such an elastic region, which is heavily deformed under the stretched state, is responsible for both the non-affine deformation and the small remaining strain.
Finally, it is worth mentioning that the g factor did not change upon the release of the stretching load for the direction parallel to the stretching direction, which is recognized when comparing the values of the g factor for α = 7.9 and the unstretched states in Table 1. In other words, not only the enhancement of the regularity in the stretching direction remained as it was upon the release of the stretching load. It is characteristic of block copolymers that the anisotropy of the degree of the packing regularity of the spherical microdomains remains in the sample recovered from the stretched state without being homogenized.
4. Conclusions
We conducted in situ 2d-SAXS measurements at room temperature during the uniaxial stretching of the elastomeric sphere-forming triblock copolymer (PCHD-PEB-PCHD) using synchrotron radiation as an X-ray source. Isotropically circular rings of the lattice peaks observed for the unstretched sample turned into deformed elliptic rings upon the uniaxial stretching, with sharpening of the peaks in the direction parallel to the stretching direction and an almost disappearing of the peaks in the perpendicular direction. By quantitatively analyzing the SAXS results, it was found that the packing regularity of the spherical microdomains was enhanced in the parallel direction while it was spoiled in the perpendicular direction under the stretched state. The enhanced regularity of packing was unchanged even if the stretching load was completely removed.
Although our result seems to indicate that the packing regularity in the parallel direction is enhanced by extensional deformation, it is unclear whether compression in the perpendicular direction plays a role or not. 2d-SAXS studies on the sample under simple compression or simultaneous biaxial stretching deserves future work. Another interesting aspect is that the state attained in the stretched state can be maintained even after the complete removal of the stretching load. Why does homogenization not take place? Considering that this result is obtained right after the release of the stretching, gradual homogenization may occur. In this case, how fast the decay rate is and what determines the decay rate deserves also future work. It is needless to say that future work should be carried out to reveal the mechanism of the enhancement of the packing regularity upon the uniaxial stretching.




| Stretching Ratio | Direction | Type of Lattice | g | d (nm) | R (nm) | σR (nm) | tI (nm) | |
|---|---|---|---|---|---|---|---|---|
| (a) shown in Figure 1 | 1.0 | ⫽ | fcc | 0.085 | 28.0 | 8.8 | 2.5 | 1.5 |
| 4.0 | ⫽ | 0.070 | 25.5 | 8.5 | 1.5 | 1.0 | ||
| 7.5 | ⫽ | bcc | 0.060 | 25.5 | 8.5 | 1.5 | 1.0 | |
| 8.0 | ⫽ | 0.050 | 25.5 | 8.5 | 1.5 | 1.0 | ||
| (b) shown in Figures 5 and 6 | 1.0 | ⫽ | 0.090 | 26.0 | 8.3 | 1.0 | 1.0 | |
| ┴ | 0.080 | 24.5 | 8.5 | 1.0 | 1.0 | |||
| 4.5 | ⫽ | 0.070 | 63.7 | 8.7 | 1.0 | 0.5 | ||
| ┴ | 0.090 | 16.6 | 5.0 | 1.2 | 1.0 | |||
| 5.4 | ⫽ | 0.065 | 69.0 | 8.7 | 0.8 | 0.5 | ||
| ┴ | 0.090 | 16.2 | 4.2 | 2.0 | 1.0 | |||
| 6.8 | ⫽ | bcc | 0.065 | 89.0 | 8.7 | 1.0 | 0.5 | |
| ┴ | 0.150 | 15.5 | 4.2 | 2.0 | 1.0 | |||
| 7.9 | ⫽ | 0.065 | 105 | 9.0 | 1.0 | 0.5 | ||
| ┴ | 0.120 | 10.5 | 4.2 | 1.5 | 1.0 | |||
| after releasing the load | ⫽ | 0.067 | 31.0 | 8.7 | 1.0 | 1.0 | ||
| ┴ | 0.080 | 22.5 | 8.0 | 1.0 | 1.0 | |||
Acknowledgments
SAXS experiments were performed at the Photon Factory of the High Energy Accelerator Research Organization (approval numbers 2003G228 and 2007G546), and at SPring-8 (approval number 2006B1125 and 2009A1573).
Appendix
Here we present the model calculation of the SAXS profiles for spheres ordered in bcc and fcc lattices based on the Hosemann's paracrystal theory. According to the Hosemann's paracrystal theory, the scattering intensity I(q) from microphase-separated block copolymers can be formulated as follows [15,16]:
References and Notes
- Holden, G.; Legge, N.R.; Quirk, R.; Schroeder, H.E.; Hanser, M. Thermoplastic Elastomers, 2nd ed.; Hanser: New York, NY, USA, 1996. [Google Scholar]
- Hashimoto, T. Order-Disorder Transition in Block Polymers. In Thermoplastic Elastomers, 2nd ed.; Holden, G., Legge, N.R., Quirk, R., Schroeder, H.E., Hanser, M., Eds.; Hanser: New York, NY, USA, 1996; pp. 429–463. [Google Scholar]
- Matsen, M.W.; Bates, F.S. Unifying Weak- and Strong-Segregation Block Copolymer Theories. Macromolecules 1996, 29, 1091–1998. [Google Scholar]
- Hamley, I.W. The Physics of Block Copolymers; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Hamley, I.W. Developments in Block Copolymer Science and Technology; John Wiley & Sons: Lodon, UK, 2004. [Google Scholar]
- Kim, J.K.; Lee, H.H.; Sakurai, S.; Aida, S.; Masamoto, J.; Nomura, S.; Kitagawa, Y.; Suda, Y. Lattice Disordering and Domain Dissolution Transitions in Polystyrene-block-poly(ethylene-co-but-1-ene)-block-polystyrene Triblock Copolymer Having a Highly Asymmetric Composition. Macromolecules 1999, 32, 6707–6717. [Google Scholar]
- Okamoto, S.; Saijo, K.; Hashimoto, T. Dynamic SAXS Studies of Sphere-Forming Block Copolymers under Large Oscillatory Shear Deformation. Macromolecules 1994, 27, 3753–3758. [Google Scholar]
- Shin, G.; Sakamoto, N.; Saijo, K.; Suehiro, S.; Hashimoto, T.; Ito, K.; Amemiya, Y. Time-Resolved SAXS Studies of a Sphere-Forming Block Copolymer under Large Oscillatory Shear Deformation. Macromolecules 2000, 33, 9002–9014. [Google Scholar]
- Imaizumi, K.; Ono, T.; Kota, T.; Okamoto, S.; Sakurai, S. Transformation of Cubic Symmetry for Spherical Microdomains from Face-Centered to Body-Centered Cubic upon Uniaxial Elongation in an Elastomeric Triblock Copolymer. J. Appl. Cryst. 2003, 36, 976–981. [Google Scholar]
- Sakurai, S. Progress in Control of Microdomain Orientation in Block Copolymers—Efficiencies of Various External Fields. Polymer 2008, 49, 2781–2796. [Google Scholar]
- Sakurai, S.; Aida, S.; Okamoto, S.; Ono, T.; Imaizumi, K.; Nomura, S. Preferential Orientation of Lamellar Microdomains Induced by Uniaxial Stretching of Cross-Linked Polystyrene-block-polybutadiene-block-polystyrene Triblock Copolymer. Macromolecules 2001, 34, 3672. [Google Scholar]
- Sakurai, S.; Isobe, D.; Okamoto, S.; Yao, T.; Nomura, S. Collapse of the Ia3d Cubic Symmetry by Uniaxial Stretching of a Double-Gyroid Block Copolymer. Phys. Rev. E 2001, 63, 061803:1–061803:5. [Google Scholar]
- Fujisawa, T.; Inoko, Y.; Yagi, N. The use of a Hamamatsu X-ray image intensifier with a cooled CCD as a solution X-ray scattering detector. J. Synchrotron Rad. 1999, 6, 1106. [Google Scholar]
- Sakurai, S.; Kota, T.; Isobe, D.; Okamoto, S.; Sakurai, K.; Ono, T.; Imaizumi, K.; Nomura, S. Synchrotron Small-Angle X-ray Scattering Studies on Flow-Induced Gyroid to Cylinder Transition in an Elastomeric SBS Triblock Copolymer. J. Macromol. Sci. Phys. 2004, 43, 1–11. [Google Scholar]
- Matsuoka, H.; Tanaka, H.; Hashimoto, T.; Ise, N. Elastic Scattering from Cubic Lattice Systems with Paracrystalline Distortion. Phys. Rev. B 1987, 36, 1754. [Google Scholar]
- Matsuoka, H.; Tanaka, H.; Iizuka, N.; Hashimoto, T.; Ise, N. Elastic Scattering from Cubic Lattice Systems with Paracrystalline Distortion. II. Phys. Rev. B 1990, 41, 3854. [Google Scholar]
- Inoue, T.; Moritani, M.; Hashimoto, T.; Kawai, H. Deformation Mechanism of Elastomeric Block Copolymers Having Spherical Domains of Hard Segments under Uniaxial Tensile Stress. Macromolecules 1971, 4, 500–507. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kota, T.; Imaizumi, K.; Sasaki, S.; Sakurai, S. Spontaneous Enhancement of Packing Regularity of Spherical Microdomains in the Body-Centered Cubic Lattice upon Uniaxial Stretching of Elastomeric Triblock Copolymers. Polymers 2011, 3, 36-50. https://doi.org/10.3390/polym3010036
Kota T, Imaizumi K, Sasaki S, Sakurai S. Spontaneous Enhancement of Packing Regularity of Spherical Microdomains in the Body-Centered Cubic Lattice upon Uniaxial Stretching of Elastomeric Triblock Copolymers. Polymers. 2011; 3(1):36-50. https://doi.org/10.3390/polym3010036
Chicago/Turabian StyleKota, Takuya, Kimio Imaizumi, Sono Sasaki, and Shinichi Sakurai. 2011. "Spontaneous Enhancement of Packing Regularity of Spherical Microdomains in the Body-Centered Cubic Lattice upon Uniaxial Stretching of Elastomeric Triblock Copolymers" Polymers 3, no. 1: 36-50. https://doi.org/10.3390/polym3010036





