Thermal Degradation Studies of Poly(2-ethyl hexyl acrylate) in the Presence of Nematic Liquid Crystals
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Thermogravimetrical Analysis
2.3. Gel permeation Chromatography
2.4. Polarized Optical Microscopy
3. Kinetic Study of Degradation
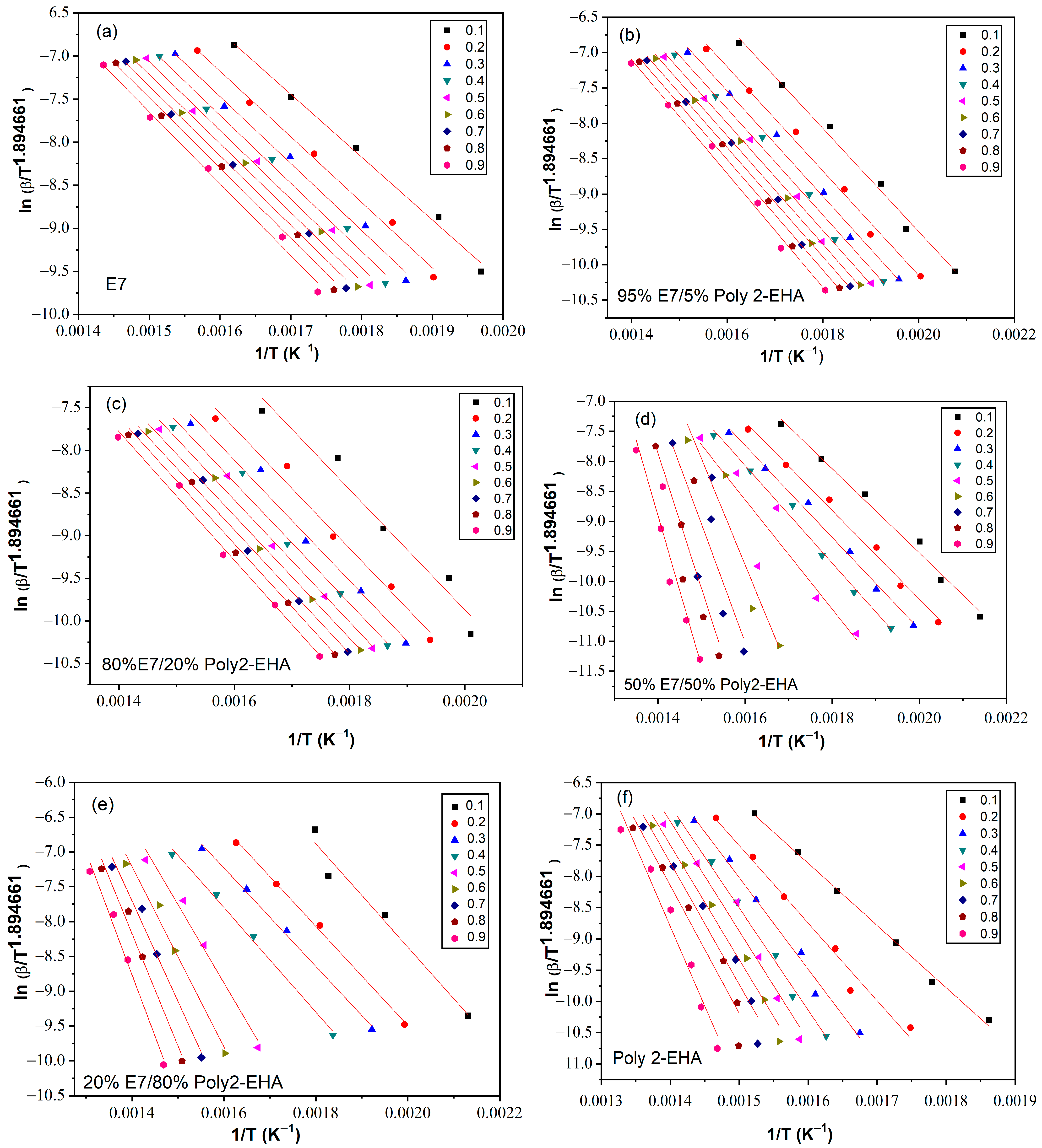
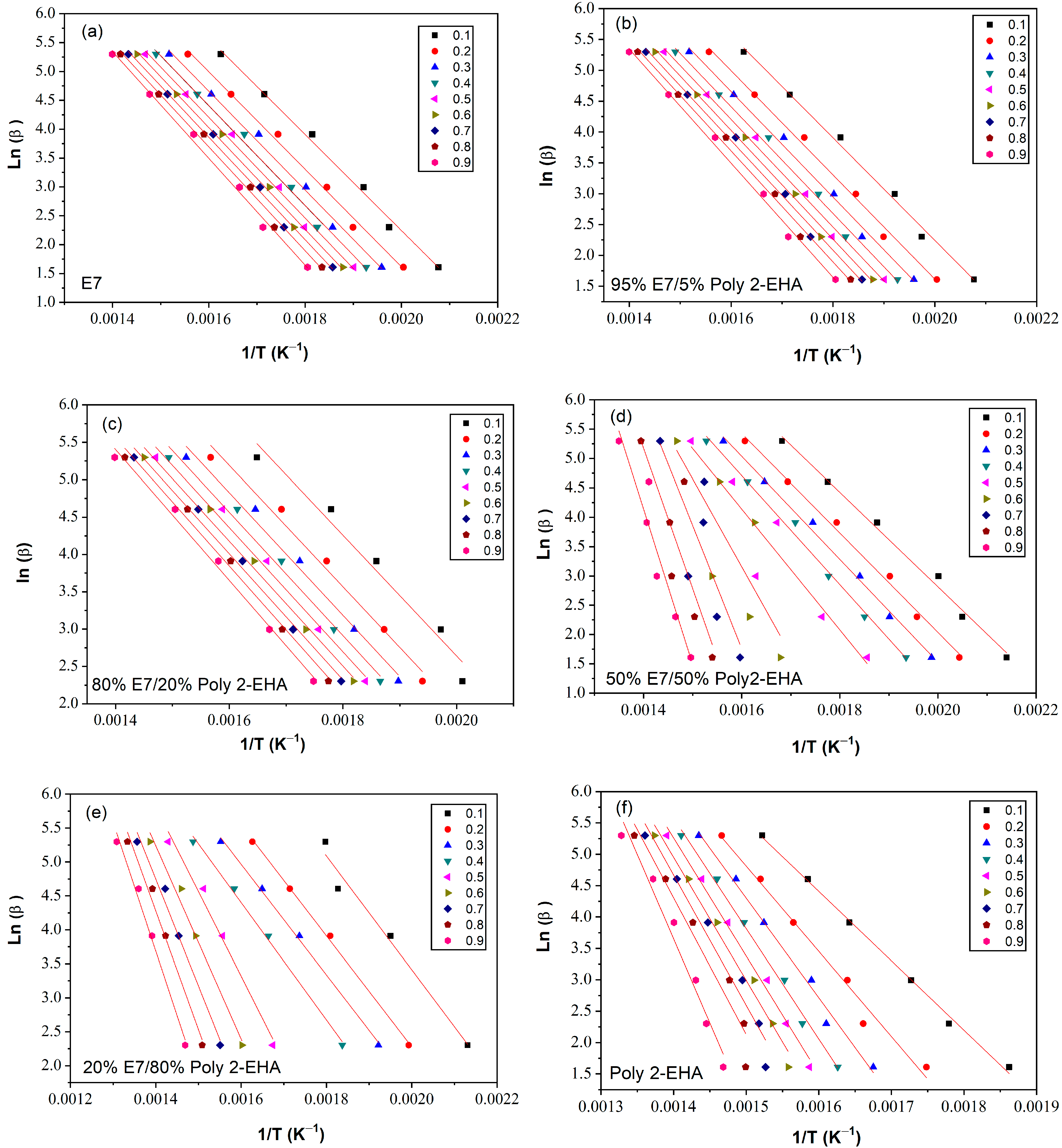
3.1. Tang Method
3.2. Flynn-Wall-Ozawa Method
3.3. Kissinger-Akahira-Sunose Method
4. Results and Discussion
4.1. Liquid Crystal E7
4.2. Poly(2-Ethylhexylacrylate)
4.3. Poly(2-EHA)/E7 Blends
4.4. Observation of Sample Morphology of Poly(2-EHA)/E7 Blends
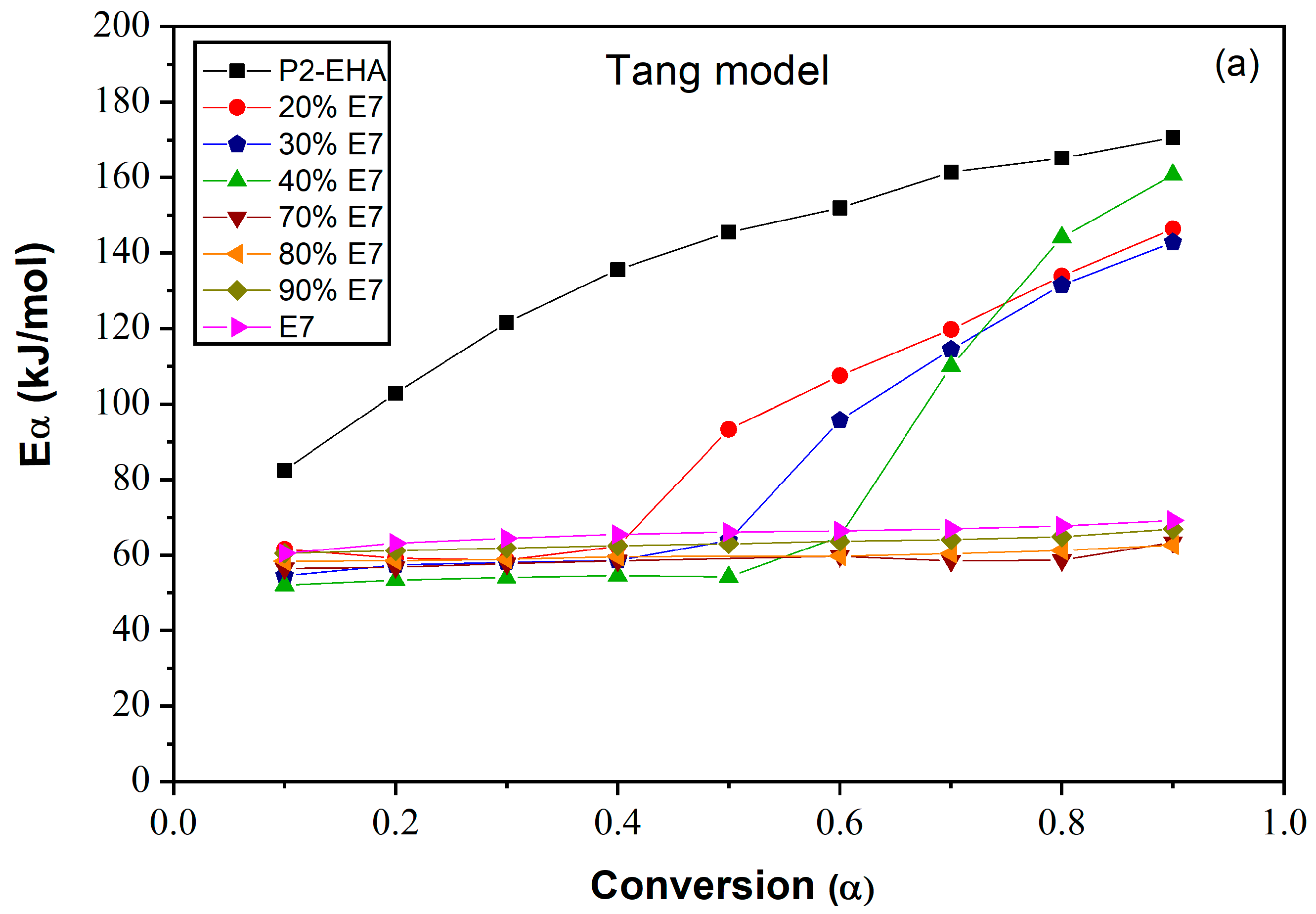
4.5. Determination of Activation Energy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, C.; Hu, Y.; Xu, J.; Yu, M.; Zou, C.; Wang, Q.; Gao, Y.; Yang, H. Research on the Morphology, Electro-Optical Properties and Mechanical Properties of Electrochromic Polymer-Dispersed Liquid Crystalline Films Doped with Anthraquinone Dyes. Crystals 2023, 13, 735. [Google Scholar] [CrossRef]
- Islam, M.S.; Chan, K.-Y.; Thien, G.S.H.; Low, P.-L.; Lee, C.-L.; Wong, S.K.; Noor, E.E.M.; Au, B.W.-C.; Ng, Z.-N. Performances of Polymer-Dispersed Liquid Crystal Films for Smart Glass Applications. Polymers 2023, 15, 3420. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Zhang, S.; Saeed, M.H.; Zhou, L.; Gao, H.; Huang, J.; Zhang, L.; Yang, H.; Xiao, J.; Gao, Y. Effects of the methacrylate monomers with different end groups on the morphologies, electro-optical and mechanical properties of polymer dispersed liquid crystals composite films. Liq. Cryst. 2021, 48, 722–734. [Google Scholar] [CrossRef]
- Hemaida, A.; Ghosh, A.; Sundaram, S.; Mallick, T.K. Evaluation of thermal performance for a smart switchable adaptive polymer dispersed liquid crystal (PDLC) glazing. Sol. Energy 2020, 195, 185–193. [Google Scholar] [CrossRef]
- Saeed, M.H.; Zhang, S.; Cao, Y.; Zhou, L.; Hu, J.; Muhammad, I.; Xiao, J.; Zhang, L.; Yang, H. Recent Advances in The Polymer Dispersed Liquid Crystal Composite and Its Applications. Molecules 2020, 25, 5510. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, G.; Shen, W.; Zhang, C.; Lanying, Z. Effect of functionality of thiol on the optical properties of liquid crystals/polymer composite films. Liq. Cryst. 2021, 48, 313–321. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Wang, Q.; Zhou, L.; Saeed, M.H.; Wang, X.; Zhang, L.; Yang, Z.; Yang, H. Fluorescence enhancement and encapsulation of quantum dots via a novel crosslinked vinyl-ether liquid crystals/polymer composite film. Polymer 2020, 207, 122834. [Google Scholar] [CrossRef]
- Jiang, J.; McGraw, G.; Ma, R.; Brown, J.; Yang, D.-K. Selective scattering polymer dispersed liquid crystal film for light enhancement of organic light emitting diode. Opt. Express 2017, 25, 3327–3335. [Google Scholar] [CrossRef]
- Seo, J.; Nam, S.; Jeong, J.; Lee, C.; Kim, H.; Kim, Y. Liquid Crystal-Gated-Organic Field-Effect Transistors with In-Plane Drain–Source–Gate Electrode Structure. ACS Appl. Mater. Interfaces 2015, 7, 504–510. [Google Scholar] [CrossRef]
- Labeeb, A.M.; Ibrahim, S.A.; Ward, A.A.; Abd-El-Messieh, S.L. Polymer/liquid crystal nanocomposites for energy storage applications. Polym. Eng. Sci. 2020, 60, 2529–2540. [Google Scholar] [CrossRef]
- Nasir, N.; Hong, H.; Rehman, M.A.; Kumar, S.; Seo, Y. Polymer-dispersed liquid-crystal-based switchable glazing fabricated via vacuum glass coupling. RSC Adv. 2020, 10, 32225–32231. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.M.; Song, J.K.; Kim, S.H. Thermal decomposition behavior and reliability evaluation of thermotropic liquid crystalline polymers. Macromol. Res. 2009, 17, 149–155. [Google Scholar] [CrossRef]
- Wadhwani, R.; Sutherland, D.; Moinuddin, K.A.M.; Joseph, P. Kinetics of pyrolysis of litter materials from pine and eucalyptus forests. J. Therm. Anal. Calorim. 2017, 130, 2035–2046. [Google Scholar] [CrossRef]
- Li, X.G. Thermogravimetric kinetics of thermotropic copolyesters containing p-oxybenzoate unit by multiple heating-rate methods. J. Appl. Polym. Sci. 1999, 74, 2016–2028. [Google Scholar] [CrossRef]
- Alashmawy, M.M.; Hassan, H.S.; Ookawara, S.A.; Elwardany, A.E. Thermal decomposition characteristics and study of the reaction kinetics of tea-waste. Biomass Convers. Biorefinery 2023, 13, 9487–9505. [Google Scholar] [CrossRef]
- Bondarchuk, I.; Bondarchuk, S.; Vorozhtsov, A.; Zhukov, A. Advanced Fitting Method for the Kinetic Analysis of Thermogravimetric Data. Molecules 2023, 28, 424. [Google Scholar] [CrossRef]
- Emiola-Sadiq, T.; Zhang, L.; Dalai, A.K. Thermal and Kinetic Studies on Biomass Degradation via Thermogravimetric Analysis: A Combination of Model-Fitting and Model-Free Approach. ACS Omega 2021, 6, 22233–22247. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Linert, W. Kinetic analysis of reversible thermal decomposition of solids. Int. J. Chem. Kinet. 1995, 27, 73–84. [Google Scholar] [CrossRef]
- Vyazovkin, S. Computational aspects of kinetic analysis: Part C. The ICTAC Kinetics Project—The light at the end of the tunnel? Thermochim. Acta 2000, 355, 155–163. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Wight, C.A. Ammonium Dinitramide: Kinetics and Mechanism of Thermal Decomposition. J. Phys. Chem. A 1997, 101, 5653–5658. [Google Scholar] [CrossRef]
- Vyazovkin, S. A Unified Approach to Nonisothermal Data. Chem. Kinet. 1996, 28, 95–101. [Google Scholar] [CrossRef]
- Wanjun, T.; Donghua, C. An integral method to determine variation in activation energy with extent of conversion. Thermochim. Acta 2005, 433, 72–76. [Google Scholar] [CrossRef]
- Budrugeac, P.; Segal, E. On the Li and Tang’s isoconversional method for kinetic analysis of solid-state reactions from thermoanalytical data. J. Mater. Sci. 2001, 36, 2707–2710. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C: Polym. Symp. 2007, 6, 183–195. [Google Scholar] [CrossRef]
- Ozawa, T. Kinetic analysis of derivative curves in thermal analysis. J. Therm. Anal. Calorim. 1970, 2, 301–324. [Google Scholar] [CrossRef]
- Smith, B.J.; Djajasasmita, M. The land molluscs of the Krakatau Islands, Indonesia. Philos. Trans. R. Soc. London. B Biol. Sci. 1988, 322, 379–400. [Google Scholar] [CrossRef]
- Li, C.-R.; Tang, T.B. A new method for analysing non-isothermal thermoanalytical data from solid-state reactions. Thermochim. Acta 1999, 325, 43–46. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Denisov, E.T. Solid-phase Radical Reactions and Mechanism of Oxidation of Carbon-chain Polymers. Russ. Chem. Rev. 1978, 47, 572–586. [Google Scholar] [CrossRef]
- Grassieker, N. Thermal Stability of Polymers; RT Conley Marcel Dekker: New York, NY, USA, 1970. [Google Scholar] [CrossRef]
- Emanuel, S.L.; Buchachenko, A.L. Chemical Physics of Polymer Degradation and Stabilization; CRC Press: Boca Raton, FL, USA, 1987. [Google Scholar]
- Nemphos, S.P. The Oxidative Degradation of Deuteropolystyrenees. J. Polym. Sci. 1957, 25, 173–187. [Google Scholar]
- Conley, R.T.; Valint, P.L. Oxidative degradation of poly(ethyl acrylate). J. Appl. Polym. Sci. 1965, 9, 785–797. [Google Scholar] [CrossRef]
- Steele, R.; Jacobs, H. Thermal-Oxidative Degradation of Poly (ethyl Acrylate). J. Appl. Polym. Sci. 1959, 2, 86–92. [Google Scholar] [CrossRef]
- Hu, Y.-H.; Chen, C.-Y.; Wang, C.-C. Thermal degradation kinetics of poly(n-butyl acrylate) initiated by lactams and thiols. Polym. Degrad. Stab. 2004, 84, 505–514. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Fan, M.; Zhang, J.; Cheng, J. Thermal degradation kinetics of poly(acrylate/α-methyl styrene) copolymers. Polym. Degrad. Stab. 2016, 128, 158–164. [Google Scholar] [CrossRef]
- Ors, J.; La Perriere, D. Thermogravimetric profile of decomposition of acrylate systems based on bornyl acrylate monomers. Polymer 1986, 27, 1999–2002. [Google Scholar] [CrossRef]
- Matsumoto, A.; Mizuta, K.; Otsu, T. Synthesis and thermal properties of poly(cycloalkyl methacrylate)s bearing bridged- and fused-ring structures. J. Polym. Sci. Part A Polym. Chem. 1993, 31, 2531–2539. [Google Scholar] [CrossRef]
- Han, X.G.; Wei, X.Y.; Wang, X.Y.; Shanks, R.A. Characterization and Thermal Behaviour of Polymer-Dispersed Liquid Crystals. Adv. Mater. Res. 2011, 152–153, 284–287. [Google Scholar] [CrossRef]
- Rusen, E.; Diacon, A.; Mitran, R.-A.; Dinescu, A.; Nistor, C.; Șomoghi, R.; Boscornea, A.C.; Mănăilă-Maximean, D. E7 nematic liquid crystal encapsulated in a polymeric photonic crystal. Eur. Polym. J. 2022, 175, 111374. [Google Scholar] [CrossRef]
- Selevou, A.; Papamokos, G.; Yildirim, T.; Duran, H.; Steinhart, M.; Floudas, G. Eutectic liquid crystal mixture E7 in nanoporous alumina. Effects of confinement on the thermal and concentration fluctuations. RSC Adv. 2019, 9, 37846–37857. [Google Scholar] [CrossRef]
- Vlad-Bubulac, T.; Serbezeanu, D.; Hamciuc, C.; Petreus, O.; Carja, I.; Lisa, G. Preparation and Phase Behavior of Blends of Polysulfone-Based Polymers with Phosphorous- Containing Smectic-A Liquid Crystals. Polym. Eng. Sci. 2013, 53, 1209–1216. [Google Scholar] [CrossRef]
- Merah, D.; Bedjaoui, L.; Zeggai, N.; Bouberka, Z.; Sarazin, J.; Boutalbi, D.; Barrera, A.; Boughrara, H.; Dubois, F.; Cazaux, F.; et al. Enhanced thermal stability of biobased crosslinked poly (isobornylacrylate-co-2-ethylhexylacrylate) copolymers. J. Polym. Res. 2022, 29, 1–11. [Google Scholar] [CrossRef]
- Haloi, D.J.; Singha, N.K. Synthesis of poly(2-ethylhexyl acrylate)/clay nanocomposite by in situ living radical polymerization. J. Polym. Sci. Part A Polym. Chem. 2011, 49, 1564–1571. [Google Scholar] [CrossRef]
- JSolorzano, J.A.P.; Moinuddin, K.A.M.; Tretsiakova-McNally, S.; Joseph, P. A Study of the Thermal Degradation and Combustion Characteristics of Some Materials Commonly Used in the Construction Sector. Polymers 2019, 11, 1833. [Google Scholar] [CrossRef]
- Li, K.; Jiang, H.; Cheng, M.; Li, Y.; Yin, Z.; Luo, D.; Sun, X.W.; Liu, Y.J. Controlling morphological and electro-optical properties via the phase separation in polymer/liquid-crystal composite materials. Liq. Cryst. 2020, 47, 238–247. [Google Scholar] [CrossRef]
- Bouriche, A.; Alachaher, L.B.; Maschke, U. Phase behaviour and electro-optical response of systems composed of nematic liquid crystals and poly (2-ethylhexylacrylate). Liq. Cryst. 2018, 45, 656–665. [Google Scholar] [CrossRef]
- Li, J.; Wen, C.-H.; Gauza, S.; Lu, R.; Wu, S.-T. Refractive Indices of Liquid Crystals for Display Applications. J. Disp. Technol. 2005, 1, 51–61. [Google Scholar] [CrossRef]
- Dhyani, V.; Kumar, J.; Bhaskar, T. Thermal decomposition kinetics of sorghum straw via thermogravimetric analysis. Bioresour. Technol. 2017, 245, 1122–1129. [Google Scholar] [CrossRef]
- Gai, C.; Zhang, Y.; Chen, W.-T.; Zhang, P.; Dong, Y. Thermogravimetric and kinetic analysis of thermal decomposition characteristics of low-lipid microalgae. Bioresour. Technol. 2013, 150, 139–148. [Google Scholar] [CrossRef]
- Tang, W.; Liu, Y.; Zhang, H.; Wang, C. New approximate formula for Arrhenius temperature integral. Thermochim. Acta 2003, 408, 39–43. [Google Scholar] [CrossRef]
- Rathore, N.S.; Pawar, A.; Panwar, N.L. Kinetic analysis and thermal degradation study on wheat straw and its biochar from vacuum pyrolysis under non-isothermal condition. Biomass Convers. Biorefinery 2021, 13, 7547–7559. [Google Scholar] [CrossRef]
- Chen, T.-J.; Lin, G.-J.; Chen, B.-Y.; Lin, B.-R.; Wu, J.-J.; Yang, Y.-J. Optimized electro-optical properties of polymer-stabilized vertical-aligned liquid crystal displays driven by an in-plane field. Displays 2015, 37, 94–99. [Google Scholar] [CrossRef]
- Doyle, C.D. Estimating isothermal life from thermogravimetric data. J. Appl. Polym. Sci. 1962, 6, 639–642. [Google Scholar] [CrossRef]
- Varma, A.K.; Lal, N.; Rathore, A.K.; Katiyar, R.; Thakur, L.S.; Shankar, R.; Mondal, P. Thermal, kinetic and thermodynamic study for co-pyrolysis of pine needles and styrofoam using thermogravimetric analysis. Energy 2021, 218, 119404. [Google Scholar] [CrossRef]
- Kissinger, H.E. Variation of peak temperature with heating rate in differential thermal analysis. J. Res. Natl. Bur. Stand. 1956, 57, 217. [Google Scholar] [CrossRef]
- Starink, M.J. Activation energy determination for linear heating experiments: Deviations due to neglecting the low temperature end of the temperature integral. J. Mater. Sci. 2007, 42, 483–489. [Google Scholar] [CrossRef]
- Krongauz, V.V. Crosslink density dependence of polymer degradation kinetics: Photocrosslinked acrylates. Thermochim. Acta 2010, 503–504, 70–84. [Google Scholar] [CrossRef]
- Sun, J.; Huang, Y.; Gong, G.; Cao, H. Thermal degradation kinetics of poly(methylphenylsiloxane) containing methacryloyl groups. Polym. Degrad. Stab. 2006, 91, 339–346. [Google Scholar] [CrossRef]
- Grassie, N.; Speakman, G. Thermal Degradation of Poly(alky1 Acrylates). I. Preliminary Investigations. J. Polym. Sci. Part A-1 Polym. Chem. 1971, 9, 919–929. [Google Scholar] [CrossRef]
- Aliev, F.; Zgonnik, V. Thermo-optics and thermal stability of poly(alkyl methacrylates) in porous matrices. Eur. Polym. J. 1991, 27, 969–973. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, Y.; Yin, W.; Guo, B.; Rao, F.; Ku, J. Isothermal Coal-Based Reduction Kinetics of Fayalite in Copper Slag. ACS Omega 2020, 5, 8605–8612. [Google Scholar] [CrossRef]
- Yao, Z.; Yu, S.; Su, W.; Wu, W.; Tang, J.; Qi, W. Kinetic studies on the pyrolysis of plastic waste using a combination of model-fitting and model-free methods. Waste Manag. Res. J. Sustain. Circ. Econ. 2020, 38, 77–85. [Google Scholar] [CrossRef] [PubMed]

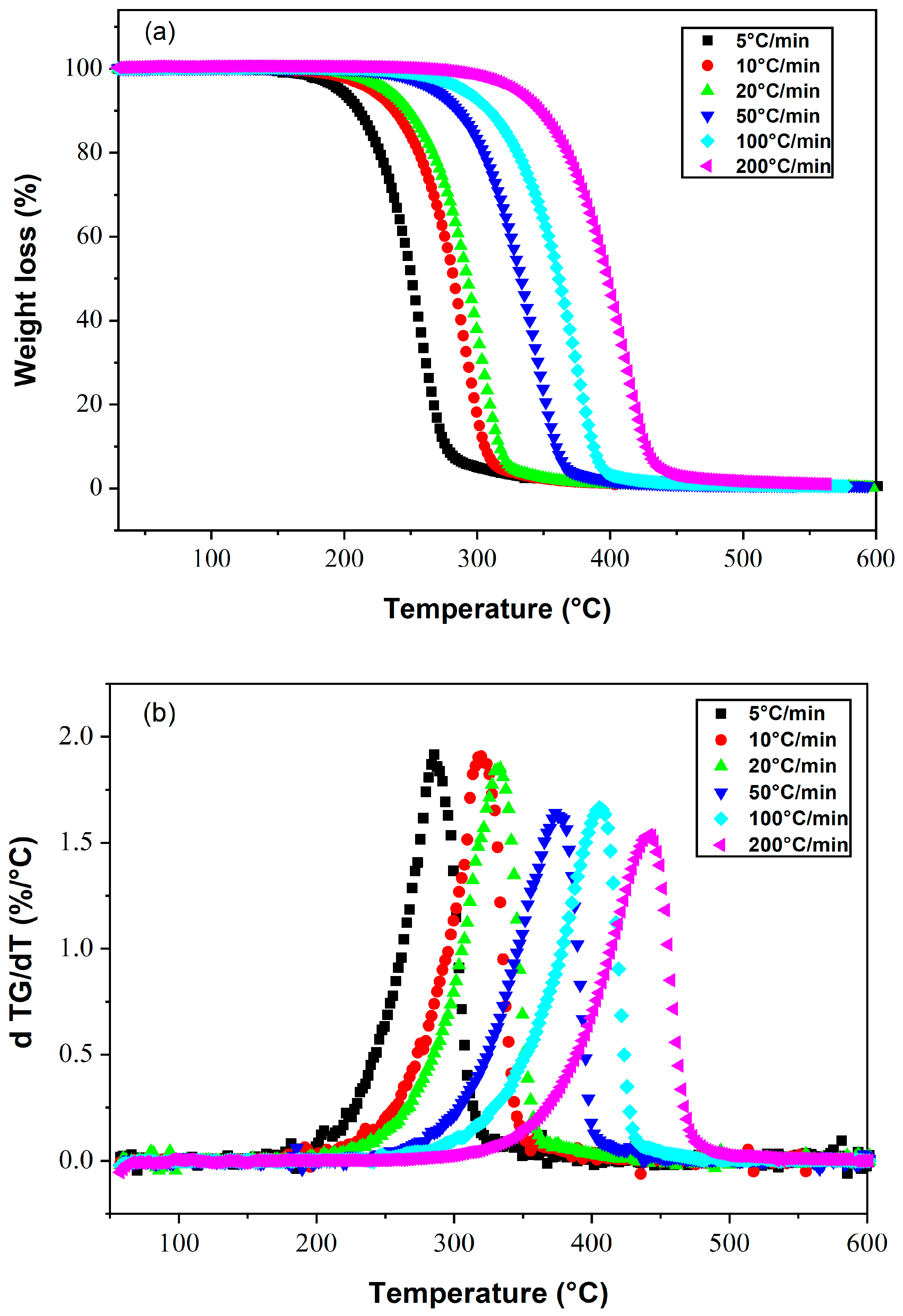
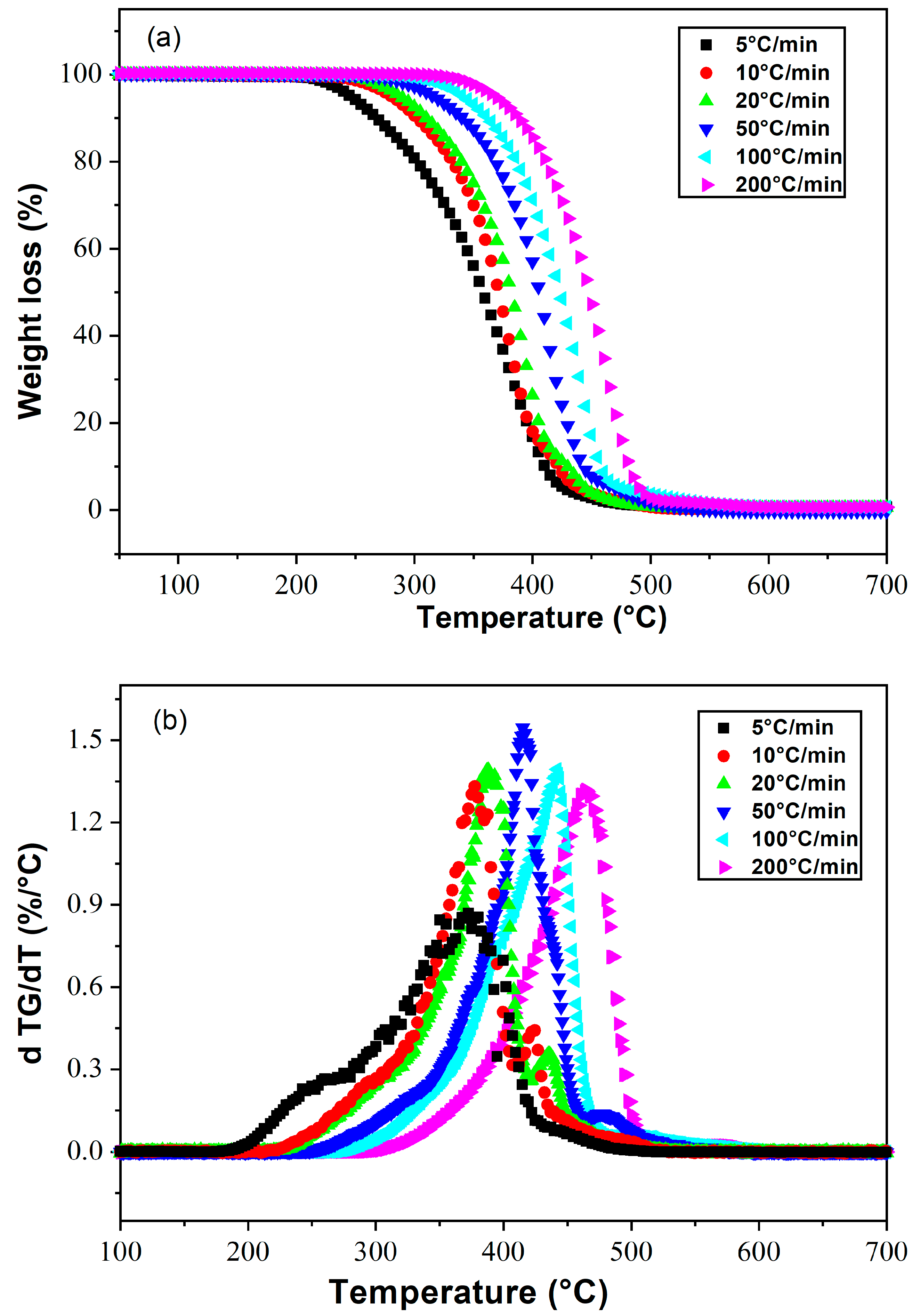
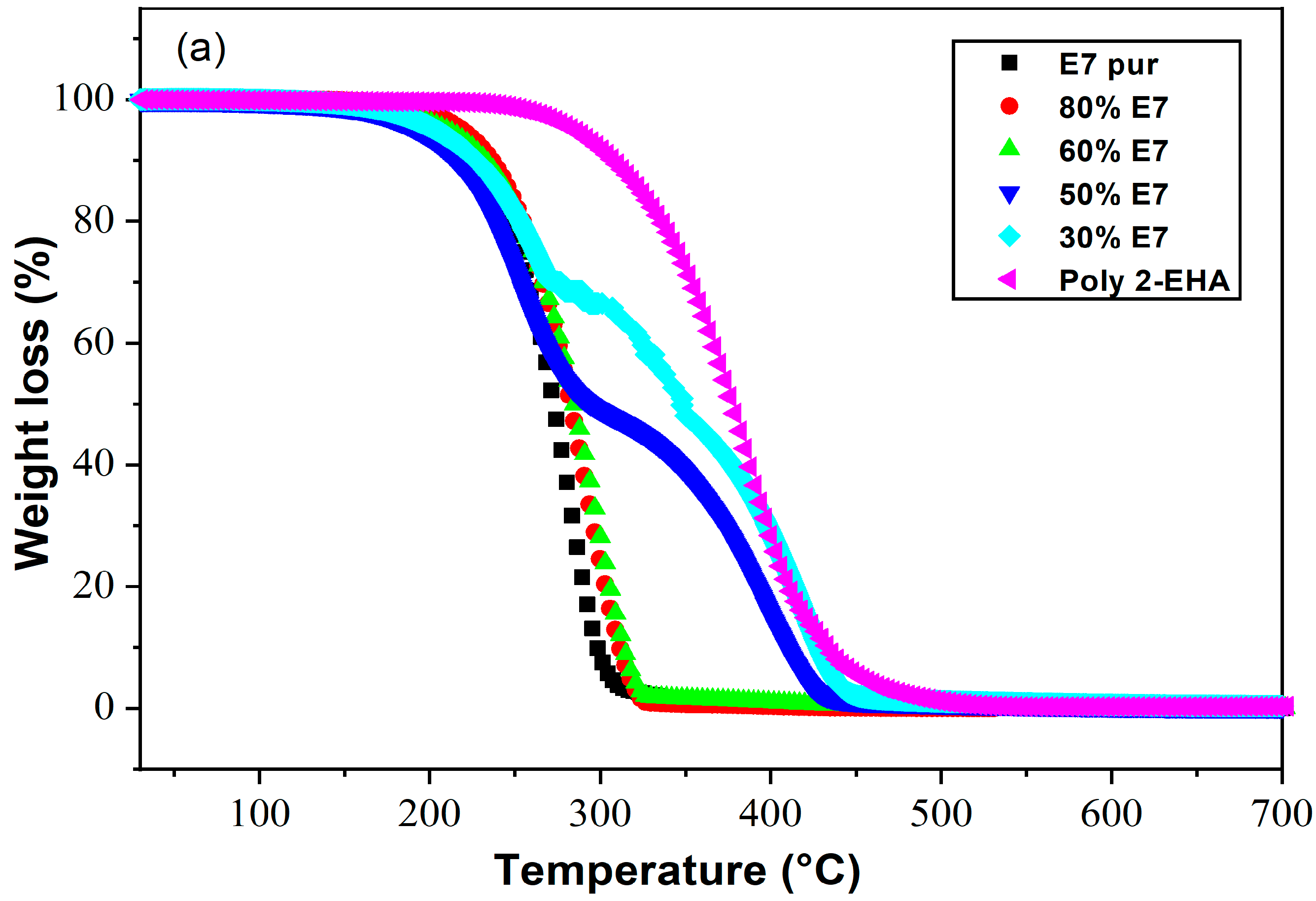
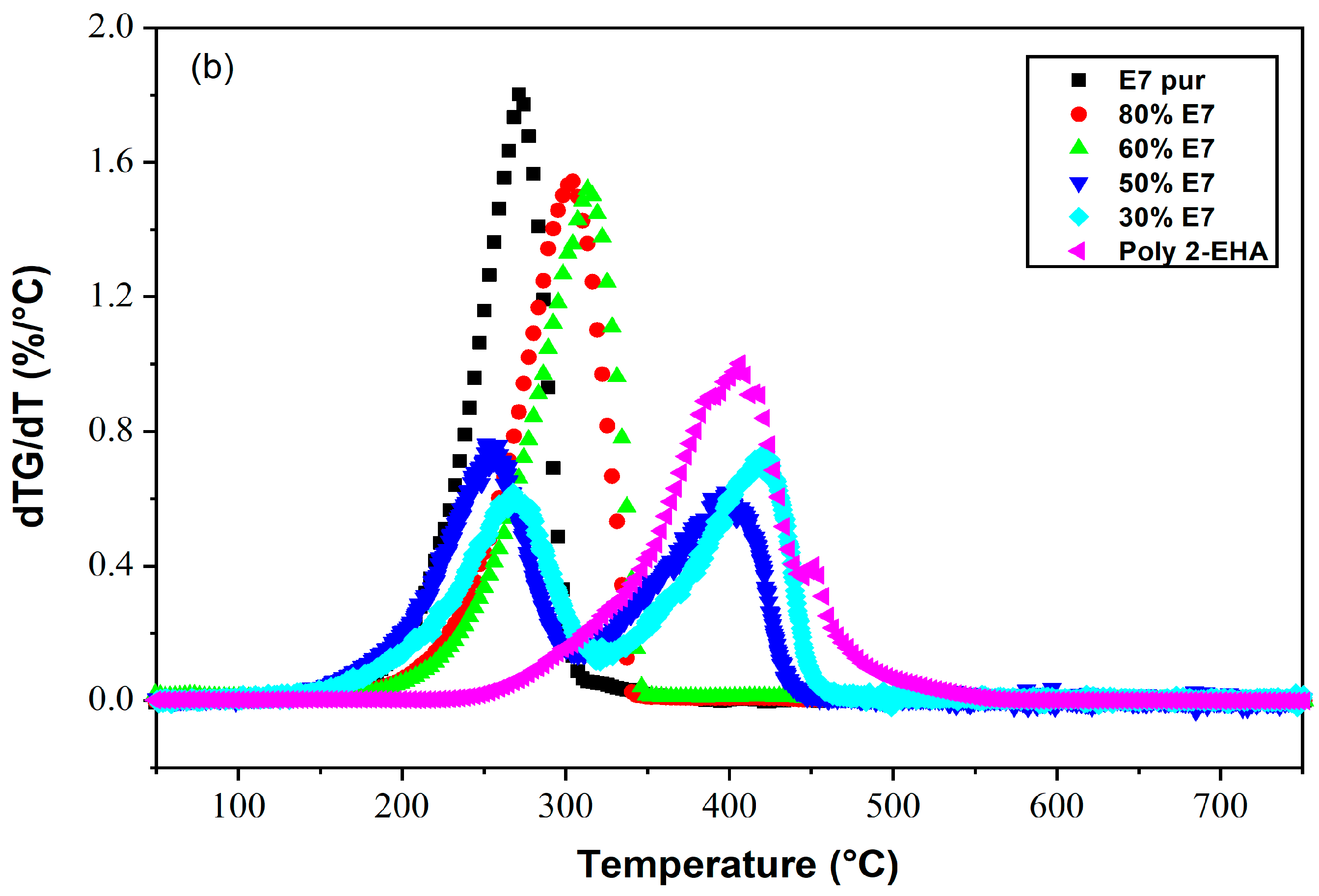


| Composition | Conversion | Tang Model | FWO Model | Kissinger Model | |||
|---|---|---|---|---|---|---|---|
| Eα (kJ/mol) | R2 | Eα (kJ/mol) | R2 | Eα (kJ/mol) | R2 | ||
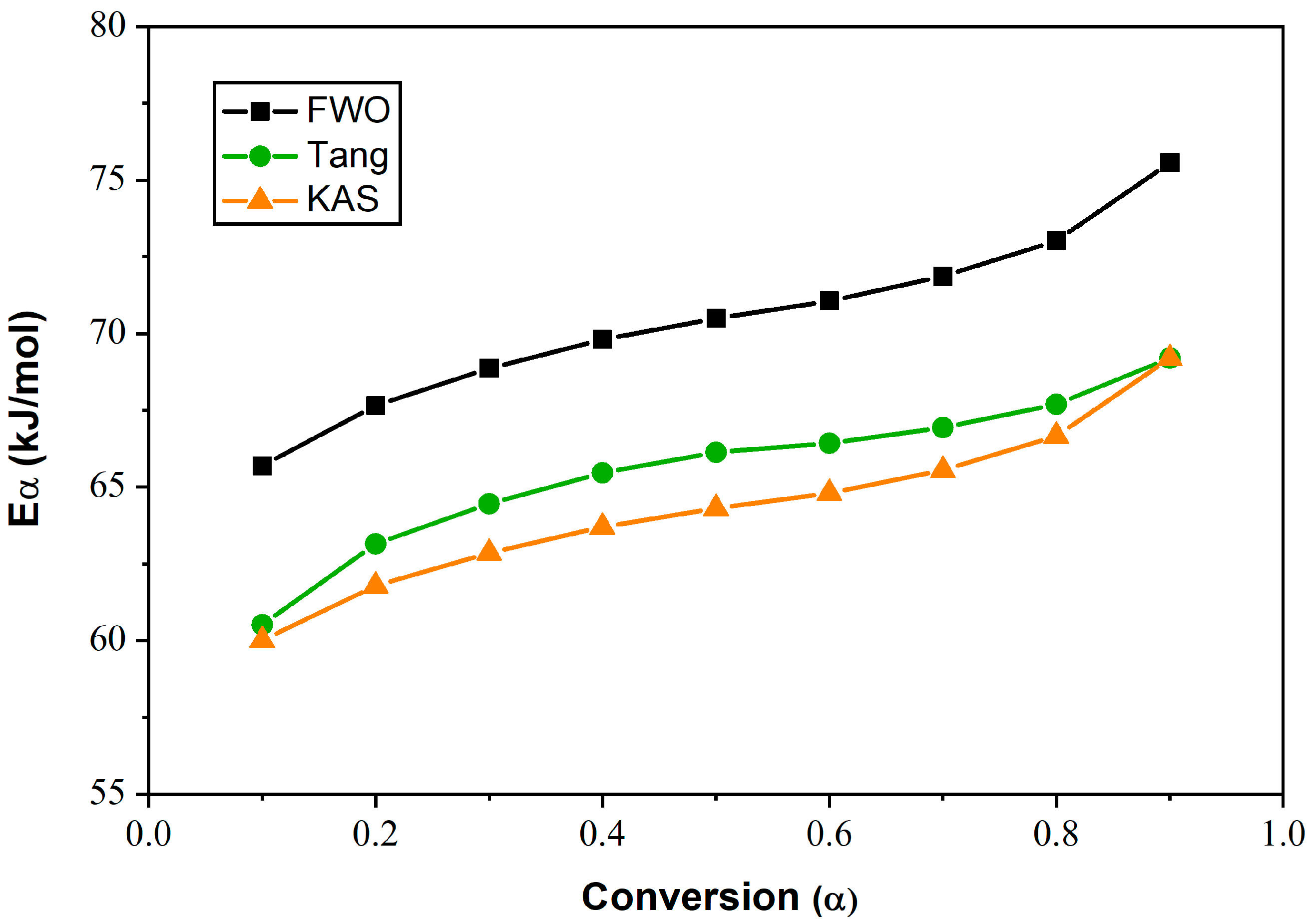
| E7 | 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 | 60.52 63.15 64.46 65.46 66.13 66.43 66.93 67.69 69.19 | 0.9933 0.9927 0.9918 0.9899 0.9900 0.9895 0.9907 0.9907 0.9912 | 65.69 67.66 68.86 69.80 70.49 71.06 71.86 73.01 75.56 | 0.9964 0.9960 0.9958 0.9951 0.9951 0.9951 0.9960 0.9966 0.9973 | 60.01 61.78 62.85 63.70 64.30 64.80 65.55 66.66 69.19 | 0.9962 0.9955 0.9948 0.9936 0.9936 0.9935 0.9945 0.9947 0.9950 |
| 95% E7 | 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 | 60.48 61.18 61.85 62.48 63.00 63.65 64.07 64.88 66.89 | 0.9905 0.9906 0.9906 0.9903 0.9903 0.9905 0.9899 0.9906 0.9909 | 65.74 66.73 67.57 68.32 68.94 69.67 70.18 71.06 73.10 | 0.9931 0.9931 0.9932 0.9930 0.9929 0.9930 0.9927 0.9932 0.9934 | 60.10 60.77 61.43 62.05 62.57 63.21 63.63 64.43 66.43 | 0.9903 0.9904 0.9905 0.9901 0.9901 0.9903 0.9898 0.9904 0.9907 |
| 80%E7 | 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 | 58.4 58.47 58.85 59.55 59.76 60.37 61.26 62.62 63.85 | 0.9484 0.9736 0.9784 0.9786 0.9800 0.9821 0.9831 0.9850 0.9860 | 63.93 64.25 64.83 65.28 65.79 66.10 66.80 67.76 69.19 | 0.9618 0.9814 0.9850 0.9851 0.9862 0.9877 0.9884 0.9898 0.9905 | 58.17 58.05 58.42 58.85 59.11 59.30 59.91 60.80 62.16 | 0.9857 0.9847 0.9827 0.9817 0.9796 0.9783 0.9779 0.9731 0.9512 |
| 50% E7 | 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 | 58.27 61.37 63.66 67.64 75.80 146.88 163.73 187.37 208.59 | 0.9873 0.9907 0.9924 0.9883 0.8292 0.8643 0.5535 0.6083 0.8893 | 63.66 66.99 69.42 73.42 81.45 118.28 166.07 188.88 209.38 | 0.9910 0.9935 0.9947 0.9917 0.8617 0.5453 0.5900 0.6391 0.8998 | 58.20 61.29 63.58 67.56 75.72 113.84 163.65 187.29 208.50 | 0.8892 0.6081 0.5532 0.4926 0.8289 0.9887 0.9924 0.9906 0.9873 |
| 20% E7 | 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 | 61.54 59.14 58.62 62.30 93.29 107.54 119.80 133.95 146.45 | 0.9582 0.9964 0.995 0.9921 0.9724 0.9752 0.9761 0.9774 0.9816 | 66.24 64.60 64.44 68.34 98.49 112.43 124.39 138.09 150.24 | 0.9671 0.9977 0.9968 0.9948 0.9783 0.9799 0.9803 0.9811 0.9845 | 61.19 58.74 58.20 61.86 92.86 107.11 119.37 133.53 146.03 | 0.9815 0.9771 0.9758 0.9749 0.9720 0.9919 0.9948 0.9963 0.9577 |
| Poly(2-EHA) | 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 | 82.50 102.87 121.60 135.64 145.50 151.96 161.41 165.16 170.64 | 0.9959 0.9788 0.9865 0.9921 0.9608 0.7164 0.9476 0.9825 0.9598 | 91.95 112.86 131.94 146.23 156.38 162.93 172.55 180.93 223.22 | 0.9964 0.9819 0.9884 0.9932 0.9909 0.9799 0.9541 0.9359 0.9640 | 82.97 102.64 121.27 135.56 144.12 153.05 171.74 191.21 214.99 | 0.9857 0.9847 0.9827 0.9817 0.9796 0.9783 0.9779 0.9731 0.9512 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouriche, A.; Alachaher-Bedjaoui, L.; Barrera, A.; Staelens, J.-N.; Maschke, U. Thermal Degradation Studies of Poly(2-ethyl hexyl acrylate) in the Presence of Nematic Liquid Crystals. Polymers 2023, 15, 3934. https://doi.org/10.3390/polym15193934
Bouriche A, Alachaher-Bedjaoui L, Barrera A, Staelens J-N, Maschke U. Thermal Degradation Studies of Poly(2-ethyl hexyl acrylate) in the Presence of Nematic Liquid Crystals. Polymers. 2023; 15(19):3934. https://doi.org/10.3390/polym15193934
Chicago/Turabian StyleBouriche, Amina, Lamia Alachaher-Bedjaoui, Ana Barrera, Jean-Noël Staelens, and Ulrich Maschke. 2023. "Thermal Degradation Studies of Poly(2-ethyl hexyl acrylate) in the Presence of Nematic Liquid Crystals" Polymers 15, no. 19: 3934. https://doi.org/10.3390/polym15193934
APA StyleBouriche, A., Alachaher-Bedjaoui, L., Barrera, A., Staelens, J.-N., & Maschke, U. (2023). Thermal Degradation Studies of Poly(2-ethyl hexyl acrylate) in the Presence of Nematic Liquid Crystals. Polymers, 15(19), 3934. https://doi.org/10.3390/polym15193934








