Temperature and Frequency Dependence of the Dynamic Viscoelastic Properties of Silicone Rubber
Abstract
:1. Introduction
2. Theory
2.1. Time–Temperature Superposition Principle
2.2. The WLF Equation
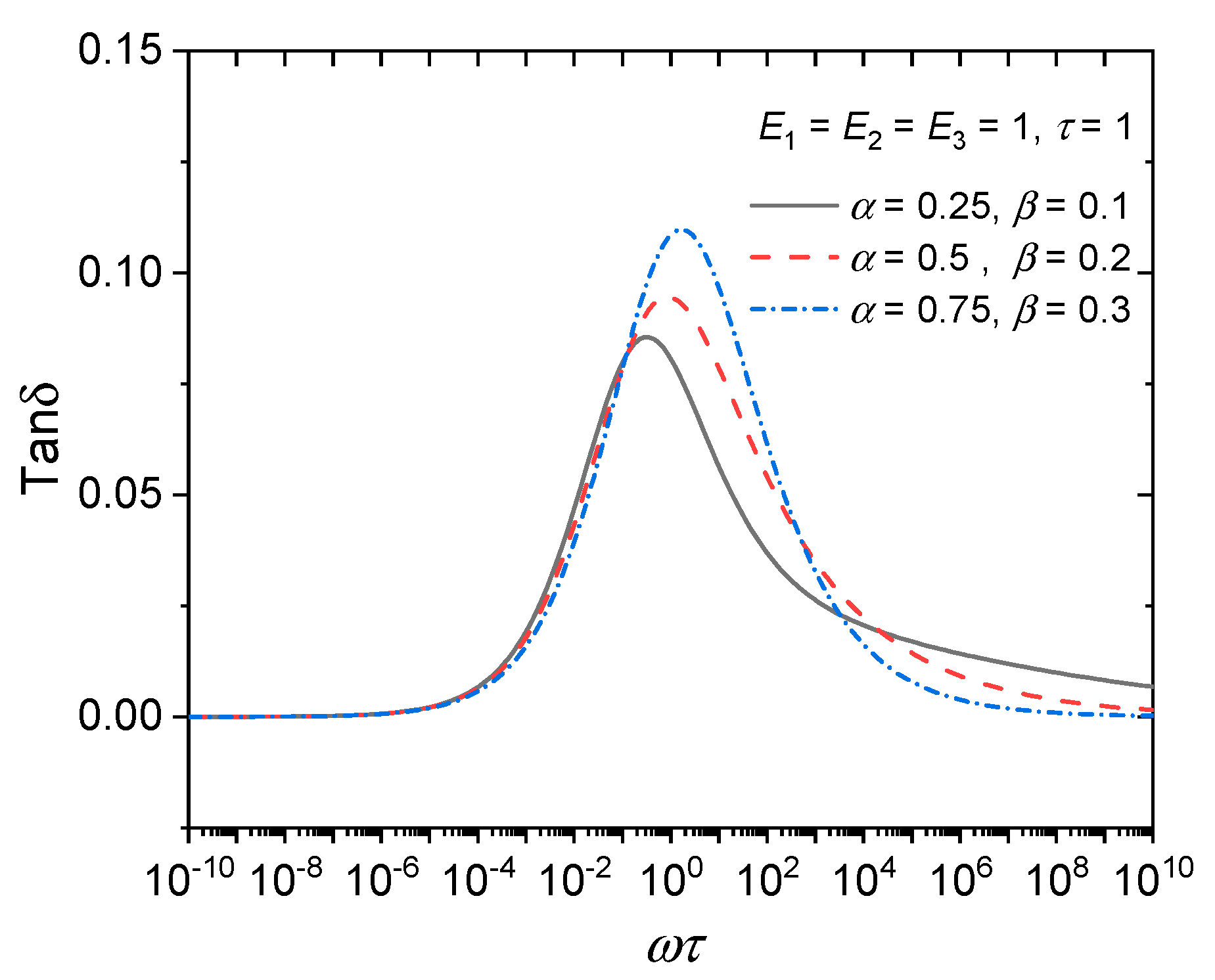
2.3. Fractional-Order Derivative Viscoelastic Model
3. Experimental Section
4. Results and Discussion
4.1. Master Curve Analysis
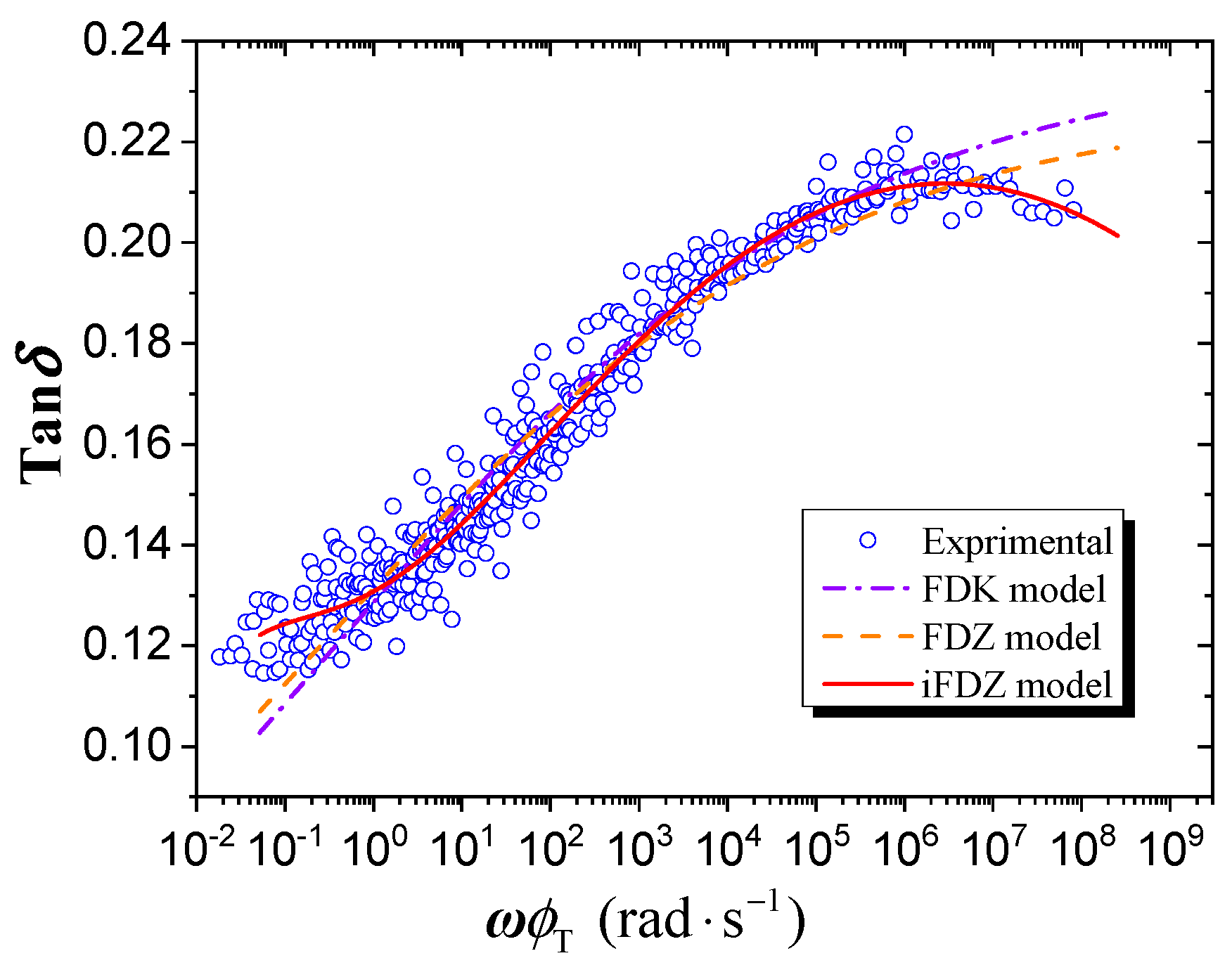
4.2. Application Analysis of Fractional Derivative Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Zhang, L.; Wang, B.; Xu, Z.; Wang, W. Effect of thermal aging on mechanical properties of EPDM rubber. Appl. Mech. Mater. 2015, 727–728, 318–321. [Google Scholar]
- Wang, L.; Zhao, S. Study on the Structure-Mechanical Properties Relationship and Antistatic Characteristics of SSBR Composites Filled with SiO2/CB. J. Appl. Polym. Sci. 2010, 118, 338–345. [Google Scholar] [CrossRef]
- Liu, B.; Wang, P.C.; Ao, Y.Y.; Zhao, Y. Effects of combined neutron and gamma irradiation upon silicone foam. Radiat. Phys. Chem. 2017, 133, 31–36. [Google Scholar] [CrossRef]
- Shit, S.C.; Shah, P. A Review on Silicone Rubber. Natl. Acad. Sci. Lett. 2013, 36, 355–365. [Google Scholar] [CrossRef]
- Wei, J.W.; Shi, X.P.; Feng, Z.Y. Strain rate dependent constitutive model of rubber. Chin. J. Phys. 2022, 36, 024205. [Google Scholar]
- Yin, B.Y.; Wen, H.B.; Luo, W.B. Effect of thermo-oxidative aging on the Payne effect and hysteresis loss of carbon-black filled rubber vulcanizates. npj. Mat. Degrad. 2022, 6, 94. [Google Scholar] [CrossRef]
- Kulik, V.M. Viscoelastic properties of silicone rubber with addition of carbon nanotubes. J. Appl. Mech. Tech. Phys. 2023, 63, 884–890. [Google Scholar] [CrossRef]
- Peleg, M. On the use of the WLF model in polymers and foods. Crit. Rev. Food Sci. 2009, 32, 59–66. [Google Scholar] [CrossRef]
- Van, D.P. Theoretical derivation of the WLF- and annealing equations. J. Non-Cryst. Solids. 2009, 356, 394–399. [Google Scholar]
- Paulo, L.; Sara, P.; Vítor, C. Rheological properties of ground tyre rubber based thermoplastic elastomeric blends. Polym. Test. 2015, 45, 58–67. [Google Scholar]
- Lin, J.R.; Chen, L.W. The mechanical-viscoelastic model and WLF relationship in shape memorized linear ether-type polyurethanes. J. Polym. Res. 1999, 6, 35–40. [Google Scholar] [CrossRef]
- Jacek, D.; Jack, F.D.; Karl, F.F. The meaning of the “universal” WLF parameters of glass-forming polymer liquids. J. Chem. Phys. 2015, 142, 014905. [Google Scholar]
- Zhang, Z.; Li, S.; Zhu, W. Temperature Spectrum Model of Dynamic Mechanical Properties for Viscoelastic Damping Materials. J. Mech. Eng. 2011, 47, 135–140. [Google Scholar] [CrossRef]
- Hu, X.L.; He, R.; Huang, Y.; Yin, B.; Luo, W.B. A method to predict the dynamical behaviors of carbon black filled natural rubber at different temperatures. Polym. Test. 2019, 79, 106067. [Google Scholar] [CrossRef]
- Liang, S.; Luo, R.; Luo, W. Fractional differential constitutive model for linear viscoelasticity of asphalt and asphalt mastic. Constr. Build. Mater. 2021, 306, 124886. [Google Scholar] [CrossRef]
- Luo, W.; Huang, Y.; Yin, B. Fatigue Life Assessment of Filled Rubber by Hysteresis Induced Self-Heating Temperature. Polymer 2020, 12, 864–874. [Google Scholar] [CrossRef] [Green Version]
- Jeong, G.; McCarthy, M. Stochastic Estimation of the In-Place Dynamic Modulus for Asphalt Concrete Pavements. J. Mater. Civil. Eng. 2015, 27, 04014181. [Google Scholar] [CrossRef]
- Kumar, A.; Lopez-Pamies, O. On the two-potential constitutive modeling of rubber viscoelastic materials. Comptes Rendus Mec. 2016, 344, 102–112. [Google Scholar] [CrossRef]
- Nutting, P.G. A new general law of deformation. J. Franklin. Inst. 1921, 191, 679–685. [Google Scholar] [CrossRef]
- Arfan, M.; Mahariq, I.; Shah, K.; Abdeljawad, T.; Laouini, G.; Mohammed, P.O. Numerical computations and theoretical investigations of a dynamical system with fractional order derivative. Alex. Eng. J. 2022, 61, 1982–1994. [Google Scholar] [CrossRef]
- Bosworth, R.C.L. A definition of plasticity. Nature 1946, 157, 447. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the Fractional Calculus Model of Viscoelastic Behavior. J. Rheol. 1998, 30, 135–155. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Chen, W. Anomalous diffusion: Fractional derivative equation models and applications in environmental flows. Sci. Sin-Phys. Mech. Astron. 2015, 45, 8–22. [Google Scholar]
- Tang, Z.; Luo, G.; Chen, W.; Yang, X. Dynamic Characteristics of Vibration System Including Rubber Isolator. J. Nanjing Univ. Aeronaut. Astronaut. 2014, 46, 285–291. [Google Scholar]
- Li, Z.; Sun, D.; Yan, B.; Sun, B.; Zhang, W. Fractional order model of viscoelastic suspension for crawler vehicle and its vibration suppression analysis. Chin. Soc. Ag. Eng. 2015, 31, 72–79. [Google Scholar]
- Wharmby, A.W.; Bagley, R.L. Modifying Maxwell’s equations for dielectric materials based on techniques from viscoelasticity and concepts from fractional calculus. Int. J. Eng. Sci. 2014, 79, 59–80. [Google Scholar] [CrossRef]
- Cao, L.; Li, Y.; Tian, G. Time domain analysis of the fractional order weighted distributed parameter Maxwell model. Comput. Math. Appl. 2013, 66, 813–823. [Google Scholar] [CrossRef]
- Himadri, B. Fundamentals of Polymer Physics and Molecular Biophysics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Haupt, P.; Lion, A.; Backhaus, E. On the dynamic behaviour of polymers under finite strains: Constitutive modelling and identification of parameters. Int. J. Solids Struct. 2000, 37, 3633–3646. [Google Scholar] [CrossRef]
- Luo, W.B.; Liang, S.; Zhang, Y. Fractional Differential Constitutive Model for Dynamic Viscoelasticity of Asphalt. China J. Highw. Transp. 2020, 33, 34–43. [Google Scholar]
- Sawai, T.; MizunoI, S.; Imamura, H. Thermal Softening Properties of Torrefied Wood Powderas a Raw Material for Production of Biomass-based Plastics. Exp. Mech. 2021, 21, 16–22. [Google Scholar]
- Placet, V.; Passard, J.; Perré, P. Viscoelastic properties of green wood across the grain measured by harmonic tests in the range 0–95 °C: Hardwood vs. softwood and normal wood vs. reaction wood. Holzforschung 2007, 61, 548–557. [Google Scholar] [CrossRef] [Green Version]
- Ouis, D. On the frequency dependence of the modulus of elasticity of wood. Wood Sci. Technal. 2002, 36, 335–346. [Google Scholar] [CrossRef]
- Gergesova, M.; Zupancic, B.; Saprunov, I. The closed form t-T-P shifting (CFS) algorithm. J. Rheol. 2011, 55, 1–16. [Google Scholar] [CrossRef]
- Zheng, Q.; Lin, Y.; Ye, Y.L.; Zhang, X.H. The Solution and Analysis on Parameters of WLF Equation in Teaching the Course Polymer Physics. Polym. Bull. 2010, 6, 99–105. [Google Scholar]
- Trinkle, S.; Walter, P.; Friedrich, C. Van Gurp-Palmen Plot II—Classification of long chain branched polymers by their topology. Rheol. Acta 2002, 41, 103–113. [Google Scholar] [CrossRef]
- Aytac, A. A new fractional derivative model for linearly viscoelastic materials and parameter identification via genetic algorithms. Rheol. Acta 2014, 53, 219–233. [Google Scholar]
- Yu, F.Y. Rheological Study on the Flow-Induced Crystallization of the Semicrystalline Polyolesfin. Ph.D. Dissertation, Shanghai Jiao Tong University, Shanghai, China, 2009. [Google Scholar]
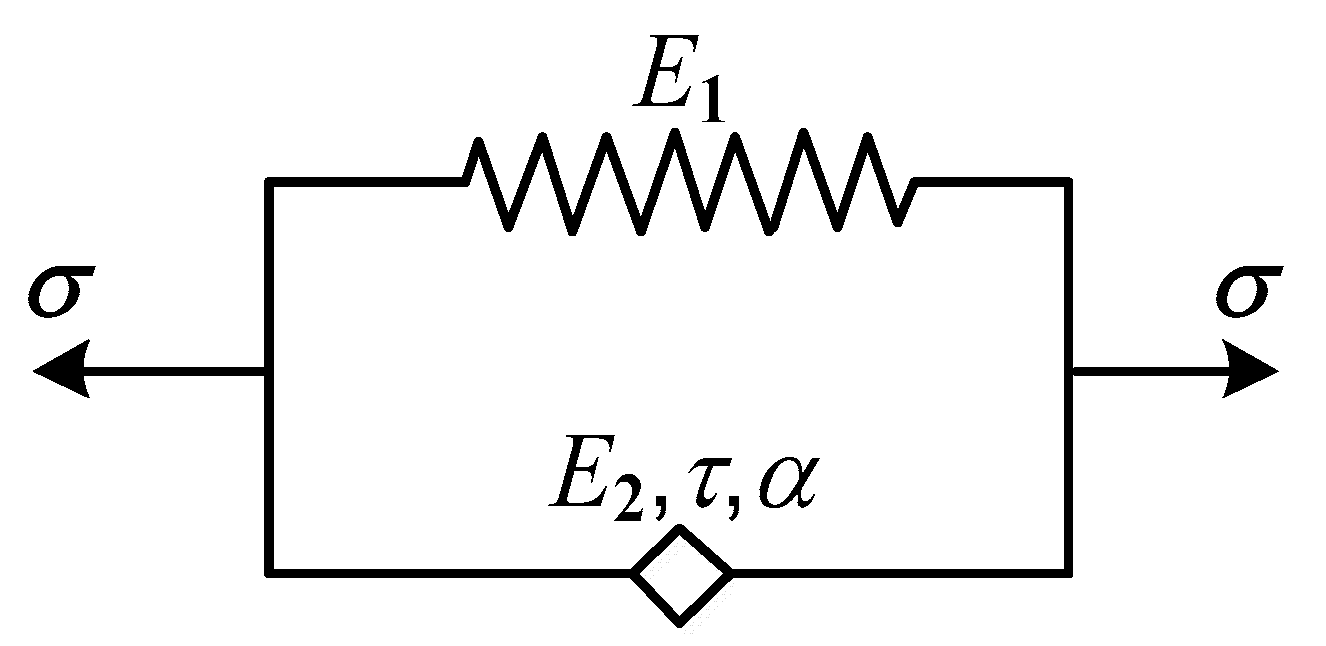
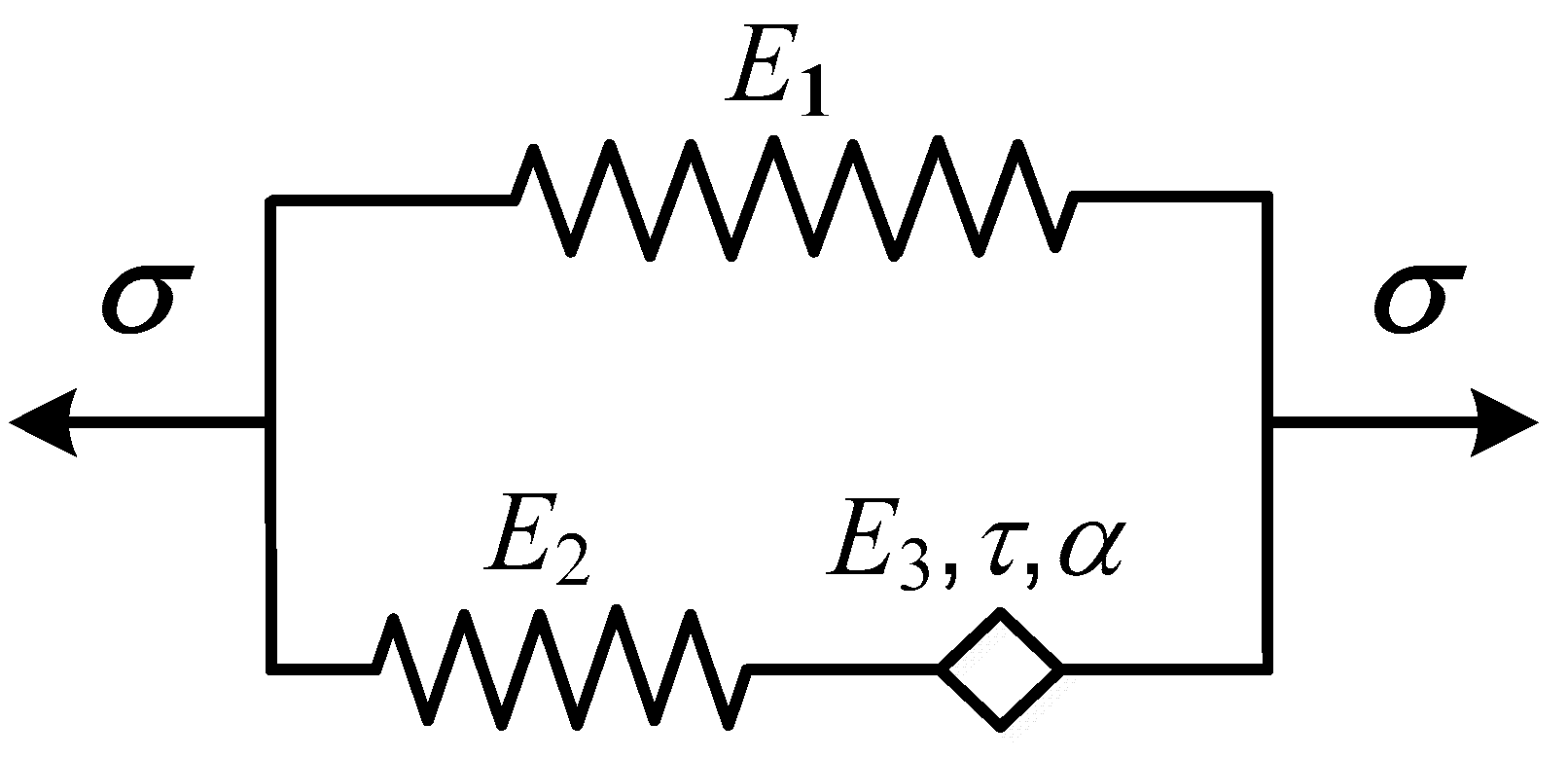
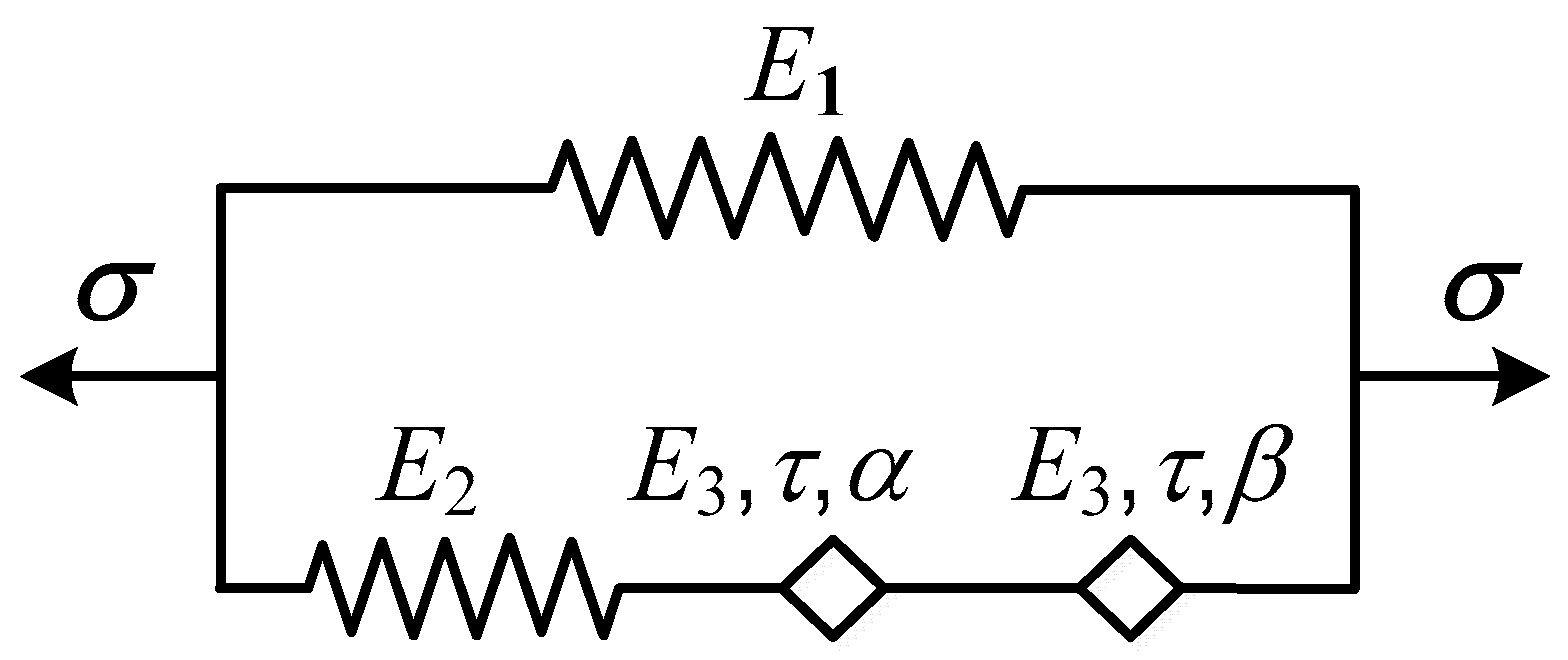


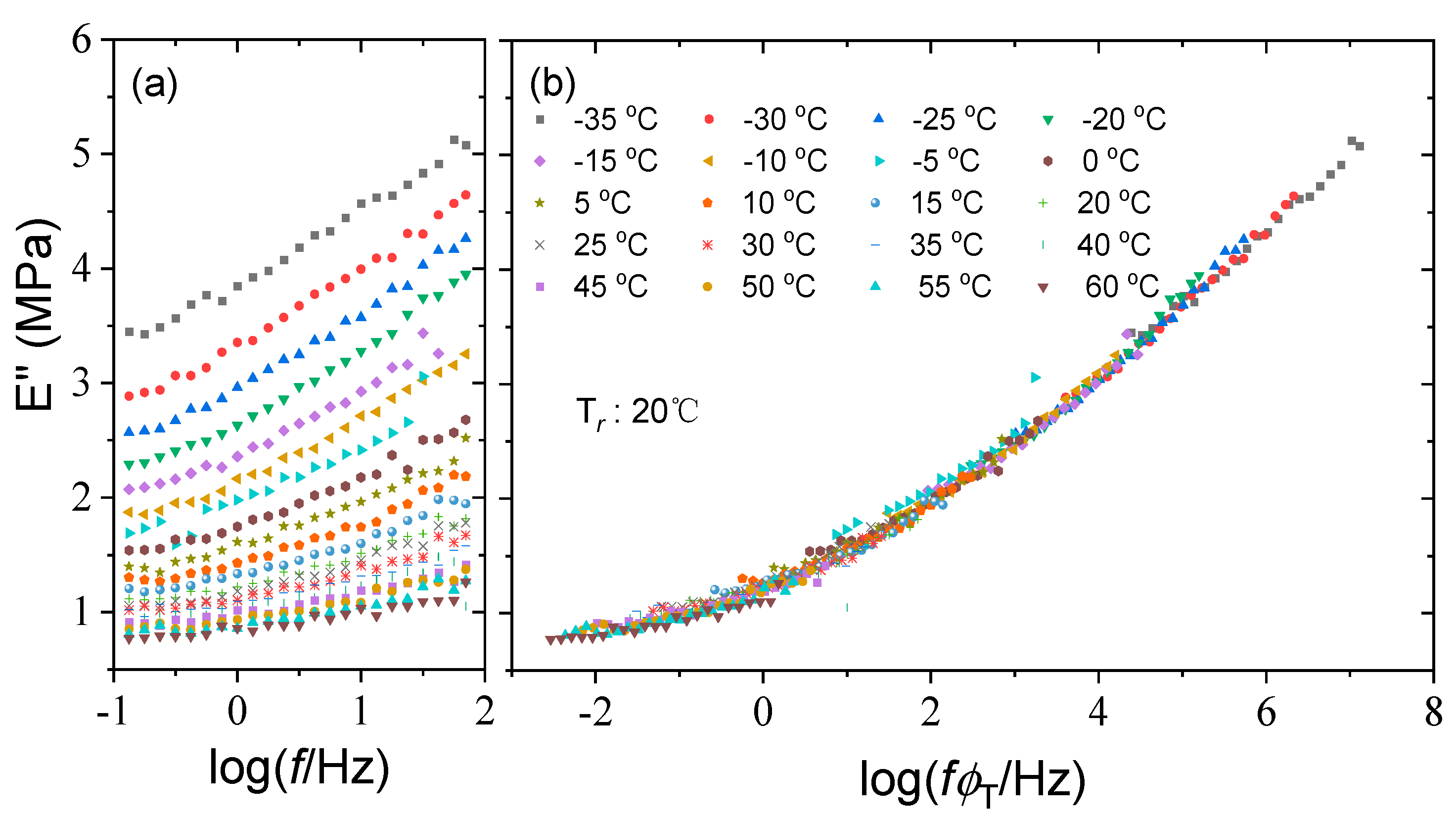
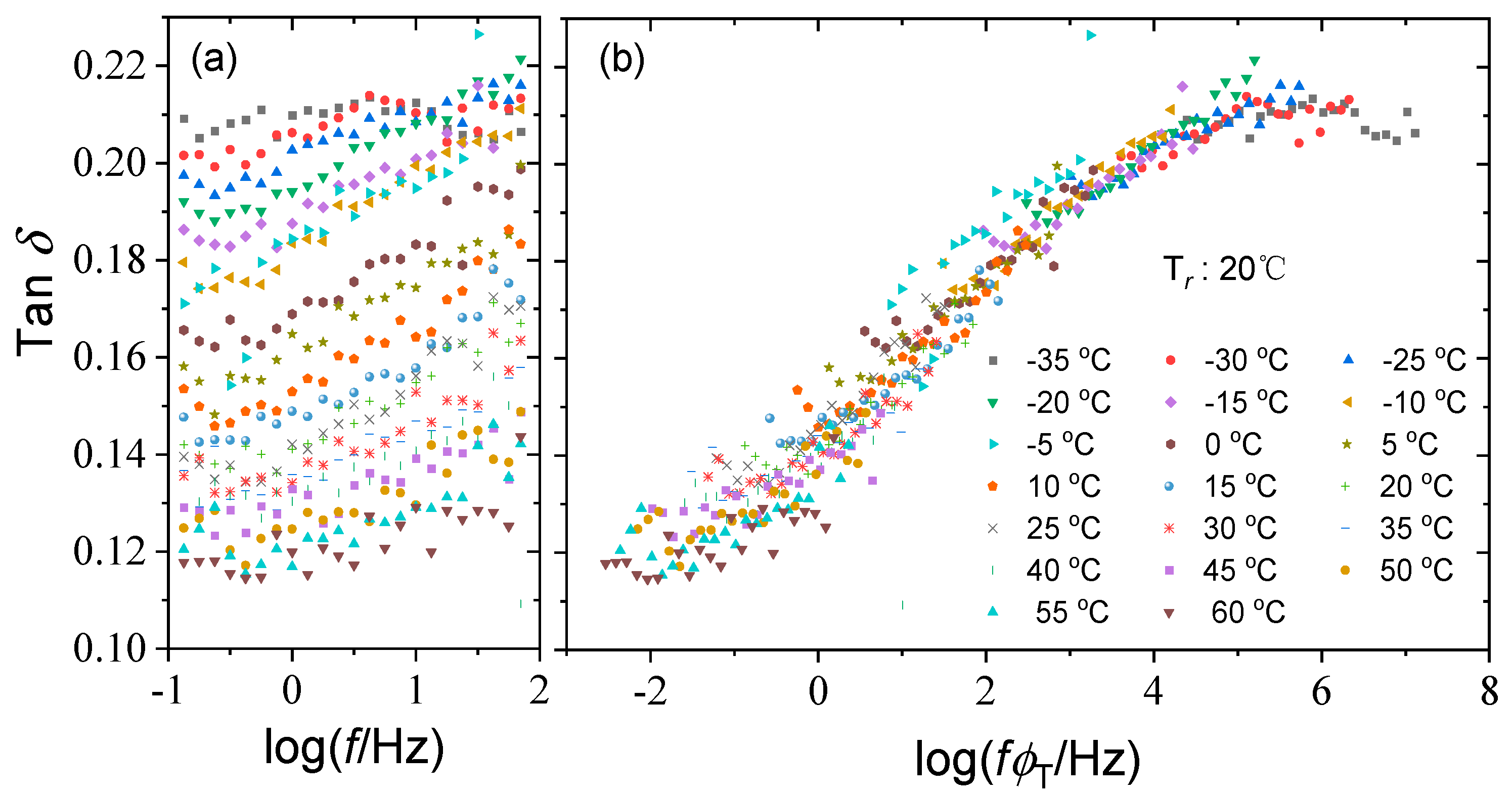
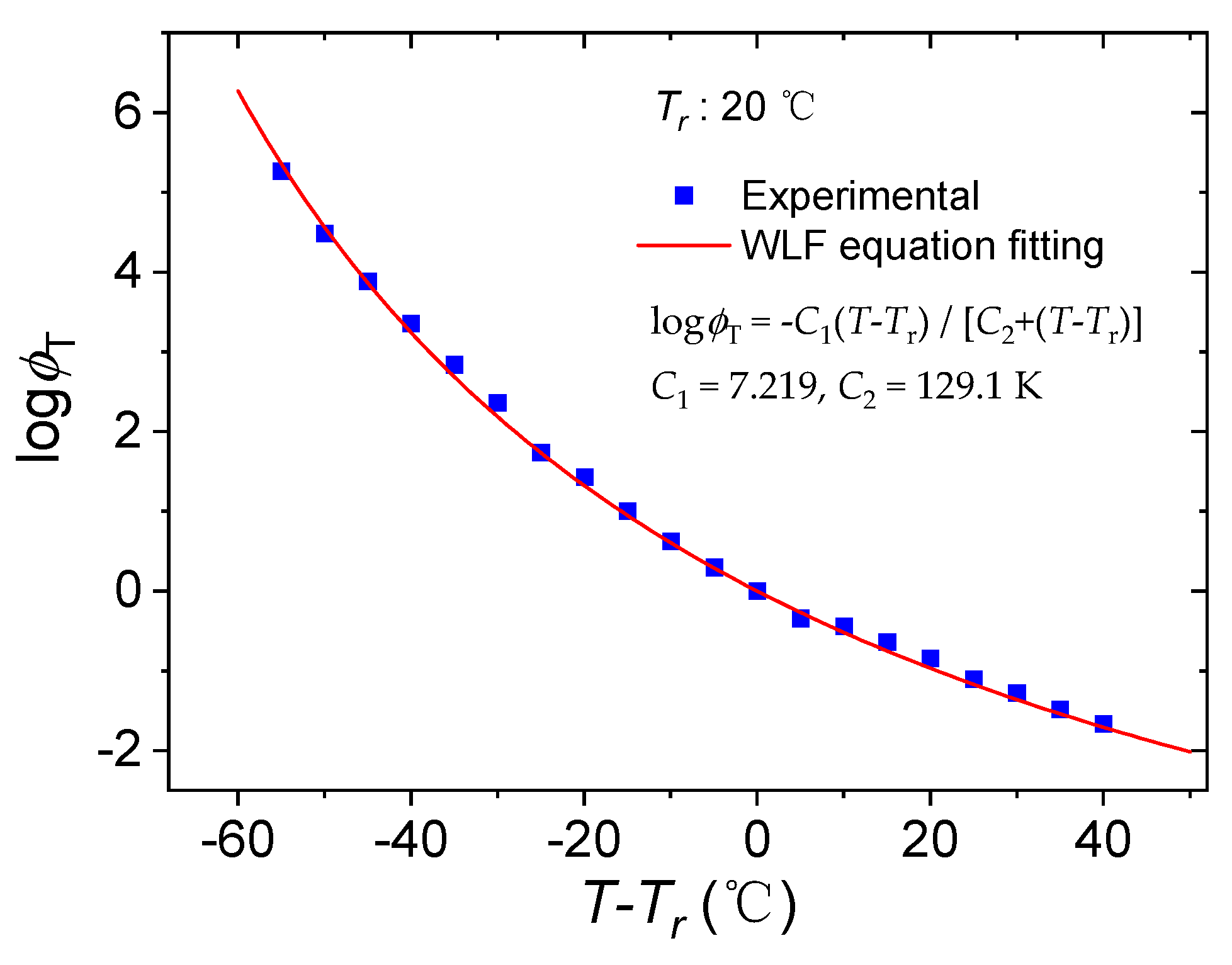
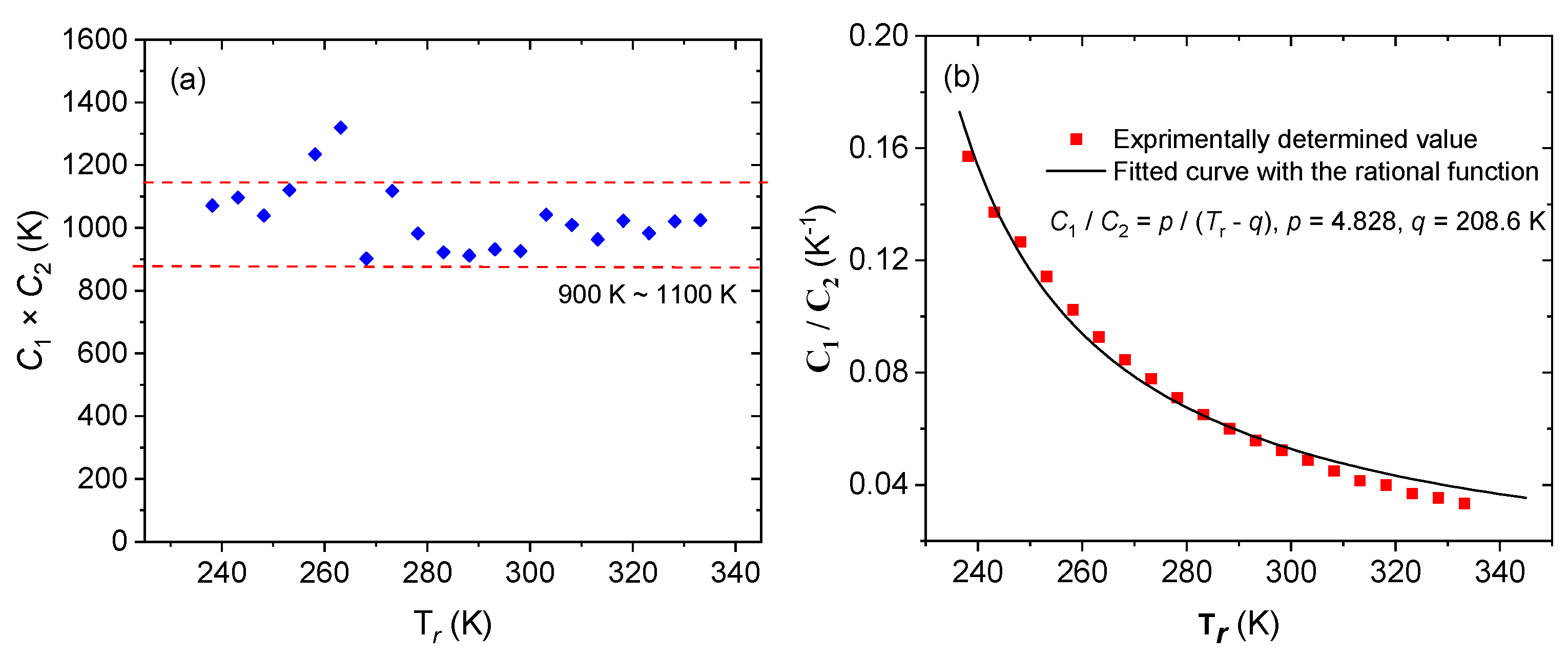



| T/°C | −35 | −30 | −25 | −20 | −15 | −10 | −5 | 0 | 5 | 10 |
| logϕT | 5.27 | 4.48 | 3.89 | 3.35 | 2.84 | 2.36 | 1.74 | 1.43 | 1.00 | 0.63 |
| T/°C | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| logϕT | 0.30 | 0 | −0.34 | −0.44 | −0.64 | −0.84 | −1.11 | −1.28 | −1.49 | −1.66 |
| Tr (K) | C1 | C2 (K) | C1 × C2 (K) | C1/C2 (K−1) | R2 | Tr (K) | C1 | C2 (K) | C1 × C2 (K) | C1/C2 (K−1) | R2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 238.15 | 12.98 | 82.55 | 1071.50 | 0.16 | 0.999 | 288.15 | 7.40 | 123.20 | 912.17 | 0.06 | 0.9984 |
| 243.15 | 12.27 | 89.38 | 1096.70 | 0.14 | 0.9988 | 293.15 | 7.22 | 129.10 | 931.97 | 0.06 | 0.9982 |
| 248.15 | 11.48 | 90.57 | 1039.74 | 0.13 | 0.999 | 298.15 | 6.97 | 132.90 | 926.58 | 0.05 | 0.9957 |
| 253.15 | 11.32 | 98.96 | 1120.23 | 0.11 | 0.9985 | 303.15 | 7.14 | 146.00 | 1042.73 | 0.05 | 0.999 |
| 258.15 | 11.25 | 109.80 | 1235.25 | 0.10 | 0.998 | 308.15 | 6.75 | 149.70 | 1010.03 | 0.05 | 0.9987 |
| 263.15 | 11.07 | 119.20 | 1319.54 | 0.09 | 0.9978 | 313.15 | 6.33 | 152.30 | 963.60 | 0.04 | 0.9985 |
| 268.15 | 8.74 | 103.20 | 902.38 | 0.08 | 0.9986 | 318.15 | 6.40 | 159.90 | 1023.20 | 0.04 | 0.999 |
| 273.15 | 9.34 | 119.80 | 1118.45 | 0.08 | 0.9989 | 323.15 | 6.04 | 162.90 | 983.59 | 0.04 | 0.9989 |
| 278.15 | 8.36 | 117.50 | 982.65 | 0.07 | 0.999 | 328.15 | 6.02 | 169.70 | 1020.92 | 0.04 | 0.999 |
| 283.15 | 7.75 | 119.00 | 922.49 | 0.07 | 0.9986 | 333.15 | 5.86 | 174.90 | 1024.91 | 0.03 | 0.999 |
| Model | E1 (MPa) | E2 (MPa) | E3 (MPa) | α | β | τ (s) | R2 | SD |
|---|---|---|---|---|---|---|---|---|
| FDK | 7.19 | 8.49 | / | 0.15 | / | 1.25 | 0.93 | 0.0079 |
| FDZ | 0.10 | 821.10 | 0.15 | 0.14 | / | 0.57 | 0.94 | 0.0073 |
| iFDZ | 0.65 | 55.21 | 0.22 | 0.16 | 0.66 | 179.70 | 0.97 | 0.0053 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhu, D.; Lin, J.; Zhang, Y. Temperature and Frequency Dependence of the Dynamic Viscoelastic Properties of Silicone Rubber. Polymers 2023, 15, 3005. https://doi.org/10.3390/polym15143005
Liu X, Zhu D, Lin J, Zhang Y. Temperature and Frequency Dependence of the Dynamic Viscoelastic Properties of Silicone Rubber. Polymers. 2023; 15(14):3005. https://doi.org/10.3390/polym15143005
Chicago/Turabian StyleLiu, Xiu, Dingxiang Zhu, Jianguo Lin, and Yongjun Zhang. 2023. "Temperature and Frequency Dependence of the Dynamic Viscoelastic Properties of Silicone Rubber" Polymers 15, no. 14: 3005. https://doi.org/10.3390/polym15143005





