Effect of Long-Term Thermal Relaxation of Epoxy Binder on Thermoelasticity of Fiberglass Plastics: Multiscale Modeling and Experiments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
- Epoxy resin KER 828, with the following main characteristics: Epoxy Group Content (EGC) 5308 mmol/kg, Epoxide Equivalent Weight (EEW) 188.5 g/eq, viscosity at 25 °C 12.7 Pa·s, HCl 116 mg/kg, and total chlorine 1011 mg/kg. Manufacturer: KUMHO P&B Chemicals, Gwangju, South Korea.
- Hardener for epoxy resin methyl tetrahydrophthalic anhydride with the following main characteristics: viscosity at 25 °C 63 Pa·s, anhydride content 42.4%, volatile fraction content 0.55%, and free acid 0.1%. Manufacturer: ASAMBLY Chemicals company Ltd., Nanjing, China.
- Alkophen (epoxy resin curing accelerator) with the following main characteristics: viscosity at 25 °C 150 Pa·s, molecular formula C15H27N3O, molecular weight 265, and amine value 600 mg KOH/g. Manufacturer: Epital JSC, Moscow, Russian Federation.
- -
- Thickness 0.190 + 0.01/−0.02 mm;
- -
- Surface density 200 + 16/−10 g/m2;
- -
- Number of yarns per 1 cm of fabric on the basis 12 +/− 1;
- -
- Number of yarns per 1 cm of fabric on the weft 8 +/− 1;
- -
- Weave—plain;
- -
- Oiling agent—paraffin emulsion.
- -
- Thickness, 0.27 + 0.01/−0.02 mm;
- -
- Surface density, 260 + 25/−25 g/m2;
- -
- Number of yarns per 1 cm of fabric on the basis 12 +/− 1;
- -
- Number of yarns per 1 cm of fabric on the weft 8 +/− 1;
- -
- Weave—plain;
- -
- Oiling agent—aminosilane.
2.2. Methods
2.2.1. Long Heat Treatment
2.2.2. Investigation of Elasticity Modulus under Heating
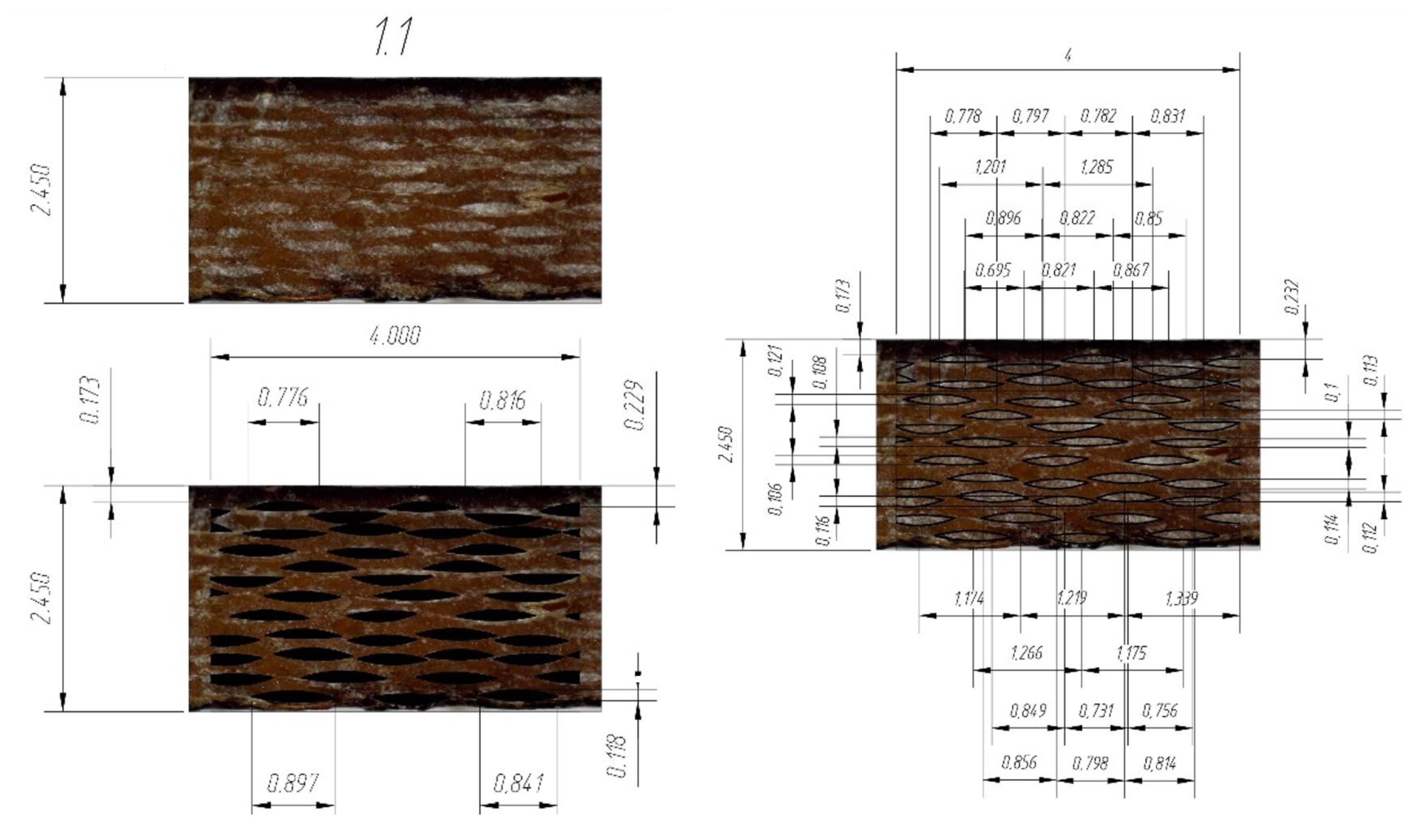
2.2.3. Prediction of the Deformation Characteristics of FRP
- -
- The fiber composite being modeled consists of isotropic linear-elastic matrix material and isotropic or transversally isotropic linear-elastic filament material;
- -
- The volume fraction of fibers in the filaments is constant;
- -
- The representative volume of the material is strictly periodic.
- -
- The following parameters are set as the initial data for the woven composite model:
- -
- Weaving type—a type of fabric weaving (plain or twill);
- -
- Fiber volume fraction—share of fiber volume in the volume of the whole RVE;
- -
- Yarn fiber volume fraction is the fraction of volume in a separate thread, which is taken up by the fiber material (glass in our case), the volume of the yarn “net”;
- -
- Shear angle—the angle in degrees of warping the fibers due to drape properties of the fabric;
- -
- Yarn spacing—the distance between the centers of cross-sections of neighboring yarns;
- -
- Fabric thickness—thickness of the modeled RVE;
- -
- Repeat count—number of elementary cells considered in the model in the direction of each coordinate;
- -
- Align with x-direction—the fibers are oriented along the x-axis (if not, they are oriented at a 45° angle to the x-axis).
3. Results
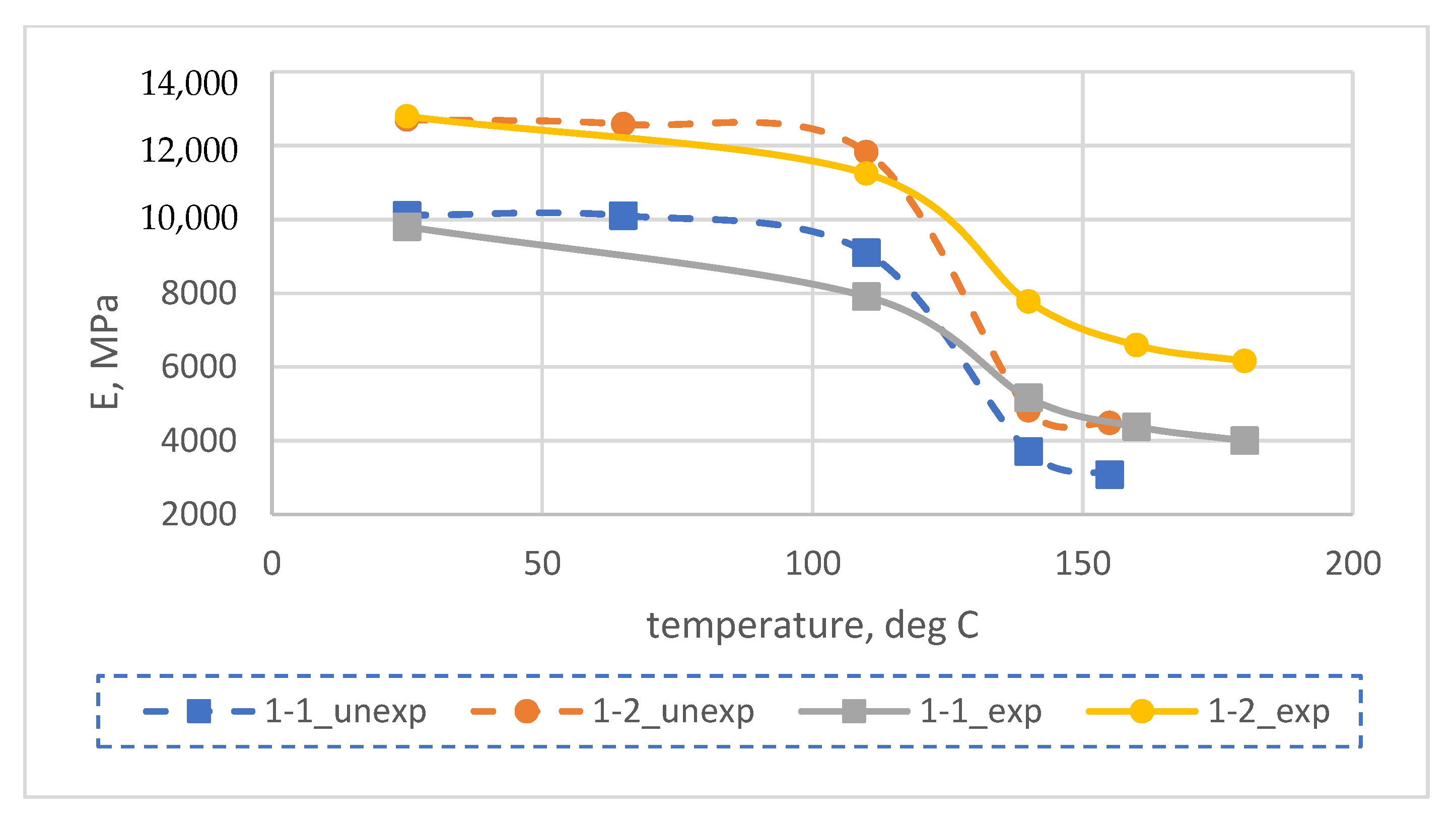
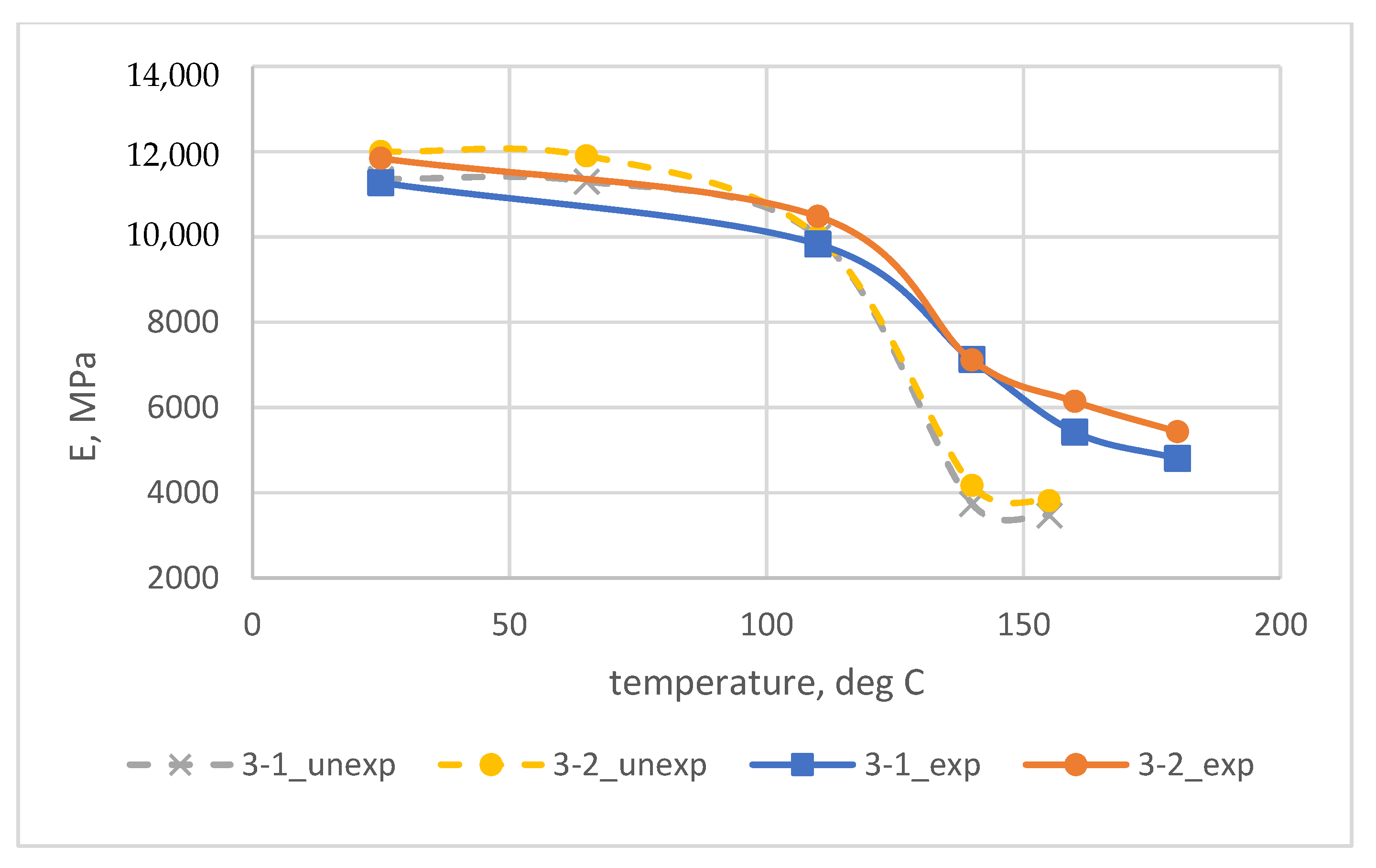
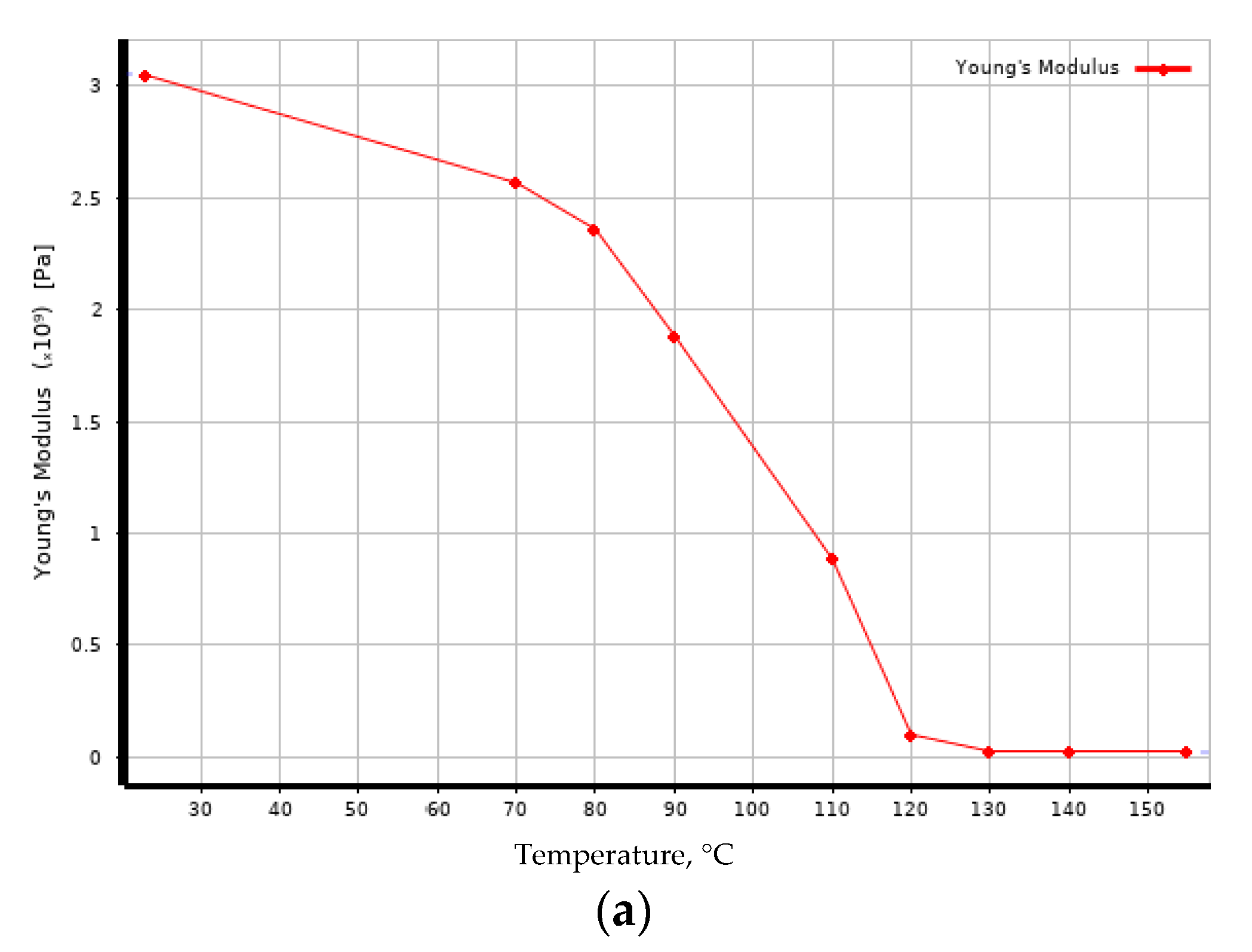
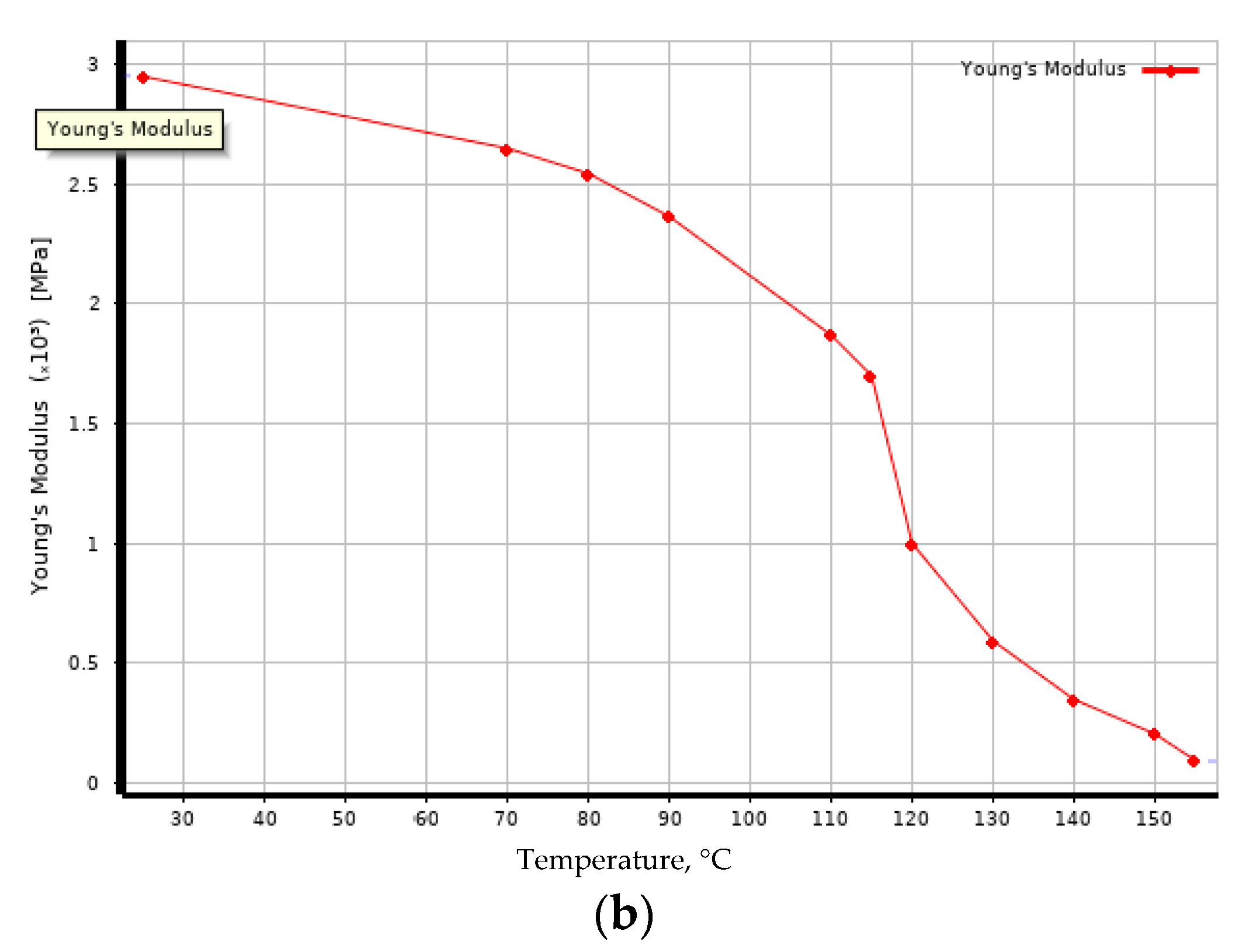
3.1. Experimental Results
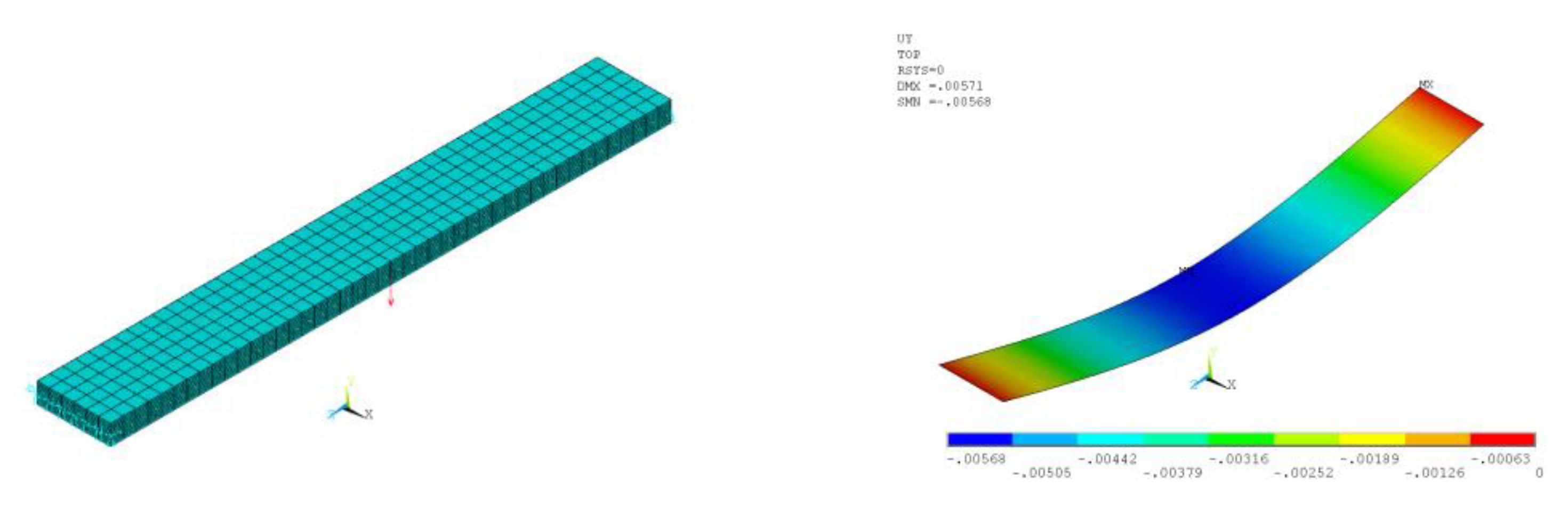
3.2. Prediction of the Thermomechanical Characteristics of Fiberglass Plastics Using the Finite Element Method
- -
- -
- Stage 2—the refinement of the elastic modulus of the multilayer composite using three-point bend modeling (for example, in the ANSYS APDL module), considering the polymer matrix interlayers between the reinforced monolayers.
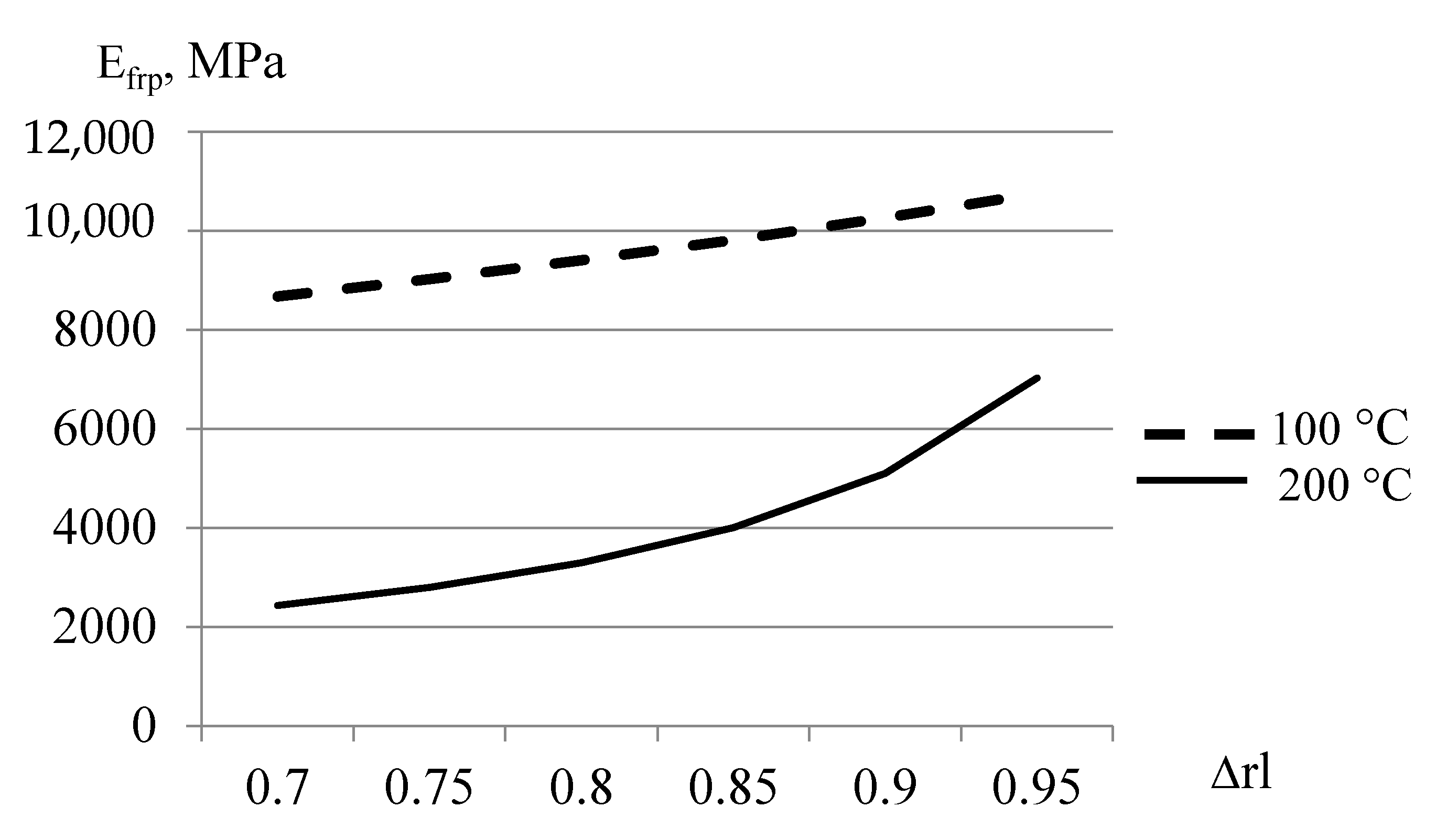
3.3. Predicting Properties Using the Entropy Approach
4. Discussion
5. Conclusions
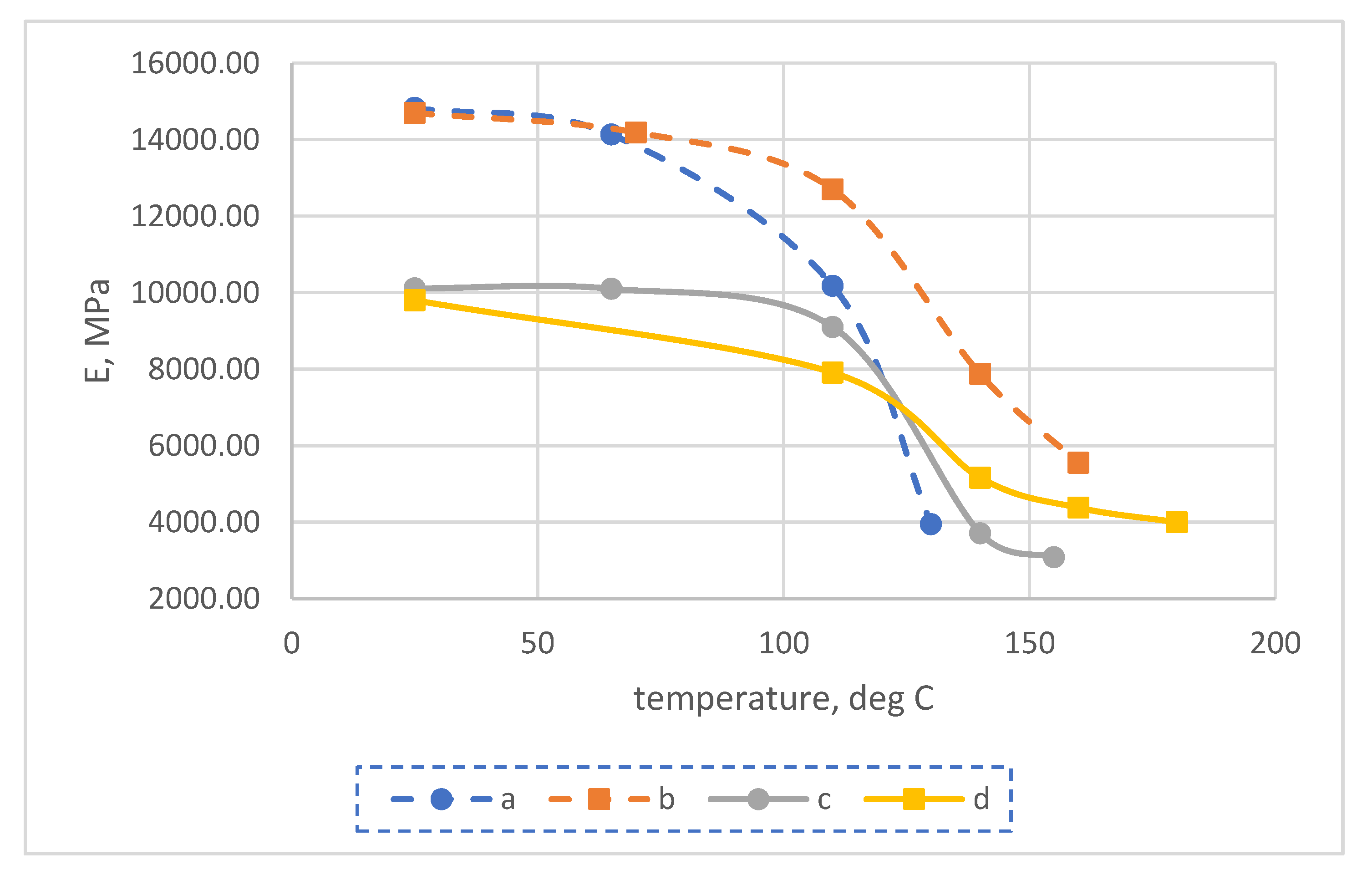
- After a prolonged exposure of the fiberglass samples (504 h in total) at temperatures higher than the initial glass transition temperature of the polymer–binder matrix, the flexural modulus at temperatures above 100 to 110 °C significantly increased (up to 1.6 times for samples on the EZ-200 fabric, up to 1.9 times for samples on the T-23 fabric), at lower temperatures the flexural modulus either did not change or decreased slightly.
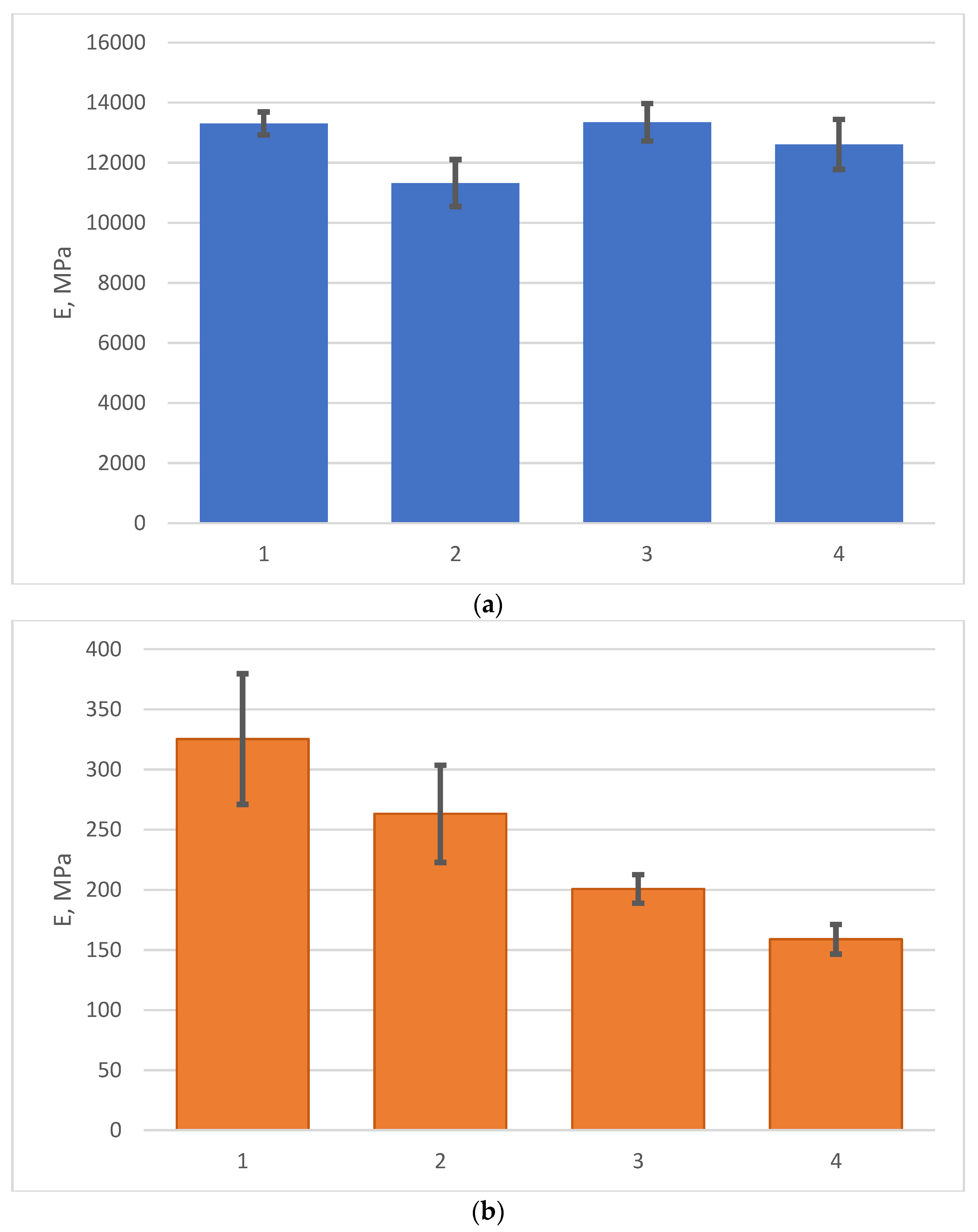
- The bending strength after curing decreased by about 16% in the samples on the EZ-200 fabric and by 8% in the samples on the T-23 fabric.
- The entropy value of fiberglass plastic was up to two times lower than that of unreinforced polymer, indicating that the composite structure was much more ordered. After thermal relaxation, the entropy level decreased by another 20% and leveled out for both types of FRP (on different types of glass fabrics). Therefore, the difference between the elastic properties of fiberglass composites on different fabrics may be related to their somewhat different fiber–matrix bonding properties.
- The calculated values of the modulus of elasticity at room temperature showed the best coincidence with the experiment (almost complete coincidence), while at elevated temperatures, the experimental values of the modulus of elasticity were higher than the predicted ones, which, on the one hand, requires additional research to clarify the reason for the difference, and on the other hand, from the standpoint of reliability for solving practical problems, it is better than overestimation, since it goes into the reliability reserve.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Plecnik, J.M.; Gerwein, P.H.; Pham, M.G. Design and Construction of World’s Tallest Free-Standing Fiberglass Stack; Civil Engineering—American Society of Civil Engineers: New York, NY, USA, 1981; Volume 51, pp. 57–59. [Google Scholar]
- O’Keefe, W. FRP Widens Use in Energy Systems. Power 1976, 120, 79–81. [Google Scholar]
- Honga, S.J.; Honga, S.H.; Doh, J.M. Materials for flue gas desulfurization systems operating in Korea and their failures. Mater. High Temp. 2007, 24, 289–293. [Google Scholar] [CrossRef]
- Astashkin, V.M.; Zholudov, V.S. Chimneys and Elements of Gas-Escape Paths Made of Polymer Composites; Гyceв Б.B.: Moscow, Russia, 2011; pp. 1–155. [Google Scholar]
- Yang, Y.; Xian, G.; Li, H.; Sui, L. Thermal aging of an anhydride-cured epoxy resin. Polym. Degrad. Stab. 2015, 118, 111–119. [Google Scholar] [CrossRef]
- Li, K.; Wang, K.; Zhan, M.S.; Wen, X. The change of thermal-mechanical properties and chemical structure of ambient cured DGEBA/TEPA under accelerated thermo-oxidative aging. Polym. Degrad. Stab. 2013, 98, 2340–2346. [Google Scholar] [CrossRef]
- Korolev, A.; Mishnev, M.; Vatin, N.I.; Ignatova, A. Prolonged Thermal Relaxation of the Thermosetting Polymers. Polymers 2021, 13, 4104. [Google Scholar] [CrossRef] [PubMed]
- Korolev, A.; Mishnev, M.; Zherebtsov, D.; Vatin, N.I.; Karelina, M. Polymers under Load and Heating Deformability: Modelling and Predicting. Polymers 2021, 13, 428. [Google Scholar] [CrossRef] [PubMed]
- Arzhakov, M. Relaxation in Physical and Mechanical Behavior of Polymers; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- García-Moreno, I.; Caminero, M.Á.; Rodríguez, G.P.; López-Cela, J.J. Effect of Thermal Ageing on the Impact and Flexural Damage Behaviour of Carbon Fibre-Reinforced Epoxy Laminates. Polymers 2019, 11, 80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Daghia, F.; Zhang, F.; Cluzel, C.; Ladeveze, P. Thermo-mechano-oxidative behavior at the ply’s scale: The effect of oxidation on transverse cracking in carbon-epoxy composites. Compos. Struct. 2015, 134, 602–612. [Google Scholar] [CrossRef]
- Martin, R. Ageing of Composites; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Kouznetsova, V.G.; Geers, M.G.D.; Brekelmans, W.A.M. Multi-scale second-order computational homogenization of multi-phase materials: A nested finite element solution strategy. Comput. Methods Appl. Mech. Eng. 2004, 193, 5525–5550. [Google Scholar] [CrossRef]
- Geers, M.G.D.; Kouznetsova, V.G.; Brekelmans, W.A.M. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
- Li, S. Boundary conditions for unit cells from periodic microstructures and their implications. Compos. Sci. Technol. 2008, 68, 1962–1974. [Google Scholar] [CrossRef]
- Bezmelnitsyn, A.V.; Sapozhnikov, S.B. Multiscale Modeling and Formation Analysis of Technological Interlaminar Stresses in Thick-Walled GFRP Rings. Perm Natl. Res. Polytech. Univ. Mech. Bull. 2017, 2, 5–22. [Google Scholar]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar]
- Pelissou, C.; Baccou, J.; Monerie, Y.; Perales, F. Determination of the size of the representative volume element for random quasi-brittle composites. Int. J. Solids Struct. 2009, 46, 2842–2855. [Google Scholar]
- Hesseler, S.; Stapleton, S.E.; Yakovlev, V.; Appel, L.; Gries, T. Micro-scale model for a multi-scale modeling approach of thermoplastic fiber reinforced polymers. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 406, p. 012049. [Google Scholar] [CrossRef]
- Rayhan, S.B.; Rahman, M.M. Modeling elastic properties of unidirectional composite materials using ansys material designer. Procedia Struct. Integr. 2020, 28, 1892–1900. [Google Scholar] [CrossRef]
- GOST 19907-83; Dielectric Fabrics Made of Glass. Twister Complex Threads. Specifications. Ministry of Chemical Industry. USSR: Moscow, Russia, 1982.
- GOST 19170-2001; Fibre Glass. Constructive Woven Fabrics. Specifications. Ministry of Chemical Industry: Moscow, Russia, 2002.
- GOST RF 56810-2015; Polymer Composites. Test Method for Flexural Flat Samples. Standardinform: Moscow, Russia, 2016.
- Ansys. Material Designer Users Guide. Theory Documentation [Electronic Resource]. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v212/en/acp_md/acp_md_theory.html (accessed on 17 April 2022).
- Li, S.; Jeanmeure, L.; Pan, Q. A composite material characterisation tool: UnitCells. J. Eng. Math. 2015, 95, 279–293. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Mechanical APDL Theory Reference; ANSYS Inc.: Canonsburg, PA, USA, 2013; Volume 15. [Google Scholar]
- Mishnev, M.V.; Zadorin, A.A.; Khoroshilov, N.A. Prediction of elastic characteristics of fiber-reinforced plastic in bending: Multi-scale finite element modeling and experiment. Constr. Unique Build. Struct. 2021, 5, 9801. [Google Scholar] [CrossRef]







| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|
| Description of FRP | Type No | Specimen No | b, mm | h, mm | E, MPa | σ, MPa | Eav, MPa | σav, MPa | Eunexp/Eexp * | σunexp/σexp * |
| Epoxy FRP on EZ-200 unexposed | 1 | 10 | 17.35 | 2.3 | 13.827 | 286 | 13,307/381 (2.86%) | 325/54 (16.7%) | 1.18 | 1.24 |
| 1 | 11 | 18.8 | 2.4 | 13.281 | 374 | |||||
| 1 | 12 | 16.55 | 2.35 | 13.380 | 270 | |||||
| 1 | 13 | 16.85 | 2.55 | 12.650 | 374 | |||||
| 1 | 14 | 18.1 | 2.35 | 13.270 | 272 | |||||
| 1 | 15 | 17.15 | 2.5 | 13.435 | 376 | |||||
| Epoxy FRP on EZ-200 exposed | 1 | 4 | 17.75 | 2.45 | 12.100 | 304 | 11,323/781 (6.90%) | 263/40.4 (15.35%) | ||
| 1 | 5 | 18.5 | 2.9 | 10.150 | 254 | |||||
| 1 | 6 | 17.6 | 2.6 | 10.700 | 278 | |||||
| 1 | 7 | 18 | 2.45 | 12.100 | 216 | |||||
| 1 | 8 | 16.85 | 2.55 | 11.610 | 308 | |||||
| 1 | 9 | 17.65 | 2.7 | 11.280 | 219 | |||||
| Epoxy FRP on T-23 unexposed | 3 | 9 | 17.6 | 2.45 | 13.540 | 205 | 13,348/622 (4.66%) | 201/11.9 (5.92%) | 1.06 | 1.26 |
| 3 | 10 | 17.7 | 2.25 | 13.160 | 186 | |||||
| 3 | 11 | 17.55 | 2.2 | 13.590 | 196 | |||||
| 3 | 12 | 16.9 | 2.45 | 12.240 | 193 | |||||
| 3 | 13 | 17.7 | 2.2 | 14.100 | 220 | |||||
| 3 | 14 | 18.65 | 2.35 | 13.460 | 205 | |||||
| Epoxy FRP on T-23 exposed | 3 | 2 | 16.35 | 2.5 | 11.600 | 146.4 | 12,612/831 (6.59%) | 159/12.4 (7.77%) | ||
| 3 | 4 | 18.6 | 2.45 | 11.790 | 147 | |||||
| 3 | 5 | 18.6 | 2.45 | 12.480 | 150 | |||||
| 3 | 6 | 17.5 | 2.3 | 13.720 | 170 | |||||
| 3 | 7 | 17.75 | 2.35 | 13.310 | 172.3 | |||||
| 3 | 8 | 18.45 | 2.45 | 12.770 | 168 |
| Description of FRP | Type No | Average Density Unexposed, kg/m3 | Average Density Exposed, kg/m3 | Average Density Change | Average Mass Change |
|---|---|---|---|---|---|
| Epoxy FRP on EZ-200 | 1 | 1607.7 | 1672.2 | 4.01% | −0.983% |
| Epoxy FRP on T-23 | 3 | 1803.7 | 1841.0 | 2.07% | −1.175% |
| Composition | Temperature, °C | Efact, MPa | S, J/J | Ecalc, MPa | % Deviation | |
|---|---|---|---|---|---|---|
| EP + EZ-200 before thermal relaxation | 25 | 11.405 | 2.4 | 1.000 | - | - |
| 65 | 11.340 | 0.698 | 10.131 | −10.7 | ||
| 110 | 10.460 | 0.398 | 7925 | −24.2 | ||
| 140 | 4265 | 0.217 | 5568 | 30.6 | ||
| 160 | 3780 | 0.103 | 3241 | −14.3 | ||
| EP + EZ-200 after thermal relaxation | 25 | 11.295 | 2.0 | 1.000 | - | |
| 110 | 9575 | 0.498 | 8741 | −8.7 | ||
| 140 | 6465 | 0.347 | 7311 | 13.1 | ||
| 160 | 5485 | 0.253 | 6081 | 10.9 | ||
| 180 | 5080 | 0.162 | 4526 | 10.9 | ||
| 200 | n/a | 0.076 | 2496 | - |
| Composition | Temperature, °C | Efact, MPa | S, J/J | Ecalc, MPa | % Deviation | |
|---|---|---|---|---|---|---|
| EP + T-23 before thermal relaxation | 25 | 11.680 | 2.42 | 1 | - | - |
| 65 | 11.600 | 0.695 | 10.362 | −10.7 | ||
| 110 | 10.000 | 0.393 | 8063 | −19.4 | ||
| 140 | 3955 | 0.210 | 5589 | 41.3 | ||
| 160 | 3640 | 0.096 | 3124 | −14.2 | ||
| EP + T-23 after thermal relaxation | 25 | 11.555 | 2.0 | 1 | - | - |
| 110 | 10.155 | 0.498 | 8942 | −11.9 | ||
| 140 | 7115 | 0.347 | 7479 | 5.1 | ||
| 160 | 5780 | 0.253 | 6221 | 7.6 | ||
| 180 | 5115 | 0.162 | 4630 | −9.5 | ||
| 200 | n/a | 0.076 | 2553 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishnev, M.; Korolev, A.; Ekaterina, B.; Dmitrii, U. Effect of Long-Term Thermal Relaxation of Epoxy Binder on Thermoelasticity of Fiberglass Plastics: Multiscale Modeling and Experiments. Polymers 2022, 14, 1712. https://doi.org/10.3390/polym14091712
Mishnev M, Korolev A, Ekaterina B, Dmitrii U. Effect of Long-Term Thermal Relaxation of Epoxy Binder on Thermoelasticity of Fiberglass Plastics: Multiscale Modeling and Experiments. Polymers. 2022; 14(9):1712. https://doi.org/10.3390/polym14091712
Chicago/Turabian StyleMishnev, Maxim, Alexander Korolev, Bartashevich Ekaterina, and Ulrikh Dmitrii. 2022. "Effect of Long-Term Thermal Relaxation of Epoxy Binder on Thermoelasticity of Fiberglass Plastics: Multiscale Modeling and Experiments" Polymers 14, no. 9: 1712. https://doi.org/10.3390/polym14091712
APA StyleMishnev, M., Korolev, A., Ekaterina, B., & Dmitrii, U. (2022). Effect of Long-Term Thermal Relaxation of Epoxy Binder on Thermoelasticity of Fiberglass Plastics: Multiscale Modeling and Experiments. Polymers, 14(9), 1712. https://doi.org/10.3390/polym14091712








