Filler Effects on H2 Diffusion Behavior in Nitrile Butadiene Rubber Blended with Carbon Black and Silica Fillers of Different Concentrations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Composition
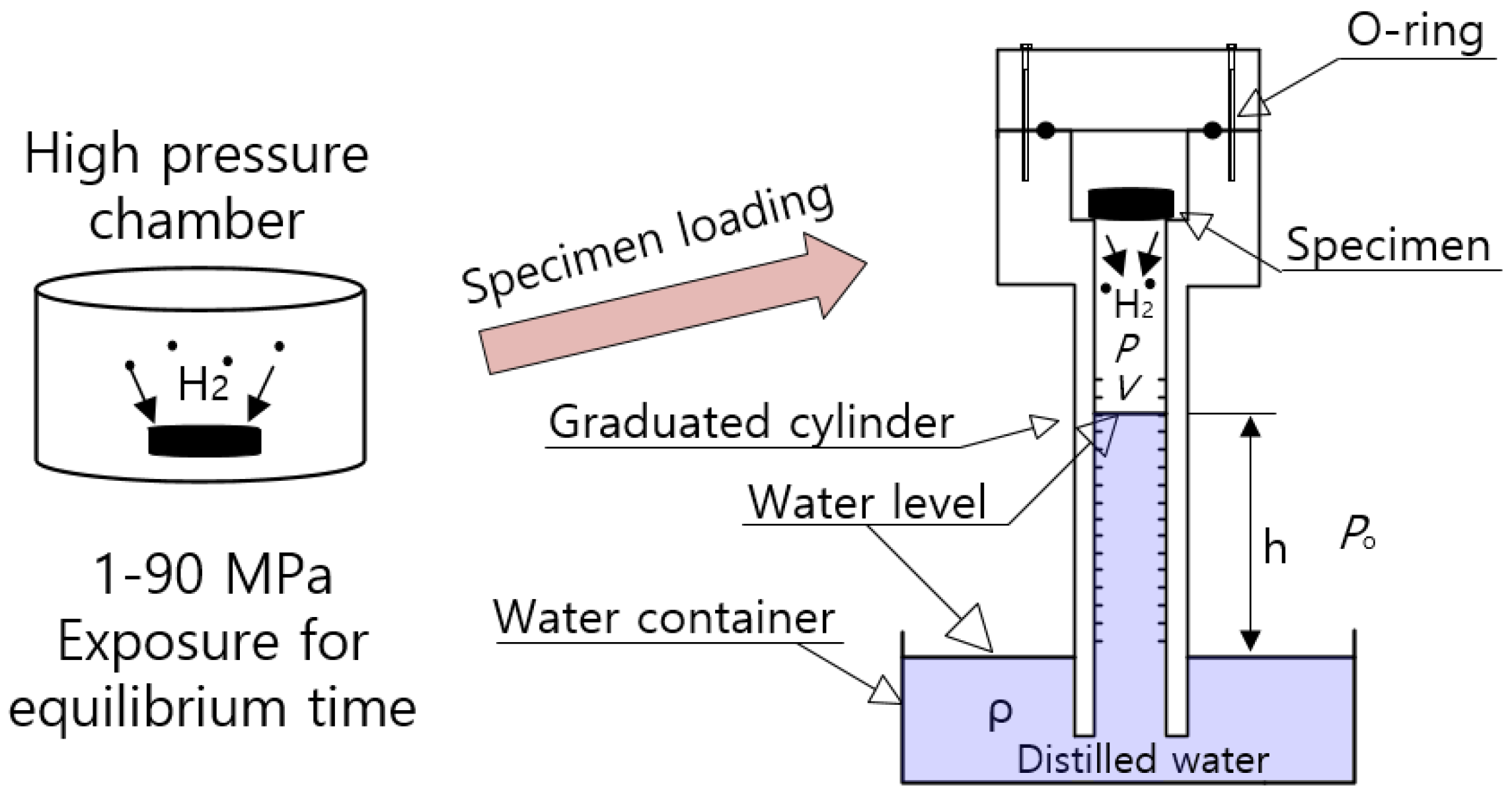
2.2. Exposure Condition to Hydrogen
3. Measurement Method and Data Analysis
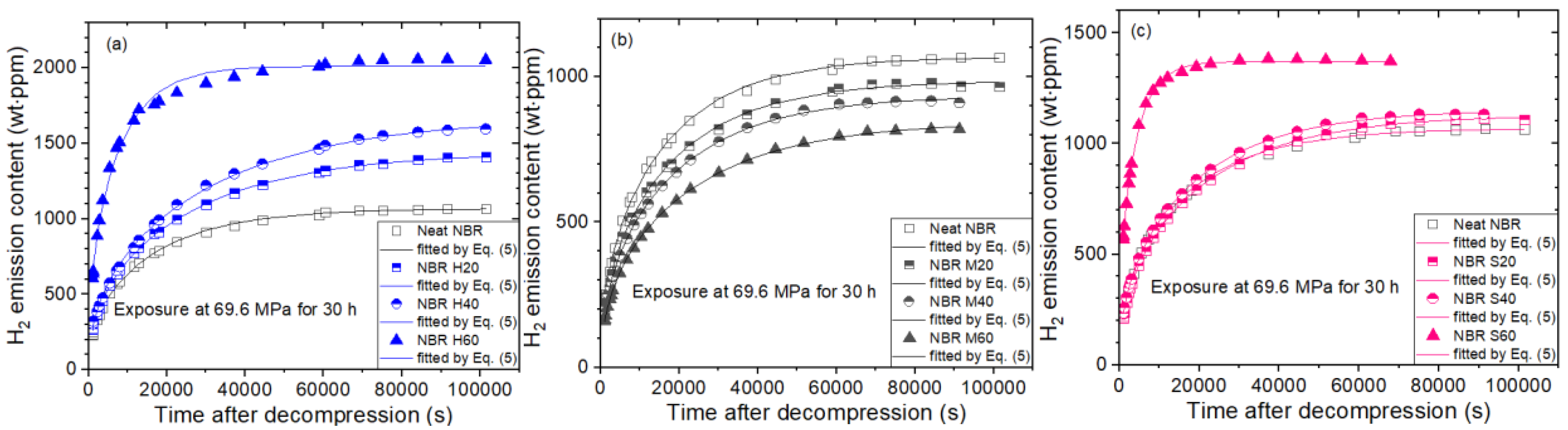
3.1. Volumetric Measurement of Emitted Hydrogen
3.2. Diffusion Analysis Program
4. Results and Discussion
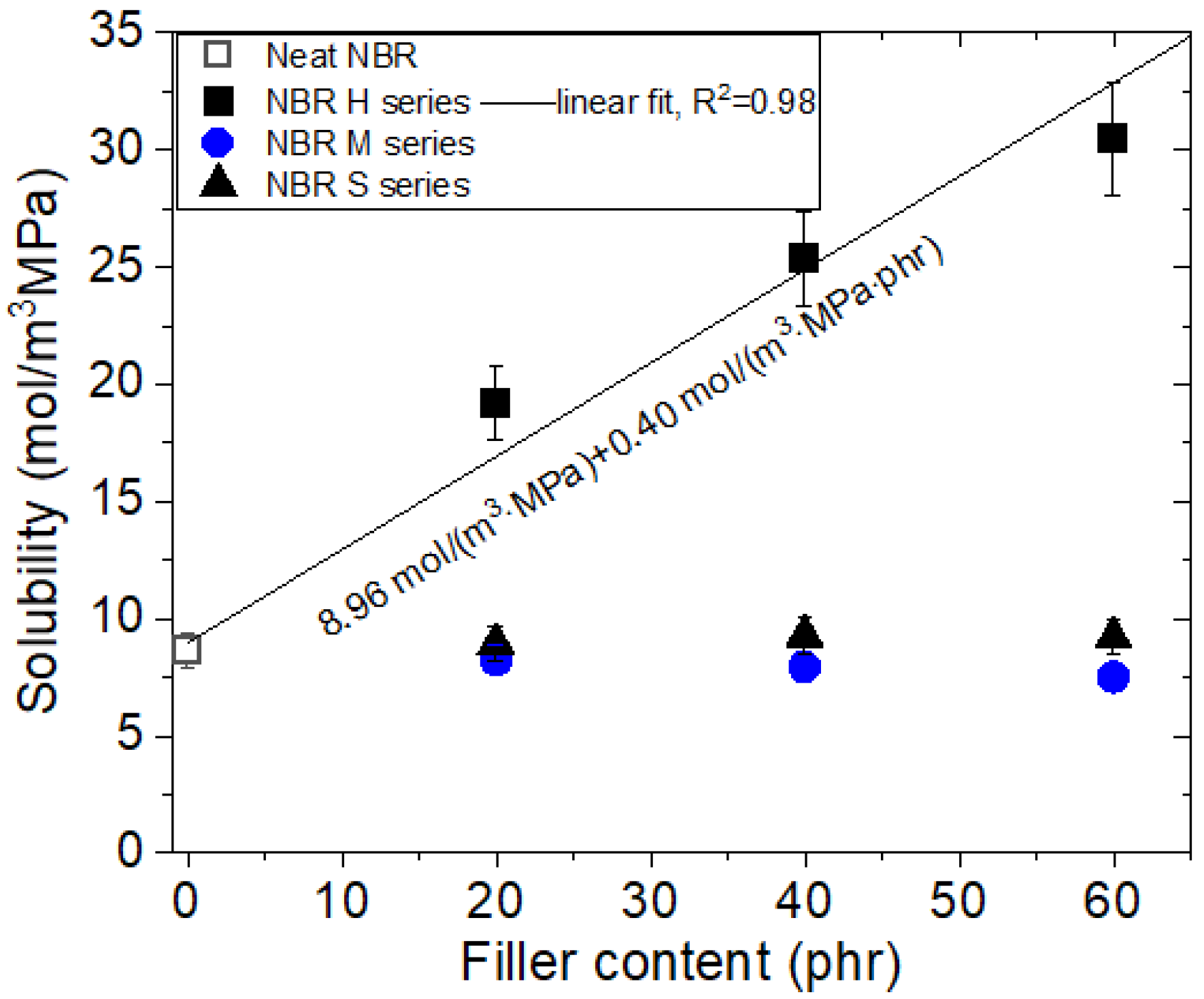
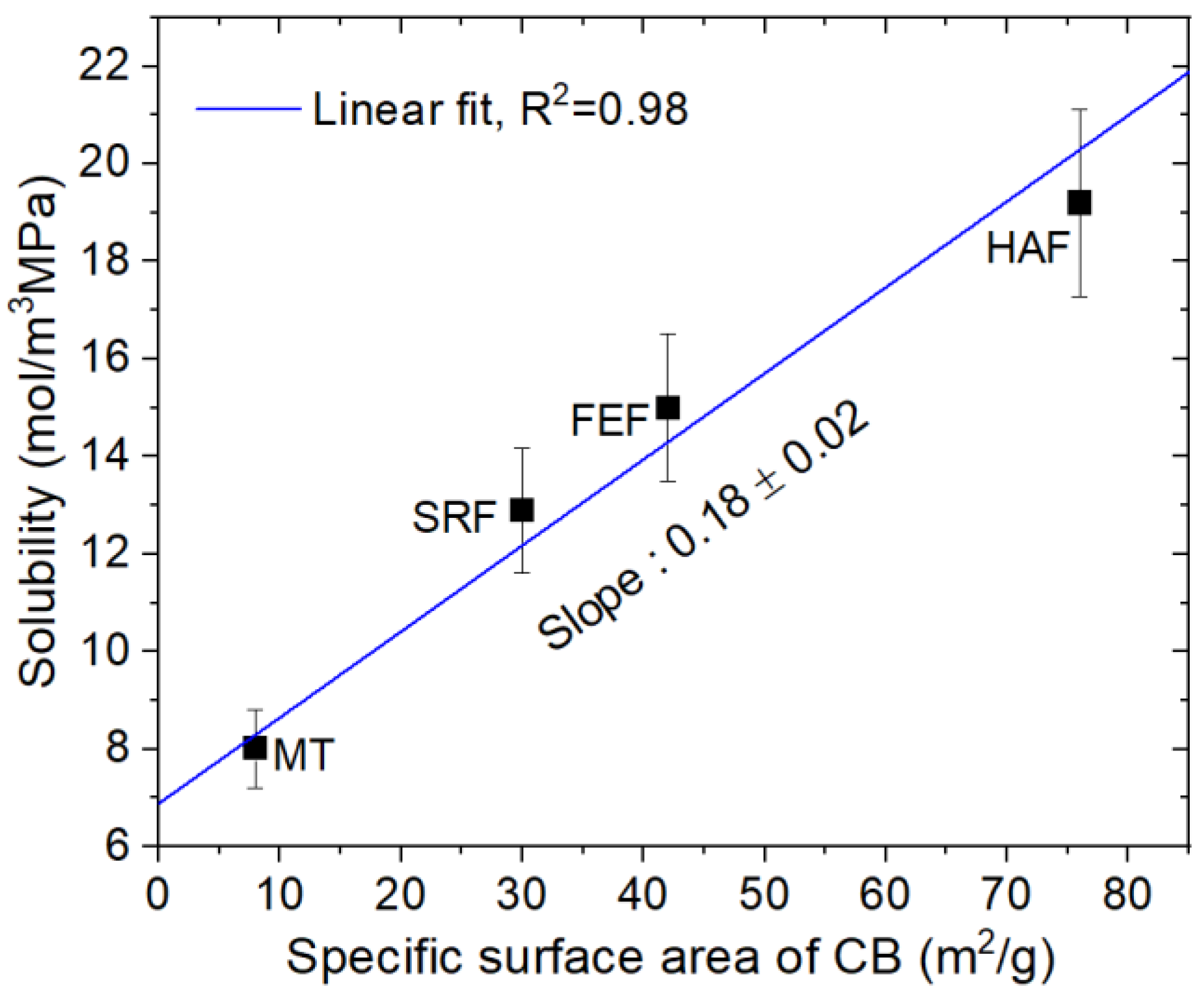
4.1. Filler Effect on Pressure-Dependent H2 Solubility
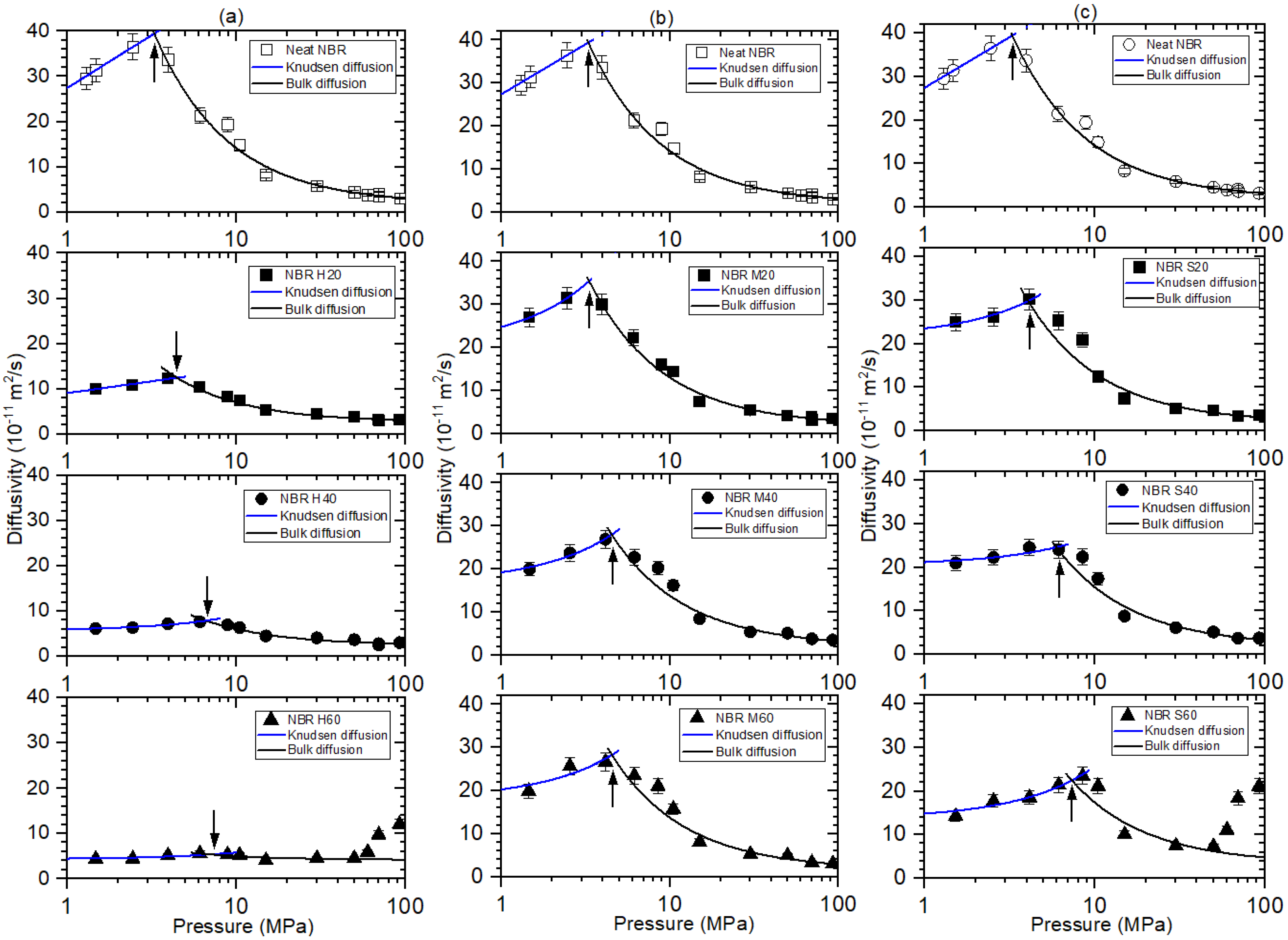
4.2. Filler Effect on Pressure-Dependent H2 Diffusivity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khawaja, M.; Sutton, A.P.; Mostofi, A.A. Molecular simulation of gas solubility in nitrile butadiene rubber. J. Phys. Chem. B 2017, 121, 287–297. [Google Scholar] [CrossRef] [Green Version]
- Fujiwara, H. Analysis of acrylonitrile butadiene rubber (NBR) expanded with penetrated hydrogen due to high pressure hydrogen exposure. Int. Polym. Sci. Technol. 2017, 44, 41–48. [Google Scholar] [CrossRef] [Green Version]
- Trelleborg Sealing Solutions. O-Rings and Back-Up Rings; Trelleborg Sealing Solutions: Trelleborg, Sweden, 2012. [Google Scholar]
- Hertz, D.L.; Bussem, H.; Ray, T.W. Nitrile rubber—Past, present and future. In Presented at a Meeting of the Rubber Division, American Chemical Society; American Chemical Society: Pittsburgh, PA, USA, 1994; pp. 1–19. [Google Scholar]
- Nanda, M.; Chaudhary, R.N.P.; Tripathy, D.K. Dielectric relaxation of conductive carbon black reinforced chlorosulfonated polyethylene vulcanizates. Polym. Compos. 2010, 31, 152–162. [Google Scholar] [CrossRef]
- Das, N.C.; Chaki, T.K.; Khastgir, D.; Chakraborty, A. Electrical and mechanical properties of conductive carbon black filled EVA, EPDM and their blends. Kautsch. Gummi Kunstst. 2002, 55, 300–306. [Google Scholar] [CrossRef]
- Karsek, L.; Sumita, M. Characterization of dispersion state of filler and polymer-filler interactions in rubber-carbon black composites. J. Mater. Sci. 1996, 31, 281–289. [Google Scholar] [CrossRef]
- Liu, J.S.; Wu, S.P.; Chen, M.Z.; Mi, Y.X. The effect of filler on the properties of silicone rubber. Mater. Sci. Forum 2009, 620–622, 311–314. [Google Scholar] [CrossRef]
- Zeng, W.; Chen, S.G.; Zhao, B.; Rong, M.Z.; Zhang, M.Q. Gas sensing conductive polymer nanocomposites filled with carbon black nanoparticles. In Physical Properties and Applications of Polymer Nanocomposites; Tjong, S.C., Mai, Y.W., Eds.; Woodhead Publishing: Sawston, UK, 2010; pp. 690–722. [Google Scholar]
- Stöckelhuber, K.W.; Svistkov, A.S.; Pelevin, A.G.; Heinrich, G. Impact of filler surface modification on large scale mechanics of styrene butadiene/silica rubber composites. Macromolecules 2011, 44, 4366–4381. [Google Scholar] [CrossRef]
- Meier, J.G.; Mani, J.W.; Klüppel, M. Analysis of carbon black networking in elastomers by dielectric spectroscopy. Phys. Rev. B 2007, 75, 054202. [Google Scholar] [CrossRef]
- Rattanasom, N.; Saowapark, T.; Deeprasertkul, C. Reinforcement of natural rubber with silica/carbon black hybrid filler. Polym. Test. 2007, 26, 369–377. [Google Scholar] [CrossRef]
- Hashim, A.S.; Azahari, B.; Ikeda, Y.; Kohjiya, S. The effect of Bis(3-Triethoxysilylpropyl) tetrasulfide on silica reinforcement of styrene-butadiene rubber. Rubber Chem. Technol. 1998, 71, 289–299. [Google Scholar] [CrossRef]
- Brinke, J.W.T.; Debnath, S.C.; Reuvekamp, L.A.E.M.; Noordermeer, J.W.M. Mechanistic aspects of the role of coupling agents in silica–rubber composites. Compos. Sci. Technol. 2003, 63, 1165–1174. [Google Scholar] [CrossRef]
- Gatos, K.G.; Karger-Kocsis, J. Effect of the aspect ratio of silicate platelets on the mechanical and barrier properties of hydrogenated acrylonitrile butadiene rubber (HNBR)/layered silicate nanocomposites. Eur. Polym. J. 2007, 43, 1097–1104. [Google Scholar] [CrossRef]
- Hussain, A.I.; Abadir, I.F.; El Marsafy, S.M. Effect of inorganic additives on some properties of NBR vulcanizates. Pigment Resin Technol. 2010, 39, 84–88. [Google Scholar] [CrossRef]
- Hanna, J.M.; Martin, G.T.; Marco, M.; Francesco, P.L.M.; Ange, N.; Kuruvilla, J.; Didier, R.; Susana, C.M.F.; Nandakumar, K.; Sabu, T. Gas Barrier, Rheological and Mechanical Properties of Immiscible Natural Rubber/Acrylonitrile Butadiene Rubber/Organoclay (NR/NBR/Organoclay) Blend Nanocomposites. Materials 2020, 13, 2654. [Google Scholar] [CrossRef]
- Fujiwara, H.; Ono, H.; Nishimura, S. Effects of fillers on the hydrogen uptake and volume expansion of acrylonitrile butadiene rubber composites exposed to high pressure hydrogen: -Property of polymeric materials for high pressure hydrogen devices. Int. J. Hydrogen Energy 2022, 47, 4725–4740. [Google Scholar] [CrossRef]
- Yang, X.; Schneider, L.K.A.; Giese, U.; Schuster, R.H. Characterization of permeability of elastomers—Part II. Kautsch. Gummi Kunstst. 2010, 496–505. [Google Scholar]
- Yamabe, J.; Nakao, M.; Fujiwara, H.; Nishimura, S. Influence of Fillers on Hydrogen Penetration Properties and Blister Fracture of EPDM Comosites Exposed to 10 MPa Hydrogen Gas. Trans. Jpn. Soc. Mech. Eng. Part A 2008, 74, 971–981. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Giese, U.; Schuster, R.H. Characterization of permeability of elastomers-Part I-HNBR. Kautsch. Gummi Kunstst. 2008, 61, 294–300. [Google Scholar]
- Yamabe, J.; Nishimura, S. Influence of fillers on hydrogen penetration properties and blister fracture of rubber composites for O-ring exposed to high-pressure hydrogen gas. Int. J. Hydrogen Energy 2009, 34, 1977–1989. [Google Scholar] [CrossRef]
- Jung, J.K.; Kim, I.G.; Kim, K.T.; Ryu, K.S.; Chung, K.S. Evaluation techniques of hydrogen permeation in sealing rubber materials. Polym. Test. 2021, 93, 107016. [Google Scholar] [CrossRef]
- Jung, J.K.; Kim, I.G.; Jeon, S.K.; Kim, K.T.; Baek, U.B.; Nahm, S.H. Volumetric analysis technique for analyzing the transport properties of hydrogen gas in cylindrical-shaped rubbery polymers. Polym. Test. 2021, 99, 107147. [Google Scholar] [CrossRef]
- Kim, G.H.; Moon, Y.; Jung, J.K.; Choi, M.C.; Bae, J.W. Influence of carbon black and silica fillers with different concentrations on dielectric relaxation in nitrile butadiene rubber investigated by impedance spectroscopy. Polymers 2022, 14, 155. [Google Scholar] [CrossRef] [PubMed]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Yang, Y.; Liu, S. Estimation and modeling of pressure-dependent gas diffusion coefficient for coal: A fractal theory-based approach. Fuel 2019, 253, 588–606. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Wang, G.; Zhang, J.; Ren, T. The influence of sorption pressure on gas diffusion in coal particles: An experimental study. Processes 2019, 7, 219. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.S.; Kamiya, Y. Evaluation of gas sorption parameters and prediction of sorption isotherms in glassy polymers. J. Polym. Sci. B Polym. Phys. 2000, 38, 883–888. [Google Scholar] [CrossRef]
- Stannett, V.T.; Koros, W.J.; Paul, D.R.; Lonsdale, H.K.; Baker, R.W. Recent advances in membrane science and technology. Adv. Polym. Sci. 1979, 32, 69–121. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, S. Estimation of pressure-dependent diffusive permeability of coal using methane diffusion coefficient: Laboratory measurements and modeling. Energy Fuels 2016, 30, 8968–8976. [Google Scholar] [CrossRef]
- Knudsen, M. Die gesetze der molekularströmung und der inneren reibungsströmung der gase durch röhren. Ann. Phys. 1909, 333, 75–130. [Google Scholar] [CrossRef] [Green Version]
- Welty, J.R.; Wicks, C.E.; Wilson, R.E. Fundamentals of Momentum, Heat, and Mass Transfer; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Fröhlich, J.; Niedermeier, W.; Luginsland, H.D. The effect of filler–filler and filler–elastomer interaction on rubber reinforcement. Compos. A Appl. Sci. Manuf. 2005, 36, 449–460. [Google Scholar] [CrossRef]
- Litvinov, V.M.; Orza, R.A.; Klüppel, M.; van Duin, M.; Magusin, P.C.M.M. Rubber–filler interactions and network structure in relation to stress–strain behavior of vulcanized, carbon black filled EPDM. Macromolecules 2011, 44, 4887–4900. [Google Scholar] [CrossRef]
- Mitchell, M.R.; Link, R.E.; Mostafa, A.; Abouel-Kasem, A.; Bayoumi, M.R.; El-Sebaie, M.G. Rubber-filler interactions and its effect in rheological and mechanical properties of filled compounds. J. Test. Eval. 2010, 38, 101942. [Google Scholar] [CrossRef]
- Lee, J.Y.; Park, N.; Lim, S.; Ahn, B.; Kim, W.; Moon, H.; Paik, H.J.; Kim, W. Influence of the silanes on the crosslink density and crosslink structure of silica-filled solution styrene butadiene rubber compounds. Compos. Interfaces 2017, 24, 711–727. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J. Statistical mechanics of cross-linked polymer networks I. Rubberlike elasticity. J. Chem. Phys. 1943, 11, 512–520. [Google Scholar] [CrossRef]
- Hrnjak-Murgic, Z.; Jelencic, J.; Bravar, M.; Marovic, M. Influence of the network on the interaction parameter in system EPDM vulcanizate-solvent. J. Appl. Polym. Sci. 1998, 65, 991–999. [Google Scholar] [CrossRef]





| Chemical Composition | Neat NBR | NBR-H20 | NBR-H40 | NBR-H60 | NBR-M20 | NBR-M40 | NBR-M60 |
|---|---|---|---|---|---|---|---|
| KNB 35 L | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| ZnO | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 |
| St/A* | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| HAF N330 | - | 20 | 40 | 60 | - | - | - |
| MT N990 | - | - | - | - | 20 | 40 | 60 |
| S | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| TBBS+ | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 |
| Chemical Composition | NBR-S20 | NBR-S40 | NBR-S60 |
|---|---|---|---|
| KBR 35 L | 100 | 100 | 100 |
| ZnO | 3.0 | 3.0 | 3.0 |
| St/A | 1.0 | 1.0 | 1.0 |
| Silica S-175 | 20 | 40 | 60 |
| Si-69× | 1.6 | 3.2 | 4.8 |
| PEG# | 0.8 | 1.6 | 2.4 |
| S | 1.5 | 1.5 | 1.5 |
| TBBS+ | 0.7 | 0.7 | 0.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.K.; Lee, C.H.; Son, M.S.; Lee, J.H.; Baek, U.B.; Chung, K.S.; Choi, M.C.; Bae, J.W. Filler Effects on H2 Diffusion Behavior in Nitrile Butadiene Rubber Blended with Carbon Black and Silica Fillers of Different Concentrations. Polymers 2022, 14, 700. https://doi.org/10.3390/polym14040700
Jung JK, Lee CH, Son MS, Lee JH, Baek UB, Chung KS, Choi MC, Bae JW. Filler Effects on H2 Diffusion Behavior in Nitrile Butadiene Rubber Blended with Carbon Black and Silica Fillers of Different Concentrations. Polymers. 2022; 14(4):700. https://doi.org/10.3390/polym14040700
Chicago/Turabian StyleJung, Jae Kap, Chang Hoon Lee, Min Seok Son, Ji Hun Lee, Un Bong Baek, Ki Soo Chung, Myung Chan Choi, and Jong Woo Bae. 2022. "Filler Effects on H2 Diffusion Behavior in Nitrile Butadiene Rubber Blended with Carbon Black and Silica Fillers of Different Concentrations" Polymers 14, no. 4: 700. https://doi.org/10.3390/polym14040700






