Small-Angle X-ray Scattering Analysis on the Estimation of Interaction Parameter of Poly(n-butyl acrylate)-b-poly(methyl methacrylate)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. ATRP Synthesis
2.2.1. Synthesis of Poly(n-butyl acrylate) (PBA) Macro Initiator
2.2.2. Synthesis of Poly(n-butyl acrylate)-b-p,oly(methyl methacrylate) (PBA-b-PMMA) Diblock Copolymer
2.2.3. Conversion Analysis
2.3. SAXS Measurements
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Braunecker, W.A.; Matyjaszewski, K. Controlled/living Radical Polymerization: Features, Developments, and Perspectives. Prog. Polym. Sci. 2007, 32, 93–146. [Google Scholar] [CrossRef]
- Tong, J.D.; Moineau, G.; Leclere, P.; Brédas, J.L.; Lazzaroni, R.; Jérôme, R. Synthesis, Morphology, and Mechanical Properties of Poly(methyl methacrylate)-b-poly(n-butyl acrylate)-b-poly(methyl methacrylate) Triblocks: Ligated Anionic Polymerization vs. Atom Transfer Radical Polymerization. Macromolecules 2000, 33, 470–479. [Google Scholar] [CrossRef]
- Destarac, M. Controlled Radical Polymerization: Industrial Stakes, Obstacles and Achievements. Macromol. React. Eng. 2010, 4, 165–179. [Google Scholar] [CrossRef]
- Matyjaszewski, K. Atom Transfer Radical Polymerization (ATRP): Current Status and Future Perspectives. Macromolecules 2012, 45, 4015–4039. [Google Scholar] [CrossRef]
- Shipp, D.A.; Wang, J.L.; Matyjaszewski, K. Synthesis of Acrylate and Methacrylate Block Copolymers Using Atom Transfer Radical Polymerization. Macromolecules 1998, 31, 8005–8008. [Google Scholar] [CrossRef]
- Moineau, C.; Minet, M.; Teyssié, P.; Jérôme, R. Synthesis and Characterization of Poly(methyl methacrylate)-block-poly(n-butyl acrylate)-block-poly(methyl methacrylate) Copolymers by Two-Step Controlled Radical Polymerization (ATRP) Catalyzed by NiBr2(PPh3)2, 1. Macromolecules 1999, 32, 8277–8282. [Google Scholar] [CrossRef]
- Garcia, M.F.; de la Fuente, J.L.; Fernandez-Sanz, M.; Madruga, E.L. The Importance of Solvent Polar Character on the Synthesis of PMMA-b-PBA Block Copolymers by Atom Transfer Radical Polymerization. Polymer 2001, 42, 9405–9412. [Google Scholar] [CrossRef]
- Guillaneuf, Y.; Gigmes, D.; Marque, S.R.; Astolfi, P.; Greci, L.; Tordo, P.; Bertin, D. First Effective Nitroxide-Mediated Polymerization of Methyl Methacrylate. Macromolecules 2007, 40, 3108–3114. [Google Scholar] [CrossRef]
- Tran, T.A.; Leonardi, F.; Bourrigaud, S.; Gerard, P.; Derail, C. All Acrylic Block Copolymers Based on Poly(methyl methacrylate) and Poly(butyl acrylate): A Link between the Physico-Chemical Properties and the Mechanical Behaviour on Impact Tests. Polym. Test. 2008, 27, 945–950. [Google Scholar] [CrossRef]
- Roos, S.G.; Müller, A.H.; Matyjaszewski, K. Copolymerization of n-Butyl Acrylate with Methyl Methacrylate and PMMA Macromonomers: Comparison of Reactivity Ratios in Conventional and Atom Transfer Radical Copolymerization. Macromolecules 1999, 32, 8331–8335. [Google Scholar] [CrossRef]
- Holden, G.; Bishop, E.; Legge, N.R. Thermoplastic Elastomers. J. Polym. Sci. Part C Polym. Symp. 1969, 26, 37–57. [Google Scholar] [CrossRef]
- Holden, G.L.; Legge, N.R.; Quirk, R.P.; Schroeder, H.E. Thermoplastic Elastomers; Hanser: Munich, Germany, 1996. [Google Scholar]
- Fetters, L.J.; Morton, M. Synthesis and Properties of Block Polymers. I. Poly(α-methyl styrene)-b-polyisoprene-b-poly(α-methylstyrene). Macromolecules 1969, 2, 453–458. [Google Scholar] [CrossRef]
- Dufour, B.; Koynov, K.; Pakula, T.; Matyjaszewski, K. PBA–PMMA 3-Arm Star Block Copolymer Thermoplastic Elastomers. Macromol. Chem. Phys. 2008, 209, 1686–1693. [Google Scholar] [CrossRef]
- Nese, A.; Mosnacek, J.; Juhari, A.; Yoon, J.A.; Koynov, K.; Kowalewski, T.; Matyjaszewski, K. Synthesis, Characterization, and Properties of Starlike Poly(n-butyl acrylate)-b-poly(methyl methacrylate) Block Copolymers. Macromolecules 2010, 43, 1227–1235. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Wang, X.; Wang, Z. The Synthesis of Bottlebrush Cellulose-Graft-Diblock Copolymer Elastomers via Atom Transfer Radical Polymerization Utilizing a Halide Exchange Technique. Chem. Commun. 2019, 55, 13904–13907. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A. Bridging Attraction by Telechelic Polymers. Macromolecules 1992, 25, 5495–5503. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Paletsky, A.A.; Gonchikzhapov, M.B.; Glaznev, R.K.; Gerasimov, I.E.; Naganovsky, Y.K.; Shundrina, I.K.; Snegirev, A.Y.; Vinu, R. Kinetics of Thermal Decomposition of PMMA at Different Heating Rates and in a Wide Temperature Range. Thermochim. Acta. 2019, 671, 17–25. [Google Scholar] [CrossRef]
- Nikolaidis, A.K.; Achilias, D.S. Thermal Degradation Kinetics and Viscoelastic Behavior of Poly(Methyl Methacrylate)/ Organomodified Montmorillonite Nanocomposites Prepared via In Situ Bulk Radical Polymerization. Polymers 2018, 10, 491. [Google Scholar] [CrossRef] [Green Version]
- Bodycomb, J.; Yamaguchi, D.; Hashimoto, T. Observation of a Discontinuity in the Value of at the Order-Disorder Transition in Diblock Copolymer/Hornopolymer and Diblock Copolymer/Diblock Copolymer Blends. Polym.J. 1996, 28, 821–824. [Google Scholar] [CrossRef] [Green Version]
- Bates, F.S.; Rosedale, J.H.; Fredrickson, G.H. Fluctuation Effects in a Symmetric Diblock Copolymer near the Order–Disorder Transition. J. Chem. Phys. 1990, 92, 6255–6270. [Google Scholar] [CrossRef]
- Abu-Sharkh, B.; AlSunaidi, A. Morphology and Conformation Analysis of Self-Assembled Triblock Copolymer Melts. Macromol. Theory Simul. 2006, 15, 507–515. [Google Scholar] [CrossRef]
- Sakamoto, N.; Hashimoto, T. Order-Disorder Transition of Low Molecular Weight Polystyrene-block-polyisoprene: 1. SAXS Analysis of Two Characteristic Temperatures. Macromolecules 1995, 28, 6825–6834. [Google Scholar] [CrossRef]
- Schwahn, D.; Willner, L. Phase Behavior and Flory-Huggins Interaction Parameter of Binary Polybutadiene Copolymer Mixtures with Different Vinyl Content and Molar Volume. Macromolecules 2002, 35, 239–247. [Google Scholar] [CrossRef] [Green Version]
- Russell, T.P.; Hjelm, R.P., Jr.; Seeger, P.A. Temperature Dependence of the Interaction Parameter of Polystyrene and Poly(methy1 methacrylate). Macromolecules 1990, 23, 890–893. [Google Scholar] [CrossRef]
- Zhao, Y.; Sivaniah, E.; Hashimoto, T. SAXS Analysis of the Order-Disorder Transition and the Interaction Parameter of Polystyrene-block-poly(methyl methacrylate). Macromolecules 2008, 41, 9948–9951. [Google Scholar] [CrossRef]
- Sakurai, S.; Mori, K.; Okawara, A.; Kimishima, K.; Hashimoto, T. Evaluation of Segmental Interaction by Small-Angle X-ray Scattering Based on the Random-Phase Approximation for Asymmetric, Polydisperse Triblock Copolymers. Macromolecules 1992, 25, 2679–2691. [Google Scholar] [CrossRef]
- Zha, W.; Han, C.D.; Lee, D.H.; Han, S.H.; Kim, J.K.; Kang, J.H.; Park, C. Origin of the Difference in Order-Disorder Transition Temperature between Polystyrene-block-poly(2-vinylpyridine) and Polystyrene-block-poly(4-vinylpyridine) Copolymers. Macromolecules 2007, 40, 2109–2119. [Google Scholar] [CrossRef]
- Tanaka, H.; Hashimoto, T. Thermal Concentration Fluctuations of Block Polymer/Homopolymer Mixtures in the Disordered State. 1. Binary Mixtures of SI/HS. Macromolecules 1991, 24, 5398–5407. [Google Scholar] [CrossRef]
- Anastasiadis, S.H.; Gancarz, I.; Koberstein, J.T. Interfacial Tension of Immiscible Polymer Blends: Temperature and Molecular Weight Dependence. Macromolecules 1988, 21, 2980–2987. [Google Scholar] [CrossRef]
- Hewel, M.; Ruland, W. Microphase Separation Transition in Block Copolymer Melts. Makromol. Chem. Macromol. Symp. 1986, 4, 197–202. [Google Scholar] [CrossRef]
- Mori, K.; Hasegawa, H.; Hashimoto, T. Small-Angle X-Ray Scattering from Bulk Block Polymers in Disordered State. Estimation of χ-Values from Accidental Thermal Fluctuations. Polym. J. 1985, 17, 799–806. [Google Scholar] [CrossRef] [Green Version]
- Leibler, L. Theory of Microphase Separation in Block Copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Burger, C.; Ruland, W.; Semenov, A.N. Polydispersity Effects on the Microphase-Separation Tran-sition in Block Copolymers. Macromolecules 1990, 23, 3339–3346. [Google Scholar] [CrossRef]
- Lynd, N.A.; Hillmyer, M.A. Influence of Polydispersity on the Self-Assembly of Diblock Copolymers. Macromolecules 2005, 38, 8803–8810. [Google Scholar] [CrossRef]
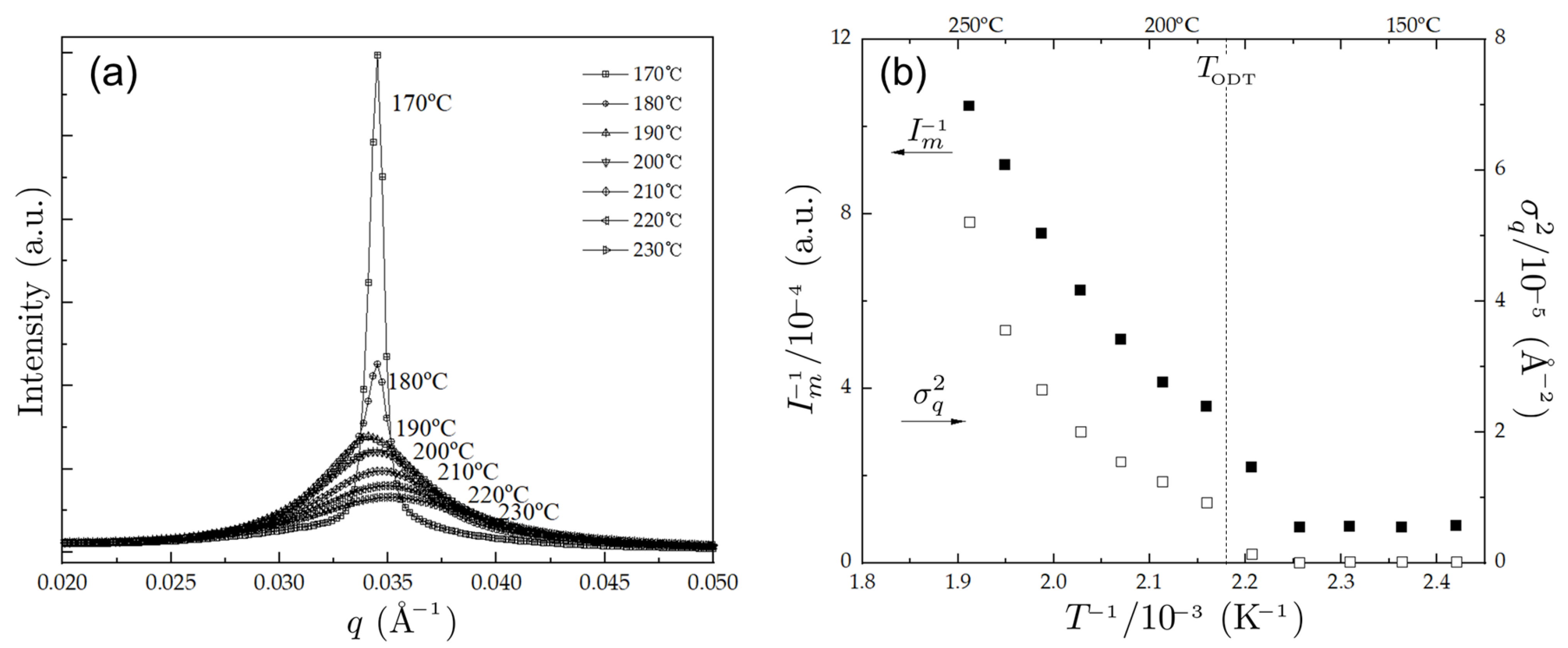
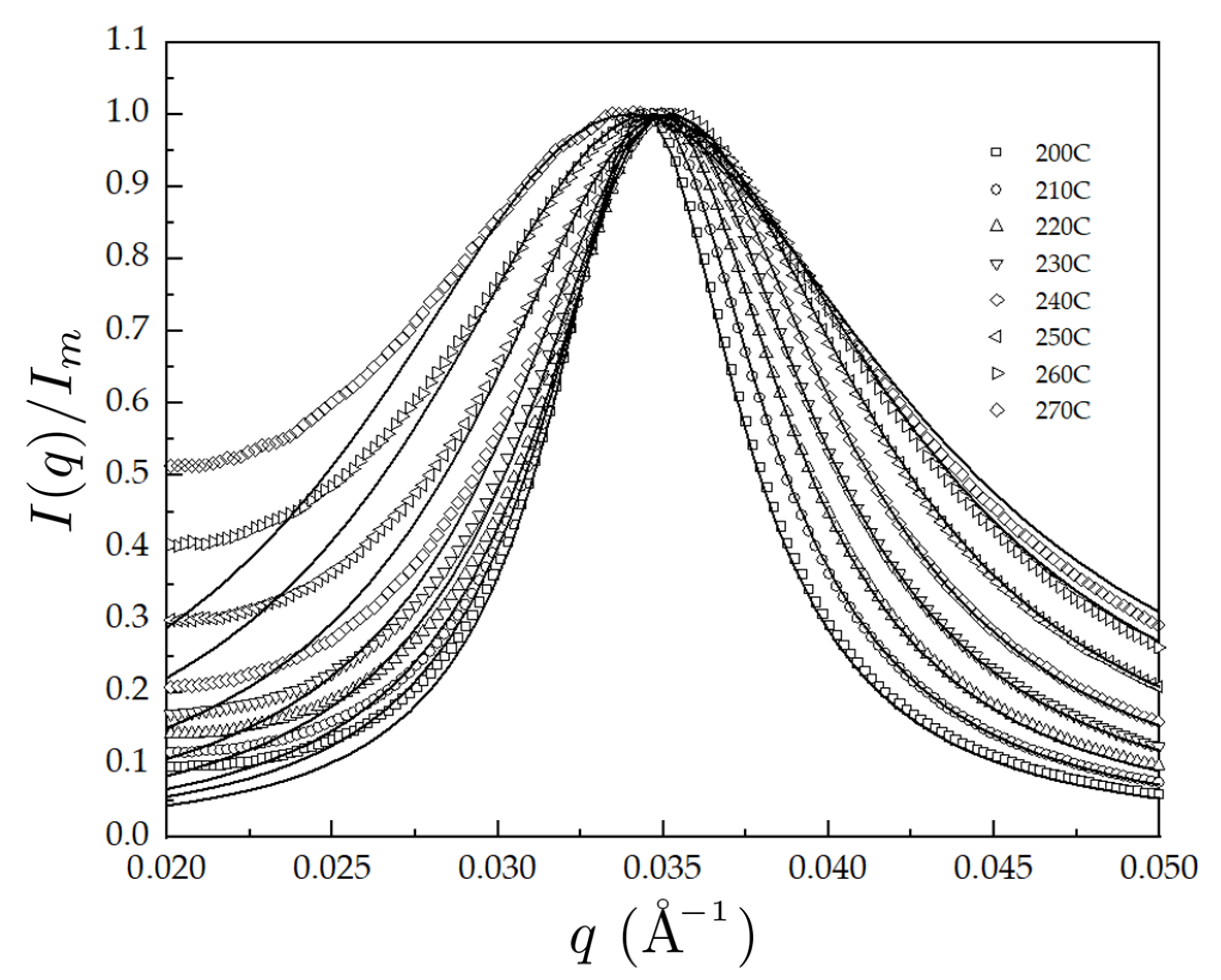
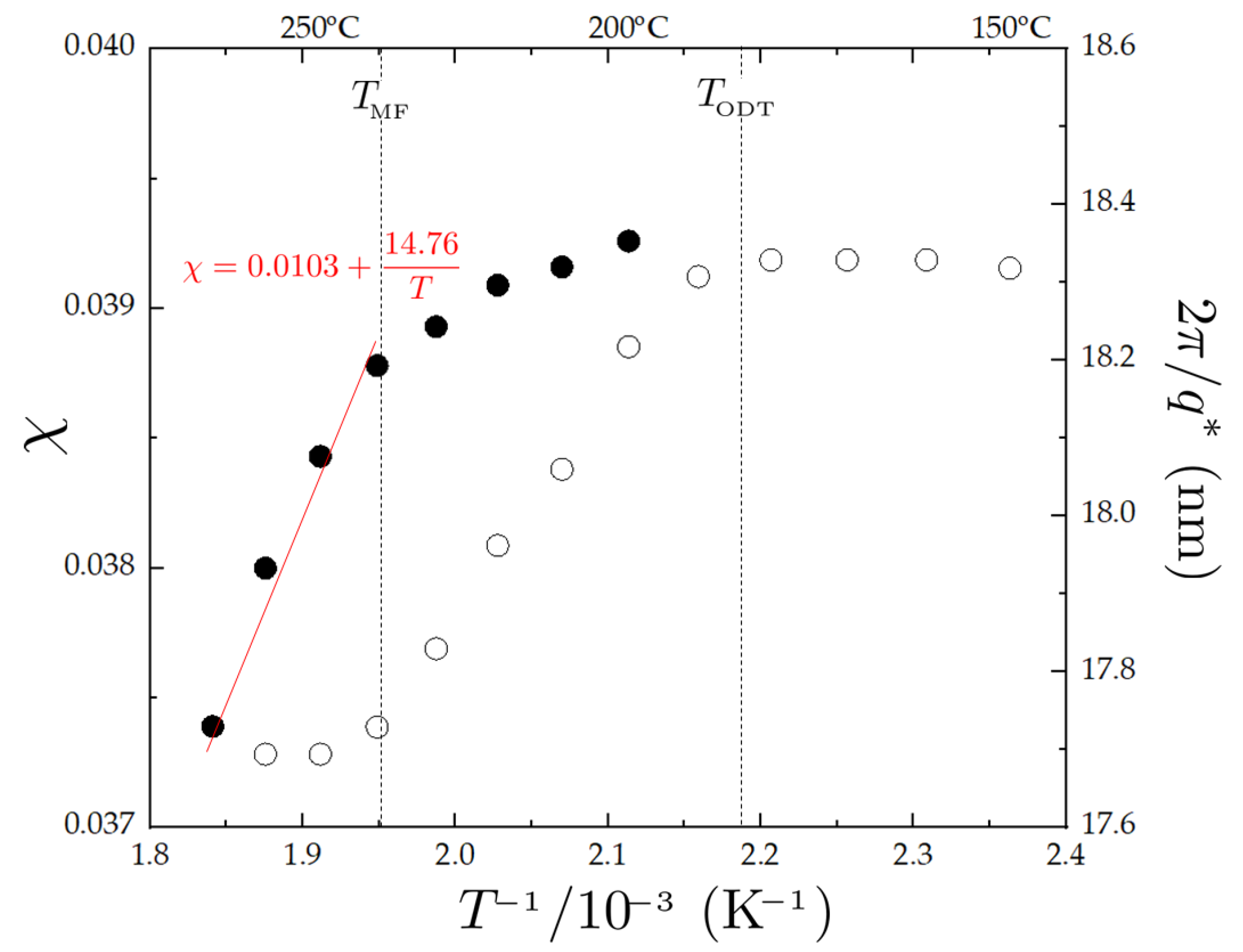
| Volume Fraction of PBA Block () | Dispersity of PBA Block () | Dispersity of PMMA Block () | Total Number of unit Segments () |
|---|---|---|---|
| 0.553 | 1.084 | 1.579 1 | 208.2 2 |
| System | Ref | |
|---|---|---|
| PS-b-PB 1 | [30] | |
| PS-b-PB 2 | [31] | |
| PS-b-PI 3 | [30] | |
| PS-b-PI 4 | [32] | |
| PBA-b-PMMA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-I.; Seo, M.-G.; Huh, J.; Paik, H.-j. Small-Angle X-ray Scattering Analysis on the Estimation of Interaction Parameter of Poly(n-butyl acrylate)-b-poly(methyl methacrylate). Polymers 2022, 14, 5567. https://doi.org/10.3390/polym14245567
Lee S-I, Seo M-G, Huh J, Paik H-j. Small-Angle X-ray Scattering Analysis on the Estimation of Interaction Parameter of Poly(n-butyl acrylate)-b-poly(methyl methacrylate). Polymers. 2022; 14(24):5567. https://doi.org/10.3390/polym14245567
Chicago/Turabian StyleLee, Sang-In, Min-Guk Seo, June Huh, and Hyun-jong Paik. 2022. "Small-Angle X-ray Scattering Analysis on the Estimation of Interaction Parameter of Poly(n-butyl acrylate)-b-poly(methyl methacrylate)" Polymers 14, no. 24: 5567. https://doi.org/10.3390/polym14245567
APA StyleLee, S.-I., Seo, M.-G., Huh, J., & Paik, H.-j. (2022). Small-Angle X-ray Scattering Analysis on the Estimation of Interaction Parameter of Poly(n-butyl acrylate)-b-poly(methyl methacrylate). Polymers, 14(24), 5567. https://doi.org/10.3390/polym14245567







