Effective Stiffness of Fused Deposition Modeling Infill Lattice Patterns Made of PLA-Wood Material
Abstract
:1. Introduction
2. Materials and Methods
2.1. PLA-Wood Material for FDM
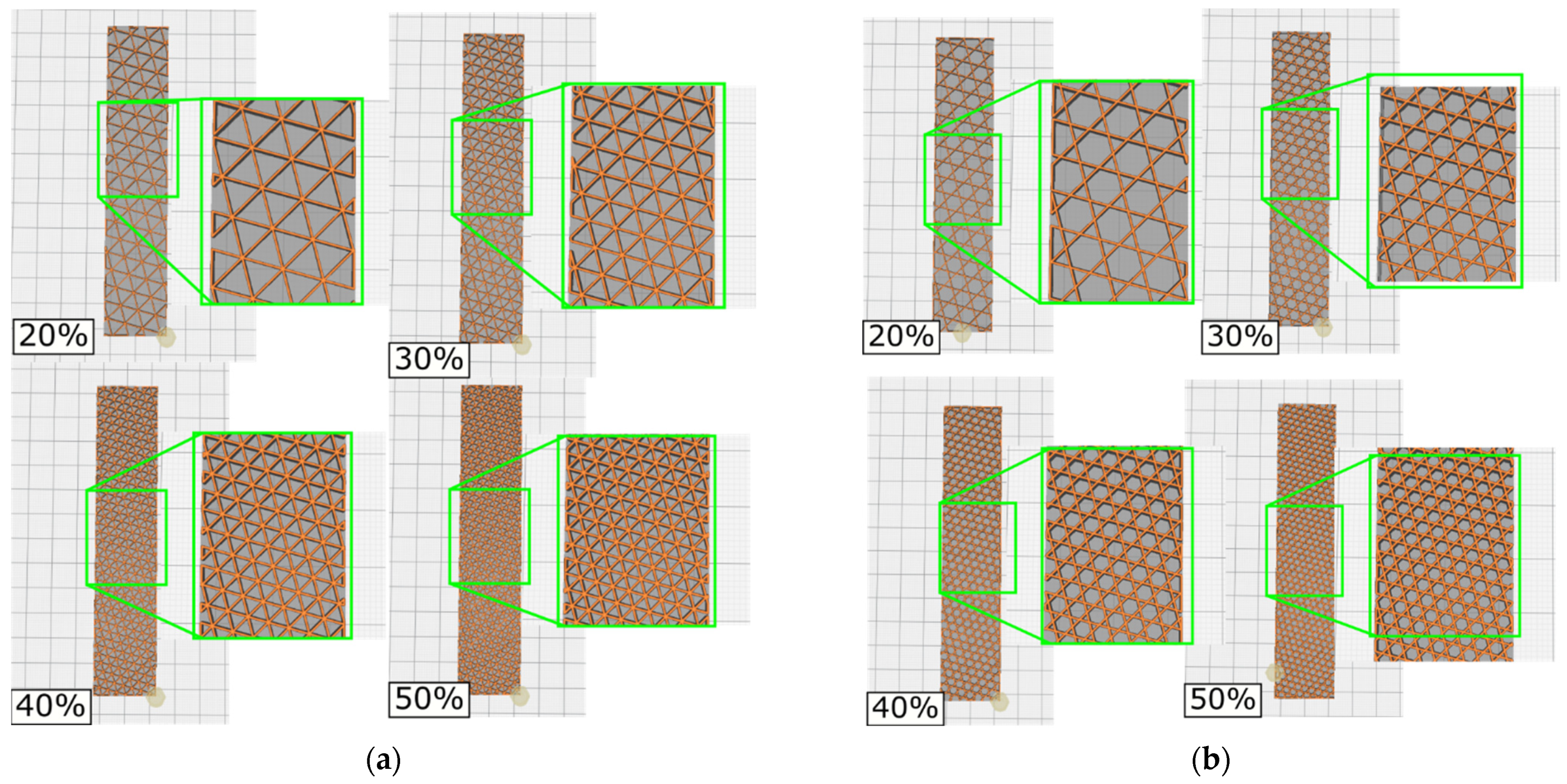
2.2. Design and Additive Manufacturing of Lattice Samples
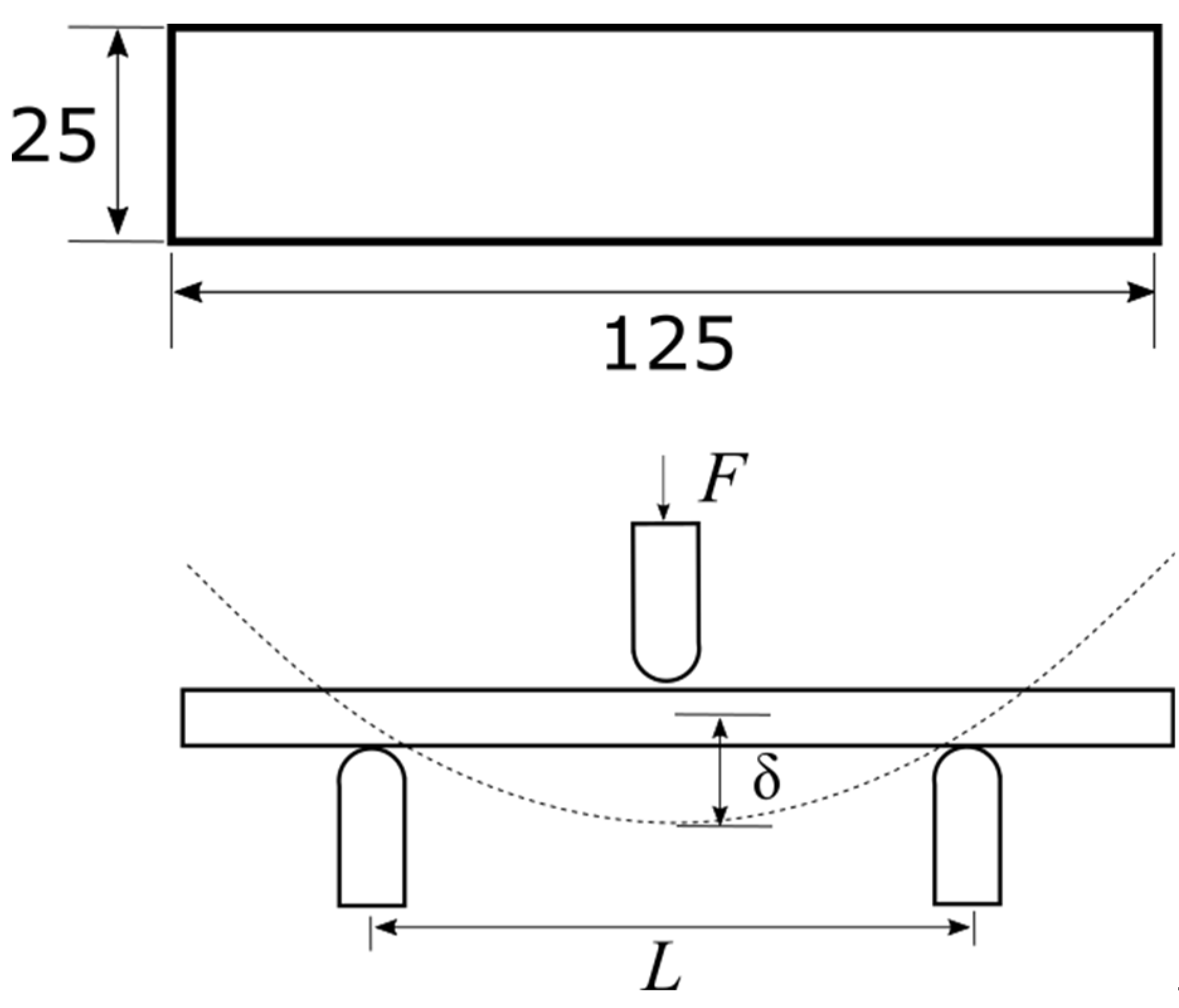
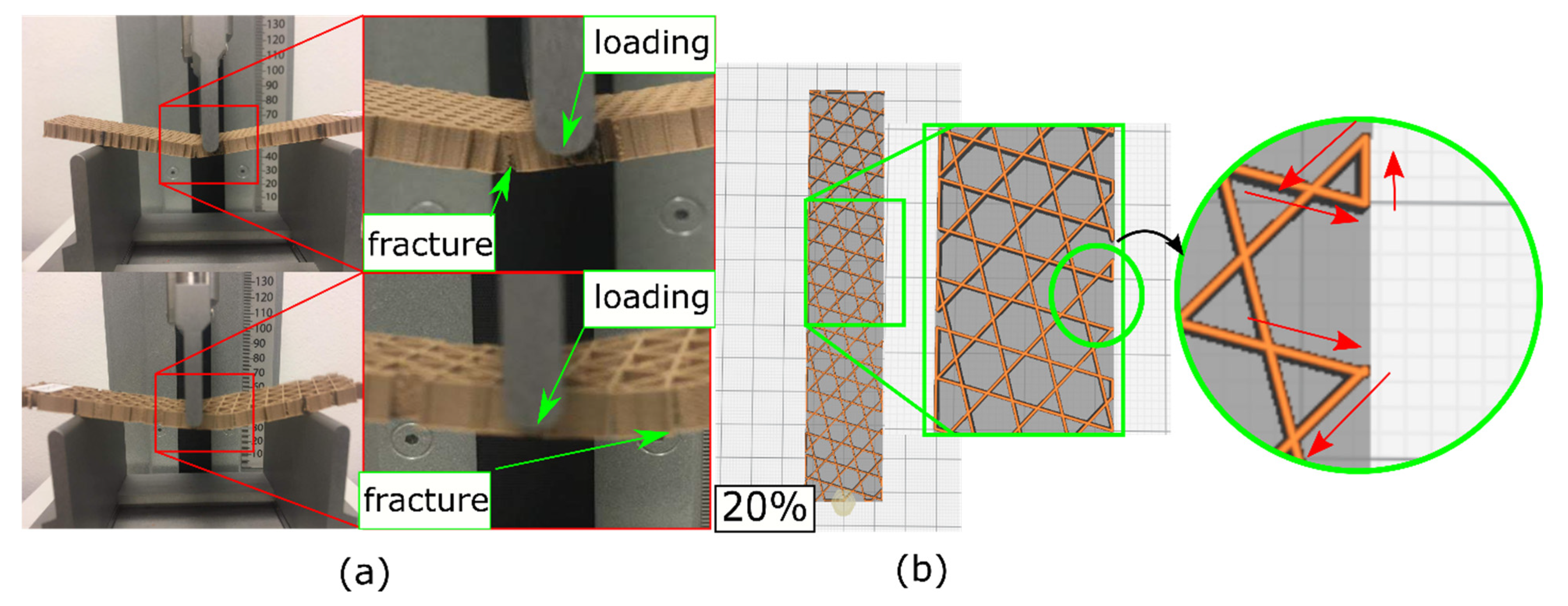
2.3. Mechanical Testing and Micro-Characterization
2.4. Statistical Analysis
3. Results
3.1. PLA-Wood Samples under 3-Point Bending
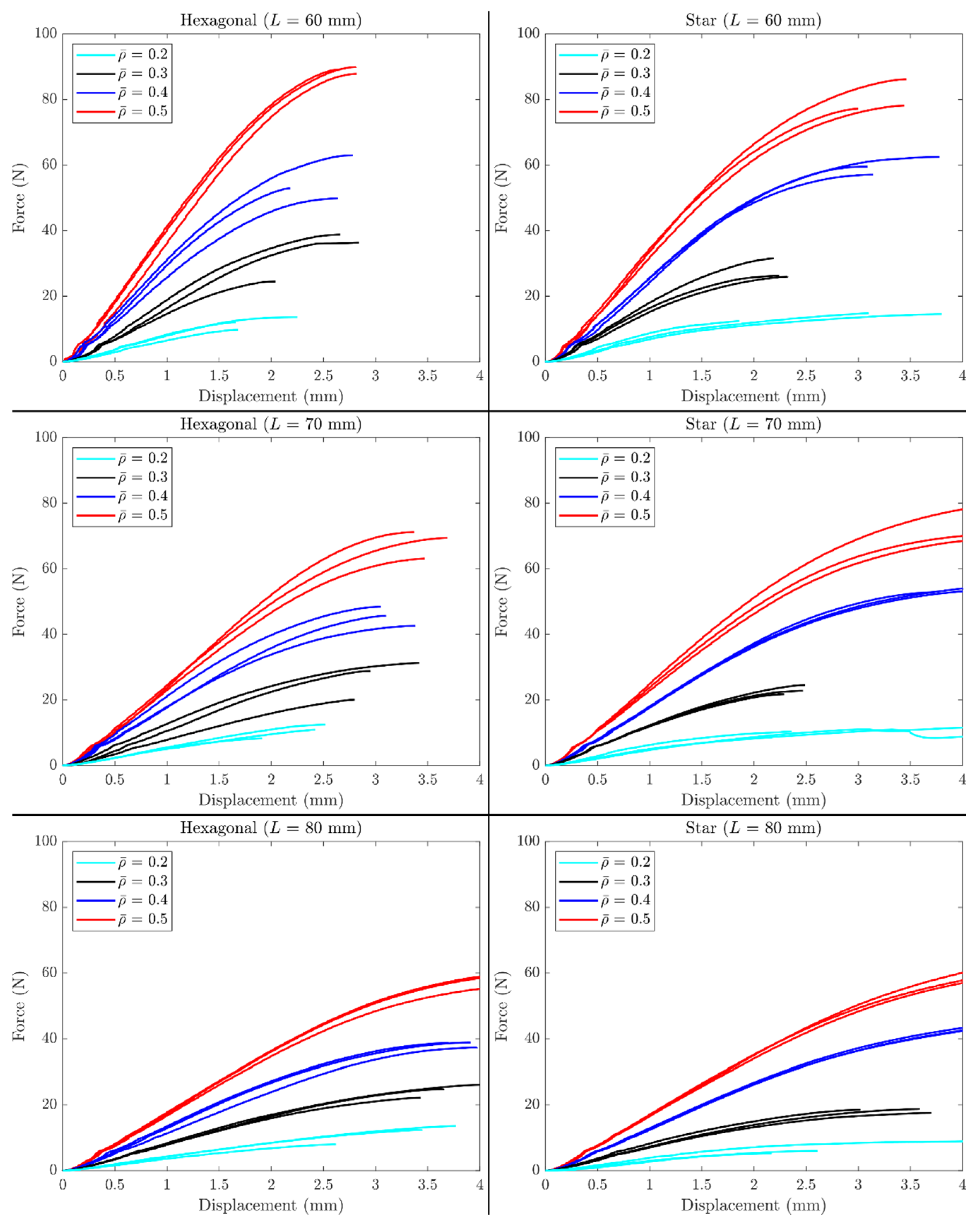
3.2. Flexural Elasticity of Lattice Beams
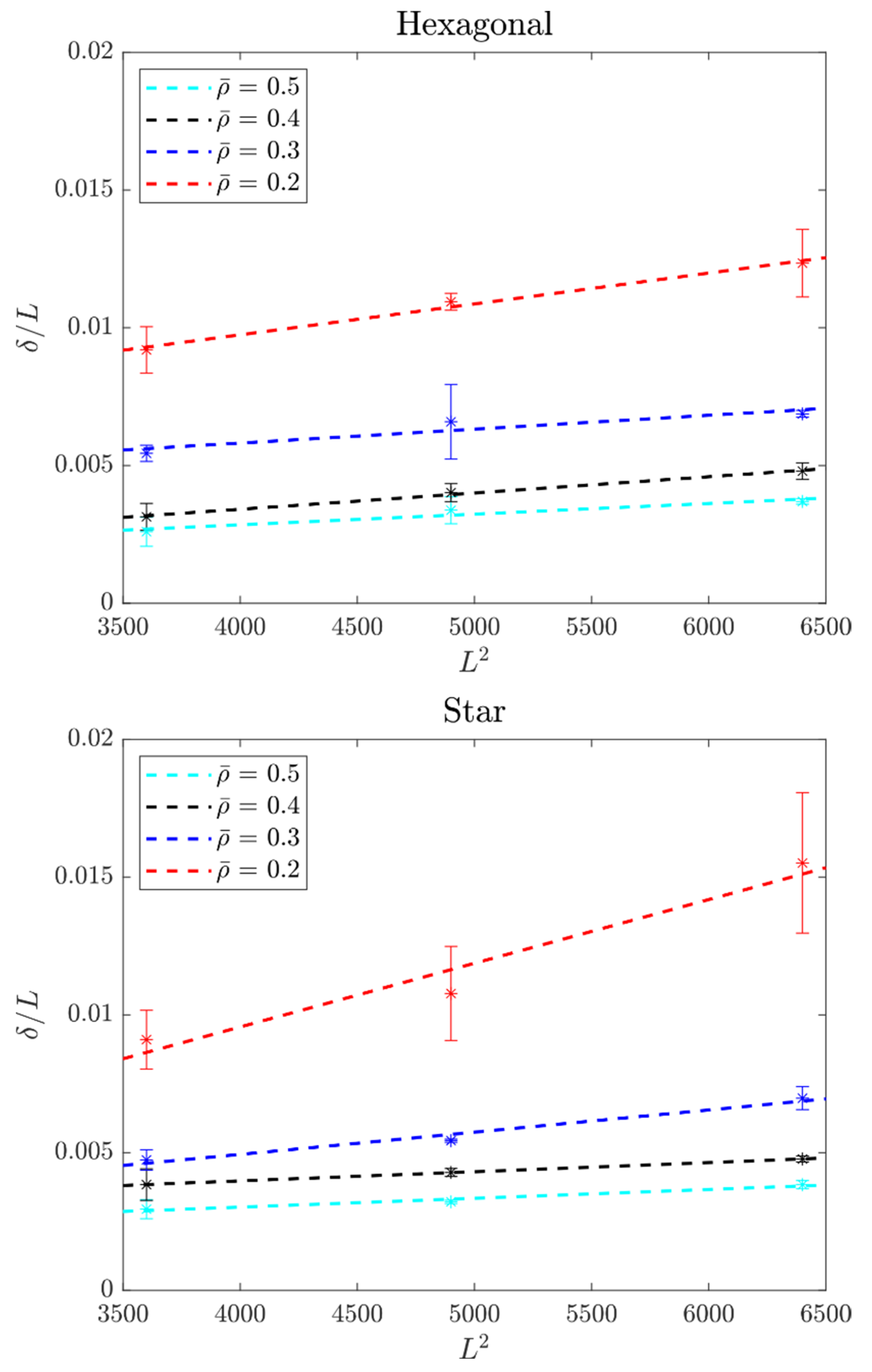
3.3. Shear Sensitivity in the Transverse Deflection of Lattice Beams
3.4. Micro-Characterization of PLA-Wood Lattices
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ashby, M.F. The Mechanical Properties of Cellular Solids. Metall. Trans. 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Wadley, H.N.G. Multifunctional Periodic Cellular Metals. Philos. Trans. A. Math. Phys. Eng. Sci. 2006, 364, 31–68. [Google Scholar] [CrossRef] [PubMed]
- Fleck, N.A.; Deshpande, V.S.; Ashby, M.F. Micro-Architectured Materials: Past, Present and Future. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 2495–2516. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Shalchy, F.; Bhaskar, A. Compressive Stiffness of Staggered Woodpile Lattices: Mechanics, Measurement, and Scaling Laws. Int. J. Mech. Sci. 2020, 187, 105932. [Google Scholar] [CrossRef]
- Yadav, P.; Sahai, A.; Sharma, R.S. Strength and Surface Characteristics of FDM-Based 3D Printed PLA Parts for Multiple Infill Design Patterns. J. Inst. Eng. Ser. C 2021, 102, 197–207. [Google Scholar] [CrossRef]
- Kiendl, J.; Gao, C. Controlling Toughness and Strength of FDM 3D-Printed PLA Components through the Raster Layup. Compos. Part B Eng. 2020, 180, 107562. [Google Scholar] [CrossRef]
- Aloyaydi, B.A.; Sivasankaran, S.; Ammar, H.R. Influence of Infill Density on Microstructure and Flexural Behavior of 3D Printed PLA Thermoplastic Parts Processed by Fusion Deposition Modeling. AIMS Mater. Sci. 2019, 6, 1033–1048. [Google Scholar] [CrossRef]
- Akhoundi, B.; Behravesh, A.H. Effect of Filling Pattern on the Tensile and Flexural Mechanical Properties of FDM 3D Printed Products. Exp. Mech. 2019, 59, 883–897. [Google Scholar] [CrossRef]
- Bhate, D.; Penick, C.A.; Ferry, L.A.; Lee, C. Classification and Selection of Cellular Materials in Mechanical Design: Engineering and Biomimetic Approaches. Designs 2019, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Gibson, L.J.; Ashby, M.F. The Mechanics of Two-Dimensional Cellular Materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Barocio, E.; Tejada-Ortigoza, V.; Pipes, R.B.; Rodriguez, C.A.; Roman-Flores, A. Characterization of the Mechanical Properties of FFF Structures and Materials: A Review on the Theoretical Approaches. Materials 2019, 12, 895. [Google Scholar] [CrossRef] [Green Version]
- Bakradze, G.; Arājs, E.; Gaidukovs, S.; Thakur, V.K. On the Heuristic Procedure to Determine Processing Parameters in Additive Manufacturing Based on Materials Extrusion. Polymers 2020, 12, 3009. [Google Scholar] [CrossRef]
- Nogales, A.; Gutiérrez-Fernández, E.; García-Gutiérrez, M.C.; Ezquerra, T.A.; Rebollar, E.; Šics, I.; Malfois, M.; Gaidukovs, S.; Gē Cis, E.; Celms, K.; et al. Structure Development in Polymers during Fused Filament Fabrication (FFF): An in Situ Small- And Wide-Angle X-Ray Scattering Study Using Synchrotron Radiation. Macromolecules 2019, 52, 9715–9723. [Google Scholar] [CrossRef]
- Gomez-Gras, G.; Jerez-Mesa, R.; Travieso-Rodriguez, J.A.; Lluma-Fuentes, J. Fatigue Performance of Fused Filament Fabrication PLA Specimens. Mater. Des. 2018, 140, 278–285. [Google Scholar] [CrossRef] [Green Version]
- Cuan-Urquizo, E.; Espinoza-Camacho, J.I.; Álvarez-Trejo, A.; Uribe, E.; Treviño-Quintanilla, C.D.; Crespo-Sánchez, S.E.; Gómez-Espinosa, A.; Roman-flores, A.; Overa-Silva, O.; Olvera-, O.; et al. Elastic Response of Lattice Arc Structures Fabricated Using Curved-Layered Fused Deposition Modeling. Mech. Adv. Mater. Struct. 2019, 28, 1498–1508. [Google Scholar] [CrossRef]
- Vicente, C.M.S.; Martins, T.S.; Leite, M.; Ribeiro, A.; Reis, L. Influence of Fused Deposition Modeling Parameters on the Mechanical Properties of ABS Parts. Polym. Adv. Technol. 2020, 31, 501–507. [Google Scholar] [CrossRef]
- Domingo-Espin, M.; Travieso-Rodriguez, J.A.; Jerez-Mesa, R. Fatigue Performance of ABS Specimens Obtained by Fused Filament Fabrication. Materials 2018, 11, 2521. [Google Scholar] [CrossRef] [Green Version]
- Moscato, S.; Bahr, R.; Le, T.; Pasian, M.; Bozzi, M.; Perregrini, L.; Tentzeris, M.M. Infill-Dependent 3-D-Printed Material Based on NinjaFlex Filament for Antenna Applications. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1506–1509. [Google Scholar] [CrossRef]
- Domingo-Espin, M.; Borros, S.; Agullo, N.; Garcia-Granada, A.-A.; Reyes, G. Influence of Building Parameters on the Dynamic Mechanical Properties of Polycarbonate Fused Deposition Modeling Parts. 3D Print. Addit. Manuf. 2014, 1, 70–77. [Google Scholar] [CrossRef]
- Rohde, S.; Cantrell, J.; Jerez, A.; Kroese, C.; Damiani, D.; Gurnani, R.; DiSandro, L.; Anton, J.; Young, A.; Steinbach, D.; et al. Experimental Characterization of the Shear Properties of 3D–Printed ABS and Polycarbonate Parts. Exp. Mech. 2018, 58, 871–884. [Google Scholar] [CrossRef]
- Goyanes, A.; Kobayashi, M.; Martínez-Pacheco, R.; Gaisford, S.; Basit, A.W. Fused-Filament 3D Printing of Drug Products: Microstructure Analysis and Drug Release Characteristics of PVA-Based Caplets. Int. J. Pharm. 2016, 514, 290–295. [Google Scholar] [CrossRef]
- Muta, S.; Ikeda, M.; Nikaido, T.; Sayed, M.; Sadr, A.; Suzuki, T.; Tagami, J. Chairside Fabrication of Provisional Crowns on FDM 3D-Printed PVA Model. J. Prosthodont. Res. 2020, 64, 401–407. [Google Scholar] [CrossRef] [PubMed]
- Zandi, M.D.; Jerez-Mesa, R.; Lluma-Fuentes, J.; Roa, J.J.; Travieso-Rodriguez, J.A. Experimental Analysis of Manufacturing Parameters’ Effect on the Flexural Properties of Wood-PLA Composite Parts Built through FFF. Int. J. Adv. Manuf. Technol. 2020, 106, 3985–3998. [Google Scholar] [CrossRef]
- Oksman, K.; Skrifvars, M.; Selin, J.F. Natural Fibres as Reinforcement in Polylactic Acid (PLA) Composites. Compos. Sci. Technol. 2003, 63, 1317–1324. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive Manufacturing of Carbon Fiber Reinforced Thermoplastic Composites Using Fused Deposition Modeling. Compos. Part B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Åkesson, D.; Vrignaud, T.; Tissot, C.; Skrifvars, M. Mechanical Recycling of PLA Filled with a High Level of Cellulose Fibres. J. Polym. Environ. 2016, 24, 185–195. [Google Scholar] [CrossRef]
- Lebedev, S.M.; Gefle, O.S.; Amitov, E.T.; Zhuravlev, D.V.; Berchuk, D.Y.; Mikutskiy, E.A. Mechanical Properties of PLA-Based Composites for Fused Deposition Modeling Technology. Int. J. Adv. Manuf. Technol. 2018, 97, 511–518. [Google Scholar] [CrossRef]
- Le Duigou, A.; Castro, M.; Bevan, R.; Martin, N. 3D Printing of Wood Fibre Biocomposites: From Mechanical to Actuation Functionality. Mater. Des. 2016, 96, 106–114. [Google Scholar] [CrossRef]
- Platnieks, O.; Barkane, A.; Ijudina, N.; Gaidukova, G.; Thakur, V.K.; Gaidukovs, S. Sustainable Tetra Pak Recycled Cellulose / Poly(Butylene Succinate) Based Woody-like Composites for a Circular Economy. J. Clean. Prod. 2020, 270, 122321. [Google Scholar] [CrossRef]
- Platnieks, O.; Sereda, A.; Gaidukovs, S.; Thakur, V.K.; Barkane, A.; Gaidukova, G.; Filipova, I.; Ogurcovs, A.; Fridrihsone, V. Adding Value to Poly (Butylene Succinate) and Nanofibrillated Cellulose-Based Sustainable Nanocomposites by Applying Masterbatch Process. Ind. Crops Prod. 2021, 169, 113669. [Google Scholar] [CrossRef]
- Martikka, O.; Kärki, T.; Wu, Q. Mechanical Properties of 3D-Printed Wood-Plastic Composites. Key Eng. Mater. 2018, 777, 499–507. [Google Scholar] [CrossRef]
- Gaidukovs, S.; Platnieks, O.; Gaidukova, G.; Starkova, O.; Barkane, A.; Beluns, S.; Thakur, V.K. Understanding the Impact of Microcrystalline Cellulose Modification on Durability and Biodegradation of Highly Loaded Biocomposites for Woody Like Materials Applications. J. Polym. Environ. 2021, 1–16. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical Behaviors of SLM Additive Manufactured Octet-Truss and Truncated-Octahedron Lattice Structures with Uniform and Taper Beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef] [Green Version]
- Grassi, G.; Lupica Spagnolo, S.; Paoletti, I. Fabrication and Durability Testing of a 3D Printed Façade for Desert Climates. Addit. Manuf. 2019, 28, 439–444. [Google Scholar] [CrossRef]
- Travieso-Rodriguez, J.A.; Zandi, M.D.; Jerez-Mesa, R.; Lluma-Fuentes, J. Fatigue Behavior of PLA-Wood Composite Manufactured by Fused Filament Fabrication. J. Mater. Res. Technol. 2020, 9, 8507–8516. [Google Scholar] [CrossRef]
- Travieso-Rodriguez, J.A.; Jerez-Mesa, R.; Llumà, J.; Gomez-Gras, G.; Casadesus, O. Comparative Study of the Flexural Properties of ABS, PLA and a PLA–Wood Composite Manufactured through Fused Filament Fabrication. Rapid Prototyp. J. 2021, 27, 81–92. [Google Scholar] [CrossRef]
- Tao, Y.; Pan, L.; Liu, D.; Li, P. A Case Study: Mechanical Modeling Optimization of Cellular Structure Fabricated Using Wood Flour-Filled Polylactic Acid Composites with Fused Deposition Modeling. Compos. Struct. 2019, 216, 360–365. [Google Scholar] [CrossRef]
- Zandi, M.D.; Jerez-Mesa, R.; Lluma-Fuentes, J.; Jorba-Peiro, J.; Travieso-Rodriguez, J.A. Study of the Manufacturing Process Effects of Fused Filament Fabrication and Injection Molding on Tensile Properties of Composite PLA-Wood Parts. Int. J. Adv. Manuf. Technol. 2020, 108, 1725–1735. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Bhaskar, A. Flexural Elasticity of Woodpile Lattice Beams. Eur. J. Mech. A Solids 2018, 67, 187–199. [Google Scholar] [CrossRef] [Green Version]
- Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain, 9th ed.; McGraw-Hill: New York, NY, USA, 1938; Volume 4. [Google Scholar] [CrossRef]
- Liu, Z.; Lei, Q.; Xing, S. Mechanical Characteristics of Wood, Ceramic, Metal and Carbon Fiber-Based PLA Composites Fabricated by FDM. J. Mater. Res. Technol. 2019, 8, 3743–3753. [Google Scholar] [CrossRef]
- Christensen, R.M. Sufficient Symmetry Conditions for Isotropy of Elastic Moduli Tensor. J. Appl. Mech. Trans. ASME 1987, 54, 772–777. [Google Scholar] [CrossRef]
- Ayas, C.; Tekoglu, C. On the Sufficient Symmetry Conditions for Isotropy of Elastic Moduli. J. Appl. Mech. Trans. ASME 2018, 85, 074502. [Google Scholar] [CrossRef]
- Wang, A.J.; McDowell, D.L. In-Plane Stiffness and Yield Strength of Periodic Metal Honeycombs. J. Eng. Mater. Technol. Trans. ASME 2004, 126, 137–156. [Google Scholar] [CrossRef]
- Arabnejad, S.; Pasini, D. Mechanical Properties of Lattice Materials via Asymptotic Homogenization and Comparison with Alternative Homogenization Methods. Int. J. Mech. Sci. 2013, 77, 249–262. [Google Scholar] [CrossRef] [Green Version]
- Petinakis, E.; Yu, L.; Edward, G.; Dean, K.; Liu, H.; Scully, A.D. Effect of Matrix-Particle Interfacial Adhesion on the Mechanical Properties of Poly(Lactic Acid)/Wood-Flour Micro-Composites. J. Polym. Environ. 2009, 17, 83–94. [Google Scholar] [CrossRef]
- Guo, R.; Ren, Z.; Bi, H.; Song, Y.; Xu, M. Effect of Toughening Agents on the Properties of Poplar Wood Flour/Poly (Lactic Acid) Composites Fabricated with Fused Deposition Modeling. Eur. Polym. J. 2018, 107, 34–45. [Google Scholar] [CrossRef]
- Sudamrao Getme, A.; Patel, B. A Review: Bio-Fiber’s as Reinforcement in Composites of Polylactic Acid (PLA). Mater. Today Proc. 2020, 26, 2116–2122. [Google Scholar] [CrossRef]
- Csikós, Á.; Faludi, G.; Domján, A.; Renner, K.; Móczó, J.; Pukánszky, B. Modification of Interfacial Adhesion with a Functionalized Polymer in PLA/Wood Composites. Eur. Polym. J. 2015, 68, 592–600. [Google Scholar] [CrossRef] [Green Version]
- Wan, L.; Zhang, Y. Jointly Modified Mechanical Properties and Accelerated Hydrolytic Degradation of PLA by Interface Reinforcement of PLA-WF. J. Mech. Behav. Biomed. Mater. 2018, 88, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Pukanszky, B.; Vörös, G. Mechanism of Interfacial Interactions in Particulate Filled Composites. Compos. Interfaces 1993, 1, 411–427. [Google Scholar] [CrossRef]
- Renner, K.; Kenyó, C.; Móczó, J.; Pukánszky, B. Micromechanical Deformation Processes in PP/Wood Composites: Particle Characteristics, Adhesion, Mechanisms. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1653–1661. [Google Scholar] [CrossRef]
- Keleş, Ö.; Anderson, E.H.; Huynh, J.; Gelb, J.; Freund, J.; Karakoç, A. Stochastic Fracture of Additively Manufactured Porous Composites. Sci. Rep. 2018, 8, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tao, Y.; Wang, H.; Li, Z.; Li, P.; Shi, S.Q. Development and Application of Wood Flour-Filled Polylactic Acid Composite Filament for 3d Printing. Materials 2017, 10, 339. [Google Scholar] [CrossRef] [PubMed] [Green Version]




| Constants | Variables | ||
|---|---|---|---|
| Layer height (mm) | 0.1 | (%) | 20, 30, 40, 50 |
| Extruder and bed temperature (°C) | 19,060 | L (mm) | 60, 70, 80 |
| Print speed (mm/s) | 30 | Infill topologies | Hexagonal, Star |
| (%) | L (mm) | ||
|---|---|---|---|
| 60 | 70 | 80 | |
| 50 | 0.00294 ± 0.00034 c,A | 0.00321 ± 0.00007 b,A | 0.00383 ± 0.00014 b,B |
| 40 | 0.00384 ± 0.00057 bc,A | 0.00428 ± 0.00015 b,AB | 0.00477 ± 0.00010 b,B |
| 30 | 0.00474 ± 0.00038 b,A | 0.00544 ± 0.00006 b,A | 0.00698 ± 0.00042 b,B |
| 20 | 0.00910 ± 0.00107 a,A | 0.01078 ± 0.00171 a,A | 0.01551 ± 0.00255 a,B |
| (%) | L (mm) | ||
|---|---|---|---|
| 60 | 70 | 80 | |
| 50 | 0.00260 ± 0.00053 c,A | 0.00338 ± 0.00049 c,AB | 0.00370 ± 0.00010 c,B |
| 40 | 0.00314 ± 0.00049 c,A | 0.00402 ± 0.00033 c,AB | 0.00480 ± 0.00030 c,B |
| 30 | 0.00544 ± 0.00029 b,A | 0.00659 ± 0.00135 b,A | 0.00688 ± 0.00013 b,A |
| 20 | 0.00920 ± 0.00084 a,A | 0.01094 ± 0.00031 a,AB | 0.01235 ± 0.00123 a,B |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuan-Urquizo, E.; Álvarez-Trejo, A.; Robles Gil, A.; Tejada-Ortigoza, V.; Camposeco-Negrete, C.; Uribe-Lam, E.; Treviño-Quintanilla, C.D. Effective Stiffness of Fused Deposition Modeling Infill Lattice Patterns Made of PLA-Wood Material. Polymers 2022, 14, 337. https://doi.org/10.3390/polym14020337
Cuan-Urquizo E, Álvarez-Trejo A, Robles Gil A, Tejada-Ortigoza V, Camposeco-Negrete C, Uribe-Lam E, Treviño-Quintanilla CD. Effective Stiffness of Fused Deposition Modeling Infill Lattice Patterns Made of PLA-Wood Material. Polymers. 2022; 14(2):337. https://doi.org/10.3390/polym14020337
Chicago/Turabian StyleCuan-Urquizo, Enrique, Alberto Álvarez-Trejo, Andrés Robles Gil, Viridiana Tejada-Ortigoza, Carmita Camposeco-Negrete, Esmeralda Uribe-Lam, and Cecilia D. Treviño-Quintanilla. 2022. "Effective Stiffness of Fused Deposition Modeling Infill Lattice Patterns Made of PLA-Wood Material" Polymers 14, no. 2: 337. https://doi.org/10.3390/polym14020337
APA StyleCuan-Urquizo, E., Álvarez-Trejo, A., Robles Gil, A., Tejada-Ortigoza, V., Camposeco-Negrete, C., Uribe-Lam, E., & Treviño-Quintanilla, C. D. (2022). Effective Stiffness of Fused Deposition Modeling Infill Lattice Patterns Made of PLA-Wood Material. Polymers, 14(2), 337. https://doi.org/10.3390/polym14020337









