Environmental Effects on Strength and Failure Strain Distributions of Sheep Wool Fibers
Abstract
:1. Introduction
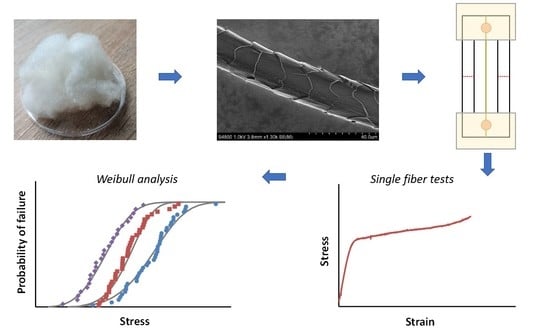
2. Materials and Methods
2.1. Wool Fibers
2.2. Single Fiber Tests
2.3. Fiber Conditioning
2.4. Scanning Electron Microscopy (SEM)
2.5. Optical Microscopy
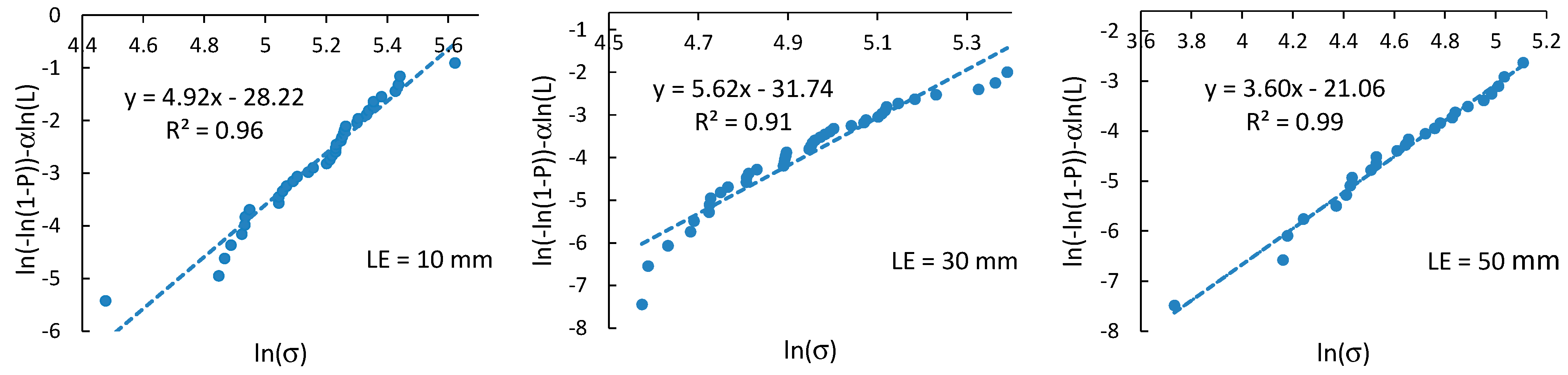
3. Statistical Analysis with Weibull Distribution
4. Results and Discussions
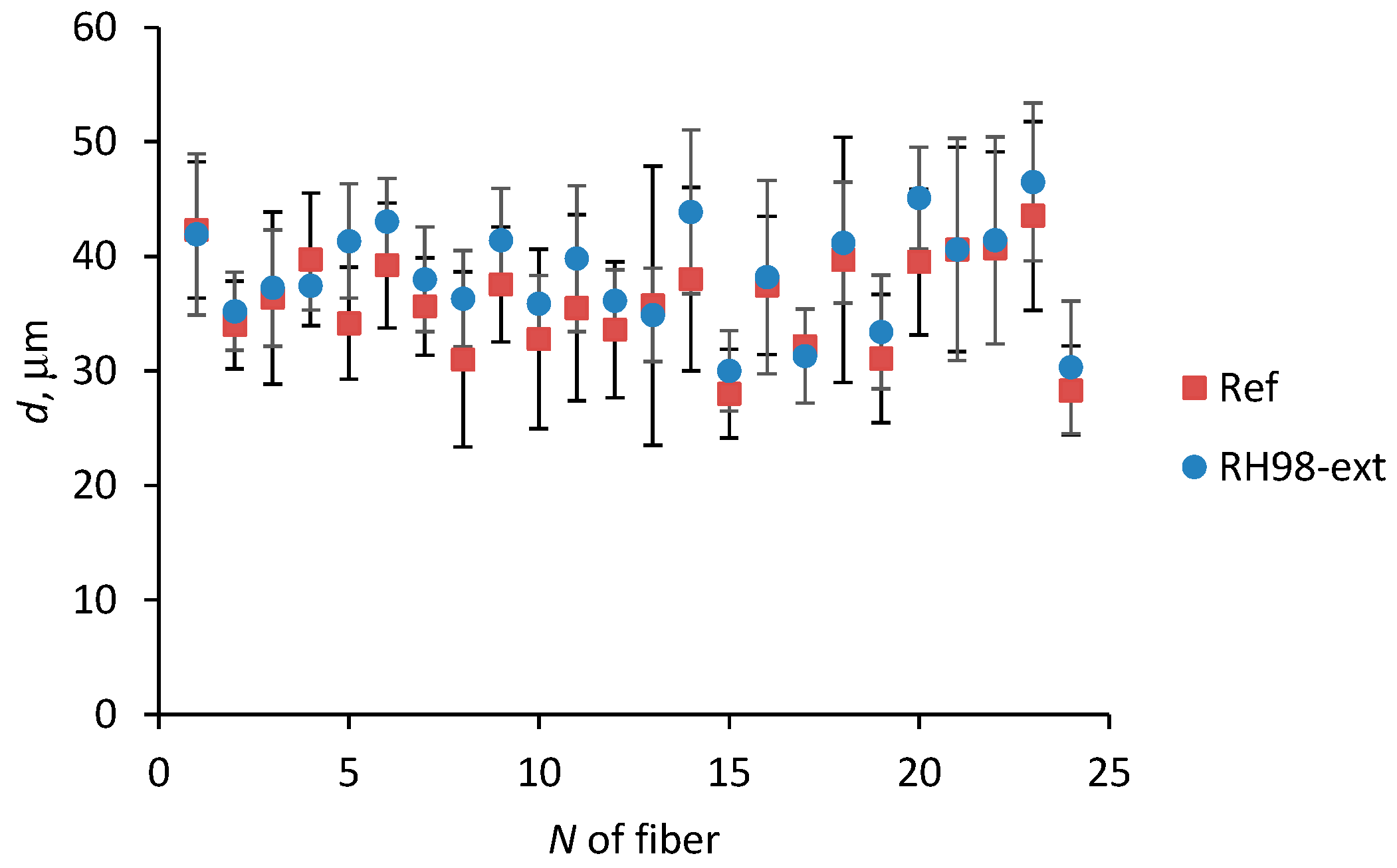
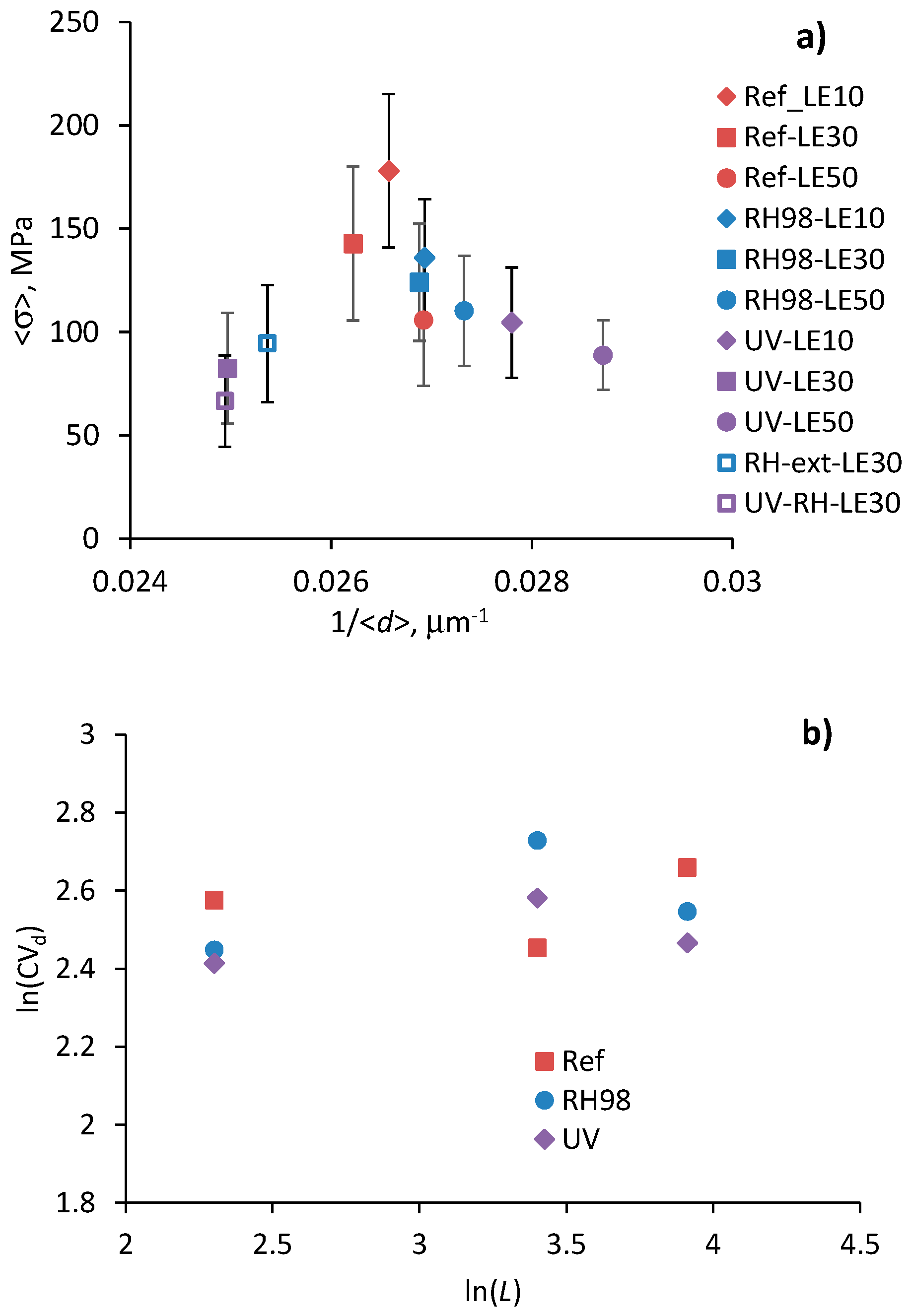
4.1. Diameter Variations
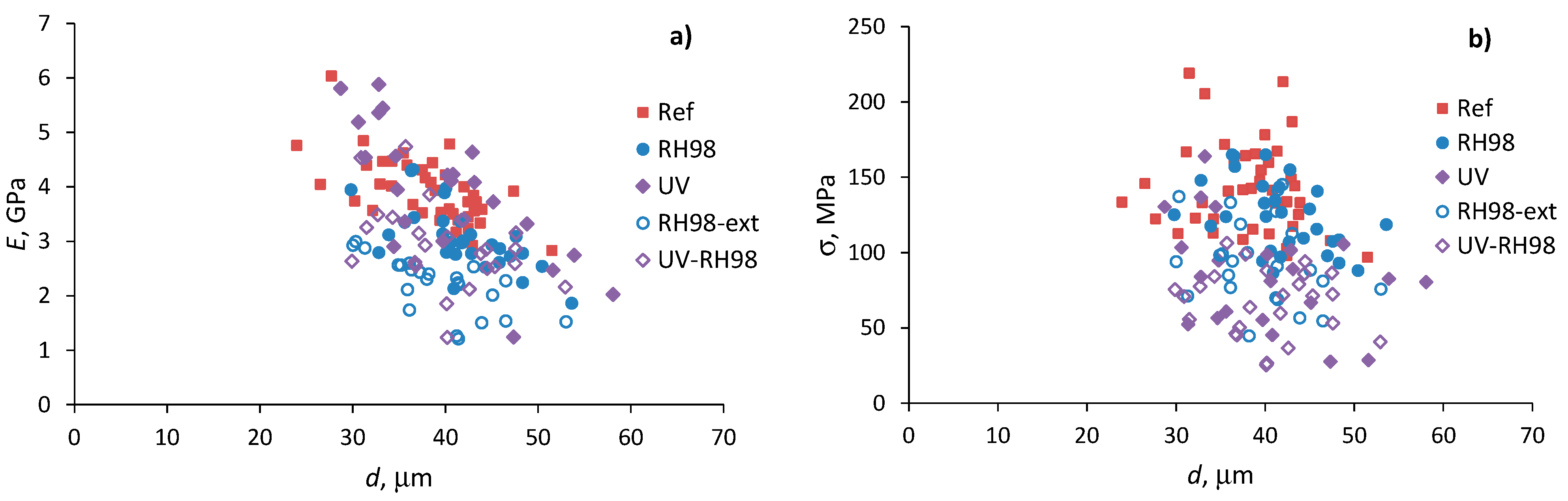
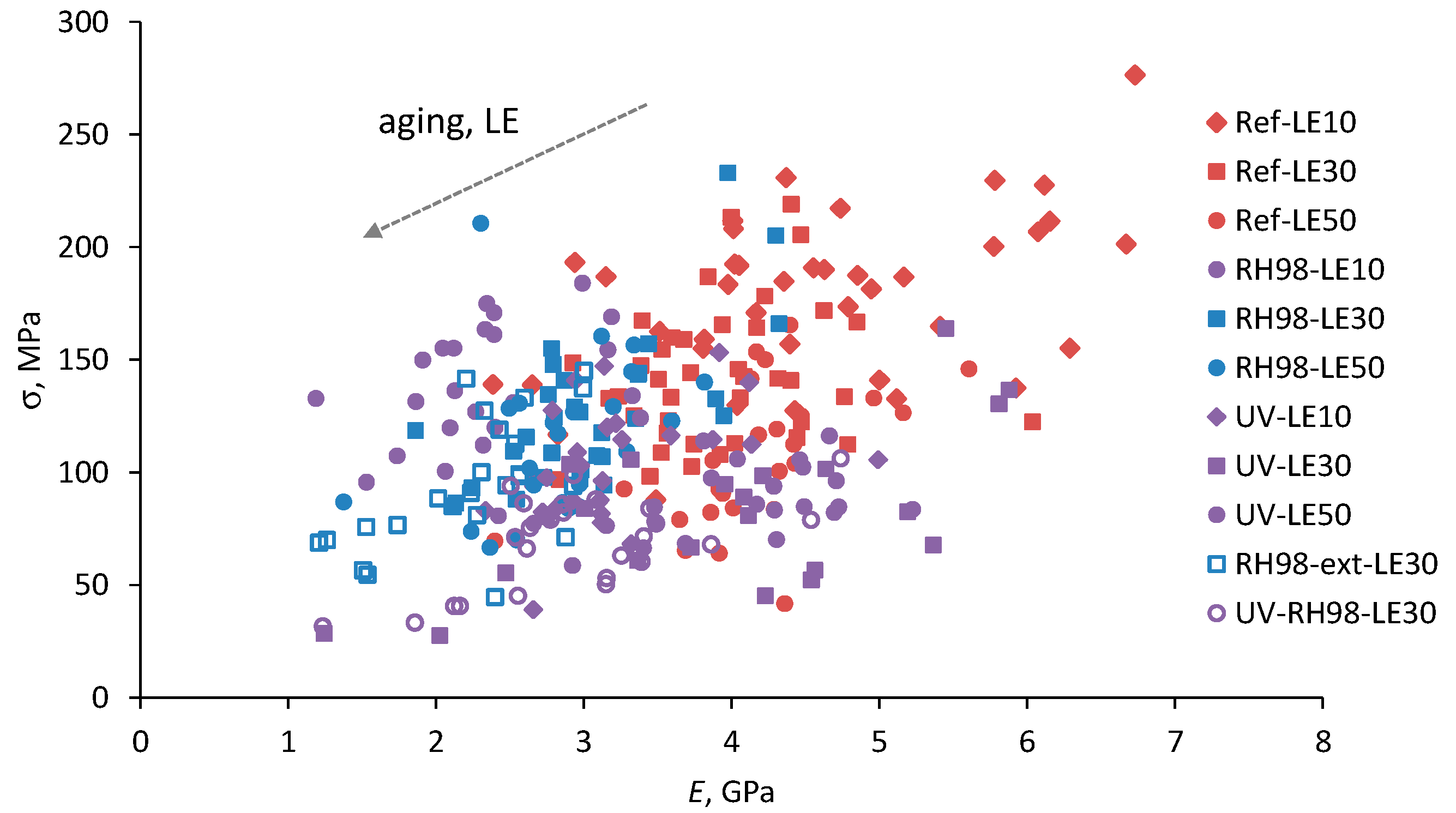
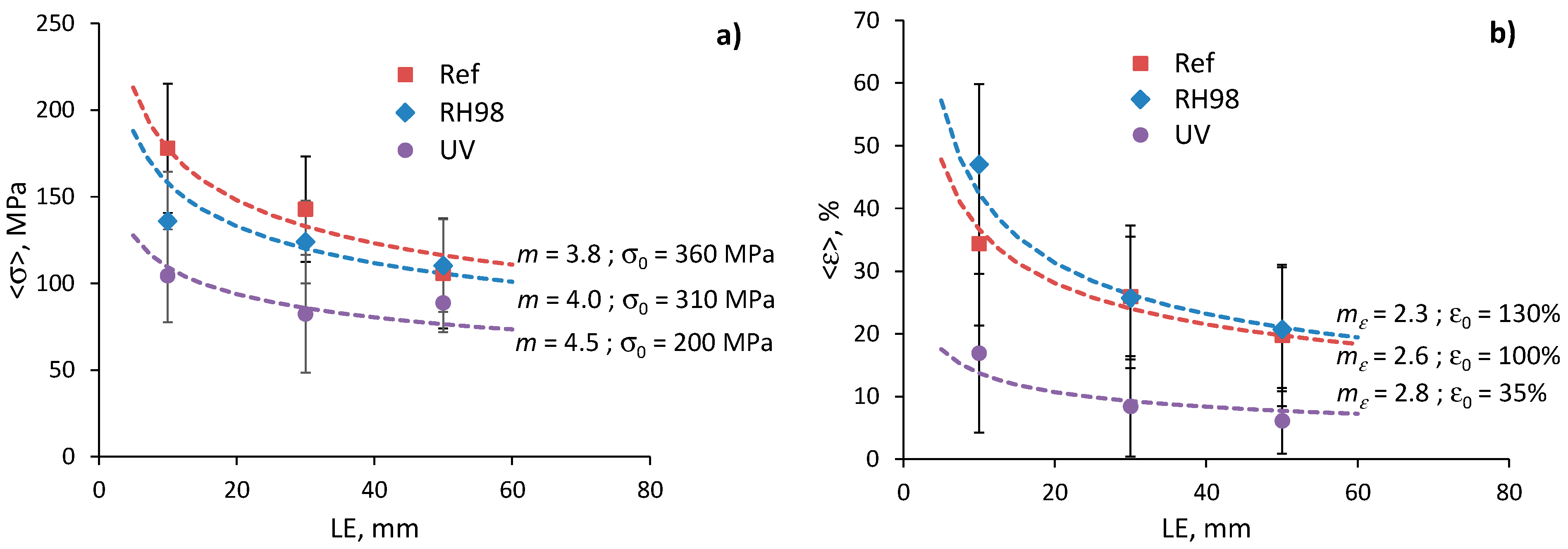
4.2. Tensile Properties of Wool Fibers
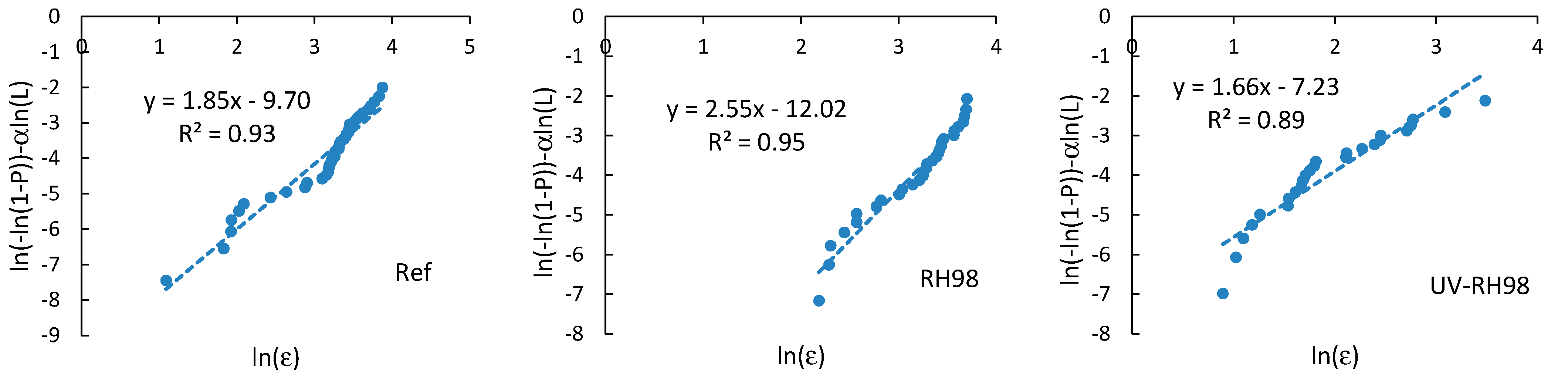
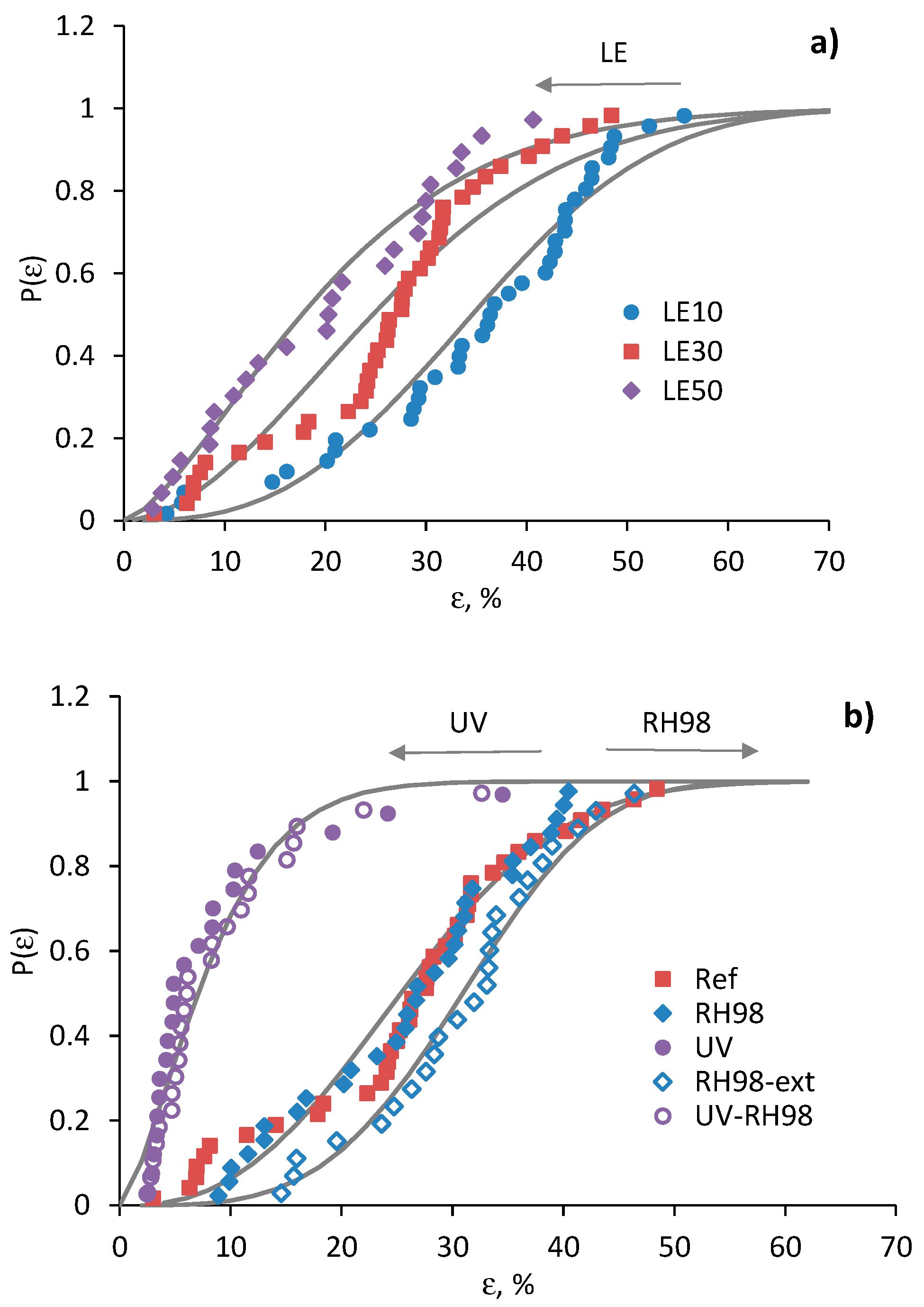
4.3. Weibull Strength Distribution Analysis
4.4. Weibull Failure Strain Distribution Analysis
4.5. Optical Microscopy and SEM Investigations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheung, H.Y.; Ho, M.P.; Lau, K.T.; Cardona, F.; Hui, D. Natural fibre-reinforced composites for bioengineering and environmental engineering applications. Compos. Part B 2009, 40, 655–663. [Google Scholar] [CrossRef]
- Ramamoorthy, S.K.; Skrifvars, M.; Persson, A. A Review of Natural Fibers Used in Biocomposites: Plant, Animal and Regenerated Cellulose Fibers. Polym. Rev. 2015, 55, 107–162. [Google Scholar] [CrossRef]
- Allafi, F.; Hossain, M.S.; Lalung, J.; Shaah, M.; Salehabadi, A.; Ahmad, M.I.; Shadi, A. Advancements in Applications of Natural Wool Fiber: Review. J. Nat. Fibers 2022, 19, 497–512. [Google Scholar] [CrossRef]
- Bosia, D.; Savio, L.; Thiebat, F.; Patrucco, A.; Fantucci, S.; Piccablotto, G.; Marino, D. Sheep wool for sustainable architecture. Energy Procedia 2015, 78, 315–320. [Google Scholar] [CrossRef] [Green Version]
- Fiore, V.; Di Bella, G.; Valenza, A. Effect of Sheep Wool Fibers on Thermal Insulation and Mechanical Properties of Cement-Based Composites. J. Nat. Fibers 2020, 17, 1532–1543. [Google Scholar] [CrossRef]
- Voikiva, V.; Zarins, A.; Avotina, L.; Barmina, I.; Rudovica, V.; Kizane, G. Influence of Biomass Combustion Products on Element Content and Thermal Stability of Latvian Sheep Breed Wool Filter Fibres. Mater. Sci. 2020, 26, 438–443. [Google Scholar] [CrossRef]
- Available online: https://appsso.eurostat.ec.europa.eu (accessed on 11 June 2022).
- Available online: https://theworldnews.net/lv-news/ (accessed on 11 June 2022).
- Jozwiak-Niedzwiedzka, D.; Fantilli, A.P. Wool-Reinforced Cement Based Composites. Materials 2020, 13, 3590. [Google Scholar] [CrossRef]
- Guna, V.; Ilangovan, M.; Vighnesh, H.R.; Sreehari, B.R.; Abhijith, S.; Sachin, H.E.; Mohan, C.B.; Reddy, N. Engineering Sustainable Waste Wool Biocomposites with High Flame Resistance and Noise Insulation for Green Building and Automotive Applications. J. Nat. Fibers 2021, 18, 1871–1881. [Google Scholar] [CrossRef]
- Beckman, I.P.; Lozano, C.; Freeman, E.; Riveros, G. Fiber Selection for Reinforced Additive Manufacturing. Polymers 2021, 13, 2231. [Google Scholar] [CrossRef]
- Alyousef, R.; Mohammadhosseini, H.; Ebid, A.A.K.; Alabduljabbar, H. An Integrated Approach to Using Sheep Wool as a Fibrous Material for Enhancing Strength and Transport Properties of Concrete Composites. Materials 2022, 15, 1638. [Google Scholar] [CrossRef]
- Parlato, M.C.M.; Cuomo, M.; Porto, S.M.C. Natural fibers reinforcement for earthen building components: Mechanical performances of a low quality sheep wool (“Valle del Belice” sheep). Constr. Build. Mater. 2020, 326, 126855. [Google Scholar] [CrossRef]
- Kim, N.K.; Lin, R.J.T.; Bhattacharyya, D. Extruded short wool fibre composites: Mechanical and fire retardant properties. Compos. Part B 2014, 67, 472–480. [Google Scholar] [CrossRef]
- Santulli, C.; Sarasini, F.; Tirillo, J.; Valente, T.; Valente, M.; Caruso, A.P.; Infantino, M.; Nisini, E.; Minak, G. Mechanical behaviour of jute cloth/wool felts hybrid laminates. Mater. Des. 2013, 50, 309–321. [Google Scholar] [CrossRef]
- Conzatti, L.; Giunco, F.; Stagnaro, P.; Patrucco, A.; Marano, C.; Rink, M.; Marsano, E. Composites based on polypropylene and short wool fibres. Compos. Part A 2013, 47, 165–171. [Google Scholar] [CrossRef]
- Manivannan, J.; Rajesh, S.; Mayandi, K.; Rajini, N.; Ismail, S.O.; Mohammad, F.; Kuzman, M.K.; Al-Lohedan, H.A. Animal fiber characterization and fiber loading effect on mechanical behaviors of sheep wool fiber reinforced polyester composites. J. Nat. Fibers 2020, 1–17. [Google Scholar] [CrossRef]
- Aida, H.J.; Nadlene, R.; Mastura, M.T.; Yusriah, L.; Sivakumar, D.; Ilyase, R.A. Natural fibre filament for Fused Deposition Modelling (FDM): A review. Int. J. Sustain. Eng. 2021, 14, 1988–2008. [Google Scholar] [CrossRef]
- Bouagga, T.; Harizi, T.; Sakli, F.; Zoccola, M. Correlation between the mechanical behavior and chemical, physical and thermal characteristics of wool: A study on Tunisian wool. J. Nat. Fibers 2020, 17, 28–40. [Google Scholar] [CrossRef]
- Rama Rao, D.; Gupta, V.B. Crystallite orientation in wool fibers. J. Appl. Polym. Sci. 1992, 46, 1109–1112. [Google Scholar] [CrossRef]
- Andersons, J.; Sparnins, E.; Joffe, R.; Wallstrom, L. Strength distribution of elementary flax fibres. Compos. Sci. Technol. 2005, 65, 693–702. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Pan, N. Weibull analysis of the tensile behavior of fibers with geometrical irregularities. J. Mater. Sci. 2002, 37, 1401–1406. [Google Scholar] [CrossRef] [Green Version]
- Sia, C.V.; Fernando, L.; Joseph, A.; Chua, S.N. Modified Weibull analysis on banana fiber strength prediction. J. Mech. Eng. Sci. 2018, 12, 3461–3471. [Google Scholar] [CrossRef]
- Andersons, J.; Poriķe, E.; Spārniņš, E. Modeling strength scatter of elementary flax fibers: The effect of mechanical damage and geometrical characteristics. Compos. Part A Appl. Sci. 2011, 42, 543–549. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, T.H.; Chen, B.W.; Cheng, L. Tensile strength analysis of palm leaf sheath fiber with Weibull distribution. Compos. Part A 2014, 62, 45–51. [Google Scholar] [CrossRef]
- Joffe, R.; Andersons, J.; Spārniņš, E. Applicability of Weibull strength distribution for cellulose fibers with highly non-linear behavior. In Proceedings of the International Conference of Composite Materials (ICCM-17), Edinburgh, UK, 27–31 July 2009. [Google Scholar]
- Shebanov, S.M. Extreme Values of the Strength of Single Filaments and Threads of a Paraaramide Fiber After Its Treatment by a Water Suspension of Carbon Nanoparticles. Mech. Compos. Mater. 2021, 57, 269–272. [Google Scholar] [CrossRef]
- Starkova, O.; Gagani, A.I.; Karl, C.W.; Rocha, I.B.C.M.; Burlakovs, J.; Krauklis, A.E. Modelling of Environmental Ageing of Polymers and Polymer Composites—Durability Prediction Methods. Polymers 2022, 14, 907. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Shi, J.; Zhou, N.; Tuo, X.; Gong, Y.; Guo, J. Study on the Relationship between Accelerated Aging, Color Characterization and Properties of Natural Fibers. J. Nat. Fibers 2021, 1–11. [Google Scholar] [CrossRef]
- Lu, D.; Yu, W.; Pan, N. Determination of the strength and elongation distribution of single wool through fiber bundle testing based on acoustic emissions. Text. Res. J. 2021, 91, 1263–1273. [Google Scholar] [CrossRef]
- Lu, D.; Yu, W. Characterization and analysis of the tensile and acoustic emission parameter distributions of single wool fibers. Text. Res. J. 2020, 90, 2454–2466. [Google Scholar] [CrossRef]
- Ntenga, R.; Saïdjo, S.; Beda, T.; Béakou, A. Estimation of the Effects of the Cross-Head Speed and Temperature on the Mechanical Strength of Kenaf Bast Fibers Using Weibull and Monte-Carlo Statistics. Fibers 2019, 7, 89. [Google Scholar] [CrossRef] [Green Version]
- Naik, D.L.; Fronk, T.H. Weibull Distribution Analysis of the Tensile Strength of the Kenaf Bast Fiber. Fibers Polym. 2016, 17, 1696–1701. [Google Scholar] [CrossRef]
- Gutans, J.A.; Tamuzh, V.P. Scale Effect of the Weibull Distribution of Fibre Strength. Mech. Compos. Mater. 1984, 6, 1107–1109. [Google Scholar]
- Watson, A.S.; Smith, R.L. An examination of statistical theories for fibrous materials in the light of experimental data. J. Mater. Sci. 1985, 20, 3260–3270. [Google Scholar] [CrossRef]
- Karimah, A.; Ridho, M.R.; Munawar, S.S.; Adi, D.S.; Ismadi; Damayanti, R.; Subiyanto, B.; Fatriasari, W.; Fudholi, A. A review on natural fibers for development of eco-friendly bio-composite: Characteristics, and utilizations. J. Mater. Res. Technol. 2021, 13, 2442–2458. [Google Scholar] [CrossRef]
- Starkova, O.; Platnieks, O.; Sabalina, A.; Gaidukovs, S. Hydrothermal Ageing Effect on Reinforcement Efficiency of Nanofibrillated Cellulose/Biobased Poly(butylene succinate) Composites. Polymers 2022, 14, 221. [Google Scholar] [CrossRef]
- Nogueira, A.C.S.; Dicelio, L.E.; Joekes, I. Photochem. About photo-damage of human hair. Photobiol. Sci. 2006, 5, 165–169. [Google Scholar] [CrossRef] [Green Version]
- Dyer, J.M.; Plowman, J.E.; Krsinic, G.L.; Deb-Choudhury, S.; Koehn, H.; Millington, K.R.; Clerens, S. Proteomic evaluation and location of UVB-induced photo-oxidation in wool. J. Photochem. Photobiol. B Biol. 2010, 98, 118–127. [Google Scholar] [CrossRef]
- Mozziconacci, O.; Schöneich, C. Chemical degradation of proteins in the solid state with a focus on photochemical reactions. Adv. Drug Deliv. Rev. 2015, 93, 2–13. [Google Scholar] [CrossRef]

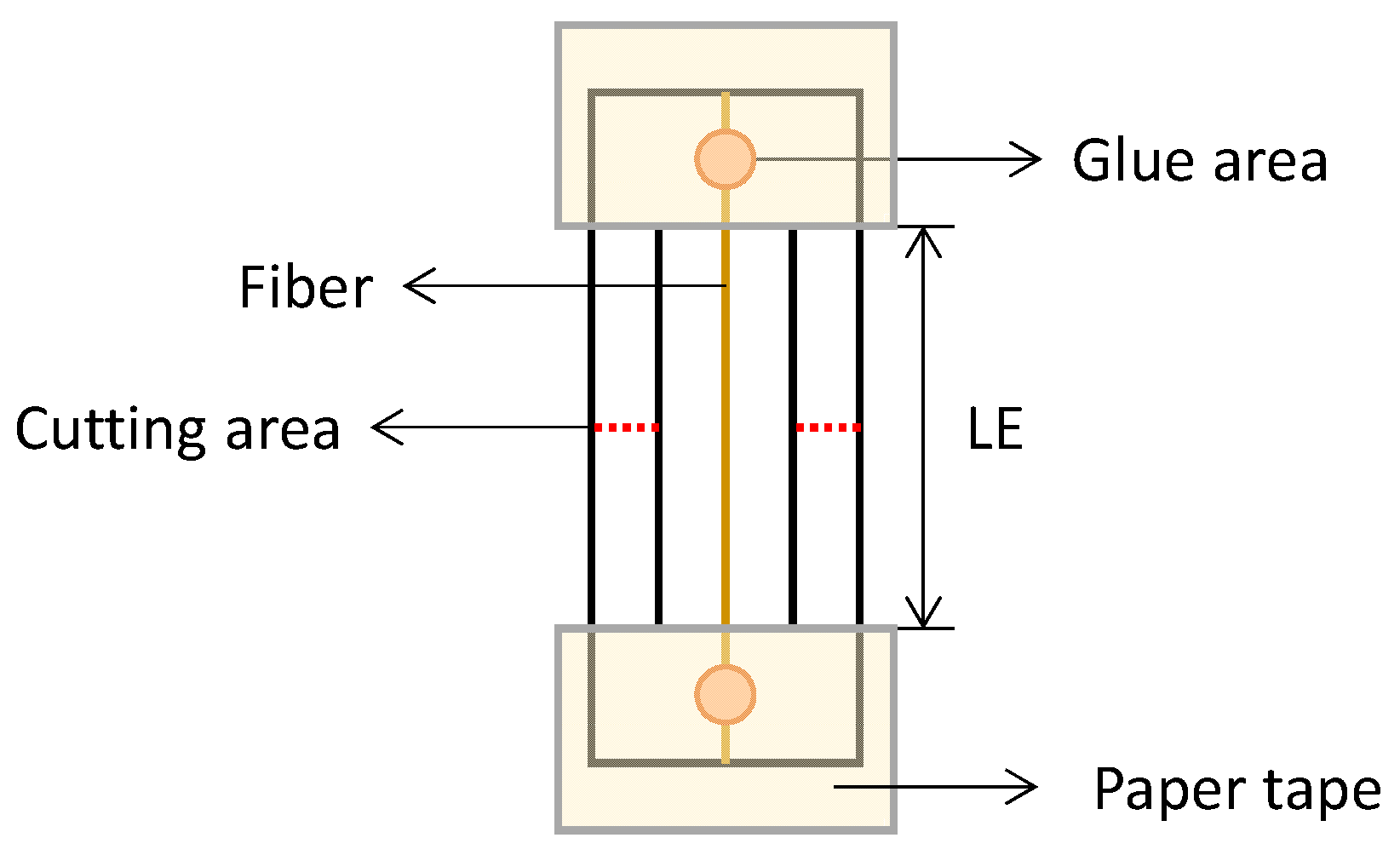






| Notation | Environment | Duration | Gauge Length (LE), mm |
|---|---|---|---|
| Ref | Ambient: RH = 37 ± 5%, T = 22 ± 2 °C | - | 10, 30, 50 |
| RH98 | RH = 98%, T = 22 ± 2 °C | 1 week | 10, 30, 50 |
| RH98-ext | RH = 98%, T = 22 ± 2 °C | 2 months | 30 |
| UV | I = 4 mW/cm2, T = 35 ± 2 °C; “Ref” fibers | 24 h | 10, 30, 50 |
| UV-RH98 | I = 4 mW/cm2, T = 35 ± 2 °C; “RH98” fibers | 24 h | 30 |
| Environment | LE, mm | Number of Tests | <d> 1, μm | <E>, GPa | <σ>, MPa | <ε>, % | m | σ0 (R2, %) 2 | (R2, %) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Ref | 10 | 20 | 37.63 (±4.50) | 4.58 (±1.13) | 178.0 (±37.2) | 34.4 (±13.1) | 4.80 | 311.6 (96%) | 2.77 | 90.6 (94%) |
| 30 | 42 | 38.14 (±5.72) | 3.93 (±0.61) | 142.8 (±30.3) | 25.9 (±11.4) | 5.62 | 283.1 (91%) | 1.85 | 190.4 (93%) | |
| 50 | 25 | 37.14 (±4.66) | 4.16 (±0.61) | 105.8 (±31.7) | 19.7 (±11.3) | 3.59 | 353.43 (98%) | 1.47 | 324.5 (96%) | |
| RH98 | 10 | 25 | 37.29 (±4.55) | 2.31 (±0.51) | 136.0 (±28.3) | 47.0 (±12.8) | 5.33 | 226.9 (98%) | 4.57 | 86.4 (95%) |
| 30 | 30 | 41.68 (±5.39) | 3.06 (±0.59) | 124.1 (±23.8) | 25.7 (±9.8) | 5.99 | 236.2 (94%) | 2.55 | 111.0 (95%) | |
| 50 | 25 | 36.97 (±3.86) | 2.84 (±0.51) | 110.3 (±26.7) | 20.7 (±9.9) | 4.65 | 279.3 (96%) | 1.88 | 191.6 (95%) | |
| RH98-ext | 30 | 24 | 39.42 (±5.52) | 2.23 (±0.53) | 94.4 (±28.3) | 30.6 (±8.6) | 3.73 | 259.9 (98%) | 3.66 | 86.6 (97%) |
| UV | 10 | 26 | 35.97 (±3.80) | 3.24 (±0.58) | 104.5 (±26.8) | 16.7 (±12.7) | 3.95 | 207.1 (95%) | 1.32 | 103.2 (94%) |
| 30 | 23 | 40.05 (±8.10) | 3.95 (±1.23) | 82.4 (±33.9) | 8.4 (±8.0) | 2.56 | 353.2 (98%) | 1.45 | 94.8 (79%) | |
| 50 | 25 | 34.83 (±5.00) | 4.02 (±0.66) | 88.8 (±16.9) | 6.1 (±5.2) | 6.06 | 182.2 (95%) | 1.72 | 65.8 (77%) | |
| UV-RH98 | 30 | 26 | 40.09 (±5.89) | 2.95 (±0.76) | 66.6 (±22.1) | 9.0 (±7.0) | 3.05 | 228.7 (98%) | 1.66 | 77.9 (89%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starkova, O.; Sabalina, A.; Voikiva, V.; Osite, A. Environmental Effects on Strength and Failure Strain Distributions of Sheep Wool Fibers. Polymers 2022, 14, 2651. https://doi.org/10.3390/polym14132651
Starkova O, Sabalina A, Voikiva V, Osite A. Environmental Effects on Strength and Failure Strain Distributions of Sheep Wool Fibers. Polymers. 2022; 14(13):2651. https://doi.org/10.3390/polym14132651
Chicago/Turabian StyleStarkova, Olesja, Alisa Sabalina, Vanda Voikiva, and Agnese Osite. 2022. "Environmental Effects on Strength and Failure Strain Distributions of Sheep Wool Fibers" Polymers 14, no. 13: 2651. https://doi.org/10.3390/polym14132651