Mechanical Testing and Modeling of the Time–Temperature Superposition Response in Hybrid Fiber Reinforced Composites
Abstract
:1. Introduction
2. Materials and Experimental Procedures
2.1. Composite Materials
2.2. Hybrid Laminates Fabrication
2.3. Three-Point Bending Test
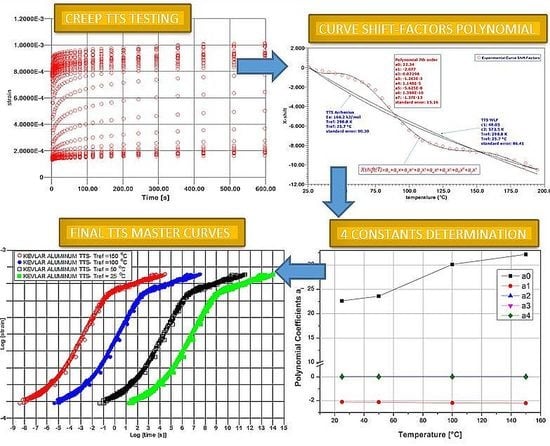
2.4. Thermomechanical Testing and Modeling
2.5. Scanning Electron Microscopy
3. Results & Discussion
3.1. Three-Point Bending Test
3.2. Thermomechanical Testing
3.2.1. Creep Time–Temperature Superposition (TTS) Testing
3.2.2. Dynamic Mechanical Analysis (DMA)
3.3. Scanning Electron Microscopy Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, Q.; Omar, M.; Dongri, S. Ultrasonic NDE Techniques for Impact Damage Inspection on CFRP Laminates. J. Mater. Sci. Res. 2012, 1. [Google Scholar] [CrossRef]
- Kiran, R.; Vasudevan, A.; Pugazhendhi, L. A review on different hybrid composites for aircraft structures. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Bin, H.; Boyao, W.; Zhanwen, W.; Shengli, Q.; Guofeng, T.; Dezhen, W. Mechanical properties of hybrid composites reinforced by carbon fiber and high-strength and high-modulus polyimide fiber. Polymer 2020, 204. [Google Scholar] [CrossRef]
- Don, C. Flexural behaviour of carbon and glass reinforced hybrid composite pipes. Composites 2021, 4. [Google Scholar] [CrossRef]
- Siva, R.; Kesavaram, B.; Martin, J.J.; Mathiselvan, G.; Bantha, N.; Sangeetha, M. Mechanical behavior of sisal and banana fiber reinforced hybrid epoxy composites. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Rana, R.S.; Buddi, T.; Purohit, R. Effect of SiC reinforcement on the mechanical properties of Kevlar fiber based hybrid epoxy composites. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Ramesh, V.; Anand, P. Evaluation of mechanical properties on Kevlar/Basalt fiber reinforced hybrid composites. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Shaari, N.; Wahab, M.F.A.; Shaari, N.S.; Jumahat, A. Unhole and open hole tensile properties of hybrid Kevlar/glass fiber polymer composites with different stacking sequence. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Zeno, M.; Mahisham, I.; Mahadi, M.F.; Mhod Amin, A.N.; Ahmad, S.I.; Mahmud, J. Deformation and failure behavior of hybrid composite laminates made of Glass Epoxy and woven Kevlar Epoxy. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Nunes, J.; Pouzada, A.; Bernardo, C. The use of a three-point support flexural test to predict the stiffness of anisotropic composite plates in bending. Polym. Test. 2002, 21, 27–33. [Google Scholar] [CrossRef] [Green Version]
- Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials; ASTM: West Conshohocken, PA, USA, 2007.
- Hallet, S. Three-point beam impact tests on T300/914 carbon-fibre composites. Compos. Sci. Technol. 2000, 60, 115–124. [Google Scholar] [CrossRef]
- Azzam, A.; Li, W. An experimental investigation on the three-point bending behavior of composite laminate. IOP Conf. Ser. Mater. Sci. Eng. 2014, 62. [Google Scholar] [CrossRef]
- Vargas, G.; Mujika, F. Determination of in-plane shear properties by three-point flexure test of ±45° anti-symmetric laminates. Polym. Test. 2011, 30, 204–215. [Google Scholar] [CrossRef]
- Ary Subagia, I.D.G.; Kim, Y.; Tijing, L.D.; Kim, C.S.; Shon, H.K. Effect of stacking sequence on the flexural properties of hybrid composites reinforced with carbon and basalt fibers. Compos. Part B Eng. 2014, 58, 251–258. [Google Scholar] [CrossRef]
- Belingardi, G.; Cavatorta, M.P. Bending fatigue stiffness and strength degradation in carbon–glass/epoxy hybrid laminates: Cross-ply vs. angle-ply specimens. Int. J. Fatigue 2006, 28, 815–825. [Google Scholar] [CrossRef]
- Carbajal, N.; Mujika, F. An experimental investigation on the three-point bending behavior of composite laminate. Polym. Test. 2009, 28, 618–626. [Google Scholar] [CrossRef]
- de Baere, I.; van Paepegem, W.; Degrieck, J. Comparison of different setups for fatigue testing of thin composite laminates in bending. Int. J. Fatigue 2009, 31, 1095–1101. [Google Scholar] [CrossRef]
- Fujihara, K.; Huang, Z.M.; Ramakrishna, S.; Hamada, H. Influence of processing conditions on bending property of continuous carbon fiber reinforced PEEK composites. Compos. Sci. Technol. 2004, 64, 2525–2534. [Google Scholar] [CrossRef]
- Tomita, Y.; Morioka, K.; Iwasa, M. Bending fatigue of long carbon fiber-reinforced epoxy composites. Mater. Sci. Eng. A 2001, 319–321, 679–682. [Google Scholar] [CrossRef]
- Naya, S.; Meneses, A.; Tarrío-Saavedra, J.; Artiaga, R.; López-Beceiro, J.; Gracia-Fernández, C. New method for estimating shift factors in time–temperature superposition models. J. Therm. Anal. Calorim. 2013, 113, 453–460. [Google Scholar] [CrossRef]
- Ionita, D.; Cristea, M.; Gaina, C. Prediction of polyurethane behaviour via time-temperature superposition: Meanings and limitations. Polym. Test. 2020, 83, 106340. [Google Scholar] [CrossRef]
- Fesko, D.G.; Tschoegl, Ν.W. Time temperature superposition in thermorheologically complex materials. J. Polym. Sci. Part C Polym. Symp. 2007, 35, 51–69. [Google Scholar] [CrossRef]
- Ljubić, D.; Stamenovic, M.; Smithon, C.; Nujkic, M.; Medo, B.; Putic, S. Time: Temperature superposition principle: Application of WLF equation in polymer analysis and composites. Zaštita Mater. 2014, 55, 395–400. [Google Scholar] [CrossRef] [Green Version]
- Nosrati, N.; Ahad, Z.; Samaneh, S. Long-term creep behaviour of E-glass/epoxy composite: Time-temperature superposition principle. Plast. Rubber Compos. 2020, 49, 254–262. [Google Scholar] [CrossRef]
- Ornaghi, H.; Almeida, J.M.; Monticeli, F.; Neves, R.; Cioffi, M.D. Time-temperature behavior of carbon/epoxy laminates under creep loading. Mech. Time-Depend. Mater. 2020, 1–15. [Google Scholar] [CrossRef]
- Guedes, R.M.; Alcides, S.; Hugo, F. Influence of moisture absorption on creep of GRP composite pipes. Polym. Test. 2007, 26, 595–605. [Google Scholar] [CrossRef]
- Guedes, R.M.; Rui, M. A viscoelastic model for a biomedical ultra-high molecular weight polyethylene using the time–temperature superposition principle. Polym. Test. 2011, 30, 294–302. [Google Scholar] [CrossRef]















| Property | Aramid Fabric | Vectran Fabric | Fiberglass/Aluminum Fabric |
|---|---|---|---|
| Tensile strength (MPa) | 2863 | 2860–3206 | 2750 |
| Elastic modulus (Gpa) | 67 | 64–72 | 75 |
| Fracture strain (%) | 3.7 | 3.3–3.7 | 1.8–3.2 |
| Mass per unit of area (gr/m2) | 460 | 200 | 200 |
| Weave | Plain | Twill 2 × 2 | Twill 2 × 2 |
| Warp (ends(threads)/cm) | 6.7 | 6 | 16.8 |
| Weft (ends(threads)/cm) | 6.7 | 6 | 12 |
| Property | Fiberglass/Aluminum-Vectran Lamina | Fiberglass/Aluminum-Aramid Lamina |
|---|---|---|
| Elastic modulus (GPa) | 11.75 | 15.30 |
| Elastic fracture strain (%) | 0.89 | 0.99 |
| Yield strength (Mpa) (@max stress) | 9.78 | 9.58 |
| Residual fracture strain (%) | 6.85 | 6.97 |
| Residual fracture strength (Mpa) | 4.16 | 1.99 |
| 25 °C | 50 °C | 100 °C | 150 °C | |
|---|---|---|---|---|
| α0 | 22.64 | 23.6 | 30.12 | 32.17 |
| α1 | −2.107 | −2.123 | −2.197 | −2.214 |
| α2 | 0.07417 | 0.07461 | 0.07703 | 0.07797 |
| α3 | −1.29 × 10−3 | −1.29 × 10−3 | −1.33 × 10−3 | −1.36 × 10−3 |
| α4 | 1.18 × 10−5 | 1.17× 10−5 | 1.21 × 10−5 | 1.24 × 10−5 |
| α5 | −5.80 × 10−8 | −5.76 × 10−8 | −5.9 × 10−8 | −6.18 × 10−8 |
| α6 | 1.46 × 10−10 | 1.43 × 10−10 | 1.50 × 10−10 | 1.56 × 10−10 |
| α7 | −1.45 × 10−13 | −1.41 × 10−13 | −1.50 × 10−13 | −1.57 × 10−13 |
| 25 °C | 50 °C | 100 °C | 150 °C | |
|---|---|---|---|---|
| α0 | 27.97 | 32.18 | 37.63 | 27.97 |
| α1 | −2.515 | −2.749 | −2.77 | −2.515 |
| α2 | 8.56 × 10−2 | 0.09439 | 0.09489 | 0.08559 |
| α3 | −1.47 × 10−3 | −1.64 × 10−3 | −1.65 × 10−3 | −1.47 × 10−3 |
| α4 | 1.35 × 10−5 | 1.53 × 10−5 | 1.54 × 10−5 | 1.35 × 10−5 |
| α5 | −6.78 × 10−8 | −7.86 × 10−8 | −7.94 × 10−8 | −6.78 × 10−8 |
| α6 | 1.74 × 10−10 | 2.08 × 10−10 | 2.12 × 10−10 | 1.74 × 10−10 |
| α7 | −1.78 × 10−13 | −2.23 × 10−13 | −2.28 × 10−13 | −1.78 × 10−13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsomichalis, A.; Kalampoukas, T.; Mouzakis, D.E. Mechanical Testing and Modeling of the Time–Temperature Superposition Response in Hybrid Fiber Reinforced Composites. Polymers 2021, 13, 1178. https://doi.org/10.3390/polym13071178
Koutsomichalis A, Kalampoukas T, Mouzakis DE. Mechanical Testing and Modeling of the Time–Temperature Superposition Response in Hybrid Fiber Reinforced Composites. Polymers. 2021; 13(7):1178. https://doi.org/10.3390/polym13071178
Chicago/Turabian StyleKoutsomichalis, Aggelos, Thomas Kalampoukas, and Dionysios E. Mouzakis. 2021. "Mechanical Testing and Modeling of the Time–Temperature Superposition Response in Hybrid Fiber Reinforced Composites" Polymers 13, no. 7: 1178. https://doi.org/10.3390/polym13071178