Hysteretic Swelling/Deswelling of Polyelectrolyte Brushes and Bilayer Films in Response to Changes in pH and Salt Concentration
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Variable Angle Spectroscopic Ellipsometry (VASE)
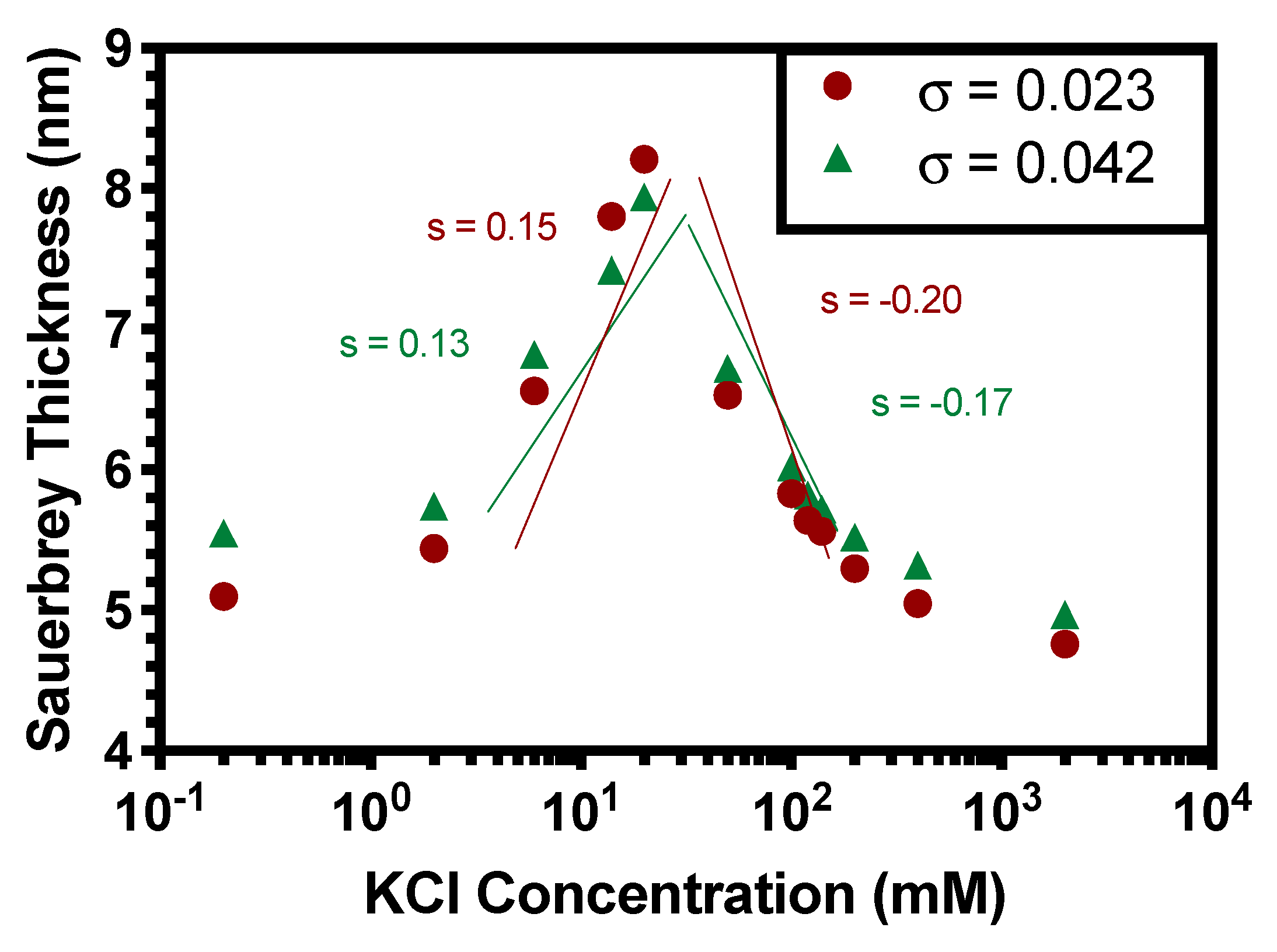
3.2. Scaling Theory for Monolayer PE Brushes and Comparison to Previous Findings
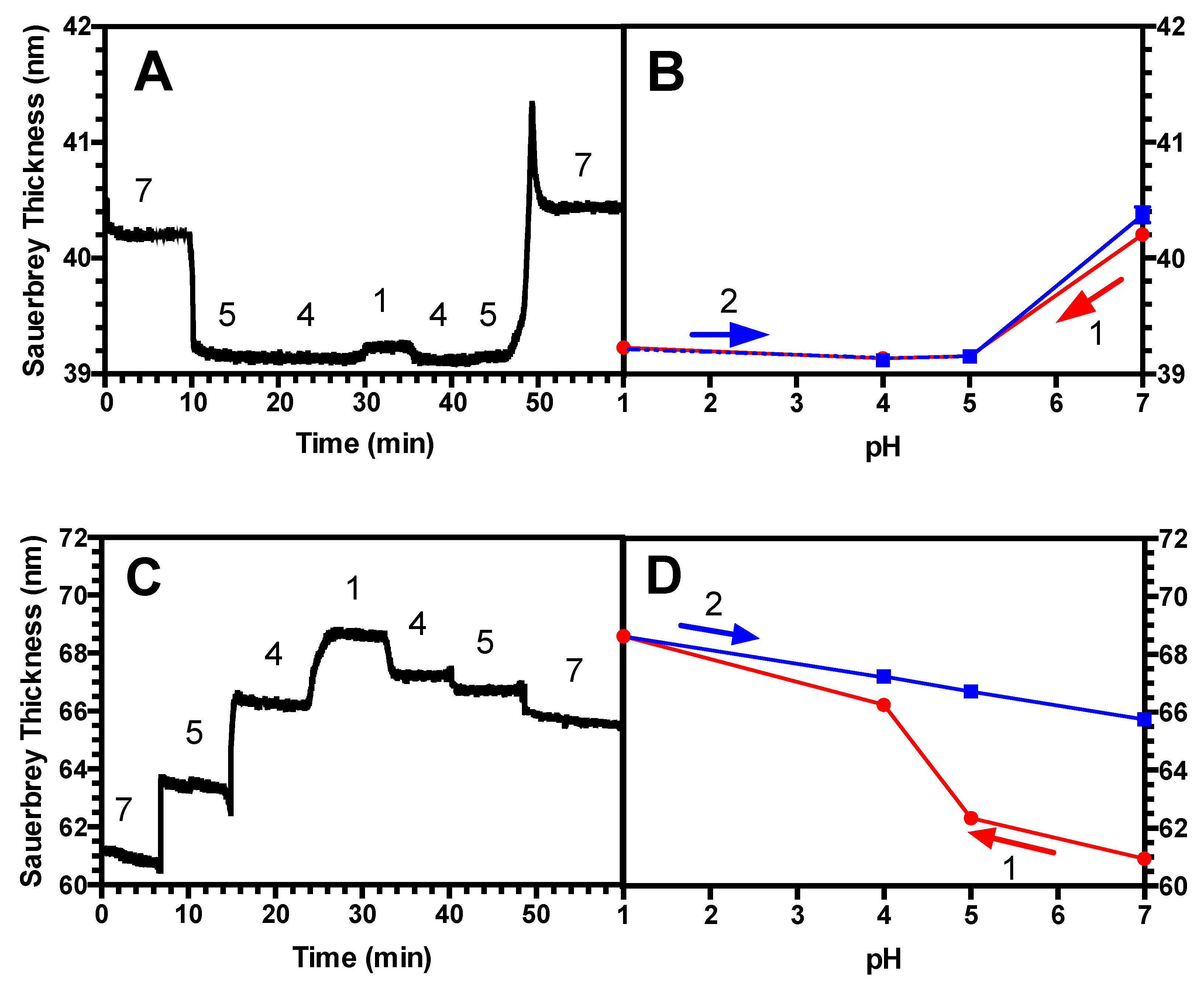
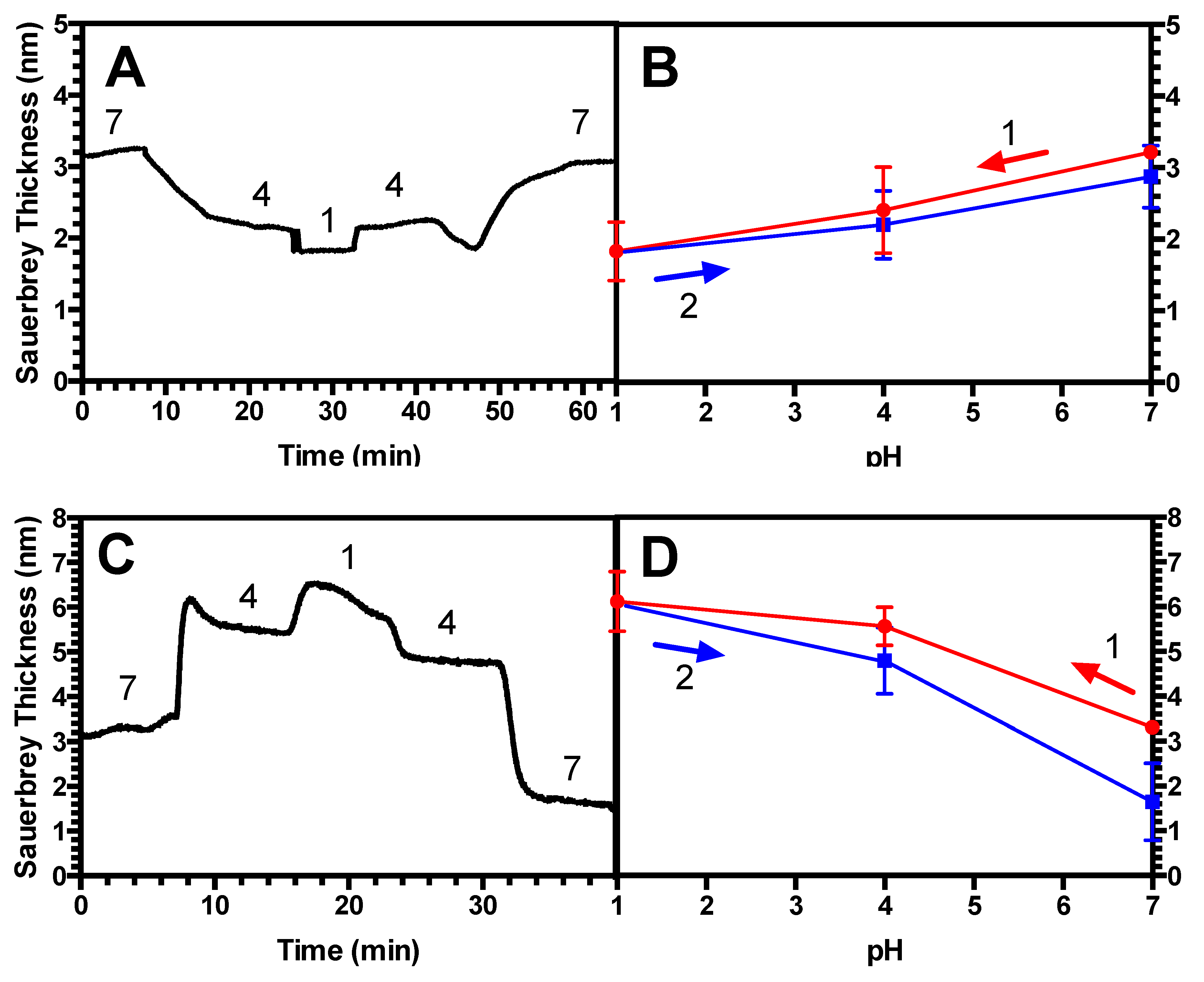
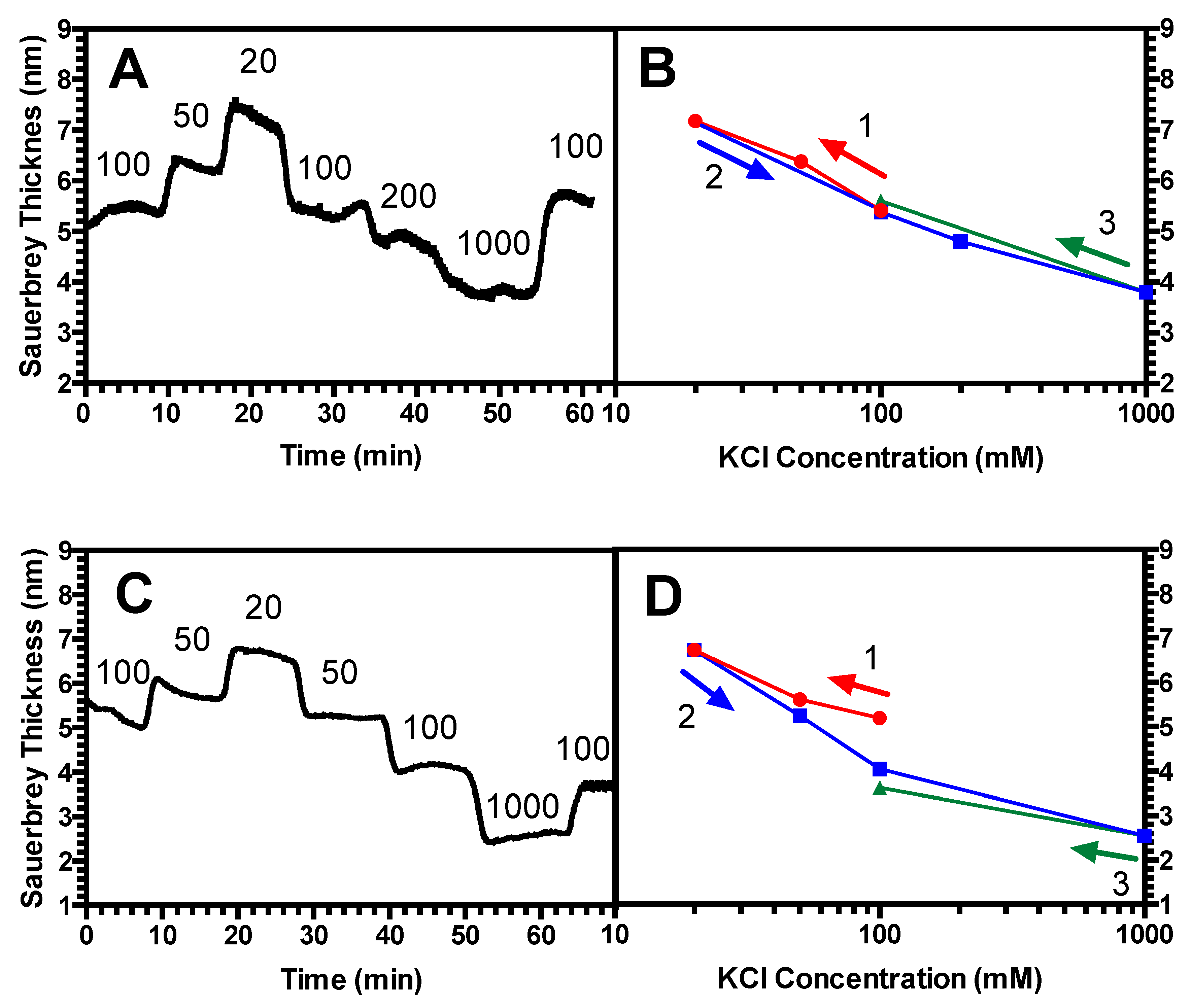
3.3. Hysteresis Studies
4. Discussion
4.1. Scaling Theory for PE Brushes in the Osmotic Brush Regime
4.2. Hysteresis in Brushes and Bilayers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pincus, P. Colloid stabilization with grafted polyelectrolytes. Macromolecules 1991, 24, 2912–2919. [Google Scholar] [CrossRef]
- Weir, M.P.; Parnell, A.J. Water Soluble Responsive Polymer Brushes. Polymers 2011, 3, 2107–2132. [Google Scholar] [CrossRef]
- Motornov, M.; Tam, K.; Pita, M.; Tokarev, I.; Katz, E.; Minko, S. Switchable selectivity for gating ion transport with mixed polyelectrolyte brushes: Approaching “smart” drug delivery systems. IOP Publ. Nanotechnol. Nanotechnol. 2009, 20, 434006–434016. [Google Scholar] [CrossRef]
- Yang, Z.; Tarabara, V.V.; Bruening, M.L. Adsorption of Anionic or Cationic Surfactants in Polyanionic Brushes and Its Effect on Brush Swelling and Fouling Resistance during Emulsion Filtration. Langmuir 2015, 31, 11790–11799. [Google Scholar] [CrossRef] [PubMed]
- Wohl, B.M.; Engbersen, J.F.J. Responsive layer-by-layer materials for drug delivery. J. Control. Release 2012, 158, 2–14. [Google Scholar] [CrossRef]
- Hammond, P.T. Engineering materials layer-by-layer: Challenges and opportunities in multilayer assembly. AIChE J. 2011, 57, 2928–2940. [Google Scholar] [CrossRef]
- Fendler, J.H. Chemical self-assembly for electronic applications. Chem. Mater. 2001, 13, 3196–3210. [Google Scholar] [CrossRef]
- Panchagnula, V.; Jeon, J.; Dobrynin, A.V. Molecular dynamics simulations of electrostatic layer-by-layer self-assembly. Phys. Rev. Lett. 2004, 93, 037801. [Google Scholar] [CrossRef]
- Van de Steeg, H.G.M.; Stuart, M.A.C.; de keizer, A.; Bijsterbosch, B.H. Polyelectrolyte Adsorption: A Subtle Balance of Forces. Langmuir 1992, 8, 2538–2546. [Google Scholar] [CrossRef]
- Patel, P.A.; Jeon, J.; Mather, P.T.; Dobrynin, A.V. Molecular Dynamics Simulations of Layer-by-Layer Assembly of Polyelectrolytes at Charged Surfaces: Effects of Chain Degree of Polymerization and Fraction of Charged Monomers. Langmuir 2005, 21, 6113–6122. [Google Scholar] [CrossRef] [PubMed]
- Salehi, A.; Larson, R.G. A transport model and constitutive equation for oppositely charged polyelectrolyte mixtures with application to layer-by-layer assembly. J. Chem. Phys. 2018, 149, 194901. [Google Scholar] [CrossRef]
- Wang, Q. Internal structure and charge compensation of polyelectrolyte multilayers: A numerical study. Soft Matter 2009, 5, 413–424. [Google Scholar] [CrossRef]
- Mecea, V.M. From Quartz Crystal Microbalance to Fundamental Principles of Mass Measurements. Anal. Lett. 2005, 38, 753–767. [Google Scholar] [CrossRef]
- Höök, F.; Kasemo, B.; Nylander, T.; Fant, C.; Sott, K.; Elwing, H. Variations in coupled water, viscoelastic properties, and film thickness of a Mefp-1 protein film during adsorption and cross-linking: A quartz crystal microbalance with dissipation monitoring, ellipsometry, and surface plasmon resonance study. Anal. Chem. 2001, 73, 5796–5804. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Zhang, G. Chapter 1: Basic Principles of QCM-D. In QCM-D Studies on Polymer Behavior at Interfaces; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; pp. 1–8. [Google Scholar]
- Hollingsworth, N.R.; Wilkanowicz, S.I.; Larson, R.G. Salt- and pH-induced swelling of a poly(acrylic acid) brush via quartz crystal microbalance w/dissipation (QCM-D). Soft Matter 2019, 15, 7838–7851. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Birshtein, T.M.; Borisov, O.V. Theory of Ionizable Polymer Brushes. Macromolecules 1995, 28, 1491–1499. [Google Scholar] [CrossRef]
- Secrist, K.E.; Nolte, A.J. Humidity Swelling/Deswelling Hysteresis in a Polyelectrolyte Multilayer Film. Macromolecules 2011, 44, 2859–2865. [Google Scholar] [CrossRef]
- Yadav, V.; Harkin, A.V.; Robertson, M.L.; Conrad, J.C. Hysteretic memory in pH-response of water contact angle on poly(acrylic acid) brushes. Soft Matter 2016, 12, 3589. [Google Scholar] [CrossRef] [PubMed]
- Aulich, D.; Hoy, O.; Luzinov, I.; Brücher, M.; Hergenröder, R.; Bittrich, E.; Eichhorn, K.-J.; Uhlmann, P.; Stamm, M.; Esser, N.; et al. In Situ Studies on the Switching Behavior of Ultrathin Poly(acrylic acid) Polyelectrolyte Brushes in Different Aqueous Environments. Langmuir 2010, 26, 12926–12932. [Google Scholar] [CrossRef] [PubMed]
- Pryamitsyn, V.A.; Leermakers, F.A.M.; Fleer, G.J.; Zhulina, E.B. Theory of the Collapse of the Polyelectrolyte Brush. Macromolecules 1996, 29, 8260–8270. [Google Scholar] [CrossRef]
- Almeida, B.; Shukla, A. Degradation of alkanethiol self-assembled monolayers in mesenchymal stem cell culture. J. Biomed. Mater. Res. Part A 2017, 105A, 464–474. [Google Scholar] [CrossRef]
- Bittrich, E.; Rodenhausen, K.B.; Eichhorn, K.-J.; Hofmann, T.; Schubert, M.; Stamm, M.; Uhlmann, P. Protein adsorption on and swelling of polyelectrolyte brushes: A simultaneous ellipsometry-quartz crystal microbalance study. Biointerphases 2010, 5, 159–167. [Google Scholar] [CrossRef] [PubMed]
- Tompkins, H.G. A User’s Guide to Ellipsometry; Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Herzinger, C.M.; Yao, H.; Snyder, P.G.; Celii, F.G.; Kao, Y.-C.; Johs, B.; Woollam, J.A. Determination of AlAs optical constants by variable angle spectroscopic ellipsometry and a multisample analysis. J. Appl. Phys. 1995, 77, 4677–4687. [Google Scholar] [CrossRef][Green Version]
- Denolf, G.C.; Sturdy, L.F.; Shull, K.R. High-Frequency Rheological Characterization of Homogeneous Polymer Films with the Quartz Crystal Microbalance. Langmuir 2014, 30, 9731–9740. [Google Scholar] [CrossRef] [PubMed]
- Sadman, K.; Wiener, C.G.; Weiss, R.A.; White, C.C.; Shull, K.R.; Vogt, B.D. Quantitative Rheometry of Thin Soft Materials Using the Quartz Crystal Microbalance with Dissipation. Anal. Chem. 2018, 90, 4079–4088. [Google Scholar] [CrossRef]
- Dixon, M.C. Quartz crystal microbalance with dissipation monitoring: Enabling real-time characterization of biological materials and their interactions. J. Biomol. Tech. 2008, 19, 151–158. [Google Scholar] [PubMed]
- Alassi, A.; Benammar, M.; Brett, D. Quartz Crystal Microbalance Electronic Interfacing Systems: A Review. Sensors 2017, 17, 2799. [Google Scholar] [CrossRef]
- Zhang, X.; Chu, S.S.; Ho, J.R.; Grigoropoulos, C.P. Excimer laser ablation of thin gold films on a quartz crystal microbalance at various argon background pressures. Appl. Phys. A Mater. Sci. Process. 1997, 64, 545–552. [Google Scholar] [CrossRef]
- Sauerbrey, G. Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung. Z. Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Chu, X.; Yang, J.; Liu, G.; Zhao, J. Swelling enhancement of polyelectrolyte brushes induced by external ions. Soft Matter 2014, 10, 5568–5578. [Google Scholar] [CrossRef]
- Zhou, T.; Qi, H.; Han, L.; Barbash, D.; Li, C.Y. Towards controlled polymer brushes via a self-assembly-assisted-grafting-to approach. Nat. Commun. 2016, 7, 11119. [Google Scholar] [CrossRef]
- Hiller, A.; Rubner, M.F. Reversible Molecular Memory and pH-Switchable Swelling Transitions in Polyelectrolyte Multilayers. Macromolecules 2003. [Google Scholar] [CrossRef]
- Silva, J.M.; Caridade, S.G.; Costa, R.R.; Alves, N.M.; Groth, T.; Picart, C.; Reis, R.L.; Mano, J.F. PH Responsiveness of Multilayered Films and Membranes Made of Polysaccharides. Langmuir 2015, 31, 11318–11328. [Google Scholar] [CrossRef]
- Sukhorukov, G.B.; Schmitt, J.; Decher, G. Reversible swelling of polyanion/polycation multilayer films in solutions of different ionic strength. Ber. Bunsenges. Phys. Chem. 1996, 100, 948–953. [Google Scholar] [CrossRef]
- Nolte, A.J.; Takane, N.; Hindman, E.; Gaynor, W.; Rubner, M.F.; Cohen, R.E. Thin film thickness gradients and spatial patterning via salt etching of polyelectrolyte multilayers. Macromolecules 2007, 40, 5479–5486. [Google Scholar] [CrossRef]
- Wu, T.; Gong, P.; Szleifer, I.; Vlček, P.; Šubr, V.; Genzer, J. Behavior of Surface-Anchored Poly(acrylic acid) Brushes with Grafting Density Gradients on Solid Substrates: 1. Experiment. Macromolecules 2007, 40, 8756–8764. [Google Scholar] [CrossRef]
- Leyte, J.C.; Arbouw-van Der Veen, H.M.R.; Zuiderweg, L.H. Irreversible potentiometric behavior of isotactic poly(methacrylic acid). J. Phys. Chem. 1972, 76, 2559–2561. [Google Scholar] [CrossRef]
- Ghasemi, M.; Larson, R.G. Role of Electrostatic Interactions in Charge Regulation of Weakly Dissociating Polyacids. Prog. Polym. Sci. 2020, 101322. [Google Scholar] [CrossRef]


| Type of Material | Chain Length PAA/PEI (kDa) | PAA Brush Grafting Density, (Chains/nm2) | Dry Thickness (nm) |
|---|---|---|---|
| (PAA/PEI) Bilayer | 2/2.5 | 0.87 | 2.80 nm ± 0.21 |
| PAA brush only | 2 | 0.87 | 2.66 nm ± 0.13 |
| (PAA/PEI) Bilayer | 14/10 | 0.060 | 1.70 nm ± 0.19 |
| PAA brush only | 14 | 0.060 | 1.29 nm ± 0.11 |
| (PAA/PEI) Bilayer | 39/25 | 0.45 | 34.3 nm ± 1.13 |
| PAA brush only | 39 | 0.45 | 27.0 nm ± 2.04 |
| (PAA/PEI) Bilayer | 39/25 | 0.023 | 2.02 nm ± 0.22 |
| PAA brush only | 39 | 0.023 | 1.27 nm ± 0.17 |
| PAA brush only | 39 | 0.042 | 2.32 nm ± 0.24 |
| Type of Material | PAA Brush Grafting Density, (Chains/nm2) | Chain Length (kDa) PAA, PEI | Hysteresis Observed |
|---|---|---|---|
| (PAA/PEI) Bilayer | 0.87 | 2, 2.5 | No |
| PAA brush only | 0.87 | 2 | No |
| (PAA/PEI) Bilayer | 0.06 | 14, 10 | ** |
| PAA brush only | 0.06 | 14 | ** |
| (PAA/PEI) Bilayer | 0.45 | 39, 25 | Yes |
| PAA brush only | 0.45 | 39 | No |
| (PAA/PEI) Bilayer | 0.023 | 39, 25 | Yes |
| PAA brush only | 0.023 | 39 | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hollingsworth, N.; Larson, R.G. Hysteretic Swelling/Deswelling of Polyelectrolyte Brushes and Bilayer Films in Response to Changes in pH and Salt Concentration. Polymers 2021, 13, 812. https://doi.org/10.3390/polym13050812
Hollingsworth N, Larson RG. Hysteretic Swelling/Deswelling of Polyelectrolyte Brushes and Bilayer Films in Response to Changes in pH and Salt Concentration. Polymers. 2021; 13(5):812. https://doi.org/10.3390/polym13050812
Chicago/Turabian StyleHollingsworth, Nisha, and Ronald G. Larson. 2021. "Hysteretic Swelling/Deswelling of Polyelectrolyte Brushes and Bilayer Films in Response to Changes in pH and Salt Concentration" Polymers 13, no. 5: 812. https://doi.org/10.3390/polym13050812
APA StyleHollingsworth, N., & Larson, R. G. (2021). Hysteretic Swelling/Deswelling of Polyelectrolyte Brushes and Bilayer Films in Response to Changes in pH and Salt Concentration. Polymers, 13(5), 812. https://doi.org/10.3390/polym13050812






