Modeling Spring-In of L-Shaped Structural Profiles Pultruded at Different Pulling Speeds †
Abstract
:1. Introduction
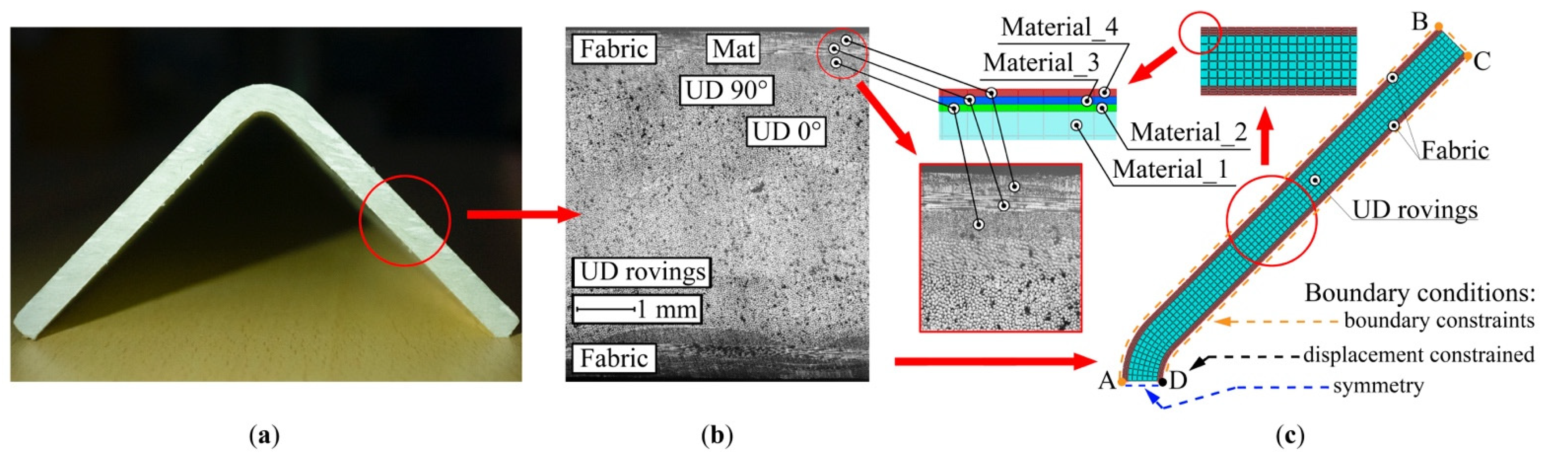
2. Materials and Methods
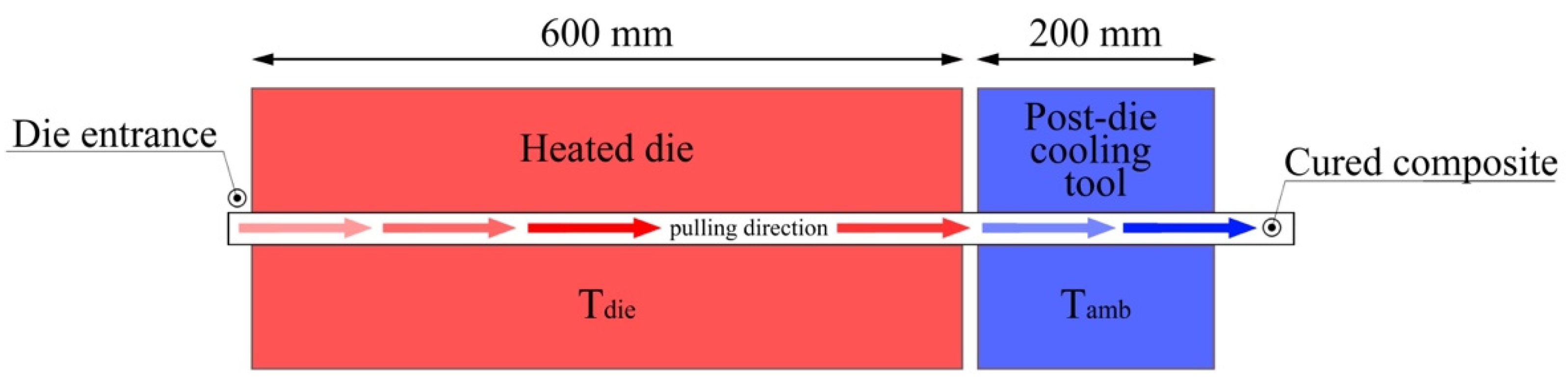
2.1. Pultrusion Manufacturing
2.2. Modeling
2.2.1. 2D Thermal Model
2.2.2. 2D Mechanical Model
2.2.3. Finite Element Modeling
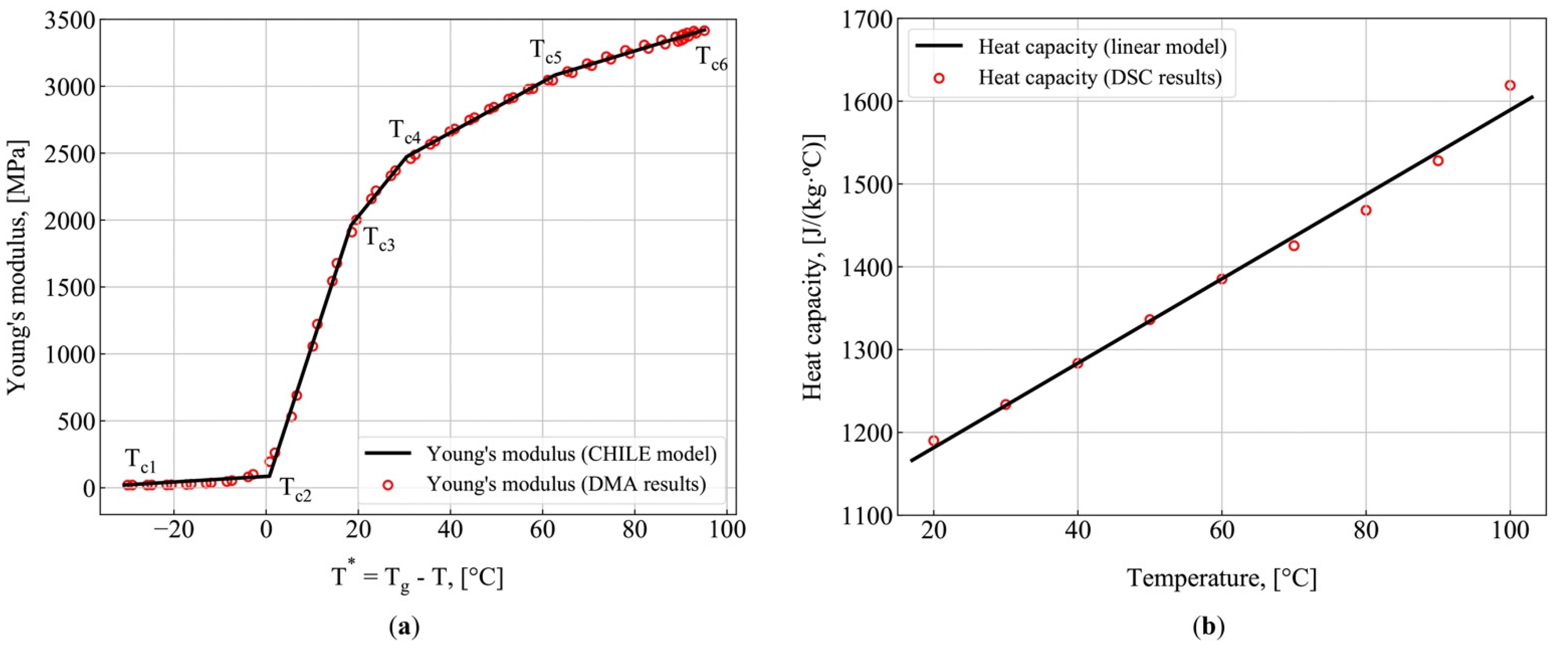
2.3. Experimental Methods to Determine Model Parameters
3. Results
3.1. Model Parameters
3.2. Finite Element Modeling Results
4. Discussion
5. Conclusions
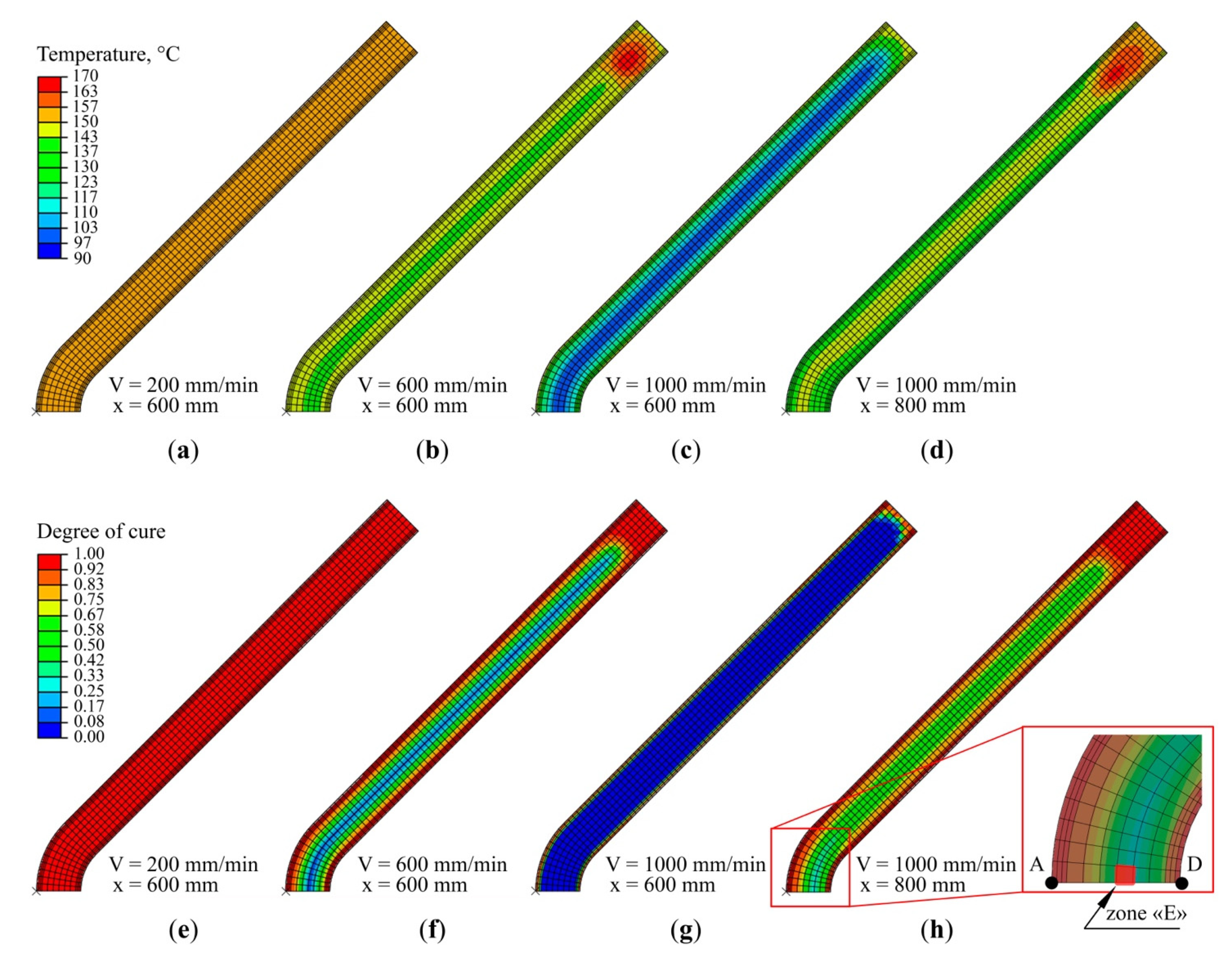
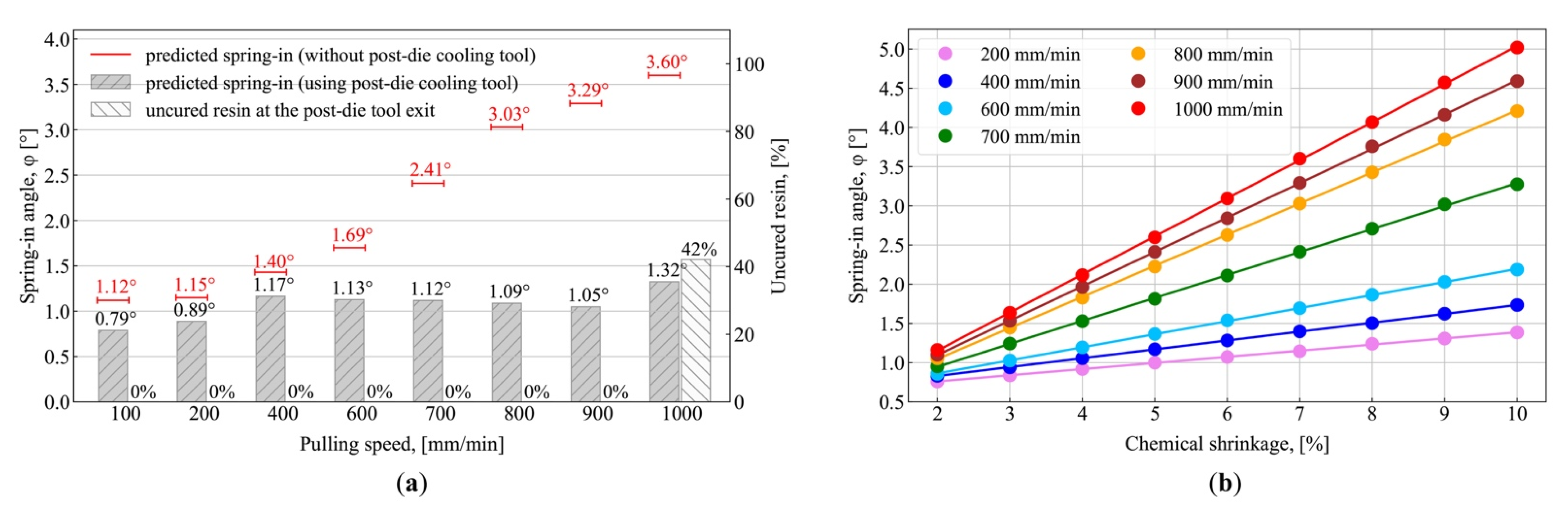
- The final value of spring-in depends on the position of the exothermic peak and vitrification point on the pultrusion line, relative to the end of the constrained region of the die, which, in turn, is determined by the selected pulling speed. The closer the exothermic peak position to the constrained region of the die, the lower the obtained spring-in values. Alternatively, higher spring-in values can be observed with the increase in the distance of the peak from the die exit because the composite can no longer sustain stresses from chemical shrinkage in the unconstrained environment of the post-die region. It was shown that higher pulling speeds result in a higher fraction of uncured material in a composite exiting the constrained environment of the die block. This leads to an increase in the total chemical shrinkage of the material under unconstrained conditions and, hence, results in increased values of spring-in;
- Starting from the pulling speed of 400 mm/min, the largest contribution to spring-in comes from the chemical shrinkage of the resin, which takes place before the exothermic peak (Stage I), and from thermal shrinkage taking place before vitrification of the composite (Stage II). However, at the cooling stage (Stage III), thermal shrinkage resulted only in a slight increase in spring-in. The higher pulling speeds increase the contribution from Stage I and reduce the role of Stage II, while the spring-in contribution from Stage III remains unchanged;
- The use of a post-die cooling tool or reduction of resin chemical shrinkage allows a minimum of 4.5 times increase in process output to be obtained while preserving the same level of spring-in.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
| density of resin, kg/m3 | |
| density of fiber, kg/m3 | |
| density of composite, kg/m3 | |
| thermal conductivity of resin, W/(m·°C) | |
| thermal conductivity of the fiber in the transverse direction, W/(m·°C) | |
| thermal conductivity of the fiber in the longitudinal direction, W/(m·°C) | |
| thermal conductivity in the cross-sectional plane, W/(m·°C) | |
| instantaneous temperature, °C | |
| temperature-dependent heat capacity of resin, J/(kg·°C) | |
| heat capacity of the fiber, J/(kg·°C) | |
| temperature-dependent heat capacity of a composite, J/(kg·°C) | |
| time, sec | |
| heat released due to the exothermic reaction in polymer matrix, kJ | |
| coordinates of a cross-section of the composite profile, mm | |
| coordinate of a composite cross-section along the pulling direction of pultrusion, mm | |
| convective heat transfer coefficient between the die block and the profile, W/(m2·°C) | |
| convective heat transfer coefficient between the ambient air and the profile after the die block exit, W/(m2·°C) | |
| resin degree of cure | |
| resin curing rate, 1/s | |
| pre-exponential coefficient, 1/s | |
| activation energy, kJ/mol | |
| universal gas constant, J/(mol·°C) | |
| order of reaction | |
| activation constant | |
| total heat released, kJ/kg | |
| temperature of material at the die block entrance, °C | |
| temperature at the die block, °C | |
| temperature at the first zone of the die block, °C | |
| temperature at the second zone of the die block, °C | |
| temperature at the third zone of the die block, °C | |
| temperature at the fourth zone of the die block, °C | |
| temperature at the fifth zone of the die block, °C | |
| temperature at the die block exit, °C | |
| ambient temperature, °C | |
| instantaneous glass transition temperature, °C | |
| glass transition temperature of uncured resin, °C | |
| glass transition temperature of fully cured resin, °C | |
| difference between the instantaneous glass transition temperature and the instantaneous temperature of the resin, °C | |
| , , , , , | critical temperatures, °C |
| instantaneous Young’s modulus of the resin, MPa | |
| Young’s modulus of resin at , MPa | |
| Young’s modulus of resin at , MPa | |
| Young’s modulus of resin at , MPa | |
| Young’s modulus of resin at , MPa | |
| Young’s modulus of resin at , MPa | |
| Young’s modulus of resin at , MPa | |
| instantaneous bulk modulus of resin, MPa | |
| bulk modulus of resin at , MPa | |
| bulk modulus of resin at , MPa | |
| instantaneous Poisson’s ratio of resin | |
| Poisson’s ratio of resin at | |
| coefficient of thermal expansion of resin at , 1/°C | |
| coefficient of thermal expansion of resin at , 1/°C | |
| Young’s modulus of glass fiber reinforcement, MPa | |
| Poisson’s ratio of glass fiber reinforcement | |
| coefficient of thermal expansion of glass fiber reinforcement, 1/°C | |
| pulling speed, mm/min | |
| volume fraction of fabric layer reinforcement | |
| volume fraction of unidirectional layer reinforcement | |
| total volumetric chemical shrinkage, % | |
| resin cure degree corresponding to the gelation | |
| material constant in Equation (10) | |
| die block length, m | |
| spring-in angle, ° | |
| thickness of the strips, mm | |
| size of the L-shaped profile legs, mm |
Appendix A
| Property | Source | Symbol | Value | Unit | ||
|---|---|---|---|---|---|---|
| Heat transfer problem | ||||||
| Density of resin | – a | 1140 | kg/m3 | |||
| Density of fiber | [49] | 2560 | kg/m3 | |||
| Thermal conductivity of resin | – e | 0.178 | W/(m·°C) | |||
| Thermal conductivity of fiber in the transverse direction | [49] | 1.04 | W/(m·°C) | |||
| Thermal conductivity of fiber in the longitudinal direction | [49] | 11.4 | W/(m·°C) | |||
| Heat capacity of resin depending on the temperature | – b | 5.1 × T + 1080 | J/(kg·°C) | |||
| Heat capacity of fiber | [49] | 670 | J/(kg·°C) | |||
| Convective heat transfer coefficient between the die block and the profile | – f | 5000 | W/(m2·°C) | |||
| Convective heat transfer coefficient between the ambient air and the profile after the die block exit | – f | 9 | W/(m2·°C) | |||
| Cure kinetics | ||||||
| Pre-exponential coefficient | [90] | 109.34 | 1/s | |||
| Activation energy | [90] | 93.3 | kJ/mol | |||
| Universal gas constant | [90] | 8.31 | J/(mol·°C) | |||
| Order of reaction | [90] | 1.91 | - | |||
| Activation constant | [90] | 102.73 | - | |||
| Total heat released | [90] | 189 | kJ/kg | |||
| Temperature conditions | ||||||
| Temperature at the die block, : | Pulling speed, mm/min | |||||
| 200 | 400 | 600 | ||||
| @ 97–103 mm (1st zone) | – a | 45 | 31 | 30 | °C | |
| @ 197–203 mm (2nd zone) | – a | 62 | 42 | 40 | °C | |
| @ 297–303 mm (3rd zone) | – a | 84 | 66 | 89 | °C | |
| @ 397–403 mm (4th zone) | – a | 127 | 95 | 119 | °C | |
| @ 497–503 mm (5th zone) | – a | 159 | 127 | 141 | °C | |
| @ 600 mm (at the die block exit) | – a | 153 | 148 | 147 | °C | |
| Temperature of material at the die block entrance | – a | 18 | °C | |||
| Ambient temperature | – a | 18 | °C | |||
| Mechanical properties of resin | ||||||
| Young’s modulus at | – c | 21 | MPa | |||
| Young’s modulus at | – c | 86 | MPa | |||
| Young’s modulus at | – c | 1961 | MPa | |||
| Young’s modulus at | – c | 2473 | MPa | |||
| Young’s modulus at | – c | 3083 | MPa | |||
| Young’s modulus at | – c | 3421 | MPa | |||
| Poisson’s ratio at | [111] | 0.35 | - | |||
| Bulk modulus at | 3801 | MPa | ||||
| Bulk modulus at | [56] | 1520 | MPa | |||
| Coefficient of thermal expansion at | – d | 60 × 10−6 | 1/°C | |||
| Coefficient of thermal expansion at | 2.5 × [56] | 150 × 10−6 | 1/°C | |||
| Mechanical properties of glass fiber reinforcement | ||||||
| Young’s modulus | [57] | 73 080 | MPa | |||
| Poisson’s ratio | [57] | 0.22 | - | |||
| Coefficient of thermal expansion | [57] | 5.04 × 10−6 | 1/°C | |||
| Other properties | ||||||
| Pulling speed | – a | 200/400/600 | mm/min | |||
| The volume fraction of reinforcement | ||||||
| Fabric layer | – a | 0.5 | - | |||
| UD layer | – a | 0.59 | - | |||
| Total volumetric chemical shrinkage | [100] | −7 | % | |||
| Glass transition temperature of the uncured resin | [56] | −41 | °C | |||
| Glass transition temperature of the fully cured resin | – c | 120.4 | °C | |||
| Resin cure degree corresponding to the gelation | – f | 0.6 | - | |||
| Material constant in Equation (10) | [49] | 0.4 | - | |||
| Die block length | – a | 0.6 | m | |||
References
- Starr, T.F. Pultrusion for Engineers; Woodhead Publishing: Cambridge, UK, 2000. [Google Scholar]
- Vedernikov, A.; Safonov, A.; Tucci, F.; Carlone, P.; Akhatov, I. Pultruded Materials and Structures: A Review. J. Compos. Mater. 2020, 54, 4081–4117. [Google Scholar] [CrossRef]
- Minchenkov, K.; Vedernikov, A.; Safonov, A.; Akhatov, I. Thermoplastic Pultrusion: A Review. Polymers 2021, 13, 180. [Google Scholar] [CrossRef]
- Zhu, R.; Li, F.; Zhao, Z.; Zhang, D.; Chen, Y. Compression Behavior of Square Pyramid Substructure of Novel Pultruded FRP-Aluminum Space Truss. J. Compos. Constr. 2020, 24. [Google Scholar] [CrossRef]
- Shekarchi, M.; Yekrangnia, M.; Biniaz, A.; Raftery, G.M. Effect of Elevated Temperatures on the Compressive Behavior of Timber Filled Steel and Pultruded GFRP Tubes. Compos. Struct. 2021, 271, 114135. [Google Scholar] [CrossRef]
- Tucci, F.; Vedernikov, A. Design Criteria for Pultruded Structural Elements. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Madenci, E.; Özkılıç, Y.O.; Gemi, L. Buckling and Free Vibration Analyses of Pultruded GFRP Laminated Composites: Experimental, Numerical and Analytical Investigations. Compos. Struct. 2020, 254, 112806. [Google Scholar] [CrossRef]
- Gemi, L.; Madenci, E.; Özkılıç, Y.O. Experimental, Analytical and Numerical Investigation of Pultruded GFRP Composite Beams Infilled with Hybrid FRP Reinforced Concrete. Eng. Struct. 2021, 244, 112790. [Google Scholar] [CrossRef]
- Li, C.; Yin, X.; Wang, Y.; Zhang, L.; Zhang, Z.; Liu, Y.; Xian, G. Mechanical Property Evolution and Service Life Prediction of Pultruded Carbon/Glass Hybrid Rod Exposed in Harsh Oil-Well Condition. Compos. Struct. 2020, 246, 112418. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, D.; Li, F.; Zhao, Q.; Zhao, Z.; Chen, Y. Bearing Strength and Failure Behaviour of Composite Pre-Tightened Multi-Tooth Joint. Compos. Struct. 2021, 272, 114208. [Google Scholar] [CrossRef]
- Tinkov, D.V.; Safonov, A.A. Design Optimization of Truss Bridge Structures of Composite Materials. J. Mach. Manuf. Reliab. 2017, 46, 46–52. [Google Scholar] [CrossRef]
- Sorina, T.G.; Safonov, A.A.; Khairetdinov, A.K. Pecularities of Using Carbon Glass-Reinforced Plastic in Pultrusion Composite Profiles for Bridge Engineering. J. Mach. Manuf. Reliab. 2010, 39, 47–51. [Google Scholar] [CrossRef]
- Zhu, R.; Li, F.; Chen, Y.; Li, R. A Hybrid Beam-Column Element for Direct Second-Order Nonlinear Analysis of PFRP Frame Structures. Compos. Struct. 2021, 271, 114171. [Google Scholar] [CrossRef]
- Sharda, A.; Manalo, A.; Ferdous, W.; Bai, Y.; Nicol, L.; Mohammed, A.; Benmokrane, B. Axial Compression Behaviour of All-Composite Modular Wall System. Compos. Struct. 2021, 268, 113986. [Google Scholar] [CrossRef]
- Toubia, E.A.; Alomari, A.; Morgan, A.B.; Klosterman, D. Influence of Heat Damage on the Bolted Double Lap Joint Strength of Pultruded E-Glass/Polyester Composites. Thin Walled Struct. 2021, 163, 107764. [Google Scholar] [CrossRef]
- Alhawamdeh, M.; Alajarmeh, O.; Aravinthan, T.; Shelley, T.; Schubel, P.; Kemp, M.; Zeng, X. Modelling Hollow Pultruded FRP Profiles under Axial Compression: Local Buckling and Progressive Failure. Compos. Struct. 2021, 262, 113650. [Google Scholar] [CrossRef]
- Rubino, F.; Nisticò, A.; Tucci, F.; Carlone, P. Marine Application of Fiber Reinforced Composites: A Review. J. Mar. Sci. Eng. 2020, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Zyka, K.; Mohajerani, A. Composite Piles: A Review. Constr. Build. Mater. 2016, 107, 394–410. [Google Scholar] [CrossRef]
- Madenci, E.; Özkılıç, Y.O.; Gemi, L. Experimental and Theoretical Investigation on Flexure Performance of Pultruded GFRP Composite Beams with Damage Analyses. Compos. Struct. 2020, 242, 112162. [Google Scholar] [CrossRef]
- Struzziero, G.; Maistros, G.M.; Hartley, J.; Skordos, A.A. Materials Modelling and Process Simulation of the Pultrusion of Curved Parts. Compos. Part A Appl. Sci. Manuf. 2021, 144, 106328. [Google Scholar] [CrossRef]
- Dubinskii, S.V.; Safonov, A.A. Composite-Friendly Approach to Certification of Advanced Materials and Fabrication Methods Used in Aviation Industry. J. Mach. Manuf. Reliab. 2017, 46, 501–506. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; AlAjarmeh, O.; Mohammed, A.A.; Salih, C.; Yu, P.; Mehrinejad Khotbehsara, M.; Schubel, P. Static Behaviour of Glass Fibre Reinforced Novel Composite Sleepers for Mainline Railway Track. Eng. Struct. 2021, 229, 111627. [Google Scholar] [CrossRef]
- Li, C.; Xian, G.; Li, H. Tension-Tension Fatigue Performance of a Large-Diameter Pultruded Carbon/Glass Hybrid Rod. Int. J. Fatigue 2019, 120, 141–149. [Google Scholar] [CrossRef]
- Jeppesen, N.; Mikkelsen, L.P.; Dahl, A.B.; Nymark, A.N.; Dahl, V.A. Quantifying Effects of Manufacturing Methods on Fiber Orientation in Unidirectional Composites Using Structure Tensor Analysis. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106541. [Google Scholar] [CrossRef]
- Corrado, A.; Polini, W.; Sorrentino, L.; Bellini, C. Geometrical Deviation Analysis of CFRP Thin Laminate Assemblies: Numerical and Experimental Results. Compos. Sci. Technol. 2018, 168, 1–11. [Google Scholar] [CrossRef]
- Hörberg, E.; Nyman, T.; Åkermo, M.; Hallström, S. Thickness Effect on Spring-in of Prepreg Composite L-Profiles—An Experimental Study. Compos. Struct. 2019, 209, 499–507. [Google Scholar] [CrossRef]
- Wisnom, M.R.; Potter, K.D.; Ersoy, N. Shear-Lag Analysis of the Effect of Thickness on Spring-in of Curved Composites. J. Compos. Mater. 2007, 41, 1311–1324. [Google Scholar] [CrossRef]
- Hörberg, E.; Åkermo, M.; Hallström, S. Moisture Effect on Shape Distortions of Curved Quasi-Isotropic Prepreg Composite Laminates. Compos. Part A Appl. Sci. Manuf. 2021, 145, 106361. [Google Scholar] [CrossRef]
- Abouhamzeh, M.; Sinke, J.; Jansen, K.M.B.; Benedictus, R. Closed Form Expression for Residual Stresses and Warpage during Cure of Composite Laminates. Compos. Struct. 2015, 133, 902–910. [Google Scholar] [CrossRef]
- Yuksel, O.; Sandberg, M.; Hattel, J.H.; Akkerman, R.; Baran, I. Mesoscale Process Modeling of a Thick Pultruded Composite with Variability in Fiber Volume Fraction. Materials 2021, 14, 3763. [Google Scholar] [CrossRef]
- Sandberg, M.; Yuksel, O.; Baran, I.; Spangenberg, J.; Hattel, J.H. Steady-State Modelling and Analysis of Process-Induced Stress and Deformation in Thermoset Pultrusion Processes. Compos. Part B Eng. 2021, 216, 108812. [Google Scholar] [CrossRef]
- Traiforos, N.; Turner, T.; Runeberg, P.; Fernass, D.; Chronopoulos, D.; Glock, F.; Schuhmacher, G.; Hartung, D. A Simulation Framework for Predicting Process-Induced Distortions for Precise Manufacturing of Aerospace Thermoset Composites. Compos. Struct. 2021, 114465. [Google Scholar] [CrossRef]
- Albert, C.; Fernlund, G. Spring-in and Warpage of Angled Composite Laminates. Compos. Sci. Technol. 2002, 62, 1895–1912. [Google Scholar] [CrossRef]
- Bapanapalli, S.K.; Smith, L.V. A Linear Finite Element Model to Predict Processing-Induced Distortion in FRP Laminates. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1666–1674. [Google Scholar] [CrossRef]
- Fernlund, G.; Rahman, N.; Courdji, R.; Bresslauer, M.; Poursartip, A.; Willden, K.; Nelson, K. Experimental and Numerical Study of the Effect of Cure Cycle, Tool Surface, Geometry, and Lay-up on the Dimensional Fidelity of Autoclave-Processed Composite Parts. Compos. Part A Appl. Sci. Manuf. 2002, 33, 341–351. [Google Scholar] [CrossRef]
- Fernlund, G.; Osooly, A.; Poursartip, A.; Vaziri, R.; Courdji, R.; Nelson, K.; George, P.; Hendrickson, L.; Griffith, J. Finite Element Based Prediction of Process-Induced Deformation of Autoclaved Composite Structures Using 2D Process Analysis and 3D Structural Analysis. Compos. Struct. 2003, 62, 223–234. [Google Scholar] [CrossRef]
- Svanberg, J.M.; Holmberg, J.A. An Experimental Investigation on Mechanisms for Manufacturing Induced Shape Distortions in Homogeneous and Balanced Laminates. Compos. Part A Appl. Sci. Manuf. 2001, 32, 827–838. [Google Scholar] [CrossRef]
- Jain, L.K.; Lutton, B.G.; Mai, Y.-W.; Paton, R. Stresses and Deformations Induced during Manufacturing. Part II: A Study of the Spring-in Phenomenon. J. Compos. Mater. 1997, 31, 696–719. [Google Scholar] [CrossRef]
- Svanberg, J.M.; Holmberg, J.A. Prediction of Shape Distortions. Part II. Experimental Validation and Analysis of Boundary Conditions. Compos. Part A Appl. Sci. Manuf. 2004, 35, 723–734. [Google Scholar] [CrossRef]
- Nielsen, M.W. Prediction of Process Induced Shape Distortions and Residual Stresses in Large Fibre Reinforced Composite Laminates: With Application to Wind Turbine Blades. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 25 June 2013. [Google Scholar]
- Hsiao, K.-T.; Gangireddy, S. Investigation on the Spring-in Phenomenon of Carbon Nanofiber-Glass Fiber/Polyester Composites Manufactured with Vacuum Assisted Resin Transfer Molding. Compos. Part A Appl. Sci. Manuf. 2008, 39, 834–842. [Google Scholar] [CrossRef]
- Corrado, A.; Polini, W. Measurement of Flexible Components in Composite Material by a 3-2-1 Locating Scheme. Compos. Sci. Technol. 2020, 189, 108036. [Google Scholar] [CrossRef]
- Sorrentino, L.; Bellini, C. Compaction Influence on Spring-in of Thin Composite Parts: Experimental and Numerical Results. J. Compos. Mater. 2015, 49, 2149–2158. [Google Scholar] [CrossRef]
- Ding, A.; Wang, J.; Ni, A.; Li, S. A New Analytical Solution for Cure-Induced Spring-in of L-Shaped Composite Parts. Compos. Sci. Technol. 2019, 171, 1–12. [Google Scholar] [CrossRef]
- Hou, M.; Ye, L.; Mai, Y.W. Manufacturing Process and Mechanical Properties of Thermoplastic Composite Components. J. Mater. Process. Technol. 1997, 63, 334–338. [Google Scholar] [CrossRef]
- Ganley, J.M.; Mawi, A.K.; Huybrechts, S. Explaining Spring-In in Filament Wound Carbon Fiber/Epoxy Composites. J. Compos. Mater. 2000, 34, 1216–1239. [Google Scholar] [CrossRef]
- Li, N.; Li, Y.; Hao, X.; Gao, J. A Comparative Experiment for the Analysis of Microwave and Thermal Process Induced Strains of Carbon Fiber/Bismaleimide Composite Materials. Compos. Sci. Technol. 2015, 106, 15–19. [Google Scholar] [CrossRef] [Green Version]
- Baran, I.; Akkerman, R.; Hattel, J.H. Modelling the Pultrusion Process of an Industrial L-Shaped Composite Profile. Compos. Struct. 2014, 118, 37–48. [Google Scholar] [CrossRef]
- Baran, I.; Tutum, C.C.; Nielsen, M.W.; Hattel, J.H. Process Induced Residual Stresses and Distortions in Pultrusion. Compos. Part B Eng. 2013, 51, 148–161. [Google Scholar] [CrossRef]
- Wisnom, M.R.; Gigliotti, M.; Ersoy, N.; Campbell, M.; Potter, K.D. Mechanisms Generating Residual Stresses and Distortion during Manufacture of Polymer-Matrix Composite Structures. Compos. Part A Appl. Sci. Manuf. 2006, 37, 522–529. [Google Scholar] [CrossRef]
- Radford, D.W.; Rennick, T.S. Separating Sources of Manufacturing Distortion in Laminated Composites. J. Reinf. Plast. Compos. 2000, 19, 621–641. [Google Scholar] [CrossRef]
- Kappel, E.; Stefaniak, D.; Hühne, C. Process Distortions in Prepreg Manufacturing—An Experimental Study on CFRP L-Profiles. Compos. Struct. 2013, 106, 615–625. [Google Scholar] [CrossRef]
- Wiersma, H.W.; Peeters, L.J.B.; Akkerman, R. Prediction of Springforward in Continuous-Fibre/Polymer L-Shaped Parts. Compos. Part A Appl. Sci. Manuf. 1998, 29, 1333–1342. [Google Scholar] [CrossRef]
- David, A. Darrow, J.; Smith, L.V. Isolating Components of Processing Induced Warpage in Laminated Composites. J. Compos. Mater. 2002, 36, 2407–2419. [Google Scholar] [CrossRef]
- Ersoy, N.; Garstka, T.; Potter, K.; Wisnom, M.R.; Porter, D.; Stringer, G. Modelling of the Spring-in Phenomenon in Curved Parts Made of a Thermosetting Composite. Compos. Part A Appl. Sci. Manuf. 2010, 41, 410–418. [Google Scholar] [CrossRef]
- Svanberg, J.M.; Holmberg, J.A. Prediction of Shape Distortions Part I. FE-Implementation of a Path Dependent Constitutive Model. Compos. Part A Appl. Sci. Manuf. 2004, 35, 711–721. [Google Scholar] [CrossRef]
- Bogetti, T.A.; Gillespie, J.W., Jr. Process-Induced Stress and Deformation in Thick-Section Thermoset Composite Laminates. J. Compos. Mater. 1992, 26, 626–660. [Google Scholar] [CrossRef]
- Arafath, A.R.A.; Vaziri, R.; Poursartip, A. Closed-Form Solution for Process-Induced Stresses and Deformation of a Composite Part Cured on a Solid Tool: Part II—Curved Geometries. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1545–1557. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Guan, Z.; Jiang, T.; Geng, K.; Li, Z. Study on Cure-Induced Residual Stresses and Spring-in Deformation of L-Shaped Composite Laminates Using a Simplified Constitutive Model Considering Stress Relaxation. Compos. Struct. 2021, 272, 114203. [Google Scholar] [CrossRef]
- Vedernikov, A.; Tucci, F.; Carlone, P.; Gusev, S.; Konev, S.; Firsov, D.; Akhatov, I.; Safonov, A. Effects of Pulling Speed on Structural Performance of L-Shaped Pultruded Profiles. Compos. Struct. 2021, 255, 112967. [Google Scholar] [CrossRef]
- Safonov, A.A.; Carlone, P.; Akhatov, I. Mathematical Simulation of Pultrusion Processes: A Review. Compos. Struct. 2018, 184, 153–177. [Google Scholar] [CrossRef]
- Struzziero, G.; Teuwen, J.J.E.; Skordos, A.A. Numerical Optimisation of Thermoset Composites Manufacturing Processes: A Review. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105499. [Google Scholar] [CrossRef]
- Vedernikov, A.; Nasonov, Y.; Korotkov, R.; Gusev, S.; Akhatov, I.; Safonov, A. Effects of Additives on the Cure Kinetics of Vinyl Ester Pultrusion Resins. J. Compos. Mater. 2021. [Google Scholar] [CrossRef]
- Safonov, A.; Gusev, M.; Saratov, A.; Konstantinov, A.; Sergeichev, I.; Konev, S.; Gusev, S.; Akhatov, I. Modeling of Cracking during Pultrusion of Large-Size Profiles. Compos. Struct. 2020, 235, 111801. [Google Scholar] [CrossRef]
- Sandberg, M.; Yuksel, O.; Baran, I.; Hattel, J.H.; Spangenberg, J. Numerical and Experimental Analysis of Resin-Flow, Heat-Transfer, and Cure in a Resin-Injection Pultrusion Process. Compos. Part A Appl. Sci. Manuf. 2020, 143, 106231. [Google Scholar] [CrossRef]
- Barkanov, E.; Akishin, P.; Miazza, N.L.; Galvez, S. ANSYS-Based Algorithms for a Simulation of Pultrusion Processes. Mech. Adv. Mater. Struct. 2017, 24, 377–384. [Google Scholar] [CrossRef]
- Safonov, A.A.; Suvorova, Y.V. Optimization of the Pultrusion Process for a Rod with a Large Diameter. J. Mach. Manuf. Reliab. 2009, 38, 572–578. [Google Scholar] [CrossRef]
- Carlone, P.; Baran, I.; Hattel, J.H.; Palazzo, G.S. Computational Approaches for Modeling the Multiphysics in Pultrusion Process. Adv. Mech. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Yuksel, O.; Sandberg, M.; Baran, I.; Ersoy, N.; Hattel, J.H.; Akkerman, R. Material Characterization of a Pultrusion Specific and Highly Reactive Polyurethane Resin System: Elastic Modulus, Rheology, and Reaction Kinetics. Compos. Part B Eng. 2020, 207, 108543. [Google Scholar] [CrossRef]
- Wang, J.; Kelly, D.; Hillier, W. Finite Element Analysis of Temperature Induced Stresses and Deformations of Polymer Composite Components. J. Compos. Mater. 2000, 34, 1456–1471. [Google Scholar] [CrossRef]
- Jain, L.K.; Mai, Y.-W. Stresses and Deformations Induced during Manufacturing. Part I: Theoretical Analysis of Composite Cylinders and Shells. J. Compos. Mater. 1997, 31, 672–695. [Google Scholar] [CrossRef]
- Ersoy, N.; Potter, K.; Wisnom, M.R.; Clegg, M.J. Development of Spring-in Angle during Cure of a Thermosetting Composite. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1700–1706. [Google Scholar] [CrossRef]
- Ruiz, E.; Trochu, F. Multi-Criteria Thermal Optimization in Liquid Composite Molding to Reduce Processing Stresses and Cycle Time. Compos. Part A Appl. Sci. Manuf. 2006, 37, 913–924. [Google Scholar] [CrossRef]
- Kravchenko, O.G.; Kravchenko, S.G.; Pipes, R.B. Chemical and Thermal Shrinkage in Thermosetting Prepreg. Compos. Part A Appl. Sci. Manuf. 2016, 80, 72–81. [Google Scholar] [CrossRef]
- Takagaki, K.; Minakuchi, S.; Takeda, N. Process-Induced Strain and Distortion in Curved Composites. Part I: Development of Fiber-Optic Strain Monitoring Technique and Analytical Methods. Compos. Part A Appl. Sci. Manuf. 2017, 103, 236–251. [Google Scholar] [CrossRef]
- Nawab, Y.; Sonnenfeld, C.; Saouab, A.; Agogué, R.; Beauchêne, P. Characterisation and Modelling of Thermal Expansion Coefficient of Woven Carbon/Epoxy Composite and Its Application to the Determination of Spring-In. J. Compos. Mater. 2017, 51, 1527–1538. [Google Scholar] [CrossRef]
- Hu, H.; Li, S.; Wang, J.; Zu, L.; Cao, D.; Zhong, Y. Monitoring the Gelation and Effective Chemical Shrinkage of Composite Curing Process with a Novel FBG Approach. Compos. Struct. 2017, 176, 187–194. [Google Scholar] [CrossRef]
- Exner, W.; Hein, R.; Mahrholz, T.; Wierach, P.; Monner, H.P.; Sinapius, M. Impact of Nanoparticles on the Process-Induced Distortions of Carbon Fiber Reinforced Plastics: An Experimental and Simulative Approach. J. Appl. Polym. Sci. 2019, 136, 47031. [Google Scholar] [CrossRef]
- Groh, F.; Kappel, E.; Hühne, C.; Brymerski, W. Investigation of Fast Curing Epoxy Resins Regarding Process Induced Distortions of Fibre Reinforced Composites. Compos. Struct. 2019, 207, 923–934. [Google Scholar] [CrossRef]
- Qiao, W.; Yao, W. Modelling of Process-Induced Deformation for Composite Parts Considering Tool-Part Interaction. Materials 2020, 13, 4503. [Google Scholar] [CrossRef]
- Shaker, K.; Nawab, Y.; Saouab, A. Experimental and Numerical Investigation of Reduction in Shape Distortion for Angled Composite Parts. Int. J. Mater. Form. 2020, 13, 897–906. [Google Scholar] [CrossRef]
- Struzziero, G.; Nardi, D.; Sinke, J.; Teuwen, J. Cure-Induced Residual Stresses for Warpage Reduction in Thermoset Laminates. J. Compos. Mater. 2020, 54, 3055–3065. [Google Scholar] [CrossRef] [Green Version]
- Vedernikov, A.N.; Safonov, A.A.; Gusev, S.A.; Carlone, P.; Tucci, F.; Akhatov, I.S. Spring-in Experimental Evaluation of L-Shaped Pultruded Profiles. IOP Conf. Ser. Mater. Sci. Eng. 2020, 747, 012013. [Google Scholar] [CrossRef]
- Vedernikov, A.; Tucci, F.; Safonov, A.; Carlone, P.; Gusev, S.; Akhatov, I. Investigation on the Shape Distortions of Pultruded Profiles at Different Pulling Speed. Procedia Manuf. 2020, 47, 1–5. [Google Scholar] [CrossRef]
- Zocher, M.A.; Groves, S.E.; Allen, D.H. A Three-Dimensional Finite Element Formulation for Thermoviscoelastic Orthotropic Media. Int. J. Numer. Methods Eng. 1997, 40, 2267–2288. [Google Scholar] [CrossRef]
- White, S.R.; Kim, Y.K. Process-Induced Residual Stress Analysis of AS4/3501-6 Composite Material. Mech. Compos. Mater. Struct. 1998, 5, 153–186. [Google Scholar] [CrossRef]
- Hill, R. A Self-Consistent Mechanics of Composite Materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Batch, G.L.; Macosko, C.W. Heat Transfer and Cure in Pultrusion: Model and Experimental Verification. AIChE J. 1993, 39, 1228–1241. [Google Scholar] [CrossRef]
- Baran, I.; Hattel, J.H.; Akkerman, R.; Tutum, C.C. Mechanical Modelling of Pultrusion Process: 2D and 3D Numerical Approaches. Appl. Compos. Mater. 2014, 22, 99–118. [Google Scholar] [CrossRef]
- Nasonov, Y.; Safonov, A.; Gusev, S.; Akhatov, I. Mathematical Simulation the Kinetics of Polymerization of Vinyl Ester Resin Using in Pultrusion. IOP Conf. Ser. Mater. Sci. Eng. 2020, 747, 12010. [Google Scholar] [CrossRef]
- Johnston, A.A. An Integrated Model of the Development of Process-Induced Deformation in Autoclave Processing of Composite Structures. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, May 1997. [Google Scholar]
- Khoun, L.; Centea, T.; Hubert, P. Characterization Methodology of Thermoset Resins for the Processing of Composite Materials—Case Study: CYCOM 890RTM Epoxy Resin. J. Compos. Mater. 2010, 44, 1397–1415. [Google Scholar] [CrossRef]
- O’Brien, D.J.; White, S.R. Cure Kinetics, Gelation, and Glass Transition of a Bisphenol F Epoxide. Polym. Eng. Sci. 2003, 43, 863–874. [Google Scholar] [CrossRef]
- Plepys, A.R.; Farris, R.J. Evolution of Residual Stresses in Three-Dimensionally Constrained Epoxy Resins. Polymer 1990, 31, 1932–1936. [Google Scholar] [CrossRef]
- Abaqus Analysis User Manual, Version 6.14. 2014. Available online: https://www.3ds.com/products-services. (accessed on 1 June 2021).
- ISO 6721-1:2011. Plastics—Determination of Dynamic Mechanical Properties—Part 1: General Principles; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- ISO 11357-4:2005. Plastics—Differential Scanning Calorimetry (DSC)—Part 4: Determination of Specific Heat Capacity; International Organization for Standardization: Geneva, Switzerland, 2005. [Google Scholar]
- ISO 22007-4:2008. Plastics—Determination of Thermal Conductivity and Thermal Diffusivity—Part 4: Laser Flash Method; International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- ISO 11359-2:1999. Plastics—Thermomechanical Analysis (TMA)—Part 2: Determination of Coefficient of Linear Thermal Expansion and Glass Transition Temperature; International Organization for Standardization: Geneva, Switzerland, 1999. [Google Scholar]
- Baran, I. Pultrusion: State-of-the-Art Process. Models. Smithers Rapra: Shropshire, UK, 2015. [Google Scholar]
- Chachad, Y.R.; Roux, J.A.; Vaughan, J.G.; Arafat, E. Three-Dimensional Characterization of Pultruded Fiberglass-Epoxy Composite Materials. J. Reinf. Plast. Compos. 1995, 14, 495–512. [Google Scholar] [CrossRef]
- Akkerman, R. On the Properties of Quasi-Isotropic Laminates. Compos. Part B Eng. 2002, 33, 133–140. [Google Scholar] [CrossRef]
- Mahrholz, T.; Stängle, J.; Sinapius, M. Quantitation of the Reinforcement Effect of Silica Nanoparticles in Epoxy Resins Used in Liquid Composite Moulding Processes. Compos. Part A Appl. Sci. Manuf. 2009, 40, 235–243. [Google Scholar] [CrossRef]
- Haider, M.; Hubert, P.; Lessard, L. Cure Shrinkage Characterization and Modeling of a Polyester Resin Containing Low Profile Additives. Compos. Part A Appl. Sci. Manuf. 2007, 38, 994–1009. [Google Scholar] [CrossRef]
- Methven, J.M.; Ghaffariyan, S.R.; Abidin, A.Z. Manufacture of Fiber-Reinforced Composites by Microwave Assisted Pultrusion. Polym. Compos. 2000, 21, 586–594. [Google Scholar] [CrossRef]
- Struzziero, G.; Teuwen, J.J.E. A Fully Coupled Thermo-Mechanical Analysis for the Minimisation of Spring-in and Process Time in Ultra-Thick Components for Wind Turbine Blades. Compos. Part A Appl. Sci. Manuf. 2020, 139. [Google Scholar] [CrossRef]
- Liu, T.; Vieira, J.D.; Harries, K.A. Predicting Flange Local Buckling Capacity of Pultruded GFRP I-Sections Subject to Flexure. J. Compos. Constr. 2020, 24. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, L.-T.; Tam, L.; Yan, L.; He, L. Effect of Bearing Length on Web Crippling Behavior of Pultruded GFRP Channel Section. Compos. Struct. 2020, 253, 112810. [Google Scholar] [CrossRef]
- Civera, M.; Boscato, G.; Zanotti Fragonara, L. Treed Gaussian Process for Manufacturing Imperfection Identification of Pultruded GFRP Thin-Walled Profile. Compos. Struct. 2020, 254, 112882. [Google Scholar] [CrossRef]
- Safonov, A.A. 3D Topology Optimization of Continuous Fiber-Reinforced Structures via Natural Evolution Method. Compos. Struct. 2019, 215, 289–297. [Google Scholar] [CrossRef]
- Poveda, R.; Gupta, N.; Porfiri, M. Poisson’s Ratio of Hollow Particle Filled Composites. Mater. Lett. 2010, 64, 2360–2362. [Google Scholar] [CrossRef]

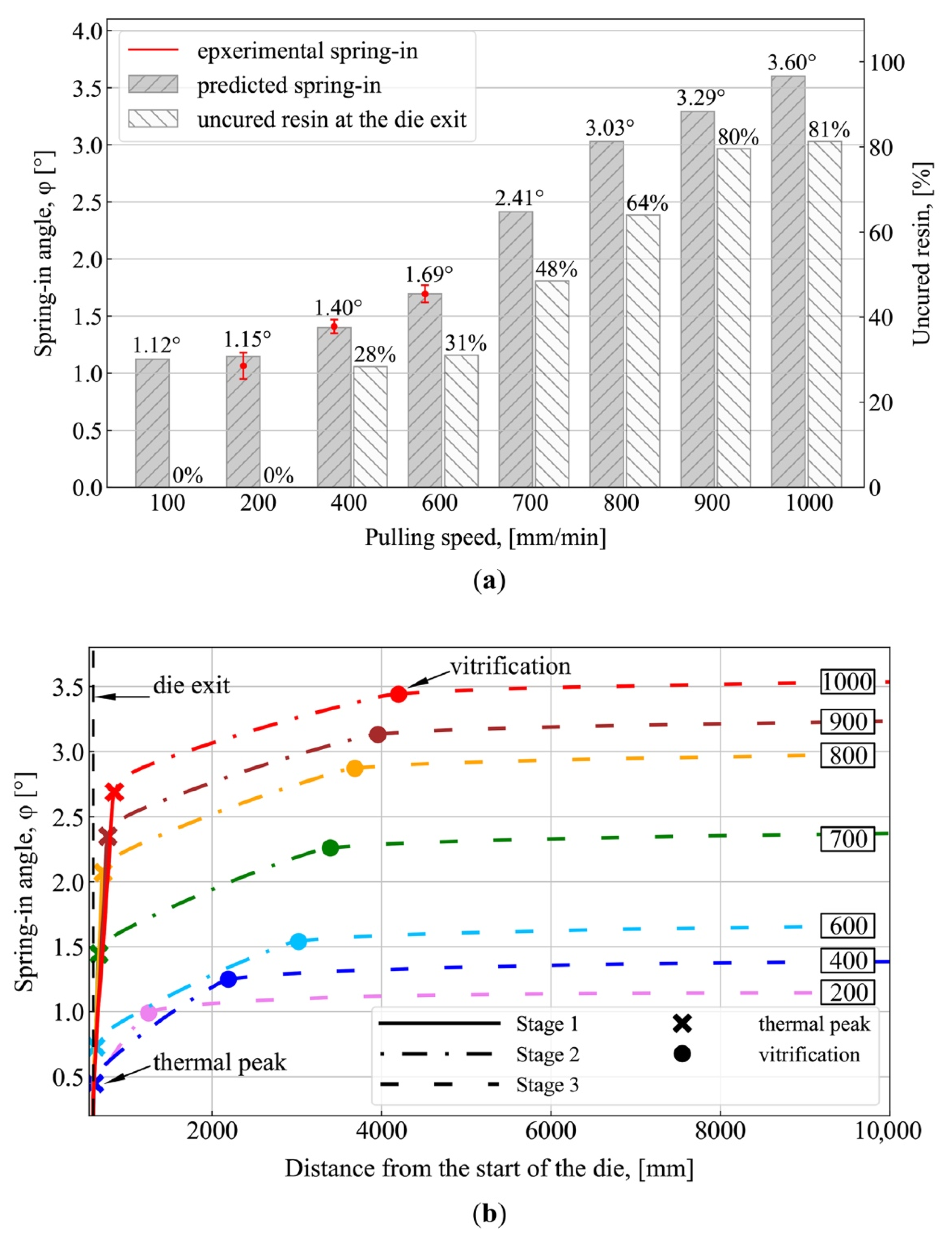
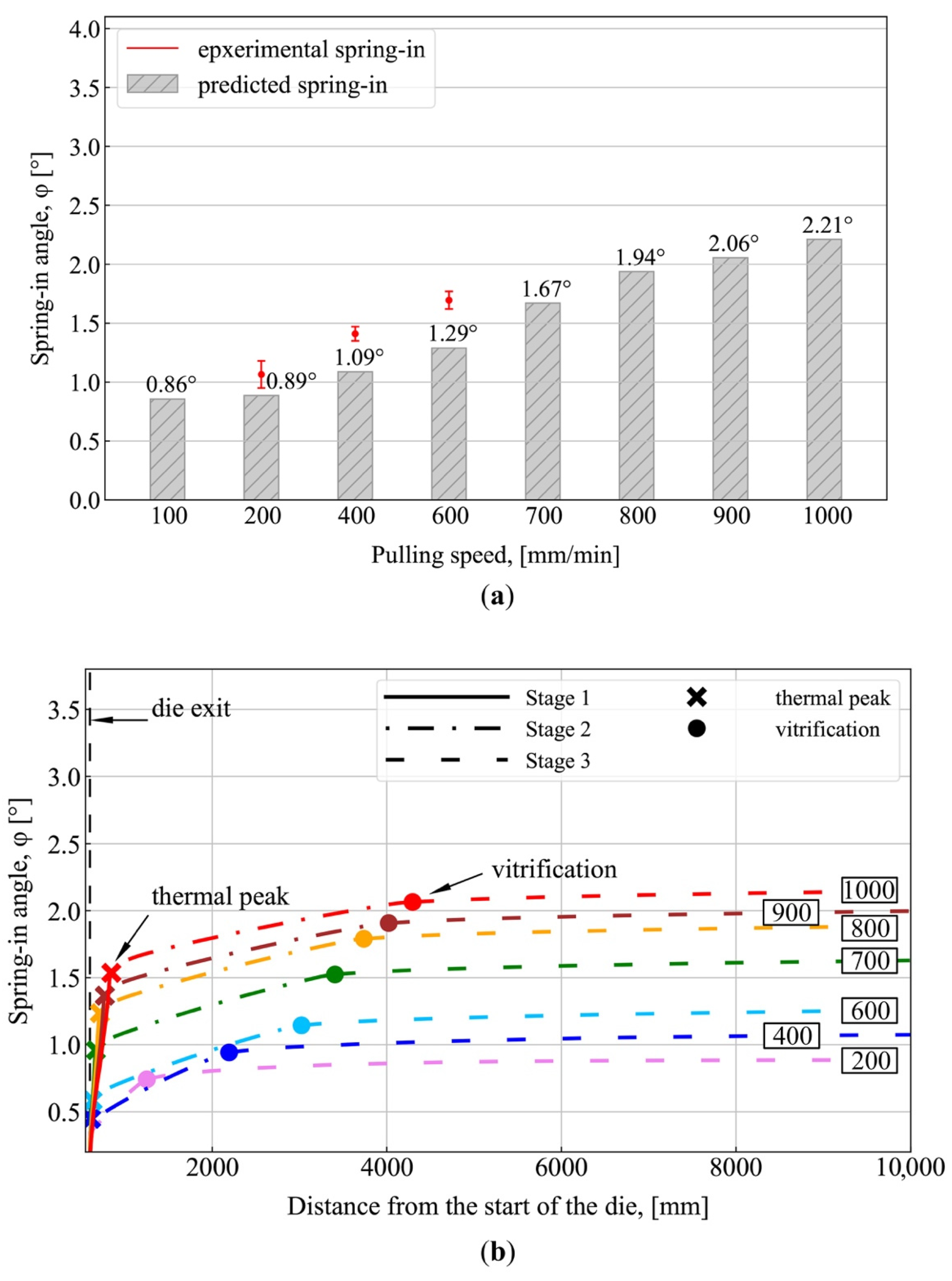
| Pulling Speed [mm/min] | Spring-In Angle [°] | |||||
|---|---|---|---|---|---|---|
| Experiment | Model | |||||
| Experiment 1 | Experiment 2 | Stage I (From the Die Block Exit to the Exothermic Peak) | Stage II (From the Exothermic Peak to the Vitrification Point) | STAGE III (From Vitrification to the Full Cooldown of the Profile) | Final Value | |
| 100 | – | – | 0 | 0.97 | 0.15 | 1.12 |
| 200 | 0.97 | 1.16 | 0 | 0.99 | 0.16 | 1.15 |
| 400 | 1.40 | 1.42 | 0.45 | 0.80 | 0.15 | 1.40 |
| 600 | 1.67 | 1.72 | 0.76 | 0.78 | 0.15 | 1.69 |
| 700 | – | – | 1.46 | 0.80 | 0.15 | 2.41 |
| 800 | – | – | 2.10 | 0.77 | 0.16 | 3.03 |
| 900 | – | – | 2.38 | 0.75 | 0.16 | 3.29 |
| 1000 | – | – | 2.72 | 0.72 | 0.16 | 3.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vedernikov, A.; Safonov, A.; Tucci, F.; Carlone, P.; Akhatov, I. Modeling Spring-In of L-Shaped Structural Profiles Pultruded at Different Pulling Speeds. Polymers 2021, 13, 2748. https://doi.org/10.3390/polym13162748
Vedernikov A, Safonov A, Tucci F, Carlone P, Akhatov I. Modeling Spring-In of L-Shaped Structural Profiles Pultruded at Different Pulling Speeds. Polymers. 2021; 13(16):2748. https://doi.org/10.3390/polym13162748
Chicago/Turabian StyleVedernikov, Alexander, Alexander Safonov, Fausto Tucci, Pierpaolo Carlone, and Iskander Akhatov. 2021. "Modeling Spring-In of L-Shaped Structural Profiles Pultruded at Different Pulling Speeds" Polymers 13, no. 16: 2748. https://doi.org/10.3390/polym13162748








