Redesign of the Geometry of Parts Produced from PBT Composite to Improve Their Operational Behavior
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
Properties of PBT-GF30 Material
2.2. Methods
2.2.1. Parts Testing Method
- The housing part was immobilized on the testing machine support;
- The device used for testing was calibrated and mounted;
- The parts were loaded, with a speed set at 35 mm/min.
2.2.2. Artificial Aging of Parts
- The parts were kept in the thermal chamber for 1250 h, at temperatures in the range of −50 °C to +140 °C;
- It was maintained for one hour at −50 °C, and for the next hour at +140 °C;
- The humidity varied between 60% and 95%.
2.2.3. Checking the Geometry of the Parts
2.2.4. Scanning Electron Microscopy (SEM) Analysis of the Sampled Surfaces in the Breaking Areas
2.2.5. PBT-GF30 Viscosity Analysis
2.2.6. Establishing the Correlation between the Design of the Part and the Modeling of the Injection Molding Process (IM)
2.2.7. Research Methodology
3. Results and Discussion
3.1. Results Obtained When Testing New Parts
3.2. Results Obtained When Testing Artificially Aged Parts
3.3. Determination of the Evolution of PBT-GF30 Viscosity
3.4. Results Obtained When Measuring the Topography of the Parts’ Breaking Surface
4. Conclusions
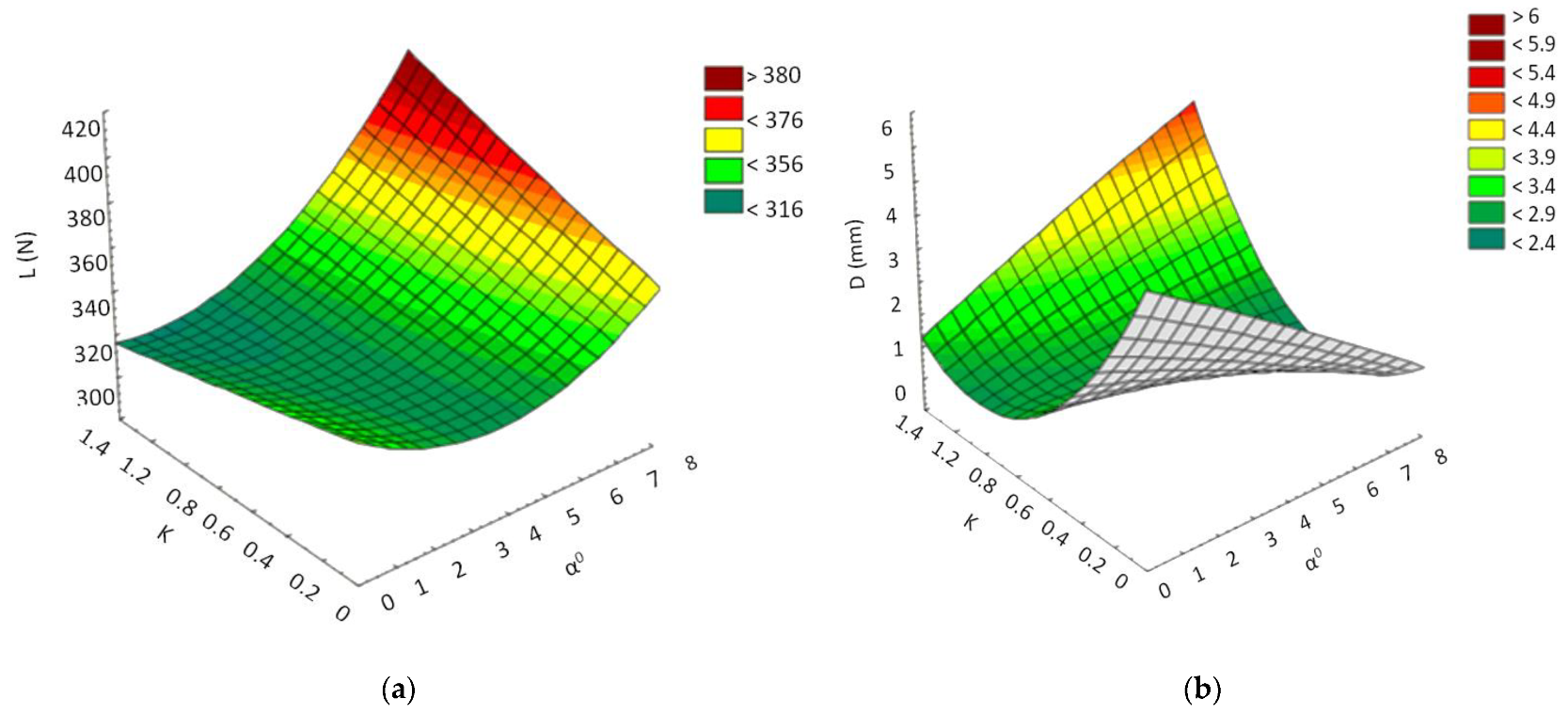
- The best values for loading or displacement, in the case of new parts, were obtained if a connection radius was adopted between the parts’ walls of R = 1.104 mm, an angle of their inclination α = 6°, and a ratio between the thickness of the walls K = 1.
- The aging process of the material in the parts causes a partial change in the values of the parameters that were taken into the analysis. Thus, their optimal values are R = 0.9 mm, α = 6°, and K = 1. In this respect, it has been observed that, in order to improve the operating performance of the parts undergoing the aging process, a reduction in the value of the connecting radius is required; this is justified by the fact that too large a connecting radius can cause a thickening of the material in the area of intersection of the walls, with negative effects on the aging process.
- The characteristics of the material in the parts deteriorate with age and, in this respect, it was found that a reduction in the size of the load at which the rupture occurs was obtained by about 21%, while the reduction in the size of the displacement was greater than about 50%.
- Aging changes the color of the matrix (PBT) in the composition of PBT-GF30 from a black to a brown color. The topographic analysis of the breaking surface also showed that, in the case of the new parts, the maximum height of roughness was 1200 µm, while the roughness in the case of the parts subjected to the aging process was at a height of 550 µm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akshat, P.; Arun, P.; Rajesh, P. An overview of Polymeric Materials for Automotive Applications. Mater. Today Proc. 2017, 4, 3807–3815. [Google Scholar] [CrossRef]
- Mahajan, G.V.; Aher, V.S. Composite Material: A Review over Current Development and Automotive Application. Int. J. Sci. Res. Publ. 2012, 2, 1–5. [Google Scholar]
- Demirci, M.T.; Düzcükoðlu, H. Wear Behaviors of Polytetrafluoroethylene and Glass Fiber Reinforced Polyamide 66 Journal Bearings. Mater. Des. 2014, 57, 560–567. [Google Scholar] [CrossRef]
- Toda, A. Temperature-Modulated Scanning Calorimetry of Melting–Recrystallization of Poly(butylene terephthalate). Polymers 2021, 13, 152. [Google Scholar] [CrossRef]
- Vendan, S.A.; Natesh, M.; Garg, A.; Gao, L. Confluence of Multidisciplinary Sciences for Polymer Joining. In Ultrasonic Welding of Polymers; Springer: Singapore, 2019; pp. 73–101. [Google Scholar]
- Dobrotă, D.; Lazăr, S.V. Ultrasonic Welding of PBT-GF30 (70% Polybutylene Terephthalate +30% Fiber Glass) and Expanded Polytetrafluoroethylene (e-PTFE). Polymers 2021, 13, 298. [Google Scholar] [CrossRef]
- Stanek, M.; Manas, M.; Manas, D.; Kyas, K.; Navratil, J.; Senkerik, V. Injection Molding Process and its Optimization. In Proceedings of the Annals of DAAAM for 2011 & Proceedings of the 22nd International DAAAM Symposium, Vienna, Austria, 23–26 November 2011; Volume 22. [Google Scholar]
- Grgac, S.; Ludwig, H.J.; Fischer, G.; McLeod, M. Water Assist Injection Moulded Structural Members. US2011316306, 2011. [Google Scholar]
- Liang, L.; Yonggang, P.; Wei, W. Recent Advances on Fluid Assisted Injection Molding Technique. Recent Pat. Mech. Eng. 2014, 7, 82–91. [Google Scholar]
- Liu, S.J.; Chen, Y.S. Water-assisted injection molding of thermoplastic materials: Effects of processing parameters. Polym. Eng. Sci. 2003, 43, 1806–1817. [Google Scholar] [CrossRef]
- Liu, S.J.; Chen, Y.S. The manufacturing of thermoplastic composite parts by water-assisted injection-molding technology. Compos. Part A Appl. Sci. Manuf. 2004, 35, 171–180. [Google Scholar] [CrossRef]
- Kleijnen, R.G.; Schmid, M.; Wegener, K. Production and Processing of a Spherical Polybutylene Terephthalate Powder for Laser Sintering. Appl. Sci. 2019, 9, 1308. [Google Scholar] [CrossRef] [Green Version]
- Wegner, A.; Oehler, M.; Ünlü, T. Development of a new polybutylene terephthalate material for laser sintering process. Procedia CIRP 2018, 74, 254–258. [Google Scholar] [CrossRef]
- Schmidt, J.; Sachs, M.; Fanselow, S.; Zhao, M.; Romeis, S.; Drummer, D.; Wirth, K.; Peukert, W. Optimized polybutylene terephthalate powders for selective laser beam melting. Chem. Eng. Sci. 2016, 156, 1–10. [Google Scholar] [CrossRef]
- Berretta, S.; Ghita, O.; Evans, K.; Anderson, A.; Newman, C. Size shape and flow of powders for use in Selective Laser Sintering (SLS). In Proceedings of the 6th International Conference on Advanced Research and Rapid Prototyping (VRAP), Leiria, Portugal, 1–5 October 2013; pp. 49–54. [Google Scholar]
- Berretta, S.; Ghita, O.; Evans, K. Morphology of polymeric powders in Laser Sintering (LS): From Polyamide to new PEEK powders. Eur. Polym. J. 2014, 59, 218–229. [Google Scholar] [CrossRef]
- Hung, B.P.; Naved, B.A.; Nyberg, E.L.; Dias, M.; Holmes, C.A.; Elisseeff, J.H.; Dorafshar, A.H.; Grayson, W.L. Three-Dimensional Printing of Bone Extracellular Matrix for Craniofacial Regeneration. ACS Biometer. Sci. Eng. 2016, 2, 1806–1816. [Google Scholar] [CrossRef] [PubMed]
- Sarode, J.S.; Firake, V.L.; Patil, A. Concept Validation and Design Synthesis of car Dashboard as per Plastic trim Standard. Int. Res. J. Eng. Technol. (IRJET) 2019, 6, 1526–1531. [Google Scholar]
- Global Automotive Plastics Market Size—Industry Report, 2018–2025x. Available online: https://www.grandviewresearch.com/industryanalysis/automotive-plastics-market (accessed on 30 July 2021).
- Kazmer, D. 27—Design of Plastic Parts. In Plastics Design Library, Applied Plastics Engineering Handbook, 2nd ed.; William Andrew Publishing: Norwich, NY, USA, 2017; pp. 593–615. [Google Scholar] [CrossRef]
- Khosravani, M.R. Influences of Defects on the Performance of Adhesively Bonded Sandwich Joints. Key Eng. Mater. 2018, 789, 45–50. [Google Scholar] [CrossRef]
- Mirzaali, M.J.; Edens, M.E.; De La Nava, A.H.; Janbaz, S.; Vena, P.; Doubrovski, E.L.; Zadpoor, A.A. Length-scale dependency of biomimetic hard-soft composites. Sci. Rep. 2018, 8, 12052. [Google Scholar] [CrossRef] [PubMed]
- Zolfagharian, A.; Khosravani, M.R.; Kaynak, A. Fracture Resistance Analysis of 3D-Printed Polymers. Polymers 2020, 12, 302. [Google Scholar] [CrossRef] [Green Version]
- Harris, M.; Potgieter, J.; Archer, R.; Arif, K.M. Effect of material and process specific factors on the strength of printed parts in fused filament fabrication: A review of recent developments. Materials 2019, 12, 1664. [Google Scholar] [CrossRef] [Green Version]
- Mercado-Colmenero, J.M.; Martin-Doñate, C.; Moramarco, V.; Attolico, M.A.; Renna, G.; Rodriguez-Santiago, M.; Casavola, C. Mechanical Characterization of the Plastic Material GF-PA6 Manufactured Using FDM Technology for a Compression Uniaxial Stress Field via an Experimental and Numerical Analysis. Polymers 2020, 12, 246. [Google Scholar] [CrossRef] [Green Version]
- Baradi, M.B. A Step towards Predicting the Mechanical Properties of Weld Lines in Injection-Molded Short Fiber-Reinforced Thermoplastics; Ecole Nationale Supérieure des Arts Et Métiers: Paris, France, 2019. [Google Scholar]
- Hnatkova, E.; Dvorak, Z. Effect of the skin-core morphology on the mechanical properties of injection-moulded parts. Mater. Tehnol. 2016, 50, 195–198. [Google Scholar] [CrossRef]
- Liparoti, S.; Speranza, V.; Pantani, Z.R.; Titomanlio, G. Modeling of the Injection Molding Process Coupled with the Fast Mold Temperature Evolution. J. Electrochem. Soc. 2019, 166, B3148–B3155. [Google Scholar] [CrossRef]
- Chang, T.C.; Faison, E. Shrinkage behaviour and optimization of injection molded parts studied by the Taguchi method. Polym. Eng. Sci. 2001, 41, 703–710. [Google Scholar] [CrossRef]
- Huang, J.; Lu, X.; Zhang, G.; Qu, J. Study on the rheological, thermal and mechanical properties of thermoplastic polyurethane/poly (butylene terephthalate) blends. Polym. Test. 2014, 36, 69–74. [Google Scholar] [CrossRef]
- Kashyap, S.; Datta, D. Process parameter optimization of plastic injection molding: A review. Int. J. Plast. Technol. 2015, 19, 1–18. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.; Viana, J.; Gaspar-Cunha, A. Using multiobjective evolutionary algorithms in the optimization of operating conditions of polymer injection molding. Polym. Eng. Sci. 2010, 50, 1667–1678. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Using Multi-objective Evolutionary Algorithms for Optimization of the Cooling System in Polymer Injection Molding. Int. Polym. Process. 2012, 27, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Li, C.T.; Isayev, A.I. Interface development and encapsulation in simultaneous coinjection molding. I. Two-dimensional modeling and formulation. J. Appl. Polym. Sci. 2003, 88, 2300–2309. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Nobrega, J.M.; Gaspar-Cunha, A. Modeling of Plasticating Injection Molding—Experimental Assessment. Int. Polym. Process. 2014, 29, 558–569. [Google Scholar] [CrossRef]
- Lou, J.; Li, Y.; He, H.; Li, D.; Wang, G.; Feng, J.; Liu, C. Interface development and numerical simulation of powder co-injection moulding. Part II. Numerical simulation and experimental verification. Powder Technol. 2017, 305, 357–363. [Google Scholar] [CrossRef]
- Jeng, Y.R.; Liu, D.S.; Yau, H.T. Fast numerical algorithm for optimization mold shape of direct injection molding process. Mater. Manuf. Process. 2013, 28, 689–694. [Google Scholar] [CrossRef]
- Papon, E.A.; Haque, A. Fracture toughness of additively manufactured carbon fiber reinforced composites. Addit. Manuf. 2019, 26, 41–52. [Google Scholar] [CrossRef]
- Mercado-Colmenero, J.M.; Rubio-Paramio, M.A.; De Juanes Marquez-Sevillano, J.; Martin-Doñate, C. A new method for the automated design of cooling systems in injection molds. Comput. Aided Des. 2018, 104, 60–86. [Google Scholar] [CrossRef]
- Ding, L.P.; Tan, J.R.; Wei, Z.; Chen, W.L.; Gao, Z. Multi-objective performance design of injection molding machine via a new multi-objective optimization algorithm. Int. J. Innov. Comput. Inf. Control. 2011, 7, 3939–3949. [Google Scholar]
- Chen, W.; Zhou, X.H.; Wang, H.F.; Wang, W. Multi-objective optimal approach for injection molding based on surrogate model and particle swarm optimization algorithm. J. Shanghai Jiaotong Univ. 2010, 15, 88–93. [Google Scholar] [CrossRef]
- Alosime, E.M. A review on Copoly (ether-ester) elastomers: Degradation and stabilization. J. Polym. Res. 2019, 26, 293. [Google Scholar] [CrossRef]
- Loyer, C.; Régnier, G.; Duval, V.; Ould, Y.; Richaud, E. PBT plasticity loss induced by oxidative and hydrolysis ageing. Polym. Degrad. Stab. 2020, 181, 109368. [Google Scholar] [CrossRef]
- Nait-Ali, L.K.; Colin, X.; Bergeret, A. Kinetic analysis and modelling of PET macromolecular changes during its mechanical recycling by extrusion. Polym. Degrad. Stabil. 2011, 96, 236–246. [Google Scholar] [CrossRef]
- Reano, A.F.; Guinault, A.; Richaud, E.; Fayolle, B. Polyethylene loss of ductility during oxidation: Effect of initial molar mass distribution. Polym. Degrad. Stab. 2018, 149, 78–84. [Google Scholar] [CrossRef]
- Jariyavidyanont, K.; Androsch, R.; Schick, C. Crystal reorganization of poly (butylene terephthalate). Polymer 2017, 124, 274–283. [Google Scholar] [CrossRef]
- Hocker, S.J.A.; Kim, W.T.; Schniepp, H.C.; Kranbuehl, D.E. Polymer crystallinity and the ductile to brittle transition. Polymers 2018, 158, 72–76. [Google Scholar] [CrossRef]
- Jose, C.; Chan, C.H.; Winie, T.; Joseph, B.; Tharayil, A.; Maria, H.J.; Volova, T.; La Mantia, F.P.; Rouxel, D.; Morreale, M.; et al. Thermomechanical Analysis of Isora Nanofibril Incorporated Polyethylene Nanocomposites. Polymers 2021, 13, 299. [Google Scholar] [CrossRef]
- Kopal, I.; Harniˇcárová, M.; Valíˇcek, J.; Kušnerová, M. Modeling the temperature dependence of dynamic mechanical properties and visco-elastic behavior of thermoplastic polyurethane using artificial neural network. Polymers 2017, 9, 519. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.C.; Guo, B.H.; Xu, J. A review on polymer crystallization theories. Crystals 2017, 7, 4. [Google Scholar] [CrossRef]
- Ekiert, M.; Młyniec, A.; Uhl, T. The influence of degradation on the viscosity and molecular mass of poly(lactide acid) biopolymer. Diagnostyka 2015, 16, 63–70. [Google Scholar]
- Prezenszkya, A.C.; Ambrósio, J.D.; Pessan, L.A.; Hage, E., Jr. Correlation between Processing, Morphology and Impact Resistance of PBT/ABS Blends. Mat. Res. 2017, 20, 452–457. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Modeling and Optimization of the Injection-Molding Process: A Review. Adv. Polym. Technol. 2018, 37, 21683. [Google Scholar] [CrossRef]
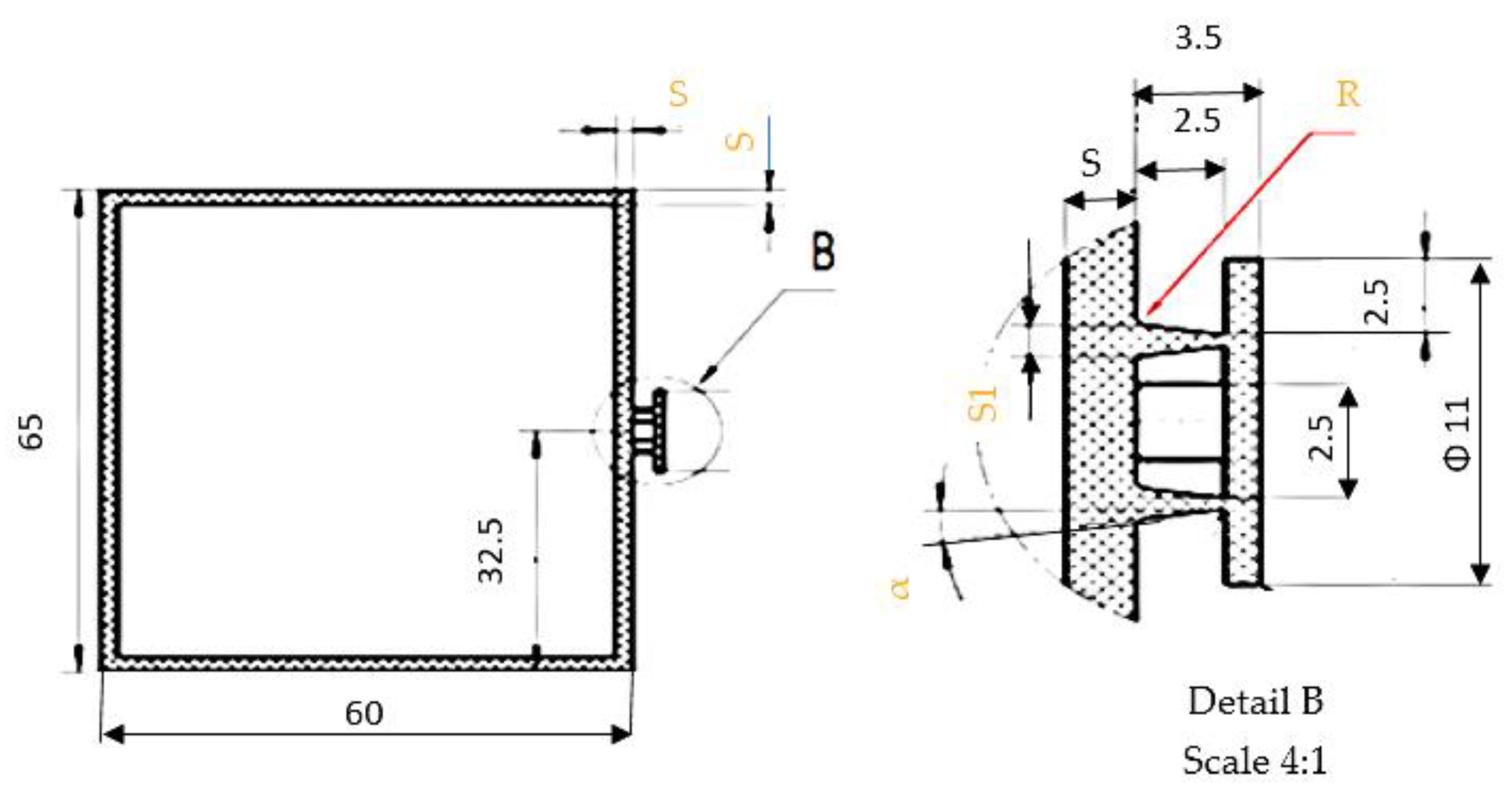
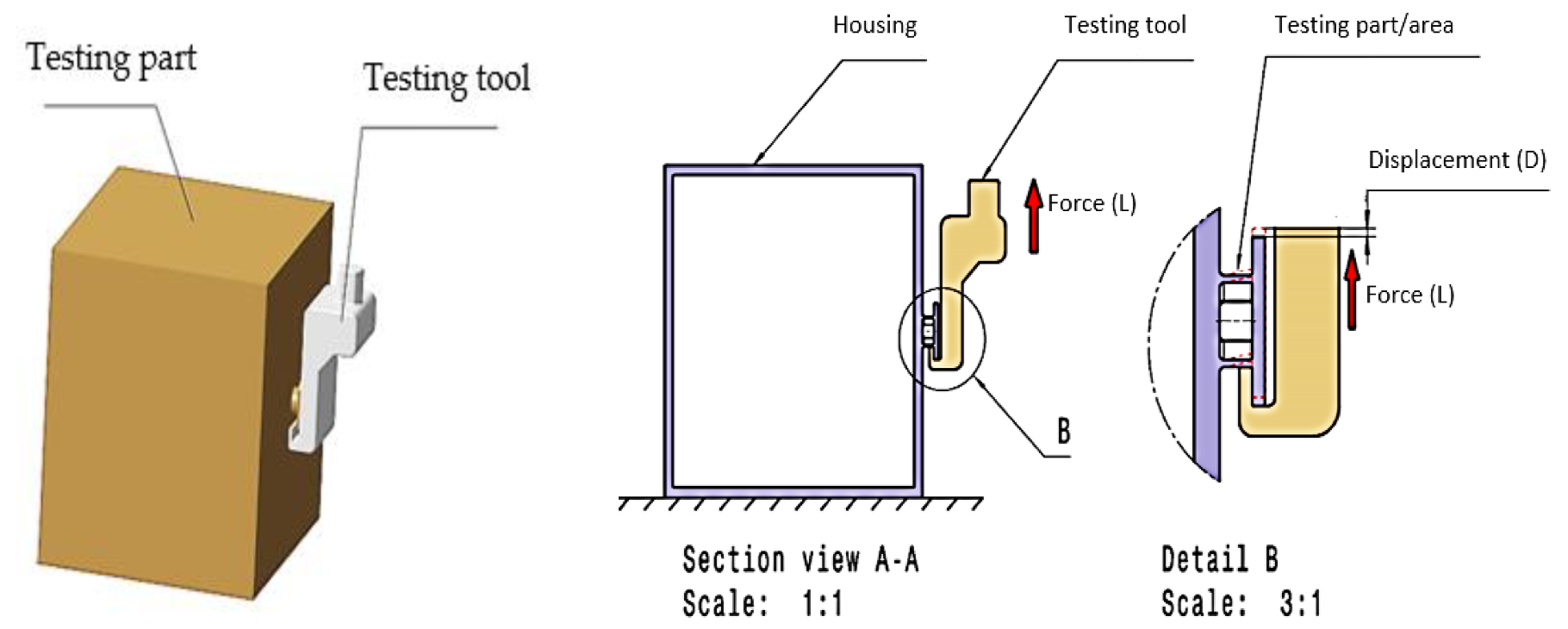


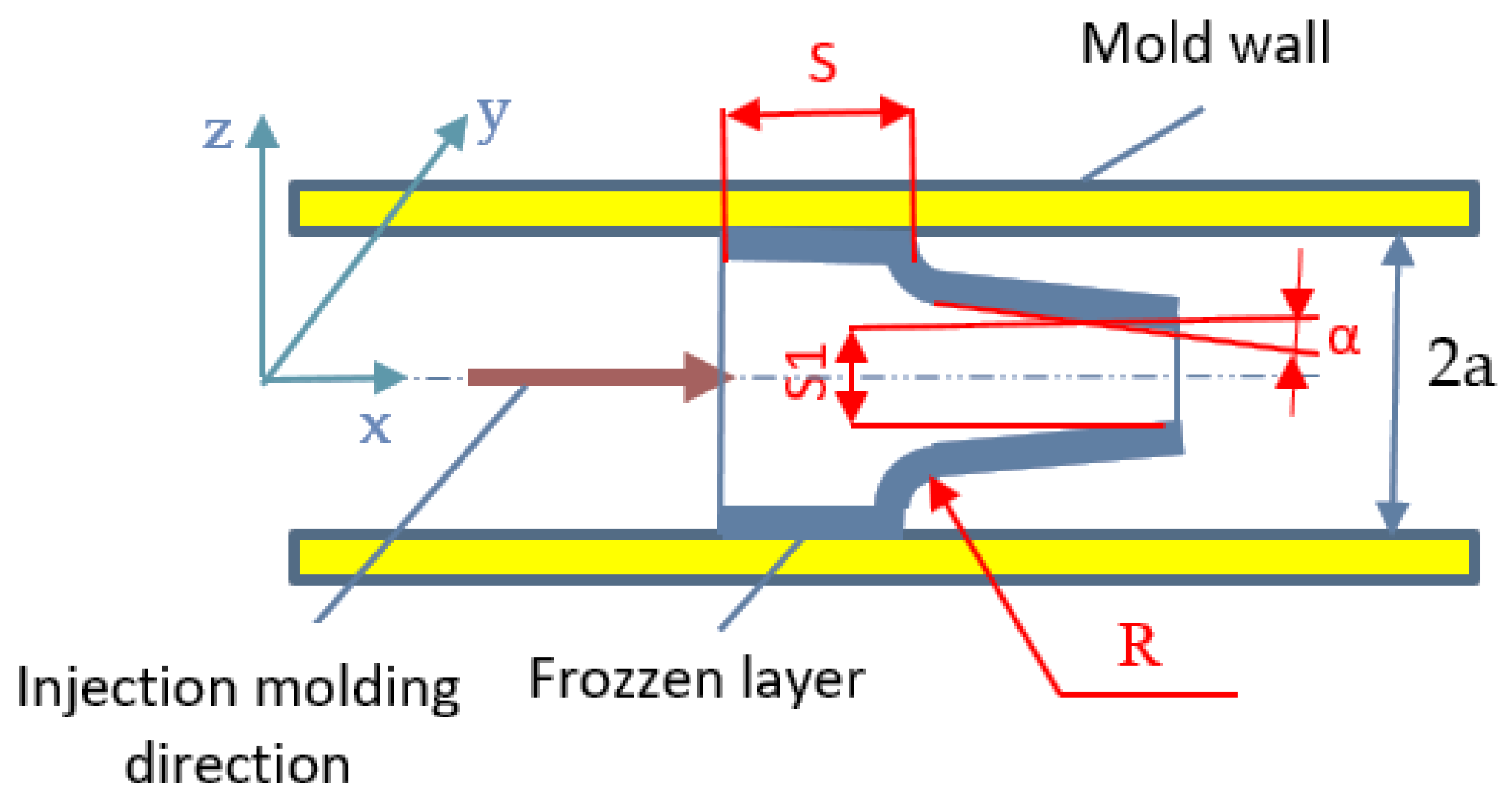



| Bulk Modulus, GPa | Compressive Strength, MPa | Elastic Limit, MPa | Hardness, MPa | Tensile Strength, MPa | Modulus of Rupture, MPa | Breakdown Potential, MV/m |
|---|---|---|---|---|---|---|
| 11.2 | 155 | 92 | 275 | 165 | 185 | 21 |
| Level | Lowest | Low | Center | High | Highest |
|---|---|---|---|---|---|
| Cod value | −1.68179 | −1 | 0 | 1 | 1.68179 |
| Connection radius, R, mm | 0.096 | 0.3 | 0.6 | 0.9 | 1.104 |
| Angle of inclination, α° | 0.636 | 2 | 4 | 6 | 7.364 |
| The report K = S1/S | 0.195 | 0.4 | 0.7 | 1.0 | 1.204 |
| Run Order | Connection Radius, R | The Angle of Inclination, α° | The Report K = S1/S |
|---|---|---|---|
| 1 | −1.00000 | −1.00000 | 1.00000 |
| 2 | 1.00000 | −1.00000 | 1.00000 |
| 3 | 1.00000 | 1.00000 | −1.00000 |
| 4 | 0.00000 | 0.00000 | 1.68179 |
| 5 | 1.00000 | 1.00000 | 1.00000 |
| 6 | 1.00000 | −1.00000 | −1.00000 |
| 7 | 0.00000 | 0.00000 | 0.00000 |
| 8 | 0.00000 | 0.00000 | 0.00000 |
| 9 | 1.00000 | 1.00000 | 1.00000 |
| 10 | 1.00000 | 1.00000 | 1.00000 |
| 11 | −1.68179 | 0.00000 | 0.00000 |
| 12 | 1.68179 | 0.00000 | 0.00000 |
| 13 | 1.00000 | 1.00000 | 1.00000 |
| 14 | 0.00000 | 0.00000 | 0.00000 |
| 15 | 0.00000 | −1.68179 | 0.00000 |
| 16 | 0.00000 | 0.00000 | 0.00000 |
| 17 | 0.00000 | 0.00000 | 0.00000 |
| 18 | 0.00000 | 0.00000 | 0.00000 |
| 19 | 0.00000 | 0.00000 | −1.68179 |
| 20 | 0.00000 | 1.68179 | 0.00000 |
| Run Order | R (mm) | α° | K | L (N) | D (mm) |
|---|---|---|---|---|---|
| 1 | 0.300 | 2.000 | 1.000 | 314.4 | 2.504 |
| 2 | 0.900 | 2.000 | 1.000 | 298.7 | 2.763 |
| 3 | 0.900 | 6.000 | 0.400 | 357.7 | 3.219 |
| 4 | 0.600 | 4.000 | 1.205 | 327.4 | 3.702 |
| 5 | 0.900 | 6.000 | 1.000 | 359.7 | 2.919 |
| 6 | 0.900 | 2.000 | 0.400 | 292.7 | 3.389 |
| 7 | 0.600 | 4.000 | 0.700 | 322.3 | 3.007 |
| 8 | 0.600 | 4.000 | 0.700 | 326.4 | 3.101 |
| 9 | 0.900 | 6.000 | 1.000 | 341.8 | 2.991 |
| 10 | 0.900 | 6.000 | 1.000 | 345.7 | 2.839 |
| 11 | 1.104 | 6.000 | 1.000 | 378.8 | 2.186 |
| 12 | 0.096 | 6.000 | 1.000 | 339.3 | 3.651 |
| 13 | 0.900 | 6.000 | 1.000 | 355.5 | 3.802 |
| 14 | 0.600 | 4.000 | 0.700 | 323.9 | 3.005 |
| 15 | 0.600 | 0.636 | 0.700 | 357.7 | 3.501 |
| 16 | 0.600 | 4.000 | 0.700 | 335.4 | 2.614 |
| 17 | 0.600 | 4.000 | 0.700 | 327.5 | 2.998 |
| 18 | 0.600 | 4.000 | 0.700 | 322.7 | 2.563 |
| 19 | 0.600 | 4.000 | 0.195 | 328.8 | 3.733 |
| 20 | 0.600 | 7.364 | 0.700 | 335.6 | 2.267 |
| Source | Force (L) | Displacement (D) | ||||
|---|---|---|---|---|---|---|
| Mean of Square | F Value | p Value Prob > F | Mean of Square | F Value | p Value Prob > F | |
| Model | 0.021 | 95.413 | <0.001 | 0.058 | 107.669 | <0.001 |
| R | 0.091 | 109.685 | <0.001 | 0.035 | 136.669 | <0.001 |
| α | 0.065 | 85.826 | <0.001 | 0.069 | 99.749 | <0.001 |
| k | 0.003 | 135.568 | <0.001 | 0.001 | 115.1478 | <0.001 |
| R·α | 4.57e−3 | 64.769 | 0.984 | 3.18e−3 | 83.616 | 0.627 |
| R·K | 2.31e−3 | 73.704 | 0.651 | 1.91e−3 | 77.750 | 0.322 |
| K·α | 3.19e−3 | 92.135 | 0.003 | 2.73e−3 | 95.994 | 0.001 |
| R·K·α | 4.13e−3 | 61.024 | 0.783 | 3.91e−3 | 67.523 | 0.211 |
| R2 | 5.98e−3 | 105.136 | 0.002 | 3.95e−3 | 111.651 | 0.118 |
| α2 | 1.43e−3 | 63.157 | 0.115 | 2.35e−3 | 105.637 | 0.189 |
| K2 | 3.35e−3 | 71.125 | 0.236 | 1.57e−3 | 83.869 | 0.003 |
| Residual | 1.17e−3 | 1.123e−3 | - | 2.95e−3 | 1.318e−3 | - |
| No. Exp. | Parameters | Force (L) | Displacement (D) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R (mm) | α° | K | Predicted Value | Actual Value | % Error | Predicted Value | Actual Value | % Error | |
| 1 | 0.1 | 1.0 | 0.2 | 229.656 | 241.358 | 5.095 | 3.037 | 2.912 | −5.977 |
| 2 | 0.4 | 2.0 | 0.4 | 276.235 | 281.667 | 1.966 | 2.755 | 2.621 | −5.112 |
| 3 | 0.7 | 4.0 | 0.6 | 350.933 | 341.821 | −2.596 | 2.658 | 2.763 | 3.800 |
| 4 | 1.0 | 5.0 | 0.8 | 350.197 | 367.742 | 5.010 | 2.622 | 2.854 | 8.101 |
| 5 | 1.1 | 6.0 | 1.1 | 374.639 | 383.372 | 2.331 | 2.572 | 2.495 | −3.086 |
| Run Order | R (mm) | α° | K | L (N) | D (mm) |
|---|---|---|---|---|---|
| 1 | 0.300 | 2.000 | 1.000 | 211.9 | 1.229 |
| 2 | 0.900 | 2.000 | 1.000 | 202.3 | 1.439 |
| 3 | 0.900 | 6.000 | 0.400 | 245.3 | 1.719 |
| 4 | 0.600 | 4.000 | 1.205 | 207.4 | 2.127 |
| 5 | 0.900 | 6.000 | 1.000 | 255.1 | 1.537 |
| 6 | 0.900 | 2.000 | 0.400 | 283.7 | 2.008 |
| 7 | 0.600 | 4.000 | 0.700 | 219.8 | 1.991 |
| 8 | 0.600 | 4.000 | 0.700 | 207.5 | 1.987 |
| 9 | 0.900 | 6.000 | 1.000 | 291.2 | 1.781 |
| 10 | 0.900 | 6.000 | 1.000 | 209.4 | 1.431 |
| 11 | 1.104 | 6.000 | 1.000 | 251.3 | 1.372 |
| 12 | 0.096 | 6.000 | 1.000 | 217.2 | 1.163 |
| 13 | 0.900 | 6.000 | 1.000 | 298.5 | 1.071 |
| 14 | 0.600 | 4.000 | 0.700 | 217.8 | 1.287 |
| 15 | 0.600 | 0.636 | 0.700 | 239.7 | 1.219 |
| 16 | 0.600 | 4.000 | 0.700 | 222.9 | 1.879 |
| 17 | 0.600 | 4.000 | 0.700 | 219.2 | 1.106 |
| 18 | 0.600 | 4.000 | 0.700 | 223.9 | 1.198 |
| 19 | 0.600 | 4.000 | 0,195 | 287.1 | 1.098 |
| 20 | 0.600 | 7.364 | 0.700 | 211.8 | 1.169 |
| Source | Force (L) | Displacement (D) | ||||
|---|---|---|---|---|---|---|
| Mean of Square | F Value | p Value Prob > F | Mean of Square | F Value | p Value Prob > F | |
| Model | 0.035 | 105.203 | <0.001 | 0.079 | 93.528 | <0.001 |
| R | 0.087 | 133.613 | <0.001 | 0.095 | 123.007 | <0.001 |
| α | 0.039 | 100.763 | <0.001 | 0.083 | 87.173 | <0.001 |
| K | 0.073 | 167.224 | <0.001 | 0.025 | 103.835 | <0.001 |
| R·α | 1.17e−3 | 82.692 | 0.058 | 2.63e−3 | 94.122 | 0.002 |
| R·K | 1.98e−3 | 103.704 | 0.003 | 3.82e−3 | 73.464 | 0.521 |
| K·α | 2.39e−3 | 92.913 | 0.031 | 2.62e−3 | 83.174 | 0.003 |
| R·K·α | 1.23e−7 | 76.347 | 0.098 | 1.97e−3 | 67.258 | 0.796 |
| R2 | 3.97e−3 | 93.173 | 0.143 | 3.81e−3 | 105.681 | 0.521 |
| α2 | 2.09e−3 | 62.526 | 0.028 | 4.89e−3 | 78.687 | 0.231 |
| K2 | 1.36e−3 | 73.231 | 0.099 | 2.11e−3 | 69.456 | 0.001 |
| Residual | 2.69e−3 | 69.523 | - | 3.29e−3 | 53.651 | - |
| No. Exp. | Parameters | Force (L) | Displacement (D) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R (mm) | α° | K | Predicted Value | Actual Value | % Error | Predicted Value | Actual Value | % Error | |
| 1 | 0.1 | 1.0 | 0.2 | 129.005 | 131.105 | 1.601 | 1.726 | 1.825 | 5.424 |
| 2 | 0.4 | 2.0 | 0.4 | 269.545 | 254.512 | −5.906 | 1.541 | 1.653 | 2.407 |
| 3 | 0.7 | 4.0 | 0.6 | 222.075 | 217.263 | −2.214 | 1.428 | 1.372 | −4.081 |
| 4 | 1.0 | 5.0 | 0.8 | 236.091 | 225.183 | −4.844 | 1.408 | 1.396 | −0.859 |
| 5 | 1.1 | 6.0 | 1.1 | 219.596 | 223.253 | 1.638 | 1.358 | 1.298 | −4.622 |
| Run Order | New Parts | Artificially Aged Parts | ||
|---|---|---|---|---|
| Reduced Viscosity (ηred), cm3/g | Degradation, % | Reduced Viscosity (ηred), cm3/g | Degradation, % | |
| 1 | 96.1 | 3.61 | 59.9 | 39.9 |
| 2 | 95.9 | 3.82 | 59.6 | 40.2 |
| 3 | 98.7 | 1.01 | 64.2 | 39.6 |
| 4 | 95.9 | 3.82 | 59.7 | 40.1 |
| 5 | 98.6 | 1.10 | 64.5 | 35.3 |
| 6 | 95.8 | 3.91 | 64.9 | 34.9 |
| 7 | 96.6 | 3.10 | 60.6 | 39.2 |
| 8 | 96.5 | 3.20 | 60.3 | 39.5 |
| 9 | 99.2 | 0.61 | 64.8 | 35.0 |
| 10 | 99.1 | 0.60 | 61.6 | 38.2 |
| 11 | 99.5 | 0.20 | 65.3 | 34.7 |
| 12 | 98.6 | 1.00 | 61.9 | 37.9 |
| 13 | 98.8 | 0.90 | 65.2 | 34.7 |
| 14 | 96.5 | 3.20 | 61.6 | 38.2 |
| 15 | 99.0 | 0.70 | 63.7 | 36.1 |
| 16 | 98.8 | 0.90 | 62.8 | 37.0 |
| 17 | 97.9 | 1.80 | 63.2 | 36.6 |
| 18 | 97.8 | 1.90 | 62.1 | 37.7 |
| 19 | 97.6 | 2.10 | 61.8 | 38.0 |
| 20 | 97.4 | 2.30 | 62.3 | 37.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobrotă, D.; Lazăr, S.V. Redesign of the Geometry of Parts Produced from PBT Composite to Improve Their Operational Behavior. Polymers 2021, 13, 2536. https://doi.org/10.3390/polym13152536
Dobrotă D, Lazăr SV. Redesign of the Geometry of Parts Produced from PBT Composite to Improve Their Operational Behavior. Polymers. 2021; 13(15):2536. https://doi.org/10.3390/polym13152536
Chicago/Turabian StyleDobrotă, Dan, and Sergiu Viorel Lazăr. 2021. "Redesign of the Geometry of Parts Produced from PBT Composite to Improve Their Operational Behavior" Polymers 13, no. 15: 2536. https://doi.org/10.3390/polym13152536






