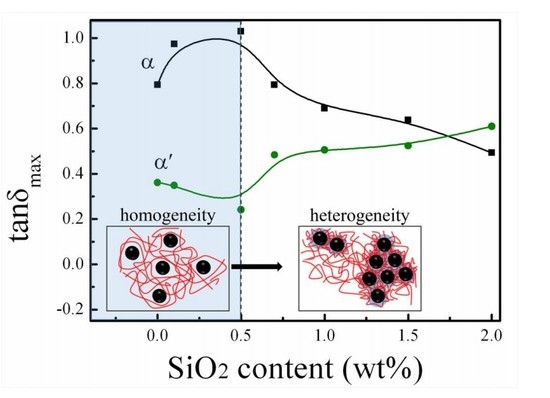
Opposite Effects of SiO2 Nanoparticles on the Local α and Larger-Scale α’ Segmental Relaxation Dynamics of PMMA Nanocomposites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials’ Preparation
2.2. Characterization
3. Results and Discussion
3.1. The Morphology and Interaction Characterization of PMMA/SiO2 Nanocomposites
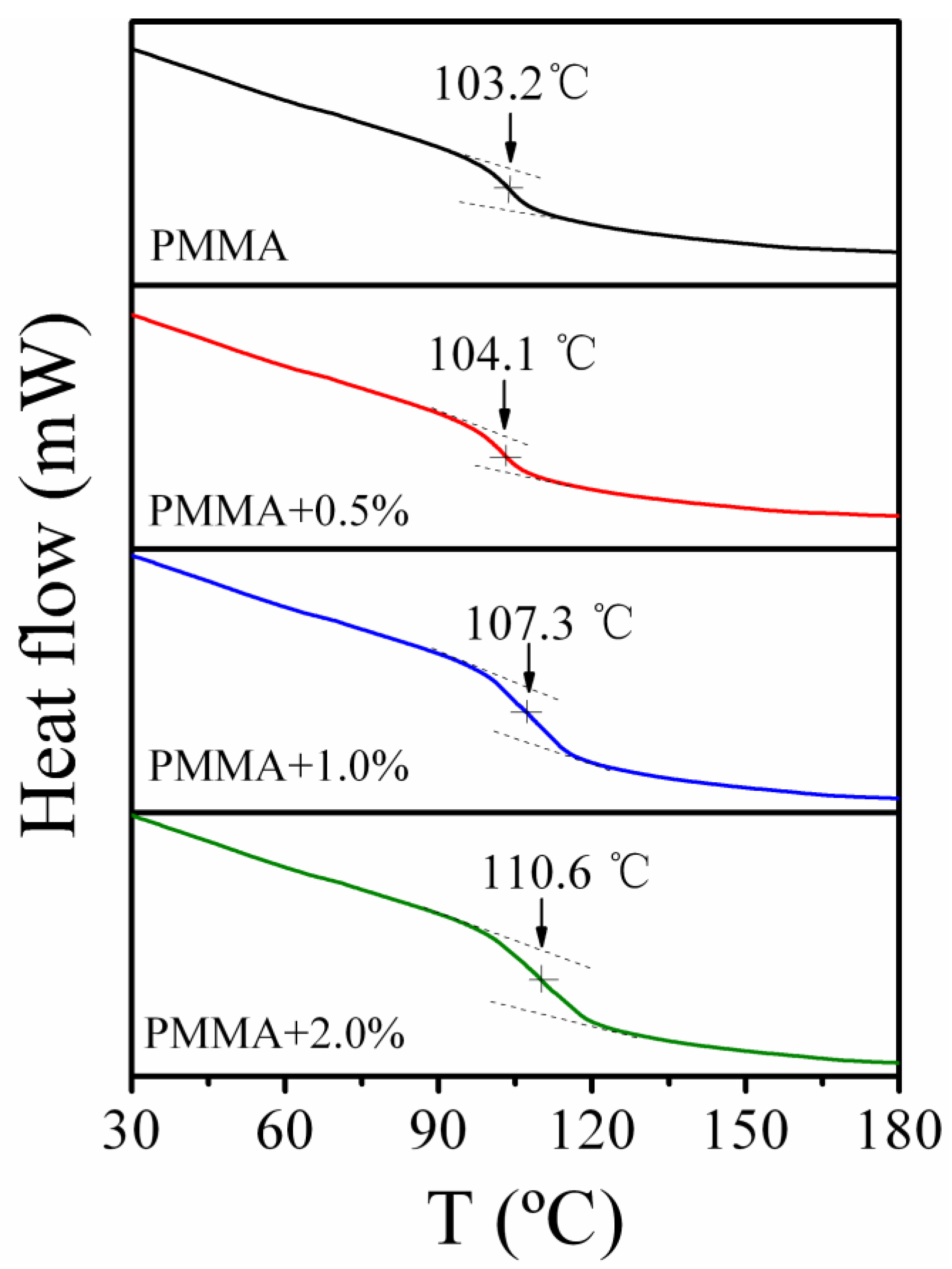
3.2. The Glass Transition of PMMA/SiO2 Nanocomposites
3.3. The Segmental Relaxation Dynamics of PMMA/SiO2 Nanocomposites
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cheng, S.; Bocharova, V.; Belianinov, A.; Xiong, S.; Kisliuk, A.; Somnath, S.; Holt, A.P.; Ovchinnikova, O.S.; Jessse, S.; Martin, H.; et al. Unraveling the mechanism of nanoscale mechanical reinforcement in glassy polymer nanocomposites. Nano Lett. 2016, 16, 3630–3637. [Google Scholar] [CrossRef] [PubMed]
- Bozzini, B.; Bocchetta, P.; Kourousias, G.; Gianoncelli, A. Electrodeposition of Mn-Co/polypyrrole nanocomposites: An electrochemical and in situ soft-X-ray microspectroscopic investigation. Polymers 2017, 9, 17. [Google Scholar] [CrossRef]
- Malas, A.; Bharati, A.; Verkinderen, O.; Goderis, B.; Moldenaers, P.; Cardinaels, R. Effect of the GO reduction method on the dielectric properties, electrical conductivity and crystalline behavior of PEO/rGO nanocomposites. Polymers 2017, 9, 613. [Google Scholar] [CrossRef] [PubMed]
- Papon, A.; Montes, H.; Lequeux, F.; Oberdisse, J.; Saalwaechter, K.; Guy, L. Solid particles in an elastomer matrix: Impact of colloid dispersion and polymer mobility modification on the mechanical properties. Soft Matter 2012, 8, 4090–4096. [Google Scholar] [CrossRef]
- Arrigo, R.; Antonioli, D.; Lazzari, M.; Gianotti, V.; Laus, M.; Montanaro, L.; Malucelli, G. Relaxation dynamics in polyethylene glycol/modified hydrotalcite nanocomposites. Polymers 2018, 10, 1182. [Google Scholar] [CrossRef] [PubMed]
- Schadler, L.S.; Kumar, S.K.; Benicewicz, B.C.; Lewis, S.L.; Harton, S.E. Designed interfaces in polymer nanocomposites: A fundamental viewpoint. MRS Bull. 2007, 32, 335–340. [Google Scholar] [CrossRef]
- Yamamoto, U.; Schweizer, K.S. Microscopic theory of the long-time diffusivity and intermediate-time anomalous transport of a nanoparticle in polymer melts. Macromolecules 2015, 48, 152–163. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Q. Time-concentration superpositioning principle accounting for the size effects of reinforcement and dissipation of polymer nanocomposites. Compos. Sci. Technol. 2018, 168, 279–286. [Google Scholar] [CrossRef]
- Behbahani, A.F.; Allaei, S.M.V.; Motlagh, G.H.; Eslami, H.; Harmandaris, V.A. Structure, dynamics, and apparent glass transition of stereoregular poly(methyl methacrylate)/graphene interfaces through atomistic simulations. Macromolecules 2018, 51, 7518–7532. [Google Scholar] [CrossRef]
- Ding, Y.; Pawlus, S.; Sokolov, A.P.; Douglas, J.F.; Karim, A.; Soles, C.L. Dielectric spectroscopy investigation of relaxation in C-60-polyisoprene nanocomposites. Macromolecules 2009, 42, 3201–3206. [Google Scholar] [CrossRef]
- Li, L.; Zhou, D.; Huang, D.; Xue, G. Double glass transition temperatures of poly(methyl methacrylate) confined in alumina nanotube templates. Macromolecules 2014, 47, 297–303. [Google Scholar] [CrossRef]
- Li, X.; Chen, L.; Li, Q.; Zhang, J.; Su, Z.; Zhang, X.; Zheng, K.; Tian, X. Double glass transitions in exfoliated poly(methyl methacrylate)/organically modified MgAl layered double hydroxide nanocomposites. RSC Adv. 2016, 6, 101941–101947. [Google Scholar] [CrossRef]
- Nusser, K.; Schneider, G.J.; Pyckhout-Hintzen, W.; Richter, D. Viscosity decrease and reinforcement in polymer-silsesquioxane composites. Macromolecules 2011, 44, 7820–7830. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Bokobza, L.; Pissis, P. Dynamics near the filler surface in natural rubber-silica nanocomposites. Polymer 2011, 52, 3175–3182. [Google Scholar] [CrossRef]
- Holt, A.P.; Sangoro, J.R.; Wang, Y.; Agapov, A.L.; Sokolov, A.P. Chain and segmental dynamics of poly(2-vinylpyridine) nanocomposites. Macromolecules 2013, 46, 4168–4173. [Google Scholar] [CrossRef]
- Bogoslovov, R.B.; Roland, C.M.; Ellis, A.R.; Randall, A.M.; Robertson, C.G. Effect of silica nanoparticles on the local segmental dynamics in poly(vinyl acetate). Macromolecules 2008, 41, 1289–1296. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, L.; Cheng, J.; Shangguan, Y.; Yu, W.; Qiu, B.; Zheng, Q. Segmental dynamics and physical aging of polystyrene/silver nanocomposites. RSC Adv. 2014, 4, 20086–20093. [Google Scholar] [CrossRef]
- Jancar, J.; Douglas, J.F.; Starr, F.W.; Kumar, S.K.; Cassagnau, P.; Lesser, A.J.; Sternstein, S.S.; Buehler, M.J. Current issues in research on structure-property relationships in polymer nanocomposites. Polymer 2010, 51, 3321–3343. [Google Scholar] [CrossRef]
- Rizos, A.K.; Jian, T.; Ngai, K.L. Determination of the coupling parameter of local segmental motion in poly(isobutylene) by photon-correlation spectroscopy. Macromolecules 1995, 28, 517–521. [Google Scholar] [CrossRef]
- Ngai, K.L.; Plazek, D.J.; Rizos, A.K. Viscoelastic properties of amorphous polymers. 5. A coupling model analysis of the thermorheological complexity of polyisobutylene in the class-rubber softening dispersion. J. Polym. Sci. Part B Polym. Phys. 1997, 35, 599–614. [Google Scholar] [CrossRef]
- Paluch, M.; Pawlus, S.; Sokolov, A.P.; Ngai, K.L. Sub-Rouse modes in polymers observed by dielectric spectroscopy. Macromolecules 2010, 43, 3103–3106. [Google Scholar] [CrossRef]
- Ngai, K.L.; Plazek, D.J. Resolution of sub-Rouse modes of polystyrene by dissolution. Macromolecules 2002, 35, 9136–9141. [Google Scholar] [CrossRef]
- Rizos, A.K.; Ngai, K.L.; Plazek, D.J. Local segmental and sub-Rouse modes in polyisobutylene by photon correlation spectroscopy. Polymer 1997, 38, 6103–6107. [Google Scholar] [CrossRef]
- Wu, X.; Liu, C.; Zhu, Z.; Ngai, K.L.; Wang, L.M. Nature of the sub-Rouse modes in the glass-rubber transition zone of amorphous polymers. Macromolecules 2011, 44, 3605–3610. [Google Scholar] [CrossRef]
- Yang, F.; Nelson, G.L. PMMA/silica nanocomposite studies: Synthesis and properties. J. Appl. Polym. Sci. 2004, 91, 3844–3850. [Google Scholar] [CrossRef]
- Qu, M.; Meth, J.S.; Blackman, G.S.; Cohen, G.M.; Sharp, K.G.; Van Vliet, K.J. Tailoring and probing particle-polymer interactions in PMMA/silica nanocomposites. Soft Matter 2011, 7, 8401–8408. [Google Scholar] [CrossRef]
- Pantaleon, R.; Gonzalez-Benito, J. Structure and thermostability of PMMA in PMMA/silica nanocomposites: Effect of high-energy ball milling and the amount of the nanofiller. Polym. Compos. 2010, 31, 1585–1592. [Google Scholar] [CrossRef]
- Salami-Kalajahi, M.; Haddadi-Asl, V.; Rahimi-Razin, S.; Behboodi-Sadabad, F.; Roghani-Mamaqani, H.; Najafi, M. Effect of loading and surface modification of nanoparticles on the properties of PMMA/silica nanocomposites prepared via in-situ free radical polymerization. Int. J. Polym. Mater. 2013, 62, 336–344. [Google Scholar] [CrossRef]
- Boucher, V.M.; Cangialosi, D.; Alegria, A.; Colmenero, J. Time dependence of the segmental relaxation time of poly(vinyl acetate)-silica nanocomposites. Phys. Rev. E 2012, 86, 041501. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, F.A.; Redondo, M.; Olmos, D.; Kuzmanovic, M.; Gonzalez-Benito, J. A near-infrared spectroscopy study on thermal transitions of PMMA and PMMA/SiO2 nanocomposites. Macromol. Symp. 2014, 339, 48–59. [Google Scholar] [CrossRef]
- Li, C.X.; Wu, J.T.; Zhao, J.; Zhao, D.L.; Fan, Q.R. Effect of inorganic phase on polymeric relaxation dynamics in PMMA/silica hybrids studied by dielectric analysis. Eur. Polym. J. 2004, 40, 1807–1814. [Google Scholar] [CrossRef]
- Hu, Y.H.; Chen, C.Y.; Wang, C.C. Viscoelastic properties and thermal degradation kinetics of silica/PMMA nanocomposites. Polym. Degrad. Stab. 2004, 84, 545–553. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, L.; Zhang, D.; Liu, Y.; Guan, A.; Wu, G. Unexpected segmental dynamics in polystyrene-grafted silica nanocomposites. Soft Matter 2016, 12, 8542–8553. [Google Scholar] [CrossRef]
- Song, Y.; Bu, J.; Zuo, M.; Gao, Y.; Zhang, W.; Zheng, Q. Glass transition of poly(methyl methacrylate) filled with nanosilica and core-shell structured silica. Polymer 2017, 127, 141–149. [Google Scholar] [CrossRef]
- Wu, X.; Xu, Q.; Shui, J.; Zhu, Z. Low-frequency mechanical spectroscopy study of conformational transition of polymer chains in concentrated solutions. Rev. Sci. Instrum. 2008, 79, 126105. [Google Scholar] [CrossRef] [PubMed]
- Kropka, J.M.; Sakai, V.G.; Green, P.F. Local polymer dynamics in polymer-C-60 mixtures. Nano Lett. 2008, 8, 1061–1065. [Google Scholar] [CrossRef]
- Rittigstein, P.; Torkelson, J.M. Polymer-nanoparticle interfacial interactions in polymer nanocomposites: Confinement effects on glass transition temperature and suppression of physical aging. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 2935–2943. [Google Scholar] [CrossRef]
- Ngai, K.L.; Plazek, D.J. Identification of different modes of molecular-motion in polymers that cause thermorheological complexity. Rubber Chem. Technol. 1995, 68, 376–434. [Google Scholar] [CrossRef]
- Wu, J.; Huang, G.; Pan, Q.; Zheng, J.; Zhu, Y.; Wang, B. An investigation on the molecular mobility through the glass transition of chlorinated butyl rubber. Polymer 2007, 48, 7653–7659. [Google Scholar] [CrossRef]
- Plazek, D.J.; Chay, I.C.; Ngai, K.L.; Roland, C.M. Viscoelastic properties of polymers. 4. Thermorheological complexity of the softening dispersion in polyisobutylene. Macromolecules 1995, 28, 6432–6436. [Google Scholar] [CrossRef] [Green Version]
- Yuan, L.X.; Fang, Q.F. Nonlinear fitting of the internal friction data and its application on the bamboo grain boundary relaxation in pure Al. Acta Metall. Sin. 1998, 34, 1016–1020. [Google Scholar]
- Wu, J.; Haddad, T.S.; Kim, G.M.; Mather, P.T. Rheological behavior of entangled polystyrene-polyhedral oligosilsesquioxane (POSS) copolymers. Macromolecules 2007, 40, 544–554. [Google Scholar] [CrossRef]
- Holt, A.P.; Griffin, P.J.; Bocharova, V.; Agapov, A.L.; Imel, A.E.; Dadmun, M.D.; Sangoro, J.R.; Sokolov, A.P. Dynamics at the polymer/nanoparticle interface in poly(2-vinylpyridine)/silica nanocomposites. Macromolecules 2014, 47, 1837–1843. [Google Scholar] [CrossRef]
- Ding, Y.F.; Sokolov, A.P. Breakdown of time-temperature superposition principle and universality of chain dynamics in polymers. Macromolecules 2006, 39, 3322–3326. [Google Scholar] [CrossRef]
- Plazek, D.J. Anomalous viscoelastic properties of polymers: Experiments and explanations. J. Non Cryst. Solids 2007, 353, 3783–3787. [Google Scholar] [CrossRef]
- Plazek, D.J. 1995 Bingham medal address: Oh, thermorheological simplicity, wherefore art thou? J. Rheol. 1996, 40, 987–1014. [Google Scholar] [CrossRef]
- Hao, N.; Boehning, M.; Schoenhals, A. Dielectric properties of nanocomposites based on polystyrene and polyhedral oligomeric phenethyl-silsesquioxanes. Macromolecules 2007, 40, 9672–9679. [Google Scholar] [CrossRef]
- Nakazawa, M.; Urakawa, O.; Adachi, K. Effect of local heterogeneity on dielectric relaxation spectra in concentrated solutions of poly(vinyl acetate) and poly(vinyl octanoate). Macromolecules 2000, 33, 7898–7904. [Google Scholar] [CrossRef]
- Fulcher, G.S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Tammann, G.; Hesse, W. Die abhangigkeit der viscositat von der temperatur bei unterkuhlten fltissigkeiten. Z. Anorg. Allg. Chem. 1926, 156, 245–257. [Google Scholar] [CrossRef]
- Vogel, H. The law of the relation between the viscosity of liquids and the temperature. Phys. Z. 1921, 22, 645–646. [Google Scholar]
- Yada, M.; Nakazawa, M.; Urakawa, O.; Morishima, Y.; Adachi, K. Effect of local heterogeneity on dielectric segmental relaxation of poly(vinyl acetate) in concentrated solution. Macromolecules 2000, 33, 3368–3374. [Google Scholar] [CrossRef]
- Wu, X.; Liu, C.; Ngai, K.L. Origin of the crossover in dynamics of the sub-Rouse modes at the same temperature as the structural alpha-relaxation in polymers. Soft Matter 2014, 10, 9324–9333. [Google Scholar] [CrossRef] [PubMed]
- Starr, F.W.; Douglas, J.F. Modifying fragility and collective motion in polymer melts with nanoparticles. Phys. Rev. Lett. 2011, 106, 115702. [Google Scholar] [CrossRef]
- Chandra, A.; Meyer, W.H. Dielectric relaxation studies of low thermal expansion polymer composites. J. Appl. Polym. Sci. 2013, 128, 2857–2864. [Google Scholar] [CrossRef]
- Wu, J.; Huang, G.; Pan, Q.; Qu, L.; Zhu, Y.; Wang, B. Study on liquid-liquid transition of chlorinated butyl rubber by positron annihilation lifetime spectroscopy. Appl. Phys. Lett. 2006, 89, 121904. [Google Scholar] [CrossRef]









| Silica Content | α Process | Sub-Rouse | Rouse | ||||
|---|---|---|---|---|---|---|---|
| T0 (K) | m | T0 (K) | T0 (K) | ||||
| 0 wt % | 1.41 × 10−3 | 349 | 230 | 2.50 × 10−3 | 367 | 3.65 × 10−3 | 402 |
| 0.1 wt % | 1.47 × 10−3 | 351 | 228 | 2.55 × 10−3 | 358 | 3.66 × 10−3 | 393 |
| 0.5 wt % | 1.49 × 10−3 | 351 | 229 | 3.12 × 10−3 | 369 | 4.26 × 10−3 | 392 |
| 0.7 wt % | 1.13 × 10−3 | 353 | 321 | 1.62 × 10−3 | 344 | 3.10 × 10−3 | 389 |
| 1.0 wt % | 1.04 × 10−3 | 354 | 336 | 1.31 × 10−3 | 332 | 2.85 × 10−3 | 386 |
| 1.5 wt % | 9.79 × 10−4 | 357 | 369 | 1.15 × 10−3 | 316 | 2.50 × 10−3 | 383 |
| 2.0 wt % | 9.22 × 10−4 | 358 | 421 | 1.06 × 10−3 | 336 | 2.42 × 10−3 | 392 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Wu, X.; Liu, C.S. Opposite Effects of SiO2 Nanoparticles on the Local α and Larger-Scale α’ Segmental Relaxation Dynamics of PMMA Nanocomposites. Polymers 2019, 11, 979. https://doi.org/10.3390/polym11060979
Wang N, Wu X, Liu CS. Opposite Effects of SiO2 Nanoparticles on the Local α and Larger-Scale α’ Segmental Relaxation Dynamics of PMMA Nanocomposites. Polymers. 2019; 11(6):979. https://doi.org/10.3390/polym11060979
Chicago/Turabian StyleWang, Na, Xuebang Wu, and C.S. Liu. 2019. "Opposite Effects of SiO2 Nanoparticles on the Local α and Larger-Scale α’ Segmental Relaxation Dynamics of PMMA Nanocomposites" Polymers 11, no. 6: 979. https://doi.org/10.3390/polym11060979