Exploring the Molecular Distributions in Dilute Polymer Solutions Using a Multi-Scale Numerical Solver
Abstract
1. Introduction
2. Governing Equations
2.1. Macroscopic Equations
2.2. Microscopic Equations
2.2.1. Fokker-Planck Approach
2.2.2. Stochastic Brownian Configuration Field Approach
3. Numerical Methods
| Algorithm 1: The iterative algorithm to solve the multi-scale model. |
 |
4. BCFsolver Implementation
4.1. Overall Structure
4.2. Domain Programming Interface
4.3. Implementation
5. Results and Discussion
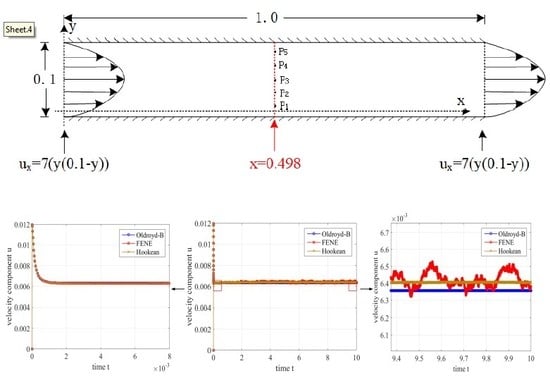
5.1. Problem Specification
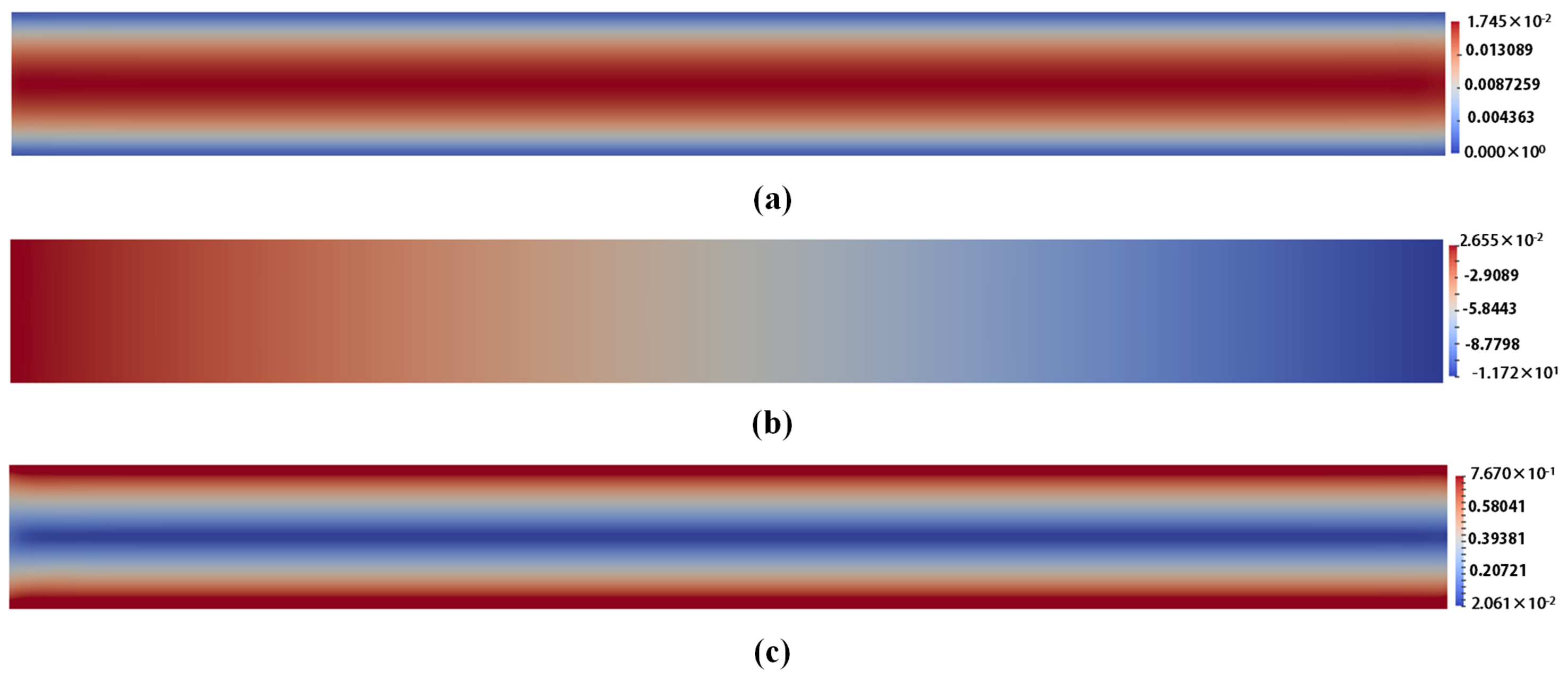
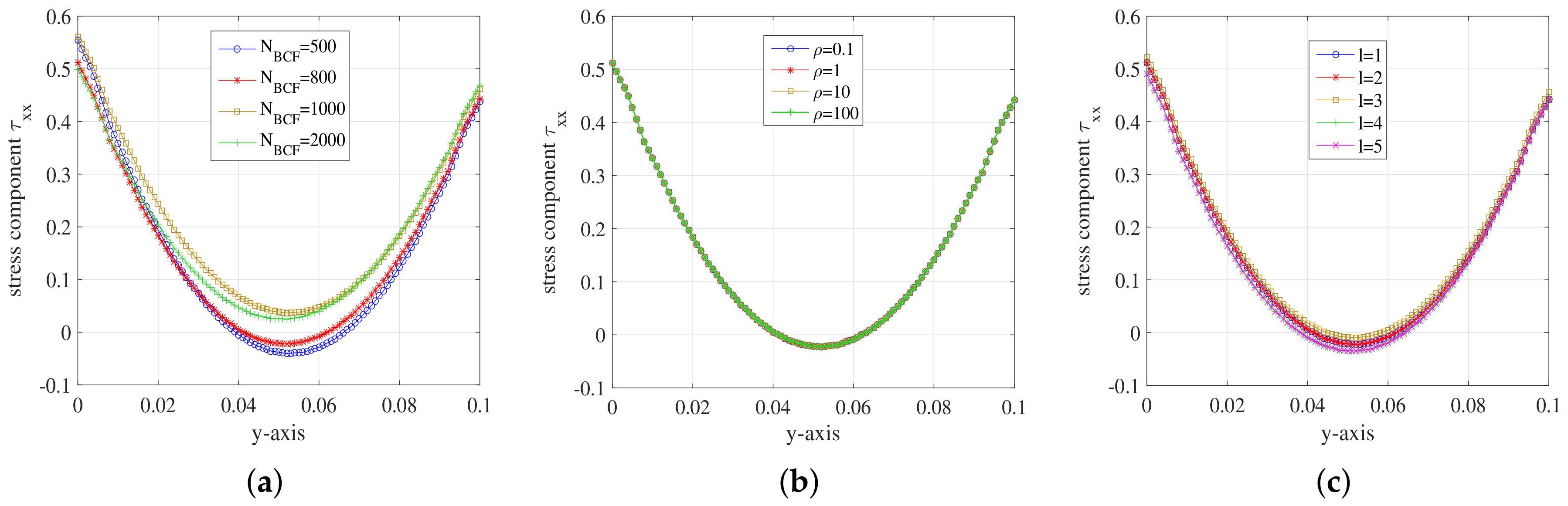
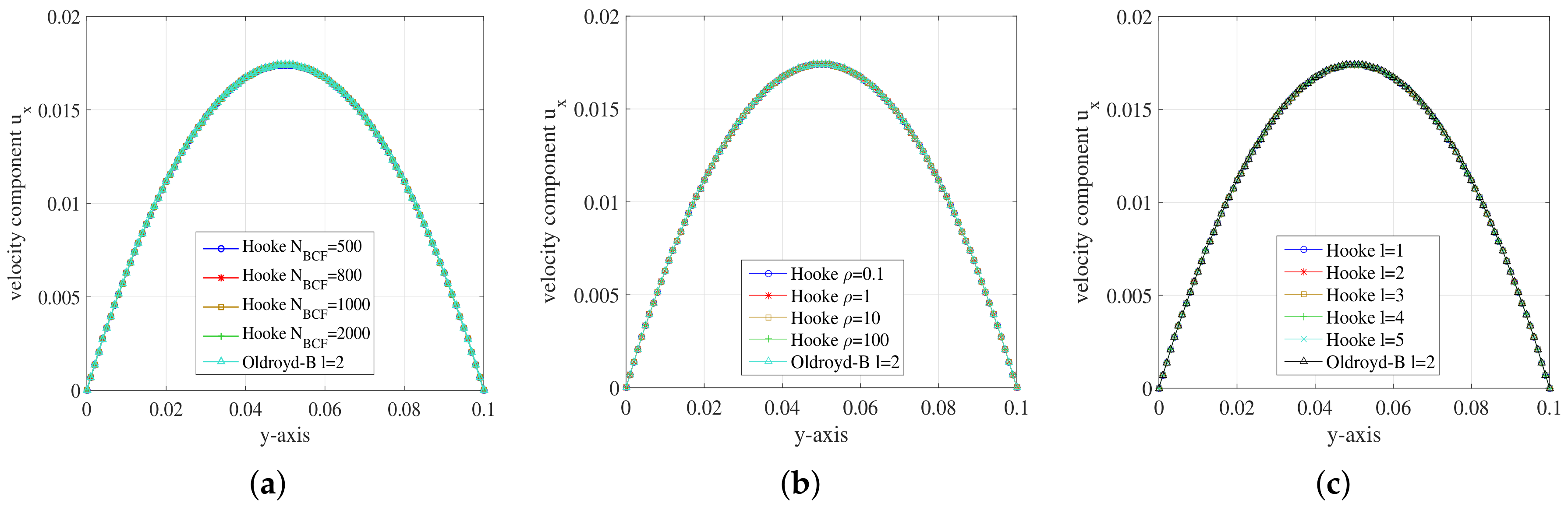
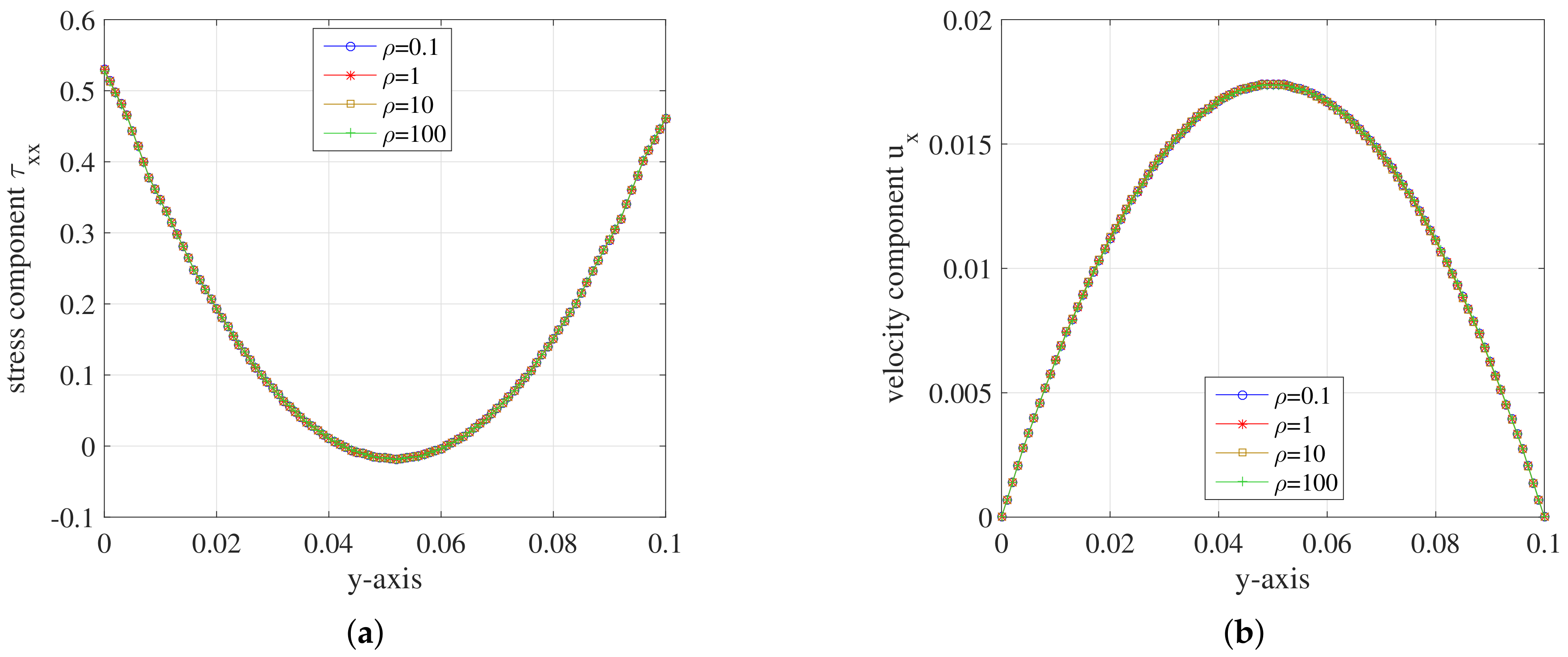
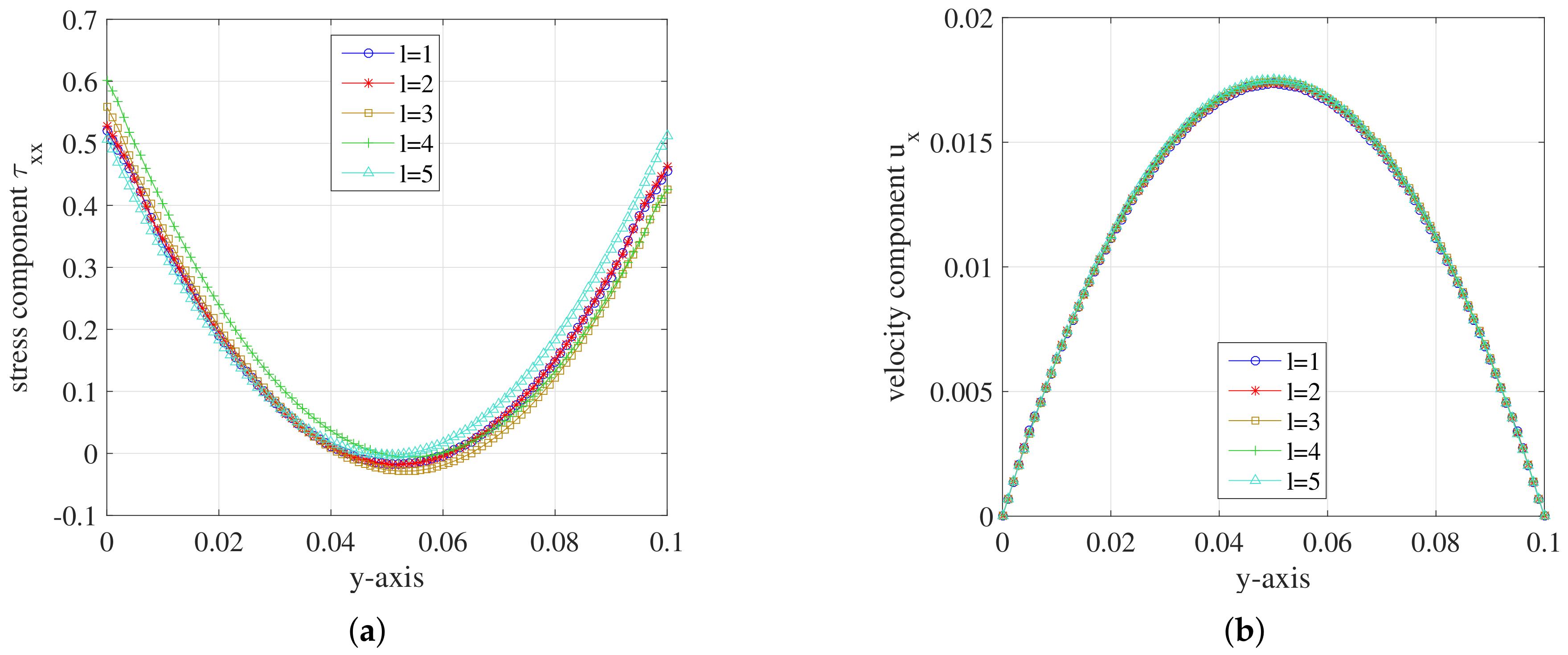
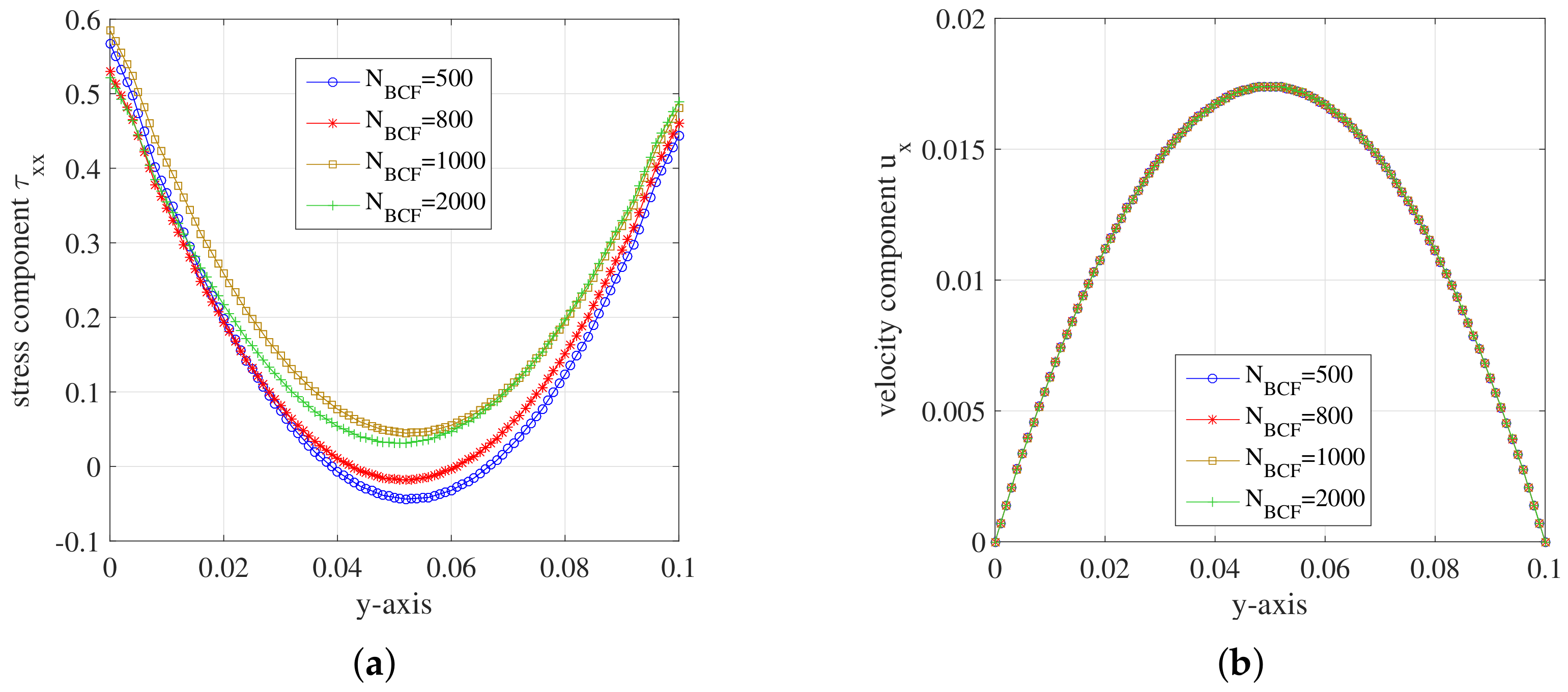
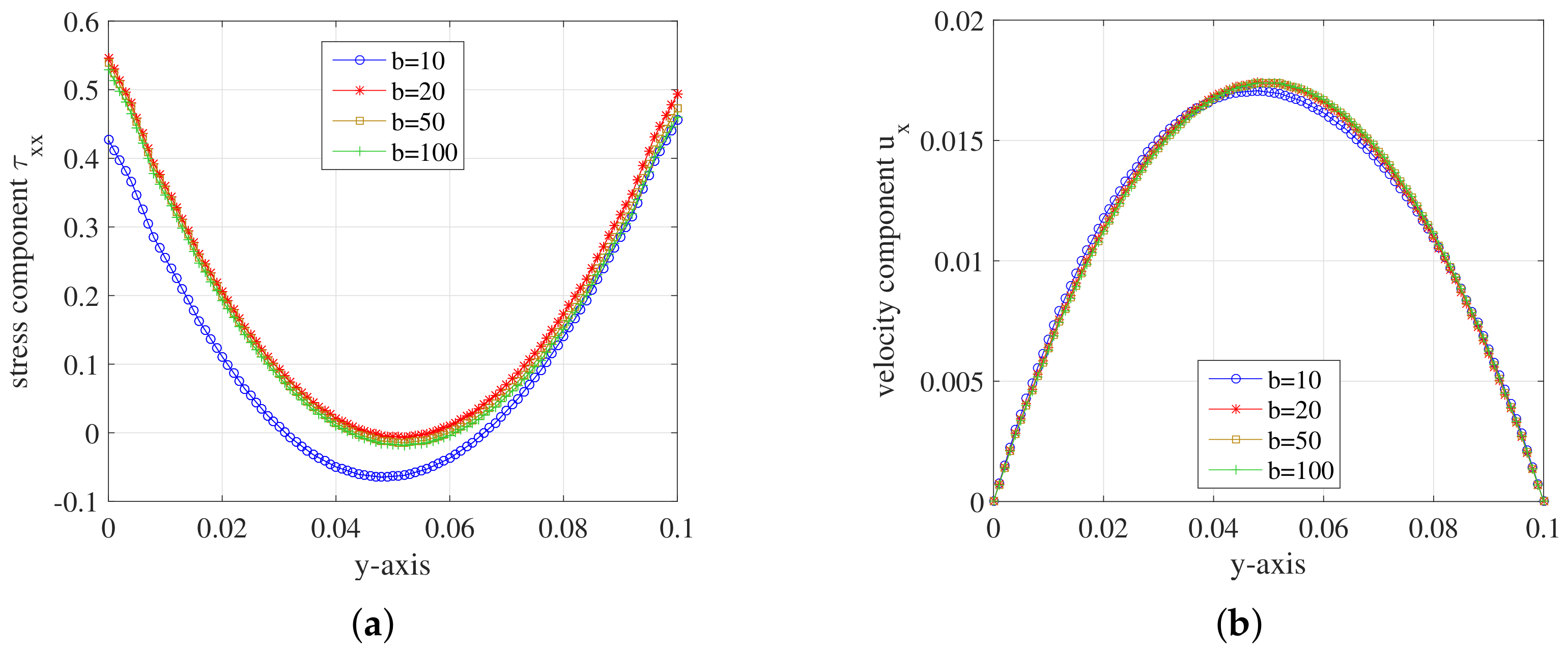
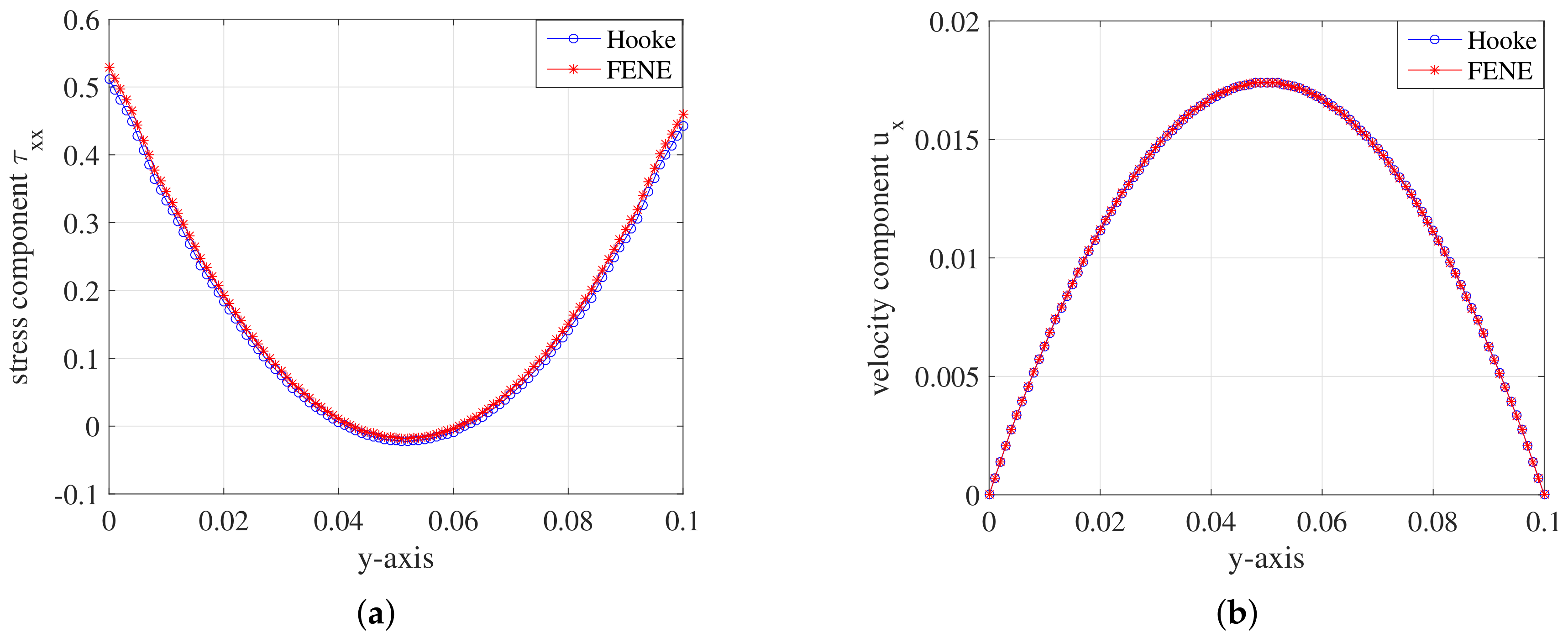
5.2. Simulation Results
5.2.1. Hooke Model
5.2.2. FENE Model
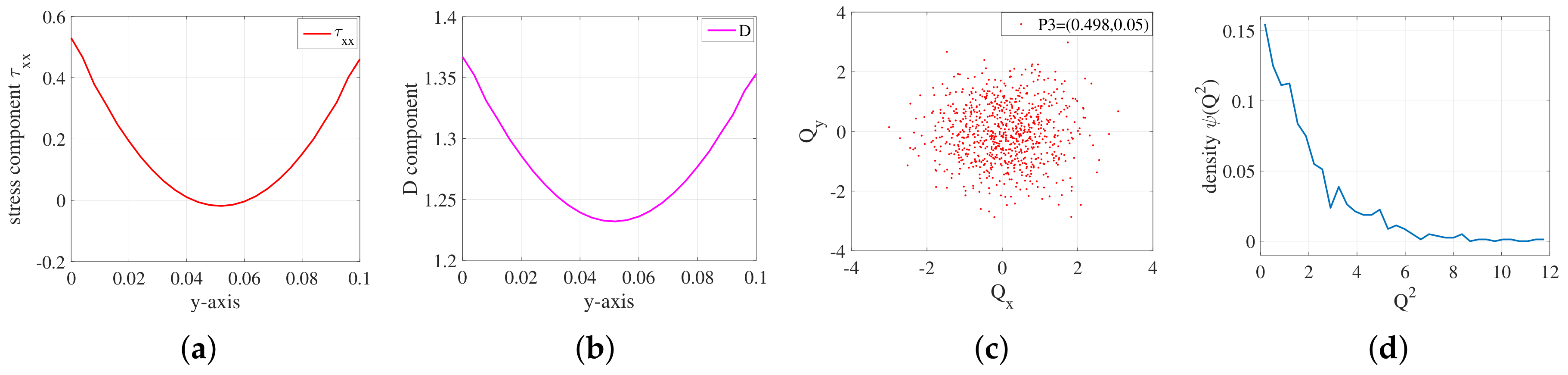
5.3. Molecular Distribution
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A review of multiscale computational methods in polymeric materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef]
- Owens, R.G.; Phillips, T.N. Computational Rheology; Imperial College Press: London, UK, 2002; ISBN 978-1-86094-186-3. [Google Scholar]
- Li, L.; Larson, R.G.; Sridhar, T. Brownian dynamics simulations of dilute polystyrene solutions. J. Rheol. 2000, 44, 291–322. [Google Scholar] [CrossRef]
- Underhill, P.T.; Doyle, P.S. On the coarse-graining of polymers into bead-spring chains. J. Non-Newton. Fluid Mech. 2004, 122, 3–31. [Google Scholar] [CrossRef]
- Peterlin, A. Hydrodynamics of macromolecules in a velocity field with longitudinal gradient. J. Polym. Sci. Part C Polym. Lett. 1966, 4, 287–291. [Google Scholar] [CrossRef]
- Lielens, G.; Keunings, R.; Legat, V. The FENE-L and FENE-LS closure approximations to the kinetic theory of finitely extensible dumbbells. J. Non-Newton. Fluid Mech. 1999, 87, 179–196. [Google Scholar] [CrossRef]
- Guo, X.W.; Xu, X.H.; Wang, Q.; Li, H.; Ren, X.G.; Xu, L.; Yang, X.J. A hybrid decomposition parallel algorithm for multi-scale simulation of viscoelastic fluids. In Proceedings of the 2016 IEEE International Confernece on Parallel and Distributed Processing Symposium, Chicago, IL, USA, 23–27 May 2016; pp. 443–452. [Google Scholar]
- Dünweg, B.; Kremer, K. Molecular dynamics simulation of a polymer chain in solution. J. Chem. Phys. 1993, 99, 6983–6997. [Google Scholar] [CrossRef]
- Aust, C.; Kröger, M.; Hess, S. Structure and dynamics of dilute polymer solutions under shear flow via nonequilibrium molecular dynamics. Macromolecules 1999, 32, 5660–5672. [Google Scholar] [CrossRef]
- Keunings, R. On the Peterlin approximation for finitely extensible dumbbells. J. Non-Newton. Fluid Mech. 1997, 68, 85–100. [Google Scholar] [CrossRef]
- Ilg, P.; Karlin, I.V.; Öttinger, H.C. Canonical distribution functions in polymer dynamics. (I). Dilute solutions of flexible polymers. Phys. A Stat. Mech. Its Appl. 2002, 315, 367–385. [Google Scholar] [CrossRef]
- Du, Q.; Liu, C.; Yu, P. FENE dumbbell model and its several linear and nonlinear closure approximations. Multiscale Model. Simul. 2005, 4, 709–731. [Google Scholar] [CrossRef]
- Wang, H.; Li, K.; Zhang, P. Crucial properties of the moment closure model FENE-QE. J. Non-Newton. Fluid Mech. 2008, 150, 80–92. [Google Scholar] [CrossRef]
- Kröger, M.; Ammar, A.; Chinesta, F. Consistent closure schemes for statistical models of anisotropic fluids. J. Non-Newton. Fluid Mech. 2008, 149, 40–55. [Google Scholar] [CrossRef]
- Kröger, M. Simple, admissible, and accurate approximants of the inverse Langevin and Brillouin functions, relevant for strong polymer deformations and flows. J. Non-Newton. Fluid Mech. 2015, 223, 77–87. [Google Scholar] [CrossRef]
- Koplik, J.; Banavar, J.R. Re-entrant corner flows of Newtonian and non-Newtonian fluids. J. Rheol. 1997, 41, 787–805. [Google Scholar] [CrossRef]
- Cieplak, M.; Koplik, J.; Banavar, J.R. Boundary conditions at a fluid-solid interface. Phys. Rev. Lett. 2001, 86, 803. [Google Scholar] [CrossRef] [PubMed]
- Busic, B.; Koplik, J.; Banavar, J.R. Molecular dynamics simulation of liquid bridge extensional flows. J. Non-Newton. Fluid Mech. 2003, 109, 51–89. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids. Volume 2: Kinetic Theory, 2nd ed.; Wiley Interscience: New York, NY, USA, 1987; ISBN 978-0-471-80244-0. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1988; ISBN 978-0-198-52033-7. [Google Scholar]
- Öttinger, H.C. Stochastic Processes in Polymeric Fluids: Tools and Examples for Developing Simulation Algorithms; Springer Science & Business Media: Berlin, Germany, 2012; ISBN 978-3-642-58290-5. [Google Scholar]
- Mangoubi, C.; Hulsen, M.; Kupferman, R. Numerical stability of the method of Brownian configuration fields. J. Non-Newton. Fluid Mech. 2009, 157, 188–196. [Google Scholar] [CrossRef]
- Laso, M.; Öttinger, H.C. Calculation of viscoelastic flow using molecular models: The CONNFFESSIT approach. J. Non-Newton. Fluid Mech. 1993, 47, 1–20. [Google Scholar] [CrossRef]
- Lozinski, A.; Owens, R.G.; Phillips, T.N. The Langevin and Fokker-Planck Equations in Polymer Rheology. In Handbook of Numerical Analysis; Glowinski, R., Xu, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 16, pp. 211–303. ISBN 978-0-444-53047-9. [Google Scholar]
- Öttinger, H.C.; Van Den Brule, B.; Hulsen, M.A. Brownian configuration fields and variance reduced CONNFFESSIT. J. Non-Newton. Fluid Mech. 1997, 70, 255–261. [Google Scholar] [CrossRef]
- Prieto, J.L.; Bermejo, R.; Laso, M. A semi-Lagrangian micro-macro method for viscoelastic flow calculations. J. Non-Newton. Fluid Mech. 2010, 165, 120–135. [Google Scholar] [CrossRef][Green Version]
- Ellero, M.; Kröger, M. The hybrid BDDFS method: Memory saving approach for CONNFFESSIT-type simulations. J. Non-Newton. Fluid Mech. 2004, 122, 147–158. [Google Scholar] [CrossRef]
- Hulsen, M.A.; Van Heel, A.P.G.; Van Den Brule, B. Simulation of viscoelastic flows using Brownian configuration fields. J. Non-Newton. Fluid Mech. 1997, 70, 79–101. [Google Scholar] [CrossRef]
- Bonvin, J.; Picasso, M. Variance reduction methods for CONNFFESSIT-like simulations. J. Non-Newton. Fluid Mech. 1999, 84, 191–215. [Google Scholar] [CrossRef]
- Xu, X.H.; Guo, X.W.; Cao, Y. Multi-scale simulation of non-equilibrium phase transitions under shear flow in dilute polymer solutions. RSC Adv. 2015, 5, 54649–54657. [Google Scholar] [CrossRef]
- Larson, R.G. Constitutive Equations for Polymer Melts and Solutions: Butterworths Series in Chemical Engineering, 1st ed.; Butterworth-Heinemann: Boston, MA, USA, 1988; ISBN 0-409-90119-9. [Google Scholar]
- Bhave, A.V.; Armstrong, R.C.; Brown, R.A. Kinetic theory and rheology of dilute, nonhomogeneous polymer solutions. J. Chem. Phys. 1991, 95, 2988–3000. [Google Scholar] [CrossRef]
- Christopher, J.; Greenshields. OpenFOAM Programmer’s Guide. Available online: http://foam.sourceforge.net/docs/Guides-a4/ProgrammersGuide.pdf (accessed on 1 January 2018).
- Guénette, R.; Fortin, M. A new mixed finite element method for computing viscoelastic flows. J. Non-Newton. Fluid Mech. 1995, 60, 27–52. [Google Scholar] [CrossRef]
- Li, C.; Yang, W.; Xu, X.; Wang, J.; Wang, M.; Xu, L. Numerical investigation of fish exploiting vortices based on the Kármán gaiting model. Ocean Eng. 2017, 140, 7–18. [Google Scholar] [CrossRef]
- Li, C.; Xu, X.; Wang, J.; Xu, L.; Ye, S.; Yang, X. A parallel multiselection greedy method for the radial basis function-based mesh deformation. Int. J. Numer. Methods Eng. 2017, 1–28. [Google Scholar] [CrossRef]







| Differential term | Explicit/implicit | Model expressions | Function name |
|---|---|---|---|
| laplace term | explicit/implicit | laplacian(phi) | |
| laplacian(Gamma,phi) | |||
| time derivative term | explicit/implicit | ddt(phi) | |
| ddt(rho,phi) | |||
| 2-nd order time derivative term | explicit/implicit | d2dt2(rho,phi) | |
| convection term | explicit/implicit | div(psi,scheme) | |
| div(psi,phi,word) | |||
| div(psi,phi) | |||
| divergence term | explicit | div(chi) | |
| gradient term | explicit | grad(chi) | |
| gGrad(phi) | |||
| lsGrad(phi) | |||
| snGrad(phi) | |||
| snGradCorrection(phi) | |||
| source term | implicit | Sp(rho,phi) |
| Field variables | Solver | Preprocessor | Error limit |
|---|---|---|---|
| p | PCG | GAMG | |
| PBiCG | GAMG | ||
| BICCG | DILU | ||
| PBiCG | DILU |
| Equation terms | Discrete format | Accuracy |
|---|---|---|
| First-order time derivative | Euler | 1st-order |
| Gradient | Gauss linear | 2nd-order |
| Divergence | Gauss Minmod/linear | 2nd-order |
| Laplace | Gauss linear corrected | 2nd-order |
| Parameter | ||||
|---|---|---|---|---|
| Value | 0.05 | 0.40 | 1.0 | 0.6 |
| l | , | Cells/direction | Total cell | |
|---|---|---|---|---|
| 1 | 0.01 | 4000 | ||
| 2 | 0.01 | 6250 | ||
| 3 | 0.01 | 16,000 | ||
| 4 | 0.01 | 25,000 | ||
| 5 | 0.01 | 64,000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yang, C.; Wu, C.-K.; Zhang, X.; Zhang, X.; Guo, X.-W. Exploring the Molecular Distributions in Dilute Polymer Solutions Using a Multi-Scale Numerical Solver. Polymers 2018, 10, 387. https://doi.org/10.3390/polym10040387
Liu Y, Yang C, Wu C-K, Zhang X, Zhang X, Guo X-W. Exploring the Molecular Distributions in Dilute Polymer Solutions Using a Multi-Scale Numerical Solver. Polymers. 2018; 10(4):387. https://doi.org/10.3390/polym10040387
Chicago/Turabian StyleLiu, Yi, Canqun Yang, Cheng-Kun Wu, Xiang Zhang, Xin Zhang, and Xiao-Wei Guo. 2018. "Exploring the Molecular Distributions in Dilute Polymer Solutions Using a Multi-Scale Numerical Solver" Polymers 10, no. 4: 387. https://doi.org/10.3390/polym10040387
APA StyleLiu, Y., Yang, C., Wu, C.-K., Zhang, X., Zhang, X., & Guo, X.-W. (2018). Exploring the Molecular Distributions in Dilute Polymer Solutions Using a Multi-Scale Numerical Solver. Polymers, 10(4), 387. https://doi.org/10.3390/polym10040387