Antisolvent Sonocrystallisation of Sodium Chloride and the Evaluation of the Ultrasound Energy Using Modified Classical Nucleation Theory
Abstract
:1. Introduction
2. Experimental Details
2.1. Materials
2.2. Supersaturation Ratio
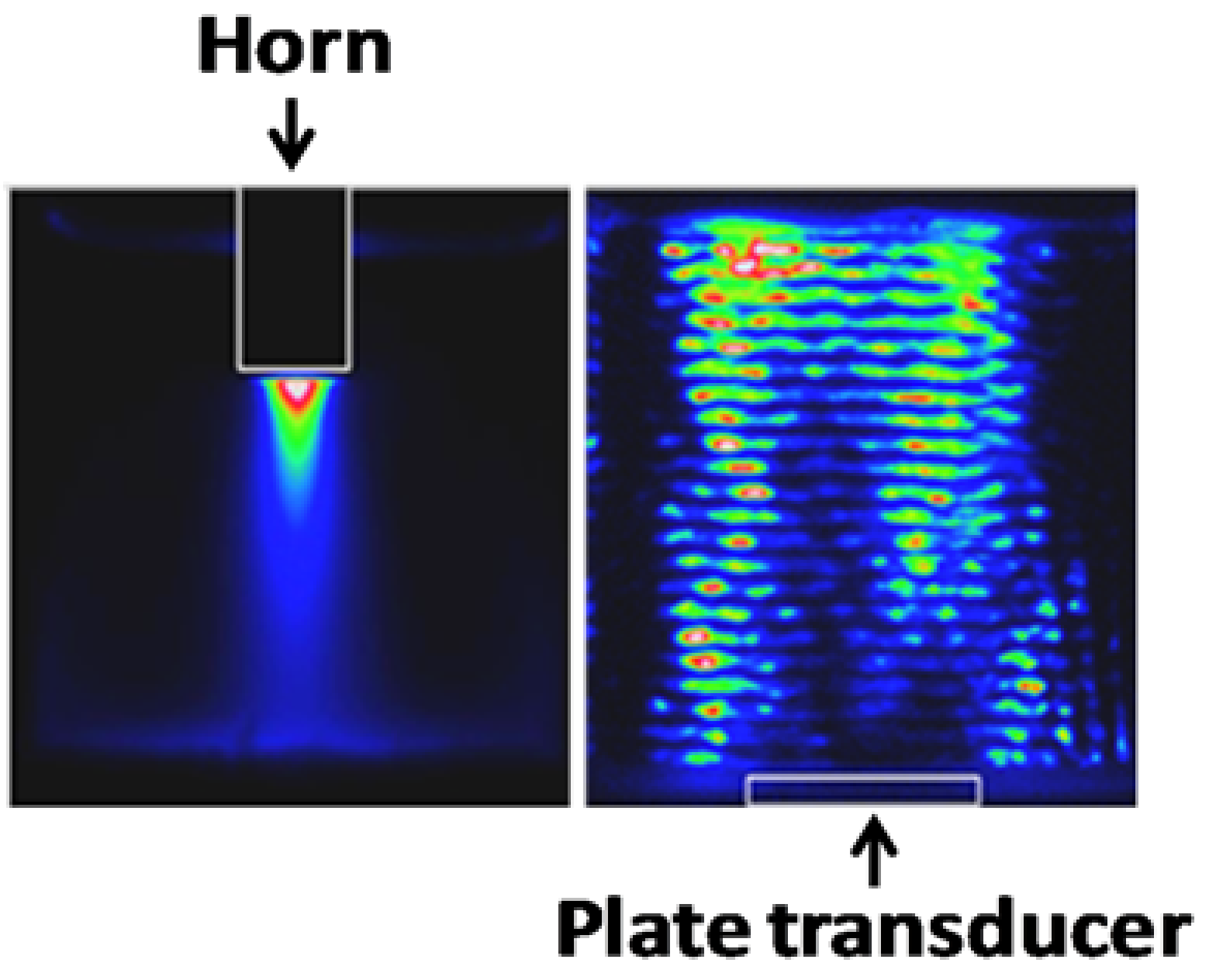
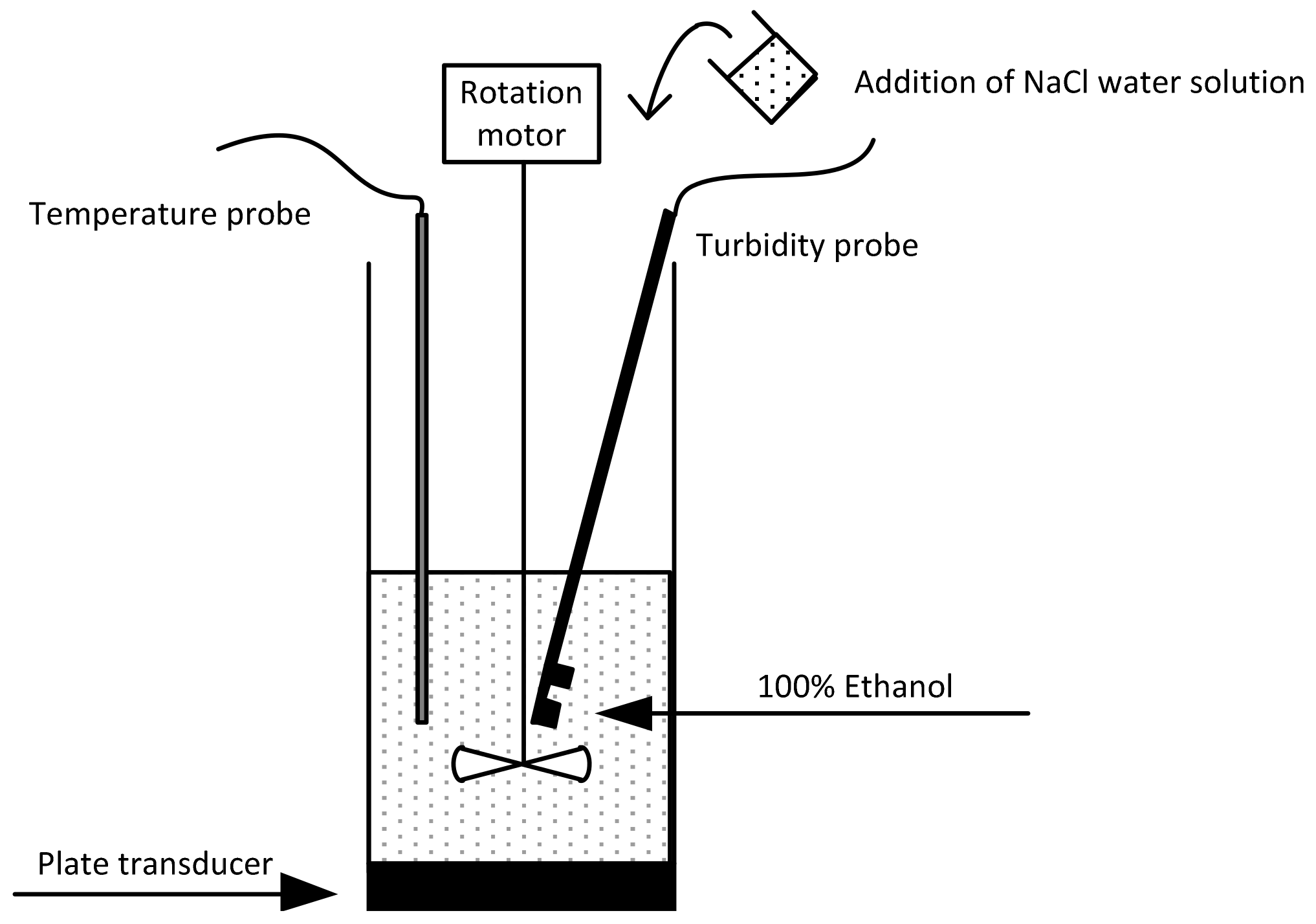
2.3. Sonocrystallisation Process
2.4. Induction Time Measurements
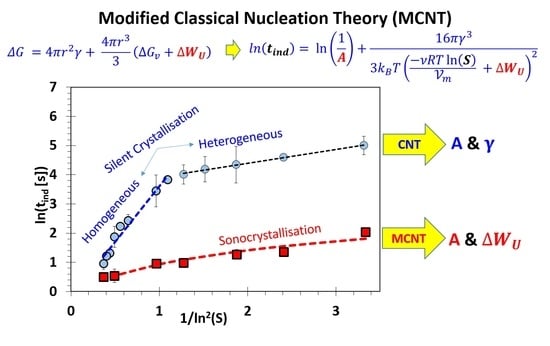
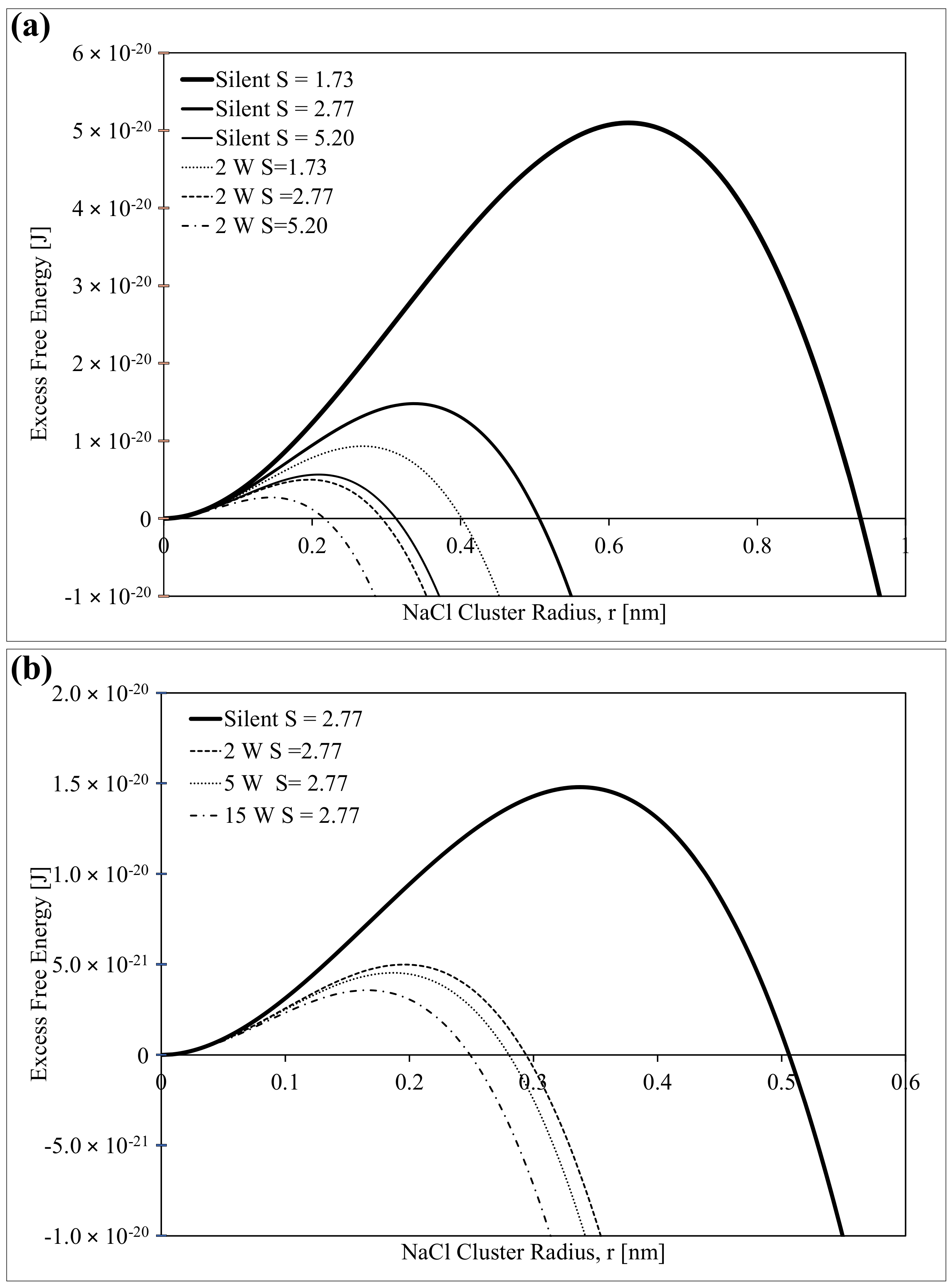
2.5. Modification of the Classical Nucleation Theory (CNT)
3. Results and Discussion
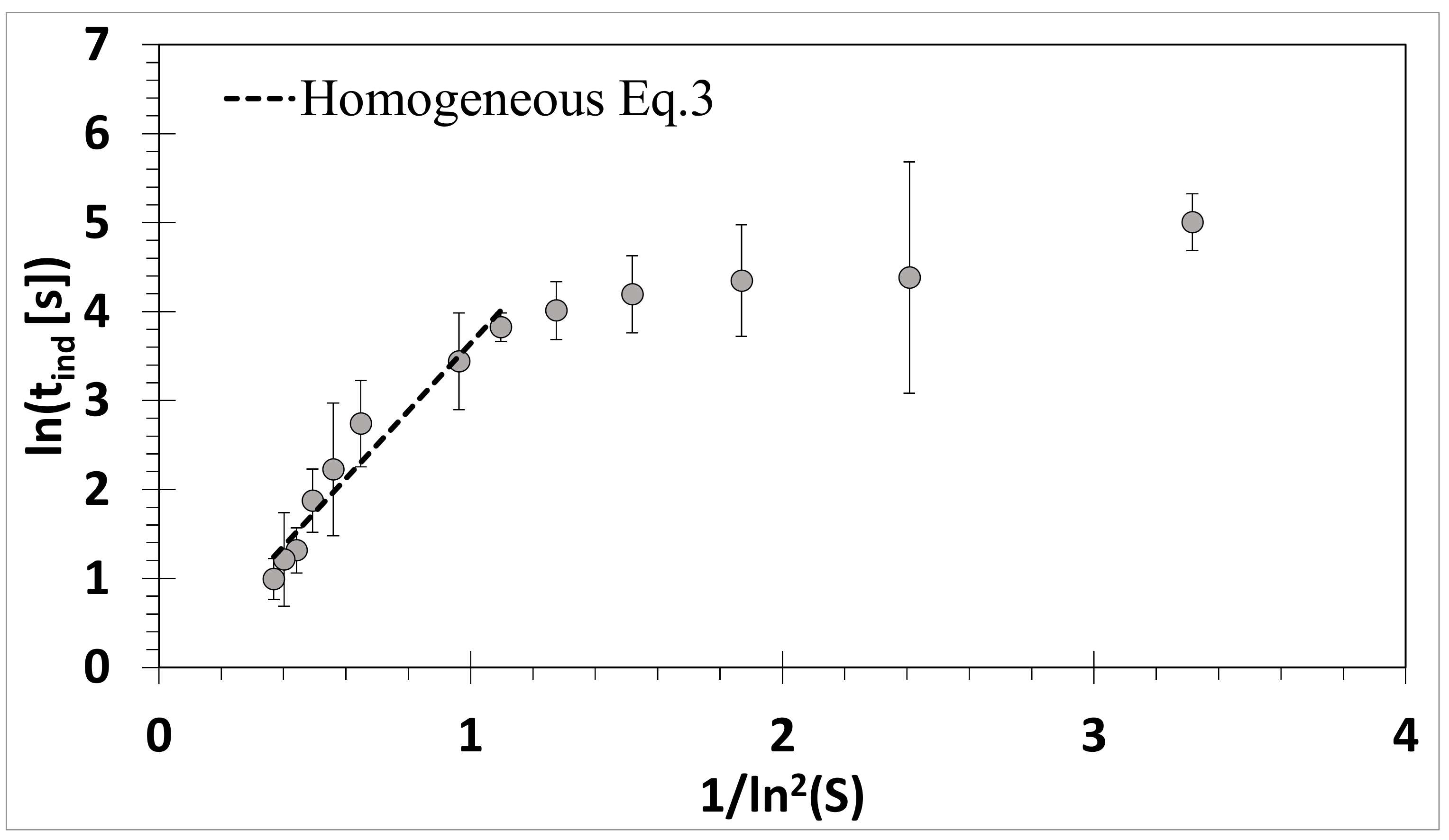
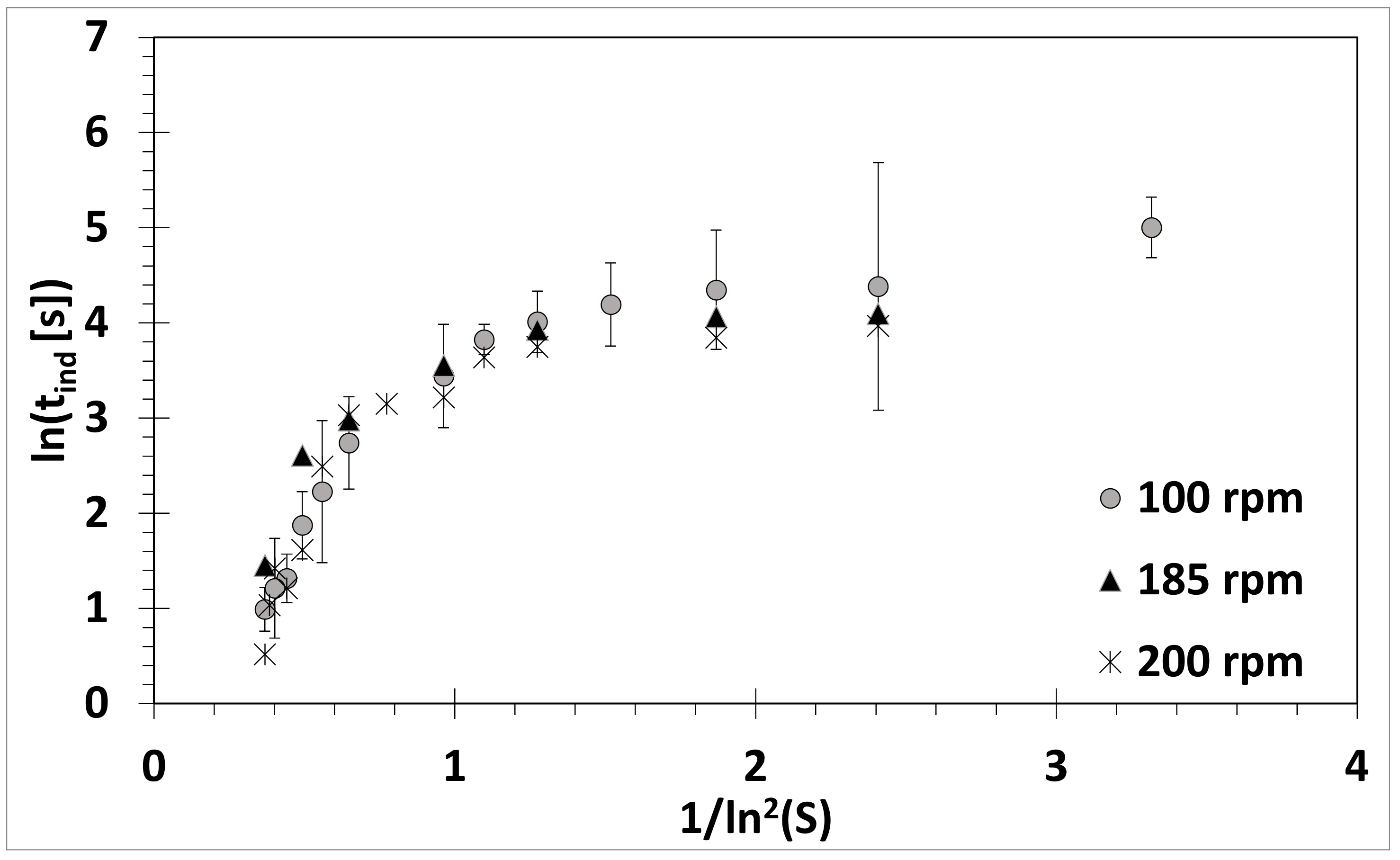
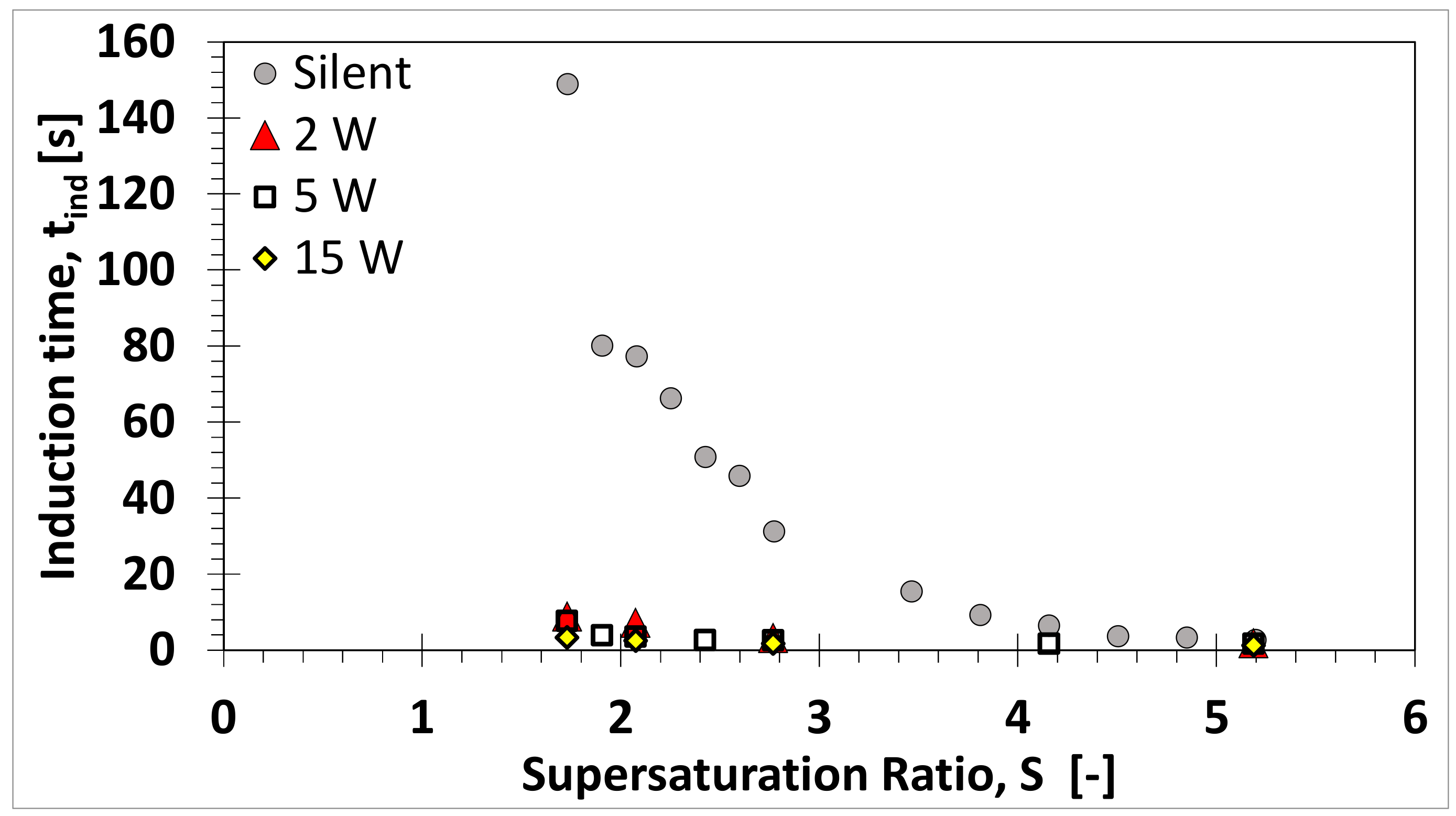
3.1. Absence of Ultrasound
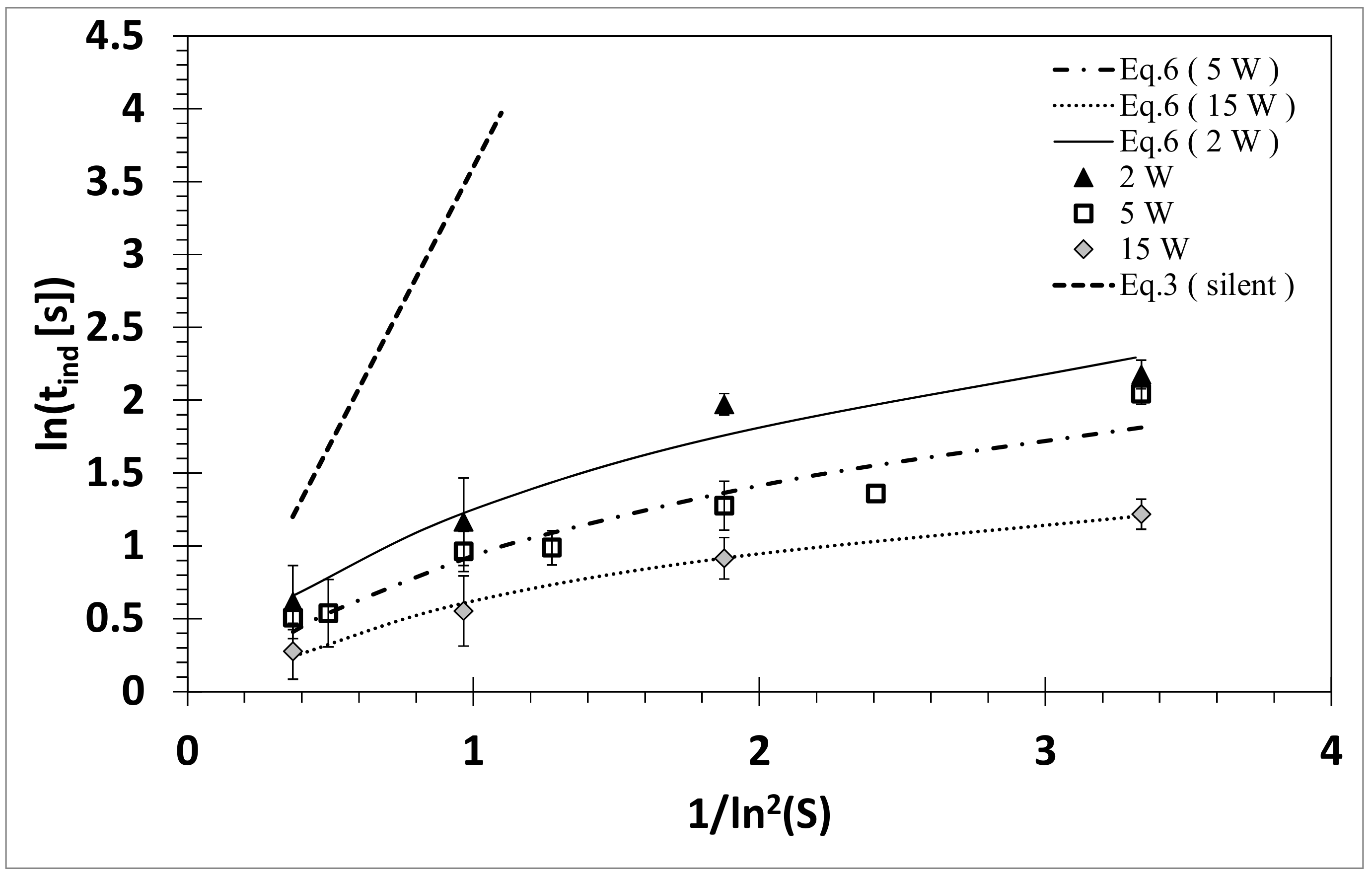
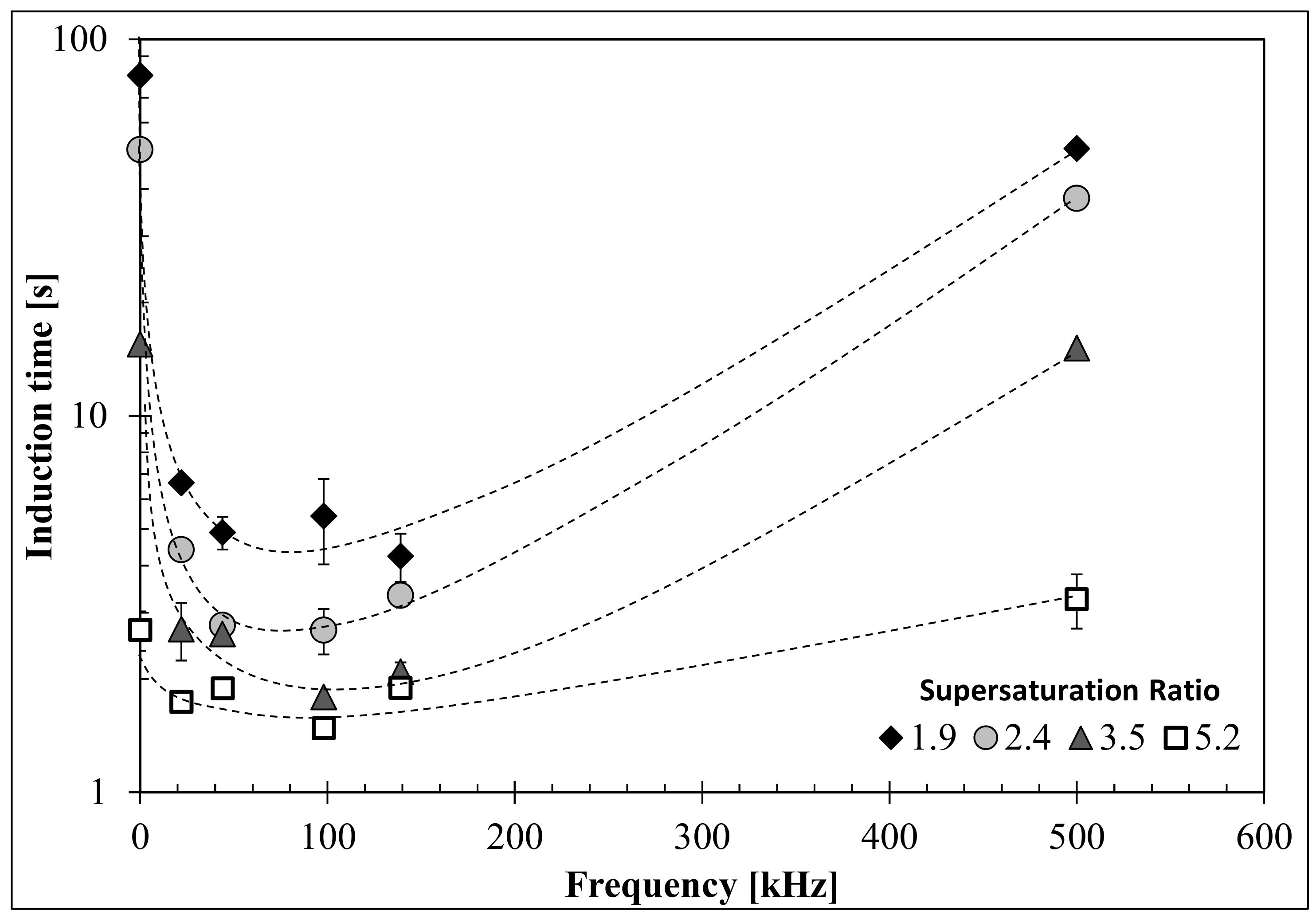
3.2. Influence of Ultrasound
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Takiyama, H. Supersaturation operation for quality control of crystalline particles in solution crystallization. Adv. Powder Technol. 2012, 23, 273–278. [Google Scholar] [CrossRef]
- Takiyama, H.; Otsuhata, T.; Matsuoka, M. Morphology of NaCl crystals in drowing-out precipitation operation. Chem. Eng. Res. Des. 1998, 76, 809–814. [Google Scholar] [CrossRef]
- Lyczko, N.; Espitalier, F.; Louisnard, O.; Schwartzentruber, J. Effect of ultrasound on the induction time and the metastable zone widths of potassium sulphate. Chem. Eng. J. 2002, 86, 233–241. [Google Scholar] [CrossRef]
- Bund, R.K.; Pandit, A.B. Sonocrystallization: Effect on lactose recovery and crystal habit. Ultrason. Sonochem. 2007, 14, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Luque de Castro, M.D.; Priego-Capote, F. Ultrasound-assisted crystallization (sonocrystallization). Ultrason. Sonochem. 2007, 14, 717–724. [Google Scholar] [CrossRef] [PubMed]
- Harzali, H.; Baillon, F.; Louisnard, O.; Espitalier, F.; Mgaidi, A. Experimental study of sono-crystallisation of ZnSO4 7H2O, and interpretation by the segregation theory. Ultrason. Sonochem. 2011, 18, 1097–1106. [Google Scholar] [CrossRef] [PubMed]
- Price, G.; Mahon, M.F.; Shannon, J.; Cooper, C. Composition of calcium carbonate polymorphs precipitated using ultrasound. Cryst. Growth Des. 2011, 11, 39–44. [Google Scholar] [CrossRef]
- Mori, Y.; Maruyama, M.; Takahashi, Y.; Ikeda, K.; Fukukita, S.; Yoshikawa, H.Y.; Okada, S.; Adachi, H.; Sugiyama, S.; Takano, K. Selective crystallization of metastable phase of acetaminophen by ultrasonic irradiation. Appl. Phys. Express 2015, 8, 065501. [Google Scholar] [CrossRef]
- Lee, J.; Ashokkumar, M.; Kentish, S. Influence of mixing and ultrasound frequency on antisolvent crystallisation of sodium chloride. Ultrason. Sonochem. 2014, 21, 60–68. [Google Scholar] [CrossRef] [PubMed]
- Bhangu, S.K.; Ashokkumar, M.; Lee, J. Ultrasound assisted crystallization of paracetamol: Crystal size distribution and polymorph control. Cryst. Growth Des. 2016, 16, 1934–1941. [Google Scholar] [CrossRef]
- Price, C. Ultrasound-the key to better crystals for the pharmaceutical industry. Pharm. Technol. Eur. 1997, 9, 78–87. [Google Scholar]
- Hem, S.L. The effect of ultrasonic vibrations on crystallization processes. Ultrasonics 1967, 5, 202–207. [Google Scholar] [CrossRef]
- Zeiger, B.W.; Suslick, K.S. Sonofragmentation of molecular crystals. J. Am. Chem. Soc. 2011, 133, 14530–14533. [Google Scholar] [CrossRef] [PubMed]
- Ratsimba, B.; Biscans, B.; Delmas, H.; Jenck, J. Sonocrystallization: The end of empiricism? Kona Powder Part. J. 1999, 17, 38–48. [Google Scholar] [CrossRef]
- Kurotani, M.; Miyasaka, E.; Ebihara, S.; Hirasawa, I. Effect of ultrasonic irradiation on the behavior of primary nucleation of amino acids in supersaturated solutions. J. Cryst. Growth 2009, 311, 2714–2721. [Google Scholar] [CrossRef]
- Nii, S.; Takayanagi, S. Growth and size control in anti-solvent crystallization of glycine with high frequency ultrasound. Ultrason. Sonochem. 2014, 21, 1182–1186. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Yasui, K.; Ashokkumar, M.; Kentish, S.E. Quantification of cavitation activity by sonoluminescence to study the sonocrystallization process under different ultrasound parameters. Cryst. Growth Des. 2018. accepted. [Google Scholar] [CrossRef]
- Grossier, R.; Louisnard, O.; Vargas, Y. Mixture segrgation by an inertial cavitation bubble. Ultrason. Sonochem. 2007, 14, 431–437. [Google Scholar] [CrossRef] [PubMed]
- Cogné, C.; Labouret, S.; Peczalski, R.; Louisnard, O.; Baillon, F.; Espitalier, F. Theoretical model of ice nucleation induced by inertial acoustic cavitation. Part 2: Number of ice nuclei generated by a single bubble. Ultrason. Sonochem. 2016, 28, 185–191. [Google Scholar] [CrossRef] [PubMed]
- Chow, R.; Atkins, D.; Singleton, S.; Mettin, R.; Lindinger, B.; Kurz, T.; Lauterborn, W.; Povey, M.; Chivers, R. High-speed observations of the nucleation of ice by power ultrasound. Water Prop. Food Pharm. Biol. Mater. 2006, 9, 613–622. [Google Scholar]
- Jordens, J.; Gielen, B.; Braeken, L.; Van Gerven, T. Determination of the effect of the ultrasonic frequency on the cooling crystallization of paracetamol. Chem. Eng. Process. Process Intensif. 2014, 84, 38–44. [Google Scholar] [CrossRef] [Green Version]
- Rossi, D.; Jamshidi, R.; Saffari, N.; Kuhn, S.; Gavriilidis, A.; Mazzei, L. Continuous-flow sonocrystallization in droplet-based microfluidics. Cryst. Growth Des. 2015, 15, 5519–5529. [Google Scholar] [CrossRef]
- Guo, Z.; Jones, A.G.; Li, N. Interpretation of the ultrasonic effect on induction time during BaSO4 homogeneous nucleation by a cluster coagulation model. J. Colloid Interface Sci. 2006, 297, 190–198. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Zhang, M.; Li, H.; Wang, J.; Kougoulos, E. Effect of ultrasound on anti-solvent crystallization process. J. Cryst. Growth 2005, 273, 555–563. [Google Scholar] [CrossRef]
- Guo, Z.; Jones, A.G.; Li, N. The effect of ultrasound on the homogeneous nucleation of during reactive crystallization. Chem. Eng. Sci. 2006, 61, 1617–1626. [Google Scholar] [CrossRef]
- Kordylla, A.; Krawczyk, T.; Tumakaka, F.; Schembecker, G. Modeling ultrasound-induced nucleation during cooling crystallization. Chem. Eng. Sci. 2009, 64, 1635–1642. [Google Scholar] [CrossRef]
- Virone, C.; Kramer, H.J.M.; van Rosmalen, G.M.; Stoop, A.H.; Bakker, T.W. Primary nucleation induced by ultrasonic cavitation. J. Cryst. Growth 2006, 294, 9–15. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2011; p. 594. [Google Scholar]
- Söhnel, O.; Mullin, J.W. Interpretation of crystallization induction periods. J. Colloid Interface Sci. 1988, 123, 43–50. [Google Scholar] [CrossRef]
- Miyasaka, E.; Ebihara, S.; Hirasawa, I. Investigation of primary nucleation phenomena of acetylsalicylic acid crystals induced by ultrasonic irradiation-ultrasonic energy needed to activate primary nucleation. J. Cryst. Growth 2006, 295, 97–101. [Google Scholar] [CrossRef]
- Monnier, H.; Wilhelm, A.M.; Delmas, H. Influence of ultrasound on mixing on the molecular scale for water and viscous liquids. Ultrason. Sonochem. 1999, 6, 67–74. [Google Scholar] [CrossRef]
- Lee, J. Importance of sonication and solution conditions on the acoustic cavitation activity. In Handbook of Ultrasonics and Sonochemistry; Ashokkumar, M., Ed.; Springer: Singapore, 2016; pp. 137–175. [Google Scholar]
- Alexander, A.J.; Camp, P.J. Single pulse, single crystal laser-induced nucleation of potassium chloride. Cryst. Growth Des. 2009, 9, 958–963. [Google Scholar] [CrossRef]
- Mersmann, A. Calculation of interfacial tensions. J. Cryst. Growth 1990, 102, 841–847. [Google Scholar] [CrossRef]
- Söhnel, O. Electrolyte crystal-aqueous solution interfacial tensions from crystallization data. J. Cryst. Growth 1982, 57, 101–108. [Google Scholar] [CrossRef]
- Mullin, J.W.; Zacek, S. The precipitation of potassium aluminium sulphate from aqueous solution. J. Cryst. Growth 1981, 53, 515–518. [Google Scholar] [CrossRef]
- Mullin, J.; Raven, K. Nucleation in agitated solutions. Nature 1961, 190, 251. [Google Scholar] [CrossRef]
- Lee, J.; Yasui, K.; Tuziuti, T.; Kozuka, T.; Towata, A.; Iida, Y. Spatial distribution enhancement of sonoluminescence activity by altering sonication and solution conditions. J. Phys. Chem. B 2008, 112, 15333–15341. [Google Scholar] [CrossRef] [PubMed]
- Mitome, H.; Kozuka, T.; Tuziuti, T. Measurement of the establishment process of acoustic streaming using laser Doppler velocimetry. Ultrasonics 1996, 34, 527–530. [Google Scholar] [CrossRef]
- Lee, J.; Ashokkumar, M.; Yasui, K.; Tuziuti, T.; Kozuka, T.; Towata, A.; Iida, Y. Development and optimization of acoustic bubble structures at high frequencies. Ultrason. Sonochem. 2011, 18, 92–98. [Google Scholar] [CrossRef] [PubMed]
- Sawamura, S.; Egoshi, N.; Setoguchi, Y.; Matsuo, H. Solubility of sodium chloride in water under high pressure. Fluid Phase Equilib. 2007, 254, 158–162. [Google Scholar] [CrossRef]
- Hatanaka, S.; Yasui, K.; Tuziuti, T.; Kozuka, T.; Mitome, H. Quenching mechanism of multibubble sonoluminescence at excessive sound pressure. Jpn. J. Appl. Phys. 2001, 40, 3856–3860. [Google Scholar] [CrossRef]
- Brotchie, A.; Grieser, F.; Ashokkumar, M. Effect of power and frequency on bubble-size distributions in acoustic cavitation. Phys. Rev. Lett. 2009, 102, 084302. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K. Influence of ultrasonic frequency on multibubble sonoluminescence. J. Acoust. Soc. Am. 2002, 112, 1405–1413. [Google Scholar] [CrossRef] [PubMed]

| Amplifier Power [W] | Calorimetric Power [W] | ΔWU [J m−3] | A |
|---|---|---|---|
| 0 | 0 | 0 | 1.22 |
| 2 | 0.73 | −1.33 × 108 | 1.01 |
| 5 | 1.8 | −1.48 × 108 | 1.24 |
| 15 | 5.5 | −1.90 × 108 | 1.32 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Yang, S. Antisolvent Sonocrystallisation of Sodium Chloride and the Evaluation of the Ultrasound Energy Using Modified Classical Nucleation Theory. Crystals 2018, 8, 320. https://doi.org/10.3390/cryst8080320
Lee J, Yang S. Antisolvent Sonocrystallisation of Sodium Chloride and the Evaluation of the Ultrasound Energy Using Modified Classical Nucleation Theory. Crystals. 2018; 8(8):320. https://doi.org/10.3390/cryst8080320
Chicago/Turabian StyleLee, Judy, and Shanshan Yang. 2018. "Antisolvent Sonocrystallisation of Sodium Chloride and the Evaluation of the Ultrasound Energy Using Modified Classical Nucleation Theory" Crystals 8, no. 8: 320. https://doi.org/10.3390/cryst8080320