Smeared Lattice Model as a Framework for Order to Disorder Transitions in 2D Systems
Abstract
:1. Introduction
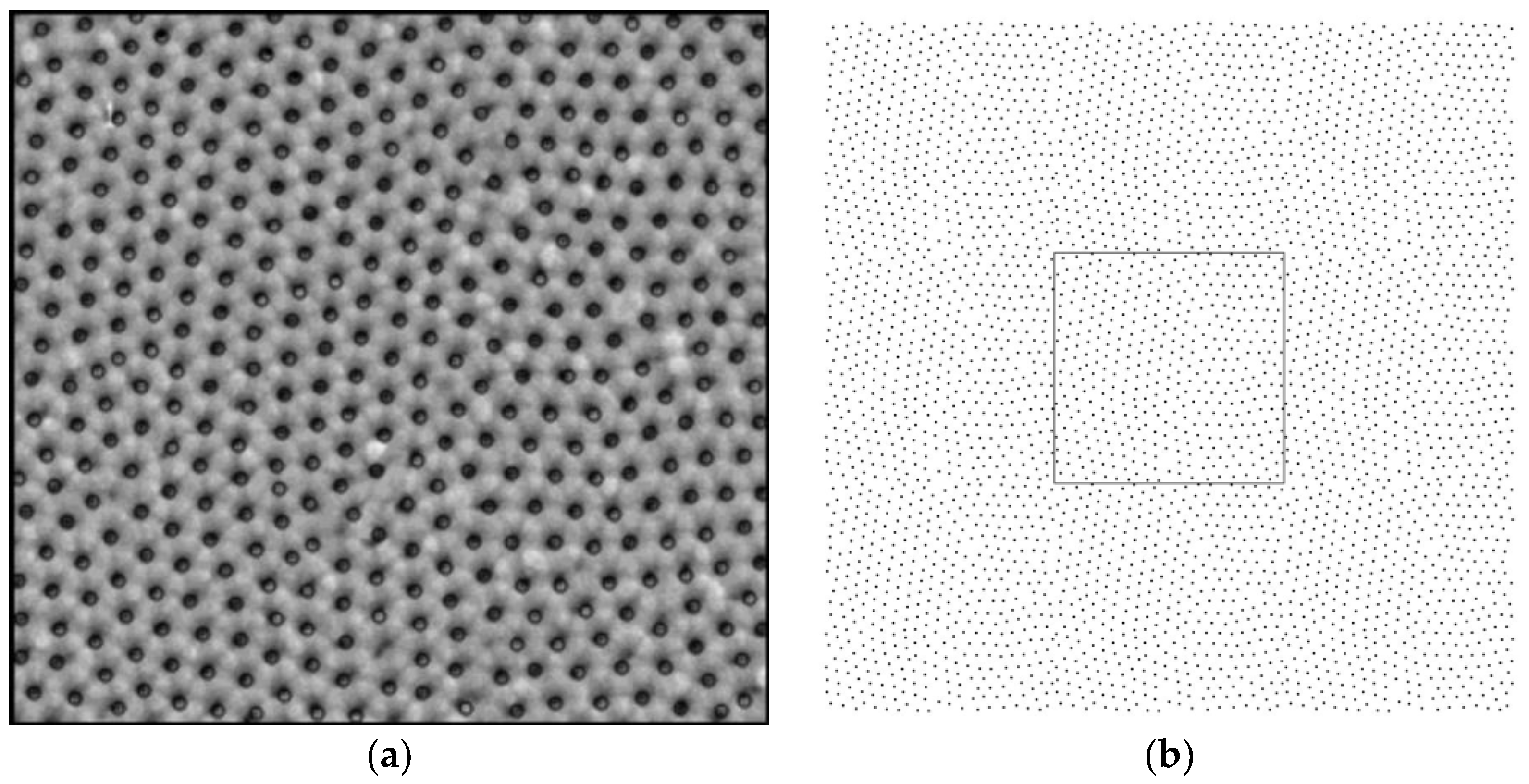
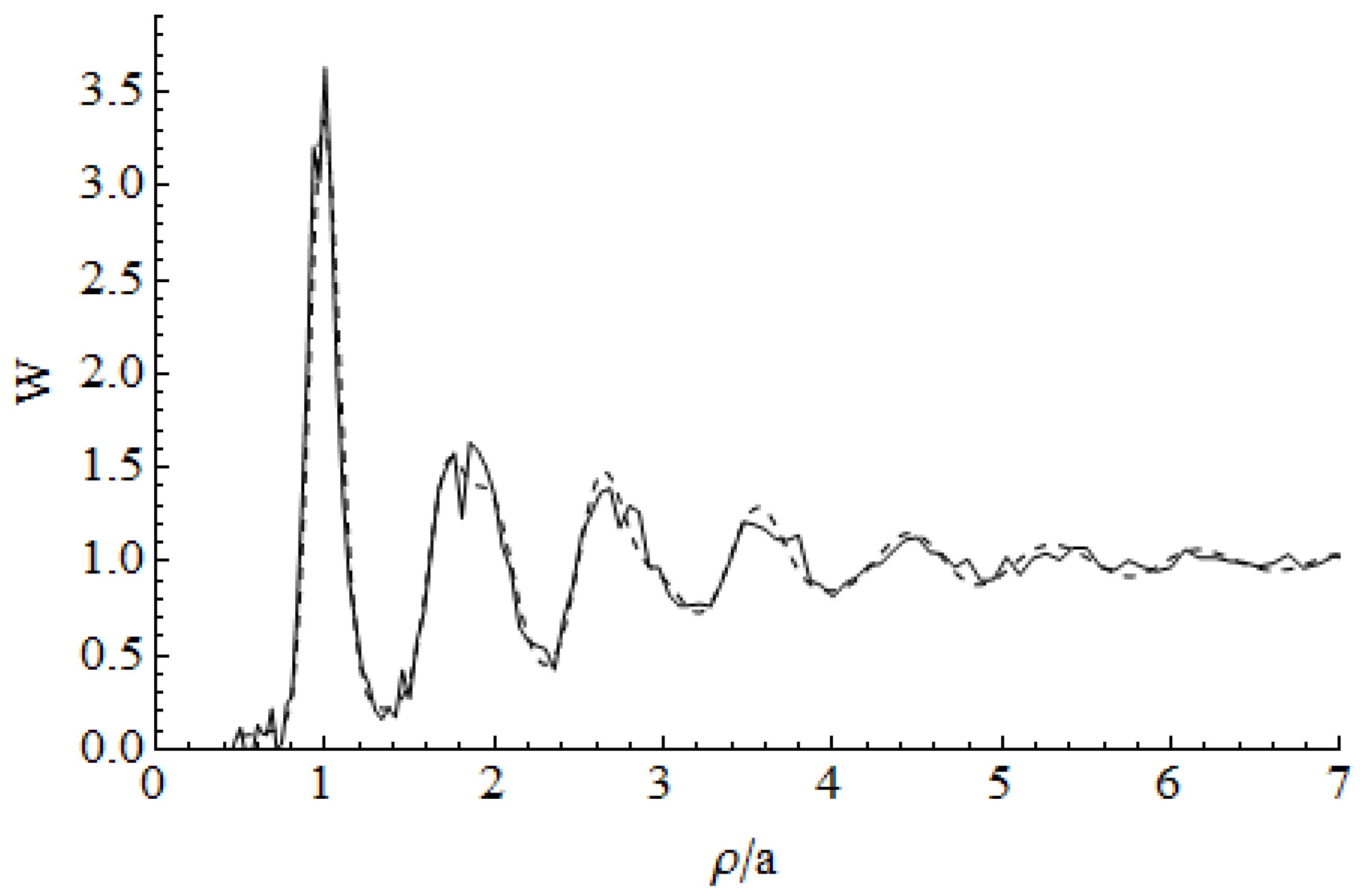
2. Radial Distribution Function for Porous Aluminum Oxide Layer
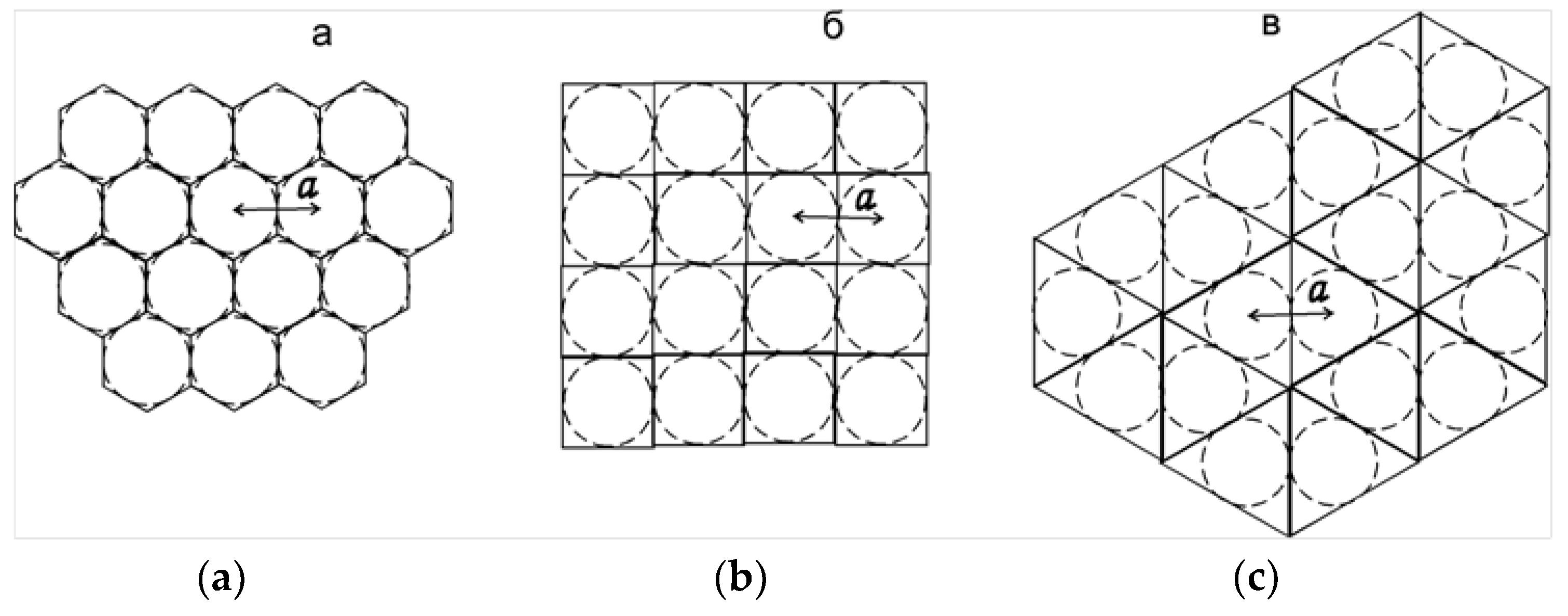
3. Hard Disks in a Plane
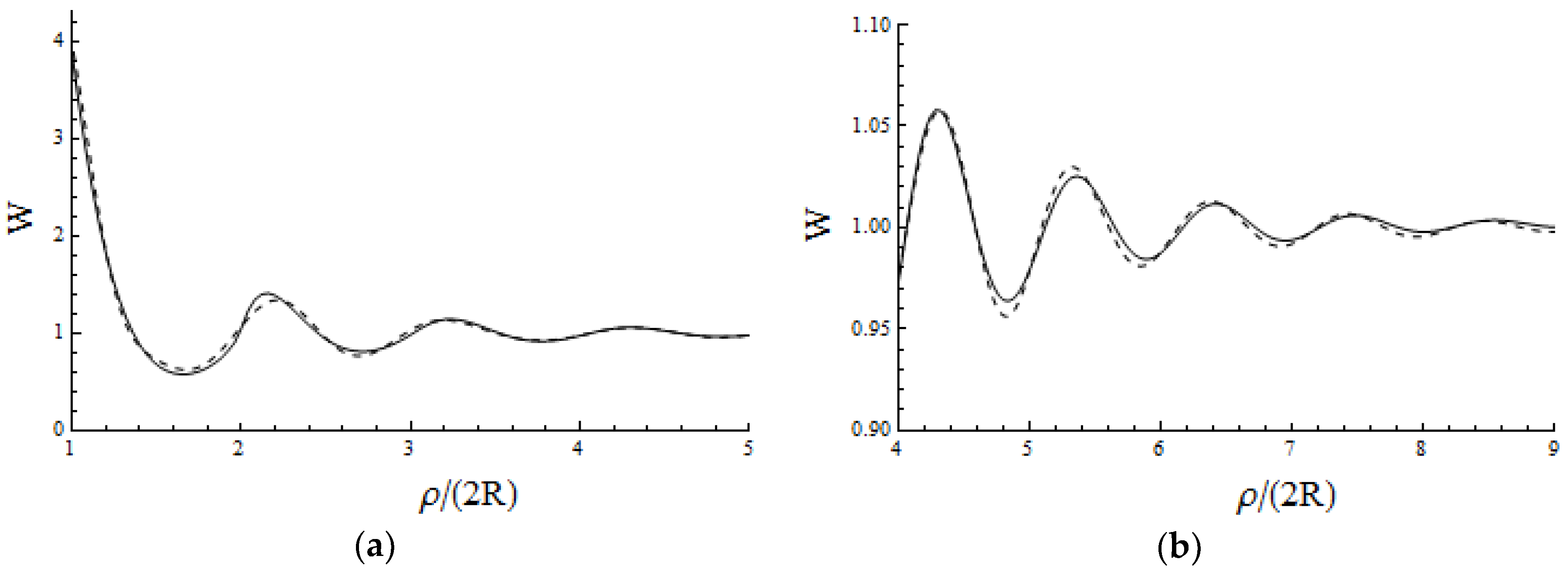
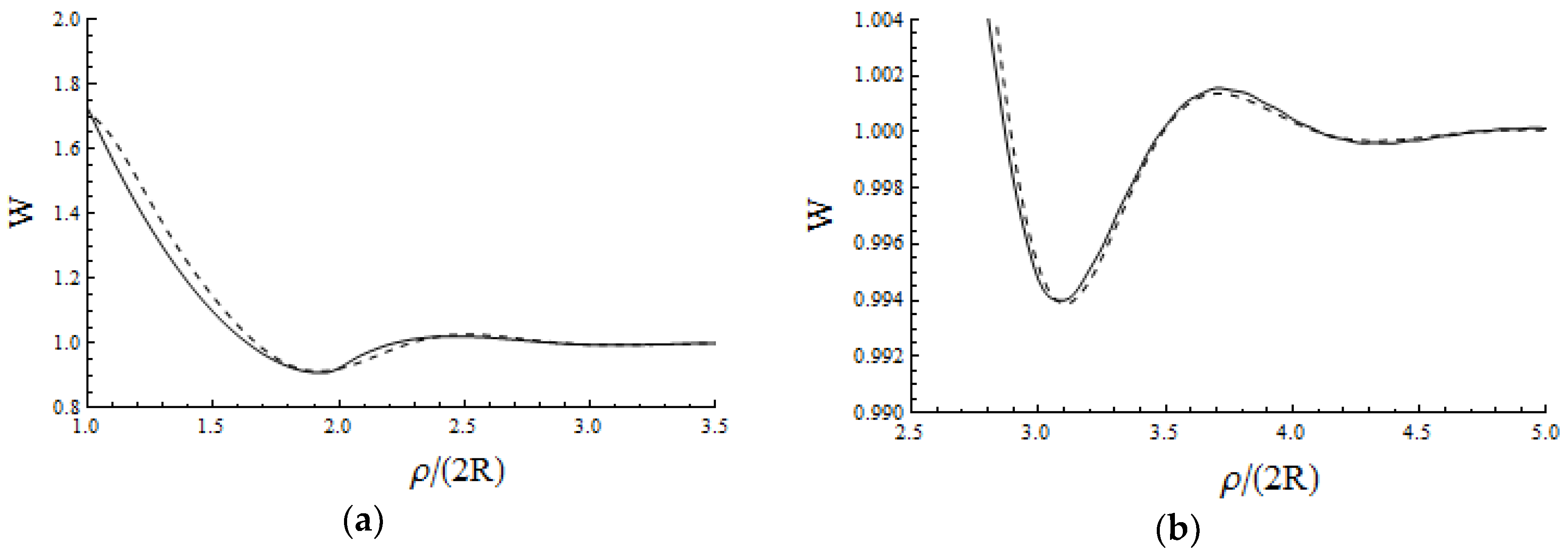
Comparison with Solutions of the Percus–Yevick Equation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Peierls, R.E. Transformation tempretures. Helv. Phys. Acta Suppl. 1934, 2, 81–83. [Google Scholar]
- Landau, L.D. On the theory of phase transitions I. Phys. Z. Sowjet. 1937, 11, 26–35. [Google Scholar] [CrossRef]
- Landau, L.D. On the theory of phase transitions II. Phys. Z. Sowjet. 1937, 11, 545–555. [Google Scholar]
- Mermin, N.D. Crystalline order in two dimensions. Phys. Rev. 1968, 176, 250–254. [Google Scholar] [CrossRef]
- Eder, F.R.; Kotakoski, J.; Kaiser, U.; Meyer, J.C. A journey from order to disorder—Atom by atom transformation from graphene to 2D carbon glass. Sci. Rep. 2014, 4, 4060. [Google Scholar] [CrossRef] [PubMed]
- Warren, B.E. X-ray Diffraction Study of the Structure of Glass. Chem. Rev. 1940, 26, 237–255. [Google Scholar] [CrossRef]
- Wright, A.C.; Thorpe, M.F. Eighty years of random networks. Phys. Status Solidi B 2013, 250, 931–936. [Google Scholar] [CrossRef]
- Prins, G.A.; Petersen, H. Theoretical diffraction patterns corresponding to some simple types of molecular arrangement in liquids. Physica 1936, 3, 147–153. [Google Scholar] [CrossRef]
- Glauberman, A.E. On the theory of a local order inliquids. Zh. Eksp. Teor. Fiz. 1952, 22, 249–250. [Google Scholar]
- Tsvetkov, V.P. About structure of the liquid metals. Izv. Vyssh. Uchebn. Zaved. Ser. Fiz. 1960, 1, 145–154. [Google Scholar]
- Franchetti, S. On a model for monoatomic liquids. Nuovo Cim. B 1968, 55, 335–347. [Google Scholar] [CrossRef]
- Medvedev, N.N.; Naberukhin, Y.I. Description of the radial distribution function of liquid argon in the quasi-crystalline model of liquids. Phys. Chem. Liq. 1978, 8, 167–187. [Google Scholar] [CrossRef]
- Baer, S. Form of the radial distribution function and the structure factor, derived from the “structural diffusion” model for liquids. Phys. A Stat. Mech. Its Appl. 1978, 91, 603–611. [Google Scholar] [CrossRef]
- Skryshevskii, A.F. Structural Analysis of Liquids and Amorphous Solids; Vysshaya Shkola: Moscow, Russia, 1980; p. 49. [Google Scholar]
- Medvedev, N.N.; Naberukhin, Y.I.; Semenova, I.Y. The radial distribution function and structure factor of liquid and amorphous gallium as described by the quasi-crystalline model. J. Non-Cryst. Solids 1984, 64, 421–432. [Google Scholar] [CrossRef]
- Miskevich, A.A.; Loiko, V.A. Coherent transmission and reflection of a two-dimensional planar photonic crystal. Zh. Eksp. Teor. Fiz. 2011, 140, 5–20. [Google Scholar] [CrossRef]
- Cherkas, N.L.; Cherkas, S.L. Model of the radial distribution function of pores in a layer of porous aluminum oxide. Crystallogr. Rep. 2016, 61, 285–290. [Google Scholar] [CrossRef]
- Masuda, H.; Fukuda, K. Ordered metal nanohole arrays made by a two-step replication of honeycomb structures of anodic alumina. Science 1995, 268, 1466–1468. [Google Scholar] [CrossRef] [PubMed]
- Jessensky, O.; Müller, F.; Gösele, U. Self-organized formation of hexagonal pore arrays in anodic alumina. Appl. Phys. Lett. 1998, 72, 1173–1175. [Google Scholar] [CrossRef]
- Nielsch, K.; Choi, J.; Schwirn, K. Self-ordering Regimes of Porous Alumina: The 10 Porosity Rule. Nano Lett. 2002, 2, 677–680. [Google Scholar] [CrossRef]
- Parkhutik, V.P.; Shershulsky, V.I. Theoretical modelling of porous oxide growth on aluminium. J. Phys. D 1992, 25, 1258–1263. [Google Scholar] [CrossRef]
- Singh, G.K.; Golovin, A.A.; Aranson, I.S. Formation of self-organized nanoscale porous structures in anodic aluminum oxide. Phys. Rev. B 2006, 73, 205422. [Google Scholar] [CrossRef]
- Cherkas, N.L. Electromagnetic wave in a medium consisting of parallel dielectric cylinders. Opt. Spektrosk. 1996, 81, 990–996. [Google Scholar]
- Yakovleva, N.M.; Yakovlev, A.N.; Gafiyatullin, M.M.; Denisov, A.I. Computer diagnostics of the mesoscopic structure of the nanoporous oxides of aluminum. Zavod. Lab. Diagn. Mater. 2009, 75, 21–26. [Google Scholar]
- Kaatz, F.H. Measuring the order in ordered porous arrays: Can bees outperformhumans? Naturwissenschaften 2006, 93, 374–378. [Google Scholar] [CrossRef] [PubMed]
- Vodopivec, A.; Kaatz, F.H.; Mohar, B. Topographical distance matrices for porous arrays. J. Math. Chem. 2010, 47, 1145–1153. [Google Scholar] [CrossRef]
- Lutich, A.A.; Gaponenko, S.V.; Gaponenko, N.V.; Molchan, I.S.; Sokol, V.A.; Parkhutik, V. Anisotropic light scattering in nanoporousmaterials: A photon density of states effect. Nano Lett. 2004, 4, 1755–1758. [Google Scholar] [CrossRef]
- Fernandez, J.F.; Alonso, J.J.; Stankiewicz, J. Melting of systems of hard disks by Monte Carlo simulations. Phys. Rev. E 1997, 55, 750–764. [Google Scholar] [CrossRef]
- Adda-Bedia, M.; Katzav, E.; Vella, D. Solution of the Percus-Yevick equation for hard disks. J. Chem. Phys. 2008, 128, 184508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kapfer, S.C.; Krauth, W. Sampling from a polytope and hard-disk Monte Carlo. J. Phys. Conf. Ser. 2013, 454, 012031. [Google Scholar] [CrossRef] [Green Version]
- Gaal, A.T. Long-range order in a hard disk model. Electron. Commun. Probab. 2014, 19, 1–9. [Google Scholar] [CrossRef]
- Atkinson, S.; Stillinger, F.H.; Torquato, S. Existence of isostatic, maximally random jammed monodisperse hard-disk packings. Proc. Natl. Acad. Sci. USA 2014, 111, 18436–18441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engel, M.; Anderson, J.A.; Glotzer, S.C.; Isobe, M.; Bernard, E.P.; Krauth, W. Hard-disk equation of state: First-order liquid-hexatic transition in two dimensions with threesimulation methods. Phys. Rev. E 2013, 87, 042134. [Google Scholar] [CrossRef] [PubMed]
- Sokołowski, S. A note on the two-dimensional radial distribution function. Czec. J. Phys. B 1978, 28, 713–720. [Google Scholar] [CrossRef]
- Kovalenko, N.P.; Fisher, I.Z. Method of integral equations in statistical theory of liquids. Uspekhi Fizicheskih Nauk 1972, 108, 209–239. [Google Scholar] [CrossRef]
- Arinshtein, E.A. A model of the liquid-crystal phase transition and the quasicrystal model of liquid. Theor. Math. Phys. 2007, 151, 571–585. [Google Scholar] [CrossRef]
| 0.62 | 1.04 | 1.1 | 0.158 | 0.027 | 0.4 |
| 0.6 | 1.056 | 1.12 | 0.176 | 0.03 | 0.41 |
| 0.55 | 1.095 | 1.14 | 0.192 | 0.1 | 0.45 |
| 0.5 | 1.11 | 1.2 | 0.2 | 0.2 | 0.53 |
| 0.45 | 1.112 | 1.3 | 0.209 | 0.5 | 0.7 |
| 0.4 | 1.115 | 1.6 | 0.213 | 0.9 | 1.1 |
| 0.35 | 1.117 | 2.1 | 0.224 | 1.4 | 0.75 |
| 0.3 | 1.12 | 2.3 | 0.236 | 2 | 0.6 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherkas, N.L.; Cherkas, S.L. Smeared Lattice Model as a Framework for Order to Disorder Transitions in 2D Systems. Crystals 2018, 8, 290. https://doi.org/10.3390/cryst8070290
Cherkas NL, Cherkas SL. Smeared Lattice Model as a Framework for Order to Disorder Transitions in 2D Systems. Crystals. 2018; 8(7):290. https://doi.org/10.3390/cryst8070290
Chicago/Turabian StyleCherkas, Nadezhda L., and Sergey L. Cherkas. 2018. "Smeared Lattice Model as a Framework for Order to Disorder Transitions in 2D Systems" Crystals 8, no. 7: 290. https://doi.org/10.3390/cryst8070290





