Crystal Structure, Hydration, and Two-Fold/Single-Fold Diffusion Kinetics in Proton-Conducting Ba0.9La0.1Zr0.25Sn0.25In0.5O3−a Oxide
Abstract
1. Introduction
- in dry hydrogen atmosphere,
- in humidified atmosphere,
Coupled and Decoupled Diffusion of Ionic Charge Carriers
2. Materials and Methods
3. Results and Discussion
3.1. Crystal Structure at Room and Elevated Temperatures
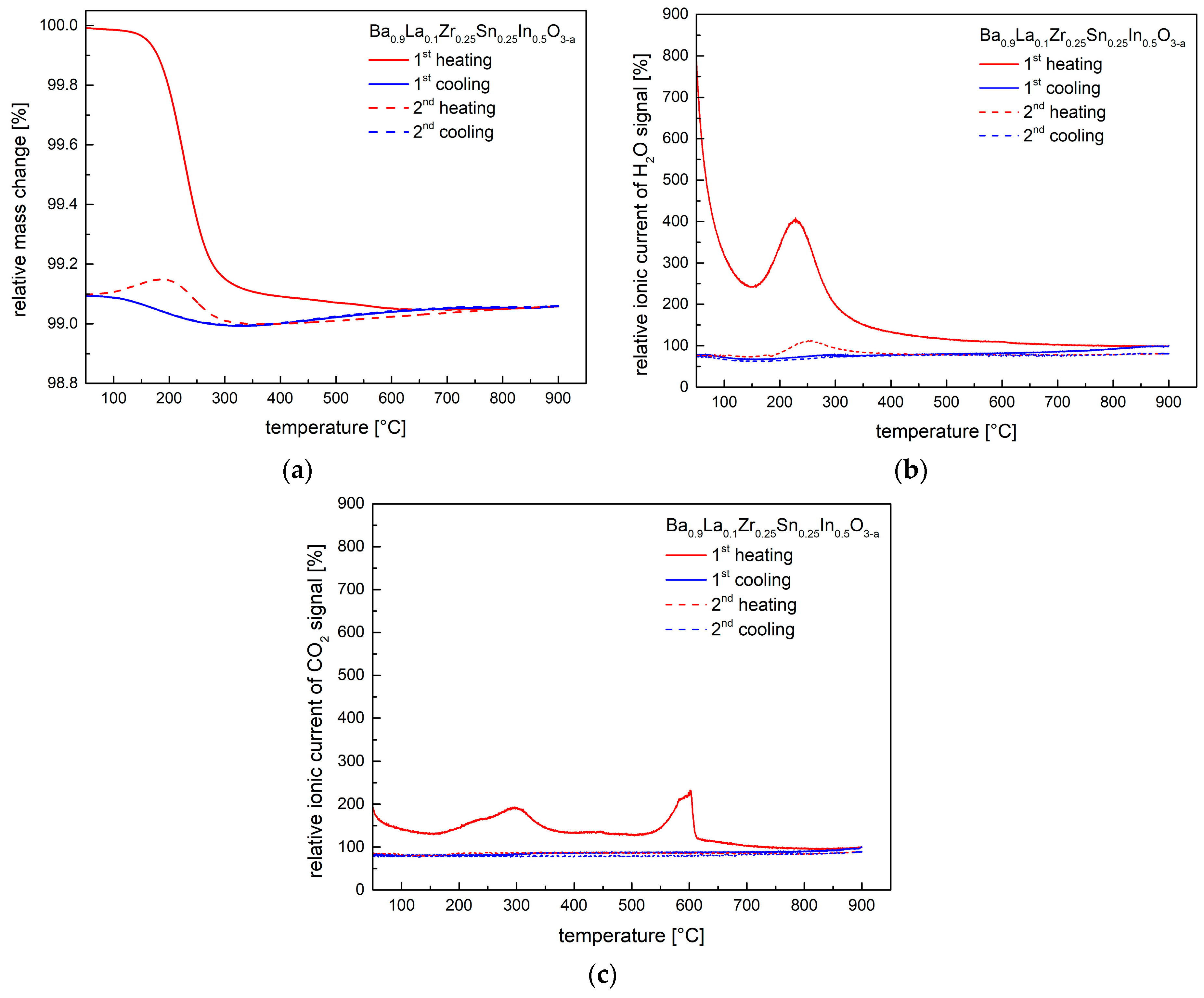
3.2. Thermogravimetric Measurements and Presence of Protons
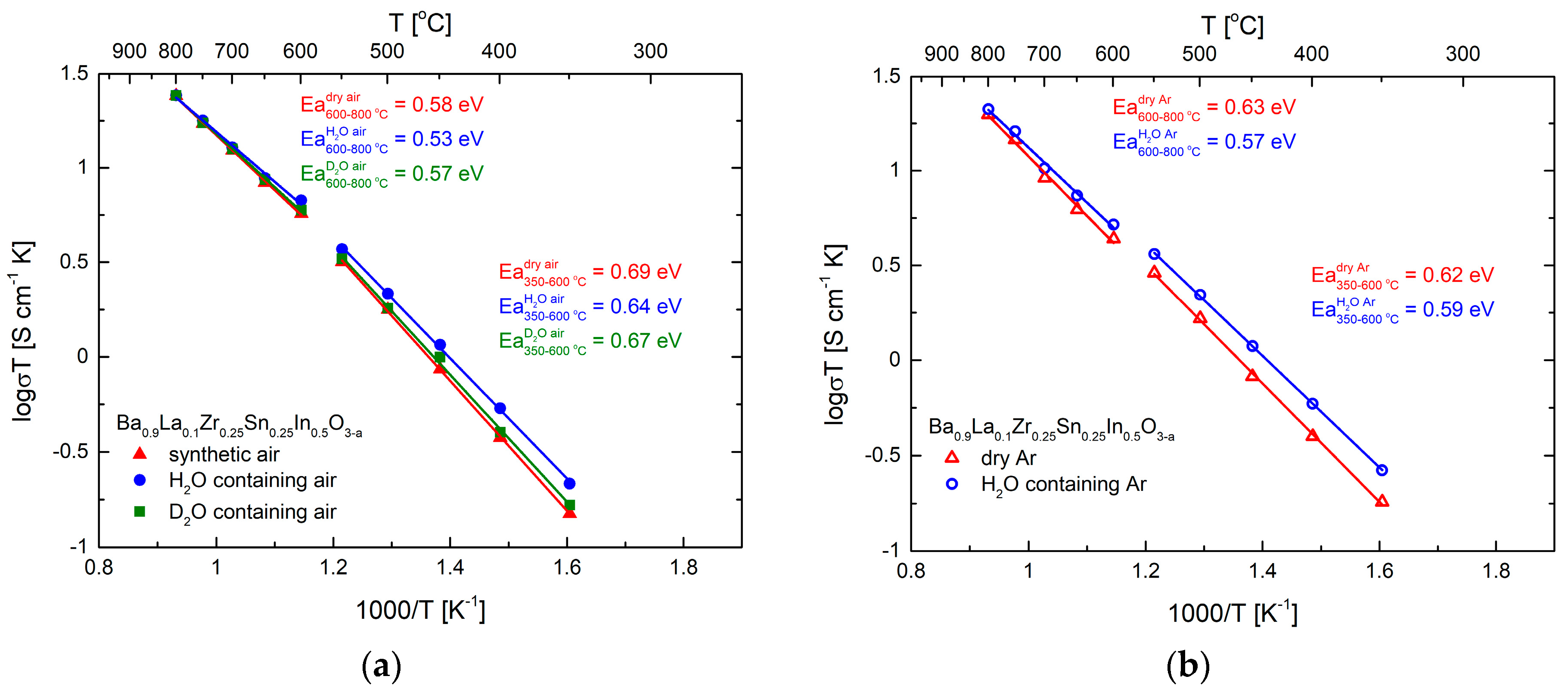
3.3. Transport Properties in Dry and Humidified Air
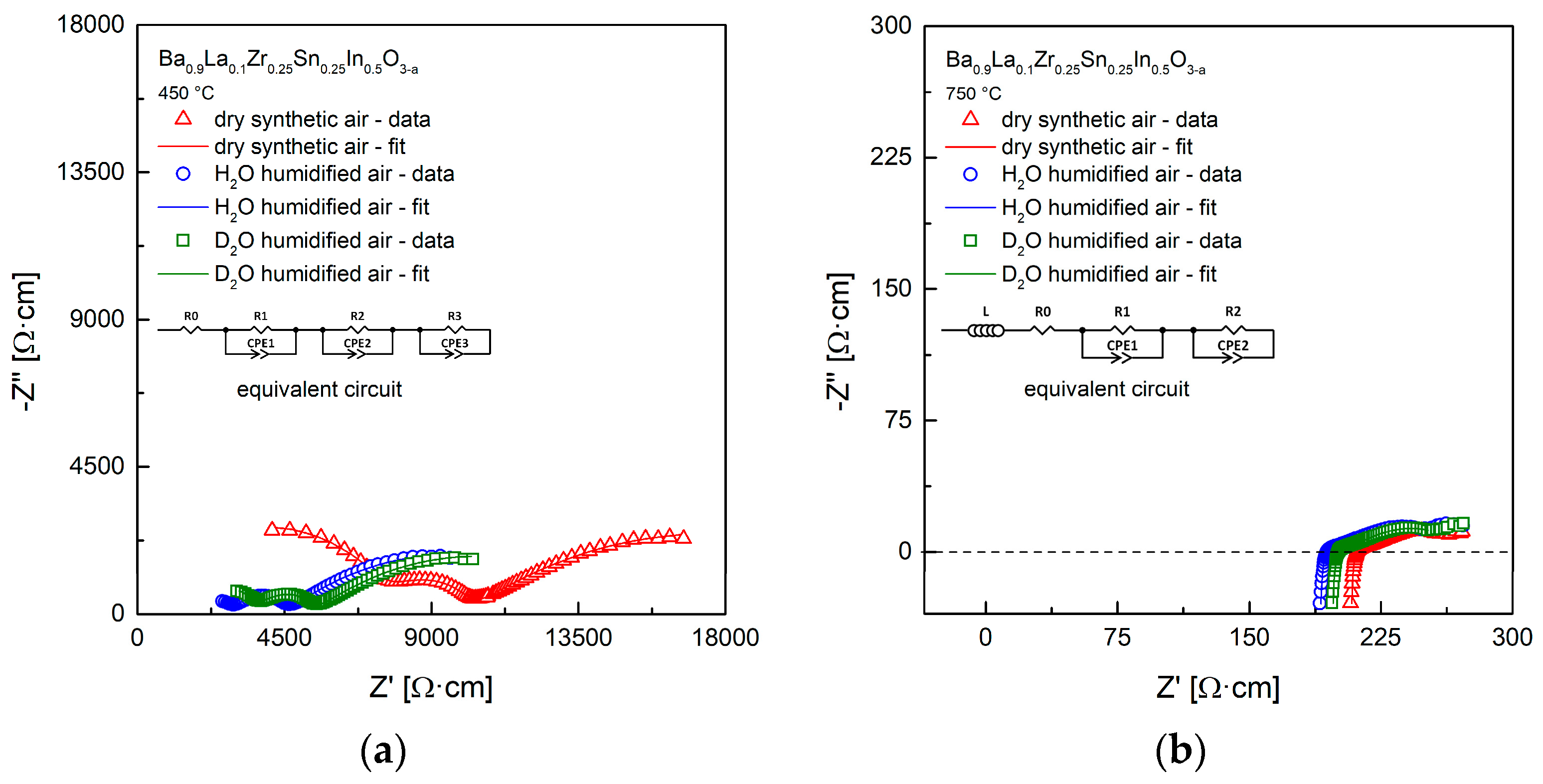
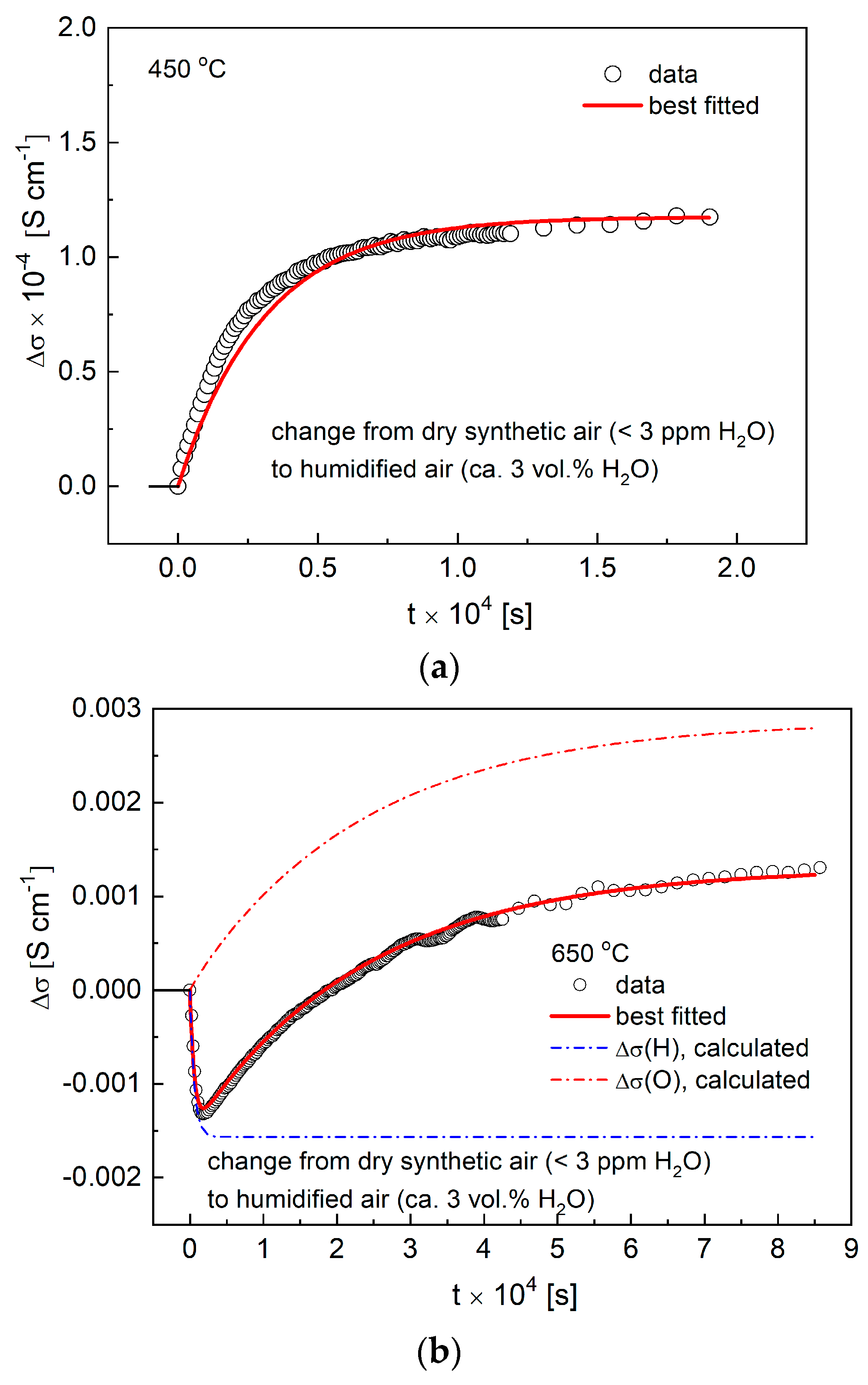
3.4. Conductivity Relaxations Studies upon Hydration
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Radenahmad, N.; Afif, A.; Petra, P.I.; Rahman, S.M.H.; Eriksson, S.-G.; Azad, A.K. Proton-conducting electrolytes for direct methanol and direct urea fuel cells—A state-of-the-art review. Renew. Sustain. Energy Rev. 2016, 57, 1347–1358. [Google Scholar] [CrossRef]
- Duan, C.; Tong, J.; Shang, M.; Nikodemski, S.; Sanders, M.; Ricote, S.; Almansoori, A.; O’Hayre, R. Readily processed protonic ceramic fuel cells with high performance at low temperatures. Science 2015, 349, 1321–1327. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, T.; Iwahara, H. Proton conduction in perovskite type oxide solid solution. Rev. Chim. Miner. 1980, 17, 243–253. [Google Scholar]
- Iwahara, H.; Uchida, H.; Maeda, N. High temperature fuel and steam electrolysis cells using proton conductive solid electrolytes. J. Power Sources 1982, 7, 293–301. [Google Scholar] [CrossRef]
- Bonano, N.; Ellis, B.; Mahmood, M.N. Construction and operation of fuel cells based on the solid electrolyte BaCeO3:Gd. Solid State Ion. 1991, 44, 305–311. [Google Scholar] [CrossRef]
- Iwahara, H.; Uchida, H.; Yamasaki, I. High-temperature steam electrolysis using SrCeO3-based proton conductive solid electrolyte. Int. J. Hydrog. Energy 1987, 12, 73–77. [Google Scholar] [CrossRef]
- Iwahara, H.; Mori, T.; Hibino, T. Electrochemical studies on ionic conduction in Ca-doped BaCeO3. Solid State Ion. 1995, 79, 177–182. [Google Scholar] [CrossRef]
- Kreuer, K.D.; Fuchs, A.; Maier, J. HD isotope effect of proton conductivity and proton conduction mechanism in oxides. Solid State Ion. 1995, 77, 157–162. [Google Scholar] [CrossRef]
- Zając, W.; Hanc, E.; Gorzkowska-Sobas, A.; Świerczek, K.; Molenda, J. Nd-doped Ba(Ce,Zr)O3−δ proton conductors for application in conversion of CO2 into liquid fuels. Solid State Ion. 2012, 225, 297–303. [Google Scholar] [CrossRef]
- Haile, S.M.; West, D.L.; Campbell, J. The role of microstructure and processing on the proton conducting properties of gadolinium-doped barium cerate. J. Mater. Res. 1998, 13, 1576–1595. [Google Scholar] [CrossRef]
- Iwahara, H.; Yajima, T.; Hibino, T.; Ushida, H. Performance of Solid Oxide Fuel Cell Using Proton and Oxide Ion Mixed Conductors Based on BaCe1− xSmxO3−α. J. Electrochem. Soc. 1993, 140, 1687–1691. [Google Scholar] [CrossRef]
- Liang, K.C.; Nowick, A.S. High-temperature protonic conduction in mixed perovskite ceramics. Solid State Ion. 1993, 61, 77–81. [Google Scholar] [CrossRef]
- Fabbri, E.; Pergolesi, D.; Traversa, E. Materials challenges toward proton-conducting oxide fuel cells: A critical review. Chem. Soc. Rev. 2010, 39, 4355–4369. [Google Scholar] [CrossRef] [PubMed]
- Haile, S.M.; Staneff, G.; Ryu, K.H. Non-stoichiometry, grain boundary transport and chemical stability of proton conducting perovskites. J. Mater. Sci. 2001, 36, 1149–1160. [Google Scholar] [CrossRef]
- Traversa, E.; Fabbri, E. Functional Materials for Sustainable Energy Applications; Kilner, J.A., Skinner, S.J., Irvine, S.J.C., Edwards, P.P., Eds.; Woodhead Publishing Series in Energy, Chapter 16; Woodhead Publishing: Sawston, UK, 2012; pp. 515–537. ISBN 9780857096371. [Google Scholar]
- Azad, A.M.; Subramaniam, S.; Dung, T.W. On the development of high density barium metazirconate (BaZrO3) ceramics. J. Alloys Compd. 2002, 334, 118–130. [Google Scholar] [CrossRef]
- Norby, T. Perovskite Oxide for Solid Oxide Fuel Cells; Ishihara, T., Ed.; Chapter 11; Springer Science Business Media: Berlin, Germany, 2009; pp. 217–241. ISBN 978-0-387-77708-5. [Google Scholar]
- Kreuer, K.D. Proton-Conducting Oxides. Annu. Rev. Mater. Rev. 2003, 33, 333–359. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, B.; Shen, J.; Lou, Y.; Ji, Y. La2Ce2O7: A promising proton ceramic conductor in hydrogen economy. J. Alloys Compd. 2015, 659, 232–239. [Google Scholar] [CrossRef]
- Malavasi, L.; Fisherb, C.; Saiful Islam, A. Oxide-ion and proton conducting electrolyte materials for clean energy applications: Structural and mechanistic features. Chem. Soc. Rev. 2010, 39, 4370–4387. [Google Scholar] [CrossRef] [PubMed]
- Marrony, M. (Ed.) Proton-Conducting Ceramics: From Fundamentals to Applied Research; PAN Stanford Publishing: Singapore, 2016; ISBN 9789814613842. [Google Scholar]
- Haugsrud, R.; Norby, T. High-temperature proton conductivity in acceptor-doped LaNbO4. Solid State Ion. 2006, 177, 1129–1135. [Google Scholar] [CrossRef]
- Quarez, E.; Noirault, S.; Caldes, M.T.; Joubert, O. Water incorporation and proton conductivity in titanium substituted barium indate. J. Power Sources 2010, 195, 1136–1141. [Google Scholar] [CrossRef]
- Jankovic, J.; Wilkinson, D.P.; Hui, R. Proton conductivity and stability of Ba2In2O5 in hydrogen containing atmospheres. J. Electrochem. Soc. 2011, 158, B61–B68. [Google Scholar] [CrossRef]
- Geffroy, P.M.; Pons, A.; Bechade, E.; Masson, O.; Fouletier, J. Characterization of electrical conduction and nature of charge carriers in mixed and ionic conductors. J. Power Sources 2017, 360, 70–79. [Google Scholar] [CrossRef]
- Agmon, N. The Grotthuss mechanism. Chem. Phys. Lett. 1995, 244, 456–462. [Google Scholar] [CrossRef]
- Kreuer, K.D. Perovskite Oxide for Solid Oxide Fuel Cells; Ishihara, T., Ed.; Chapter 12; Springer Science Business Media: Berlin, Germany, 2009; pp. 261–272. ISBN 978-0-387-77708-5. [Google Scholar]
- Norby, T.; Widerøe, M.; Glöckner, R.; Larring, Y. Hydrogen in oxides. Dalton Trans. 2004, 19, 3012–3018. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.; Yoo, H.I. Two-fold-to-single-fold transition of the conductivity relaxation patterns of proton-conducting oxides upon hydration/dehydration. Solid State Ion. 2013, 252, 132–139. [Google Scholar] [CrossRef]
- Yoo, H.I.; Yoon, J.Y.; Ha, J.S.; Lee, C.E. Hydration and oxidation kinetics of a proton conductor oxide, SrCe0.95Yb0.05O2.975. Phys. Chem. Chem. Phys. 2008, 10, 974–982. [Google Scholar] [CrossRef] [PubMed]
- Yoo, H.I.; Yeon, J.I.; Kim, J.K. Mass relaxation vs. electrical conductivity relaxation of a proton conducting oxide upon hydration and dehydration. Solid State Ion. 2009, 180, 1443–1447. [Google Scholar] [CrossRef]
- Lee, D.K.; Yoo, H.I. Unusual oxygen re-equilibration kinetics of TiO2−δ. Solid State Ion. 2006, 177, 1–9. [Google Scholar] [CrossRef]
- Yoo, H.I.; Lee, C.E. Two-Fold Diffusion Kinetics of Oxygen Re-Equilibration in Donor-Doped BaTiO3. J. Am. Ceram. Soc. 2005, 88, 617–623. [Google Scholar] [CrossRef]
- Yu, J.H.; Lee, J.S.; Maier, J. Peculiar nonmonotonic water incorporation in oxides detected by local in situ optical absorption spectroscopy. Angew. Chem. Int. Ed. 2007, 46, 8992–8994. [Google Scholar] [CrossRef] [PubMed]
- Kreuer, K.D.; Schönherr, E.; Maier, J. Proton and oxygen diffusion in BaCeO3 based compounds: A combined thermal gravimetric analysis and conductivity study. Solid State Ion. 1994, 70, 278–284. [Google Scholar] [CrossRef]
- Lim, D.K.; Choi, M.B.; Lee, K.T.; Yoon, H.S.; Wachsman, E.D.; Song, S.J. Conductivity Relaxation of Proton-Conducting BaCe0.85Y0.15O3−δ Upon Oxidation and Reduction. J. Electrochem. Soc. 2011, 158, B852–B856. [Google Scholar] [CrossRef]
- Singh, K.K.; Ganguly, P.; Rao, C.N. Structural transitions in (La,Ln)2CuO4 and La2(Cu,Ni)O4 systems. Mater. Res. Bull. 1982, 17, 493–500. [Google Scholar] [CrossRef]
- Kanai, H.; Mizusaki, J.; Tagawa, H.; Hoshiyama, S.; Hirano, K.; Fujita, K.; Tezuka, M.; Hashimoto, T. Defect Chemistry of La2−xSrxCuO4−δ: Oxygen Nonstoichiometry and Thermodynamic Stability. J. Solid State Chem. 1997, 131, 150–159. [Google Scholar] [CrossRef]
- Colomban, P.; Tran, C.; Zaafrani, O.; Slodczyk, A. Aqua oxyhydroxycarbonate second phases at the surface of Ba/Sr-based proton conducting perovskites: A source of confusion in the understanding of proton conduction. J. Raman Spectrosc. 2013, 44, 312–321. [Google Scholar] [CrossRef]
- Zhang, G.B.; Smyth, D.M. Protonic conduction in Ba2In2O5. Solid State Ion. 1995, 82, 153–160. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: New York, NY, USA, 1975; ISBN 0198533446. [Google Scholar]
- Han, D.; Majima, M.; Uda, T. Structure Analysis of BaCe0.8Y0.2O3-δ in Dry and Wet Atmospheres by High-Temperature X-ray Diffraction Measurement. J. Solid State Chem. 2013, 205, 122–128. [Google Scholar] [CrossRef]
- Świerczek, K.; Skubida, W.; Niemczyk, A.; Olszewska, A.; Zheng, K. Structure and transport properties of proton-conducting BaSn0.5In0.5O2.75 and A-site substituted Ba0.9Ln0.1Sn0.5In0.5O2.8 (Ln = La, Gd) oxides. Solid State Ion. 2017, 307, 44–50. [Google Scholar] [CrossRef]
- Skubida, W.; Świerczek, K. Structural properties and presence of protons in Ba0.9Gd0.1Zr1−x−ySnxInyO3−(y−0.1)/2 perovskites. Funct. Mater. Lett. 2016, 9, 1641005. [Google Scholar] [CrossRef]
- Andersson, A.K.E.; Selbach, S.M.; Knee, S.C.; Grande, T. Chemical Expansion Due to Hydration of Proton-Conducting Perovskite Oxide Ceramics. J. Am. Ceram. Soc. 2014, 97, 2654–2661. [Google Scholar] [CrossRef]
- Han, D.; Shinoda, K.; Uda, T. Dopant Site Occupancy and Chemical Expansion in Rare Earth-Doped Barium Zirconate. J. Am. Ceram. Soc. 2014, 97, 643–650. [Google Scholar] [CrossRef]
- Kreuer, K.D. On the complexity of proton conduction phenomena. Solid State Ion. 2000, 136, 149–160. [Google Scholar] [CrossRef]
- Babilo, P.; Uda, T.; Haile, S.M. Processing of yttrium-doped barium zirconate for high proton conductivity. J. Appl. Phys. 2007, 22, 1322–1330. [Google Scholar] [CrossRef]




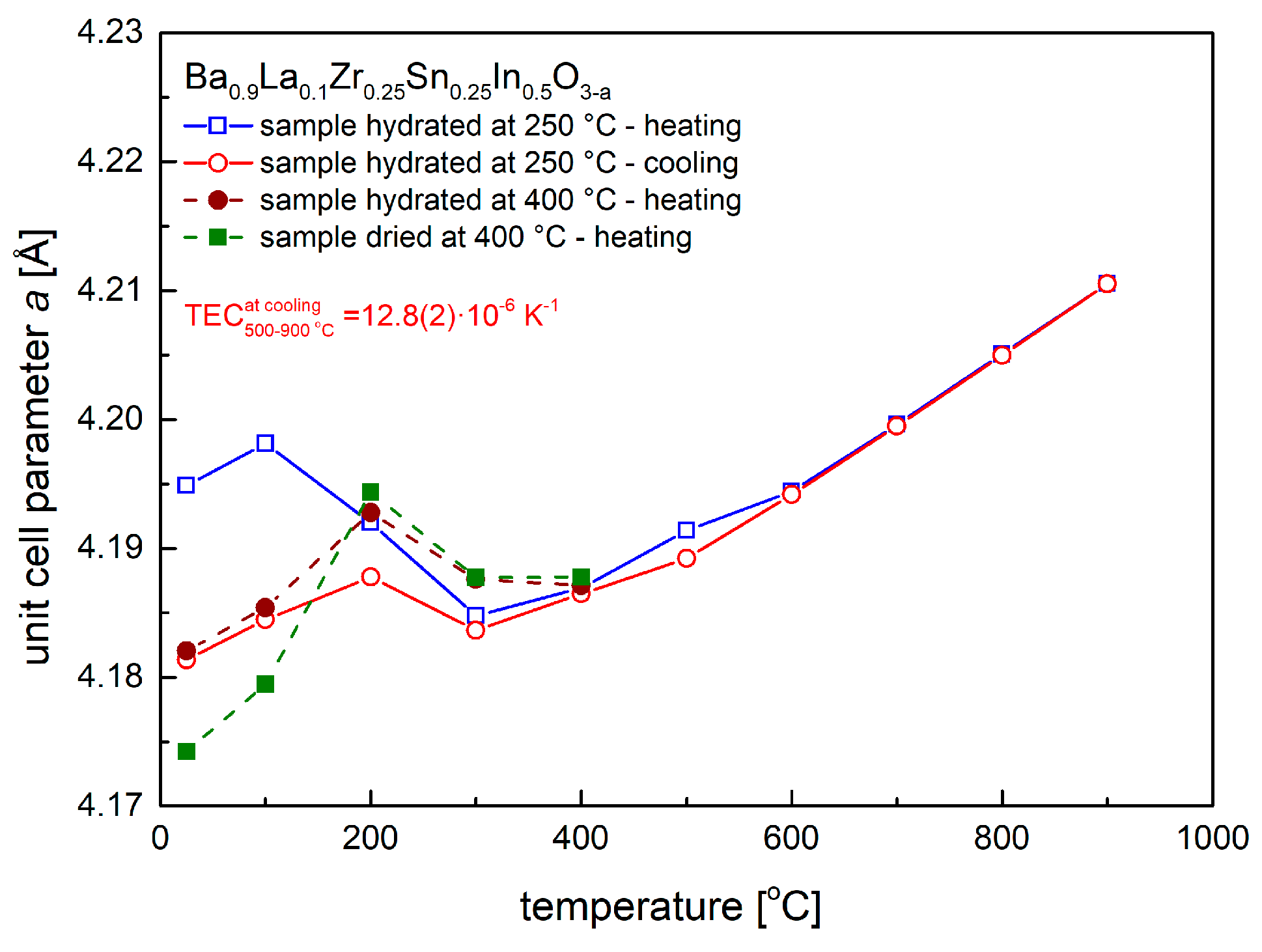

| Conditions | Unit Cell Parameter a [Å] | Unit Cell Volume V [Å3] | (Ba,La)-O Distance [Å] | (Zr,Sn,In)-O Distance [Å] | χ2/Rwp [%] | Uiso·100 [Å2] CationsO |
|---|---|---|---|---|---|---|
| stored sample | 4.1893(1) | 73.53(1) | 2.9623(1) | 2.0947(1) | 4.125/3.53 | 2.39(2)/4.6(1) |
| material hydrated at 250 °C (data at RT) | 4.1949(1) | 73.82(1) | 2.9662(1) | 2.0974(1) | 1.548/2.79 | 2.08(2)/3.1(1) |
| data recorded at 600 °C in synthetic air | 4.1944(1) | 73.79(1) | 2.9659(1) | 2.0972(1) | 2.291/3.45 | 2.09(2)/4.3(2) |
| data recorded at 900 °C in synthetic air | 4.2105(1) | 74.64(1) | 2.9773(1) | 2.1053(1) | 1.959/3.21 | 2.83(2)/5.7(2) |
| Temperature [°C] | σH = σwet − σdry [S cm−1] | σD = σwet − σdry [S cm−1] | tH = σH/σwet | tD = σD/σwet | ||
|---|---|---|---|---|---|---|
| Air | Ar | Air | Air | Ar | Air | |
| 650 | 5.0 × 10−4 | 1.3 × 10−3 | 3.3 × 10−4 | 0.05 | 0.16 | 0.04 |
| 600 | 6.2 × 10−4 | 9.5 × 10−4 | 2.3 × 10−4 | 0.08 | 0.16 | 0.03 |
| 550 | 6.4 × 10−4 | 9.0 × 10−4 | 1.5 × 10−4 | 0.14 | 0.20 | 0.04 |
| 500 | 4.8 × 10−4 | 7.1 × 10−4 | 3.9 × 10−5 | 0.17 | 0.25 | 0.02 |
| 450 | 4.1 × 10−4 | 5.1 × 10−4 | 1.9 × 10−4 | 0.25 | 0.31 | 0.13 |
| 400 | 2.4 × 10−4 | 2.9 × 10−4 | 3.8 × 10−5 | 0.30 | 0.33 | 0.06 |
| 350 | 1.1 × 10−4 | 1.4 × 10−4 | 2.6 × 10−5 | 0.30 | 0.32 | 0.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skubida, W.; Niemczyk, A.; Zheng, K.; Liu, X.; Świeczek, K. Crystal Structure, Hydration, and Two-Fold/Single-Fold Diffusion Kinetics in Proton-Conducting Ba0.9La0.1Zr0.25Sn0.25In0.5O3−a Oxide. Crystals 2018, 8, 136. https://doi.org/10.3390/cryst8030136
Skubida W, Niemczyk A, Zheng K, Liu X, Świeczek K. Crystal Structure, Hydration, and Two-Fold/Single-Fold Diffusion Kinetics in Proton-Conducting Ba0.9La0.1Zr0.25Sn0.25In0.5O3−a Oxide. Crystals. 2018; 8(3):136. https://doi.org/10.3390/cryst8030136
Chicago/Turabian StyleSkubida, Wojciech, Anna Niemczyk, Kun Zheng, Xin Liu, and Konrad Świeczek. 2018. "Crystal Structure, Hydration, and Two-Fold/Single-Fold Diffusion Kinetics in Proton-Conducting Ba0.9La0.1Zr0.25Sn0.25In0.5O3−a Oxide" Crystals 8, no. 3: 136. https://doi.org/10.3390/cryst8030136
APA StyleSkubida, W., Niemczyk, A., Zheng, K., Liu, X., & Świeczek, K. (2018). Crystal Structure, Hydration, and Two-Fold/Single-Fold Diffusion Kinetics in Proton-Conducting Ba0.9La0.1Zr0.25Sn0.25In0.5O3−a Oxide. Crystals, 8(3), 136. https://doi.org/10.3390/cryst8030136







