Light-Induced Current Oscillations in the Charge-Ordered State of (TMTTF)2SbF6
Abstract
:1. Introduction
- Non-equilibrium charge carriers: modification of the charge carrier number or the mobility.
- Space-charge distribution: for instance impurity bands.
- Electrically induced phase transitions: modification of the electronic system or the crystalline structure.
- Ionic motion in the host material: forming of conductive filaments.
- Sliding charge density waves or charge order.
- Domain wall motions or excitations of solitons.
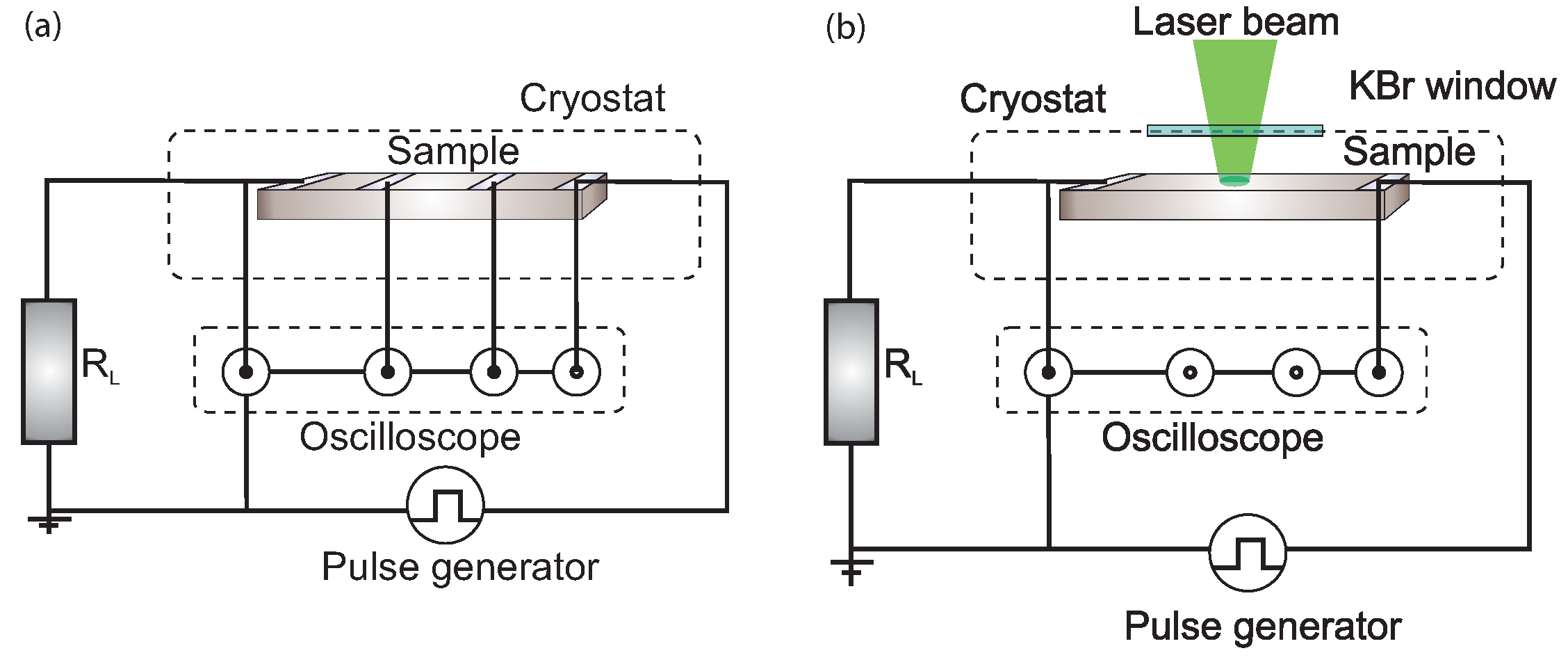
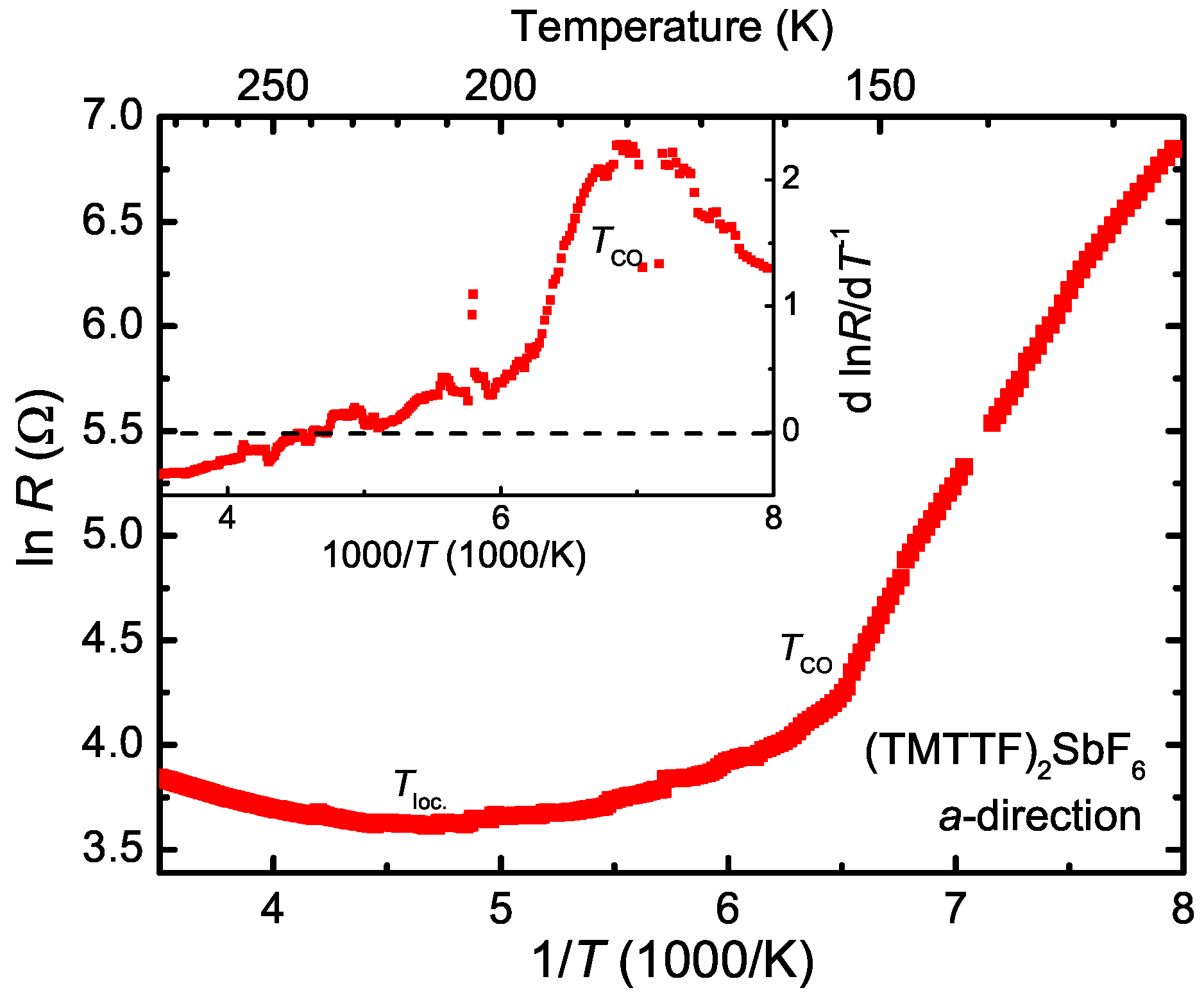
2. Experimental Details
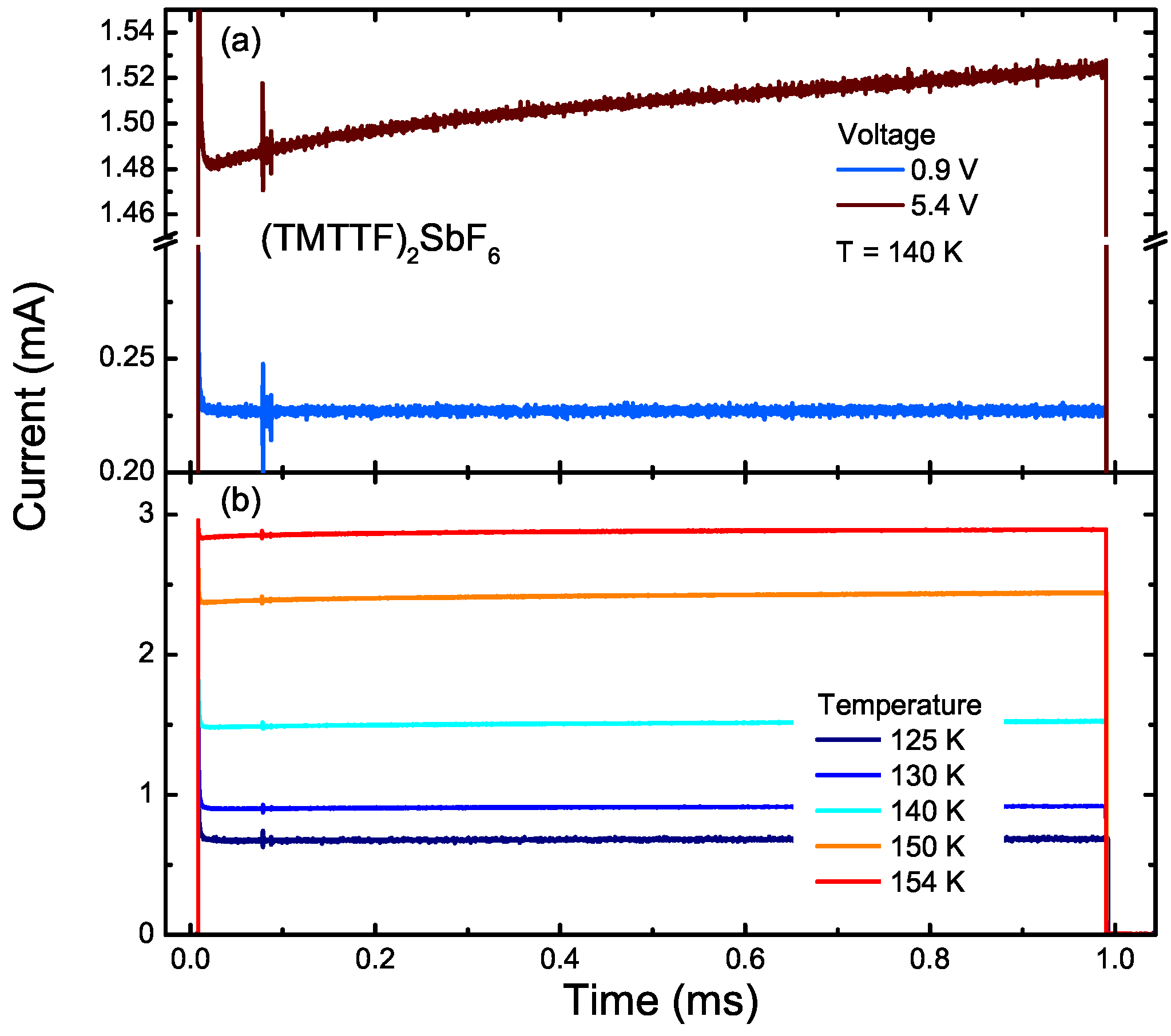
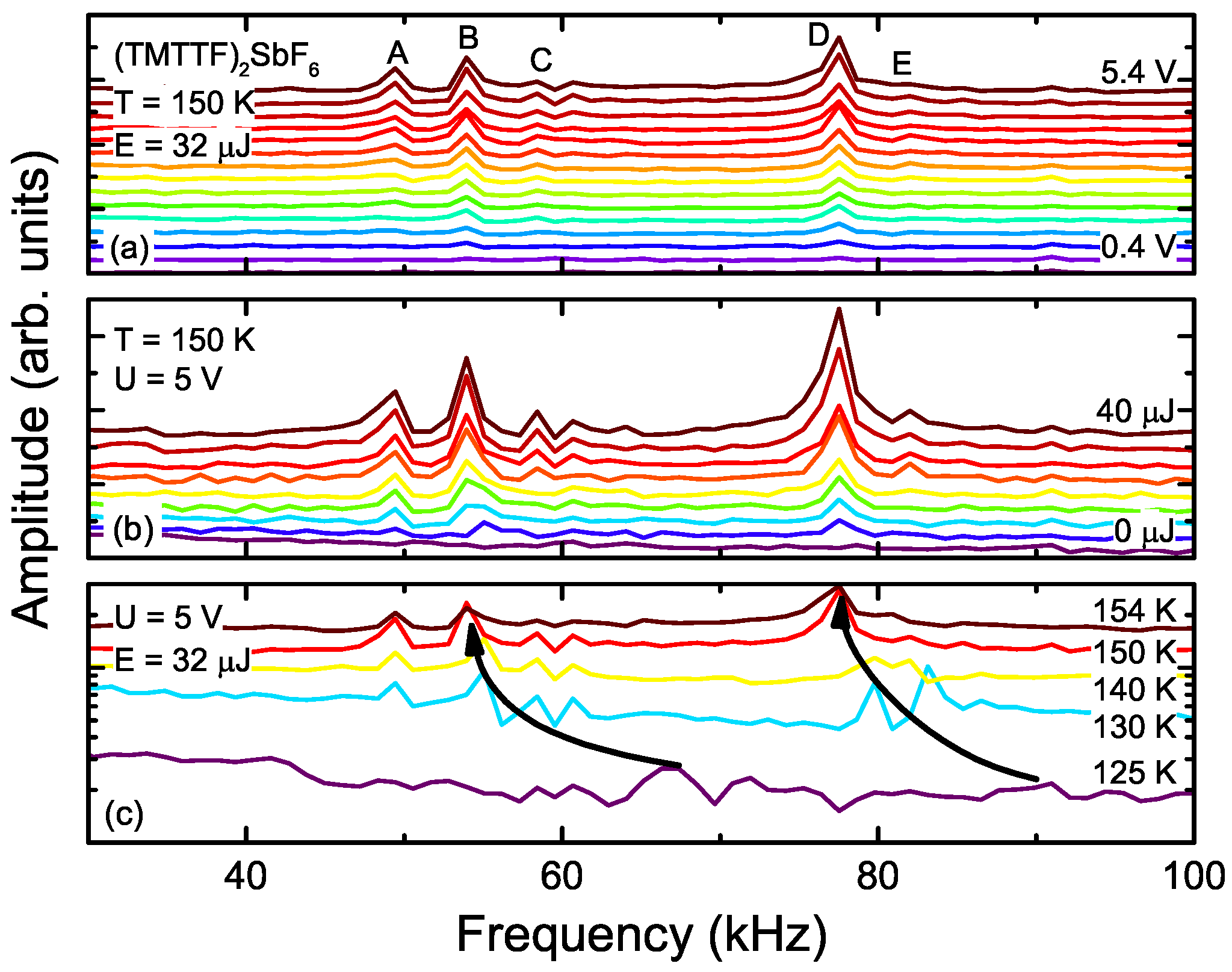
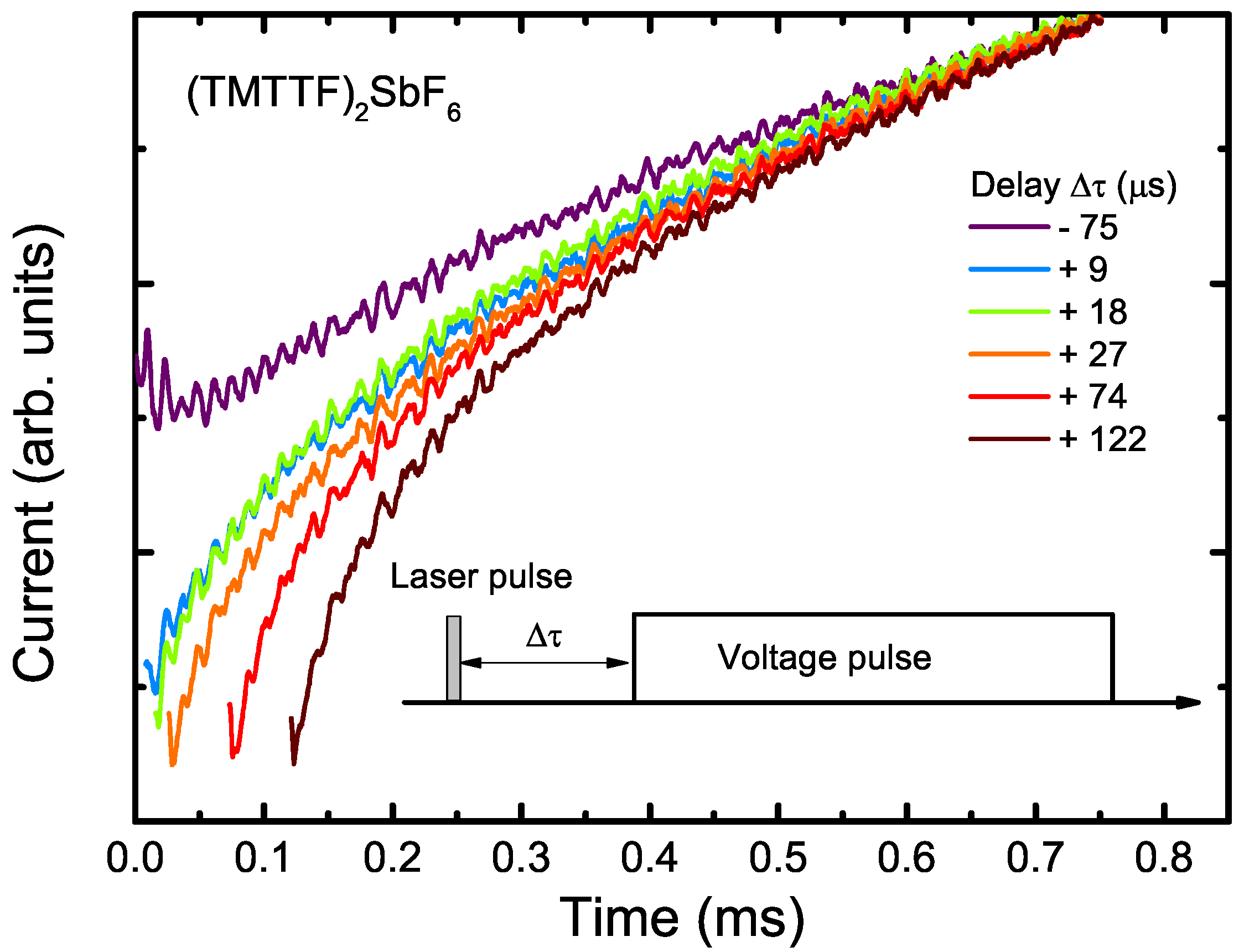
3. Response to Electric Fields
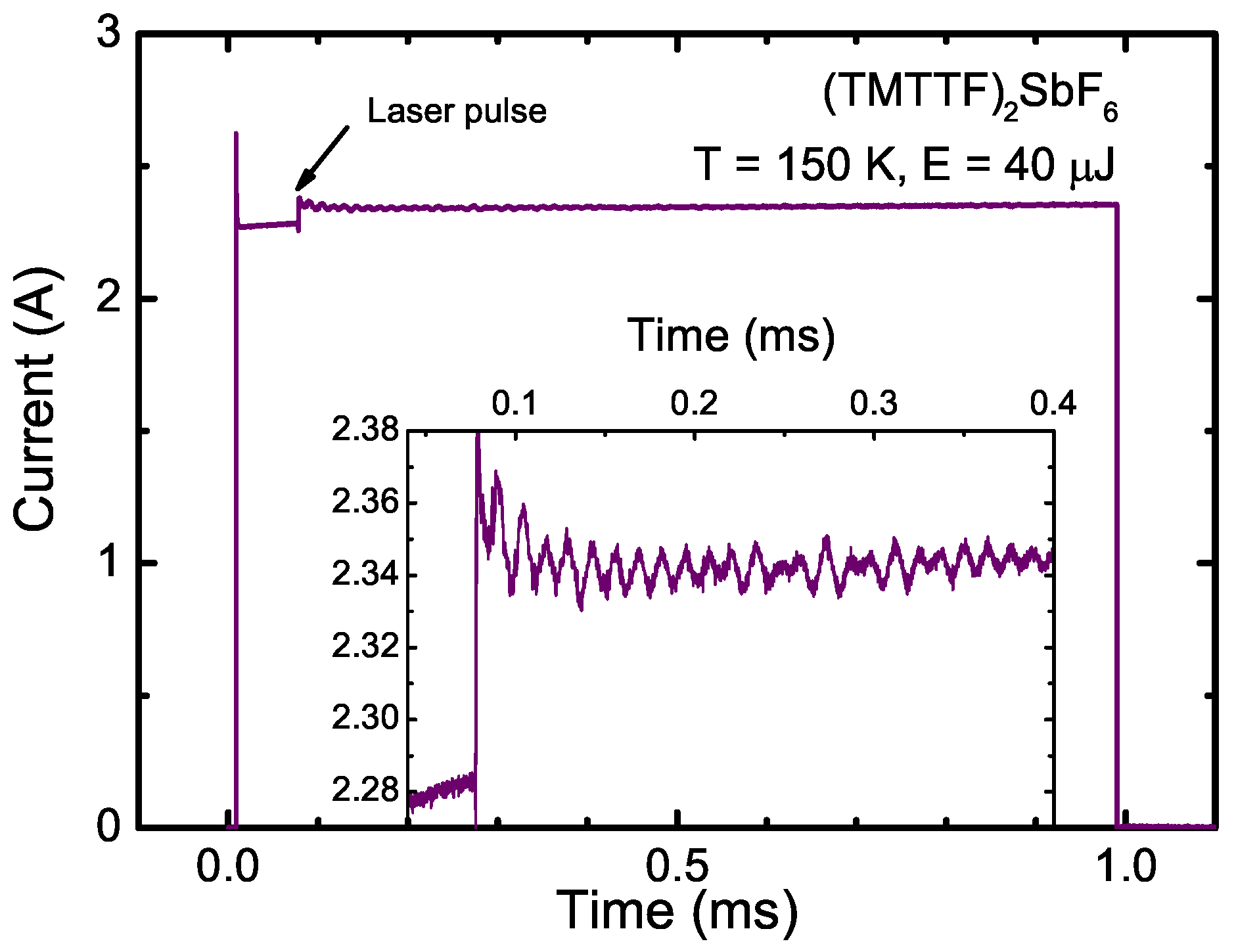
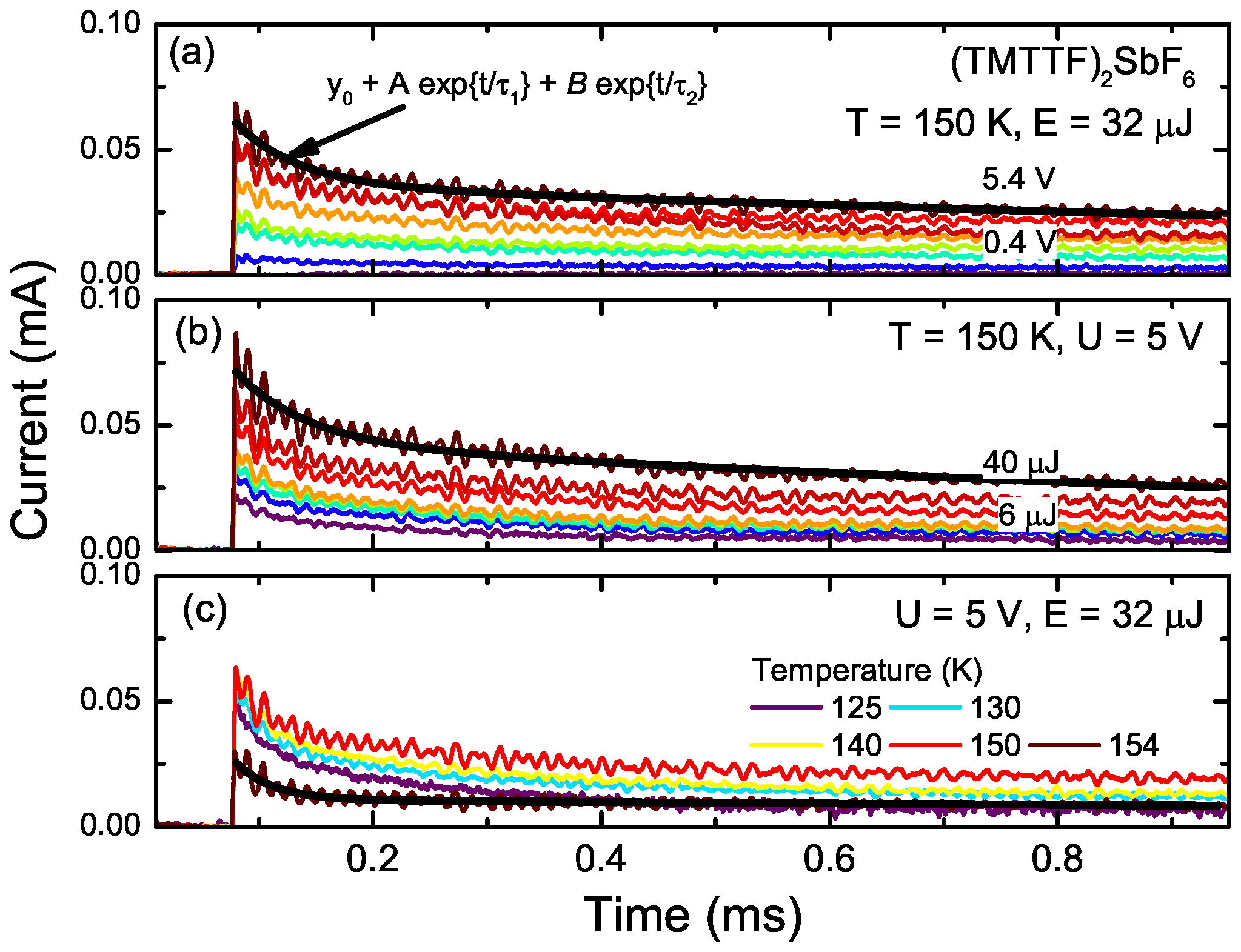
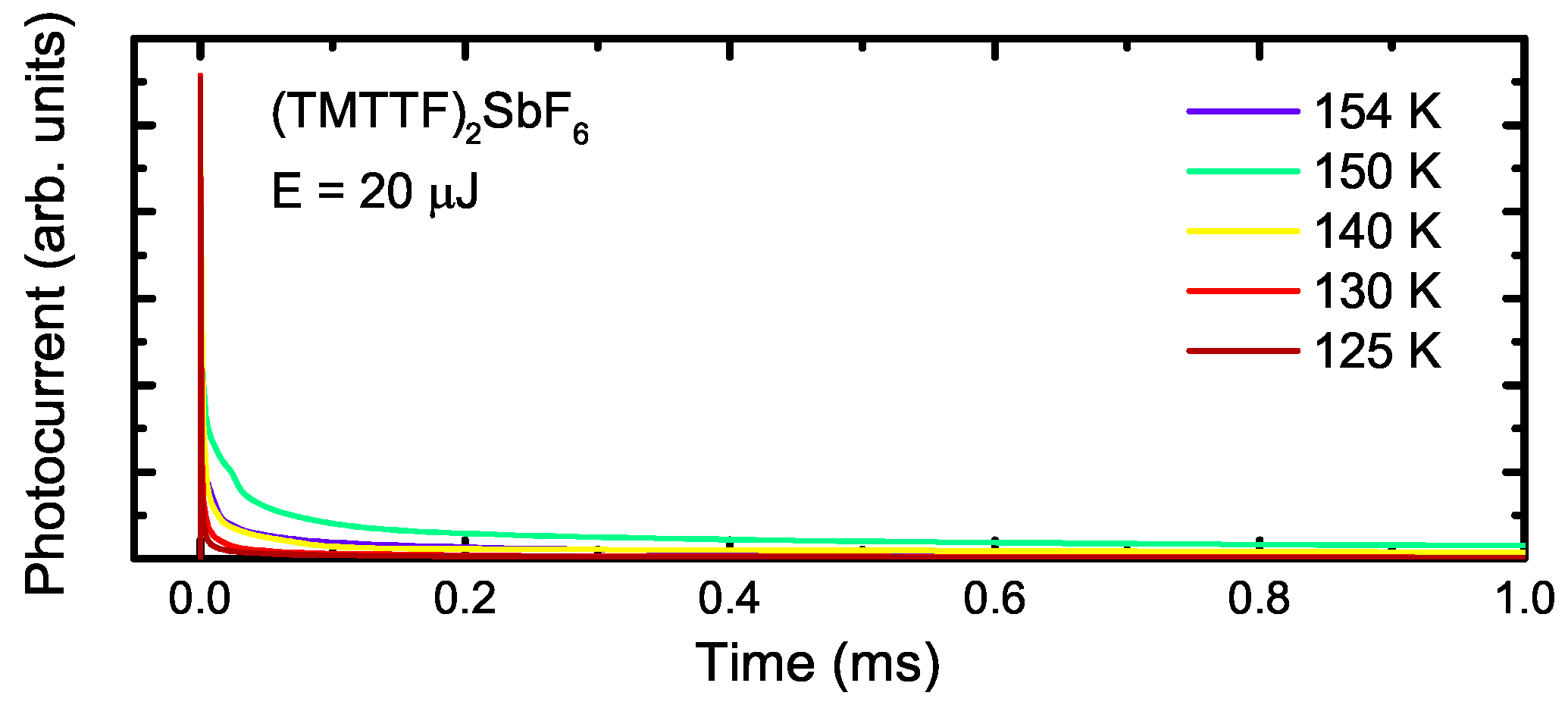
4. Response to Laser Pulses
5. Discussion
- A free electron and hole can be created, which get separated from each other by the electric field, leading to the photocurrent signal. However, they can recombine before they reach the electrodes or become trapped. In general, the lifetime of free carries is between nanoseconds and microseconds.
- After a few picoseconds the excited electronic states couple to the lattice phonons and intramolecular vibrations. By this, energy is transferred to the lattice subsystem and the sample is warmed up.
- Afterwards, the excited electrons decay back into their initial state by emitting a red-shifted photon. The latter can be reabsorbed or detected as a photo-luminescence signal. Also, a radiation-free decay is possible into the lowest excited (mid-infrared) band.
- Otherwise, the excited charge can relax into a low-lying unoccupied band, triggering a charge transfer from one cation to its neighboring molecule in the picture of a molecular chain. This can induce a phase transition from the charge-ordered to the metallic state.
- Recently, in photo-luminescence spectra of a two-dimensional organic Mott insulator the creation of an exciton was suggested [71]. The theory of photo-induced transitions [72] proposes that higher excited states can be populated and excitons brake up; Frenkel excitons becomes charge-transfer excitons and propagate. The separation of excitons may also stimulate a light-induced transition. Especially in low-dimensional system fluctuations as well as electron-electron and electron-phonon interactions play a crucial role, eventually destabilizing the equilibrium state. This picture is similar to the model suggested for the photo-induced phase transition in TTF-CA [70,73].
- In the 1960s and 1970s transport measurements on silicon with two Schottky contacts revealed current oscillations in the kHz regime, which were ascribed to double current injection at the contacts [74]. However, the frequency could be varied by changing the voltage bias or temperature and the oscillations occur only above a critical threshold field [75].
- The well-known creation of hot or non-equilibrium electrons in semiconductors such as GaAs [33] leads to electric field-dependent charge carrier velocities, causing a negative-differential resistance. One of the related phenomena is the famous Gunn effect, yielding current oscillations in the microwave regime. In this case, the frequency can be tuned by the sample length or by the applied voltage.
- Similar to the negative-differential resistance current oscillations in pure semiconductors, self-oscillating (photo-)currents were observed in superlattice structures, consisting of two different direct semiconductors such as GaAs-AlAs [76]. Due to the different energy levels in the quantum wells and the tunneling effect between the layers, a negative differential velocity regime is created as a function of the external electric field. The electric field reveals a spatial variation within the superlattice structure. Thereby, the different regions separated by domain walls get unstable and hence cause the oscillations. The resonance frequency can be tuned by the bias voltage or laser power [77,78].
- It is known that ferroelectric materials render a modification of the polarization by light stimulation, which can be detected by photoconductivity measurements [84]. Here, the detected signal is generally composed in of three different terms [85,86,87]: first, a fast decay of the excited states within a few microseconds, in addition a pyroelectric signal that can last several milliseconds, and finally piezoelectric oscillations superimposed on the decaying current due to the thickness variation of the sample by sound waves. Since the Fabre salts are charge-ordered ferroelectric crystals [50,88], they resemble the behavior of well-known inorganic ferroelectric, such as LiNbO.
- Above a certain threshold field, voltage oscillations (in the range of a few 100 mV/cm) occur in CDW systems [50,60], such as NbSe, TaS or KMoO, which are attributed to the collective sliding of the charge density wave. There, the resonance frequency depends on the applied voltage and temperature. However, only very few photoconductivity studies were conducted on CDW materials [89,90]. Experiments utilizing a lock-in technique do not directly provide the time-dependent behavior of the photocurrent. It was reported that the threshold voltage between the creeping and sliding state of the CDW can be raised by increasing the light intensity.
6. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Ab Initio Calculations
Appendix A.1. Band Structure
Appendix A.2. Optical Spectra
References
- Ishiguro, T.; Yamaji, K.; Saito, G. Organic Superconductors, 2nd ed.; Springer: Berlin, Germany, 1998. [Google Scholar]
- Lebed, A. (Ed.) The Physics of Organic Superconductors and Conductors; Springer Series in Materials Science; Springer: Berlin, Germany, 2008; Volume 110. [Google Scholar]
- Dressel, M. Spin-charge separation in quasi one-dimensional organic conductors. Naturwissenschaften 2003, 90, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Dressel, M. Ordering phenomena in quasi-one-dimensional organic Conductors. Naturwissenschaften 2007, 94, 527–541. [Google Scholar] [CrossRef] [PubMed]
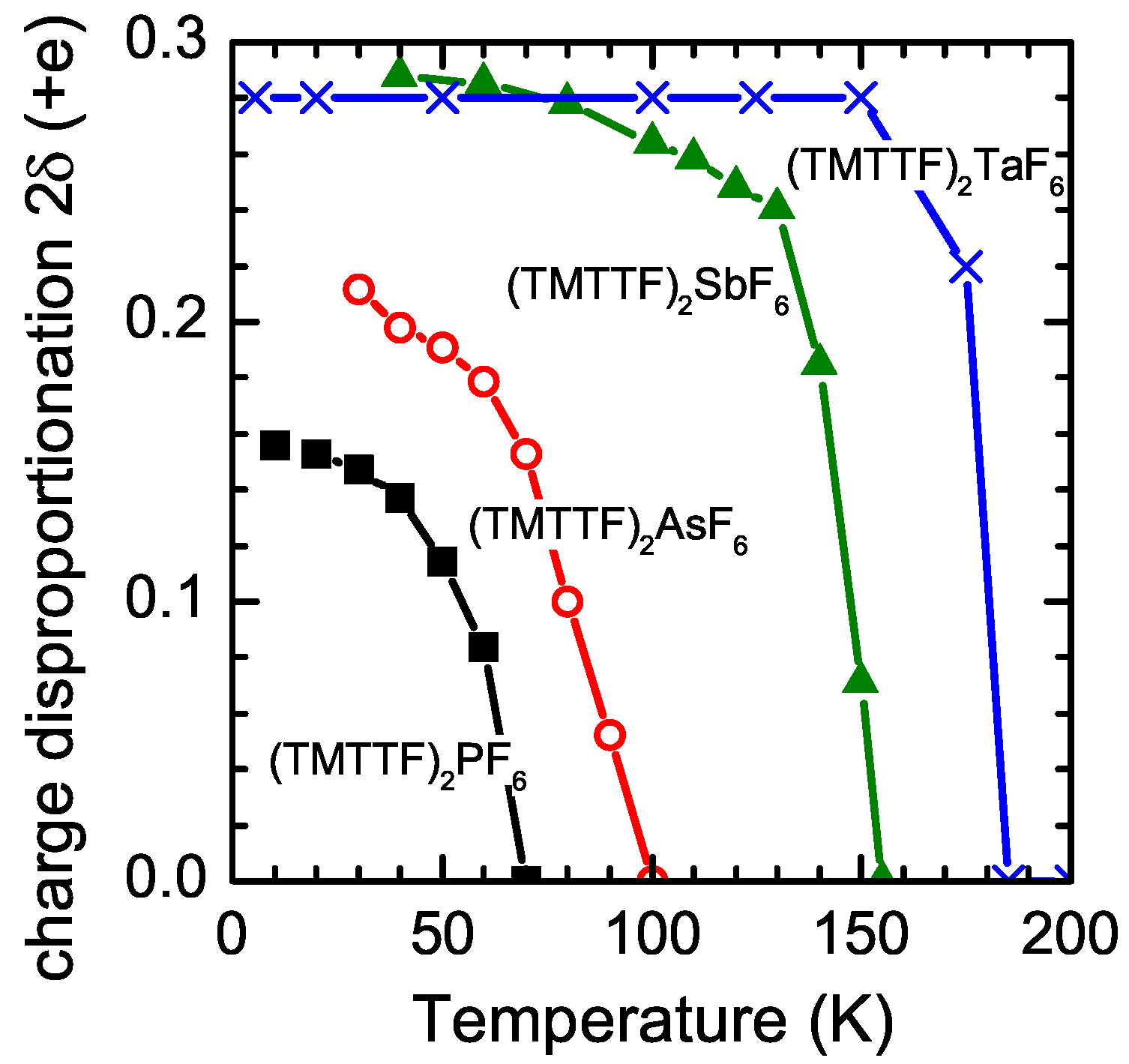
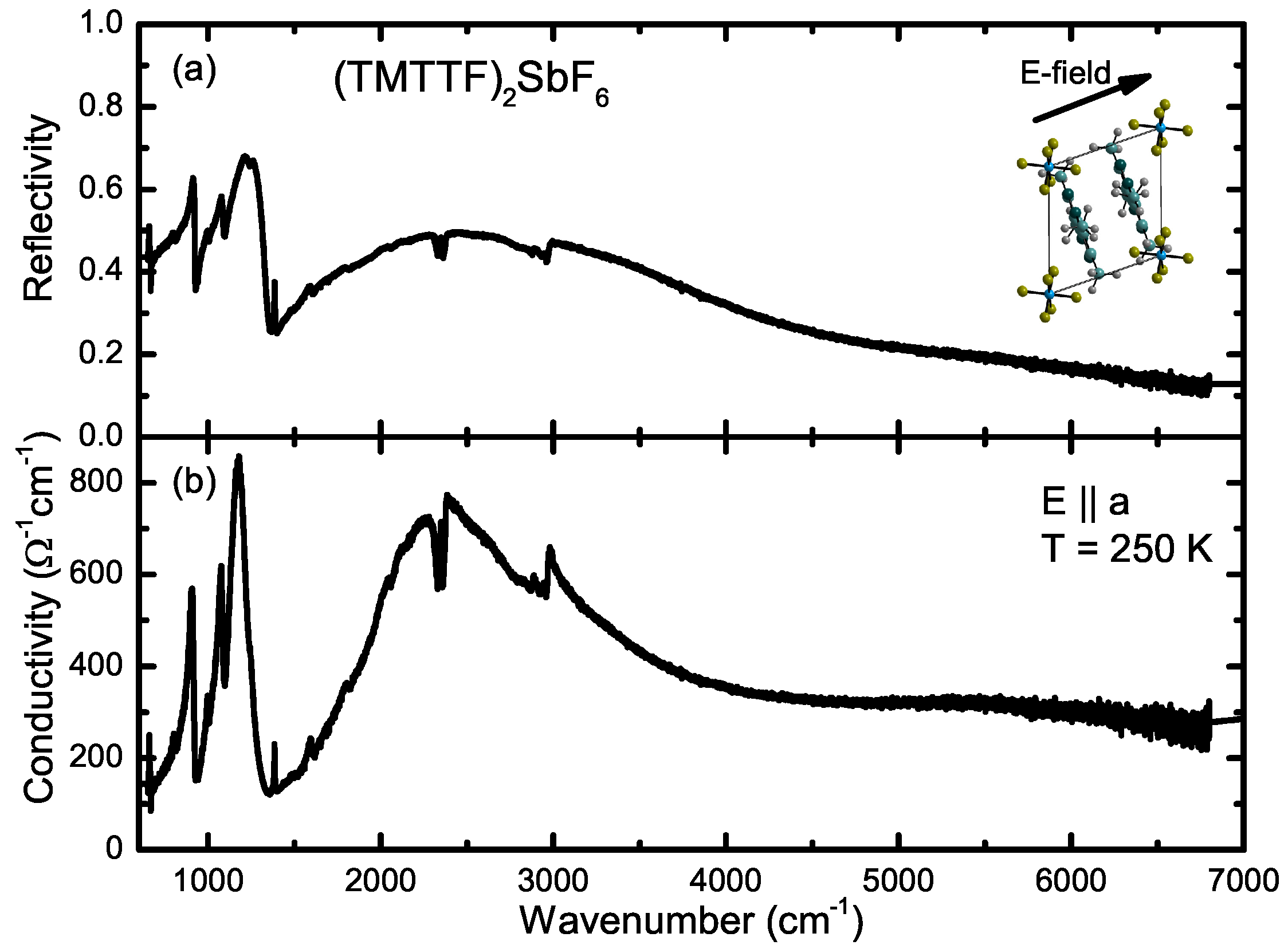
- Dumm, M.; Abaker, M.; Dressel, M. Mid-infrared response of charge-ordered quasi-1D organic conductors (TMTTF)2X. J. Phys. IV 2005, 131, 55–58. [Google Scholar] [CrossRef]
- Knoblauch, T.; Dressel, M. Charge disproportionation in (TMTTF)2X (X= PF6, AsF6 and SbF6) investigated by infrared spectroscopy. Phys. Status Solidi (C) 2012, 9, 1158–1160. [Google Scholar] [CrossRef]
- Dressel, M.; Dumm, M.; Knoblauch, T.; Masino, M. Comprehensive Optical Investigations of Charge Order in Organic Chain Compounds (TMTTF)2X. Crystals 2012, 2, 528–578. [Google Scholar] [CrossRef]
- Voloshenko, I.; Herter, M.; Beyer, R.; Pustogow, A.; Dressel, M. Pressure-dependent optical investigations of Fabre salts in the charge-ordered state. J. Phys. Condens. Matter 2017, 29, 115601. [Google Scholar] [CrossRef] [PubMed]
- Świetlik, R.; Barszcz, B.; Pustogow, A.; Dressel, M. Raman spectroscopy evidence of domain walls in the organic electronic ferroelectrics (TMTTF)2X (X = SbF6, AsF6, PF6). Phys. Rev. B 2017, 95, 085205. [Google Scholar] [CrossRef]
- Köhler, B.; Rose, E.; Dumm, M.; Untereiner, G.; Dressel, M. Comprehensive transport study of anisotropy and ordering phenomena in quasi-one-dimensional (TMTTF)2X salts (X = PF6, AsF6, SbF6, BF4, ClO4, ReO4). Phys. Rev. B 2011, 84, 035124. [Google Scholar] [CrossRef]
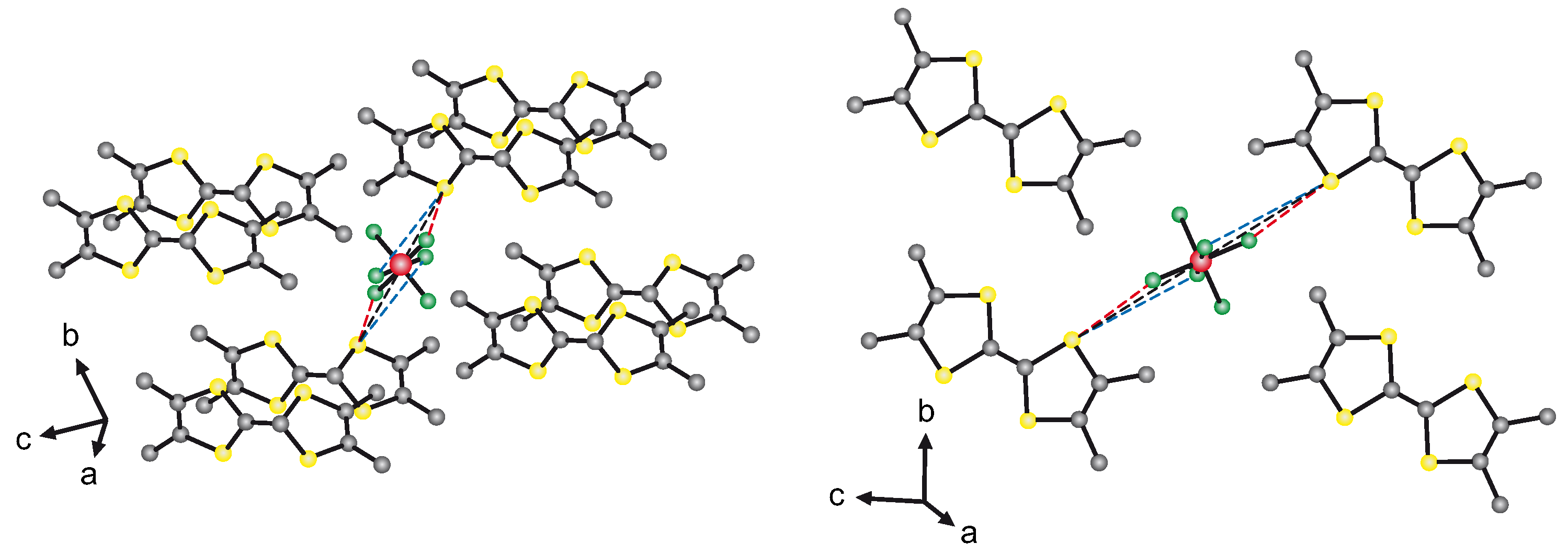
- Pouget, J.P. Structural Aspects of the Bechgaard and Fabre Salts: An Update. Crystals 2012, 2, 466–520. [Google Scholar] [CrossRef]
- Pustogow, A.; Peterseim, T.; Kolatschek, S.; Engel, L.; Dressel, M. Electronic correlations versus lattice interactions: Interplay of charge and anion orders in (TMTTF)2X. Phys. Rev. B 2016, 94, 195125. [Google Scholar] [CrossRef]
- Rose, E.; Loose, C.; Kortus, J.; Pashkin, A.; Kuntscher, C.A.; Ebbinghaus, S.G.; Hanfland, M.; Lissner, F.; Schleid, T.; Dressel, M. Pressure-dependent structural and electronic properties of quasi-one-dimensional (TMTTF)2PF6. J. Phys. Condens. Matter 2013, 25, 014006. [Google Scholar] [CrossRef] [PubMed]
- Jacko, A.C.; Feldner, H.; Rose, E.; Lissner, F.; Dressel, M.; Valentí, R.; Jeschke, H.O. Electronic properties of Fabre charge-transfer salts under various temperature and pressure conditions. Phys. Rev. B 2013, 87, 155139. [Google Scholar] [CrossRef]
- Medjanik, K.; de Souza, M.; Kutnyakhov, D.; Gloskovskii, A.; Müller, J.; Lang, M.; Pouget, J.P.; Foury-Leylekian, P.; Moradpour, A.; Elmers, H.J.; et al. Hard X-ray photoemission study of the Fabre salts (TMTTF)2X (X = SbF6 and PF6). Eur. Phys. J. B 2014, 87, 256. [Google Scholar] [CrossRef]
- Salameh, B.; Yasin, S.; Dumm, M.; Untereiner, G.; Montgomery, L.; Dressel, M. Spin dynamics of the organic linear chain compounds (TMTTF)2X (X = SbF6, AsF6, BF4, ReO4, and SCN). Phys. Rev. B 2011, 83, 205126. [Google Scholar] [CrossRef]
- Yasin, S.; Salameh, B.; Rose, E.; Dumm, M.; von Nidda, H.A.K.; Loidl, A.; Ozerov, M.; Untereiner, G.; Montgomery, L.; Dressel, M. Broken magnetic symmetry due to charge-order ferroelectricity discovered in (TMTTF)2X salts by multifrequency ESR. Phys. Rev. B 2012, 85, 144428. [Google Scholar] [CrossRef]
- Dressel, M.; Dumm, M.; Knoblauch, T.; Köhler, B.; Salameh, B.; Yasin, S. Charge Order Breaks Magnetic Symmetry in Molecular Quantum Spin Chains. Adv. Condens. Matter Phys. 2012, 2012, 398721. [Google Scholar] [CrossRef]
- Matsunaga, N.; Hirose, S.; Shimohara, N.; Satoh, T.; Isome, T.; Yamomoto, M.; Liu, Y.; Kawamoto, A.; Nomura, K. Charge ordering and antiferromagnetism in (TMTTF)2SbF6. Phys. Rev. B 2013, 87, 144415. [Google Scholar] [CrossRef]
- Bertaina, S.; Dutoit, C.E.; Van Tol, J.; Dressel, M.; Barbara, B.; Stepanov, A. Rabi oscillations of pinned solitons in spin chains: A route to quantum computation and communication. Phys. Rev. B 2014, 90, 060404. [Google Scholar] [CrossRef]
- Dutoit, C.E.; Bertaina, S.; Orio, M.; Dressel, M.; Stepanov, A. Charge-ordering induces magnetic axes rotation in organic materials (TMTTF)2X (with X = SbF6, AsF6, and PF6). Low Temp. Phys. 2015, 41, 942–944. [Google Scholar] [CrossRef]
- Dressel, M.; Grüner, G.; Pouget, J.; Breining, A.; Schweitzer, D. Field and frequency dependent transport in the two-dimensional organic conductor α-(BEDT-TTF)2I3. J. Phys. I 1994, 4, 579–594. [Google Scholar] [CrossRef]
- Dressel, M.; Grüner, G.; Pouget, J.; Breining, A.; Schweitzer, D. Non-linear transport in α-(BEDT-TTF)2I3. Synth. Met. 1995, 70, 929–930. [Google Scholar] [CrossRef]
- Ivek, T.; Korin-Hamzić, B.; Milat, O.; Tomić, S.; Clauss, C.; Drichko, N.; Schweitzer, D.; Dressel, M. Collective Excitations in the Charge-Ordered Phase of α-(BEDT-TTF)2I3. Phys. Rev. Lett. 2010, 104, 206406. [Google Scholar] [CrossRef] [PubMed]
- Ivek, T.; Korin-Hamzić, B.; Milat, O.; Tomić, S.; Clauss, C.; Drichko, N.; Schweitzer, D.; Dressel, M. Electrodynamic response of the charge ordering phase: Dielectric and optical studies of α-(BEDT-TTF)2I3. Phys. Rev. B 2011, 83, 165128. [Google Scholar] [CrossRef]
- Ito, A.; Nakamura, Y.; Nakamura, A.; Kishida, H. Measurement of the Nonlinear Conducting States of α-(BEDT-TTF)2I3 Using Electronic Raman Scattering. Phys. Rev. Lett. 2013, 111, 197801. [Google Scholar] [CrossRef] [PubMed]
- Itose, F.; Kawamoto, T.; Mori, T. Collective response to alternating current in the organic conductor a-(bis(ethylenedithio)tetrathiafulvalene)2I3. J. Appl. Phys. 2013, 113, 213702. [Google Scholar] [CrossRef]
- Peterseim, T.; Ivek, T.; Schweitzer, D.; Dressel, M. Electrically induced phase transition in α-(BEDT-TTF)2I3: Indications for Dirac-like hot charge carriers. Phys. Rev. B 2016, 93, 245133. [Google Scholar] [CrossRef]
- Tajima, N.; Fujisawa, J.I.; Naka, N.; Ishihara, T.; Kato, R.; Nishio, Y.; Kajita, K. Photo-induced insulator metal transition in an organic conductor α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2005, 74, 511–514. [Google Scholar] [CrossRef]
- Dearnaley, G.; Stoneham, A.M.; Morgan, D.V. Electrical phenomena in amorphous oxide films. Rep. Prog. Phys. 1970, 33, 1129–1191. [Google Scholar] [CrossRef]
- Mori, T.; Kawamoto, T.; Terasaki, I.; Kakiuchi, T.; Sawa, H. Nonlinear conductivity with an extremely small threshold electric field in the organic conductor (TSM-TTP)(I3)5/3. Phys. Rev. B 2007, 75, 235103. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. (Eds.) Physics of Semiconductor Devices, 3rd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Yu, P.; Cardona, M. (Eds.) Fundamentals of Semiconductors: Physics and Material Properties, 4th ed.; Graduate Texts in Physics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Potember, R.S.; Poehler, T.O.; Cowan, D.O. Electrical switching and memory phenomena in Cu-TCNQ thin films. Appl. Phys. Lett. 1979, 34, 405–407. [Google Scholar] [CrossRef]
- Tokura, Y.; Okamoto, H.; Koda, T.; Mitani, T.; Saito, G. Nonlinear electric transport and switching phenomenon in the mixed-stack charge-transfer crystal tetrathiafulvalene-p-chloranil. Phys. Rev. B 1988, 38, 2215–2218. [Google Scholar] [CrossRef]
- Kumai, R.; Okimoto, Y.; Tokura, Y. Current-induced insulator-metal transition and pattern formation in an organic charge-transfer complex. Science 1999, 284, 1645–1647. [Google Scholar] [CrossRef]
- Inagaki, K.; Terasaki, I.; Mori, H.; Mori, T. Large Dielectric Constant and Giant Nonlinear Conduction in the Organic Conductor θ-(BEDT-TTF)2CsZn(SCN)4. J. Phys. Soc. Jpn. 2004, 73, 3364–3369. [Google Scholar] [CrossRef]
- Sawano, F.; Terasaki, I.; Mori, H.; Mori, T.; Watanabe, M.; Ikeda, N.; Nogami, Y.; Noda, Y. An organic thyristor. Nature 2005, 437, 522–524. [Google Scholar] [CrossRef] [PubMed]
- Dumm, M.; Loidl, A.; Fravel, B.W.; Starkey, K.P.; Montgomery, L.K.; Dressel, M. Electron spin resonance studies on the organic linear-chain compounds (TMTCF)2X (C = S, Se; X = PF6, AsF6, ClO4, Br). Phys. Rev. B 2000, 61, 511–521. [Google Scholar] [CrossRef]
- Monceau, P.; Nad, F.Y.; Brazovskii, S. Ferroelectric Mott-Hubbard Phase of Organic (TMTTF)2X Conductors. Phys. Rev. Lett. 2001, 86, 4080–4083. [Google Scholar] [CrossRef] [PubMed]
- Fujiyama, S.; Nakamura, T. Redistribution of Electronic Charges in Spin-Peierls State in (TMTTF)2AsF6 Observed by 13C NMR. J. Phys. Soc. Jpn. 2006, 75, 014705. [Google Scholar] [CrossRef]
- Oka, Y.; Matsunaga, N.; Nomura, K.; Kawamoto, A.; Yamamoto, K.; Yakushi, K. Charge Order in (TMTTF)2TaF6 by Infrared Spectroscopy. J. Phys. Soc. Jpn. 2015, 84, 114709. [Google Scholar] [CrossRef]
- Pashkin, A.; Dressel, M.; Kuntscher, C.A. Pressure-Induced Deconfinement of the Charge Transport in the Quasi-One-Dimensional Mott Insulator (TMTTF)2AsF6. Phys. Rev. B 2006, 74, 165118. [Google Scholar] [CrossRef]
- Pashkin, A.; Dressel, M.; Hanfland, M.; Kuntscher, C.A. Deconfinement transition and dimensional crossover in the Bechgaard-Fabre salts: Pressure- and temperature-dependent optical investigations. Phys. Rev. B 2010, 81, 125109. [Google Scholar] [CrossRef]
- Ivek, T.; Kovačević, I.; Pinterić, M.; Korin-Hamzić, B.; Tomić, S.; Knoblauch, T.; Schweitzer, D.; Dressel, M. Cooperative dynamics in charge-ordered state of α-(BEDT-TTF)2I3. Phys. Rev. B 2012, 86, 245125. [Google Scholar] [CrossRef]
- Joshi, N.V. Photoconductivity: Art, Science and Technology; Marcel Dekker: New York, NY, USA; Basel, Switzerland, 1990. [Google Scholar]
- Peterseim, T.; Dressel, M.; Dietrich, M.; Polity, A. Optical properties of VO2 films at the phase transition: Influence of substrate and electronic correlations. J. Appl. Phys. 2016, 120, 075102. [Google Scholar] [CrossRef]
- Peterseim, T.; Dressel, M. Molecular Dynamics at Electrical- and Optical-Driven Phase Transitions: Time-Resolved Infrared Studies Using Fourier-Transform Spectrometers. J. Infrared Millim. Terahertz Waves 2017, 38, 104–123. [Google Scholar] [CrossRef]
- De Souza, M.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.P.; Lang, M. Evidence for Lattice Effects at the Charge-Ordering Transition in (TMTTF)2X. Phys. Rev. Lett. 2008, 101, 216403. [Google Scholar] [CrossRef] [PubMed]
- Monceau, P. Electronic crystals: An experimental overview. Adv. Phys. 2012, 61, 325–581. [Google Scholar]
- Jérome, D.; Schulz, H.J. Organic Conductors and Superconductors. Adv. Phys. 1982, 31, 299–490. [Google Scholar] [CrossRef]
- Kagoshima, S.; Nagasawa, H.; Sambongi, T. One-Dimensional Conductors; Springer: Berlin, Germany, 1988. [Google Scholar]
- Organic Conductors; Farges, J.P. (Ed.) Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- Devreese, J.T.; Evrand, R.P.; von Doren, V.E. (Eds.) Highly Conducting One-Dimensional Solids; Plenum Press: New York, NY, USA; London, UK, 1979. [Google Scholar]
- Tanaka, S.; Uchinokura, K. (Eds.) Physics and Chemistry of Quasi One-Dimensional Conductors; Physica B; North-Holland: Amsterdam, The Ntherlands, 1986; Volume 143. [Google Scholar]
- Jérome, D.; Caron, L. (Eds.) Low-Dimensional Conductors and Superconductors; Nato ASI, Series B: Physics; Plenum Press: New York, NY, USA; London, UK, 1987; Volume 155. [Google Scholar]
- Delhaes, P.; Drillon, M. (Eds.) Organic and Inorganic Low-Dimensional Crystalline Materials; Nato ASI, Series B: Physics; Plenum Press: New York, NY, USA; London, UK, 1987; Volume 168. [Google Scholar]
- Saito, G.; Kagoshima, S. (Eds.) The Physics and Chemistry of Organic Superconductors; Springer Proceedings in Physics; Springer: Berlin, Germany, 1990; Volume 51. [Google Scholar]
- Bernier, P.; Lafrant, S.; Bidan, G. (Eds.) Advances in Synthetic Metals: Twenty Years of Progress in Science and Technology; Elsevier: Amsterdam, The Ntherlands, 1999. [Google Scholar]
- Grüner, G. The dynamics of charge-density waves. Rev. Mod. Phys. 1988, 60, 1129–1181. [Google Scholar]
- Dressel, M.; Drichko, N.; Kaiser, S. Collective charge-order excitations. Physica C 2010, 470, S589–S591. [Google Scholar] [CrossRef]
- Iimori, T.; Naito, T.; Ohta, N. Photoinduced Phase Transition in the Organic Conductor α-(BEDT-TTF)2I3 at Temperatures near the Metal–Insulator Phase Transition. Chem. Lett. 2007, 36, 536. [Google Scholar] [CrossRef]
- Iimori, T.; Naito, T.; Ohta, N. Photoresponse of electrical conductivity in an organic superconductor investigated by time-resolved resistance measurements. Physica B 2010, 405, S347–S349. [Google Scholar] [CrossRef]
- Tsutsumi, J.; Yamada, T.; Matsui, H.; Haas, S.; Hasegawa, T. Competition between Charge-Transfer Exciton Dissociation and Direct Photocarrier Generation in Molecular Donor-Acceptor Compounds. Phys. Rev. Lett. 2010, 105, 226601. [Google Scholar] [CrossRef] [PubMed]
- Iimori, T.; Ohta, N. Tuning of Electrical Conductivity by Photoirradiation and Electric Fields. J. Phys. Chem. C 2014, 118, 7251–7260. [Google Scholar] [CrossRef]
- Iwasa, Y.; Koda, T.; Tokura, Y.; Koshihara, S.; Iwasawa, N.; Saito, G. Switching effect in organic charge transfer complex crystals. Appl. Phys. Lett. 1989, 55, 2111–2113. [Google Scholar] [CrossRef]
- Iwasa, Y.; Koda, T.; Koshihara, S.; Tokura, Y.; Iwasawa, N.; Saito, G. Intrinsic negative-resistance effect in mixed-stack charge-transfer crystals. Phys. Rev. B 1989, 39, 10441–10444. [Google Scholar] [CrossRef]
- Ozawa, T.; Tamura, K.; Bando, Y.; Kawamoto, T.; Mori, T.; Terasaki, I. Giant nonlinear conductivity in an organic conductor with a sharp metal-insulator transition: β″-(BEDT-TTF)3(HSO4)2. Phys. Rev. B 2009, 80, 155106. [Google Scholar] [CrossRef]
- Mori, T.; Ozawa, T.; Bando, Y.; Kawamoto, T.; Niizeki, S.; Mori, H.; Terasaki, I. Nonlinear dynamics of conduction electrons in organic conductors. Phys. Rev. B 2009, 79, 115108. [Google Scholar] [CrossRef]
- Dressel, M.; Peterseim, T. Infrared Investigations of the Neutral-Ionic Phase Transition in TTF-CA and Its Dynamics. Crystals 2017, 7, 17. [Google Scholar] [CrossRef]
- Drichko, N.; Hackl, R.; Schlueter, J. Localized states in the Mott insulator κ-(BEDT-TTF)2Cu[N(CN)2]Cl as probed by photoluminescence. Phys. Rev. B 2013, 88, 115109. [Google Scholar] [CrossRef]
- Nasu, K. (Ed.) Relaxations of Excited States and Photo-Induced Structural Phase Transitions. Springer Series in Solid State Science. In Proceedings of the 19th Taniguchi Sumposium, Kashikojima, Japan, 18–23 July 1996; Springer: Berlin, Germany, 1997; Volume 124. [Google Scholar]
- Peterseim, T.; Haremski, P.; Dressel, M. Random-walk annihilation process of photo-induced neutral-ionic domain walls in TTF-CA. Europhys. Lett. 2015, 109, 67003. [Google Scholar] [CrossRef]
- Kassing, R.; Kähler, E. Low-frequency current oscillations in high-resistivity, Au-doped silicon junctions with two Schottky contacts. Phys. Status Solidi (A) 1972, 12, 209–213. [Google Scholar] [CrossRef]
- Holonyak, N.; Bevacqua, S.F. Oscillations in semiconductors due to deep levels. Appl. Phys. Lett. 1963, 2, 71–73. [Google Scholar] [CrossRef]
- Kastrup, J.; Hey, R.; Ploog, K.H.; Grahn, H.T.; Bonilla, L.L.; Kindelan, M.; Moscoso, M.; Wacker, A.; Galán, J. Electrically tunable GHz oscillations in doped GaAs-AlAs superlattices. Phys. Rev. B 1997, 55, 2476–2488. [Google Scholar] [CrossRef]
- Hosoda, M.; Mimura, H.; Ohtani, N.; Tominaga, K.; Watanabe, T.; Fujiwara, K.; Grahn, H.T. Current self-oscillations in photoexcited type-II GaAs-AlAs superlattices. Appl. Phys. Lett. 1996, 69, 500–502. [Google Scholar] [CrossRef]
- Tomlinson, A.M.; Fox, A.M.; Cunningham, J.E.; Jan, W.Y. Photocurrent self-oscillations in a spatially direct GaAs/AlGaAs superlattice. Appl. Phys. Lett. 1999, 75, 2067–2069. [Google Scholar] [CrossRef]
- Mori, T.; Bando, Y.; Kawamoto, T.; Terasaki, I.; Takimiya, K.; Otsubo, T. Giant Nonlinear Conductivity and Spontaneous Current Oscillation in an Incommensurate Organic Superconductor. Phys. Rev. Lett. 2008, 100, 037001. [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Ozawa, T.; Bando, Y.; Kawamoto, T.; Mori, T. Voltage oscillation associated with nonlinear conductivity in the organic conductor α-(BEDT-TTF)2I3. J. Appl. Phys. 2010, 107, 103716. [Google Scholar] [CrossRef]
- Wakita, H.; Ozawa, T.; Bando, Y.; Mori, T. Nonlinear Conductivity in Dicyanoquinonediimine Complexes. J. Phys. Soc. Jpn. 2010, 79, 094703. [Google Scholar] [CrossRef]
- Kishida, H.; Ito, T.; Ito, A.; Nakamura, A. Room-Temperature Current Oscillation Based on Negative Differential Resistance in a One-Dimensional Organic Charge-Transfer Complex. Appl. Phys. Express 2011, 4, 031601. [Google Scholar] [CrossRef]
- Ivek, T.; Čulo, M.; Kuveždić, M.; Korin-Hamzić, B.; Tutiš, E.; Basletić, M.; Mihaljević, B.; Tafra, E.; Löhle, A.; Dressel, M.; et al. Semimetallic and charge-ordered α-(BEDT-TTF)2I3: On the role of disorder in dc transport and dielectric properties. Phys. Rev. B 2017, 96, 123456. [Google Scholar] [CrossRef]
- Lines, M.; Glass, A. (Eds.) Principles and Applications of Ferroelectrics and Related Materials; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 1977. [Google Scholar]
- Glass, A.M.; Abrams, R.L. Study of Piezoelectric Oscillations in Wideband Pyroelectric LiTaO3 Detectors. J. Appl. Phys. 1970, 41, 4455–4459. [Google Scholar] [CrossRef]
- Glass, A.; Auston, D. Excited state dipole moments of impurities in polar crystals. Opt. Commun. 1972, 5, 45–49. [Google Scholar] [CrossRef]
- Glass, A.M.; Auston, D.H. Excited state dipole moments of impurities in pyroelectric crystals and their applications. Ferroelectrics 1974, 7, 187–189. [Google Scholar] [CrossRef]
- Tomic, S.; Dressel, M. Ferroelectricity in molecular solids: A review of electrodynamic properties. Rep. Prog. Phys. 2015, 78, 096501. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, N.; Shiraga, A.; Kondo, R.; Kagoshima, S.; Miyano, K. Photocontrol of Dynamic Phase Transition in the Charge-Density Wave Material K0.3MoO3. Phys. Rev. Lett. 2001, 87, 256401. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, N.; Miyano, K.; Brazovski, S. Optical excitation in the creep phase of plastic charge-density waves. Phys. Rev. B 2005, 71, 075118. [Google Scholar] [CrossRef]
- Tiedje, T.; Haering, R.; Jericho, M.; Roger, W.; Simpson, A. Temperature dependence of sound velocities in TTF-TCNQ. Solid State Commun. 1977, 23, 713–718. [Google Scholar] [CrossRef]
- Chaikin, P.; Tiedje, T.; Bloch, A. Sound velocity measurements on (TMTSF)2PF6. Solid State Commun. 1982, 41, 739–742. [Google Scholar] [CrossRef]
- Zherlitsyn, S.; Bruls, G.; Goltsev, A.; Alavi, B.; Dressel, M. Acoustical properties of (TMTSF)2PF6 in the spin-density-wave ground state. Phys. Rev. B 1999, 59, 13861–13871. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Galigne, J.L.; Liautard, B.; Peytavin, S.; Brun, G.; Fabre, J.M.; Torreiles, E.; Giral, L. Etude Structurale Du Bromure de Tetramethyltetrathiofulvalene, (TMTTF)2Br. Acta Crystallogr. B 1978, 34, 620–624. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peterseim, T.; Dressel, M. Light-Induced Current Oscillations in the Charge-Ordered State of (TMTTF)2SbF6. Crystals 2017, 7, 278. https://doi.org/10.3390/cryst7090278
Peterseim T, Dressel M. Light-Induced Current Oscillations in the Charge-Ordered State of (TMTTF)2SbF6. Crystals. 2017; 7(9):278. https://doi.org/10.3390/cryst7090278
Chicago/Turabian StylePeterseim, Tobias, and Martin Dressel. 2017. "Light-Induced Current Oscillations in the Charge-Ordered State of (TMTTF)2SbF6" Crystals 7, no. 9: 278. https://doi.org/10.3390/cryst7090278





