Ice Microstructure and Fabric of Guliya Ice Cap in Tibetan Plateau, and Comparisons with Vostok3G-1, EPICA DML, and North GRIP
Abstract
:1. Introduction
2. Measurements
3. Results
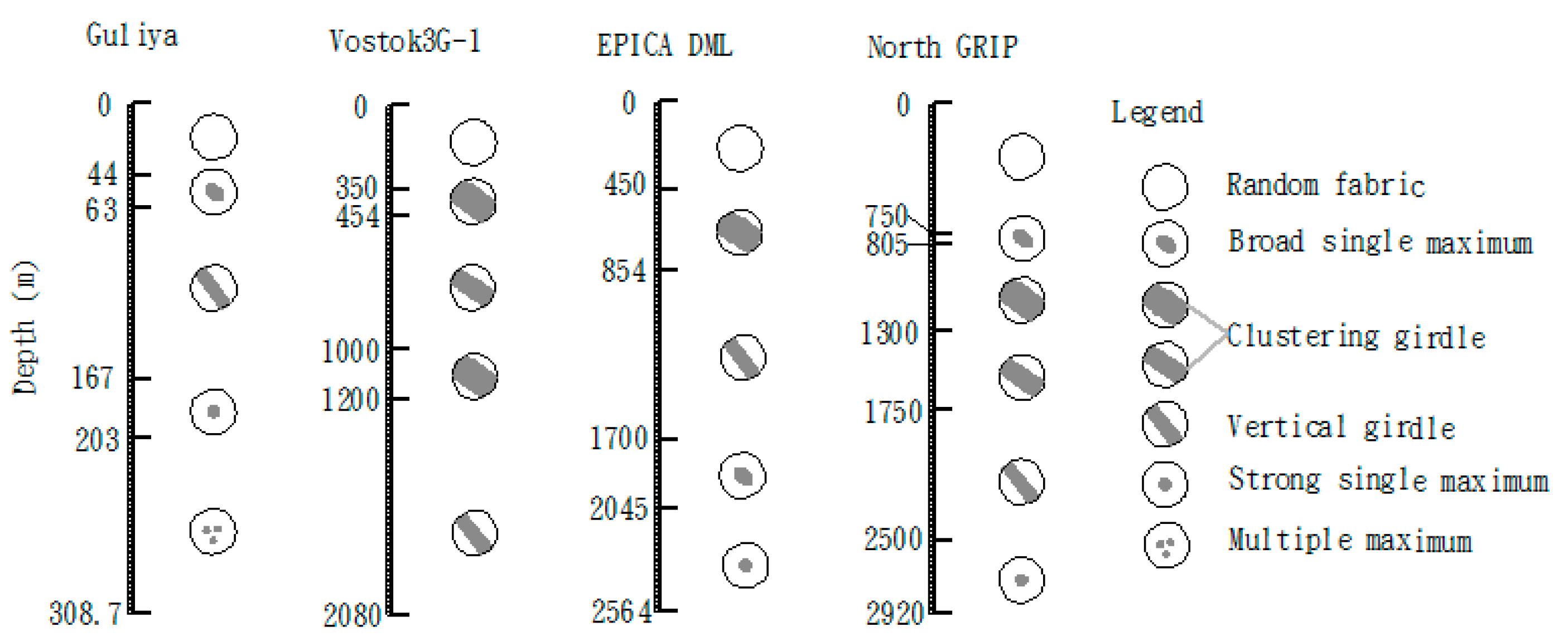
3.1. Microstructure and Fabric Variation with Depth
3.2. Comparison with the Vostok3G-1, EPICA DML, and North GRIP Ice Cores
4. Discussion
4.1. Grain Growth
4.2. Vertical Girdle
4.3. Simple Shear and Single-Maximum
4.4. Polygonization and Migration Recrystallization
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Butter Worth Heinemann: Oxford, UK, 2010. [Google Scholar]
- Kipfstuhl, S.; Hamann, I.; Lambrecht, A.; Freitag, J.; Faria, S.H.; Grigoriev, D.; Azuma, N. Microstructure mapping: A new method for imaging deformation-induced microstructural features of ice on the grain scale. J. Glaciol. 2006, 52, 398–406. [Google Scholar] [CrossRef]
- Thorsteinsson, T. Fabric development with nearest-neighbour interaction and dynamic recrystallization. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Wang, Y.; Kipfstuhl, S.; Azuma, N.; Thorsteinsson, T.; Miller, H. Ice-fabrics study in the upper 1500 m of the Dome C (East Antarctica) deep ice core. Ann. Glaciol. 2003, 37, 97–104. [Google Scholar] [CrossRef]
- Weikusat, I.; Kipfstuhl, S.; Faria, S.H.; Azuma, N.; Miyamoto, A. Subgrain boundaries and related microstructural features in EDML (Antarctica) deep ice core. J. Glaciol. 2009, 55, 461–472. [Google Scholar] [CrossRef]
- Kennedy, J.H.; Pettit, E.C. The response of fabric variations to simple shear and migration recrystallization. J. Glaciol. 2015, 61, 537–550. [Google Scholar] [CrossRef]
- Alley, R.B. Fabrics in polar ice sheets-Development and prediction. Science 1988, 240, 493–495. [Google Scholar] [CrossRef] [PubMed]
- Alley, R.B. Flow-law hypotheses for ice-sheet modeling. J. Glaciol. 1992, 38, 245–256. [Google Scholar] [CrossRef]
- Castelnau, O.; Canova, G.R.; Lebensohn, R.A.; Duval, P. Modeling viscoplastic behavior of anisotropic polycrystalline ice with a self-consistent approach. Acta Mater. 1997, 45, 4823–4834. [Google Scholar]
- Faria, S.H.; Ktitarev, D.; Hutter, K. Modeling evolution of anisotropy in fabric and microstructure of polar ice. Ann. Glaciol. 2002, 35, 545–555. [Google Scholar] [CrossRef]
- Gagliardini, O.; Meyssonnier, J. Lateral boundary conditions for a local anisotropic ice flow model. Ann. Glaciol. 2002, 35, 503–509. [Google Scholar] [CrossRef]
- Gillet-Chaulet, F.; Gagliardini, O.; Meyssonnier, J.; Montagnat, M.; Casteinau, O. A user-friendly anisotropic flow law for ice-sheet modeling. J. Glaciol. 2005, 41, 3–14. [Google Scholar] [CrossRef]
- Durand, G.; Gillet-Chaulet, F.; Svensson, A.; Gagliardini, O.; Kipfstuhl, S.; Meyssonnier, J.; Parrenin, F.; Duval, P.; Dahl-Jensen, D. Change in ice rheology during climate variations-implications for ice flow modeling and dating of the EPICA Dome C core. Clim. Past 2007, 3, 155–167. [Google Scholar] [CrossRef]
- Langway, C.C., Jr.; Shoji, H.; Azuma, N. Crystal size and orientation patterns in the Wisconsin-age ice from Dye 3, Greenland. Ann. Glaciol. 1988, 10, 109–115. [Google Scholar] [CrossRef]
- Thorsteinsson, T.; Kipfstuhl, J.; Miller, H. Microstructures and fabrics in the GRIP ice core. J. Geophys. Res. 1997, 102, 26583–26599. [Google Scholar] [CrossRef]
- Gow, A.J.; Meese, D.A.; Alley, R.B.; Fitzpatrick, J.J.; Anandakrishnan, S.; Woods, G.A.; Elder, B.C. Physical and structural properties of the Greenland ice sheet project 2 ice core: A review. J. Geophys. Res. 1997, 102, 26559–26575. [Google Scholar] [CrossRef]
- Svensson, A.; Schmidt, K.G.; Dahl-Jensen, D.; Johnsen, S.J.; Wang, Y.; Kipfstuhl, J.; Thorsteinsson, T. Properties of ice crystals in North GRIP late-mid Holocene ice. Ann. Glaciol. 2003, 37, 113–118. [Google Scholar] [CrossRef]
- EPICA Community Members. Eight glacial cycles from an Antarctic ice core. Nature 2004, 429, 623–628. [Google Scholar]
- Durand, G.; Svensson, A.; Persson, A.; Gagliardini, O.; Gillet-Chaulet, F.; Sjolte, J.; Montagnat, M.; Dahl-Jensen, D. Evolution of the microstructure along the EPICA Dome C Ice Core. Low Temp. Sci. 2009, 68, 91–105. [Google Scholar]
- Seddik, H.; Greve, R.; Placidi, L.; Hamann, I.; Gagliardini, O. Application of a continuum-mechanical model for the flow of anisotropic polar ice to the EDML core, Antarctica. J. Glaciol. 2008, 54, 631–642. [Google Scholar] [CrossRef]
- Azuma, N.; Wang, Y.; Yoshida, Y.; Narita, H.; Hondoh, T.; Shoji, H.; Watanabe, O. Crystallographic analysis of the Dome Fuji ice core. In Physics of Ice Core Records; Hondoh, T., Ed.; Hokkaido University Press: Sapporo, Japan, 2000. [Google Scholar]
- Huang, M.H.; Gao, X.; Jin, Z.M. Ice microstructures and their development of an ice core extracted from the Guliya ice cap, Kunlun Mountains. J. Glaciol. Geocryol. 1995, 17, 39–44. [Google Scholar]
- Lipenkov, V.Y.; Barkov, N.I.; Duval, P.; Pimienta, P. Crystalline texture of the 2083 m ice core at Vostok Station, Antarctica. J. Glaciol. 1989, 35, 392–398. [Google Scholar] [CrossRef]
- EPICA Community Members. One-to-one coupling of glacial climate variability in Greenland and Antarctica. Nature 2006, 444, 195–197. [Google Scholar]
- Huybrechts, P.; Rybak, O.; Pattyn, F.; Ruth, U.; Steinhage, D. Ice thinning, upstream advection, and non-climatic biases for the upper 89% of the EDML ice core from a nested model of the Antarctic ice sheet. Clim. Past 2007, 3, 577–589. [Google Scholar] [CrossRef]
- Weikusat, I.; Kipfstuhl, S.; Azuma, N.; Faria, S.H.; Miyamoto, A. Deformation microstructures in an Antarctic ice core (EDML) and in experimentally deformed artificial ice. Low Temp. Sci. 2009, 68, 115–123. [Google Scholar]
- Wang, Y.; Thorsteinsson, T.; Kipfstuhl, J.; Miller, H.; Dahl-Jensen, D.; Shoji, H. A vertical girdle fabric in the North GRIP deep ice core, North Greenland. Ann. Glaciol. 2002, 35, 515–520. [Google Scholar] [CrossRef]
- Dahl-Jensen, D.; Gundestrup, N.S.; Miller, H.; Watanabe, O.; Johnsen, S.J.; Steffensen, J.P.; Clausen, H.B.; Svensson, A.; Larsen, L.B. The North GRIP deep drilling programme. Ann. Glaciol. 2002, 35, 1–4. [Google Scholar] [CrossRef]
- Durand, G.; Persson, A.; Samyn, D.; Svensson, A. Relation between neighbouring grains in the upper part of the North GRIP ice core: Implications for rotation recrystallization. Earth Planet. Sci. Lett. 2008, 265, 666–671. [Google Scholar] [CrossRef]
- Faria, S.H.; Weikusat, I.; Azuma, N. The microstructure of polar ice. Part I: Highlights from ice core research. J. Struct. Geol. 2014, 61, 2–20. [Google Scholar] [CrossRef]
- Faria, S.H.; Weikusat, I.; Azuma, N. The microstructure of polar ice. Part II: State of the art. J. Struct. Geol. 2014, 61, 21–49. [Google Scholar] [CrossRef]
- Yao, T.; Jiao, K.; Zhang, X.; Yang, Z. Study on the glaciology of Guliya ice cap. J. Glaciol. Geocryol. 1992, 14, 233–241. [Google Scholar]
- Thompson, L.G.; Yao, T.; Davis, M.E.; Henderson, K.A.; Thompson, E.; Lin, P.N.; Beer, J.; Synal, H.A.; Cole-Dai, J.; Bolzan, J.F. Tropical climate instability: The Last Glacial Cycle from a Qinghai–Tibetan ice core. Science 1997, 276, 1821–1825. [Google Scholar] [CrossRef]
- Pickering, F.B. The Basis of Quantitative Metallography; Metals and Metallurgy Trust for the Institute of Metallurgical Technicians: Whetsone, UK, 1976. [Google Scholar]
- Langway, C.C., Jr. Ice Fabrics and the Universal Stage; SIPRE Technical Report 62; SIPRE: Vicksburg, MS, USA, 1958. [Google Scholar]
- Kamb, B. Refraction corrections for universal stage measurements. I. Uniaxial crystals. Am. Mineral. 1962, 47, 227–245. [Google Scholar]
- Wilson, C.J.L.; Russell-Head, D.S.; Sim, H.M. The application of an automated fabric analyzer system to the textural evolution of folded ice layers in shear zones. Ann. Glaciol. 2003, 37, 7–17. [Google Scholar] [CrossRef]
- Wang, Y.; Azuma, N. A new automatic ice-fabric analyzer which uses imageanalysis techniques. Ann. Glaciol. 1999, 29, 155–162. [Google Scholar]
- Faria, S.H.; Freitag, J.; Kipfstuhl, S. Polar ice structure and the integrity of ice core paleoclimate records. Quat. Sci. Rev. 2010, 29, 338–351. [Google Scholar] [CrossRef]
- Kipfstuhl, S.; Faria, S.H.; Azuma, N.; Freitag, J.; Hamann, I.; Kaufmann, P.; Miller, H.; Weiler, K.; Wilhelms, F. Evidence of dynamic recrystallization in polar firn. J. Geophys. Res. 2009, 114, B05204. [Google Scholar] [CrossRef]
- Faria, S.H.; Kipfstuhl, S.; Lambrecht, A. The EPICA-DML Deep Ice Core; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Alley, R.B.; Gow, A.J.; Meese, D.A. Mapping c-axis fabrics to study physical processes in ice. J. Glaciol. 1995, 41, 197–203. [Google Scholar] [CrossRef]
- Duval, P.; Castelnau, O. Dynamic recrystallization of ice in polar ice sheets. J. Phys. IV (Paris) 1995. [Google Scholar] [CrossRef]
- De la Chapelle, S.; Castelnau, O.; Lipenkov, V.; Duval, P. Dynamic recrystallization and microstructure development in ice as revealed by the study of deep ice cores in Antarctica and Greenland. J. Geophys. Res. 1998, 103, 5091–5105. [Google Scholar] [CrossRef]
- Duval, P.; Arnaud, L.; Brissaud, O.; Montagnat, M.; de la Chapelle, S. Deformation and recrystallization processes of ice from polar ice sheets. Ann. Glaciol. 2000, 30, 83–87. [Google Scholar] [CrossRef]
- Montagnat, M.; Duval, P. Rate controlling processes in the creep of polar ice, influence of grain boundary migration associated with recrystallization. Earth Planet. Sci. Lett. 2000, 183, 179–186. [Google Scholar] [CrossRef]
- Fujita, S.; Nakawo, M.; Mae, S. Orientation of the 700-m Mizuho core and its strain history. In Proceedings of the Ninth Symposium on Polar Meteorology and Glaciology, Tokyo, Japan, 1 December 1986; Matsuda, T., Ed.; National Institute of Polar Research: Tokyo, Japan, 1987; pp. 122–131. [Google Scholar]
- Pimienta, P.; Duval, P. Rate controlling processes in the creep of polar glacier ice. J. Phys. (Paris) 1987. [Google Scholar] [CrossRef]
- Weikusat, I.; Miyamoto, A.; Faria, S.H.; Kipfstuhl, S.; Azuma, N.; Hondoh, T. Subgrain boundaries in Antarctic ice quantified by X-ray Laue diffraction. J. Glaciol. 2011, 57, 85–94. [Google Scholar] [CrossRef]
- Azuma, N.; Higashi, A. Formation processes of ice fabric pattern in ice sheets. Ann. Glaciol. 1985, 6, 130–134. [Google Scholar] [CrossRef]
- Barkov, N.I. Rezul’taty issledovaniya skvazhiny i ledyanogo kerna na Stantsii Vostok v 1970–1972 [Results of the study of the borehole and ice core at Vostok Station, 1970–1972]. Materialy Glyatsiologicheskikh Issledovaniy Khronika Ohsuzhdeniya 1973, 22, 77–81. [Google Scholar]
- Dahl-Jensen, D.; Gundestrup, N.S. Constitutive properties of ice at Dye 3, Greenland. In The Physical Basis of Ice Sheet Modelling—Symposium, Vancouver; International Association of Hydrological Sciences Publication: Wallingford, UK, 1987; Volume 17, pp. 31–43. [Google Scholar]
- Shoji, H.; Langway, C.C., Jr. Flow-law parameters of Dye 3, Greenland, deep ice core. Ann. Glaciol. 1988, 10, 146–150. [Google Scholar] [CrossRef]
- Paterson, W.S.B. Why ice-age ice is sometimes “soft”. Cold Reg. Sci. Technol. 1991, 20, 75–98. [Google Scholar] [CrossRef]
- Dahl-Jensen, D.; Thorsteinsson, T.; Alley, R.B.; Shoji, H. Flow properties of the ice from the Greenland Ice Core Project ice core: The reason for folds? J. Geophys. Res. Atmos. 1997, 1022, 26831–26840. [Google Scholar] [CrossRef]
- Dahl-Jensen, D.; Gundestrup, N.; Keller, K.R.; Johnsen, S.J.; Gogineni, S.P.; Allen, C.T.; Chuah, T.S.; Miller, H.; Kipstuhl, S.; Waddington, E.D. A search in north Greenland for a new ice-core drill site. J. Glaciol. 1997, 43, 300–306. [Google Scholar] [CrossRef]
- Budd, W.F.; Jacka, T.H. A review of ice rheology for ice sheet modelling. Cold Reg. Sci. Technol. 1989, 16, 107–144. [Google Scholar] [CrossRef]
- Bons, P.D.; Jessell, M.W. Micro-shear zones in experimentally deformed octachloropropane. J. Struct. Geol. 1999, 21, 323–334. [Google Scholar] [CrossRef]
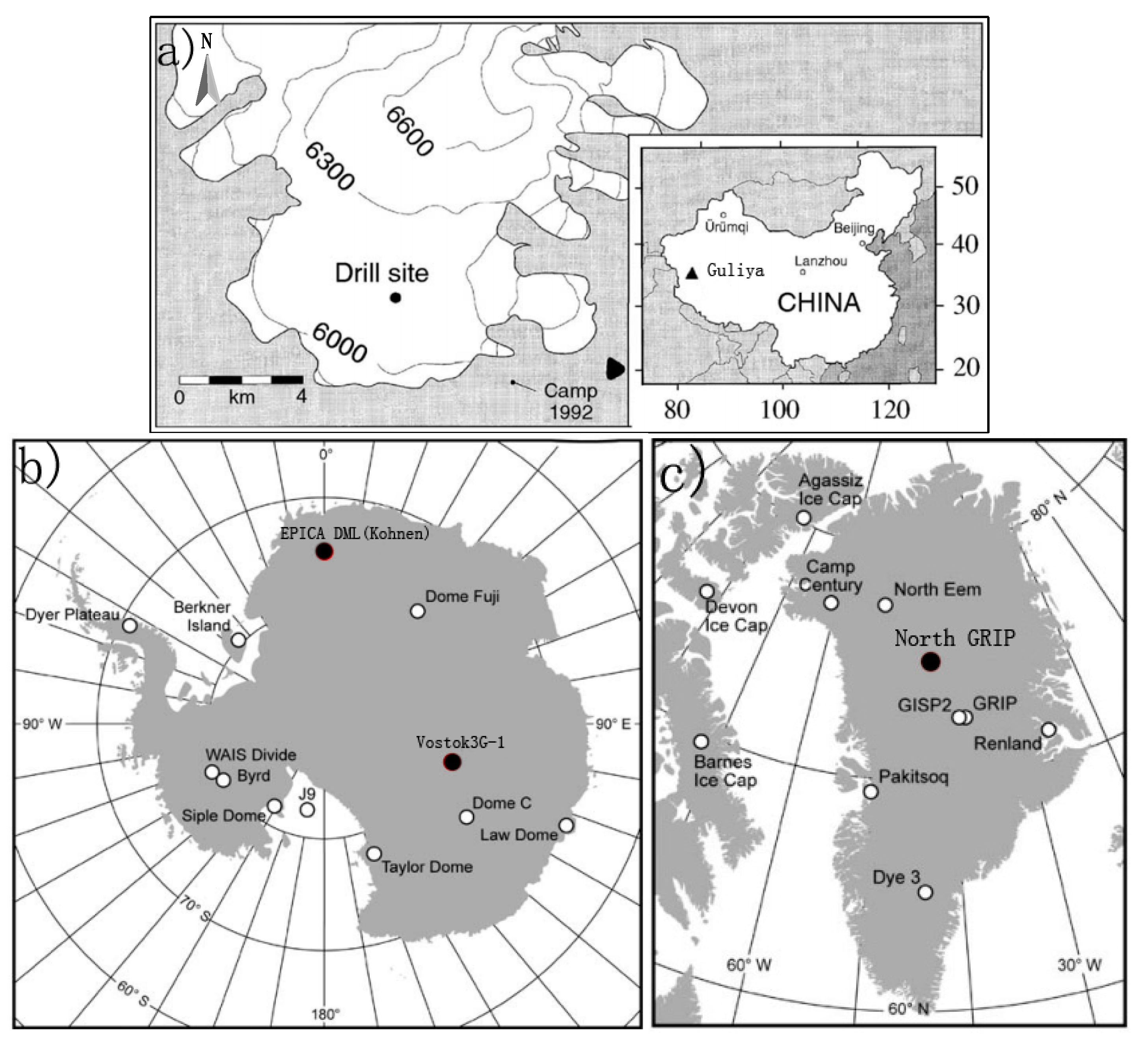

| Ice Core Project | Geographical Site | Position | Elevation (m) | Topography | Ann. M S T(°C)/T 10 m B S or B (°C) † | Snow Accumulation Rate | Ice Core Length (m)/Ice Thickness (m) |
|---|---|---|---|---|---|---|---|
| Guliya | Western Kunlun Mountains, Tibetan Plateau, China | 35°21′ N, 81°31′ E | 6200 | Ice cap top-flatted | −17.8/−15.6 (−10 m) | 25.2 cm a−1 | 308.7/c.350 |
| Vostok 3G-1 | Former Soviet Antarctic station, Antarctica | 78 °28′ S, 106 °48′ E | 3488 | Above an ice lake | −55.5/−3 (Bottom) | 2.2–2.5 g cm−2·a−1 | 2083/c.3700 |
| EPICA DML | Interior of DML, Antarctica | 75°00′ S, 0°04′ E | 2892 | Ridge/Divide | c.−45/c.−3 (Bottom) | 6.4 g cm−2 a−1 | c.2774/2782 |
| North GRIP | Ice ridge 325 km N-NW of Summit, Greenland | 75°01′ N, 42°03′ W | 2917 | Ridge/Divide | −32/−2.4 (Bottom) | 19.5 cm a−1 | 3085/3085 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Kipfstuhl, S.; Huang, M. Ice Microstructure and Fabric of Guliya Ice Cap in Tibetan Plateau, and Comparisons with Vostok3G-1, EPICA DML, and North GRIP. Crystals 2017, 7, 97. https://doi.org/10.3390/cryst7040097
Li Y, Kipfstuhl S, Huang M. Ice Microstructure and Fabric of Guliya Ice Cap in Tibetan Plateau, and Comparisons with Vostok3G-1, EPICA DML, and North GRIP. Crystals. 2017; 7(4):97. https://doi.org/10.3390/cryst7040097
Chicago/Turabian StyleLi, Yuan, Sepp Kipfstuhl, and Maohuan Huang. 2017. "Ice Microstructure and Fabric of Guliya Ice Cap in Tibetan Plateau, and Comparisons with Vostok3G-1, EPICA DML, and North GRIP" Crystals 7, no. 4: 97. https://doi.org/10.3390/cryst7040097





