The Orbital Angular Momentum Modes Supporting Fibers Based on the Photonic Crystal Fiber Structure
Abstract
:1. Introduction
2. Design of Fibers Supporting OAM Modes
2.1. OAM Modes in Optical Fiber
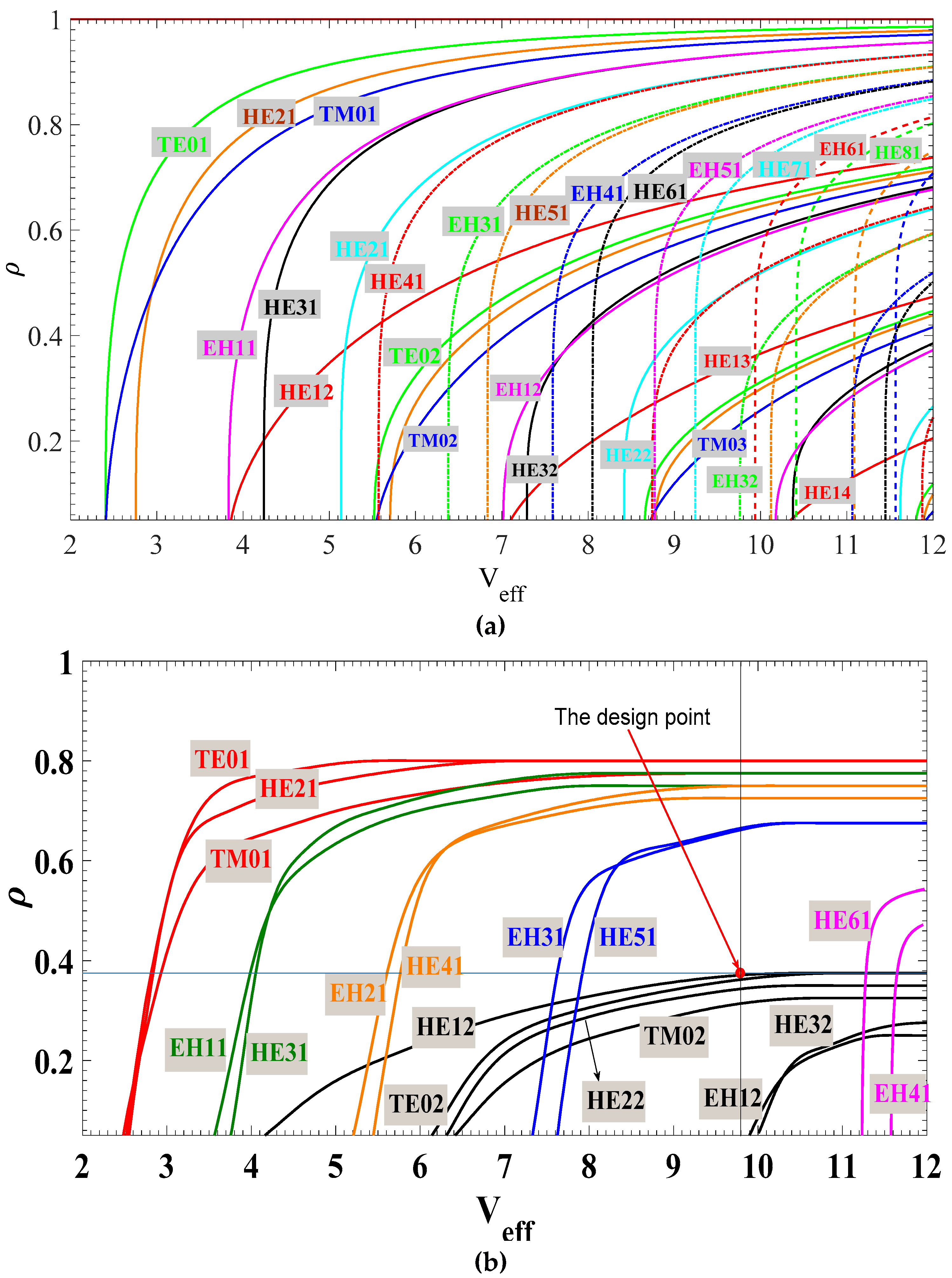
2.2 Design Requirements of OAM Fibers
3. Review of OAM Fibers Based on Photonic Crystal Fiber Structure
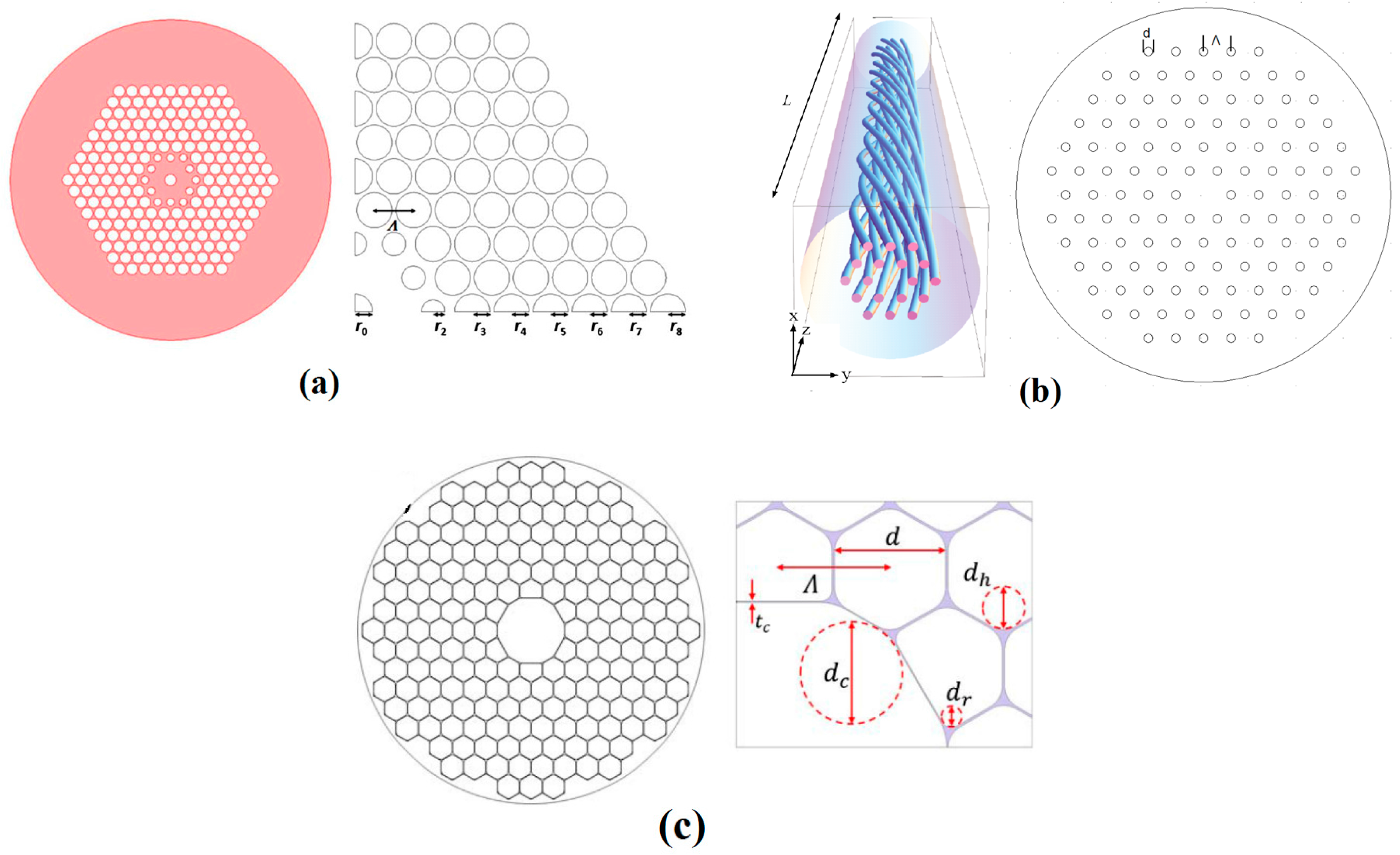
3.1. Hexagonal Lattice PCFs
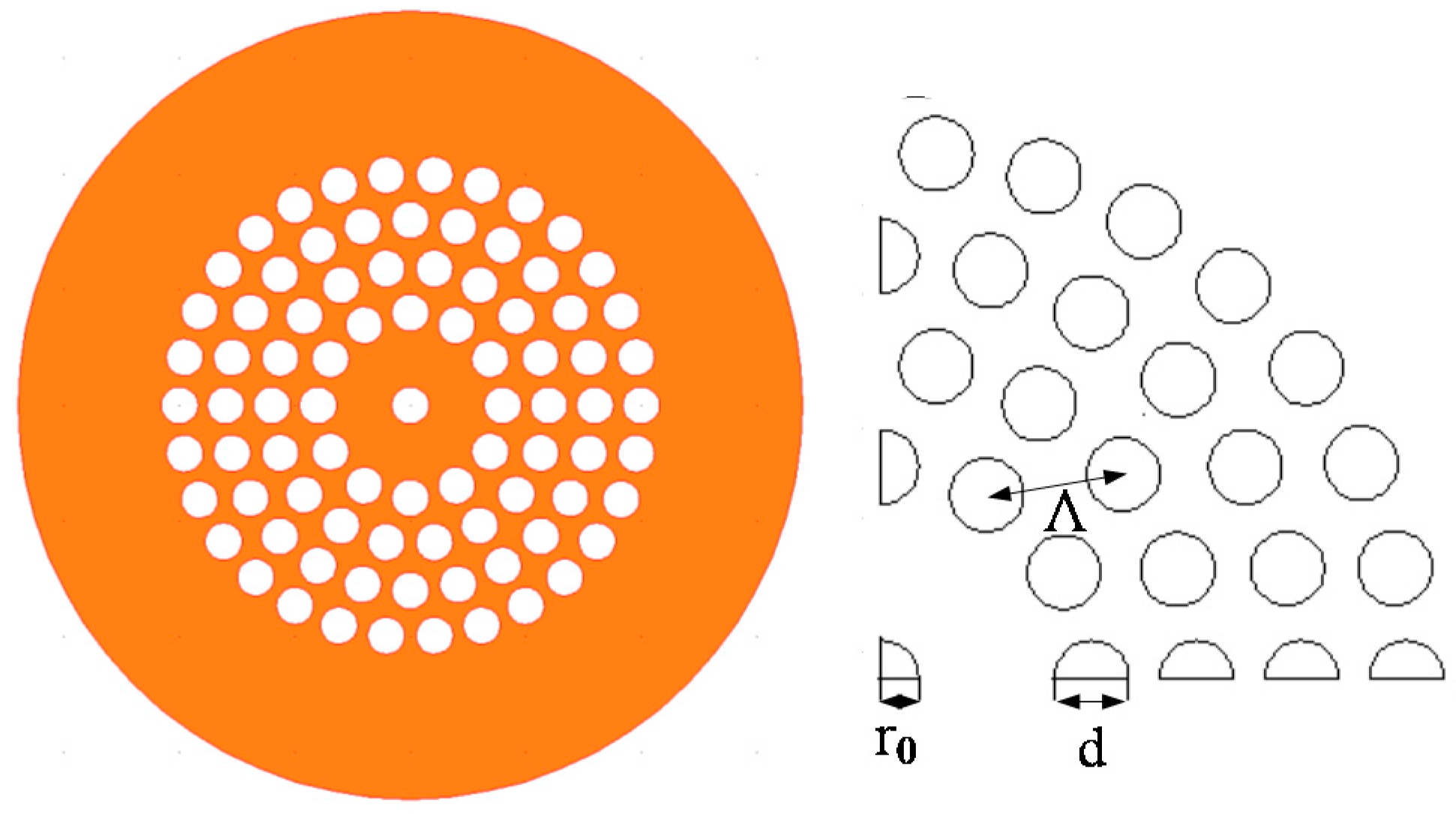
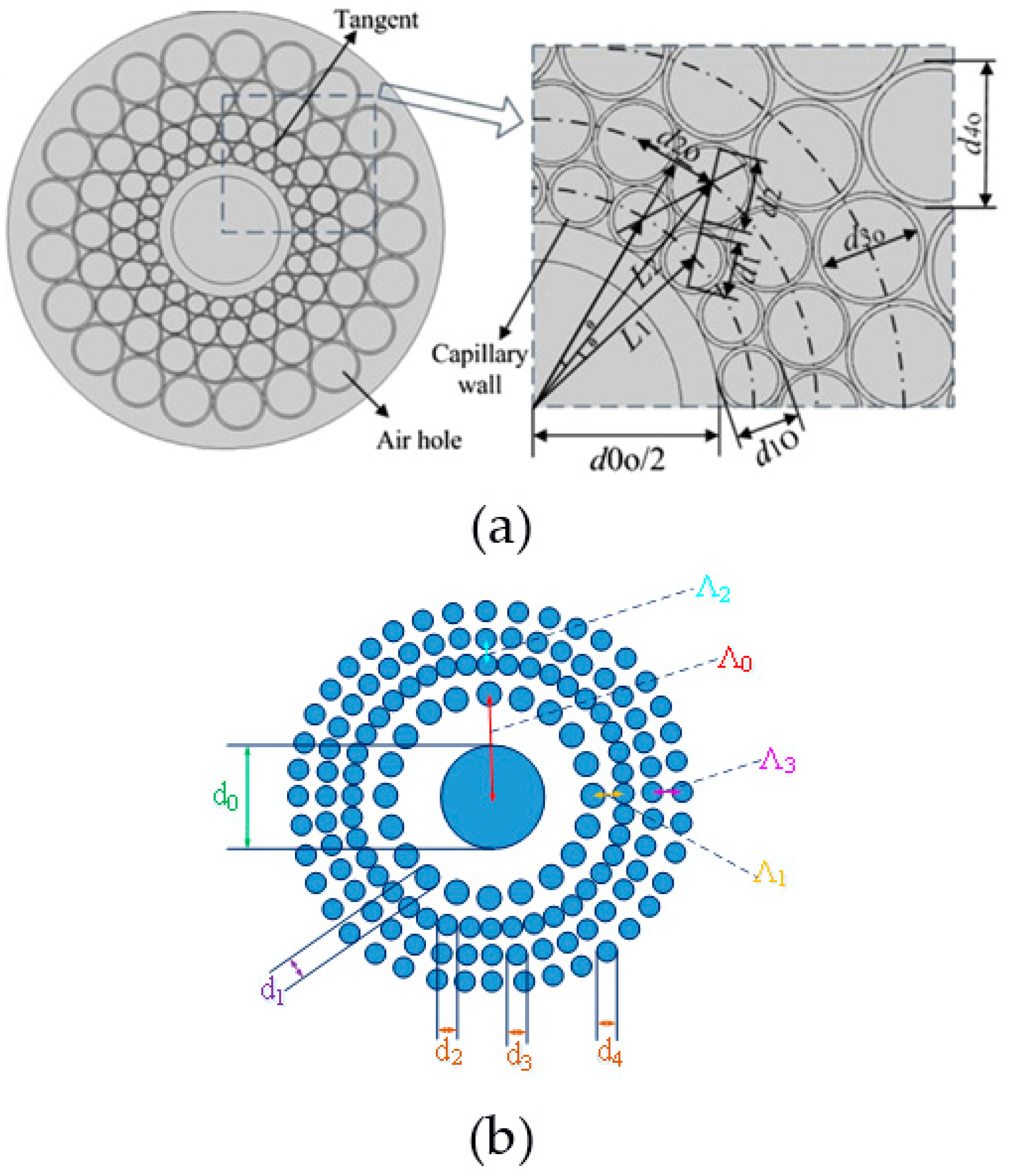
3.2 Circular PCFs
3.3 Kagome Lattice PCFs
4. Challenges and Prospects
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photon. 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Zhu, B.; Taunay, T.F.; Fishteyn, M.; Liu, X.; Chandrasekhar, S.; Yan, M.F.; Fini, J.M.; Monberg, E.M.; Dimarcello, F.V. 112-Tb/s Space-division multiplexed DWDM transmission with 14-b/s/Hz aggregate spectral efficiency over a 76.8-km seven-core fiber. Opt. Exp. 2011, 19, 16665–16671. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, J.; Puttnam, B.J.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T.; Imamura, K.; Inaba, H.; Mukasa, K.; et al. 19-core fiber transmission of 19×100×172-Gb/s SDMWDM-PDM-QPSK signal at 305 Tb/s. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 4–8 March 2012; pp. 1–3, paper PDP5C.1. [Google Scholar]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, S.; Kristensen, P.; Yan, M.F. Generation and propagation of radially polarized beams in optical fibers. Opt. Lett. 2009, 34, 2525–2527. [Google Scholar] [CrossRef] [PubMed]
- Yao, A.M.; Padgett, M. J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photon. 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Golowich, S. Asymptotic theory of strong spin-orbit coupling in optical fiber. Opt. Lett. 2014, 39, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Randel, S.; Ryf, R.; Sierra, A.; Winzer, P.J.; Gnauck, A.H.; Bolle, C.A.; Essiambre, R.-J.; Peckham, D.W.; McCurdy, A.; Lingle, R. 6×56-Gb/s mode-division multiplexed transmission over 33-km few-mode fiber enabled by 6×6 MIMO equalization. Opt. Exp. 2011, 19, 16697–16707. [Google Scholar] [CrossRef] [PubMed]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Sierra, A.; Mumtaz, S.; Esmaeelpour, M.; Burrows, E.C.; Essiambre, R.-J.; Winzer, P.J.; et al. Mode-division multiplexing over 96 km of few-mode fiber using coherent 6×6 Mimo processing. J. Lightwave Technol. 2012, 30, 521–531. [Google Scholar] [CrossRef]
- Li, S.; Wang, J. Multi-orbital-angular-momentum multi-ring fiber for high-density space-division multiplexing. IEEE Photon. J. 2013, 5, 7101007. [Google Scholar]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [PubMed]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photon. 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Carpenter, J.A.; Thomsen, B.C.; Wilkinson, T.D. Optical vortex based mode division multiplexing over graded-index multimode fibre. In Proceedings of the Optical Fiber Communication Conference/National Fiber Optic Engineers Conference, Anaheim, CA, USA, 17–21 March 2013; pp. 1–3. [Google Scholar]
- Ramachandran, S.; Kristensen, P. Optical vortices in fiber. Nanophotonics 2013, 2, 455–474. [Google Scholar] [CrossRef]
- Yan, Y.; Yue, Y.; Huang, H.; Yang, J.; Chitgarha, M.R.; Ahmed, N.; Tur, M.; Dolinar, S.J.; Willner, A.E. Efficient generation and multiplexing of optical orbital angular momentum modes in a ring fiber by using multiple coherent inputs. Opt. Lett. 2012, 37, 3645–3647. [Google Scholar] [CrossRef] [PubMed]
- Yue, Y.; Yan, Y.; Ahmed, N.; Yang, J.; Zhang, L.; Ren, Y.; Huang, H.; Birnbaum, K.M.; Erkmen, B.I.; Dolinar, S.; et al. Mode properties and propagation effects of optical orbital angular momentum (OAM) modes in a ring fiber. IEEE Photon. J. 2012, 4, 535–543. [Google Scholar]
- Gregg, P.; Kristensen, P.; Golowich, S.; Olsen, J.; Steinvurzel, P.; Ramachandran, S. Stable transmission of 12 oam states in air-core fiber. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 9–14 June 2013; pp. 1–3. [Google Scholar]
- Brunet, C.; Ung, B.; Messaddeq, Y.; LaRochelle, S.; Bernier, E.; Rusch, L.A. Design of an optical fiber supporting 16 OAM modes. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 9–13 March 2014; pp. 1–3. [Google Scholar]
- Brunet, C.; Ung, B.; Bélanger, P.A.; Messaddeq, Y.; LaRochelleand, S.; Rusch, L.A. Vector mode analysis of ring-core fibers: Design tools for spatial division multiplexing. J. Lightwave Technol. 2014, 32, 4046–4057. [Google Scholar] [CrossRef]
- Brunet, C.; Vaity, P.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Design, fabrication and validation of an OAM fiber supporting 36 states. Opt. Express 2014, 22, 26117–26127. [Google Scholar] [CrossRef] [PubMed]
- Brunet, C.; Ung, B.; Vaity, P.; Wang, L.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Design of a family of ring-core fibers for OAM transmission studies. Opt. Express 2015, 23, 10553–10563. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, S.; Gregg, P.; Kristensen, P.; Golowich, S.E. On the scalability of ring fiber designs for OAM multiplexing. Opt. Express 2015, 23, 3721–3730. [Google Scholar] [CrossRef] [PubMed]
- Gregg, P.; Kristensen, P.; Ramachandran, S. Conservation of orbital angular momentum in air core optical fibers. Optica 2015, 2, 2334–2536. [Google Scholar] [CrossRef]
- Brunet, C.; Rusch, L.A. Optical fibers for the transmission of orbital angular momentum modes. Opt. Fiber Technol. 2016, 31, 172–177. [Google Scholar] [CrossRef]
- Russell, P.S.J. Photonic crystal fibers. J. Lightwave Technol. 2006, 24, 4729–4749. [Google Scholar] [CrossRef]
- Benabid, F.; Russell, P.S.J. Hollow core photonic crystal fibers: progress and prospects. Proc. SPIE 2005, 5733, 176–189. [Google Scholar]
- Mortensen, N.A.; Nielsen, M.D.; Folkenberg, J.R.; Petersson, A.; Simonsen, H.R. Improved large-mode-area endlessly single-mode photonic crystal fibers. Opt. Lett. 2003, 28, 393–395. [Google Scholar] [CrossRef] [PubMed]
- Amezcua-Correa, R.; Broderick, N.G.; Petrovich, M.N.; Poletti, F.; Richardson, D.J. Design of 7 and 19 cells core air-guiding photonic crystal fibers for low-loss, wide bandwidth and dispersion controlled operation. Opt. Express 2007, 15, 17577–17586. [Google Scholar] [CrossRef] [PubMed]
- Lægsgaard, J.; Roberts, P.J.; Bache, M. Tailoring the dispersion properties of photonic crystal fibers. Opt. Quant. Electron. 2007, 39, 995–1008. [Google Scholar] [CrossRef]
- Yue, Y.; Zhang, L.; Yan, Y.; Ahmed, N.; Yang, J.; Huang, H.; Ren, Y.; Dolinar, S.; Tur, M.; Willner, A.E. Octave-spanning supercontinuum generation of vortices in an As2S3 ring photonic crystal fiber. Opt. Lett. 2012, 37, 1889–1891. [Google Scholar] [CrossRef] [PubMed]
- Wong, G.K.; Kang, M.S.; Lee, H.W.; Biancalana, F.; Conti, C.; Weiss, T.; Russell, P.S. Excitation of orbital angular momentum resonances in helically twisted photonic crystal fiber. Science 2012, 337, 446–449. [Google Scholar] [CrossRef] [PubMed]
- Xi, X.M.; Wong, G.K.L.; Frosz, M.H.; Babic, F.; Ahmed, G.; Jiang, X.; Euser, T.G.; Russell, P.S.J. Orbital angular-momentum-preserving helical Bloch modes in twisted photonic crystal fiber. Optica 2014, 1, 165–169. [Google Scholar] [CrossRef]
- Xi, X.M.; Weiss, T.; Wong, G.K.L.; Biancalana, F.; Barnett, S.M.; Padgett, M.J.; Russell, P.S.J. Optical activity in twisted solid-core photonic crystal fibers. Phys. Rev. Lett. 2013, 110, 143903. [Google Scholar] [CrossRef] [PubMed]
- Russell, P.S.J.; Bevarat, R.; Wong, G.K.L. Helically twisted photonic crystal fibres. Phil. Trans. R. Soc. A 2017, 375, 20150440. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Li, Y.; Han, Y.; Deng, D.; Guo, Z.; Gao, J.; Sun, Q.; Liu, Y.; Qu, S. Excitation and separation of vortex modes in twisted air-core fiber. Opt. Express 2016, 24, 8310–8316. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, W.; Xi, L.; Tang, X.; Tian, W.; Zhang, X.; Zhang, X. Design of a Circular Photonic Crystal Fiber Supporting OAM Modes. In Proceedings of the Asia Communications and Photonics Conference, Hong Kong, China, 19–23 November 2015; pp. 1–3. [Google Scholar]
- Chen, C.; Zhou, G.; Zhou, G.; Xu, M.; Hou, Z.; Xia, C.; Yuan, J. A multi-orbital-angular-momentum multi-ring micro-structured fiber with ultra-high-density and low-level crosstalk. Opt. Commun. 2016, 368, 27–33. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, C.; Xu, M.; Xia, C.; Hou, Z. Design and Analysis of a Microstructure Ring Fiber for Orbital Angular Momentum Transmission. IEEE Photon. J. 2016, 8, 7802512. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W.; Xi, L.; Tang, X.; Zhang, X.; Zhang, X. A New Type Circular Photonic Crystal Fiber for Orbital Angular Momentum Mode Transmission. IEEE Photon. Technol. Lett. 2016, 28, 1426–1429. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, Y.; Luo, A.; Cui, H.; Luo, Z.; Xu, W. Photonic crystal fiber for supporting 26 orbital angular momentum modes. Opt. Express 2016, 24, 17285–17291. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Ren, G.; Lian, Y.; Zhu, B.; Tang, M.; Zhao, Y.; Jian, S. Broadband orbital angular momentum transmission using a hollow-core photonic bandgap fiber. Opt. Lett. 2016, 41, 3591–3594. [Google Scholar] [CrossRef] [PubMed]
- Tian, W.; Zhang, H.; Zhang, X.; Xi, L.; Zhang, W.; Tang, X. A circular photonic crystal fiber supporting 26 OAM modes. Opt. Fiber Technol. 2016, 30, 184–189. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W.; Xi, L.; Tang, X.; Zhang, X. A New Design of a Circular Photonic Crystal Fiber Supporting 42 OAM Modes. In Proceedings of the Australian Conference on Optical Fibre Technology, Sydney, Australia, 5–8 September 2016; pp. 1–2. [Google Scholar]
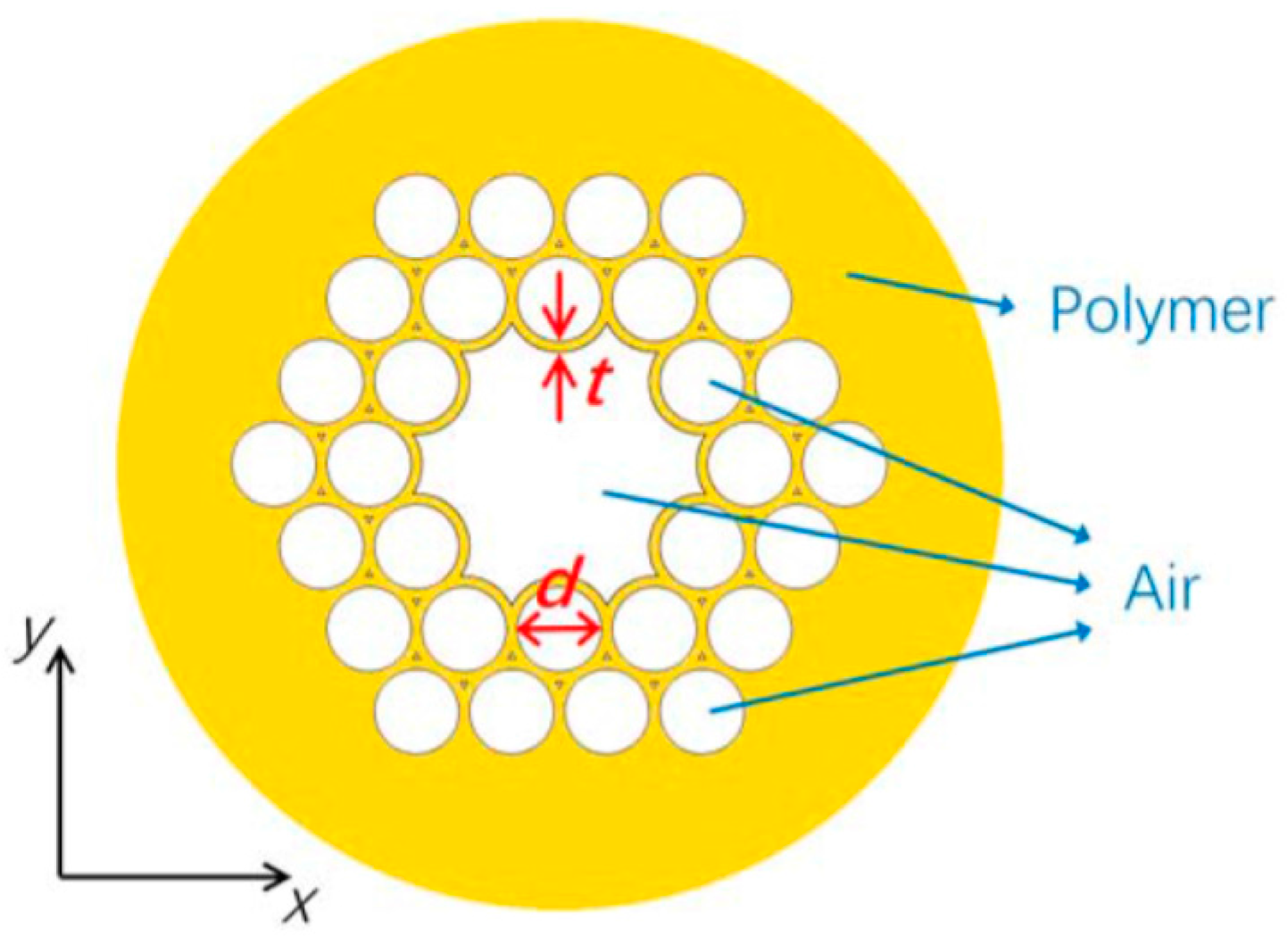
- Li, H.; Ren, G.; Zhu, B.; Gao, Y.; Yin, B.; Wang, J.; Jian, S. Guiding terahertz orbital angular momentum beams in multimode Kagome hollow-core fibers. Opt. Lett. 2017, 42, 179–183. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, X.; Li, H.; Deng, Y.; Zhang, X.; Xi, L.; Tang, X.; Zhang, W. A design strategy of the circular photonic crystal fiber supporting good quality orbital angular momentum mode transmission. Opt. Commun. 2017, 397, 59–66. [Google Scholar] [CrossRef]
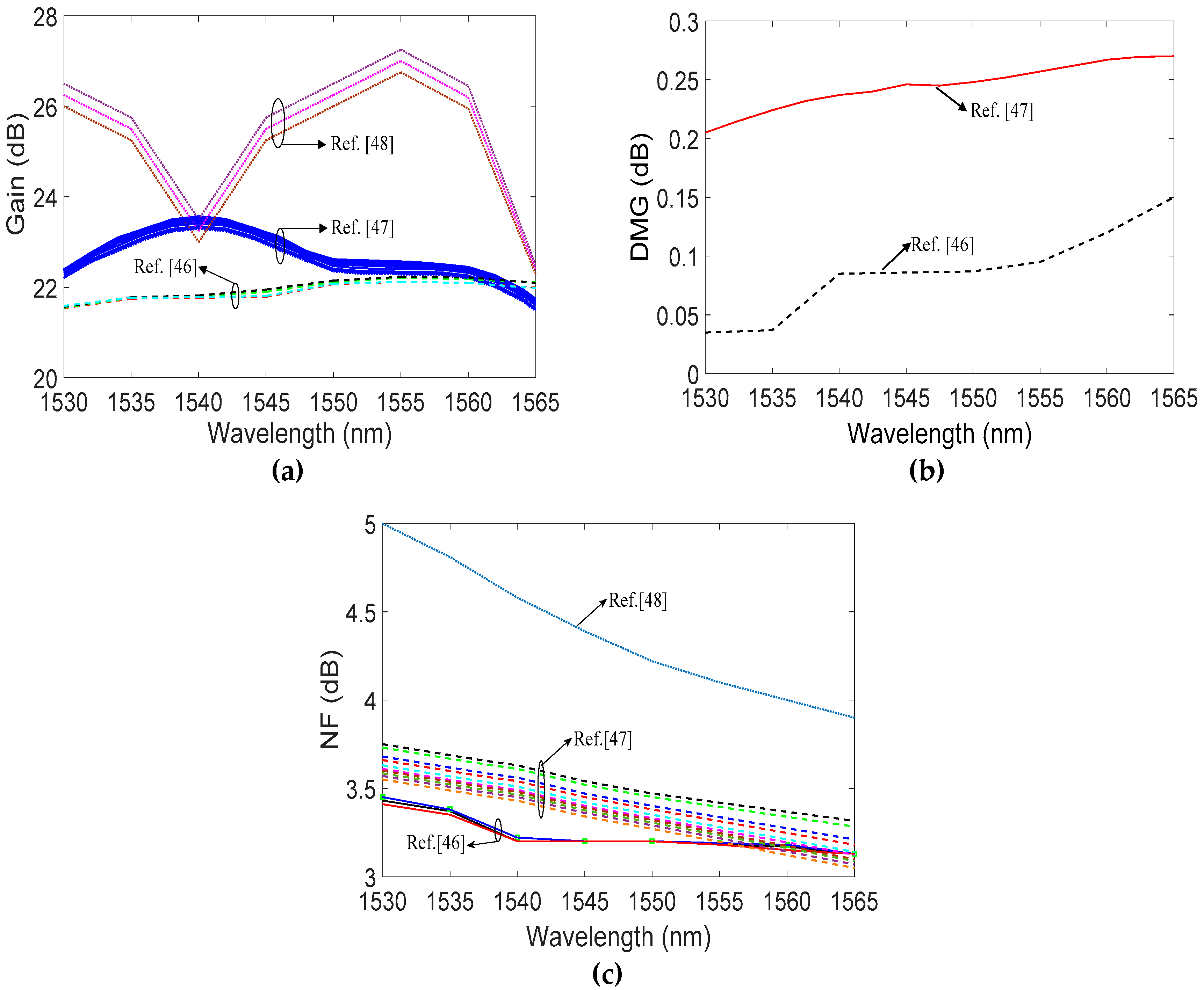
- Deng, Y.; Zhang, H.; Li, H.; Tang, X.; Zhang, X.; Xi, L.; Zhang, W.; Zhang, X. Erbium-doped amplification in circular photonic crystal fiber supporting orbital angular momentum modes. Appl. Opt. 2017, 56, 1748–1752. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Xia, F.; Li, S.; Wang, J. Design of Orbital Angular Momentum (OAM) Erbium Doped Fiber Amplifier with Low Differential Modal Gain. In Proceedings of the Optical Fiber Communication Conference/National Fiber Optic Engineers Conference, Los Angeles, CA, USA, 24–26 March 2015; pp. 1–3. [Google Scholar]
- Kang, Q.; Gregg, P.; Jung, Y.; Lim, E.L.; Alam, S.; Ramachandran, S.; Richardson, D.J. Amplification of 12 OAM Modes in an air-core erbium doped fiber. Opt. Express 2015, 23, 28341–28348. [Google Scholar] [CrossRef] [PubMed]

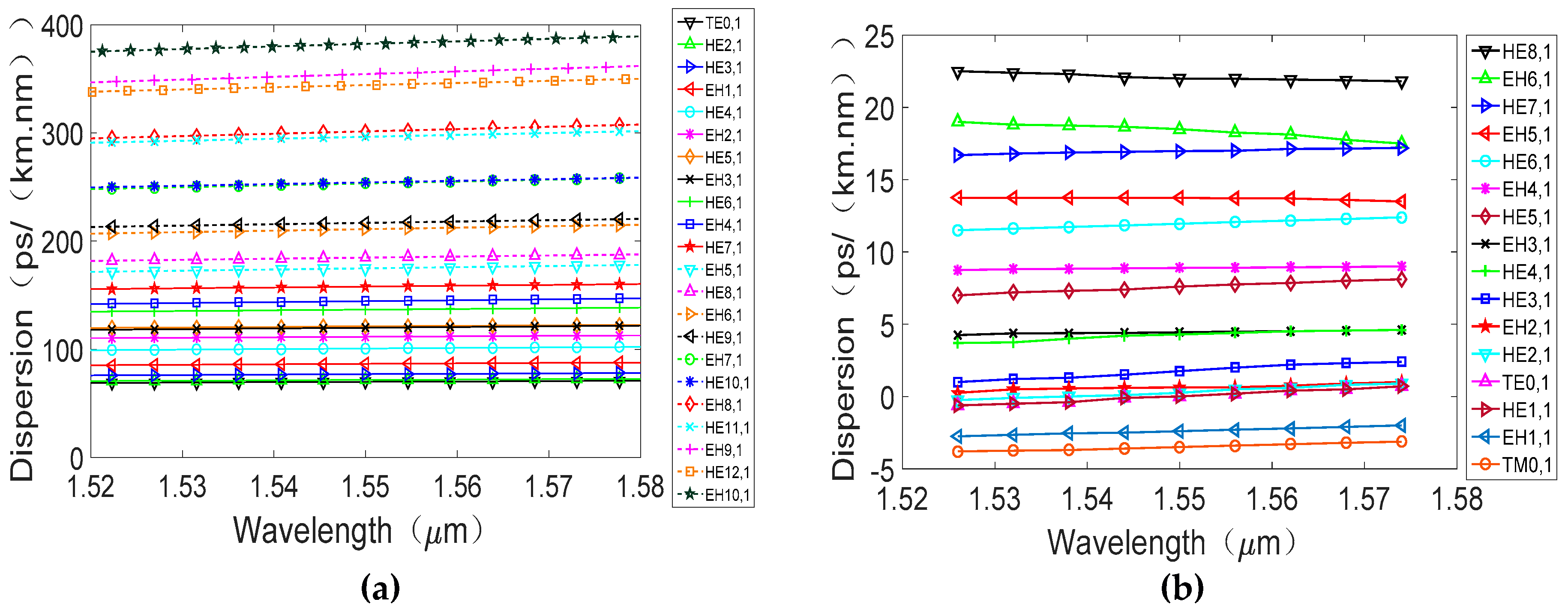
| C-PCF 1# | C-PCF 2# | C-PCF 3# | |
|---|---|---|---|
| Refractive index | Silica: n = 1.444, air holes: n = 1.000; ncl = 1.231, (nco/ncl)2 = 1.376 | ||
| Common parameters | Air hole pitch: Λ = 2.0 μm, diameters of the air holes: dn = 1.6 μm, dn/Λ = 0.8 | ||
| Outer radius | r = 3.2 μm | r = 5.2 μm | r = 7.2 μm |
| Effective normalized frequency | Veff = 9.79 | Veff = 15.91 | Veff = 22.04 |
| OAM modes | l = 1~4, 14 states | l = 1~7, 26 states | l = 1~11, 42 states |
| Bandwidth | 560 nm (1.25–1.81 μm) | 480 nm (1.25–1.73 μm) | 460 nm (1.25–1.71 μm) |
| Year | Author | Lattice | Material | Number of OAM Modes | Supported OAM Modes | Bandwidth | Reference |
|---|---|---|---|---|---|---|---|
| 2012 | Y. Yue et al. | Hexagon | As2S3 | 2 | OAM1,1 | 522 nm | [30] |
| 2012 | G.K.L.Wong et al. | Hexagon | SiO2 | 1 | OAM+1,1 ( OAM−1,1) | [31] | |
| 2015 1 | H. Zhang et al. | Circular | SiO2 | 10 | OAM1,1 OAM2,1 OAM3,1 | [36] | |
| 2016 | C. Chen et al. | Circular | SiO2 | 34 | OAM1,1, …, OAM9,1 | 60 nm | [37] |
| 2016 | G. Zhou et al. | Circular | SiO2 | 34 | OAM1,1, …, OAM9,1 | [38] | |
| 2016 2 | H. Zhang et al. | Circular | SiO2 | 14 | OAM1,1, …, OAM4,1 | 560 nm | [39] |
| 2016 | W. Tian et al. | Circular | SiO2 | 26 | OAM1,1, …, OAM7,1 | 750 nm | [42] |
| 2016 | Z. Hu et al. | Circular | As2S3 | 26 | OAM1,1, …, OAM7,1 | [40] | |
| 2017 | H. Li et al. | Hexagon(PBG) | SiO2 | 2 | OAM1,1 | 240 nm | [41] |
| 2017 | H. Li et al. | Kagome | Polymer | 3 | , , | 0.25 THz | [44] |
| 2017 | H. Zhang et al. | Circular | SiO2 | 42 | OAM1,1, …, OAM11,1 | 460 nm | [45] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, X.; Li, H.; Deng, Y.; Xi, L.; Tang, X.; Zhang, W. The Orbital Angular Momentum Modes Supporting Fibers Based on the Photonic Crystal Fiber Structure. Crystals 2017, 7, 286. https://doi.org/10.3390/cryst7100286
Zhang H, Zhang X, Li H, Deng Y, Xi L, Tang X, Zhang W. The Orbital Angular Momentum Modes Supporting Fibers Based on the Photonic Crystal Fiber Structure. Crystals. 2017; 7(10):286. https://doi.org/10.3390/cryst7100286
Chicago/Turabian StyleZhang, Hu, Xiaoguang Zhang, Hui Li, Yifan Deng, Lixia Xi, Xianfeng Tang, and Wenbo Zhang. 2017. "The Orbital Angular Momentum Modes Supporting Fibers Based on the Photonic Crystal Fiber Structure" Crystals 7, no. 10: 286. https://doi.org/10.3390/cryst7100286






