2.1. PZN-PT and PMN-PT
It is always a great challenge to grow single crystals of complex compounds. The successful growth of PMN-PT and PZN-PT single crystals became a real breakthrough that started a new era in relaxor-PT-based ferroelectric crystal research. Binary PMN-PT and PZN-PT solid-solutions, which present a perovskite phase, can be synthesized from complex oxide systems of PbO-MgO(ZnO)-Nb
2O
5-TiO
2. However, the formation of the parasitic pyrochlore phase was the most problematic in the crystal growth process, causing instability in crystallization and generating defects and polycrystals [
15,
16]. Several other challenges to the growth of large single crystals include volatilization of PbO, the high melting point of the oxides and the composition segregation of the solid solutions [
15,
16].
PMN-PT and PZN-PT crystals were first grown by the flux method, which demonstrated ultrahigh piezoelectric coefficients and strain levels with low hysteresis [
4,
10]. The flux method is a type of high temperature solution growth, which is based on the spontaneous nucleation that occurs when supersaturation happens in a slow cooling process. The method has been broadly adopted in the growth of new crystal materials, especially those that melt incongruently or volatilize seriously before reaching melting temperature [
17]. Difficulty in crystallization orientation control, slow growth rate, small crystal size and flux inclusions are common limitations of the flux growth method. To overcome these limitations, several improved high temperature solution growth methods, including top-seeded solution growth (TSSG) and solution-Bridgman growth, have been developed based on the basic flux method for the growth of PMN-PT and PZN-PT crystals [
18,
19]. In top-seeded solution growth, by introducing a perovskite seed crystal into the solution, it became possible to trigger single nucleation and control the crystallization orientation to obtain large-sized single crystals. The solution-Bridgman growth combines the flux growth and the vertical Bridgman growth, which is more suitable for growing large crystals. Currently, PMN-PT and PZN-PT single crystals grown by high temperature solution methods have reached the sizes of 35 mm in edge length or two inches in diameter.
The effective crystal growth technologies have been explored extensively after the extraordinary piezoelectric performance of PMN-PT and PZN-PT crystals were revealed. DTA study indicated that PMN-PT melts congruently [
16,
20,
21], suggesting the possibility of growing PMN-PT crystals from the melt directly. These studies also showed that PMN-PT has a more stable perovskite phase and exhibits less of a tendency to form the parasitic pyrochlore phase compared to PZN-PT. By pre-synthesizing PMN-PT and using sealed Pt crucibles to prevent the volatilization of PbO at high temperature, PMN-PT single crystals have been grown directly from the melt using the Bridgman method [
22,
23]. Compared to flux growth, the Bridgman technique can grow large-sized single crystal boules along specific crystallographic orientations with a higher growth rate, which can potentially reduce the cost of PMN-PT crystals, to be competitive with the high quality piezoelectric ceramics used in high-end applications.
It was indicated that the formation of inclusions/voids, spontaneous nucleation, crystallization orientation control and reduction of the composition variation are the major challenges in the growth of large-sized and high quality PMN-PT crystals by the Bridgman process [
15,
16,
22,
23]. Owing to the large difference in melting point and density between each oxide, especially between PbO (
Tm = 886 °C, ρ = 9.53 g/cm
3) and MgO (
Tm = 2852 °C, ρ = 3.58 g/cm
3), it is usually difficult to get a homogeneousperovskite phase by directly mixing the oxides without the presence of a minor amount of the pyrochlore phase [
16]. Pre-synthesized PMN-PT using a modified columbite precursor method has been proven to be the most efficient way to eliminate the pyrochlore phase [
24]. In this method, instead of using oxides, MgO and Nb
2O
5, columbite precursor, MgNb
2O
6, which has a similar structure to the perovskite phase, was synthesized by solid-state reaction and used as the raw material to bypass the intermediate pyrochlore phase reaction. The high-quality PMN-PT compound can also be synthesized by different routes, including the coprecipitation method [
25] and the molten salt synthesis method [
26]. The inclusions/voids formation, dendrite growth and polycrystal formation are all largely attributed to the pyrochlore phase formed in the raw material; however, such defects can be also induced by other factors, such as the non-stoichiometry of the raw material, impurities and too fast of a growth rate.
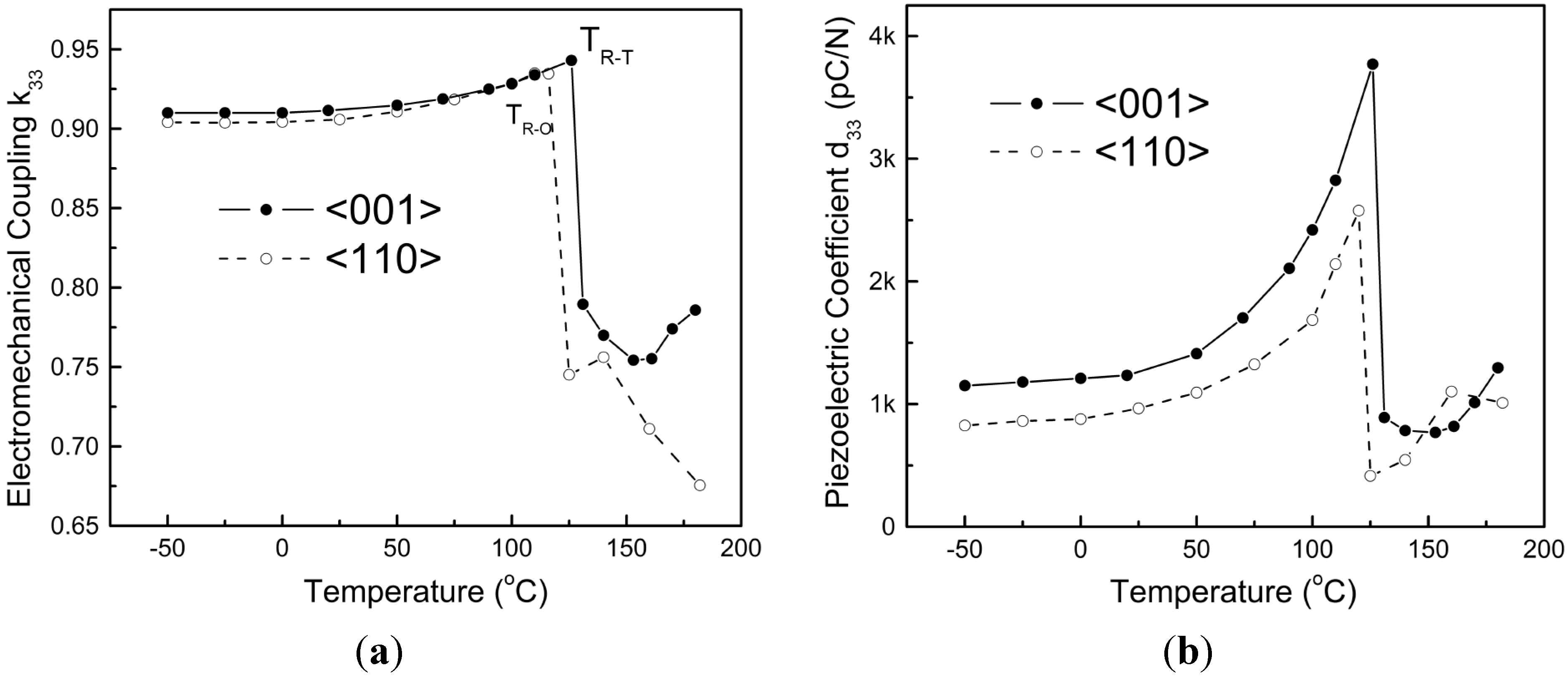
Since PMN-PT crystal exhibits the highest piezoelectric response along the <001> orientation, <001>-cut wafers have become highly demanded [
16]. Owing to the inevitable axial composition segregation of this solid-solution in the Bridgman process [
22,
27], highly uniform (001) wafers can only be produced by successful and repeatable <001>-oriented crystal growth. However, since PMN-PT presents the slowest growth rate along the low-index <001> orientation (R
<001> < R
<110> < R
<111>), the Bridgman growth of bulk PMN-PT crystal along <001> becomes the most challenging. Spontaneous nucleation is apt to happen and dominate the crystallization process, forming polycrystals instead of a single crystal. The growth process in Bridgman growth has to be finely controlled to avoid the spontaneous nucleation on the solid-liquid interface.
Significant progress has been made in the Bridgman growth of PMN-PT in recent years. High-quality and large-sized PMN-PT crystals without macro-defects have been successfully grown along different crystallographic orientations, including <001>, <110> and <111>. Currently, <001>-oriented PMN-PT crystals with a 100-mm diameter are commercially available.
Figure 2 shows a 100-mm diameter crystal boule grown along <001> and the (001) wafers cut from it.
Figure 2.
A 100-mm diameter Pb(Mg1/3Nb2/3)O3-PbTiO3 (PMN-PT) crystal grown along <001> (a) and 100-mm diameter (001) wafers (in comparison with 75-mm diameter ones); (b) courtesy of TRS Technologies Inc., State College, PA, USA.
Figure 2.
A 100-mm diameter Pb(Mg1/3Nb2/3)O3-PbTiO3 (PMN-PT) crystal grown along <001> (a) and 100-mm diameter (001) wafers (in comparison with 75-mm diameter ones); (b) courtesy of TRS Technologies Inc., State College, PA, USA.
Although the Bridgman method is a very promising technique, the composition segregation issue has to be addressed. Since PMN-PT is a complete solid-solution system, as shown by its high temperature phase diagram, it inevitably exhibits an inhomogeneous composition distribution along crystal boules grown by the Bridgman method [
22,
27], resulting in the variation of dielectric and piezoelectric properties along the growth direction. Even though the composition variation along the growth direction can be restrained to some degree by applying a higher growth rate and a lower axial temperature gradient across the solid-liquid interface, it can never be eliminated due to the thermodynamic nature of the solid solution system [
27]. The composition distribution can be simulated by a well-established equation used for describing the composition segregation behavior in solid solution systems during the normal solidification process [
17]:
Where
ke is the effective segregation coefficient,
Cs and
C0 the solute concentration in the crystal and the starting melt and
g the solidified fraction.
It was verified by chemical analysis that, except for Pb, all other elements in PMN-PT crystals exhibit composition segregation during crystal growth, with effective segregation coefficients of Nb and Mg larger than one, while that of Ti is smaller than one.
Figure 3 compares the piezoelectric property (
d33) variation with the composition distributions measured by EPMA and simulated by the above equation [
28], which shows the region between two peaks roughly corresponding to a PT (PbTiO
3) concentration of 31% to 35%, which is basically consistent with the broad MPB region between rhombohedral and tetragonal phases proposed by Guo
et al. [
29,
30]. The simulated effective segregation coefficient of Ti in this run was around 0.83. Studies show that the mixed phases, including metastable ferroelectric monoclinic (FE
m) and ferroelectric orthorhombic (FE
o) phases, are possibly present in this region [
29,
30,
31].
Figure 3.
Comparison of piezoelectric property (
d33) variation with the composition distribution. Reprinted with permission from [
28]. Copyright 2008 CRC Press.
Figure 3.
Comparison of piezoelectric property (
d33) variation with the composition distribution. Reprinted with permission from [
28]. Copyright 2008 CRC Press.
As described above, the existence of the composition segregation-induced longitudinal property variation is one of the main disadvantages of Bridgman growth. Although the <001>-oriented Bridgman growth can produce desirable (001) wafers with very high lateral uniformity in each wafer, it cannot eliminate the wafer-to-wafer variation. Usually, only a portion of each boule possesses the required PT composition range that meets the desired piezoelectric and dielectric properties. To further reduce or even eliminate the composition segregation in PMN-PT crystals, several innovative crystal growth methods were proposed, including, zone leveling [
16], continuous feeding Bridgman growth [
32] and solid-state crystal growth [
28,
33].
Zone leveling, a type of zone-melting crystal growth method, has been developed to produce a uniform, or level, distribution of solute in polycrystals and single crystals in many applications [
34], which was proposed as an alternative method to prevent composition segregation in PMN-PT crystal growth [
16]. Theoretically, zone leveling can produce a flat composition distribution except for the initial and last frozen regions (zones). The zone melting growth of PMN-PT crystals was conducted in both RF induction heated and resistance heated furnaces [
27,
28]. Constant composition at PT = 32% was observed over ~60 mm of total boule length (~80 mm) in a zone-leveled boule compared with the constantly changing composition usually observed in Bridgman grown crystals [
27].
As proposed, continuous feeding Bridgman is a modified Bridgman method, in which PMN powder or pellets are charged slowly into the melt during crystal growth to keep the concentration of Mg, Nb and Ti constant. The challenge of this method is to minimize the thermal disturbance to the melt, as well as to prevent PbO from evaporation during the feeding operation. This technique was demonstrated successfully by the growth of 80-mm diameter PMN-PT crystals [
35]. Curie temperature (
TC) was controlled to a range of 130–138 °C in a 116-mm-long portion of such a crystal, which is much narrower than that in the crystals grown by the regular Bridgman technique (usually 120–160 °C). As
TC is strongly correlated to the composition, it is indicated that the crystal possesses a much narrower composition distribution along the length.
Solid-state crystal growth (SSCG) is based on an abnormal grain growth in the sintering of polycrystalline ceramics, in which a small number of grains is grow quickly by consuming surrounding fine matrix grains [
28]. In SSCG of a PMN-PT crystal, a small BZT (Ba(Zr
0.1Ti
0.9)O
3) single crystal is used as a seed to control the nucleation of abnormal grains, so that a large single crystal can be obtained in the polycrystalline matrix. Since the polycrystalline ceramic matrix is not melted, the composition segregation does not happen. The other advantages that the SSCG method provides include low process temperature, no need for Pt crucibles and crystal growth of incongruently melting compositions. However, in this process, it is hard to completely eliminate the porosity in the crystals, which may affect the mechanical and optical properties [
33]. Currently, PMN-PT crystals larger than 50 × 50 × 10 mm
3 can be produced by the SSCG method [
28].
2.2. High TC Relaxor-PT Binary Crystals
Even though large-sized and high-quality PMN-PT crystals can be grown directly from the melt, their low ferroelectric-to-ferroelectric phase transition temperatures and low coercive field restrict their applications largely. The piezoelectric/dielectric properties of rhombohedral-phase PMN-PT crystals have a strong temperature dependence. For instance, PMN-29%PT exhibit a 52% change in the dielectric constant from room temperature to 55 °C. This change negatively affects the transducer impedance and matching circuitry and, therefore, the power delivery system. Furthermore, the rhombohedral-to-tetragonal ferroelectric phase transition temperature (
Trt) for PMN-PT crystals with near MPB compositions is as low as 85 °C to 95 °C, which becomes the maximum applicable temperature. In addition to the temperature stability, PMN-PT crystals have a coercive field as low as 2–2.5 kV/cm, limiting the amplitude of the driving field and the power output. High Curie temperature piezoelectric crystals are desired to expand the operational temperature and electric field, to reduce the properties’ temperature dependence and to increase the acoustic power output [
36].
Table 1 lists broadly investigated binary relaxor-PT systems, among which the Pb(Sc
1/2Nb
1/2) O
3-PbTiO
3 (PSN-PT), Pb(In
1/2Nb
1/2)O
3-PbTiO
3 (PIN-PT) and Pb(Yb
1/2Nb
1/2)O
3-PbTiO
3 (PYN-PT) were found to possess relatively high Curie temperatures near their MPB compositions [
5,
37,
38]. Henceforth, numerous research has focused on these binary systems in single crystal form in order to achieve high performance over a wide temperature range [
24,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50].
Table 1.
Morphotropic phase boundaries in perovskite Pb(BIBII)O3-PT ceramic systems.
Table 1.
Morphotropic phase boundaries in perovskite Pb(BIBII)O3-PT ceramic systems.
| Binary System | PT (x) at MPB | TC (°C) at MPB | TR-T (°C) at MPB |
|---|
| (1−x)Pb(Zn1/3Nb2/3)O3-xPbTiO3 (PZN-PT) | ~0.09 | ~180 | 95 |
| (1−x)Pb(Mg1/3Nb2/3)O3-xPbTiO3 (PMN-PT) | ~0.33 | ~150 | 80 |
| (1−x)Pb(Ni1/3Nb2/3)O3-xPbTiO3 (PNN-PT) | ~0.40 | ~130 | – |
| (1−x)Pb(Co1/3Nb2/3)O3-xPbTiO3 (PCN-PT) | ~0.38 | ~250 | – |
| (1−x)Pb(Sc1/2Nb1/2)O3-xPbTiO3 (PSN-PT) | ~0.43 | ~260 | 100 |
| (1−x)Pb(Sc1/2Ta1/2)O3-xPbTiO3 (PST-PT) | ~0.45 | ~205 | – |
| (1−x)Pb(Fe1/2Nb1/2)O3-xPbTiO3 (PFN-PT) | ~0.07 | ~140 | – |
| (1−x)Pb(In1/2Nb1/2)O3-xPbTiO3 (PIN-PT) | ~0.37 | ~320 | 120 |
| (1−x)Pb(Yb1/2Nb1/2)O3-xPbTiO3 (PYN-PT) | ~0.50 | ~360 | 160 |
| (1−x)Pb(Mg1/2W1/2)O3-xPbTiO3 (PMW-PT) | ~0.55 | ~60 | – |
| (1−x)Pb(Co1/2W1/2)O3-xPbTiO3 (PCW-PT) | ~0.45 | ~310 | – |
PSN-PT single crystals with MPB compositions were successfully grown by the flux method using PbO-B
2O
3 as the flux [
39,
40,
41]. The growth temperature range and B
2O
3 ratio in the flux are deemed very important because of the perovskite stability. The perovskite crystal size obtained was found to be 2–15 mm in length. PSN-33%PT crystals were reported to possess a high Curie temperature,
TC ~ 206 °C (30–50 °C higher than PMN-PT and PZN-PT systems), while the electromechanical coupling factor (
k33) and dielectric constant were found to be only 72% and 960, respectively.
Single crystals of PIN-PT and their electromechanical properties were also studied. It was reported that PIN-28PT crystals could be grown using the flux method with PbO-PbF
2-B
2O
3. The obtained crystals were 20 × 10 × 5 mm
3 in size, which is much larger compared to PSN-PT crystals [
42]. The Curie temperature was reported to be 260 °C with a rhombohedral-to-tetragonal phase transition temperature,
Trt, around 100 °C. The electromechanical coupling in the longitudinal mode (
k33) was estimated to be 85% at room temperature [
42]. The same research group also reported growing PIN-PT crystals by the solution Bridgman method using PbO-B
2O
3 as the flux, in which a crystal with 10 mm in diameter and 10 mm in length was obtained and the growth direction was determined along the [110] direction. The
TC and
Trt were found to be 300 °C and 120 °C, respectively, for PIN-31%PT crystals [
43]. It was also reported the PIN-34%PT crystals were grown by using PMNT31 as a seed crystal. The obtained crystals were found to have high piezoelectric coefficients
d33 ~ 2000 pC/N and electromechanical coupling
k33 of about 94%, comparable to the PMN-PT system, while exhibiting higher
TC at 200 °C [
44].
For the systems mentioned above,
TC on the order of 200–300 °C has been found; however,
Trt is still in the range of only 70–120 °C. PYN-PT with MPB composition was found to possess the highest
TC of about 360 °C among all of the lead-based relaxor-PT systems, similar to the commercial PZT5A ceramics. Piezoelectric single crystals in the PYN-PT system were grown using the flux method with Pb
3O
4 or Pb
3O
4/B
2O
3 as the flux. Perovskite PYN-PT solid solutions were prepared using the “wolframite process”, which consists of the synthesized B-site precursor, YbNbO
4, prior to reaction with PbO and TiO
2 [
24,
45,
46]. The obtained crystals were light yellow in color and 2–8 mm in size.
Table 2 summarized the detailed dielectric and piezoelectric properties of different relaxor-PT single crystal systems, in which it can be seen that all of the single crystals possess high electromechanical coupling, except for PSN-PT. The dielectric and piezoelectric properties were found to not only depend on the composition, but also depend on the Curie temperature: the higher Curie temperature the crystal system possesses, the lower dielectric constant and piezoelectric properties were observed; however, higher coercive fields were found with higher
TC.
Table 2.
Detailed dielectric and piezoelectric properties of relaxor-PT single crystals.
Table 2.
Detailed dielectric and piezoelectric properties of relaxor-PT single crystals.
| Crystal | Tc (°C) | TR-T (°C) | Ec (kV/cm) | ![Crystals 04 00306 i001]() | d33 (pC/N) | k33 | Reference |
|---|
| PMN-31PT | 143 | 90 | 2.5 | 5100 | 2000 | 90% | [47] |
| PZN-4.5PT | 155 | 120 | 3.2 | 4400 | 2100 | 90%–91% | [47] |
| PZN-8PT | 170 | 100 | 4 | 6000 | 2500 | 93% | [47] |
| PZN-12PT | 190 | – | 8.5 | 870 | 576 | 86% | [48] |
| PSN-33PT | 206 | – | 6 | 960 | – | 72% | [39] |
| PIN-28PT | 260 | 100 | 18 | 1500 | 700 | 85% | [42,49] |
| PIN-34PT | 200 | <100 | – | 5000 | 2000 | 94% | [44] |
| PYN-40PT | 270 | 168 | 10 | 2700 | 1200 | 88% | [47] |
| PYN-45PT | 325 | 160 | 12.5 | 2000 | 2000 | 88%–90% | [46] |
| BS-57PT | 402 | 349 | 13.7 | 3000 | 1150 | 91% | [50] |
2.3. High TC PMN-PT-Based Ternary Crystals
As described above, all of the binary relaxor-PT single crystals that have a Curie temperature higher than that of PMN-PT single crystals could only be grown by the flux method. Owing to the instability of the perovskite phase of these binary compositions, commercialization of these high
TC crystals was hindered by the availability of large-sized crystals. Recently, it was demonstrated that, by adding PMN-PT into some of the high
TC binary systems, the formed PMN-PT-based ternary compositions could have a relatively stable perovskite phase, offering the possibility to grow large crystals with a pure perovskite phase [
51,
52].
Among the broadly studied ternary systems, substantial progress has been made on the growth of large-sized PIN-PMN-PT crystals by the Bridgman process. For the preparation of PIN-PMN-PT, both a wolframite precursor, InNbO
4, and a columbite precursor, MgNb
2O
6, were firstly synthesized, respectively, by calcination of oxides at 1000–1200 °C. Using these precursors, PIN-PMN-PT with a pure perovskite phase was synthesized by another calcination process at lower temperature (750–900 °C). Like PMN-PT crystals, PIN-PMN-PT crystals with a pure perovskite phase form during solidification, so the crystals can be grown directly from the melt by the Bridgman process. By presenting a seed crystal, PIN-PMN-PT crystals with a diameter up to 75 mm have been grown along the preferred crystallographic orientations, including <001>, <110> and <111>.
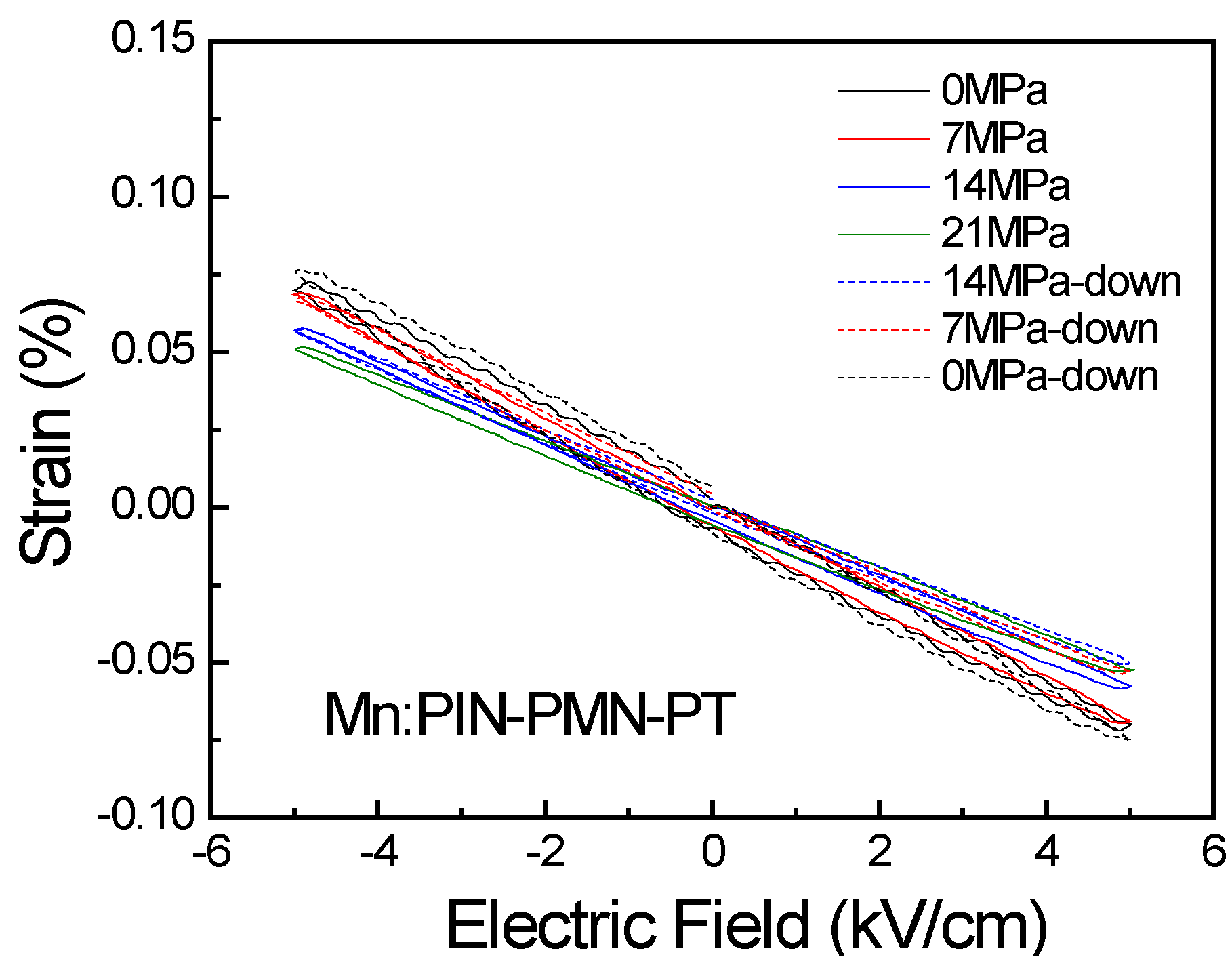
Figure 4 shows the as-grown PIN-PMN-PT crystals. It was found that the
Trt and
TC of PIN-PMN-PT (26%–36%PIN) crystals reach 120–140 °C and 160–200 °C, respectively, marking a 35–40 °C increase compared to PMN-PT crystals with a similar PT concentration. Furthermore, they exhibit a similar
d33 value (1100–2200 pC/N) as PMN-PT crystals, but a much higher coercive field (4.5–6 kV/cm).
Figure 4.
Seventy five-millimeter and 50-mm diameter <001>-oriented PIN-PMN-PT crystals grown by the Bridgman process (courtesy of TRS Technologies, Inc., State College, PA, USA).
Figure 4.
Seventy five-millimeter and 50-mm diameter <001>-oriented PIN-PMN-PT crystals grown by the Bridgman process (courtesy of TRS Technologies, Inc., State College, PA, USA).
PZT ceramics have been the mainstay for high-performance piezoelectric applications. However, the attempt to grow single-crystal PZT has not been successful. So far, only very small crystals of PZT can be produced by high temperature solution growth, which cannot provide samples for complete property measurement. As PMN-PT crystals, chemically homogeneous PMN-PZT crystals were also successfully grown by the solid-state crystal growth (SSCG) process [
53]. By this delicately controlled sintering process, the as-grown PMN-PZT crystals achieved a similar size and quality as SSCG-grown PMN-PT crystals. Interestingly, the
TC of all PMN-PZT crystals is approximately 200 °C; however, by changing the PMN/PZ/PT ratio,
Trt could be adjusted in the range of 100–160 °C, while
d33 in the range of 1000–2000 pC/N [
53].
Recently, some other PMN-PT-based ternary solid solution systems, including Pb(Yb
1/2Nb
1/2)O
3-Pb(Mg
1/3Nb
2/3)O
3-PbTiO
3 (PYN-PMN-PT), Pb(In
1/2Nb
1/2)O
3-Pb(Zn
1/3Nb
2/3)O
3-PbTiO
3 (PIN-PZN-PT) and Pb(Fe
1/2Nb
1/2)O
3-Pb(Yb
1/2Nb
1/2)O
3-PbTiO
3 (PFN-PYN-PT), have been investigated [
54,
55,
56,
57]. By the top-seeded solution growth (TSSG) method, crystals with compositions near an MPB have been grown, which show comparable piezoelectric properties to PMN-PT crystals, but higher Curie temperature and/or coercive field. As the TSSG method has been successfully applied to the large-scale production of some nonlinear optical crystals, such as β-BaBO
4 (BBO) and KTiOPO
4 (KTP) crystals, it is possible that it can be tailored to produce large crystals of these ternary solid solution crystals. Currently, PYN-PMN-PT crystals with a length and width over 3 cm have been obtained by the TSSG method. As complex flux systems are required to facilitate crystallization and to achieve a high crystal growth rate, the main challenge in the TSSG growth of crystals of these complex ternary compositions is to repeatedly produce high quality crystals that maintain consistent properties.
Table 3 summarizes the major piezoelectric and dielectric properties of PMN-PT-based ternary solid solution crystals that can operate at higher temperature and a higher electric field than current state-of-the-art PMN-PT single crystals.
Table 3.
Detailed dielectric and piezoelectric properties of PMN-PT-based ternary crystals.
Table 3.
Detailed dielectric and piezoelectric properties of PMN-PT-based ternary crystals.
| Crystal | Tc (°C) | TR-T (°C) | Ec (kV/cm) | ![Crystals 04 00306 i001]() | d33 (pC/N) | k33 | Reference |
|---|
| PMN-29PT | 135 | 96 | 2 | 5400 | 1540 | 91% | [58] |
| PMN-31PT | 143 | 90 | 2.5 | 5100 | 2000 | 90% | [47] |
| PIN-PMN-PT * | 160~200 | 120~140 | 4.5–6 | 4000–5000 | 1100–2200 | 89%–93% | [59] |
| PMN-PZT ** | 190~200 | 100~160 | >5 | 3000–6000 | 1000–2000 | 89%–92% | [53] |
| 20PYN-40PMN-40PT | 180 | 130 | 5.4 | 2400 | 2440–2580 | 90.9% | [54] |
| 15PYN-53PMN-32PT | 205 | 50 | 7 | 6270 | 1800 | 90% | [55] |
| 30PIN–33PbZN–37PT | 236 | 175 | 14.3 | 2500 | 1900–2100 | 86% | [56] |
| 10PFN–38PYN–52PT | 325 | 155 | 10.3 | 1620 | 1100 | 70% | [57] |






 = Pr<111>/
= Pr<111>/  [61,62,63]. As expected, the Pr values for the different orientations obtained from Figure 5a corresponded well to the predicted values. From Figure 5b, it is seen that in the sequence of orientation, <001>, <011> and <111>, the electric field required to reverse the domain (coercive field EC) increased, which is consistent with that indicated by the polarization hysteresis, while the positive strain achieved after the domain reorientation decreased.
[61,62,63]. As expected, the Pr values for the different orientations obtained from Figure 5a corresponded well to the predicted values. From Figure 5b, it is seen that in the sequence of orientation, <001>, <011> and <111>, the electric field required to reverse the domain (coercive field EC) increased, which is consistent with that indicated by the polarization hysteresis, while the positive strain achieved after the domain reorientation decreased.