Electronic Origin of the Orthorhombic Cmca Structure in Compressed Elements and Binary Alloys
Abstract
:1. Introduction
 |
2. Results and Discussion
2.1. Structural Characteristics of oC16-Cmca Phases
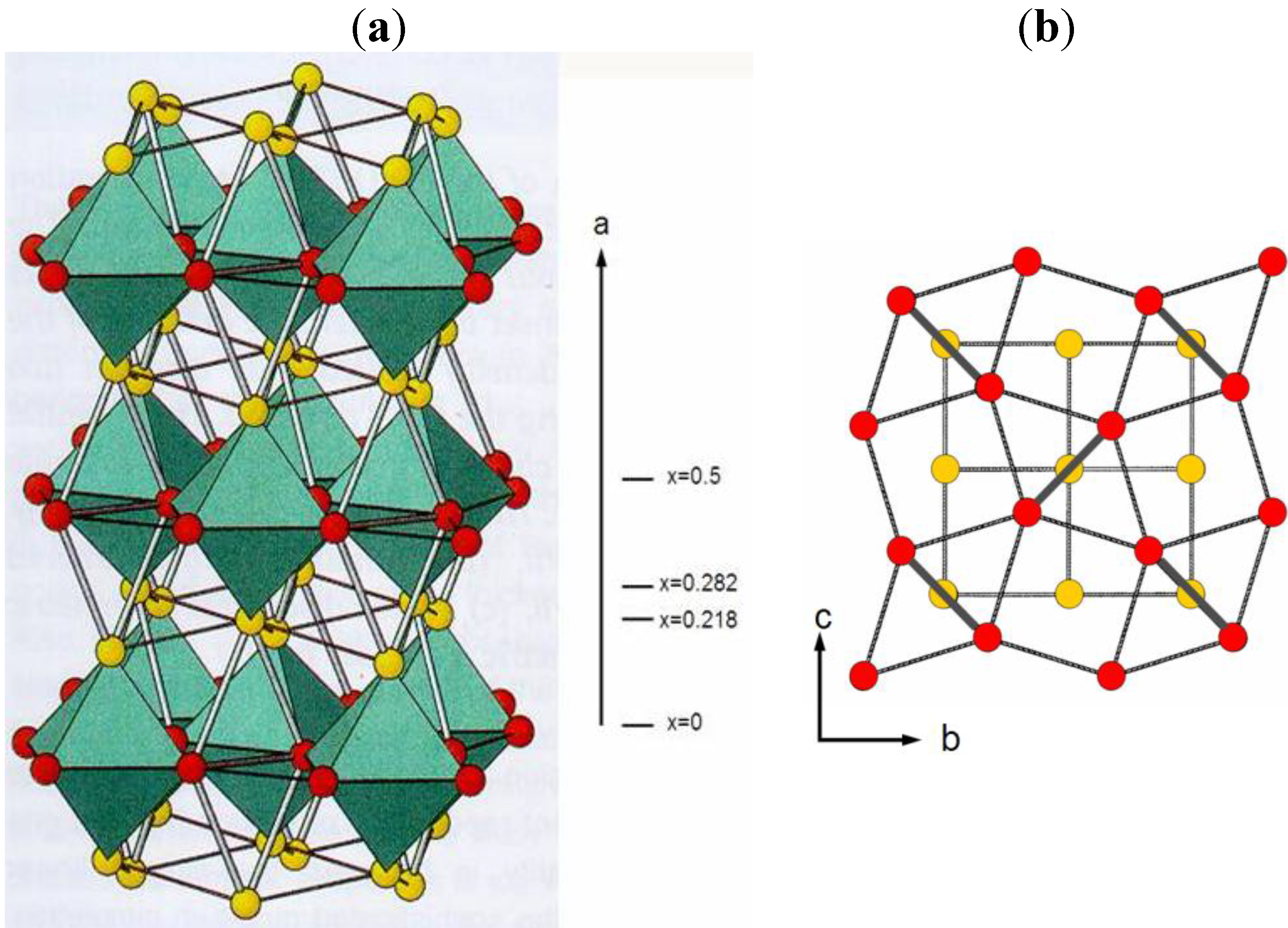
| Phase | Si-VI 38.4 GPa [5] | Ge 135 GPa [16] | Cs-V 12 GPa [4] | Rb-VI 48.1 GPa [17] | K-VI 112 GPa [18] | Bi-IV 3.2 GPa 465 K [19] | Bi40Sn60 5.8 GPa [20] | Bi80Pb20 quenched from 1.7 GPa [21] | Bi70In30 quenched from 2.0 GPa [21] |
|---|---|---|---|---|---|---|---|---|---|
| a (Å) | 8.024 | 7.885 | 11.205 | 9.372 | 8.032 | 11.191 | 10.7345 | 11.209 | 11.236 |
| b (Å) | 4.796 | 4.655 | 6.626 | 5.5501 | 4.753 | 6.622 | 6.3270 | 6.672 | 6.555 |
| c (Å) | 4.776 | 4.651 | 6.595 | 5.5278 | 4.716 | 6.608 | 6.3115 | 6.658 | 6.531 |
| Vat(Å3) | 11.49 | 10.67 | 30.60 | 17.97 | 11.25 | 30.61 | 26.79 | 31.12 | 30.07 |
| V/Vo | 0.565 | 0.470 | 0.264 | 0.194 | 0.150 | 0.864 | 0.882 | 0.905 | 0.921 |
| a/c | 1.680 | 1.695 | 1.699 | 1.689 | 1.703 | 1.693 | 1.701 | 1.684 | 1.721 |
| b/c | 1.004 | 1.001 | 1.005 | 1.004 | 1.004 | 1.002 | 1.002 | 1.002 | 1.004 |
| dshort(Å) | 2.340 | 2.315 | 3.235 | 2.764 | 2.317 | 3.275 | 2.985 | 3.242 | 3.146 |
| y (8f) | 0.173 | 0.173 | 0.164 | 0.170 | 0.173 | 0.170 | 0.167 | 0.172 | 0.170 |
| z (8f) | 0.327 | 0.328 | 0.313 | 0.318 | 0.327 | 0.320 | 0.333 | 0.328 | 0.330 |
| x (8d) | 0.216 | 0.218 | 0.218 | 0.211 | 0.216 | 0.210 | 0.212 | 0.214 | 0.212 |
2.2. Electronic Origin of Stability for oC16 Phases: Hume-Rothery Effects
2.2.1. Group IV Elements Si and Ge with the oC6 Structure
2.2.2. Structure oC16 in Bi and Bi-alloys
2.2.3. Structure oC16 in Alkali Elements: Core Ionization
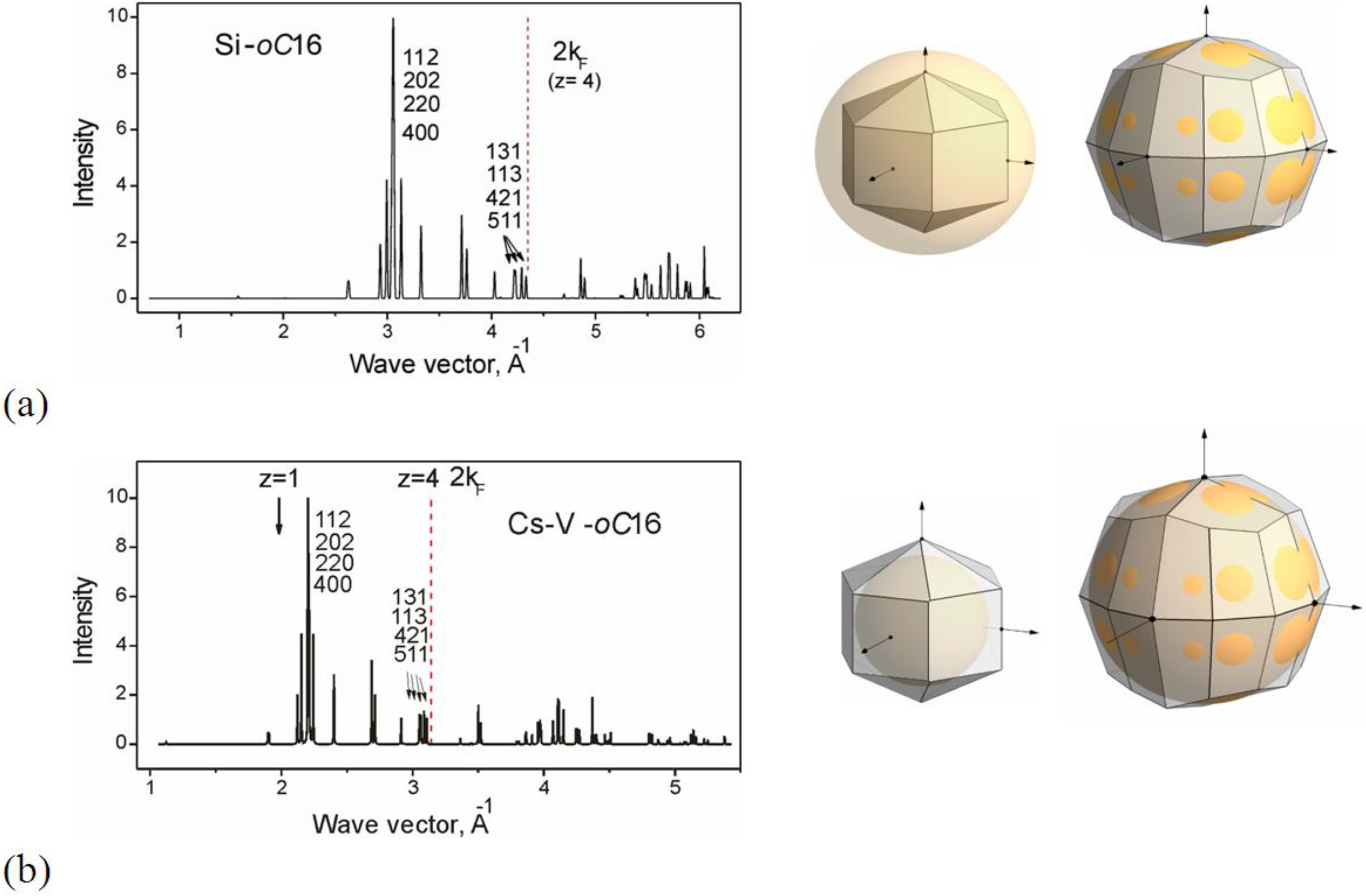
2.3. Structure Stability and Correlation with Properties within the Hume-Rothery Mechanism
3. Method of Analysis
4. Conclusions
Acknowledgments
Conflict of Interest
References
- McMahon, M.I.; Nelmes, R.J. High-pressure structures and phase transformations in elemental metals. Chem. Soc. Rev. 2006, 35, 943–963. [Google Scholar] [CrossRef]
- Degtyareva, V.F. Simple metals at high pressures: The Fermi sphere–Brillouin zone interaction model. Phys. Usp. 2006, 49, 369–388. [Google Scholar]
- Degtyareva, O. Crystal structure of simple metals at high pressures. High Press. Res. 2010, 30, 343–371. [Google Scholar] [CrossRef]
- Schwarz, U.; Takemura, K.; Hanfland, M.; Syassen, K. Crystal structure of cesium-V. Phys. Rev. Lett. 1998, 81, 2711–2714. [Google Scholar] [CrossRef]
- Hanfland, M.; Schwarz, U.; Syassen, K.; Takemura, K. Crystal structure of the high-pressure phase silicon VI. Phys. Rev. Lett. 1999, 82, 1197–1200. [Google Scholar] [CrossRef]
- Schwarz, U.; Jepsen, O.; Syassen, K. Electronic structure and bonding in the Cmca phases of Si and Cs. Solid State Commun. 2000, 113, 643–648. [Google Scholar] [CrossRef]
- Mott, N.F.; Jones, H. The Theory of the Properties of Metals and Alloys; Oxford University Press: London, UK, 1936. [Google Scholar]
- Jones, H. The Theory of Brillouin Zones and Electron States in Crystals; North-Holland Publishing Company: Amsterdam, Holland, 1962. [Google Scholar]
- Hume-Rothery, W.; Coles, B.R. Atomic Theory for Students of Metallurgy; Institute of Metals: London, UK, 1988. [Google Scholar]
- Ross, M.; McMahan, A.K. Systematics of the s → d and p → d electronic transition at high pressure for the elements I through La. Phys. Rev. B 1982, 26, 4088–4093. [Google Scholar] [CrossRef]
- Degtyareva, V.F.; Degtyareva, O. Structure stability in the simple element sodium under pressure. New J. Phys. 2009, 11, 063037:1–1063037:16. [Google Scholar]
- Pearson, W.B. Crystal Chemistry and Physics of Metals and Alloys; Wiley-Interscience: New York, NY, USA, 1972. [Google Scholar]
- Kubiak, R.; Wolcyrz, M. Refinement of crystal structures of AuSn4 and PdSn4. J. Less Common Met. 1984, 97, 265–269. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; JohnWiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chaleogenides. Acta Cryst. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Takemura, K.; Schwarz, U.; Syassen, K.; Hanfland, M.; Christensen, N.; Novikov, D.; Loa, I. High-pressure Cmca and hcp phases of germanium. Phys. Rev. B 2000, 62, R10603–R10606. [Google Scholar] [CrossRef]
- Schwarz, U.; Syassen, K.; Grzechnik, A.; Hanfland, M. The crystal structure of rubidium-VI near 50 GPa. Solid State Commun. 1999, 112, 319–322. [Google Scholar] [CrossRef]
- Lundegaard, L.F.; Marqués, M.; Stinton, G.; Ackland, G.J.; Nelmes, R.J.; McMahon, M.I. Observation of the oP8 crystal structure in potassium at high pressure. Phys. Rev. B 2009, 80, 020101:1–020101:4. [Google Scholar]
- Chaimayo, W.; Lundegaard, L.F.; Loa, I.; Stinton, G.W.; Lennie, A.R.; McMahon, M.I. High-pressure, high-temperature single-crystal study of Bi-IV. High Press. Res. 2012, 32, 442–449. [Google Scholar] [CrossRef]
- Degtyareva, V.F.; Degtyareva, O.; Allan, D.R. Ordered Si-VI-type crystal structure in BiSn alloy under high pressure. Phys. Rev. B 2003, 67, 212105:1–212105:4. [Google Scholar]
- Degtyareva, V.F. Crystal structure of a high-pressure phase in Bi-based alloys related to Si-VI. Phys. Rev. B 2000, 62, 9–12. [Google Scholar] [CrossRef]
- Degtyareva, V.F.; Smirnova, I.S. BRIZ: A vizualization program for Brillouin zone–Fermi sphere configuration. Z. Kristallogr. 2007, 222, 718–721. [Google Scholar] [CrossRef]
- Sato, H.; Toth, R.S. Fermi Surface of Alloys. Phys. Rev. Lett. 1962, 8, 239–241. [Google Scholar] [CrossRef]
- Harrison, W.A. Pseudopotentials. In the Theory of Metals; Elsevier: New York, NY, USA, 1966. [Google Scholar]
- Bundy, F.P. Phase diagram of bismuth to 130,000 kg/cm2, 500°C. Phys. Rev. 1958, 110, 314–318. [Google Scholar] [CrossRef]
- McMahon, M.I.; Degtyareva, O.; Nelmes, R.J. Ba-IV-type incommensurate crystal structure in group-V metals. Phys. Rev. Lett. 2000, 85, 4896–4899. [Google Scholar] [CrossRef]
- Ponyatovskii, E.G.; Degtyareva, V.F. Specific Features of T-C-P diagrams for binary systems of B-elements. High Press. Res. 1989, 1, 163–184. [Google Scholar] [CrossRef]
- Mizutani, U. Introduction to the Electron. Theory of Metals; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Mizutani, U. Hume-Rothery Rules for Structurally Complex Alloy Phases. Taylor & Francis US: London, UK, 2010. [Google Scholar]
- Häussler, P. Interrelations between atomic and electronic structures–Liquid and amorphous metals as model systems. Phys. Rep. 1992, 222, 65–143. [Google Scholar] [CrossRef]
- Stiehler, M.; Rauchhaupt, J.; Giegengack, U.; Häussler, P. On modifications of the well-known Hume-Rothery rules: Amorphous alloys as model systems. J. Non-Cryst. Solids 2007, 353, 1886–1891. [Google Scholar] [CrossRef]
- Berger, R.F.; Walters, P.L.; Stephen Lee, S.; Hoffmann, R. Connecting the Chemical and Physical Viewpoints of What Determines Structure: From 1-D Chains to γ-Brasses. Chem. Rev. 2011, 111, 4522–4545. [Google Scholar] [CrossRef]
- Von Schnering, H.G.; Nesper, R. How nature adapts chemical structures to curved surfaces. Angew. Chem. Int. Ed. Engl. 1987, 26, 1059–1080. [Google Scholar] [CrossRef]
- Nesper, R.; Grin, Yu. Periodic Space Partitioners (PSP) and their relations to crystal chemistry. Z. Kristallogr. 2011, 226, 692–710. [Google Scholar] [CrossRef]
- Ma, Y.; Eremets, M.; Oganov, A.R.; Xie, Y.; Trojan, I.; Medvedev, S.; Lyakhov, A.O.; Valle, M.; Prakapenka, V. Transparent dense sodium. Nature 2009, 458, 182–186. [Google Scholar] [CrossRef]
- Marqués, M.; Ackland, G.J.; Lundegaard, L.F.; Stinton, G.; Nelmes, R.J.; McMahon, M.I. Potassium under pressure: A pseudobinary ionic compound. Phys. Rev. Lett. 2009, 103, 115501:1–115501:4. [Google Scholar]
- Degtyareva, V.F.; Afonikova, N.S. Simple metal binary phases based on the body centered cubic structure: Electronic origin of distortions and superlattices. J. Phys. Chem. Solids 2013, 74, 18–24. [Google Scholar] [CrossRef]
- Hirsch, J.E.; Hamlin, J.J. Why non-superconducting metallic elements become superconducting under high pressure. Phys. C Supercond. 2010, 470, S937–S939. [Google Scholar] [CrossRef]
- Hirsch, J.E. Materials and mechanisms of hole superconductivity. Phys. C Supercond. 2012, 472, 78–82. [Google Scholar] [CrossRef]
- Wittig, J. Pressure-Induced Superconductivity in Cesium and Yttrium. Phys. Rev. Lett. 1970, 24, 812–815. [Google Scholar] [CrossRef]
- Erskine, D.; Yu, P.Y.; Chang, K.J.; Cohen, M.L. Superconductivity and Phase Transitions in Compressed Si to 45 GPa. Phys. Rev. Lett. 1986, 57, 2741–2744. [Google Scholar] [CrossRef]
- Degtyareva, V.F. Electronic origin of the incommensurate modulation in the structure of phosphorus IV. J. Phys. Conf. Ser. 2010, 226, 012019:1–012019:5. [Google Scholar]
- Degtyareva, V.F.; Degtyareva, O. Potassium under pressure: Electronic origin of complex structures. In Presented at the XXVIII International Conference on Interaction of Intense Energy Fluxes with Matter, Elbrus, Kabardino-Balkaria, Russia, 1–6 March 2013.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Degtyareva, V.F. Electronic Origin of the Orthorhombic Cmca Structure in Compressed Elements and Binary Alloys. Crystals 2013, 3, 419-430. https://doi.org/10.3390/cryst3030419
Degtyareva VF. Electronic Origin of the Orthorhombic Cmca Structure in Compressed Elements and Binary Alloys. Crystals. 2013; 3(3):419-430. https://doi.org/10.3390/cryst3030419
Chicago/Turabian StyleDegtyareva, Valentina F. 2013. "Electronic Origin of the Orthorhombic Cmca Structure in Compressed Elements and Binary Alloys" Crystals 3, no. 3: 419-430. https://doi.org/10.3390/cryst3030419
APA StyleDegtyareva, V. F. (2013). Electronic Origin of the Orthorhombic Cmca Structure in Compressed Elements and Binary Alloys. Crystals, 3(3), 419-430. https://doi.org/10.3390/cryst3030419




