Electronic Principles of Hydrogen Incorporation and Dynamics in Metal Hydrides
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Basic Features of the Metal-Hydrogen Interaction
- • The EMT is based on the Density Functional Theory (DFT), so its results could be easily related to the results of the state-of-art computations, especially in Local Density Approximation (LDA), although the relations to other approximations for exchange-correlation interaction have been made [75].
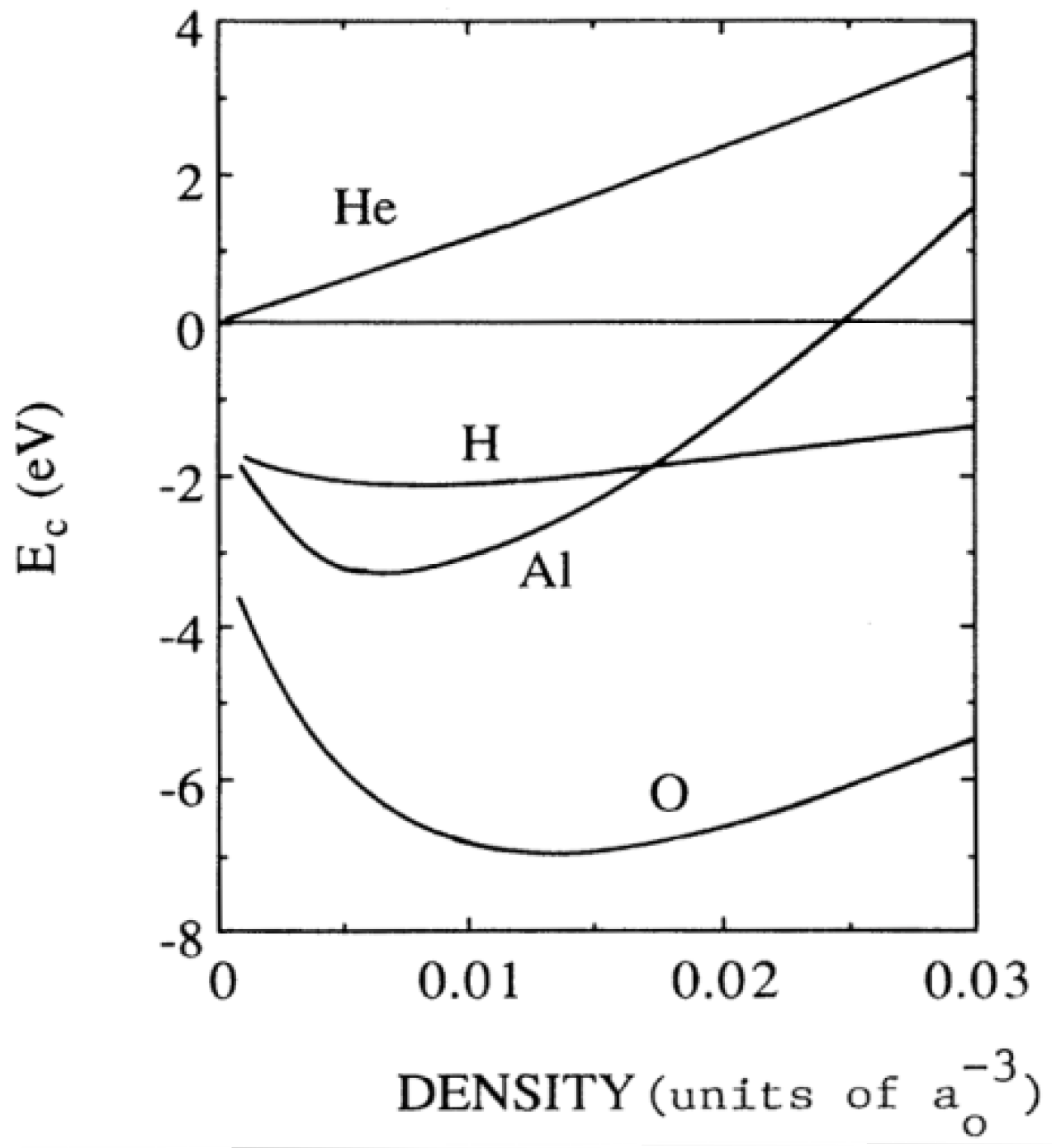
- 1. The most significant contribution to ΔEcoh(ρ) comes from the tendency of H to form a negative ion, so the models based on covalency or similar concepts are inappropriate for the description of M–H interaction.
- 2. As the electron affinity of H (AH) is smaller than the metal work function (φM), H goes to the neutral atom limit far from the metal surface (if H–H→H2 recombination does not take place)
- 3. The minimum of ΔEhom(ρ) for H is placed in the ρ range between 0.002 a.u. [74], 0.0055 a.u. [75] and 0.012 a.u. [70], so one can expect that H will prefer to occupy the positions with electron densities in that range, or as close as possible to it. This means that H2 may approach the more open and low electron density metallic surfaces closer (in general bcc closer than fcc [74], in particular the hypothetic (100) of the fcc Mg closer than the (0001) of the hcp Mg [77]), and experience smaller adsorption barriers. For instance the adsorption barrier for H on Al surface is deeper and more distant from the surface than for Mg, and it almost vanishes for low electron density Na surface [74].
2.2. H2 Adsorption and Dissociation of H2 on Mg (0001) Surface
- • There is an activation barrier for H2 adsorption on the Mg (0001) surface, which directs it toward the atom (A) (above the Mg atom) position, where H2 is placed parallel to the surface. The adsorption barrier arises because the H2 interaction with the surface charge starts to weaken the H–H bond before H–Mg bonding appears. This produces the first “delay” in the H absorption kinetics on the Mg (0001) surface.
- • Dissociation of H2 at the (A) position is hindered with another activation barrier (of about 0.5 eV), but H2 is almost free to move above the surface toward the bridge (B) site above the line connecting two neighboring surface Mg atoms. This produces the second “delay” in the H absorption kinetics on the Mg (0001) surface.
- • Dissociation barrier at the (B) position is quite low (about 0.1 eV, producing the third “delay” in the H absorption kinetics on the Mg (0001) surface), and after dissociation, one H atom goes into the surface Cfcc site, and the other into the surface Chcp site, and then quickly move into the first neighboring unoccupied Cfcc site (producing the fourth “delay” in the H absorption kinetics on the Mg (0001) surface), which is energetically most favorable for H adsorption. These Cfcc sites are the starting positions for H diffusion into the bulk of Mg metal.
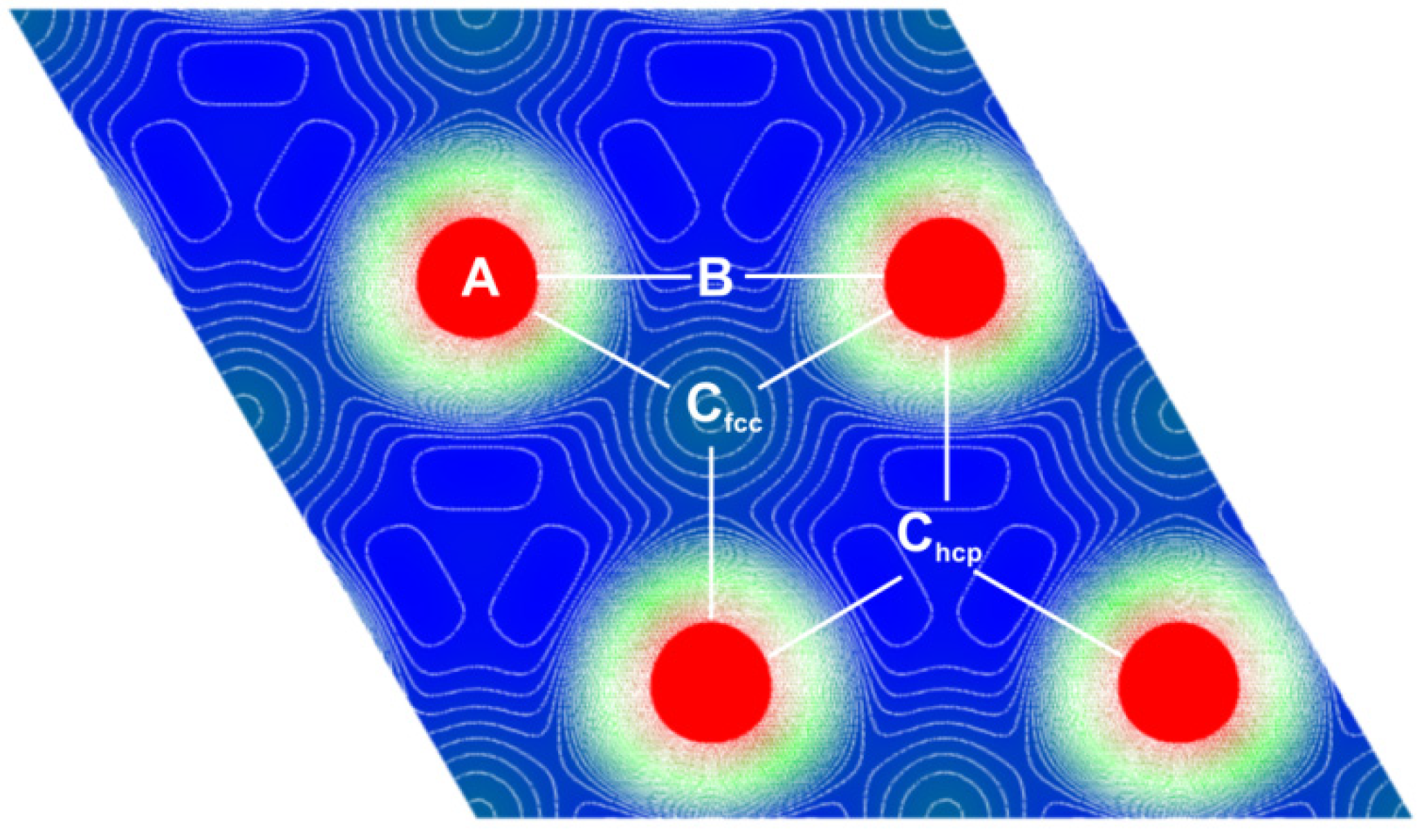
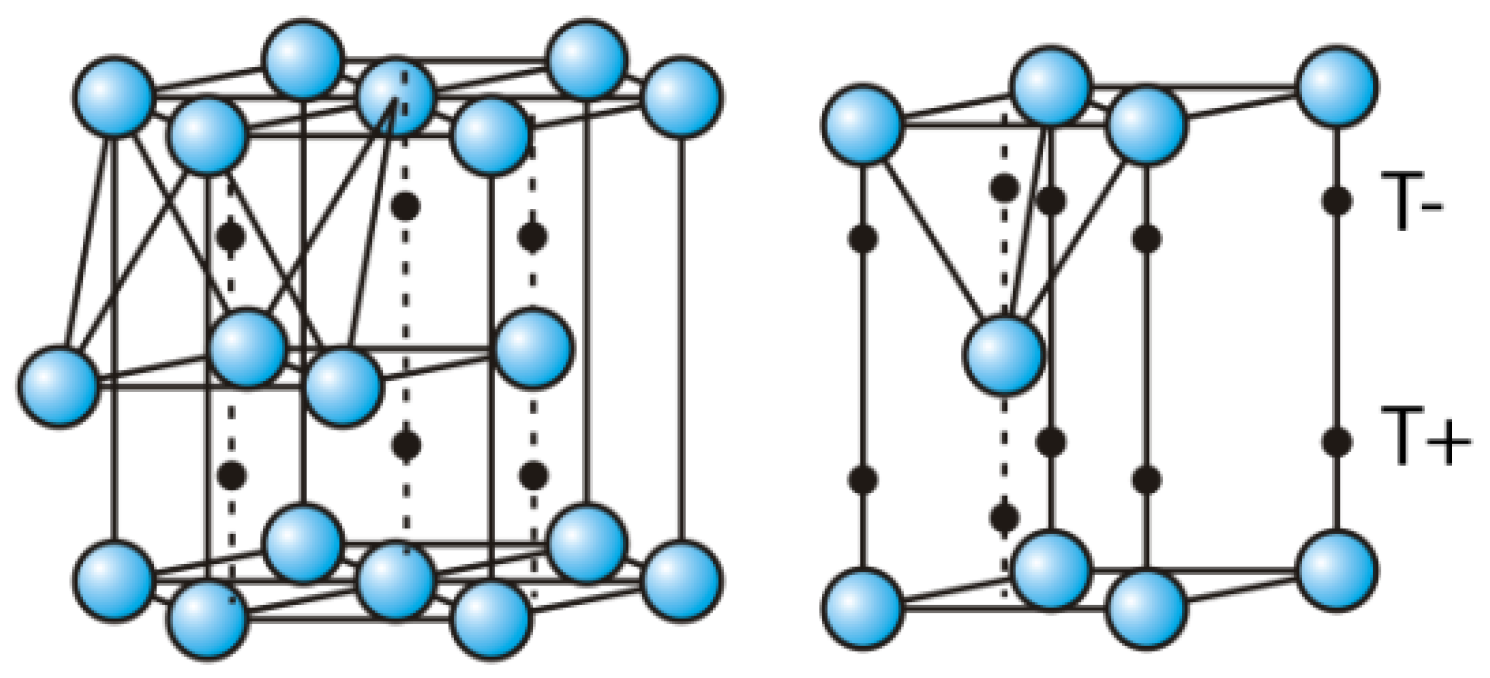
2.3. H Diffusion into the Bulk of Mg, and Hydrides Phase Formation
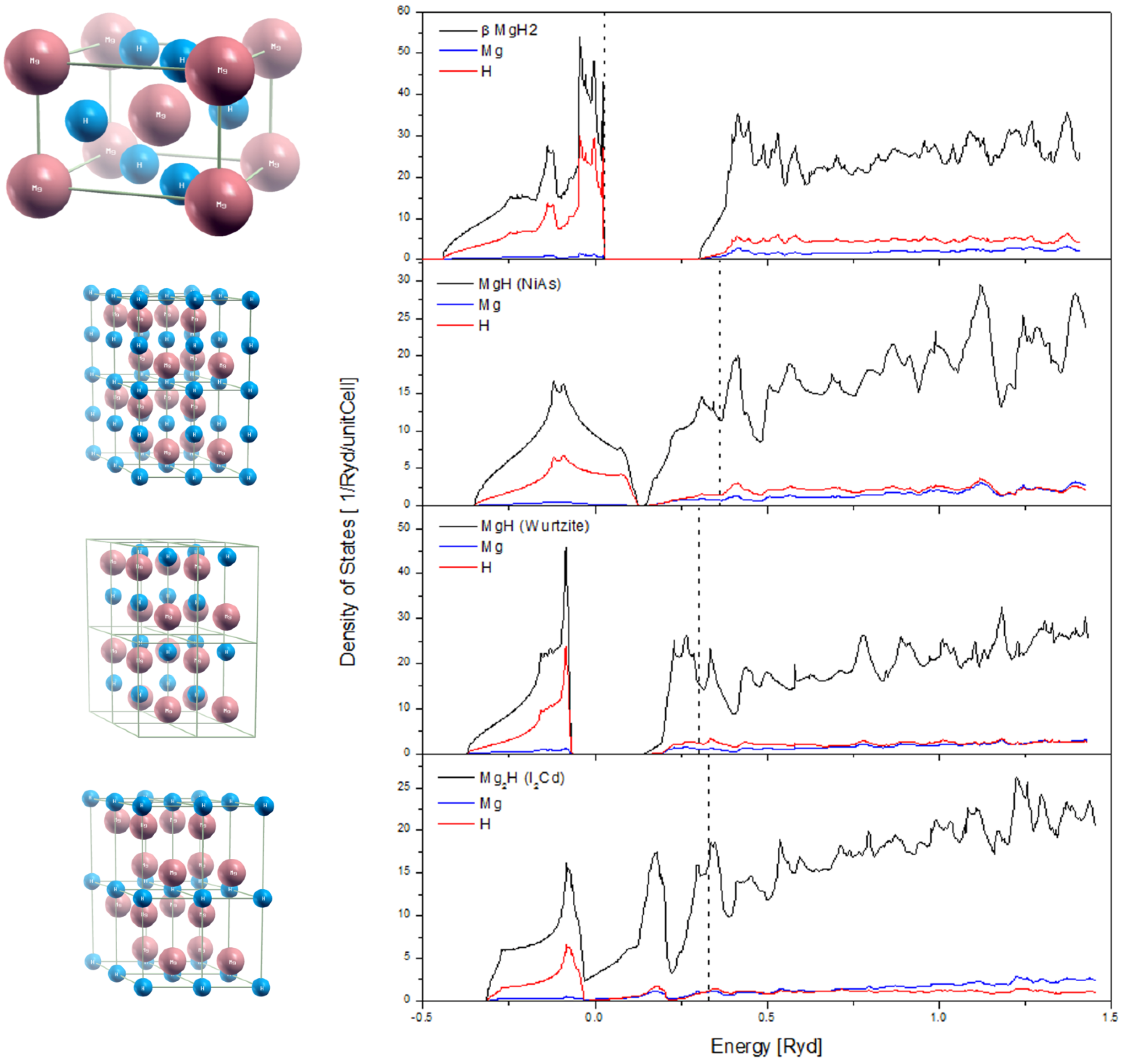
2.4. Desorption of H (H2) from MgH2, and Its Decomposition during Dehydrogenation
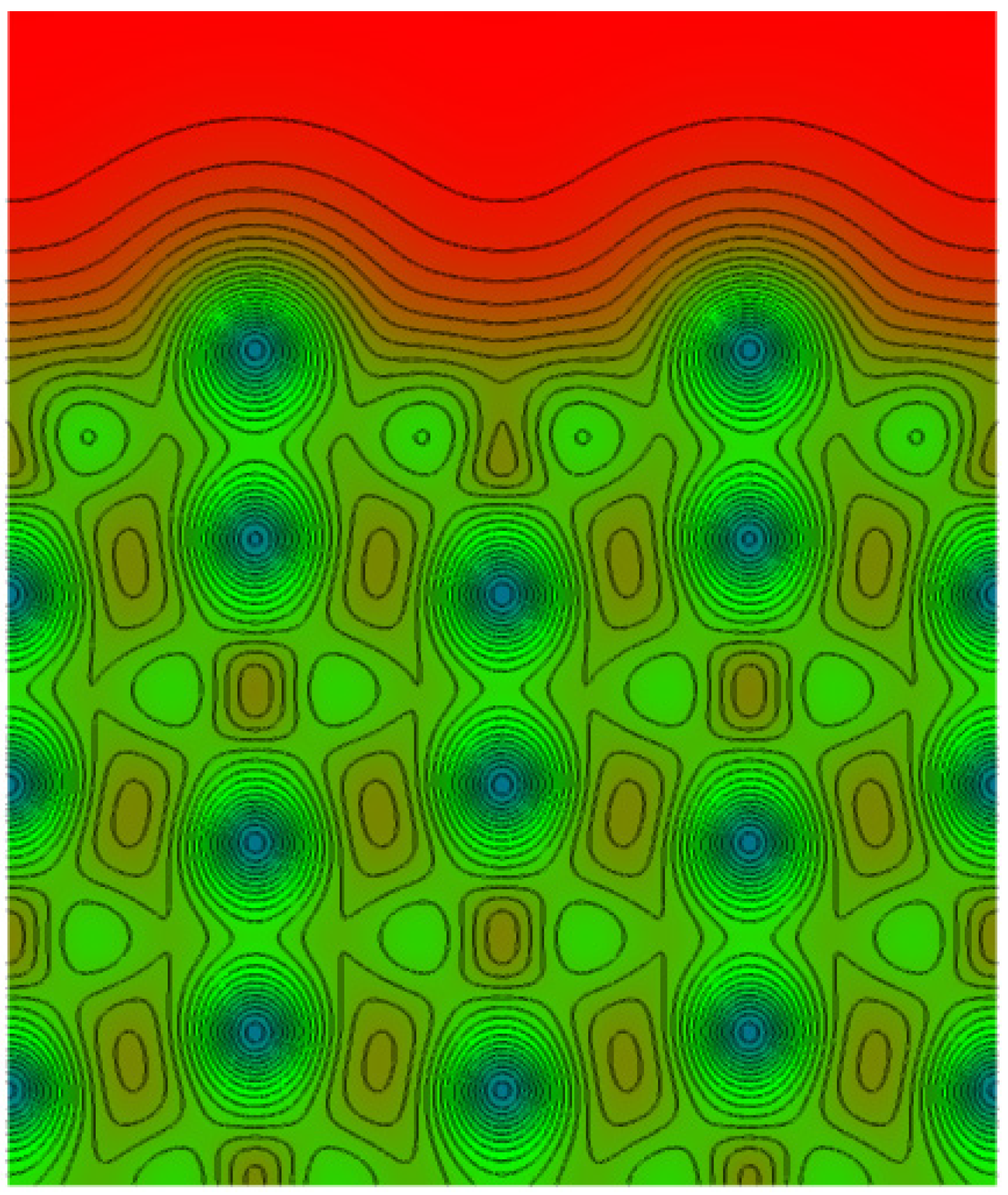

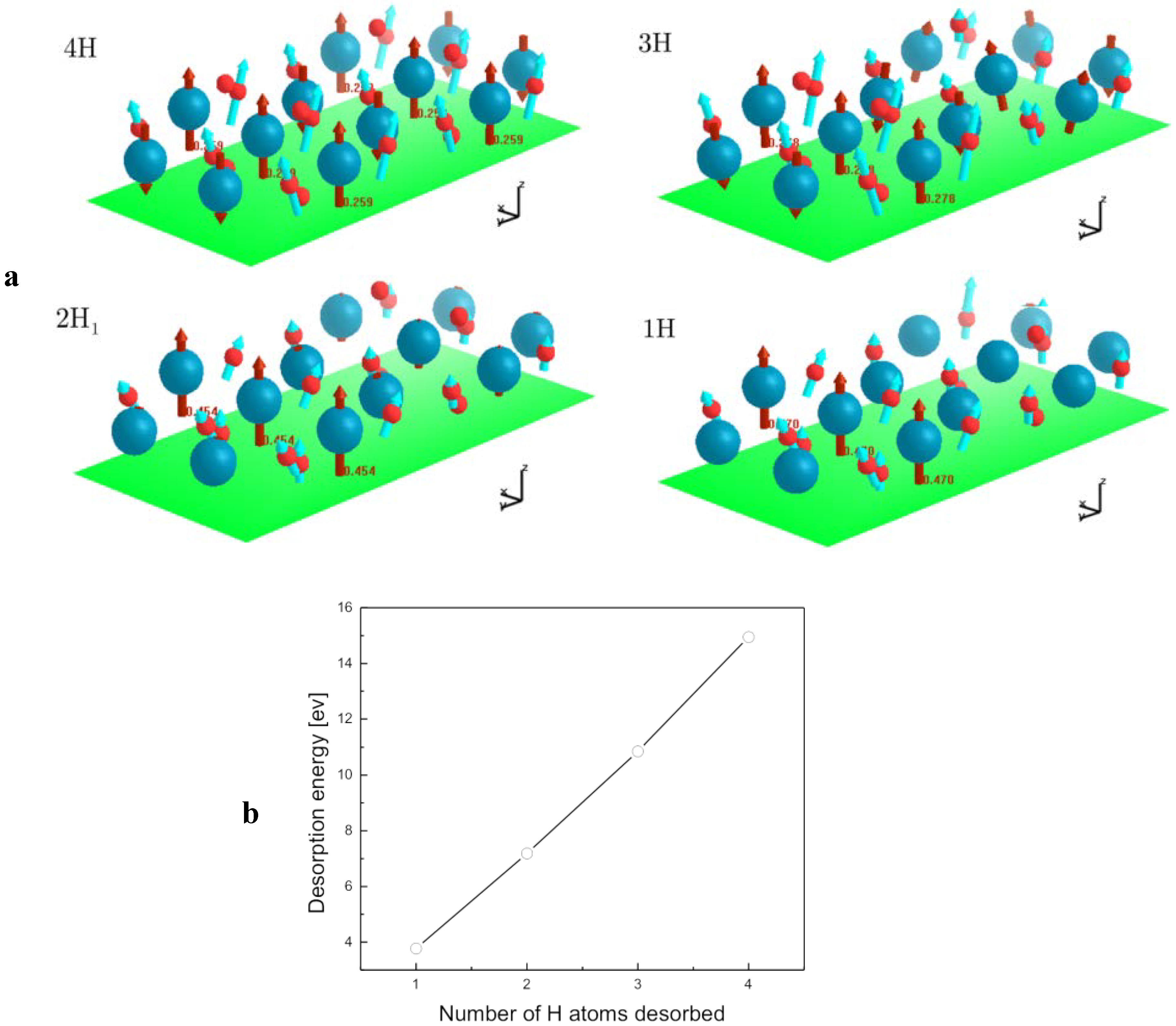
2.5. Possibilities for Improvement of the Mg/MgH2 Hydrogenation/Dehydrogenation Performances

| Compound | Distances [Å] | Etot | Δ H | ||||
|---|---|---|---|---|---|---|---|
| Atom | nn H4 | nn H2 | nn Mg | nnn H | |||
| MgH2 | Mg | 1.952 | 1.953 | 3.019 | 3.424 | −806.08 | −69.51 |
| MgH2:Ti | Ti | 1.916 | 1.905 | 3.041 | 3.440 | −7755.53 | −60.64 |
| MgH2:Co | Co | 1.789 | 1.802 | 3.025 | 3.458 | −8834.79 | −53.23 |
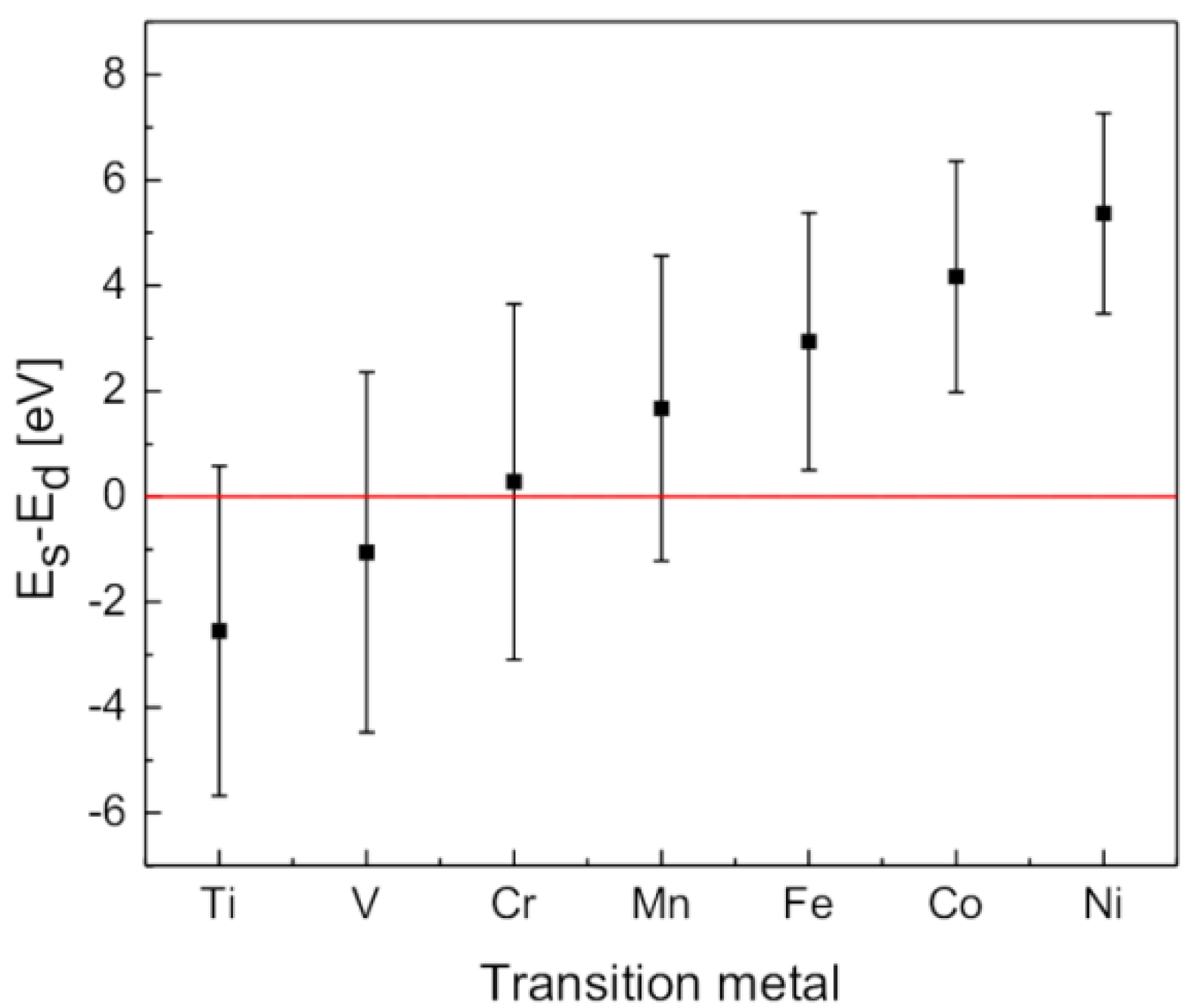
2.6. Few Words about “Modern” Complex Hydrides
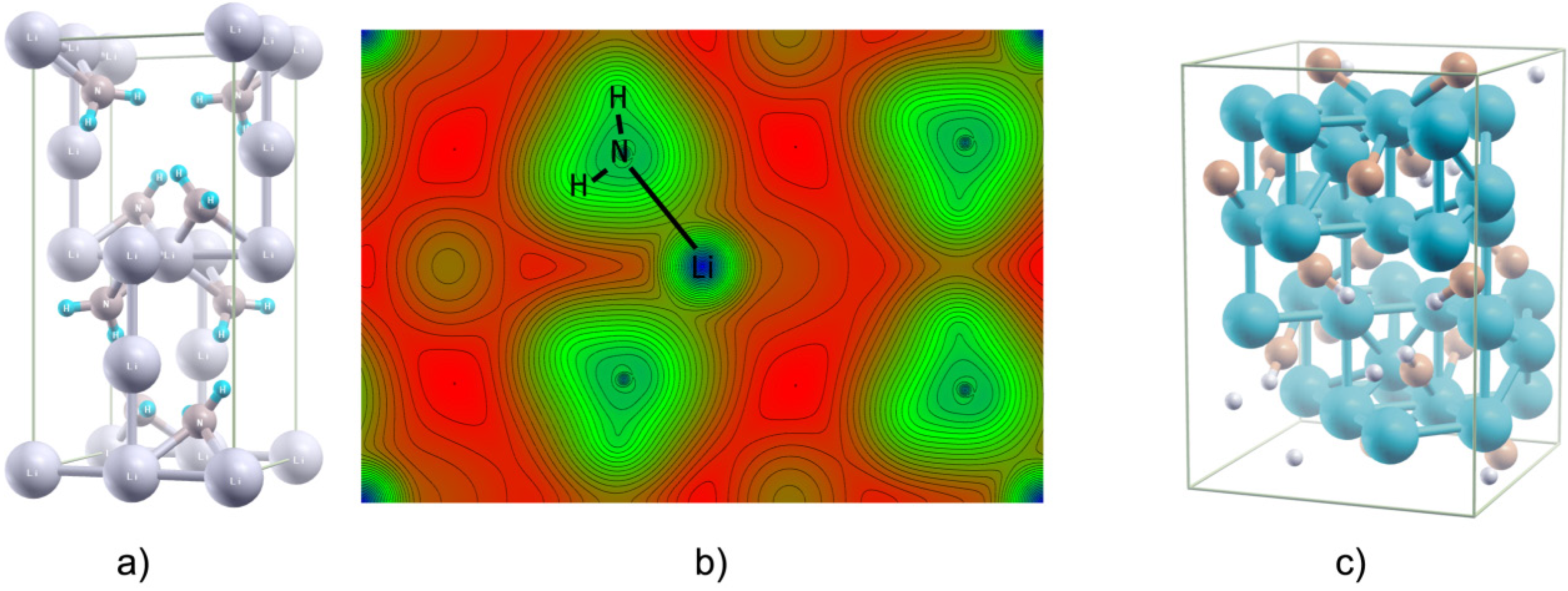
3. Summary and Perspectives
Acknowledgments
Conflict of Interest
References
- Schlapbach, L.; Zuttel, A. Hydrogen-storage materials for mobile applications. Nature 2001, 414, 353–358. [Google Scholar] [CrossRef]
- Zuttel, A. Materials for hydrogen storage. Mater. Today 2003, 6, 24–33. [Google Scholar] [CrossRef]
- Bobet, J.-L.; Even, C.; Nakamura, Y.; Akiba, E.; Darriet, B. Synthesis of magnesium and titanium hydride via reactive mechanical alloying. Influence of 3D-metal addition on MgH2 synthesize. J. Alloys Compounds 2000, 298, 279–284. [Google Scholar] [CrossRef]
- Liang, G.; Huot, J.; van Neste, A.; Schulz, R. Catalytic effect of transition metals on hydrogen sorption in nanocrystalline ball milled MgH2-Tm (Tm = Ti, V, Mn, Fe and Ni) systems. J. Alloys Compounds 1999, 292, 247–252. [Google Scholar] [CrossRef]
- Jain, I.P.; Lal, Ch.; Jain, A. Hydrogen storage in Mg: A most promising material. Int. J. Hydrogen Energy 2010, 35, 5133–5144. [Google Scholar]
- Liang, G.; Schulz, R. Synthesis of Mg-Ti alloy by mechanical alloying. J. Mater. Sci. 2003, 38, 1179–1184. [Google Scholar] [CrossRef]
- Zaluski, L.; Zaluska, A.; Strom-Olsen, J.O. Nanocrystalline metal hydrides. J. Alloys Compounds 1997, 253–254, 70–79. [Google Scholar] [CrossRef]
- Bassetti, A.; Bonetti, E.; Pasquini, L.; Montone, A.; Grbovic, J.; Vittori Antisari, M. Hydrogen desorption from ball milled MgH2 catalyzed with Fe. Eur. Phys. J. B 2005, 43, 19–27. [Google Scholar] [CrossRef]
- Gupta, R.B. Hydrogen Fuel Production Transport and Storage, 1st ed; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Varin, R.A.; Czujko, T.; Wronski, Z.S. Nanomaterials for Solid State Hydrogen Storage,1st ed.; Springer Science Bussines Media: New York, NY, USA, 2009. [Google Scholar]
- Hirscher, M. Handbook of Hydrogen Storage: New Materials for Future Energy Storage, 1st ed; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2010. [Google Scholar]
- Walker, G. Solid-state hydrogen storage. In Materials and Chemistry, 1st ed; Woodhead Publishing Limited: Cambridge, UK, 2008. [Google Scholar]
- Fukai, Y. The Metal–Hydrogen System, 2nd ed; Springer: Berlin, Germany, 2005. [Google Scholar]
- Borgschulte, A.; Schlapbach, L. Hydrogen as A Future Energy Carrier, 1st; Zuttel, A., Ed.; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2008. [Google Scholar]
- Bowman, R.C. Cohesive energies of the alkali hydrides and deuterides. J. Phys. Chem. 1971, 75, 1251–1255. [Google Scholar] [CrossRef]
- Luaña, V.; Pueyo, L. Simulation of ionic crystals: The ab initio perturbed-ion method and application to alkali hydrides and halides. Phys. Rev. B 1990, 41, 3800–3814. [Google Scholar] [CrossRef]
- Wolverton, C.; Ozoliņš, V.; Asta, M. Hydrogen in aluminum: First-principles calculations of structure and thermodynamics. Phys. Rev. B 2004, 69, 144109:1–144109:16. [Google Scholar]
- Vidal-Valat, G.; Vidal, J.-P.; Kurki-Suonio, K.; Kurki-Suonio, R. Evidence on the breakdown of the Born-Oppenheimer approximation in the charge density of crystalline 7LiH/D. Acta Cryst. 1992, A48, 46–60. [Google Scholar]
- Blat, D.K.; Zein, N.E.; Zinenko, V.I. Calculations of phonon frequencies and dielectric constants of alkali hydrides via the density functional method. J. Phys. Condens. Matter 1991, 3, 5515–5524. [Google Scholar] [CrossRef]
- Ivanović, N.; Novaković, N.; Colognesi, D.; Radisavljević, I.; Ostojić, S. Electronic principles of some trends in properties of metallic hydrides. Int. J. Mod. Phys. B 2010, 24, 703–710. [Google Scholar]
- Smithson, H.; Marianetti, C.A.; Morgan, D.; van der Ven, A.; Predith, A.; Ceder, G. First-principles study of the stability and electronic structure of metal hydrides. Phys. Rev. B 2002, 66, 144107:1–144107:10. [Google Scholar]
- Lebegue, S.; Alouani, M.; Arnuad, B.; Pickett, W.E. Pressure-induced simultaneous metal-insulator and structural-phase transitions in LiH: A quasiparticle study. Europhys. Lett. 2003, 63, 562–568. [Google Scholar] [CrossRef]
- Novaković, N.; Radisavljević, I.; Colognesi, D.; Ostojić, S.; Ivanović, N. First principle calculations of alkali hydride electronic structures. J. Phys. Condens. Matter 2007, 19, 406211:1–406211:14. [Google Scholar]
- Vajeeston, P. Theoretical Modeling of Hydrides. Ph.D. Thesis, University of Oslo, Oslo, Norway, 2004. [Google Scholar]
- Ravindran, P.; Vajeeston, P.; Fjellvåg, H.; Kjekshus, A. Chemical-bonding and high-pressure studies on hydrogen-storage materials. Comput. Mater. Sci. 2004, 30, 349–357. [Google Scholar] [CrossRef]
- Ceriotti, M.; Miceli, G.; Pietropaolo, A.; Colognesi, D.; Nale, A.; Catti, M.; Bernasconi, M.; Parrinello, M. Nuclear quantum effects in ab initio dynamics: Theory and experiments for lithium imide. Phys. Rev. B 2010, 82, 174306:1–174306:5. [Google Scholar]
- Bogdanović, B.; Schwickardi, M. Ti-doped alkali metal aluminium hydrides as potential novel reversible hydrogen storage materials. J. Alloys Compounds 1997, 253–254, 1–9. [Google Scholar] [CrossRef]
- Bogdanović, B.; Brand, R.A.; Marjanović, A.; Schwickardi, M.; Tölle, J. Metal-doped sodium aluminium hydrides as potential new hydrogen storage materials. J. Alloys Compounds 2000, 302, 36–58. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Vidya, R.; Fjellvåg, H.; Kjekshus, A. Pressure-induced phase of NaAlH4: A potential candidate for hydrogen storage? Appl. Phys. Lett. 2003, 82, 2257–2259. [Google Scholar]
- Chen, P.; Xiong, Z.; Luo, J.; Lin, J.; Tan, K.L. Interaction of hydrogen with metal nitrides and imides. Nature 2002, 420, 302–304. [Google Scholar]
- Luo, W.; Rönnebro, E. Towards a viable hydrogen storage system for transportation application. J. Alloys Compounds 2005, 404–406, 392–359. [Google Scholar] [CrossRef]
- Ivanović, N.; Radisavljević, I.; Novaković, N.; Manasijević, M.; Colognesi, D. Calculations of molecular structures and processes important for hydrogen behaviour in the Li-amide/imide system. Acta Phys. Pol. 2011, 119, 242–245. [Google Scholar]
- Dyck, W.; Jex, H. Lattice dynamics of alakali hydrides and deuterides with the NaCl type structure. J. Phys. C Solid State Phys. 1981, 14, 4193–4215. [Google Scholar] [CrossRef]
- Yu, R.; Lam, P.K. Electronic and structural properties of MgH2. Phys. Rev. B 1988, 37, 8730–8737. [Google Scholar] [CrossRef]
- Kunz, A.B.; Mickish, D.J. Electronic structure of LiH and NaH. Phys. Rev. B 1975, 11, 1700–1704. [Google Scholar]
- Grosso, G.; Parravicini, G.P. Hartree-Fock energy bands by the orthogonalized-plane-wave method: Lithium hydride results. Phys. Rev. B 1979, 20, 2366–2372. [Google Scholar]
- Zeng, K.; Klassen, T.; Oelerich, W.; Bormann, R. Critical assessment and thermodynamic modeling of the Mg–H system. Int. J. Hydrogen Energy 1999, 24, 989–1004. [Google Scholar]
- Miademma, A.R. The electronegativity parameter for transition metals: Heat of formation and charge transfer in alloys. J. Less Common Metals 1973, 32, 117–136. [Google Scholar] [CrossRef]
- Rao, B.K.; Jena, P. Switendick criterion for stable hydrides. Phys. Rev. B 1985, 31, 6726–6730. [Google Scholar] [CrossRef]
- Sakintuna, B.; Lamari-Darkrim, F.; Hirscher, M. Metal hydride materials for solid hydrogen storage: A review. Int. J. Hydrogen Energy 2007, 32, 1121–1140. [Google Scholar]
- Bazzanella, N.; Checchetto, R.; Miotello, A. Catalytic effect on hydrogen desorption in Nb-doped microcrystalline MgH2. Appl. Phys. Lett. 2004, 85, 5212–5214. [Google Scholar] [CrossRef]
- Schimmel, H.G.; Johnson, M.R.; Kearley, G.J.; Ramirez-Cuesta, A.J.; Huot, J.; Mulder, F.M. Structural information on ball milled magnesium hydride from vibrational spectroscopy and ab initio calculations. J. Alloys Compounds 2005, 393, 1–4. [Google Scholar] [CrossRef]
- Gross, K.J.; Chartouni, D.; Leroy, E.; Zuttel, A.; Schlapbach, L. Mechanically milled Mg composites for hydrogen storage: The relationship between morphology and kinetics. J. Alloys Compounds 1998, 269, 259–270. [Google Scholar] [CrossRef]
- Grbović Novaković, J.; Brdarić, T.; Novaković, N.; Matović, Lj.; Montone, A.; Mentus, S. Experimental and theoretical investigation of hydrogen storage magnesium based composites. Mat. Sci. Forum 2007, 555, 343–348. [Google Scholar] [CrossRef]
- Matović, Lj.; Novaković, N.; Kurko, S.; Šiljegović, M.; Matović, B.; Romčević, N.; Kačarević-Popović, Z.; Ivanović, N.; Grbović Novaković, J. Structural destabilisation of MgH2 obtained by heavy ion irradiation. Int. J. Hydrogen Energy 2009, 34, 7275–7282. [Google Scholar]
- Grbović Novaković, J.; Matović, Lj.; Milovanović, S.; Drvendžija, M.; Novaković, N.; Rajnović, D.; Šiljegović, M.; Kačarević-Popović, Z.; Ivanović, N. Changes of hydrogen storage properties of MgH2 induced by heavy ion irradiation. Int. J. Hydrogen Energy 2008, 33, 1876–1879. [Google Scholar]
- Westerwaal, R.J.; Broedersz, C.P.; Gremaud, R.; Slaman, M.; Borgschulte, A.; Lohstroh, W.; Tscherisch, K.G.; Fleischhauer, H.P.; Dam, B.; Griessen, R. Study of the hydride forming process of in situ grown MgH2 thin films by activated reactive evaporation. Thin Solid Films 2008, 516, 4351–4359. [Google Scholar]
- Stander, C.M.; Pacey, R.A. The lattice energy of magnesium hydride. J. Phys. Chem. Solid 1978, 39, 829–832. [Google Scholar] [CrossRef]
- Noritake, T.; Aoki, M.; Towata, S.; Seno, Y.; Hirose, Y.; Nishibori, E.; Takata, M.; Sakata, M. Chemical bonding of hydrogen in MgH2. Appl. Phys. Lett. 2002, 81, 2008–2010. [Google Scholar]
- Schimmel, H.G.; Kearley, G.J.; Huot, J.; Mulder, F.M. Hydrogen diffusion in magnesium metal (α phase) studied by ab initio computer simulations. J. Alloys Compounds 2005, 404–406, 235–237. [Google Scholar]
- Kelkar, T.; Kanhere, D.G.; Pal, S. First principles calculations of thermal equations of state and thermodynamical properties of MgH2 at finite temperatures. Comput. Mat. Sci. 2008, 42, 510–516. [Google Scholar]
- Ares, J.R.; Leardini, F.; Díaz-Chao, P.; Bodega, J.; Fernández, J.F.; Ferrer, I.J.; Sánchez, C. Ultrasonic irradiation as a tool to modify the H-desorption from hydrides: MgH2 suspended in decane. Ultrason. Sonochem. 2009, 16, 810–816. [Google Scholar]
- Imamura, H.; Yoshihara, K.; Yoo, M.; Kitazawa, I.; Sakata, Y.; Ooshima, S. Dehydriding of Sn/MgH2 nanocomposite formed by ball milling of MgH2 with Sn. Int. J. Hydrogen Energy 2007, 32, 4191–4194. [Google Scholar] [CrossRef]
- Pfrommer, B.; Elasässer, C.; Fähnle, M. Possibility of Li–Mg and Al–Mg hydrides being metallic. Phys. Rev. B 1994, 50, 5089–5093. [Google Scholar]
- Montone, A.; Grbović, J.; Stamenković, Lj.; Fiorini, A.L.; Pasquini, L.; Bonetti, E.; Vittori Antisari, M. Desorption Behaviour in Nanostructured MgH2–Co. Mater. Sci. Forum 2006, 518, 79–84. [Google Scholar] [CrossRef]
- Berlouis, L.E.A.; Cabrera, E.; Hall-Barientos, E.; Hall, P.J.; Dodd, S.B.; Morris, S.; Imam, M.A. Thermal analysis investigation of hydriding properties of nanocrystalline Mg–Ni- and Mg–Fe-based alloys prepared by high-energy ball milling. J. Mater. Res. 2001, 16, 45–57. [Google Scholar]
- Montone, A.; Grbović, J.; Vittori Antisari, M.; Bassetti, A.; Bonetti, E.; Fiorini, A.L.; Pasquini, L.; Mirenghi, L.; Rotolo, P. Nano-micro MgH2–Mg2NiH4 composites: Tayloring a multichannel system with selected hydrogen sorption properties. Int. J. Hydrogen Energy 2007, 32, 2026–2934. [Google Scholar]
- Bassetti, A.; Bonetti, E.; Fiorini, A.L.; Grbovic, J.; Montone, A.; Pasquini, L.; Vittori Antisari, M. Microstructure and hydrogen desorption in nanostructured MgH2–Fe. Mater. Sci. Forum 2004, 453-454, 205–212. [Google Scholar] [CrossRef]
- Hanada, N.; Ichikava, T.; Fujii, H. Catalytic effect of nanoparticle 3d-transition metals on hydrogen storage properties in magnesium hydride MgH2 prepared by mechanical milling. J. Phys. Chem. B 2005, 109, 7188–7194. [Google Scholar]
- Bobet, J.-L.; Akiba, E.; Nakamura, Y.; Darrie, B. Study of Mg–M (M = Co, Ni and Fe) mixture elaborated by reactive mechanical alloying—Hydrogen sorption properties. Int. J. Hydrogen Energy 2000, 25, 987–996. [Google Scholar] [CrossRef]
- Oelerich, W.; Klassen, T.; Bormann, R. Comparison of the catalytic effects of V, V2O5, VN and VC on the hydrogen sorption of nanocrystalline Mg. J. Alloys Compounds 2001, 322, L5–L9. [Google Scholar] [CrossRef]
- Gulicovski, J.; Rašković-Lovre, Ž.; Kurko, S.; Vujasin, R.; Jovanović, Z.; Matović, Lj.; Grbović Novaković, J. Influence of vacant CeO2 nanostructured ceramics on MgH2 hydrogen desorption properties. Ceram. Int. 2012, 38, 1181–1186. [Google Scholar]
- Aguey-Zinsou, K.-F.; Ares Fernandez, J.R.; Klassen, T.; Bormann, R. Effect of Nb2O5 on MgH2 properties during mechanical milling. Int. J. Hydrogen Energy 2007, 32, 2400–2407. [Google Scholar] [CrossRef]
- Sun, D.; Gingl, F.; Enoki, H.; Ross, D.K.; Akiba, E. Phase components of the sintered Mg–X wt.% LaNi5 (X = 20–50) composites and their hydrogenation properties. Acta Mater. 2000, 48, 2363–2372. [Google Scholar]
- Novaković, N.; Matović, Lj.; Grbović Novaković, J.; Manasijević, M.; Ivanović, N. Ab Initio Study of MgH2 Formation. Mater. Sci. Eng. B 2009, 165, 235–238. [Google Scholar] [CrossRef]
- Borgschulte, A.; Gremaud, R.; Griessen, R. Interplay of diffusion and dissociation mechanisms during hydrogen absorption in metals. Phys. Rev. B 2008, 78, 094106:1–094106:16. [Google Scholar]
- Du, A.J.; Smith, S.C.; Yao, X.D.; Lu, G.Q. The role of Ti as a catalyst for the dissociation of hydrogen on a Mg (0001) Surface. J. Phys. Chem. B 2005, 109, 18037–18041. [Google Scholar]
- Song, Y.; Guo, Z.X.; Yang, R. Influence of selected alloying elements on the stability of magnesium dihydride for hydrogen storage applications: A first principle investigation. Phys. Rev. B 2004, 69, 094205:1–094205:11. [Google Scholar]
- Shang, C.X.; Bououdina, M.; Song, Y.; Guo, Z.X. Mechanical alloying and electronic simulations of (MgH2–M) systems (M = Al, Ti, Fe, Ni, Cu and Nb) for hydrogen storage. Int. J. Hydrogen Energy 2004, 29, 73–80. [Google Scholar] [CrossRef]
- Vegge, T.; Hedegaard-Jensen, L.S.; Bonde, J.; Munter, T.R.; Norskov, J.K. Trends in hydride formation energies for magnesium-3d transition metal alloys. J. Alloys Compounds 2005, 386, 1–7. [Google Scholar] [CrossRef]
- Larsson, P.; Moyses Araújo, C.; Larsson, J.A.; Jena, P.; Ahuja, R. Role of catalysts in dehydrogenation of MgH2 nanoclusters. Proc. Natl. Acad. Sci. USA 2008, 105, 8227–8231. [Google Scholar]
- Novaković, N.; Grbović Novaković, J.; Matović, Lj.; Manasijević, M.; Radisavljević, I.; Paskaš-Mamula, B.; Ivanović, N. Ab initio calculations of MgH2, MgH2:Ti and MgH2:Co compounds. Int. J. Hydrogen Energy 2010, 35, 598–608. [Google Scholar]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. WIEN2k, An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Properties; Karlheinz Schwarz, Techn. Universtät: Wien, Austria, 2001. [Google Scholar]
- Nørskov, J.L.; Lang, N.D. Effective-medium theory of chemical binding: Application to chemisorptions. Phys. Rev. B 1980, 21, 2131–2136. [Google Scholar]
- Puska, M.J.; Nieminen, R.M. Atoms embedded in an electron gas: Beyond the local-density approximation. Phys. Rev. B 1991, 43, 12221–12233. [Google Scholar]
- Nieminen, R.M.; Puska, M.J.; Mannienen, M. Many-Atom Interactions in Solids (Springer Proceedings in Physics); Springer-Verlang: Berlin/Heidelberg, Germany, 1990; Volume 48. [Google Scholar]
- Nørskov, J.K.; Houmøller, A.; Johansson, P.K.; Lundquist, B.I. Adsorption and dissociation of H2 on Mg surface. Phys. Rev. Lett. 1981, 46, 257–260. [Google Scholar]
- Nørskov, J.K.; Besenbacher, F.; Bøttiger, J.; Nielsen, B.B.; Pisarev, A.A. Interaction of hydrogen with defects in metals: Interplay between theory and experiment. Phys. Rev. Lett. 1982, 49, 1420–1423. [Google Scholar]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Cote, M.; et al. ABINIT: First-principles approach of materials and nanosystem properties. Comp. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Wu, G.; Liu, S.; Zhang, J.; Wu, Y.; Chou, K.; Bao, X. Density functional theory study on hydrogenation mechanism in catalyst-activated Mg (0001) surface. Trans. Nonferrous Met. Soc. China 2009, 19, 383–388. [Google Scholar] [CrossRef]
- Sprunger, P.T.; Plummer, E.W. An experimental study of the interaction of hydrogen with the Mg (0001) surface. Chem. Phys. Lett. 1991, 187, 559–564. [Google Scholar] [CrossRef]
- Johansson, M.; Ostenfeld, C.W.; Chorkendorff, I. Adsorption of hydrogen on clean and modified magnesium films. Phys. Rev. B 2006, 74, 193408:1–193408:4. [Google Scholar]
- Cheung, S.; Deng, W.-Q.; van Duin, A.C.T.; Goddard, W.A., III. ReaxFFMgH reactive force field for magnesium hydride systems. J. Phys. Chem. A 2005, 109, 851–859. [Google Scholar]
- Du, A.J.; Smith, S.C.; Yao, X.D.; Lu, G.Q. Ab initio studies of hydrogen desorption from low index magnesium hydride surface. Surf. Sci. 2006, 600, 1854–1859. [Google Scholar] [CrossRef]
- Du, A.J.; Smith, S.C.; Lu, G.Q. First-principle studies of the formation and diffusion of hydrogen vacancies in magnesium hydride. J. Phys. Chem. C 2007, 111, 8360–8365. [Google Scholar]
- Wu, G.; Zhang, J.; Li, Q.; Wu, Y.; Chou, K.; Bao, X. Dehydrogenation kinetics of magnesium hydride investigated by DFT and experiment. Comput. Mater. Sci. 2010, 49, S144–S149. [Google Scholar]
- Park, M.S.; Janotti, A.; van de Walle, C.G. Formation and migration of charged native point defects in MgH2: First-principles calculations. Phys. Rev. B 2009, 80, 064102:1–064102:5. [Google Scholar]
- Fernandez, J.F.; Sanchez, C.R. Rate determining step in the absorption and desorption of hydrogen by magnesium. J. Alloys Compounds 2002, 340, 189–198. [Google Scholar] [CrossRef]
- Huot, J.; Liang, G.; Baily, S.; van Neste, A.; Schulz, R. Structural study and hydrogen sorption kinetics of ball-milled magnesium hydride. J. Alloys Compounds 1999, 293–295, 495–500. [Google Scholar]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory, 1st ed; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Novaković, N. Ab initio Study of Alkali, Alkali-earth, and Transition Metals Hydrides’ properties. Ph.D. Thesis (in Serbian), Faculty of Physics, University of Belgrade, Belgrade, Serbia, 2010. [Google Scholar]
- Milanović, I. A theoretical study of surface effects on desorption kinetics o hydrogen from MgH2. Master Thesis (in Serbian), Faculty of Physical Chemistry, University of Belgrade, Belgrade, Serbia, 2011. [Google Scholar]
- Kurko, S.; Paskaš-Mamula, B.; Matović, L.J.; Grbović Novaković, J.; Novaković, N. The influence of boron doping concentration on MgH2 electron structure. Acta Phys. Pol. A 2011, 120, 238–241. [Google Scholar]
- Kurko, S.; Matović, L.J.; Novaković, N.; Matović, B.; Jovanović, Z.; Paskaš-Mamula, B.; Grbović Novaković, J. Changes of hydrogen storage properties of MgH2 induced by boron ion irradiation. Int. J. Hydrogen Energy 2011, 36, 1184–1189. [Google Scholar]
- Kecik, D.; Aydinal, M.K. Density functional and dynamics study of the dissociative adsorption of hydrogen on Mg (0001) surface. Surf. Sci. 2009, 603, 304–310. [Google Scholar] [CrossRef]
- Gellat, C.D., Jr.; Ehrenreich, H.; Weis, J.A. Transition-metal hydrides: Electronic structure and the heats of formation. Phys. Rev. B 1978, 17, 1940–1957. [Google Scholar]
- Nørskov, J.K.; Besenbacher, F. Theory of hydrogen interaction with metals. J. Less-Common Metals 1987, 130, 475–490. [Google Scholar]
- Hammer, B.; Nørskov, J.K. Electronic factors determining the reactivity of metal surfaces. Surf. Sci. 1995, 343, 211–220. [Google Scholar]
- Harrison, W.A. Elementary Electronic Structure; World Scientific: Singapore, 1999; p. 539. [Google Scholar]
- Van Essen, R.M.; Buschow, K.H.J. Hydrigen absorption in various zirconium and hafnium based intermetallic compounds. J. Less-Common Metals 1979, 64, 277–284. [Google Scholar]
- Kadir, K.; Sakai, T.; Uehara, I. Synthesis and structure determination of a new series of hydrogen storage alloys: RMg2Ni9 (R = La, Ce, Pr, Nd, Sm and Gd) build from MgNi2 laves-type layers alternating with AB5 layer. J. Alloys Compounds 1997, 257, 115–121. [Google Scholar] [CrossRef]
- Tatsumi, K.; Tanaka, I.; Inui, H.; Tanaka, K.; Yamaguchi, M.; Adachi, H. Atomic structures and energetics of LaNi5-H solid solution and hydrides. Phys. Rev. B 2001, 64, 184105:1–184105:10. [Google Scholar]
- Riabov, A.B.; Yartys, V.A. An interrelation of RHx coordination and H ordering in the structures of intermetalic hydrides. J. Alloys Compounds 2002, 330–332, 234–240. [Google Scholar] [CrossRef]
- Soubeyroux, J.L.; Fruchart, D.; Derdour, S.; Vuillet, P.; Rouault, A. Localization of hydrogen (deuterium) in Hf2FeDx (x = 0–5). J. Less-Common Metals 1987, 129, 187–195. [Google Scholar] [CrossRef]
- Vuillet, P.; Teisseron, G.; Oddou, J.L.; Jeandey, C.; Yaouanc, A. Changes in the crystallographic and magnetic properties of Hf2Fe on hydrogen absorption. J. Less-Common Metals 1984, 104, 13–20. [Google Scholar] [CrossRef]
- Ivanović, N.; Rodić, D.; Koteski, V.; Radisavljević, I.; Novaković, N.; Marjanović, D.; Manasijević, M.; Koički, S. Cluster approach to the Ti2Ni structure type. Acta Crystallogr. B 2006, 62, 1–8. [Google Scholar]
- Cekić, B.; Ivanović, N.; Koteski, V.; Koički, S.; Manasijević, M. The electronic structure of Hf2Co: Perturbed angular correlation study and first principle calculations. J. Phys. Condens. Matter 2004, 16, 3015–3026. [Google Scholar]
- Koteski, V.; Ivanović, N.; Cekić, B.; Milošević, Z. FP-LAPW study of Hf2Ni: Structure, electronic properties and electric field gradients. J. Phys. Soc. Jpn. 2004, 73, 2158–2163. [Google Scholar] [CrossRef]
- Akbarzadeh, A.R.; Ozoliņš, V.; Wolverton, C. First-principles determination of multicomponent hydride phase diagrams: Application to the Li–Mg–N–H system. Adv. Mater. 2007, 19, 3233–3239. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. Theoretical modeling of hydrogen storage materials: Prediction of structure, chemical bond character, and high-pressure behaviour. J. Alloys Compounds 2005, 404–406, 377–383. [Google Scholar]
- Ravindran, P.; Vajeeston, P.; Vidja, R.; Fjellvåg, H.; Kjekshus, A. Modeling of hydrogen storage materials by density-functional calculations. J. Power Sources 2006, 159, 88–99. [Google Scholar]
- Kim, K.C.; Sholl, D.S. Crystal structures and thermodinamic investigation of LiK(BH4)2, KBH4, NaBH4, from first principle calculations. J. Phys. Chem. C 2010, 114, 678–686. [Google Scholar]
- Hector, L.G., Jr.; Herbst, J.F. Density functional theory for hydrogen storage materials: successes and opportunities. J. Phys. Condens. Matter 2008, 20, 064229:1–064229:11. [Google Scholar]
- Balogh, M.P.; Jones, C.Y.; Herbst, J.F.; Hector, L.G., Jr.; Kundrat, M. Crystal structures and phase transformation of deuterated lithium imide, Li2ND. J. Alloys Compounds 2006, 420, 326–336. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ivanović, N.; Novaković, N.; Radisavljević, I.; Matović, L.; Grbović Novaković, J. Electronic Principles of Hydrogen Incorporation and Dynamics in Metal Hydrides. Crystals 2012, 2, 1261-1282. https://doi.org/10.3390/cryst2031261
Ivanović N, Novaković N, Radisavljević I, Matović L, Grbović Novaković J. Electronic Principles of Hydrogen Incorporation and Dynamics in Metal Hydrides. Crystals. 2012; 2(3):1261-1282. https://doi.org/10.3390/cryst2031261
Chicago/Turabian StyleIvanović, Nenad, Nikola Novaković, Ivana Radisavljević, Ljiljana Matović, and Jasmina Grbović Novaković. 2012. "Electronic Principles of Hydrogen Incorporation and Dynamics in Metal Hydrides" Crystals 2, no. 3: 1261-1282. https://doi.org/10.3390/cryst2031261
APA StyleIvanović, N., Novaković, N., Radisavljević, I., Matović, L., & Grbović Novaković, J. (2012). Electronic Principles of Hydrogen Incorporation and Dynamics in Metal Hydrides. Crystals, 2(3), 1261-1282. https://doi.org/10.3390/cryst2031261




