Next Article in Journal
Molecular Dynamics Simulation of Single-Crystal 4H-SiC Nano Scratching with Different Scratching Directions of the Tool
Previous Article in Journal
Phase Compositions and Microwave Dielectric Properties of Na1+xSrB5O9+0.5x Ceramics
Previous Article in Special Issue
Study on Growth Interface of Large Nd:YAG Crystals
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 13
Issue 7
10.3390/cryst13071043
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structural Evolution in a Series of Isomorphous Rare Earth Compounds as Response of Lanthanide Contraction

by
Hans Reuter
*,
Marcel Böltken
,
Maik Horstmann
and
Markus Haase
Chemistry, Department of Biology/Chemistry, Osnabrück University, Barbarastr. 7, 49069 Osnabrück, Germany
*
Author to whom correspondence should be addressed.
Crystals 2023, 13(7), 1043; https://doi.org/10.3390/cryst13071043
Submission received: 9 June 2023 / Revised: 22 June 2023 / Accepted: 26 June 2023 / Published: 30 June 2023
(This article belongs to the Special Issue Emerging Rare-Earth Doped Materials)
Browse Figures
Versions Notes

Abstract

:
The structural parameters of the rare-earth diacetate halide trihydrates, RE(OAc)2Hal·3H2O with RE = Ce − (Pm) − Lu and Hal = Cl, Br, have been determined by low temperature, high-resolution SCXRD in order to examine the effect of lanthanide contraction on the coordination geometry in this series of isomorphous compounds consisting of cationic, acetate-bridged, non-linear, one-dimensional coordination polymers of composition [RE(H2O)3(OAc)2]+ and laterally hydrogen bonded halide ions, Hal−. Although the shrinkage of the unit cell volume follows lanthanide contraction very well over the complete range of investigated RE elements, many other parameters (i.e., lattice constants, angles and distances in the RE··· RE alignment, RE-O bond lengths, etc.) exhibit a more complex response on lanthanide contraction often expressed by sigmoid curves that can be ascribed to a continuous transition from CN9 (RE = Ce) to CN8 (RE = Lu) as one acetate group loses the chelate function, an effect accompanied by significant structural changes of the carboxylate group. Therefore, data are best analyzed by use of two subsets represented by the two different structure types of Ce and Lu, the structural features of which change with decreasing/increasing the size of RE3+, up to the borderline between both subsets.

1. Introduction

In the chemistry of the rare-earth elements, RE, usually comprising the elements of the scandium group (Sc, Y, La) and lanthanides (Ln = Ce to Lu), oxidation state +III plays an important role. Within this group the lanthanide contraction, the shrinkage of atomic and ion radii of Ln with increasing atomic number Z as a result of the lower shielding of the valence orbitals through the diffuse 4f orbitals is a well-known phenomenon not only responsible for the chemical similarity of these elements but also for the nearly identical atomic radii of the second- and third-row d-block elements. In the case of the pure lanthanide metals with valence electron configuration (6s)2(5d)1(4f)n(6p)0, contraction of the metal atom radii [1] exhibits discontinuities for Ln = Eu, Yb as a result of their half-filled and full-filled, respectively, 4f orbitals, but for Ln3+ ions the ionic radii [2] decrease continuously without interruption from 1.196 Å for Ce to 1.032 Å for Lu (Figure 1, Table S1). With RE3+ ionic radii of 1.075, and 1.216 Å the two rare-earth elements Y and La blend in quite well with the other RE elements while the much smaller element Sc [r(Sc3+) = 0.87 Å, CN8] takes an exceptional position.
On the other side, the coordination number, CN, is strongly correlated to the size of a specific metal atom. The highest possible CN this metal atom can achieve in a given oxidation state strongly correlates with its size: the bigger the atom the higher its maximal accessible CN. Consequently, the larger RE elements should expose larger coordination numbers than the smaller ones in a series of isomorphous compounds.
This relationship between lanthanide contraction and coordination number is the reason why the existence range of RE3+ compounds of identical composition is sometimes limited to some few, direct neighboring RE elements and why certain rare-earth compounds with identical composition occur in different structure types.
In case of mononuclear RE3+ coordination compounds, this relationship is less pronounced especially with small, unidentate ligands such as H2O, as the classical examples of RE(III) ethylsulfates, [RE(H2O)9][EtO-SO3]3, RE = La, Ln without Pm, CN9 [3]), and trifluoromethansulfonates, [RE(H2O)9][CF3-SO3]3, RE = La, Ln without Pm, Ho, Er, Tm, CN9 [4]) prove. In both series of compounds crystal structure determinations confirm at both ends CN9 and tricapped trigonal-prismatic coordination of the RE3+ ion.
The relationship becomes more important in di- and polynuclear RE3+ coordination compounds, especially with bidentate, bridging ligands such as the acetate group, OAc: the existence range of rare earth triacetate tetrahydrates, RE(OAc)3·4H2O (dimeric, CN9, monocapped square antiprismatic), i.e., is well-documented by SCXRD only for RE = Sm − Lu [5,6,7], whereas two different structure types (Ho-structure type, CN8, bicapped trigonal-prismatic, RE = Sm − Er, Y [8]; Lu-structure type, CN7, monocapped trigonal-prismatic RE = Tm − Lu, [8]) dominate the structure chemistry of the pure rare earth triacetates, RE(OAc)3.
In literature, a remarkable exception from this trend is documented for the rare-earth diacetate chloride trihydrates, RE(OAc)2Cl·3H2O. Their crystallographic data [RE = Ce − (Pm)-Lu, Y] obtained from X-ray powder diffraction at room temperature [9] refer to a series of isomorphous compounds, whereas some few single crystal structure determinations (RE = Eu [10], Gd [11], and Tb = [12]) demonstrate that their structures are built up of one-dimensional coordination polymers with bridging acetate ligands and CN9 of the RE atoms. With 13/14 data points of RE (as usual, Pm was not investigated because of its radioactivity), this set of compounds provides the best preconditions to study the influence of lanthanide contraction on the structural evolution within a given class of polymeric RE3+ coordination compounds where one expects a reduction of the coordination number from the lightest/largest (Ce) to heaviest/smallest (Lu) rare-earth metal [9].
By chance, we become aware of this class of compounds when searching for improved crystallization conditions of anhydrous rare-earth triacetates as precursors in the synthesis of NaREF4 and LiYF4 core and core/shell nanocrystals [13]. When recrystallizing Eu(OAc)3 · xH2O, originally prepared via the reaction sequence EuCl3·6H2O − Eu2O3 − Eu(OAc)3, we found a few single crystals of Eu(OAc)2Cl·3H2O as side product obviously resulting from the uncomplete chloride-to-oxide transformation.
As the above-mentioned single crystal X-ray structure determinations have been performed using different measurement strategies at different temperatures [295 K, Eu; 150 K, Gd; 123 K, Tb] and as the atomic radii of their rare-earth elements are just in the middle of those from Ce and Lu, we decided to perform a systematic study on the crystal structures of these class of compounds applying uniform measurement conditions in order to obtain comparable and valid data. In addition, we extended the existence range of the class of rare-earth diacetate halide trihydrates, RE(OAc)2Hal·3H2O, to those with Hal = Br.

2. Materials and Methods

2.1. Preparation

All compounds can easily be prepared by solving anhydrous, RE(OAc)3, hydrated, RE(OAc)3 · nH2O, or acetic acid solvated, RE(OAc)3 · nAcOH, rare-earth triacetates in acetic acid, AcOH(aq), and addition of diluted hydrochloric, HCl(aq), or hydrobromic, HBr(aq), acid in a molar ratio of 1:1. A typical reaction equation based on the use of a tetrahydrate is sketched out in Scheme 1. Additional procedures for the preparation of the chlorides are described in the literature [9].
With adhesive solvent, crystals are very sensitive towards moisture free of remaining solvent; they are stable at ambient conditions over periods of hours and days. For X-ray diffraction experiments, crystals have been selected without drying; for elemental analyses and spectroscopic measurements, they have been dried between two filtering papers.
All compounds have been characterized with respect to their C and H content. Mid-infrared and Raman spectra have been recorded for RE = Tb, Dy, Ho, Er, Tm, Yb, Lu, and both halides. These spectra are very similar with only slight differences in wavenumbers and intensities.
All compounds constitute transparent, colorless crystals without those of Yb (pink), and Pr (greenish). Crystal morphology is characterized by a prismatic habit (Figure 2) resulting from the combination of the pinacoids {100}, {010}, and {001}, often elongated along the a-axis, the propagation direction of the coordination polymer (see below).
Typical procedure: 205.0 mg (0.5 mmol) Tb(OAc)3 · 4H2O are dissolved in a 50 mL roll-rim glass by stirring at ambient temperature in about 20 mL concentrated acetic acid, AcOH(aq), before 0.5 mL of 1M hydrobromic acid (0.5 mmol) are added via a syringe. Thereafter, the excess of water and acetic acid is allowed to evaporate at atmosphere up to the crystallization of Tb(OAc)2Br·3H2O.
Analysis (found/calc): C = 12.97/13.11%, H = 3.18/3.30%.

2.2. Spectroscopic Measurement and Elemental Analyses

Mid-infrared spectra were collected on a VERTEX 70 Fourier transform IR spectrometer using the attenuated total reflectance (ATR) technique, Raman spectra with the Fourier transform Raman module RAM II (both: Bruker AXS GmbH, Karlsruhe, Germany). Carbon and hydrogen microanalyses were performed on a vario MICRO cube from Elementar Analysensysteme GmbH, Hanau, Germany.

2.3. Single Crystal X-ray Structure Determinations

Details of sample handling, single crystal X-ray equipment, data collection and processing, structure solution, and refinement have been described previously [13].
All H atoms including those of the water molecules were clearly identified in difference-Fourier syntheses. Hydrogen atoms of the methyl groups were refined with idealized positions and allowed to ride on their parent carbon atoms with d(C-H) = 0.98 Å and common isotropic temperature factors for all three hydrogen atoms of each methyl group. Whenever these values became extraordinarily large, the final difference in Fourier syntheses indicated hydrogen positions of a second methyl orientation. In these cases, both orientations have been included in the structure model with different site occupations but common (now smaller) isotropic temperature factors. Hydrogen atoms of the water molecules were refined with a common O-H distance of 0.96 Å and an angle of 104.95° before they were fixed and allowed to ride on the corresponding oxygen atom with common isotropic temperature factors.
Details on the crystallographic data, data collection parameters, and structure refinement results are summarized in Table 1 (Hal = Cl) and Table 2 (Hal = Br). The listed CCDC numbers contain the supplementary crystallographic data for this paper. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre via https://www.ccdc.cam.ac.uk/structures (accessed on 25 June 2023). Additional tables of bond lengths and angles prepared by SHELXL [14], as well as the results of the structure validation program Checkcif [15] are documented for each compound in the supplementary data.
Molecular graphics were prepared using DIAMOND [16], Mercury [17], and POV-Ray [18], respectively. With the exception of the hydrogen atoms that were drawn as spheres of arbitrary radii, all other atoms are shown in ball-and-stick models as thermal displacement ellipsoids of the 50% level.

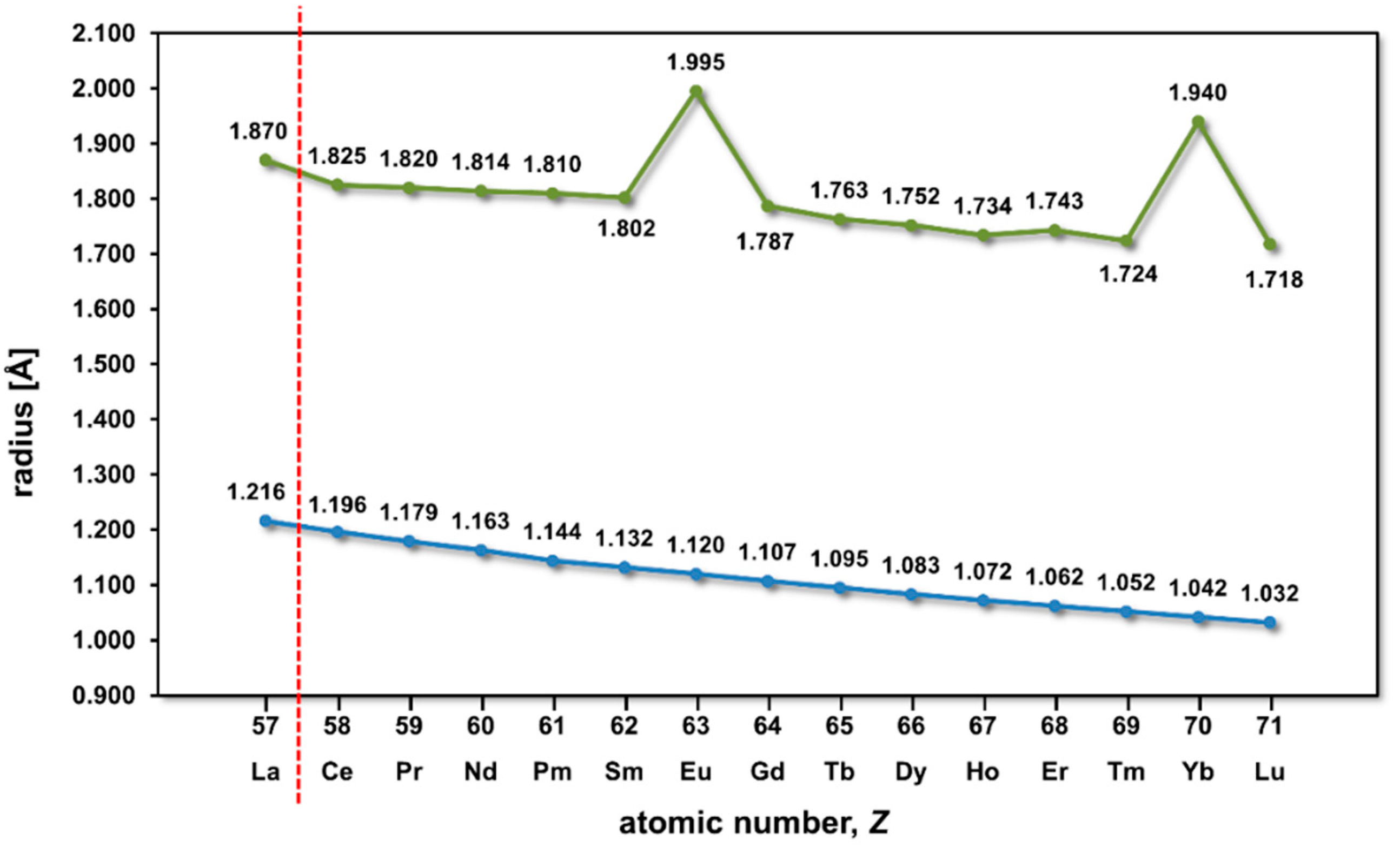
3. Results and Discussion

Our single crystal X-ray measurements in the series of isomorphous RE(OAc)2Hal·3H2O compounds confirm the previous results of a cationic, non-linear, one-dimensional coordination polymer of composition {RE(H2O)3(μ2-OAc)2}+ with two different RE···RE-distances propagating along the a-axis of a monoclinic unit cell of space group P21/n linked together via hydrogen bonds to the halide anions, Hal−. Moreover, they show that a similar series of isomorphous compounds exist for Hal = Br, structurally related to the former one.
Atoms of all compounds were labeled according to the common numbering scheme depicted in Figure 3.

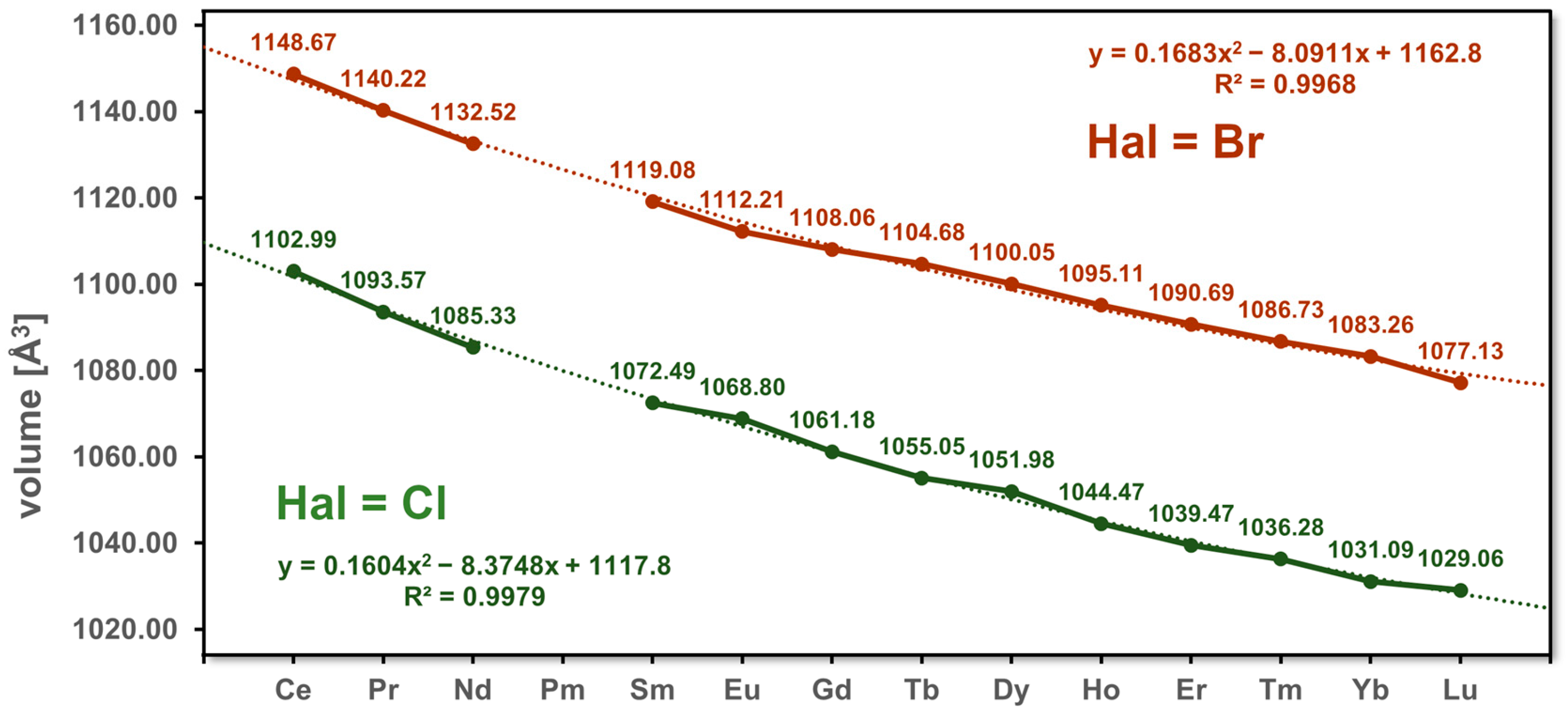
3.1. Unit Cell Volumes and Lattice Parameters

In the two series of RE(OAc)2Hal·3H2O compounds, there are two different size effects with influence on the external (lattice parameters, unit cell volume) as well as internal (bond lengths, bond angle, hydrogen bonds, etc.) structural parameters: the size of the rare-earth elements, RE, and the size of the halide ion, Hal.
The progression of the unit cell volumes as a function of the atomic number of RE is shown in Figure 4. From the larger RE (CE) to the smallest one (Lu), the unit cell volumes decrease almost uniformly and to the same extent for both halides, Hal = Cl [ΔVCe-Lu = 73.93 Å3] as well as Hal = Br [ΔVCe-Lu = 71.54 Å3].
To visualize lanthanide contraction such graphs are usually fitted by use of linear [V(x) = Ax + B] or quadratic [V(x) = Ax2 + Bx + C] regression analyses [19]. In the present case, linear regression analyses (Figure S3) result in quite well reliability factors RCl/Br [0.9872/0.9831] but reveal systematic errors, too: volumes calculated using the fitting parameters are too large for the lighter and heavier RE elements and too small for elements in between (Figure S4). Even if these differences are very small and in the range of some permille they are significant and of the same kind and quantity in both series of halide compounds. In contrast, regression analysis by use of quadratic equations (Figure 4) works better [RCl/Br = 0.9979/0.9968] and produces errors ΔV = Vobs − Vcalc that only show a statistical distribution (Figure S5).
The difference d ¯ (VBr − VCl) between the unit cell volumes of compounds with the same RE but different halide ions amount to 48.3(25) Å3. In the same extent as unit cell volumes decrease, densities increase [RCl/Br = 0.9978/0.9988, quadratic equations].
Although the unit cell volumes reflect both the lanthanide contraction and the size of the different halide ions very well, changes in the lattice parameters must follow other rules, because the lanthanide contraction should predominate in the direction of the crystallographic a-axis (=the propagation axis of the coordination polymer) whereas the size of the halide ions interconnecting the coordination polymers via hydrogen bonds should cause stacking variations with a larger influence on the lattice parameters b, c, and ß.
With respect to the a-axis, the size of the halide ions should have a negligible effect as they are not involved in the formation of the coordination polymer. Changes in lengths of a-axes with increasing atomic number Z of RE are graphically plotted in Figure 5 for both halides. As expected from lanthanide contraction, the length of this axis decreases significantly [Δ(aCe − aLu)Cl/Br = 0.1957/0.1986 Å] from RE = CeCl/Br [7.9625(3)/7.9597(3) Å] to RE = LuCl/Br [7.7668(3)/7.7611(3) Å]. Applying quadratic regression analyses over the complete datasets results in quite well R factors RCl/BR [0.9885/0.9592]. Differences between observed and calculated values are very small for the early RE elements (Ce to Gd) but become larger for the late ones (Tb to Lu).
On the first view, one might suggest that the greater deviations at the right end of the diagram are caused by experimental errors perhaps resulting from absorption effects as the linear absorption coefficients μ(MoKα) increase with increasing Z of the RE element. A more detailed analysis taking into account the evolution of all sets of internal and external structural parameters (see below), however, shows that the response of the atom arrangement in the structures of the RE(OAc)2Hal·3H2O compounds on lanthanide contraction is more complex than expected and is inadequately described by use of only one fitting equation over the complete range of the 6f-bloc metals. Thus, most of the parameters analyzed in this paper show significant chances when comparing their progress in the area of the early RE elements, eRE = Ce − Gd, with that in the area of the late ones, lRE = Tb − Lu, very similar to the situation just described for the a-axis. As a consequence, we will handle the data of both groups of RE elements separately throughout the paper whenever meaningful.
In the case of the early RE elements, differences between acl and aBr are very small (for Ce −Sm they are marginal), and both series can be fitted with high reliability [RCl/Br = 0.9964/0.9979] by use of quadratic equations (Figure 5) for the convex curvatures. In the case of the late RE elements, the graphs, however, display concave curvatures. On the foregoing statements, this contrary behavior seems implausible but becomes more reasonable when taking into account that the alignment of the RE atoms (distances, angles) in the coordination polymer acts as a further adjusting screw to bring lanthanide contraction, coordination geometry, and hydrogen bonded halide ions into structural balance. Obviously, these interactions are very complex in the case of the late RE elements as even the quadratic regression analyses of the data are of limited precession [RCl/Br = 0.9331/0.8857]
As mentioned above, all other lattice parameters should be much more infected by the size of the halide ion as they crosslink the individual rods of coordination polymers via hydrogen bonds in the bc-plane.
The lengths of the c-axes (Figure S6) decrease with decreasing size of RE, too, from 17.6973(6)/18.0642(8) Å for RE = CeCl/Br to 17.0618(7)/17.2952(6) Å for RE = LuCl/Br. The decrease is independent of the halide ion, but for Hal = Br lengths of the c-axes are longer [from 0.3859 Å for Pr up to 0.2334 Å for Lu] than for Hal = Cl. In both subsets, data can be fit very reliably with quadratic equations [RCl/Br(eRE) = 0.9922/0.9961, RCl/Br(lRE) = 0.9960/0.9955].
Much more complex behavior is observed for the b-axes (Figure S7). For Hal = Cl the length of the b-axis decreases slightly [Δb(Cl) = −0.0979 Å] from Ce [7.9276(3) Å] to Lu [7.8297(3) Å]. The b-axes are longer for Hal = Br than for Hal = Cl but in contrast to the c-axis the differences between both increase from RE = Ce [0.1166 Å] to Lu [0.2405 Å]. This is due to the fact that the lengths of the b-axis increase with decreasing size of RE from 8.0442(3) Å for Ce to 8.0702(3) Å, RE = Lu for Hal = Br [Δb(Br) = +0.026 Å]. When fitting the data of both sectors using quadratic equations the reliability factors are moderate in the case of the early RE elements [RCl/Br(eRE) = 0.9856/0.9334] but poor [RCl/Br(LRE) = 0.7738/0.9220] in the case of the late RE elements reflecting a complicated interaction between the structure constituting building units.
The foregoing statement becomes obvious when analyzing the monoclinic angle ß (Figure S8). First, ß is always smaller for Hal = Br than for Hal = Cl. The difference between both decreases from RE = Ce [ΔßBr/Cl = 2.39°] to RE = Lu [ΔßBr/Cl = 1.24°] as the decrease of the absolute values [Δß = ßCe − ßLu] between Ce and Lu is less expressed for Hal = Br [Δß = 0.63°] than for Hal = Cl [Δß = 1.79°]. As before the dataset of the chlorides can be split into two separate datasets but there is no need as the R-value [0.9977] of the quadratic regression analysis over the complete series of RE elements is excellent. Splitting, however, is obviously necessary for the data of the bromides [R = 0.8347, complete dataset, quadratic equation]. For eRE, these data show a concave curvature, and those of lRE show a convex one resembling the course of the a-axis in this subset. The corresponding fits are acceptable [ReRE/lRE = 0.9805/0.9796, quadratic equation].

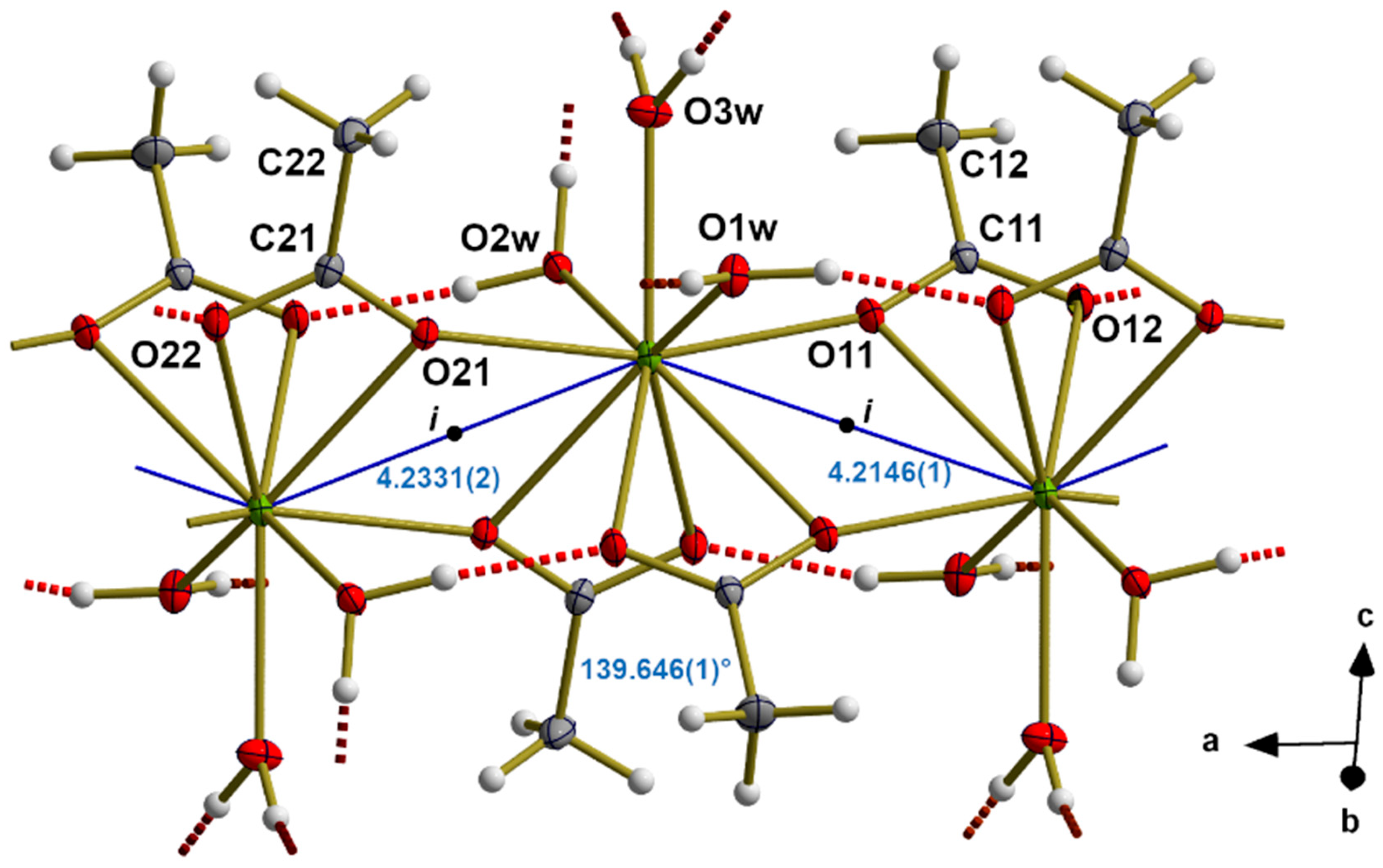
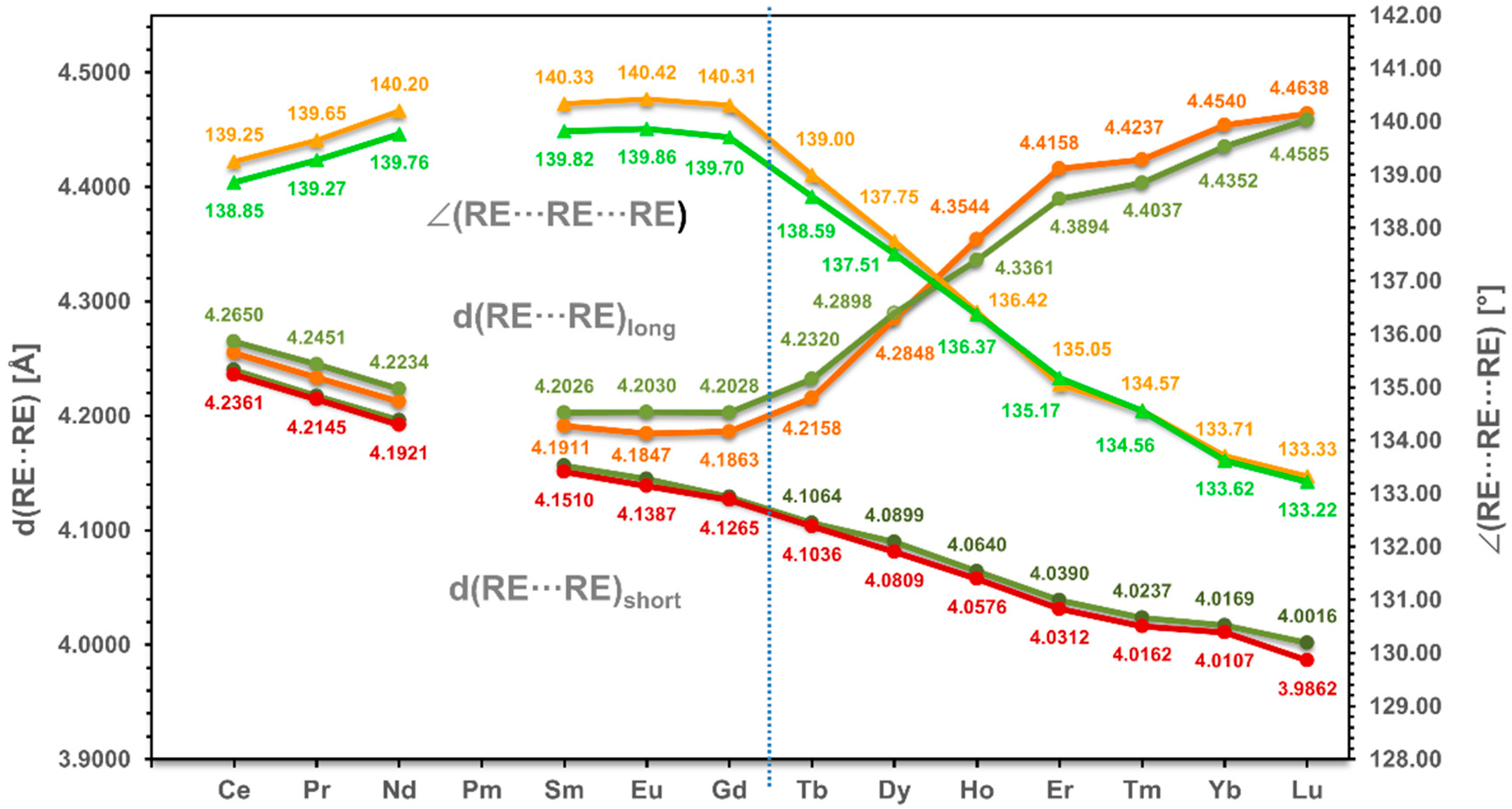
3.2. Alignment of RE in the Coordination Polymer

The first information about the response of the atom arrangement in the RE(OAc)2Hal·3H2O structure on the shrinkage of the ion radius with increasing Z results from the alignment of the RE atoms within the coordination polymer. Its repeat unit is characterized by two different interatomic RE···RE distances and one angle, ∠(RE···RE···RE), resulting from the non-linear arrangement of the RE atoms. The shorter of both interatomic distances, d(RE···RE)short, results from the bridging via the acetate ligand OAc_2 (atoms O21-C22, see below), the longer one, d(RE···RE)long, from the bridging via acetate group OAc_1 (atoms O11-C12, see below). The corresponding data as a function of increasing Z are summarized in Table S2 and visualized in Figure 6.
At first glance, d(RE···RE)short decreases continuously with decreasing size of RE from CeCl/Br = 4.2361/4.2549 Å to LuCl/Br = 3.9862/4.0016 Å [ΔCl/Brd(RE···RE)short = 0.2499/0.2533 Å]. This parameter is almost independent of the size of the counterion and can adequately be described by a linear equation [RCl/Br = 0.9953/0.9956] over the complete dataset.
Comparable RE···RE distances are found in many dimeric and polymeric RE coordination compounds. For the reason of comparability, we will restrict the discussion to pure acetate compounds measured exactly on the same conditions as in the present paper. Values from the literature may differ as a result of different measurement and refinement strategies. The relations between d(RE···RE) of RE(OAc)2Hal·3H2O to those in other RE acetate compounds are graphically represented in Figure S9. In the dimeric molecules of the triacetate tetrahydrates the curve of the RE···RE distances shows an almost similar behavior over the complete range of its existence range [RE = Sm − Lu] but with an offset of about +0.05 Å. In the one-dimensional coordination polymer of the rare earth triacetate diacetic acid solvates, RE(OAc)3 ·2AcOH with RE = Nd − Gd [13], the length of both different RE ···RE distances are of the same magnitude as the RE···RE distances discussed here, whereas the shorter one is considerably stronger. Further values come from the two structure types of pure rare-earth triacetates. In the structures of the Eu(OAc)3-structure type the curve of the interatomic RE··· RE distances runs parallel with an offset of about −0.05 Å over the complete set of data [RE = Eu − Er], whereas the RE···RE distances in the Lu(OAc)3-structure type [RE = Tm − Lu] are more than 1 Å longer.
d(RE···RE)long decreases with decreasing size of RE, too, up to minima in the range of RE = Sm, Eu, Gd. Thereafter, however, the values increase rapidly giving both curves the appearance of a sinusoidal function with a point of inflection around RE = Dy/Ho. For d(RE···RE)long, the minimal and maximal values differ by 0.2557/0.2778 Å for Hal = Cl/Br. The complex behavior of this structural parameter is completely different from what one would expect from lanthanide contraction and is one of the strongest indicators to separate the whole dataset into two subsets for eRE and lRE as regression analyses work well only therein. Thus, values d(RE···RE)long can be described by use of a quadratic equation with high reliability [RCl/Br = 0.9990/0.9987, concave] in the first subset, and [RCl/Br = 0.9911/0.9989, concave] in the second subset. Looking into more detail, the decrease of d(RE···RE)short exhibits a similar, but very flat sigmoid curvature in the opposite direction to d(RE···RE)long. Division of the corresponding data into two subsets results in somewhat better fits by quadratic equations (RCl/Br = 0.9961/0.9989, concave, subset 1/RCl/Br = 0.9950/9924, convex, subset 2) than the regression analysis over the complete set (see above).
The long RE···RE distances show in contrast to the short ones a significant impact from the size of the halide ion as they are shorter for Hal = Br for the larger RE atoms, whereas the situation inverts on the ascending branch of the curves with decreasing size of RE after a crossing point of both curves at RE = Dy.
The progress of the angles between the RE atoms exhibits a behavior inverse to the behavior of the long RE···RE distances: first, they increase with decreasing size of RE up to maxima around RE = Sm, Eu, Gd, then the values decrease rapidly up to Lu giving the complete curve a sinusoidal appearance with a point of inflection around RE = Ho. As before, the progress of this parameter can be explained quite well by splitting the whole dataset into two different subsets. Regarding the two subsets, the values in the eRE subset differ by 1.01°/1.27° and those in the lRE subset by 5.37°/5.67°. Within the subsets, all curves can be fit as usual with quadratic equations of quite good [RCl/Br = 0.9684/0.9731, eRE subset, concave] to very good [RCl/Br = 0.9971/0.9950, lRE subset, convex] reliability factors.

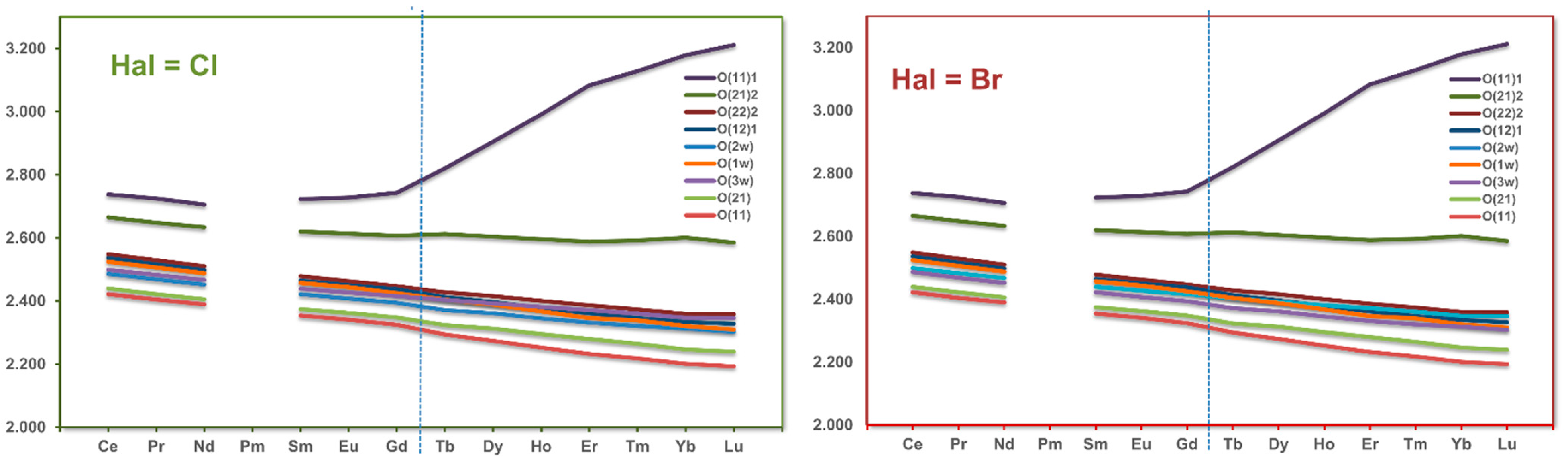
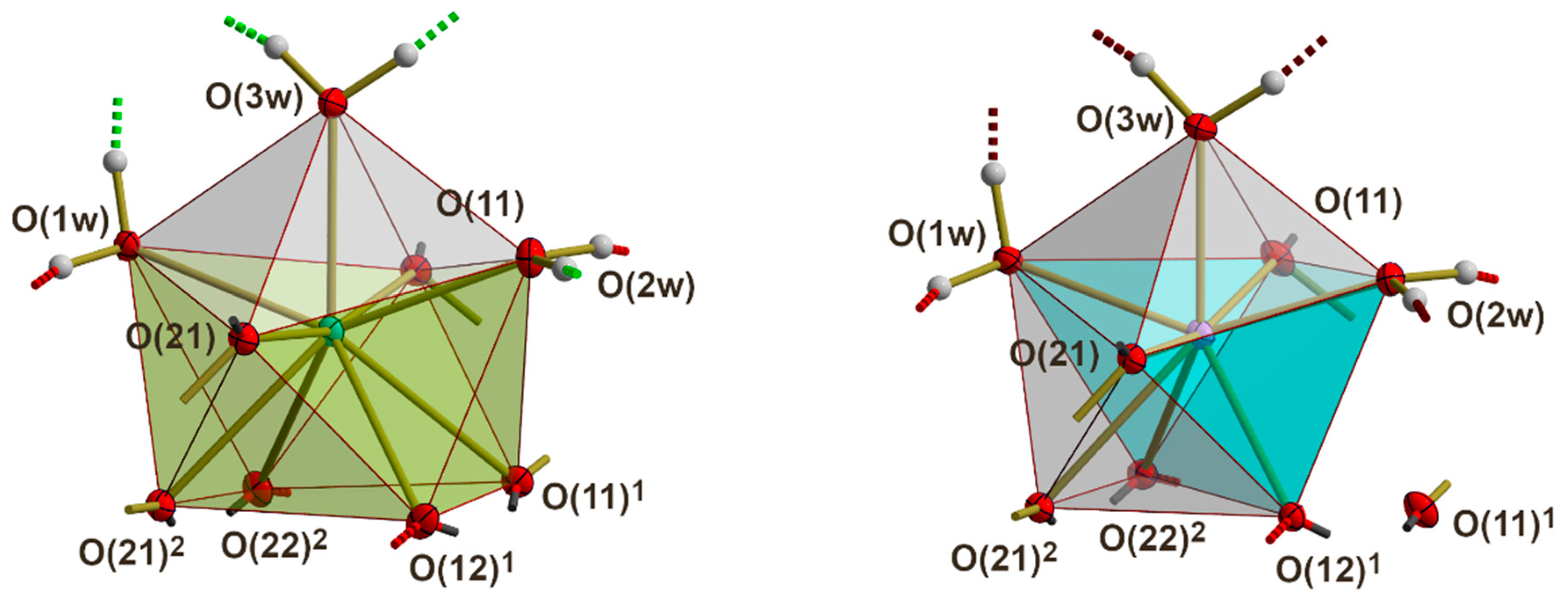
3.3. RE Coordination

Further information on the interaction of lanthanide contraction, halide size, and atom arrangement comes from the coordination sphere around the RE atoms. This coordination sphere only consists of oxygen atoms, delivered from three water molecules and two acetate anions. The corresponding RE-O distances are summarized in Table 3 and visualized as a function of increasing atomic number Z of RE in Figure 7.
RE-O distances for a given RE element cover ranges of 0.316/0.329 Å for RE = CeCl/Br, and 1.018/1.050 Å for RE = LuCl/Br. Although most of the different RE-O distances decrease with increasing Z of RE, i.e., the shortest one [RE-O(11)], by 0.229 Å for both halides, the longest ones, [RE-O(11)1], first decrease, too, up to minima at RE = Eu before they increase again giving the curves a similar sigmoid shape as observed for d(RE···RE)long (see above). From Ce to Lu these bonds become longer by 0.473 Å for Hal = Cl and 0.492 Å for Hal = Br. As a result, the coordination number of RE decreases from CN9 for Ce to CN8 for Lu accompanied by a change of the coordination polyhedra from distorted, monocapped square antiprismatic for Ce to distorted, bicapped trigonal prismatic for Lu (Figure 8). In this context, it seems advised to speak of two different structure types, represented by the atom arrangement of these two RE elements. Both structure types are correlated to each other in the way that the structural parameters of the Ce-structure type change in direction.
Again, quadratic regression analyses work quite well when splitting the dataset and fitting the data of both subsets separately. Parameters of the resulting equations and reliability factors R are given in Figure S10 for d(RE···OAc) and in Figure S11 for d(RE···H2O).
Besides this general trend, the data provide an interesting feature highlighting the transition between both coordination polyhedra at the common border of both subsets. To recognize this feature, the evolution of the RE-O distances with decreasing size of RE has to be analyzed in more detail looking separately at the RE-H2O distances (Figure 9).
In both polyhedra, the three water molecules act as monodentate ligands. Therefore, one might expect that the corresponding bond lengths decrease continuously and uniformly from Ce to Lu, in accordance with lanthanide contraction and with the observation in several other classes of isostructural compounds such as the nonahydrate triflates and ethylsulfates mentioned above. In the present case, however, two significant alterations can be deduced from Figure 9: (i) there is a significant jump in the bond lengths between the first (eRE, Ce-structure) and second subset (lRE, Lu-structure type), and (ii) the RE···H2O_1 bond becomes much stronger/shorter with increasing Z than the two other RE···H2O bonds in the lRE-subset. At the right end (RE = Lu) of the RE elements this bond is as strong/short as the RE···H2O_2 bond.
This behavior corresponds very well with the fact that the oxygen atom of H2O_1 occupies a position in the coordination sphere of RE just opposite to O(11)1 of OAc_1. In the way this oxygen moves out of the RE coordination sphere (with decreasing size of RE) the stronger becomes the RE···H2O_1 bond.

3.4. Coordination Modes of the Acetate Ligands

Both acetate groups act as bidentate, bridging ligands independently from whether the coordination number is 8 or 9. Differences in coordination numbers result from the fact that one acetate group (OAc_2) acts as a chelating ligand over the complete series of RE elements, in contrast to the other one (OAc_1), which loses this chelating function with decreasing size of RE (Figure 10a).
Besides the above-mentioned global view on the RE-OAc bond lengths, a detailed inspection of bond lengths and angles within the acetate groups will give a deeper insight into the structural evolution within both structure types as a consequence of lanthanide contraction. In the following, we will use the Harris symbol as described by Coxall et al. [20] for the different acetate coordination modes to distinguish the two different crystallographic acetate ligands shown in Figure 10a. The first one (atoms labeled 1n) exhibits a bridging 2.11 (1κO; 2κO′) coordination mode. In addition, these acetate ligands act as hydrogen acceptors in hydrogen bonds.
Bond lengths and angles within the acetate groups are listed in Table S4. C-C bonds only slightly vary in the range of the standard deviations. For OAc_2 they are in general a little bit shorter [ d ¯ (C(21)-C(22)Cl/Br = 1.490(4)/1.492(2) Å] than for OAc_1 [ d ¯ (C(11)-C(12)Cl/Br = 1.494(3)/1.496(3) Å].
In OAc_2 the two different C-O bonds differ on average by 0.020/0.022 Å [Cl/Br] with the longer/weaker [ d ¯ Cl/BrO(21)-C(21) = 1.279(2)/1.279(2) Å] bonds to O(21) and the shorter/stronger [ d ¯ Cl/BrO(22)-C(21) = 1.259(3)/1.257(2) Å] one to O(22), both less affected from the size of the RE3+ ion are negligible as the standard deviations show (Figure S11). Bond angles in these acetate groups (Figure S12) are unaffected by lanthanide contraction only in the case of the O(22)-C(21)-C(22) bond angles, the angles opposite to the bridging RE atoms [ d ¯ Cl/Br(∠O(21)-C(21) = 121.2(2)°/120.0(3)°]. On the other hand, bond angles between both oxygen atoms decrease by 1.5°/0.6° from CeCl/Br [119.0(2)°/119.3(2)°] to LuCl/Br [117.5(2)°/118.2(3)°] and increase the bond angles O(21)-C(21)-C(22) by 1.4°/0.5° from CeCl/Br [119.7(2)°/120.1(2)°] to LuCl/Br [121.1(3)°/120.6(3)°] in this acetate ligand.
In Oac_1, the O-C bonds are strongly correlated with the coordination behavior of the acetate groups. Thus, the bonds between O(12) and C(11) increase in length with the increasing length of the chelate bond. The slight increase finds expression when calculating the standard deviations of the mean values [ d ¯ Cl/Br(O12)-C(11) = 1.261(3)/1.261(5) Å]. In contrast, bonds between O(22) and C(11) become shorter/stronger [dCl(O12-C11)Ce-Lu = 1.273(3) − 1.257(2) Å/dBr(O12-C11)Ce-Lu = 1.273(3) − 1.2534) Å,] with decreasing size of RE3+ featuring a sigmoid curve inverse to the sigmoid curve of the corresponding RE-O(11)1 bonds of Figure 7. From RE = Ho up to RE = Lu, this bond is stronger than the second C-O bond as a result of the loss of the chelate function. In Oac_1, the bond angles (Figure S12) increase between the oxygen atoms [∠Cl/Br(O11-C11-O12)] by 1.9°/2.4° from CeCl/Br [119.5(2)°/119.3(2)°] to LuCl/Br [121.4(2)°/121.7(3)°] also as a result of the loss of the chelate function. To the same extent [1.9°/2.2°] as the bond angles O(12)-C(11)-C(12), the bond angles opposite to the O-RE bridges decrease. Only the bond angles between O(22) and C(22) remain almost constant [ ¯ Cl/Br(O12-C11-C12) = 120.6(2)°/120.6(2)°] over the complete series of RE elements.
Weakening and loss of the chelating function is accompanied by a movement of the acetate group OAc_1 as a whole as visualized in Figure 10b. With decreasing size of the RE atom the acetate groups perform a rotation in the plane of the metal and oxygen atoms so that the RE-O(11)1 bonds lose their chelate function. This rotation is accompanied by a movement of the methyl group in the direction of the central part of the coordination polymer. In some cases (see above: Single crystals X-ray structure determination), this movement opens additional space for a second orientation of this methyl group.
A significant influence of the halide ions and their sizes on the structure parameters of the acetate ligand is not recognizable. Changes of bond angles in the two different acetate groups of RE(OAc)2Cl·3H2O as a function of Z of RE are visualized in Figure 11.

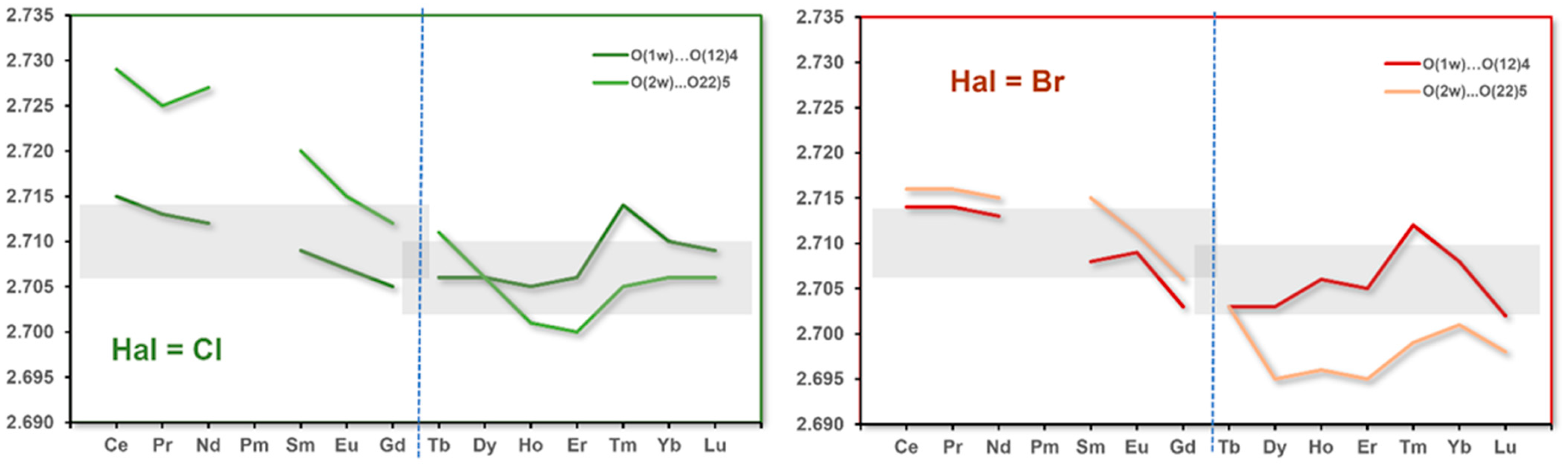
3.5. Hydrogen Bonds

In addition to coordinative RE-O and electrostatic anion-cation interactions, there exist hydrogen bonds between the water molecules and halide ions. Some specific data characterizing these hydrogen bonds are summarized in Table S4.
-OH···O hydrogen bonds are restricted to water molecules between neighboring RE-atoms alongside the surface of the coordination polymer (Figure 3). Accordingly, they are responsible—besides the μ2-acetate groups—for the constitution of the coordination polymer but also depend on lanthanide contraction and the alignment of the RE atoms. With d ¯ (O···O)Cl/Br = 2.707(3)/2.708(4) Å the hydrogen bonds [O(1w)···O(12)4] alongside the short RE···RE distances are relatively strong and almost independent from lanthanide contraction and size of the halide ion (Figure S12). Moreover, these hydrogen bonds are of similar strength in both subsets.
By way of contrast, the O···O distances alongside the long RE···RE distances [O(2w)···O(22)5] depend on the size of the halide ion [Br < Cl] (Figure 12).
In addition, they are longer than the former one [especially for Hal = Cl and RE = Ce, Δ(O···O)long-short = 15 pm], and decrease in length/becomes stronger in the case of the early RE elements [Δ(O···O)Cl/Br = 15/10 pm] as the distances between the metal atoms increase (Figure 6). In the case of the late RE elements most of these hydrogen bonds, Hal = Cl as well as Hal = Br, are stronger than the previous one in the same subset whereas their variations follow similar trends. In the first subset, the regression analyses of these O···O distances show less accuracies [R = 0.9611–0.9958], for the late RE elements the corresponding values spread around a mean value of 2.698(3)/2.705.4(4) Å for Hal = Cl/Br.
Additional hydrogen bonds exist between the water molecules of the coordination polymer and the laterally located halide ions. Changes of O···Hal distances of these hydrogen bonds are depicted in Figure 13 as a function of Z.
In the subset of eRE, the O···Hal distances only slightly increase with Z. With the exception of the longest/weakest hydrogen bond [O3w···Hal6 = 3.170(7)/3.305(6) Å], variations in bond lengths are small, which is why it seems justified to describe these hydrogen bonds by use of mean values [ d ¯ (O3w···Cl3/Br3) = 3.073(4), 3.074(2) Å, d ¯ (O2w···Cl/Br) = 3.134(2)/3.206(2) Å, and d ¯ (O1w···Cl3/Br3) = 3.274(4), 2.275(3) Å]. With respect to the halide ion, the differences between the two strongest hydrogen bonds are only marginal [0.001 Å] for Hal = Cl, but significant [0.021 Å] for Hal = Br.
Some other trends are observed in the case of the O···Hal distances in the subset of lRE. Although the two strongest/shortest hydrogen bonds slightly increase [0.006,0.006/0.008, 0.004 Å, Hal = Cl/Br] with decreasing size of the RE3+ ion, the weakest/longest one increases significantly [0.023/0.019 Å]. A completely different behavior is found in the case of the second weakest hydrogen bonds as their values decrease markedly, more expressed for Hal = Br [0.046 Å] than for Hal = Cl [0.024 Å]. All changes described result from lanthanide contraction, and its influence on the RE alignment and coordination including the positions of the water molecules that directly influence the stacking of the coordination polymers within the ab-plane and in the c-direction as the discussion on the variation of the lattice parameters with decreasing size of RE documented (see above).

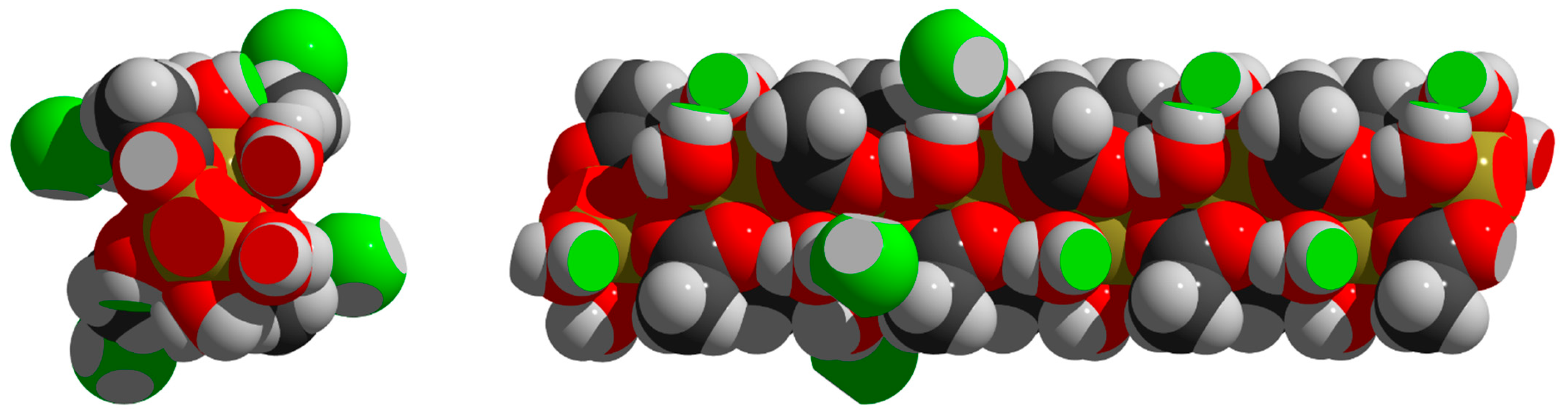
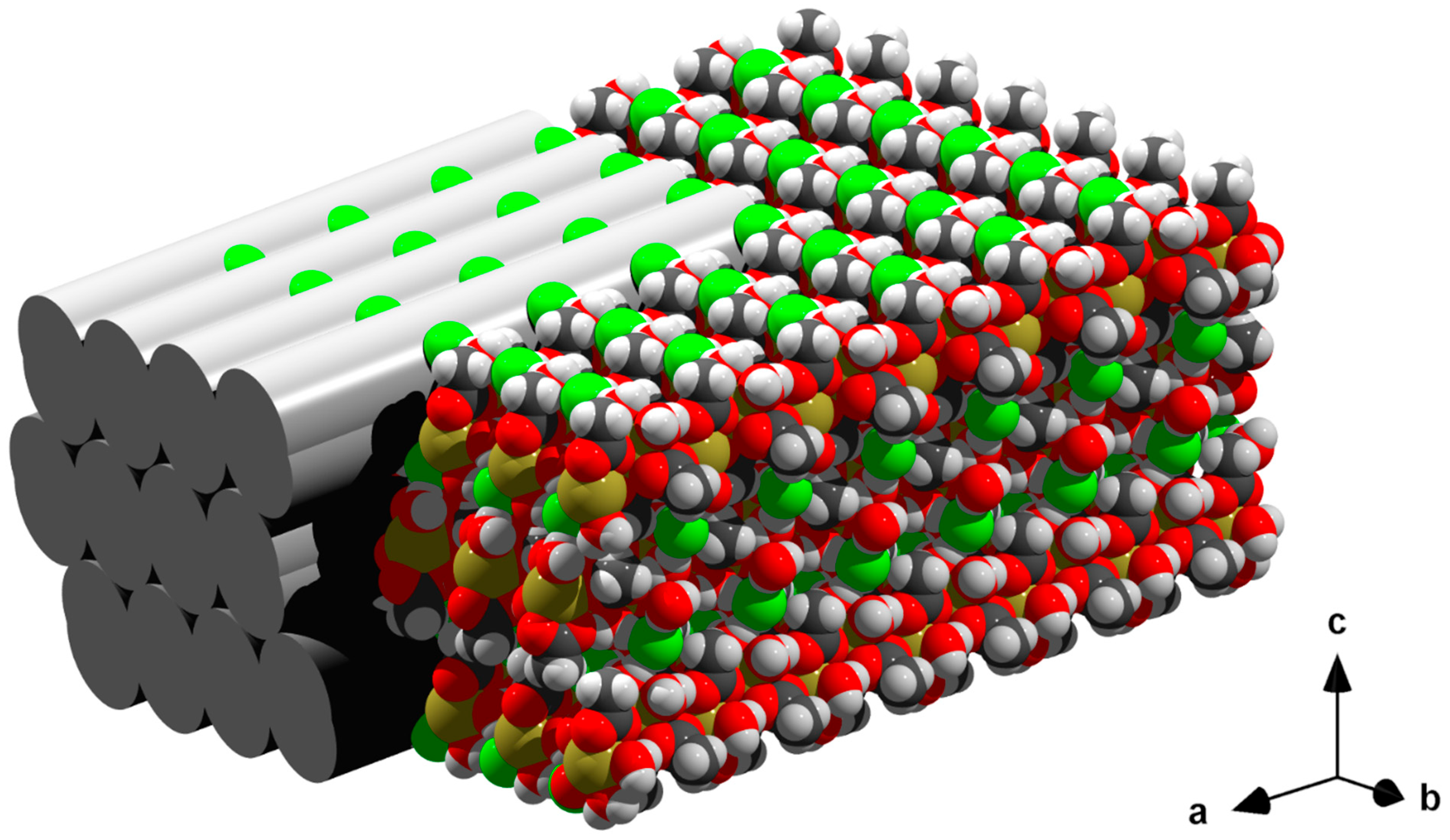
3.6. Packing

In summary, the one-dimensional coordination polymers constitute linear rods with an elliptical cross-section, constricted in the middle to some extent (Figure 14). Its surfaces consist alternately of apolar methyl groups and polar water molecules. The latter are involved in -OH O hydrogen bonds alongside the rods or hydrogen bonds to the halide ions.
The interaction of these rods (Figure 15) via the hydrogen bonds with the halide ions results in their sheet-like arrangement within the ab-plane and the stacking of these sheets in the direction of the c-axis with the monoclinic angle ß.

4. Conclusions

Our SXRD data underline the important role of lanthanide contraction and size of the halide ion on the structural evolution in the series of isomorphous RE(OAc)2Hal·3H2O compounds and reveal the complex response of a given atom arrangement on these two variables.
Some parameters such as the unit cell volumes reflect the shrinkage of the rare-earth element throughout the complete series of compounds as confirmed by quadratic regression analyses whereas some others including lattice constants and most bond lengths and angles exhibit a more complex behavior often associated with sigmoid curves. These findings are best described by separating the datasets into two subsets, one with the data of the early RE elements and one with the data for the late RE elements. As a result, most of the data in the individual datasets can be simulated with high reliability using quadratic regression analyses often with different curvatures (concave/convex) in the two datasets. Both subsets are represented by different structure types, the Ce-structure type in case of the early RE elements and the Lu-structure type in case of the late ones, both with structure parameters that converge towards each other with decreasing/increasing RE3+ radius up to the borderline between both groups of elements giving rise to a continuous transition from CN9, distorted monocapped square antiprismatic for the Ce-structure type to CN8, distorted bicapped trigonal prismatic for the Lu-structure type. These and many other structural changes are facilitated by the flexibility of the RE alignment within the non-linear, one-dimensional coordination polymer to adjust both the lanthanide contraction and the spatial requirements of the hydrogen bonds to the halide ions. Moreover, our data show that the reduction of the coordination number as a consequence of lanthanide contraction is accompanied by the loss of the chelate function of one of the two acetate groups with a strong influence on its internal structure parameters and on the free rotation of its methyl group.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst13071043/s1, Table S1: REatom and RE3+ ionic radii; Figure S1: MIR spectrum of Tb(OAc)2Br·3H2O; Figure S2: Raman spectrum of Tb(OAc)2Br·3H2O, Figure S3: Unit cell volume and linear fit, Figure S4: ΔV(linear) = Vobs − Vcalc, Figure S5: ΔV(quadratic) = Vobs − Vcalc,, Figure S6: c-axis, Figure S7: b-axis, Figure S8: angle ß, Table S2: Structural data of RE···RE interaction, Figure S9: d(RE···RE) with additional data, Figure S10: RE-OAc bond lengths, Figure S11: RE-H2O bond lengths and quadratic regression analyses, Table S3: Bond lengths and angles within acetate groups, Figure S12: OAc bond lengths, Figure S13: OAc bond angles, Table S4: data of hydrogen bonds.

Author Contributions

Conceptualization, M.H. (Markus Haase), and H.R.; resources, M.B. (Hal = Cl) and M.H. (Maik Horstmann) (Hal = Br); original draft preparation, H.R.; visualization, H.R.; funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Deutsche Forschungsgemeinschaft, HA 1649/7-1.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article or Supplementary Materials.

Acknowledgments

We thank the Deutsche Forschungsgemeinschaft and the Government of Lower-Saxony for funding the diffractometer and acknowledge support by Deutsche Forschungsgemeinschaft (DFG).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Holleman/Wiberg-Anorganische Chemie. Nebengruppenelemente, Lanthanoide, Actinoide, Transactinoide-Table V, 103rd ed.; Wiberg, N., Ed.; Walter de Gruyter: Berlin, Germany; Boston, MA, USA, 2016; Volume 2. [Google Scholar]
  2. Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomie Distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
  3. Gerkin, R.E.; Reppart, W.J. The structures of the lanthanide ethyl sulfate enneahydrates, M(C2H5SO4)3.9H2O [M = La -Lu (except Pm), at 171 K. Acta Cryst. 1984, C40, 781–786. [Google Scholar] [CrossRef]
  4. Chatterjee, A.; Maslen, E.N.; Watson, K.J. The Effect of Lanthanoid Contraction on the Nonaaqualanthanoid(III) Tris(trifluoromethanesulfonates). Acta Cryst. 1988, B44, 381–386. [Google Scholar] [CrossRef]
  5. Junk, P.C.; Kepert, C.J.; Wei-Min, L.; Skelton, B.W.; White, A.H. Structural Systematics of Rare Earth Complexes. X. (‘Maximally’) Hydrated Rare Earth Acetates. Austr. J. Chem. 1999, 52, 437–457. [Google Scholar] [CrossRef]
  6. Arias, J.L.; Cabrera, A.; Sharma, P.; Rosas, N.; Garcia, J.L.; Hernandez, S. Catalytic auto-condensation of 2,4-pentanedione promoted by Sm(III) acetylacetonate: The X-ray strcutre of a novel complex [Sm(CH3COO)3(H2O)2](H2O)2. Inorg. Chim. Acta 2000, 310, 261–264. [Google Scholar] [CrossRef]
  7. Yu, Q.; Zhou, X.; Liu, M.; Chen, J.; Zhou, Z.; Yin, X.; Cai, Y. Syntheses, characterization, and luminescence of two lanthanide complexes [Ln2(acetate)6(H2O)4]·4H2O (Ln = Tb(1), Sm(2)). J. Rare Earth 2008, 26, 178–184. [Google Scholar] [CrossRef]
  8. Lossin, A.; Meyer, G. Wasserfreie Selten-Erd-Acetate, M(CH3COO)3 (M = Sm-Lu, Y) mit Kettenstruktur. Kristallstrukturen von Lu(CH3COO)3 und Ho(CH3COO)3. Z. Anorg. Allg. Chem. 1993, 619, 1609–1615. [Google Scholar] [CrossRef]
  9. Lossin, A.; Meyer, G. Dimers and chains in lanthanide acetate-chloride hydrates [M(CH3COO)2(H2O)3]Cl (M = Ce-Lu, Y) and [M(CH3COO)(H2O)6]Cl2 H2O (M = La-Sm): A survey of their synthesis, crystal chemistry and thermal decomposition. J. Less Common Met. 1991, 175, 301–308. [Google Scholar] [CrossRef]
  10. Schleid, T.; Meyer, G. Synthese und Kristallstruktur von Europium(III)-diacetatotriaquo-chlorid, [Eu(CH3COO)2(H2O)3]Cl. Z. Naturforsch. 1989, 44b, 1007–1010. [Google Scholar] [CrossRef] [Green Version]
  11. Cesur, N.; Pantenburg, I.; Meyer, G. Crystal structure of catena-[triaqua-bis(acetato-O,O′)gadolinium(III)]chloride, [Gd(CH3COO)2(H2O)3Cl. Z. Kristallogr. New Cryst. Struct. 2005, 220, 631–632. [Google Scholar] [CrossRef]
  12. Chen, W.-T.; Luo, Z.-G.; Yao, Z.-L. Synthesis, crystal structure and fluorescense of an unusual terbium carboxylate. Acta Chim. Slov. 2012, 59, 949–953. [Google Scholar] [PubMed]
  13. Haase, M.; Rissiek, P.; Gather-Steckhan, M.; Henkel, F.; Reuter, H. Structural Evolution in the RE(OAc)3·2AcOH Structure Type. A Non-Linear, One-Dimensional Coordination Polymer with Unequal Interatomic Rare Earth Distances. Crystals 2021, 11, 768. [Google Scholar] [CrossRef]
  14. Sheldrick, G.M. A short history of SHELX. Acta Cryst. 2015, C71, 3–8. [Google Scholar] [CrossRef] [Green Version]
  15. Spek, A.L. checkCIF validation ALERTS: What they mean and how to respond. Acta Cryst. 2020, E76, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Brandenburg, K. Diamond-Crystal and Molecular Visualization; Crystal Impact: Bonn, Germany, 2006. [Google Scholar]
  17. Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriquez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0-new features for the visualization and investigation of crystal structures. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
  18. POV-Ray: The Persistence of Vision Retracer; Pty. Ltd.: Victoria, Australia, 2004.
  19. Jordan, R.B. Lanthanide Contraction: What is Normal? Inorg. Chem. 2023, 62, 3715–3721. [Google Scholar] [CrossRef] [PubMed]
  20. Coxall, R.A.; Harris, S.G.; Hernderson, D.K.; Parsons, S.; Takser, P.A.; Winpenny, E.P. Inter-ligand reactions: In situ formation of new polydentate ligands. J. Chem. Soc. Dalton Trans. 2000, 2349–2356. [Google Scholar] [CrossRef]
Crystals 13 01043 g001 550
Figure 1. Evolution of atomic radii [1] and effective RE3+ ionic radii [2] throughout the series of rare earth elements of the 6th period PSE as a function of the atomic number, Z; dotted, vertical line (red) indicating the boundary between lanthanides and the element La of the scandium group.
Figure 1. Evolution of atomic radii [1] and effective RE3+ ionic radii [2] throughout the series of rare earth elements of the 6th period PSE as a function of the atomic number, Z; dotted, vertical line (red) indicating the boundary between lanthanides and the element La of the scandium group.
Crystals 13 01043 g001
Crystals 13 01043 sch001 550
Scheme 1. Reaction equation for the formation of rare-earth diacetate bromide trihydrates by use of tetrahydrates as starting material.
Scheme 1. Reaction equation for the formation of rare-earth diacetate bromide trihydrates by use of tetrahydrates as starting material.
Crystals 13 01043 sch001
Crystals 13 01043 g002 550
Figure 2. Typical prismatic shape (left) of crystals of RE(OAc)2Hal·3H2O compounds (here: greenish crystals of RE = Pr, Hal = Cl), and microscopic image (right) showing an assemblage (here: RE = Lu, Hal = Cl) of crystals in the mother liquor.
Figure 2. Typical prismatic shape (left) of crystals of RE(OAc)2Hal·3H2O compounds (here: greenish crystals of RE = Pr, Hal = Cl), and microscopic image (right) showing an assemblage (here: RE = Lu, Hal = Cl) of crystals in the mother liquor.
Crystals 13 01043 g002
Crystals 13 01043 g003 550
Figure 3. Ball-and-stick model showing the general building concept of the one-dimensional coordination polymers in the RE(OAc)2Hal·3H2O structure type (here: RE = Pr, Hal = Br) with atom labeling scheme of the asymmetric unit; hydrogen atoms not labeled and the position of the halide atom not shown for clarity; hydrogen bonds visualized as dashed sticks (-OH···H = red, -OH··· Br = brown) and covalent bonds to adjacent, symmetry-related atoms as shortened sticks; the non-linear, unsymmetrical arrangement of the RE atoms is visualized by blue lines with distances [Å] and angle; black dots labeled i show the positions of the crystallographic centers of symmetry.
Figure 3. Ball-and-stick model showing the general building concept of the one-dimensional coordination polymers in the RE(OAc)2Hal·3H2O structure type (here: RE = Pr, Hal = Br) with atom labeling scheme of the asymmetric unit; hydrogen atoms not labeled and the position of the halide atom not shown for clarity; hydrogen bonds visualized as dashed sticks (-OH···H = red, -OH··· Br = brown) and covalent bonds to adjacent, symmetry-related atoms as shortened sticks; the non-linear, unsymmetrical arrangement of the RE atoms is visualized by blue lines with distances [Å] and angle; black dots labeled i show the positions of the crystallographic centers of symmetry.
Crystals 13 01043 g003
Crystals 13 01043 g004 550
Figure 4. Unit cell volumes [Å3] in the series of isomorphous RE(OAc)2Hal·3H2O compounds for Hal = Cl (dark green), and Hal = Br (brown); dotted lines represent the graphs of the quadratic regression analyses with parameters and reliability factors R given.
Figure 4. Unit cell volumes [Å3] in the series of isomorphous RE(OAc)2Hal·3H2O compounds for Hal = Cl (dark green), and Hal = Br (brown); dotted lines represent the graphs of the quadratic regression analyses with parameters and reliability factors R given.
Crystals 13 01043 g004
Crystals 13 01043 g005 550
Figure 5. Variation of the a-axis [Å] in the RE(OAc)2Hal·3H2O compounds for Hal = Cl (dark red) and Hal = Br (brown) as a function of Z, by a horizontal, dotted line (blue).
Figure 5. Variation of the a-axis [Å] in the RE(OAc)2Hal·3H2O compounds for Hal = Cl (dark red) and Hal = Br (brown) as a function of Z, by a horizontal, dotted line (blue).
Crystals 13 01043 g005
Crystals 13 01043 g006 550
Figure 6. Distances [Å], and angles [°] between the RE atoms in the RE(OAc)2Hal·3H2O compounds with Hal = Cl (dark green, olive, green), and Hal = Br (dark red, brown, orange), for reasons of clarity all curves are drawn over the complete datasets without interruption at the borderline (dotted, blue) between the early and late RE elements.
Figure 6. Distances [Å], and angles [°] between the RE atoms in the RE(OAc)2Hal·3H2O compounds with Hal = Cl (dark green, olive, green), and Hal = Br (dark red, brown, orange), for reasons of clarity all curves are drawn over the complete datasets without interruption at the borderline (dotted, blue) between the early and late RE elements.
Crystals 13 01043 g006
Crystals 13 01043 g007 550
Figure 7. Overview on the evolution of the RE-O distances [Å] in RE(OAc)2Cl·3H2O with RE = Ce-(Pm)-Lu and Hal = Cl, Br; Symmetry transformations used to generate equivalent atoms: (1) −x, −y + 1, −z + 1; (2) −x + 1, −y + 1, −z + 1; for reasons of clarity all curves are drawn over the complete datasets without interruption at the borderline (blue) between of early and late RE elements.
Figure 7. Overview on the evolution of the RE-O distances [Å] in RE(OAc)2Cl·3H2O with RE = Ce-(Pm)-Lu and Hal = Cl, Br; Symmetry transformations used to generate equivalent atoms: (1) −x, −y + 1, −z + 1; (2) −x + 1, −y + 1, −z + 1; for reasons of clarity all curves are drawn over the complete datasets without interruption at the borderline (blue) between of early and late RE elements.
Crystals 13 01043 g007
Crystals 13 01043 g008 550
Figure 8. Distorted monocapped square-antiprismatic, ninefold coordination of RE = CeCl (left) and distorted bicapped trigonal prismatic, eightfold coordination of RE = LuBr (right); color codes: caps = grey, square antiprism = green, trigonal prism = blue; hydrogen bonds are indicated by short dashed sticks with color codes: -OH···O = red, -OH···Cl = green, -OH···Br = brown; symmetry codes used to generate equivalent atoms: (1) −x, −y + 1, −z + 1; (2) −x + 1, −y + 1, −z + 1.
Figure 8. Distorted monocapped square-antiprismatic, ninefold coordination of RE = CeCl (left) and distorted bicapped trigonal prismatic, eightfold coordination of RE = LuBr (right); color codes: caps = grey, square antiprism = green, trigonal prism = blue; hydrogen bonds are indicated by short dashed sticks with color codes: -OH···O = red, -OH···Cl = green, -OH···Br = brown; symmetry codes used to generate equivalent atoms: (1) −x, −y + 1, −z + 1; (2) −x + 1, −y + 1, −z + 1.
Crystals 13 01043 g008
Crystals 13 01043 g009 550
Figure 9. Overview of the evolution of the RE-H2O distances [Å] in RE(OAc)2Hal·3H2O compounds with Hal = Cl (left) and Hal = Br (right); the connecting line between both subsets has been omitted as have been added the lines of regression analysis in case of the early RE elements in order to show the jumps of the properties.
Figure 9. Overview of the evolution of the RE-H2O distances [Å] in RE(OAc)2Hal·3H2O compounds with Hal = Cl (left) and Hal = Br (right); the connecting line between both subsets has been omitted as have been added the lines of regression analysis in case of the early RE elements in order to show the jumps of the properties.
Crystals 13 01043 g009
Crystals 13 01043 g010 550
Figure 10. (a) Ball-and-stick model of the two extreme acetate coordination in the series of RE(OAc)2Hal·3H2O compounds (Hal = Cl, RE = Ce (left of a), RE = Lu (right of a); bonds from oxygen to the two RE atoms are indicated by shortened sticks, hydrogen bonds by short, dashed sticks in red. (b) Schematic stick model showing the motion of OAc_1 in the metal-oxygen plane with respect to the common inversion center.
Figure 10. (a) Ball-and-stick model of the two extreme acetate coordination in the series of RE(OAc)2Hal·3H2O compounds (Hal = Cl, RE = Ce (left of a), RE = Lu (right of a); bonds from oxygen to the two RE atoms are indicated by shortened sticks, hydrogen bonds by short, dashed sticks in red. (b) Schematic stick model showing the motion of OAc_1 in the metal-oxygen plane with respect to the common inversion center.
Crystals 13 01043 g010
Crystals 13 01043 g011 550
Figure 11. Changes of bond angles [°] in the two different acetate groups of RE(OAc)2Cl·3H2O as a function of decreasing size of RE; mean values are indicated by broad, the standard deviations simulating bars (grey).
Figure 11. Changes of bond angles [°] in the two different acetate groups of RE(OAc)2Cl·3H2O as a function of decreasing size of RE; mean values are indicated by broad, the standard deviations simulating bars (grey).
Crystals 13 01043 g011
Crystals 13 01043 g012 550
Figure 12. Progress of the interatomic d(O···O) distances [Å] in the hydrogen bonds between the water molecules; mean values are indicated by broad, the standard deviations simulating bars (grey); symmetry transformations used to generate equivalent atoms: (4) x + 1, yes, z; (5) x − 1, y, z.
Figure 12. Progress of the interatomic d(O···O) distances [Å] in the hydrogen bonds between the water molecules; mean values are indicated by broad, the standard deviations simulating bars (grey); symmetry transformations used to generate equivalent atoms: (4) x + 1, yes, z; (5) x − 1, y, z.
Crystals 13 01043 g012
Crystals 13 01043 g013 550
Figure 13. Progress of interatomic O···Hal [Å] distances in the hydrogen bonds between the water molecules and halide anions (Hal = Cl left, Hal = Br, right) as a function of Z; mean values are indicated by broad, the standard deviations simulating bars (grey); symmetry transformations used to generate equivalent atoms: (3) x, y − 1, z; (6) −x + 1/2, y − 1/2, −z + 3/2.
Figure 13. Progress of interatomic O···Hal [Å] distances in the hydrogen bonds between the water molecules and halide anions (Hal = Cl left, Hal = Br, right) as a function of Z; mean values are indicated by broad, the standard deviations simulating bars (grey); symmetry transformations used to generate equivalent atoms: (3) x, y − 1, z; (6) −x + 1/2, y − 1/2, −z + 3/2.
Crystals 13 01043 g013
Crystals 13 01043 g014 550
Figure 14. Space-filling model showing a detail (cross-section, looking down the a-axis left, side view right) of the one-dimensional coordination polymer in the crystal structures of RE(OAc)2Hal·3H2O compounds (here: RE = Ce, Hal = Cl); color code: oxygen = red, carbon = black, hydrogen = white, cerium = brassy; rvdW: O = 1.52, C = 1.65, H = 1.2, Ce = 2.2, Cl = 1.75 Å; interactions with additional atoms are visualized by cutting off the overlapping cap and coloring the interface using the color of the auxiliary atom.
Figure 14. Space-filling model showing a detail (cross-section, looking down the a-axis left, side view right) of the one-dimensional coordination polymer in the crystal structures of RE(OAc)2Hal·3H2O compounds (here: RE = Ce, Hal = Cl); color code: oxygen = red, carbon = black, hydrogen = white, cerium = brassy; rvdW: O = 1.52, C = 1.65, H = 1.2, Ce = 2.2, Cl = 1.75 Å; interactions with additional atoms are visualized by cutting off the overlapping cap and coloring the interface using the color of the auxiliary atom.
Crystals 13 01043 g014
Crystals 13 01043 g015 550
Figure 15. Space-filling model showing a detail of the three-dimensional stacking of the one-dimensional coordination polymers (denoted as rods) in the crystal structures of RE(OAc)2Hal·3H2O compounds (here: RE = Ce, Hal = Cl); atom colors and sizes as in the previous figure.
Figure 15. Space-filling model showing a detail of the three-dimensional stacking of the one-dimensional coordination polymers (denoted as rods) in the crystal structures of RE(OAc)2Hal·3H2O compounds (here: RE = Ce, Hal = Cl); atom colors and sizes as in the previous figure.
Crystals 13 01043 g015
Table
Table 1. Crystallographic data, summary of data collection parameters and results of structure refinement for RE(OAc)2Cl·3H2O.
Table 1. Crystallographic data, summary of data collection parameters and results of structure refinement for RE(OAc)2Cl·3H2O.
CePrNdPmSmEuGdTbDyHoErTmYbLu
Empirical formulaC4H23CeClO7C4H12ClO7PrC4H12ClNdO7 C4H12ClO7SmC4H12ClEuO7C4H12ClGdO7C4H12ClO7TbC4H12ClDyO7C4H12ClHoO7C4H12ClErO7C4H12ClO7TmC4H12ClO7YbC4H12ClLuO7
Formula weight [g/mol]347.71348.50351.83 357.94359.55364.84366.51370.09372.52374.85376.52380.63382.56
Temperature [K]100(2) 100(2)
Crystal systemmonoclinic Monoclinic
Space groupP 21/n P 21/n
a [Å]7.9625(3)7.9333(3)7.9059(3) 7.8503(3)7.8412(2)7.8219(4)7.8003(2)7.8106(4)7.7993(3)7.7927(3)7.7747(2)7.7710(3)7.7668(3)
b [Å]7.9276(3)7.9139(3)7.9008(3) 7.8844(3)7.8769(2)7.8592(4)7.8539(2)7.8433(4)7.8345(3)7.8301(5)7.8392(2)7.8224(3)7.8297(3)
b [Å]17.6973(6)17.6327(6)17.5852(7) 17.5192(6)17.4901(5)17.4434(8)17.3942(5)17.3400(8)17.2564(7)17.1904(7)17.1517(5)17.1055(8)17.0618(7)
β99.122(2)°98.94798.856(2) 98.483(2)98.354(1)°98.265(2)98.075(2)°97.978(2)°97.881(2)°97.695(2)97.552(1)97.422(2)97.336(2)
Volume [Å3]1102.99(7)1093.57(7)1085.33(7) 1072.49(7)1068.80(5)1061.18(9)1055.05(5)1051.98(9)1044.47(7)1039.47(7)1036.28(5)1031.09(7)1029.06(7)
Z,Z′,dcalc [g/mol]4, 1, 2.0944, 1, 2.1174, 1, 2.153 4, 1, 2.2174, 1, 2.2344, 1, 2.2844, 1, 2.3074, 1, 2.3374, 1, 2.3694, 1, 2.3954, 1, 2.4134, 1, 2.4524, 1, 2.469
μ [mm−1]4.3734.7035.034 5.7286.1226.5096.9607.3617.8358.3358.8239.3339.857
F(000)668672676 684688692696700704708712716720
2Ѳmax56° 56°
Reflections collected101277125986122829 130814798281227421261094923713342193.61710871570583100183
Reflections unique, Rint2664, 0.04602645, 0.03982621, 0.0566 2595, 0.03442587, 0.03992569, 0.03582551, 0.05172547, 0.03282528, 0.03582514, 0.03052504, 0.03972491, 0.07212490, 0.0653
Data/restraints/parameters2664/0/1252645/0/1252621/0/125 2595/0/1262587/0/1252569/0/1262551/0/1252547/0/1262528/0/1262514/0/1262504/0/1252491/0/1252490/0/125
Goodness of fito n F21.2241.1011.062 1.1331.0941.0901.0541.1841.1761.4091.1321.0611.034
R1/wR2 [I > 2σ(I)]0.0177, 0.03550.0125, 0.02800.0122, 0.0270 0.0101, 0.02330.0131, 0.03270.0094, 0.02060.0108, 0.02450.0127, 0.02660.0103, 0.02340.0135, 0.02920.0108, 0.02400.0162, 0.03020.0119, 0.0264
R1/wR2 [all data]0.0186, 0.03580.0134, 0.02830.0142, 0.0275 0.0105, 0.02350.0137, 0.03300.0100, 0.02080.0131, 0.02530.0131, 0.02670.0106, 0.02350.0135, 0.02920.0113, 0.02410.0217, 0.03180.0143, 0.0269
Extinction coefficientN/A 0.00104(8)N/A0.00122(7)N/A0.0045(1)0.00185(8)0.00115(9)N/A
±∆e[eÅ−3]0.532/−0.8110.457/−0.6090.387/−0.358 0.381/−0.5280.470/−0.7030.348/−0.4740.486/−0.3920.489/−0.6520.364/−0.4360.524/−0.6030.386/−0.5790.522/−0.4800.365/−0.421
CCDC number226082422608312260827 2260830226082222608282260829226082022608322260823226082522608212206826
Table
Table 2. Crystallographic data, summary on data collection parameters and results of structure refinement for RE(OAc)2Br·3H2O.
Table 2. Crystallographic data, summary on data collection parameters and results of structure refinement for RE(OAc)2Br·3H2O.
CePrNdPmSmEuGdTbDyHoErTmYbLu
Empirical formulaC4H23BrCeO7C4H12BrO7PrC4H12BrNdO7 C4H12BrO7SmC4H12BrEuO7C4H12BrGdO7C4H12BrO7TbC4H12BrDyO7C4H12BrHoO7C4H12BrErO7C4H12BrO7TmC4H12BrO7YbC4H12BrLuO7
Formula weight [g/mol]392.17392.96396.29 402.40404.01409.30410.97414.55416.98419.31420.98425.09427.02
Temperature [K]100(2) 100(2)
Crystal systemmonoclinic Monoclinic
Space groupP 21/n P 21/n
a [Å]7.9597(3)7.9293(3)7.9027(3) 7.8473(3)7.8318(3)7.8191(2)7.7972(3)7.8038(3)7.8117(3)7.8069(3)7.7868(5)7.7854(3)7.7611(3)
b [Å]8.0442(3)8.0327(3)8.0349(3) 8.0230(3)8.0121(3)8.0130(2)8.0263(3)8.0288(3)8.0361(4)8.0529(3)8.0675(5)8.0625(3)8.0702(3)
b [Å]18.0642(8)18.0186(6)17.9481(6) 17.8722(7)17.8214(7)17.7804(6)17.7443(8)17.6550(7)17.5440(9)17.4494(7)17.3994(7)17.3573(7)17.2952(6)
β96.732(2)°96.533(2)°96.414(2)°°95.987(2)°95.972(2)°95.929(2)°95.862(2)°96.034(2)°96.096(3)°96.154(2)°96.154(2)°96.142(29)°96.098(2)°
Volume [Å3]1148.67(8)1140.22(7)1132.52(7) 1119.08(7)1112.21(7)1108.06(5)1104.68(8)1100.05(7)1095.11(9)1090.69(7)1086.73(11)1083.26(7)1077.13(7)
Z,Z′,dcalc [g/mol]4, 1, 2.2684, 1, 2.2894, 1, 2.324 4, 1, 2.3884, 1, 2.4134, 1, 2.4534, 1, 2.4714, 1, 2.5034, 1, 2.5294, 1, 2.5444, 1, 2.5734, 1, 2.6064, 1, 2.633
μ [mm−1]7.4467.7818.117 8.8229.2369.59510.02310.42910.87811.36211.84512.32612.879
F(000)740744748 756760764768772776780784788792
2Ѳmax56° 56°
Reflections collected11330592529132337 1113760118192132199124829101683102663121.468112602120213103545
Reflections unique, Rint2770, 0.05722753, 0.04972735, 0.0553 2708, 0.07012696, 0.05162690, 0.04102683, 0.04592666, 0.04442655, 0.07342636, 0.04132626, 0.04882616, 0.04602596, 0.0753
Data/restraints/parameters2770/0/1252753/0/1252735/0/125 2708/0/1252696/0/1252690/0/1252683/0/1252666/0/1262655/0/1252636/0/1262626/0/1252616/0/1252596/0/125
Goodness of fito n F21.0711.0781.051 1.0841.1001.1341.1221.1181.0491.1821.0831.0731.054
R1/wR2 [I>2σ(I)]0.0142, 0.03100.0141, 0.02950.0129, 0.0300 0.0150, 0.03050.0131, 0.03000.0155, 0.04030.0133, 0.03010.0129, 0.03210.148, 0.03360.0114, 0.02530.0118, 0.02650.0121, 0.02610.0184, 0.0417
R1/wR2 [all data]0.0173, 0.03210.0175, 0.03050.0154, 0.0307 0.0201, 0.03210.0157, 0.03090.0168, 0.04100.0151, 0.03060.0140, 0.03250.196, 0.03530.0123, 0.02550.0141, 0.02720.0141, 0.02660.0233, 0.0437
Extinction coefficientN/A N/A0.00126(9)N/A0.00082(5)N/A
±∆e[eÅ−3]0.368/−0.3740.441/−0.4990.402/−0.415 0.442/−0.4430.408/−0.4080.695/−0.9770.554/−0.4070.779/−0.6010.508/−0.5790.364/−0.4670.383/−0.2260.4607/−0.5811.131/−1.209
CCDC number226120722611992261203 2261208226120622612052261209226120022611982261201226120222612042261210
Table
Table 3. RE-O distances [Å] with standard deviations in parentheses of the RE(OAc)2Hal·3H2O compounds with Hal = Cl, Br.
Table 3. RE-O distances [Å] with standard deviations in parentheses of the RE(OAc)2Hal·3H2O compounds with Hal = Cl, Br.
RECePrNdPmSmEuGdTbDyHoErTmYbLu
Hal = Cl
RE(1)-O(11)2.422(2)2.404(1)2.390(1) 2.351(1)2.341(1)2.325(1)2.294(1)2.274(1)2.252(1)2.232(2)2.218(1)2.201(2)2.193(1)
RE(1)-O(21)2.440(2)2.422(1)2.406(1) 2.373(1)2.362(1)2.346(1)2.323(1)2.312(1)2.295(1)2.280(2)2.265(1)2.246(2)2.239(1)
RE(1)-O(2W)2.486(2)2.468(1)2.452(1) 2.421(1)2.407(1)2.393(1)2.403(1)2.361(2)2.345(1)2.331(2)2.320(1)2.312(2)2.302(2)
RE(1)-O(3W)2.499(2)2.482(1)2.467(1) 2.438(1)2.427(1)2.418(1)2.403(1)2.392(1)2.381(1)2.372(2)2.360(1)2.347(2)2.346(2)
RE(1)-O(1W)2.524(2)2.506(1)2.487(1) 2.457(1)2.444(1)2.425(1)2.404(1)2.388(1)2.367(1)2.346(2)2.339(1)2.320(2)2.309(2)
RE(1)-O(12) 12.536(2)2.516(1)2.498(1) 2.462(1)2.450(1)2.436(1)2.413(1)2.396(2)2.378(1)2.362(2)2.346(1)2.334(2)2.327(2)
RE(1)-O(22) 22.548(2)2.529(1)2.510(1) 2.475(1)2.462(1)2.449(1)2.428(1)2.416(1)2.400(1)2.386(2)2.373(1)2.359(2)2.358(2)
RE(1)-O(21) 22.665(2)2.648(1)2.633(1) 2.620(1)2.613(1)2.607(1)2.612(1)2.604(1)2.596(1)2.588(2)2.592(1)2.601(2)2.585(2)
RE(1)-O(11) 12.738(2)2.725(1)2.706(1) 2.723(1)2.728(1)2.740(1)2.820(1)2.905(2)2.991(1)3.083(2)3.128(2)3.178(2)3.211(2)
Hal = Br
RE(1)-O(11)2.417(1)2.401(1)2.388(1) 2.349(2)2.338(1)2.324(2)2.294(2)2.269(1)2.248(2)2.229(1)2.216(2)2.201(2)2.188(2)
RE(1)-O(21)2.431(1)2.416(1)2.403(1) 2.370(2)2.356(1)2.343(2)2.322(1)2.307(1)2.294(2)2.280(1)2.266(1)2.251(1)2.238(2)
RE(1)-O(2W)2.489(1)2.471(1)2.457(1) 2.425(2)2.409(2)2.398(2)2.381(2)2.365(1)2.346(2)2.338(1)2.325(2)2.316(2)2.305(2)
RE(1)-O(3W)2.490(2)2.476(1)2.461(1) 2.431(2)2.420(2)2.412(2)2.398(2)2.386(2)2.366(2)2.347(2)2.353(2)2.344(2)2.338(2)
RE(1)-O(1W)2.526(1)2.504(1)2.490(1) 2.459(2)2.442(2)2.426(2)2.405(2)2.389(1)2.373(2)2.360(2)2.336(2)2.322(2)2.306(2)
RE(1)-O(12) 12.536(1)2.516(2)2.499(1) 2.466(2)2.450(2)2.439(2)2.417(2)2.395(2)2.376(2)2.365(2)2.342(2)2.333(3)2.323(2)
RE(1)-O(22) 22.539(1)2.527(1)2.504(1) 2.471(2)2.459(2)2.447(2)2.429(2)2.412(2)2.395(2)2.382(1)2.368(2)2.358(2)2.350(2)
RE(1)-O(21) 22.666(1)2.652(1)2.632(1) 2.623(2)2.615(1)2.608(2)2.612(2)2.603(1)2.591(2)2.582(1)2.587(2)2.594(2)2.577(2)
RE(1)-O(11) 12.746(1)2.730(1)2.711(1) 2.722(2)2.720(2)2.733(2)2.808(2)2.917(2)3.026(2)3.129(2)3.165(2)3.213(2)3.238(2)
Symmetry transformations used to generate equivalent atoms: (1) −x, −y + 1, −z + 1; (2) −x + 1, −y + 1, −z + 1.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Reuter, H.; Böltken, M.; Horstmann, M.; Haase, M. Structural Evolution in a Series of Isomorphous Rare Earth Compounds as Response of Lanthanide Contraction. Crystals 2023, 13, 1043. https://doi.org/10.3390/cryst13071043

AMA Style

Reuter H, Böltken M, Horstmann M, Haase M. Structural Evolution in a Series of Isomorphous Rare Earth Compounds as Response of Lanthanide Contraction. Crystals. 2023; 13(7):1043. https://doi.org/10.3390/cryst13071043

Chicago/Turabian Style

Reuter, Hans, Marcel Böltken, Maik Horstmann, and Markus Haase. 2023. "Structural Evolution in a Series of Isomorphous Rare Earth Compounds as Response of Lanthanide Contraction" Crystals 13, no. 7: 1043. https://doi.org/10.3390/cryst13071043

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop