A Novel Catalytic Micro-Combustor Inspired by the Nasal Geometry of Reindeer: CFD Modeling and Simulation
Abstract
:1. Introduction
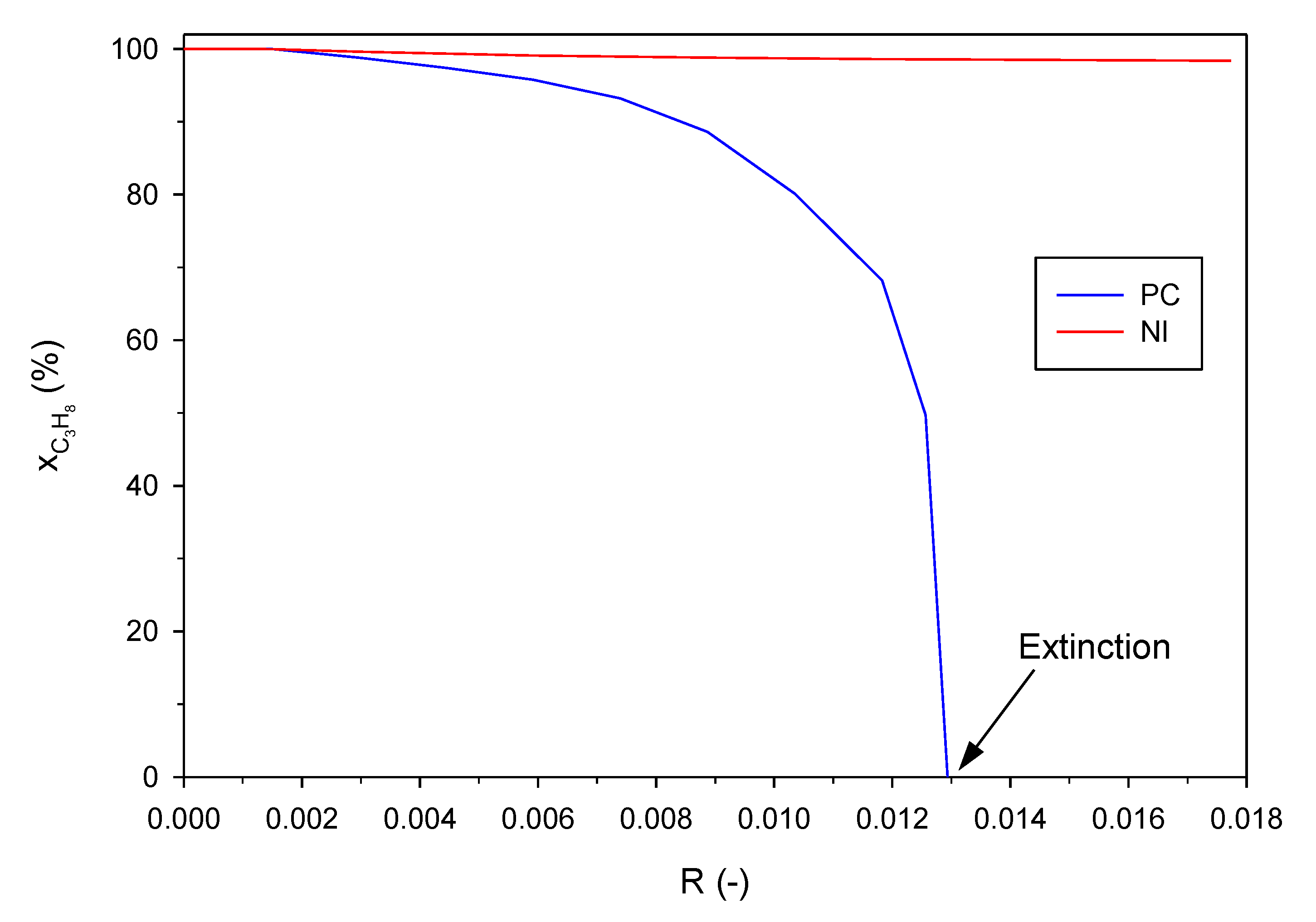
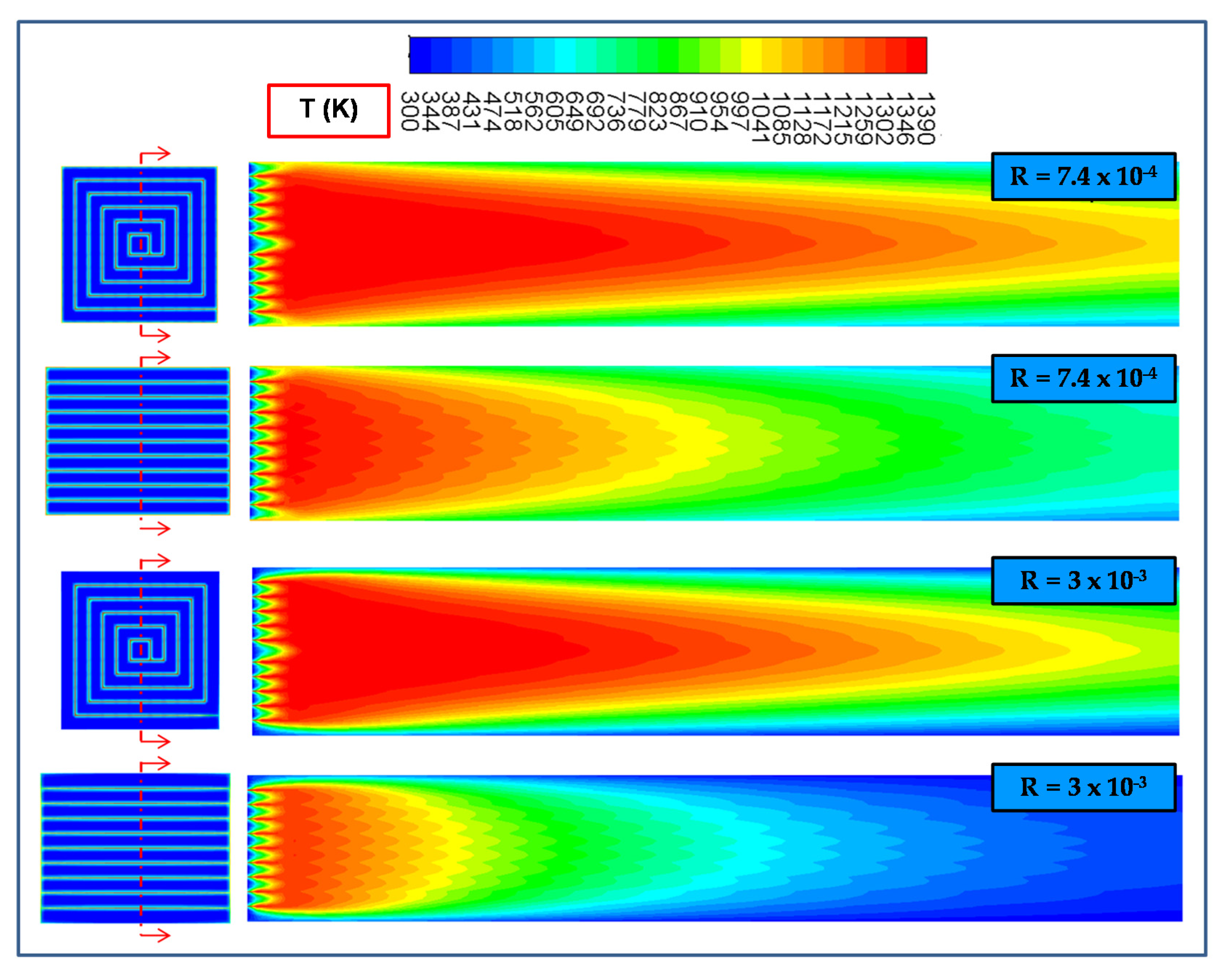
2. Results and Discussion
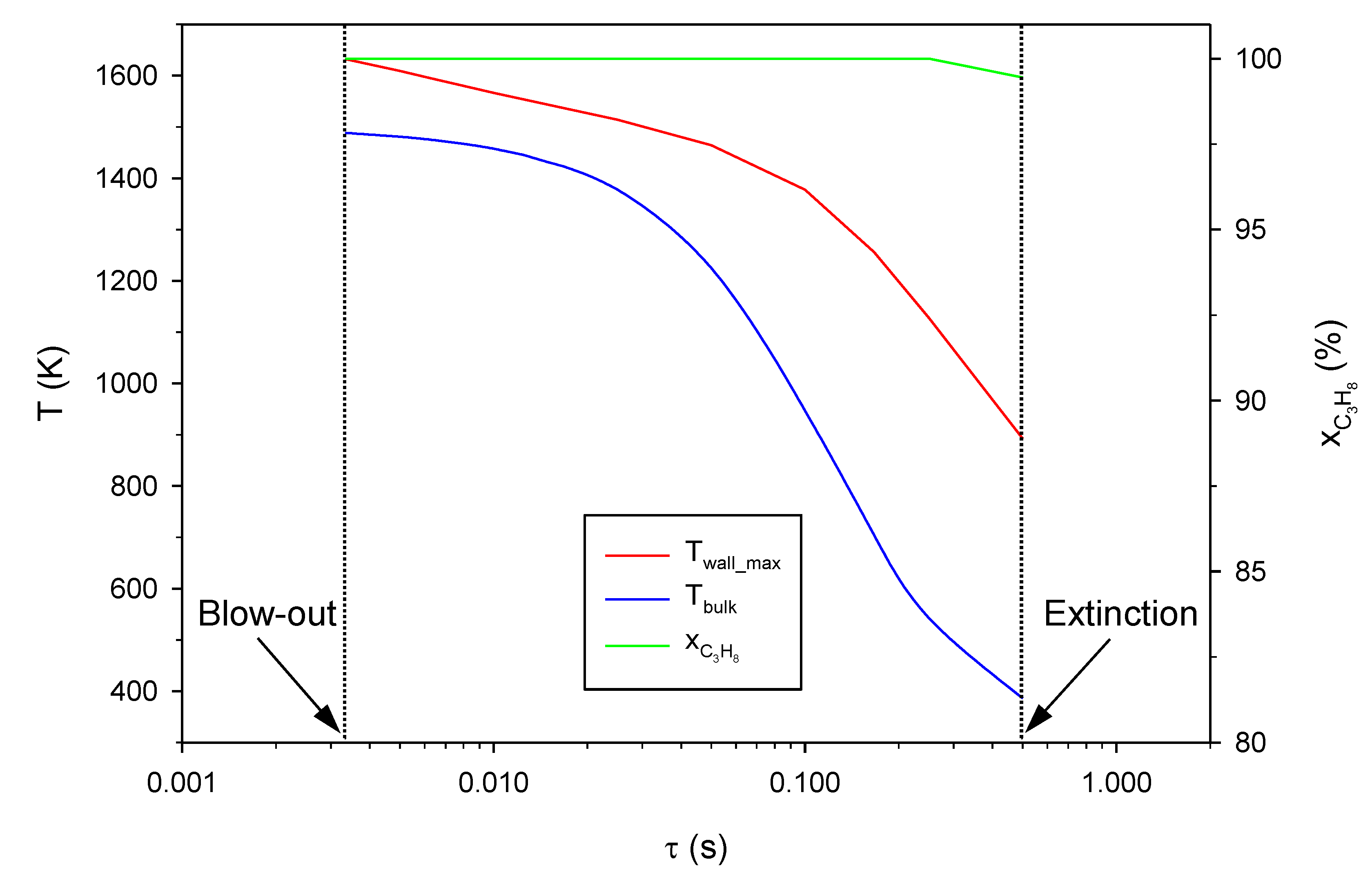
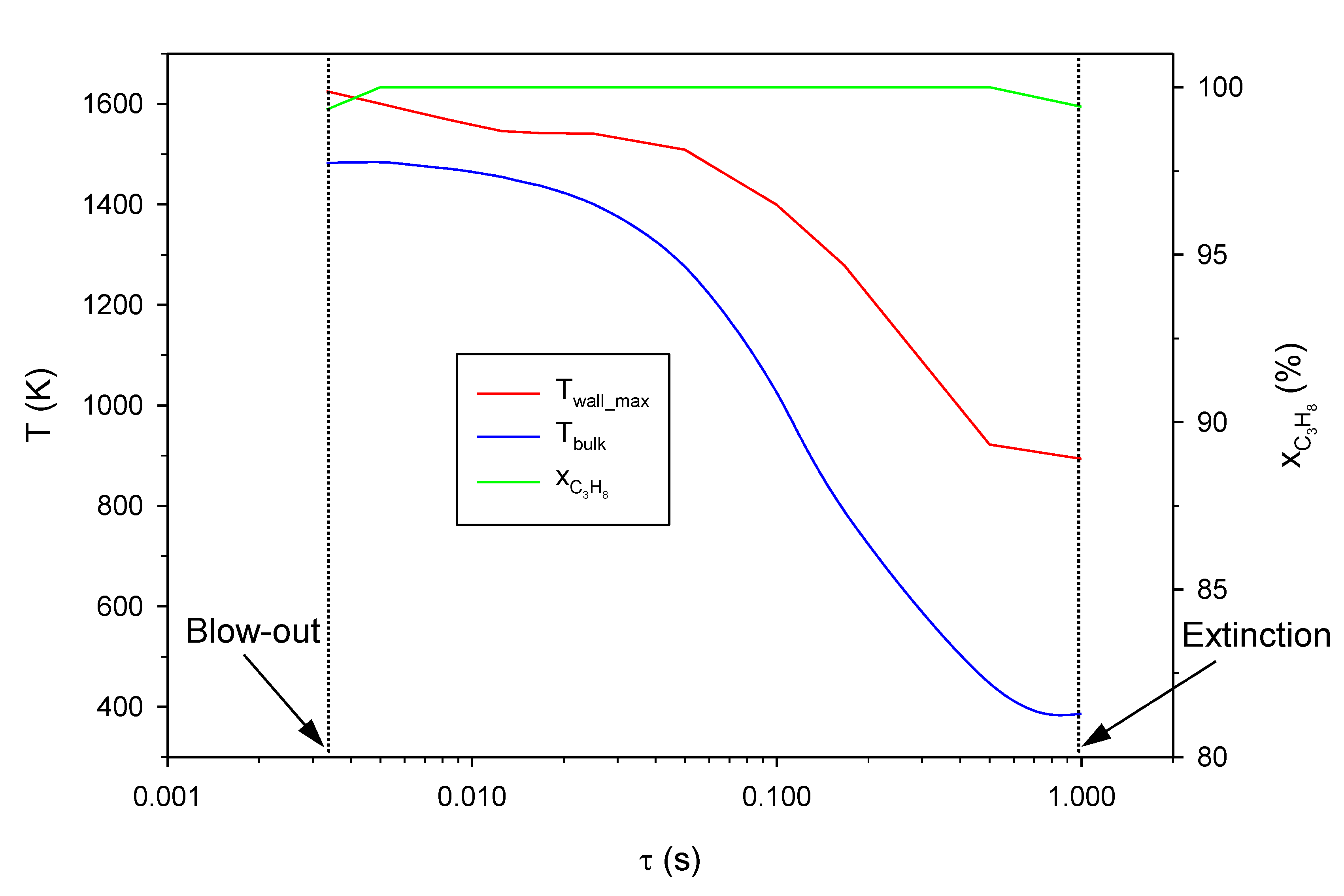
2.1. Effect of the Inlet Gas Velocity (i.e., Residence Time)
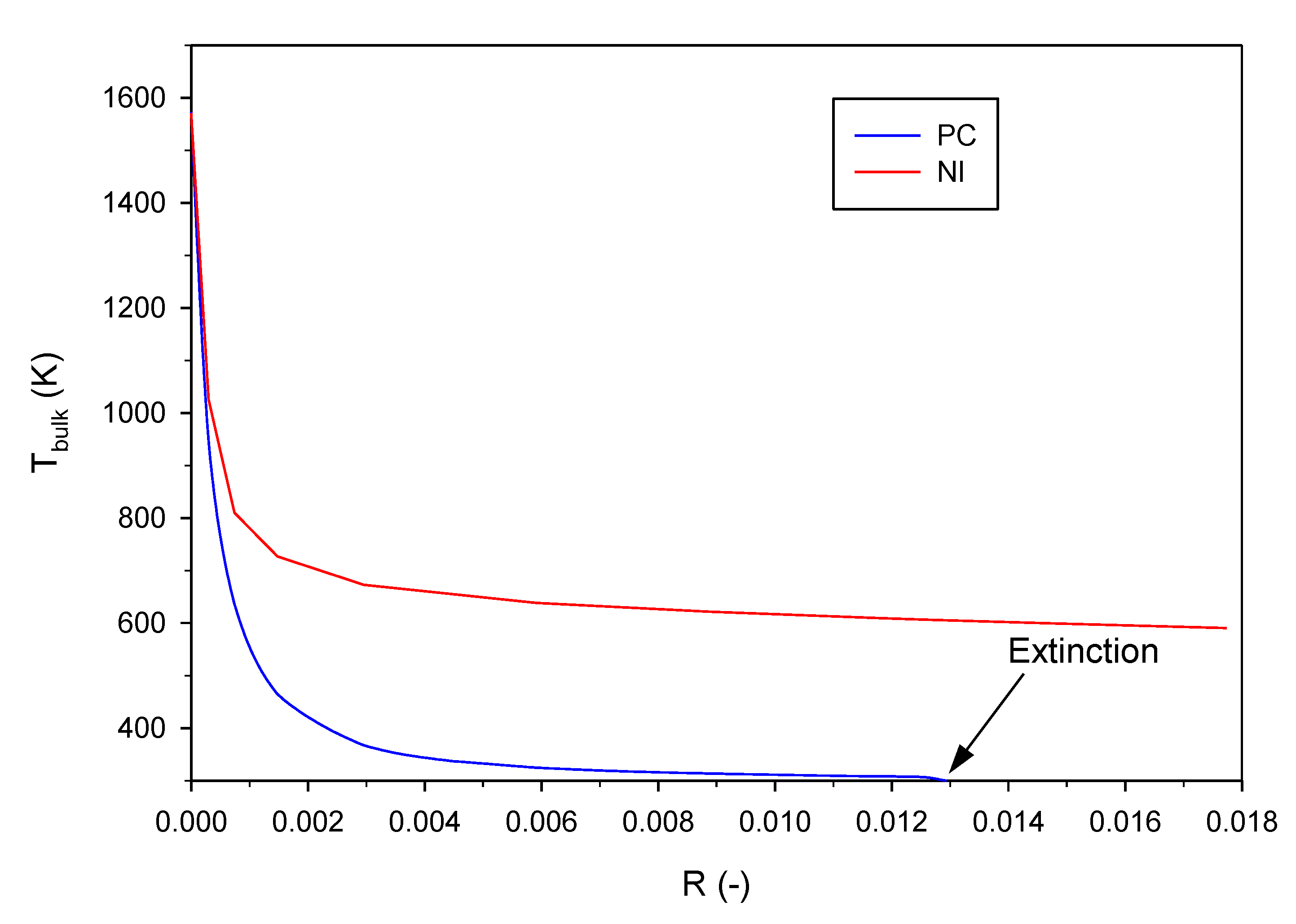
2.2. Effect of the (External Convective) Heat Transfer Coefficient
3. Mathematical Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fernandez-Pello, A.C. Micropower generation using combustion: Issues and approaches. Prog. Energy Combust. Sci. 2002, 29, 883–899. [Google Scholar] [CrossRef] [Green Version]
- Kaisare, N.S.; Vlachos, D.G. A review on microcombustion: Fundamentals, devices and applications. Prog. Energy Combust. Sci. 2012, 38, 321–359. [Google Scholar] [CrossRef]
- Kletz, T.; Amyotte, P. Process Plants: A Handbook for Inherently Safer Design, 2nd ed.; CRC Press (Taylor & Francis Group): Boca Raton, FL, USA; London, UK; New York, NY, USA, 2010; p. 53. [Google Scholar]
- Norton, D.G.; Wetzel, E.D.; Vlachos, D.G. Thermal management in catalytic microreactors. Ind. Eng. Chem. Res. 2006, 45, 76–84. [Google Scholar] [CrossRef]
- Karagiannidis, S.; Mantzaras, J.; Jackson, G.; Boulouchos, K. Hetero-/homogeneous combustion and stability maps in methane-fueled catalytic microreactors. Proc. Combust. Inst. 2007, 31, 3309–3317. [Google Scholar] [CrossRef]
- Kaisare, N.S.; Deshmukh, S.R.; Vlachos, D.G. Stability and performance of catalytic microreactors: Simulations of propane catalytic combustion on Pt. Chem. Eng. Sci. 2008, 63, 1098–1116. [Google Scholar] [CrossRef]
- Di Benedetto, A.; Di Sarli, V. Steady-state multiplicity in catalytic microcombustors. Ind. Eng. Chem. Res. 2010, 49, 2130–2134. [Google Scholar] [CrossRef]
- Di Benedetto, A.; Di Sarli, V.; Russo, G. Effect of geometry on the thermal behavior of catalytic micro-combustors. Catal. Today 2010, 155, 116–122. [Google Scholar] [CrossRef]
- Barbato, P.S.; Di Benedetto, A.; Di Sarli, V.; Landi, G.; Pirone, R. High-pressure methane combustion over a perovskyte catalyst. Ind. Eng. Chem. Res. 2012, 51, 7547–7558. [Google Scholar] [CrossRef]
- Kaisare, N.S.; Vlachos, D.G. Extending the region of stable homogeneous micro-combustion through forced unsteady operation. Proc. Combust. Inst. 2007, 31, 3293–3300. [Google Scholar] [CrossRef]
- Federici, J.A.; Wetzel, E.D.; Geil, B.R.; Vlachos, D.G. Single channel and heat recirculation catalytic microburners: An experimental and computational fluid dynamics study. Proc. Combust. Inst. 2009, 32, 3011–3018. [Google Scholar] [CrossRef]
- Chen, J.; Song, W.; Xu, D. Thermal management in catalytic heat-recirculating micro-combustors: A computational fluid dynamics study. Appl. Therm. Eng. 2019, 160, 114073. [Google Scholar] [CrossRef]
- Kim, N.I.; Kato, S.; Kataoka, T.; Yokomori, T.; Maruyama, S.; Fujimori, T.; Maruta, K. Flame stabilization and emission of small Swiss-roll combustors as heaters. Combust. Flame 2005, 141, 229–240. [Google Scholar] [CrossRef]
- Zhong, B.-J.; Wang, J.-H. Experimental study on premixed CH4/air mixture combustion in micro Swiss-roll combustors. Combust. Flame 2010, 157, 2222–2229. [Google Scholar] [CrossRef]
- Di Benedetto, A.; Landi, G.; Di Sarli, V.; Barbato, P.S.; Pirone, R.; Russo, G. Methane catalytic combustion under pressure. Catal. Today 2012, 197, 206–213. [Google Scholar] [CrossRef]
- Landi, G.; Di Benedetto, A.; Barbato, P.S.; Russo, G.; Di Sarli, V. Transient behavior of structured LaMnO3 catalyst during methane combustion at high pressure. Chem. Eng. Sci. 2014, 116, 350–358. [Google Scholar] [CrossRef]
- Barbato, P.S.; Di Sarli, V.; Landi, G.; Di Benedetto, A. High pressure methane catalytic combustion over novel partially coated LaMnO3-based monoliths. Chem. Eng. J. 2015, 259, 381–390. [Google Scholar] [CrossRef]
- Di Sarli, V.; Barbato, P.S.; Di Benedetto, A.; Landi, G. Start-up behavior of a LaMnO3 partially coated monolithic combustor at high pressure. Catal. Today 2015, 242, 200–210. [Google Scholar] [CrossRef]
- Di Benedetto, A.; Di Sarli, V.; Russo, G. A novel catalytic-homogenous micro-combustor. Catal. Today 2009, 147, S156–S161. [Google Scholar] [CrossRef]
- Kunte, A.; Raghu, A.K.; Kaisare, N.S. A spiral microreactor for improved stability and performance for catalytic combustion of propane. Chem. Eng. Sci. 2018, 187, 87–97. [Google Scholar] [CrossRef]
- Yedala, N.; Raghu, A.K.; Kaisare, N.S. A 3D CFD study of homogeneous-catalytic combustion of hydrogen in a spiral microreactor. Combust. Flame 2019, 206, 441–450. [Google Scholar] [CrossRef]
- Magnanelli, E.; Wilhelmsen, Ø.; Acquarone, M.; Folkow, L.P.; Kjelstrup, S. The nasal geometry of the reindeer gives energy-efficient respiration. J. Non-Equilib. Thermodyn. 2017, 42, 59–78. [Google Scholar] [CrossRef] [Green Version]
- Westbrook, C.K.; Dryer, F.L. Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Spadaccini, C.M.; Peck, J.; Waitz, I.A. Catalytic combustion systems for microscale gas turbine engines. J. Eng. Gas Turbines Power 2007, 129, 49–60. [Google Scholar] [CrossRef] [Green Version]
- Canu, P. Simulation and interpretation of catalytic combustion experimental data. Catal. Today 2001, 64, 239–252. [Google Scholar] [CrossRef]


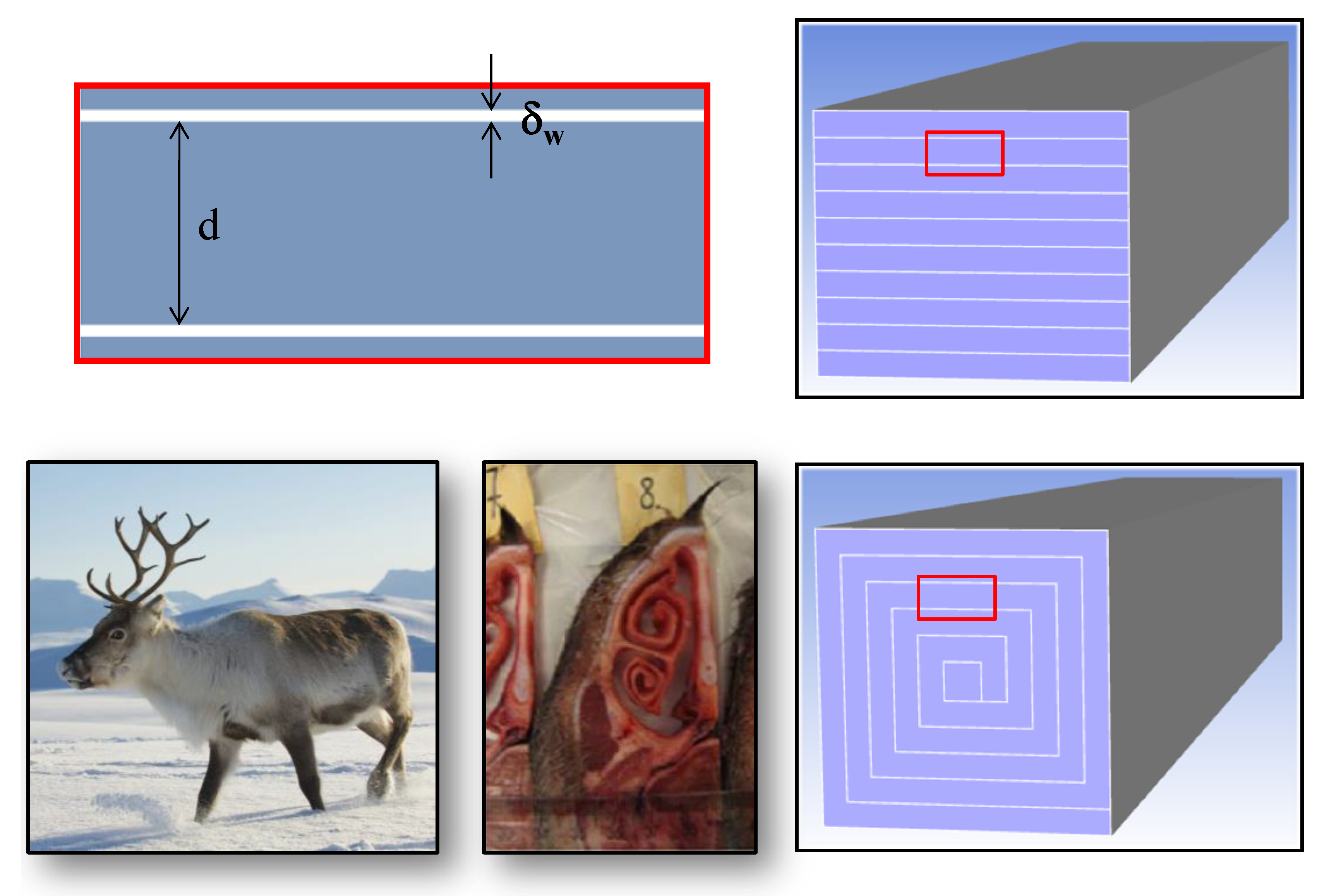

| Parameter | Value |
|---|---|
| Distance between catalytic walls, d (mm) | 0.783 |
| Thickness of the catalytic walls, δw (mm) | 0.045 |
| Length of the micro-reactor, L (mm) | 50 |
| Total catalytic surface area of the micro-reactor, Acat (mm2) | 11053 |
| Total catalytic surface area/volume of the micro-reactor, PC/NI, Acat/V (mm−1) | 2.56/2.42 |
| External surface area of the micro-reactor, PC/NI, Aext (mm2) | 1868/1911 |
| Parameter | Value |
|---|---|
| Inlet gas temperature, Tin (K) | 300 |
| Inlet fuel equivalence ratio (-) | 0.5 |
| Solid thermal conductivity, kw (W/m K) | 18 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Sarli, V.; Trofa, M.; Di Benedetto, A. A Novel Catalytic Micro-Combustor Inspired by the Nasal Geometry of Reindeer: CFD Modeling and Simulation. Catalysts 2020, 10, 606. https://doi.org/10.3390/catal10060606
Di Sarli V, Trofa M, Di Benedetto A. A Novel Catalytic Micro-Combustor Inspired by the Nasal Geometry of Reindeer: CFD Modeling and Simulation. Catalysts. 2020; 10(6):606. https://doi.org/10.3390/catal10060606
Chicago/Turabian StyleDi Sarli, Valeria, Marco Trofa, and Almerinda Di Benedetto. 2020. "A Novel Catalytic Micro-Combustor Inspired by the Nasal Geometry of Reindeer: CFD Modeling and Simulation" Catalysts 10, no. 6: 606. https://doi.org/10.3390/catal10060606





