1. Introduction
The folk theorem tells us that any feasible and individually rational (FIR) payoff is an equilibrium, when the players are patient enough [
1,
2,
3,
4]. However, the players may not be extremely patient but they rather have some intermediate value for the discount factor. This paper finds the smallest discount factor value for which the FIR payoffs are the equilibrium payoffs in the symmetric
supergames. This extends the folk theorem by solving exactly how patient the players need to be as a function of the stage-game payoffs. This reveals why and in what type of games extreme patience is required in the folk theorem and what payoffs are difficult to obtain.
This paper compares three types of strategies: pure strategies with and without public correlation and mixed strategies without public correlation. We want to examine how these assumptions affect the results. In some applications, it may be reasonable to assume that the players may only use pure strategies and they may not be able to coordinate their actions using a correlation device. The pure-strategy model has been examined in [
5,
6,
7,
8]. These papers characterize the subgame-perfect equilibria with a set-valued fixed-point equation, which forms the basis of our analysis. The mixed-strategy model has been studied in the more general model of imperfect public monitoring [
9,
10,
11]; see also [
12,
13] for the model examined in this paper.
The computation of the payoff set has been examined in [
14,
15,
16,
17,
18]. These papers assume public correlation, which makes the payoff set convex and simplifies the computation dramatically. References [
19,
20] have developed a method for computing pure-strategy equilibria without public correlation.
The main result of this paper is to solve the critical values, i.e., the smallest discount factor value for which the players obtain all the FIR payoffs as equilibrium payoffs. The results are based on solving analytically and geometrically the fixed-point equation of [
7,
8]. This idea has been presented in [
21] where the critical values are solved in a class of prisoner’s dilemma games under public randomization; see also Sections 2.5.3 and 2.5.6 in [
11]. The pure-strategy model without public correlation is a quite straightforward extension of [
21], but the mixed-strategy model requires analyzing totally new types of strategies with complicated payoffs; see [
12,
13]. We restrict our analysis to the symmetric
games since the set of pure-strategy equilibria may be empty in asymmetric games, it may be difficult to find the smallest equilibrium payoffs [
22], and it is tedious to examine all the asymmetric games.
The results of this paper can be used (i) to identify the games where the players have trouble in obtaining all the payoffs and to find the payoffs that are difficult to obtain, (ii) to understand better how the equilibrium payoffs depend on the discount factor, and (iii) to find a range of discount factor values for which the computation of equilibria is easy. For example, we know that the payoff set coincides with the FIR payoffs for all the discount factor values above the critical value, and there is no need to compute the payoff set for these values. We also observe discontinuities in the critical values, which means that the set of equilibria may not behave well, i.e., small changes in the stage-game payoffs may affect dramatically the payoff set.
We organize the games into groups based on the equations that determine the critical values and provide a useful visualization of the critical values in different games. From the figures, it is easy to see when the high level of patience is needed and to make the comparison between the different strategies.
2. The Repeated Game
2.1. Stage Games
In a repeated game, a stage game is played again and again by the same players. A stage game is defined by a finite set of players , a finite set of pure actions for each player , , and the players’ utilities for each action profile , where is the set of pure-action profiles. Moreover, a pure action of player i is denoted and a pure-action profile is .
Each player may randomize over his pure actions . This defines a mixed action such that for each and . The set of probability distributions over is denoted and . A mixed-action profile is denoted by . A support of a mixed action is the set of pure actions that is played with a strictly positive probability: . We also define , and for each , we let be the probability that the action profile a is realized if the mixed-action profile q is played: . In pure strategies, we make the restriction that for one action .
In a model with public correlation, the players observe a realization of a public lottery and they can condition their action based on the signal . For example, two players may agree to take action if and otherwise. This way the players can coordinate their actions such that they randomize between the outcomes and , and avoid the outcomes and . The latter outcomes would be realized if standard mixed strategies were used and no public correlation device was available.
The stage-game payoffs are given by function
. For example, if the players choose a mixed-action profile
, then player
i receives an expected payoff of
Let denote player i’s opponents’ actions. Now, an action profile q is a Nash equilibrium in the stage game if no player has a profitable deviation, i.e.,
The twelve symmetric strict ordinal
games are presented in
Figure 1, see ref. [
23] for the taxonomy. Strict ordinality means that all of the payoffs must be unequal and there can be no indifferences. The two actions are C (cooperate) and D (defect), and they give the players the payoffs
,
,
and
; the corresponding action profiles are also denoted by letters
. For example, if the players choose the action profile
, the players receive payoffs
and
.
2.2. Repeated Games
We examine a model where the stage game is repeated infinitely many times and these games are sometimes called as supergames. We assume that the players observe all the past realized pure actions but not the probabilities that the other players are using in their mixed strategies. The public past play is denoted by the set of histories , where is the empty set and corresponds to the beginning of the game. Thus, the history contains all the pure actions that were played in the previous rounds. The set of all possible histories is . A behavior strategy of player is a mapping that assigns a probability distribution over player i’s pure actions for each possible history . The set of player i’s strategies is . The players’ strategies form a strategy profile , a strategy profile of all players except player i is denoted by and the set of strategy profiles is given by . A pure strategy assigns a pure action for each possible history . With public correlation, the players observe a public signal on each round k before making their decisions, and thus the history contains all the past pure actions, signals and the current signal.
We assume that the players discount the future payoffs with a common discount factor
. They have the same discount factor since we examine symmetric games. The expected discounted payoff of a strategy profile
to player
i is
where
is the payoff of player
i at round
k induced by the strategy profile
. A strategy profile
is a Nash equilibrium if no player has a profitable deviation, i.e.,
and it is a subgame-perfect equilibrium (SPE) if it induces a Nash equilibrium in every subgame, i.e.,
where
is the restriction of the strategy profile after history
. From now on, by equilibrium we mean subgame-perfect equilibrium.
2.3. Critical Discount Factor Values
Let V be the compact set of SPE payoffs and we also use when we want to emphasize the players’ discount factor . By , and we refer to the equilibria in pure strategies with and without public correlation, and mixed strategies, respectively.
The player
i’s minimum equilibrium payoff, which is also called the punishment payoff, is denoted by
, when
is non-empty; and this is the case in the symmetric
supergames. Similarly, the maximum equilibrium payoff is
. The minimax payoff is
Please note that the minimax payoffs can be different in pure and mixed strategies. However, it holds under perfect monitoring that
,
[
4,
11]. The player’s minimum and maximum payoffs in a compact set
W are denoted by
and
, respectively. Moreover,
is the maximum symmetric payoff in the set
W.
Let
be the set of feasible payoffs, where
denotes the convex hull of the set. The set of feasible and individually rational (FIR) payoffs are
Let us denote the critical discount factor by
which gives the smallest discount factor value when the payoff set coincides with the FIR payoffs. Please note that
is convex and thus
for all
by Theorem 3.
Please note that the minimum equilibrium payoff
may be strictly higher than the minimax payoff
, and then it is impossible to obtain all the FIR payoffs for given
. The minimum pure-strategy payoffs have been studied in [
24], and [
22] present an algorithm for finding the punishment paths and payoffs.
For most of the symmetric games, the minimum equilibrium payoffs in pure strategies are equal to the minimax payoffs for all discount factors. No conflict, its anti-game and anti-stag hunt games are the only exceptions. In these games, the minimum payoffs are equal to the minimax values when the players are patient enough. This issue does not affect the results, since it can be shown the required levels of patience are smaller than the critical values.
The minimax payoffs in mixed strategies are the same as in pure strategies, except in leader, battle of the sexes, coordination and anti-coordination games. In these games, the minimax payoff is given by a mixed-strategy Nash equilibrium. Thus, for all in mixed strategies. It can be shown that the FIR payoffs are not obtained for any in these games.
2.4. The Characterization of Equilibria
A pair
of an action profile
and a continuation payoff
is admissible with respect to
W if it satisfies
This incentive-compatibility condition means that it is better for player i to take action and get the continuation payoff than to deviate and then obtain .
For a set of continuation payoffs
W, the set of supportable action profiles is denoted by
For
, we denote the set of admissible continuation payoffs as
Let
be an affine mapping that corresponds to an action profile
and a discount factor
where
I is an
identity matrix and
T is an
diagonal matrix with the discount factor
on the diagonal. The mapping
is also defined for sets; then the addition is the Minkowski sum and
. Finally, we denote the admissible payoffs that start with an action profile
by
.
Theorem 1. The set of pure-strategy subgame-perfect equilibrium payoffs is the unique largest compact set satisfying the fixed-point [8,11] The payoff set under public correlation
is given by the largest compact set satisfying [
11]
Let us now characterize the set of equilibria in mixed strategies [
12,
13]. In a repeated game, the play at each round is strategically equivalent to playing an augmented stage game, where the continuation payoffs are included in the payoffs. For each action profile
, the payoff in the augmented game is given by
where
is the continuation payoff after
a. Please note that in pure strategies there are only two continuation payoffs for each player:
if the player follows the equilibrium path or
if the player deviates. In mixed strategies, there can be a different continuation payoff
after each action profile
. Let
denote the set of Nash equilibrium payoffs in a stage game with payoffs
,
.
Now, we are ready to state the characterization for the subgame-perfect equilibrium payoffs [
12,
13]. This result has been derived earlier in a more general model of imperfect monitoring [
11].
Theorem 2. The payoff set is the largest compact fixed point of : This means that the payoff set corresponds to the set of equilibria in augmented stage games where the payoffs are and each can be chosen from the set .
2.5. Monotonicity and Helpful Results
In this subsection, by
we refer to the sets
,
and
, depending on which strategies are in question. A set
W is called self-generating if
. The following result follows directly from Theorems 1 and 2 and Equation (
13).
Proposition 1. If a bounded set W is self-generating then .
The following shows that the payoff set is monotone in the discount factor when it is convex [
8,
11,
24,
25].
Theorem 3. Suppose is convex then for .
Let
,
,
and
be the corners of a quadrilateral set
W corresponding to payoffs
,
,
and
. For example, if
and
are the payoffs in the northeast and northwest corners of
, then
and
are the northeast and the northwest corners of the sets
and
; see
Figure 2a. Moreover, let
This is the right-hand side of Equation (
8) for the column that contains the maximum payoff in the game.
Remark 1. If , , then for all a and i where player i can deviate to the maximum payoff of the stage game.
The following result describes how the sets , , may cover the boundaries of . The result implies that we need as many sets , , to cover the FIR payoffs as there are corner points in .
Proposition 2. The set , , may only cover the corner point of closest to . It cannot cover the other corner points or the boundary of between these other corner points.
Proof. By the definition of , the set is contracted by and is thus strictly smaller than . The translation part moves the set towards . ☐
3. Results for Different Strategies
We present now the results for the three different strategies, and the proofs are given in the appendix.
Section 4 gives an example of the proofs in a prisoner’s dilemma game. The proofs for the mixed strategies are novel in
Appendix C. However, the principle behind the proofs is the same but finding all the mixed-strategy payoffs is more complicated.
The results are based on Theorems 1 and 2 and Equation (
13), which tell that the payoff set coincides with the FIR payoffs when the admissible payoffs cover all the payoffs in
. To find the critical value
, we need to find the smallest discount factor for this to happen. The main idea is to find the last payoff point
that is covered when the discount factor is increased to
. The value
is typically solved from a condition that two sets, say
and
intersect. In the proofs, we show both the necessary and sufficient conditions for
: the point
is not covered for a smaller discount factor value and all the other FIR payoffs are covered for the given value
.
The results are given in
Table 1,
Table 2 and
Table 3. They show the values of
for different groups of games. Please note that the group boundaries cross the game boundaries. For example, there are two groups of prisoner’s dilemma (PD) games in pure strategies without public correlation: the quadrilateral PDs belong to Group I (see example in
Figure 2a) and the triangle PDs in Group IIIb, and the boundary between these groups is given by the equation
. Also, different games may belong to the same group: the triangle PDs and triangle chicken games all belong to Group IIIb.
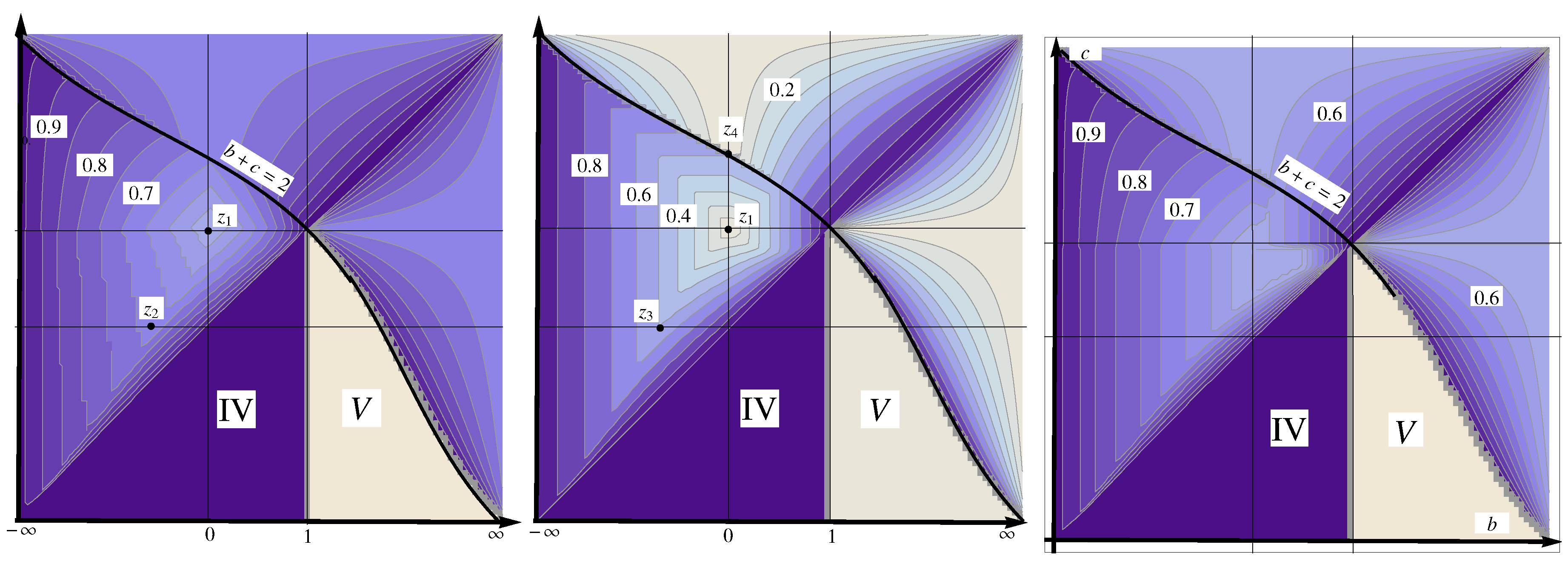
Figure 3 shows the groups for the different strategies. The thick grey lines show that there are discontinuities of
between the groups. This means that the value of
is not continuous and there may be a jump, when
b and
c are changed.
Figure 4 shows the values of
in different games.
The groups are based on the equations that determine the value of and the location of the last payoff . We note that our classification is heuristic, and the games could be organized differently into groups. In pure strategies without public correlation: in Group I, is found on the upper edge of between and , on the bottom edge between and in Group II, and in the middle in Groups IIIa-d. In Group IV, we have and in Group V, .
With public correlation, the groups are based on the last corner point to be covered: in Group I, the last corner is in the northwest, corresponding to or , the corner in Group II, and the corner in Group III.
In mixed strategies, the groups are the following. In Group Ia, the last point to be covered is on the boundary between and , i.e., the intersection of and . Group Ib corresponds to the triangle games, where and intersect. In Group II, a corner point determines the value of : corner is last to be covered in Group IIa and corner in Group IIb. The intersection of and determines the value for Group III.
The overview of the values of is similar for all the strategies. Groups IV and V are the same, and the locations of the high and low values are about the same. However, the values of are much lower with public correlation. The scale with public correlation is between 0 and 1, and between or to 1 with the other strategies. The smallest and the highest values within the game classes are shown with to . The difference between the pure and mixed strategies is surprisingly small; the values are typically smaller than in quadrilateral games and smaller than in triangle games.
We note that for all groups, there are some payoff parameters for which , except in Group V where for all payoffs. For example, when for prisoner’s dilemma, stag hunt and coordination games. This means that we cannot extend the folk theorem unless these extreme payoff parameters can be ruled out.
We can observe that the value of depends on how large is compared to . When is small, it is difficult to play certain actions in the game and the value of is high. For example, it is difficult to play the actions b and c in a prisoner’s dilemma when . Geometrically, this means that stays almost the same but keeps increasing, making the proportion of to smaller. On the other hand, if is large then is smaller. Please note that Groups IV and V are exceptions, where is a constant and thus independent of and .
We also note that there are discontinuities in
on some of the group boundaries; see the thick grey lines in
Figure 3. The discontinuity means that small changes in the payoffs can affect dramatically the payoff set and how large
is. The discontinuity between the prisoner’s dilemma games is surprising and it shows that a small geometric change from the triangle-shape to the quadrangle-shape may affect whether the Pareto efficient payoffs are obtained or not.
For mixed strategies, we have a few remarks. The necessary and sufficient conditions for are more difficult to prove, since the strategies and their payoffs are more complicated. For Groups IIb and III, the values are only upper bounds since we only use the sufficient conditions. In all leader, battle of the sexes, coordination and anti-coordination games, but in the figure we use the values for which the pure-strategy FIR payoffs are obtained as a comparison.
4. Group I in Pure Strategies without Public Correlation
This group is defined by parameters
and
. These are the prisoner’s dilemmas where
is a quadrilateral with an obtuse angle in
corner; see
Figure 2a. It is enough to examine the upper half of
where
since
is symmetric with respect to the center line. Thus, the last point
that is covered is only defined in the upper half of
.
The point
in Group I is located on the upper edge between
and
. This point and the corresponding discount factor
are solved from the intersection of
and
. It is enough to consider only player 1’s payoffs:
On the second line, the first payoff can be solved from the right-hand side of the admissibility condition.
We first show that , , if . Since the sets and intersect at , it means that does not belong to either or for . Moreover, the sets and cannot cover on the boundary of by Proposition 2.
Now, let us show that every
for some
and
. We divide
into three regions. If
then
since
coincides with
for all
by Remark 1. If
and
then we show that
. We show that all corner points
,
and
belong to
.
is the Nash equilibrium and belongs to
for any
. Also,
belongs to
if
belongs to
, because
is higher than
due to
. So for the last corner, we need to show that
. It holds that
and
and the above condition holds if
. Using Equation (
16), this is equal to
and this is true in this group.
Finally, if and then we show that . The corner points are , , and . belongs to trivially by the definition of . since is at the upper edge and covers the edge all the way to . since coincides with for all when by Remark 1. Again, ensures that and thus since .
5. Conclusions
This paper examines the discount factor values for which the subgame-perfect equilibrium payoffs coincide with the FIR payoffs in the symmetric supergames. The main motivation is to study if the folk theorem could be extended in a class of games and find out the reasons why a high level of patience such as is required in some games. We find that the main reason is that it is impossible to obtain payoffs close to the minimax values: (1) this happens in Group IV in all strategies, (2) it is a result of the fact that the mixed-strategy punishment payoff is strictly smaller than the pure-strategy punishment in leader, battle of the sexes, coordination and its anti-game in mixed strategies, and (3) it is due to geometrical reasons in some games, i.e., how the stage-game payoffs are located and how large the FIR payoffs are in proportion to feasible payoffs . If is small, which also means that it is difficult to play certain actions in the game, then a high level of patience is required.
We also examine how the public correlation and the mixed strategies affect the results. The games are organized into a few groups based on the equation that determines the smallest discount factor value as a function of the stage-game payoffs. The groups and the equations are a bit different under different strategies, but the overview looks similar. Even though a lower level of patience is required with public randomization, the highest and the lowest values are obtained in the same regions. The limit is obtained when , when , when and , or in certain anti-games. Thus, it is not possible to extend the folk theorem in any of the typical game classes, such as prisoner’s dilemma, chicken and stag hunt games, unless certain extreme payoffs can be ruled out. Furthermore, the public correlation or mixed strategies do not provide a remedy in these games and it holds that under all strategies.
The results of this paper help in determining the payoff set for high discount factor values. If the discount factor is higher than , then all the FIR payoffs are subgame-perfect equilibrium payoffs. Moreover, it is a bit surprise how small can be with public correlation. It was also observed that there are certain boundaries where is discontinuous, which means that small changes in the payoffs may affect dramatically the equilibrium payoffs.
It should be noted that this kind of analysis could be done in asymmetric games with more than two actions and more than two players. Furthermore, it is left for future research how to compute efficiently all the equilibrium payoffs when the discount factors are smaller than .