The Evolvability of Cooperation under Local and Non-Local Mutations
Abstract
:1. Introduction
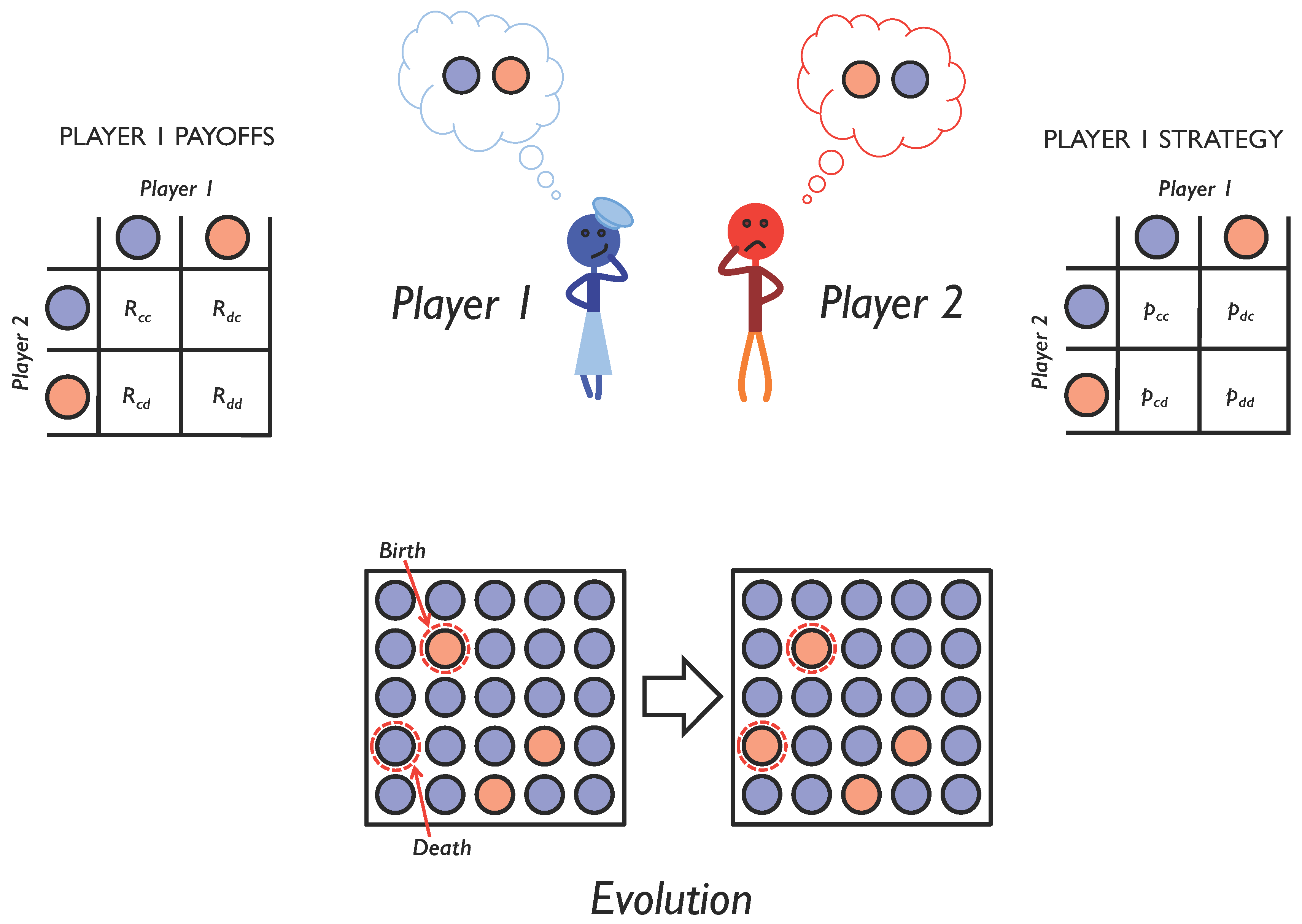
2. Results
2.1. Iterated Two-Player Games
2.2. Adaptive Dynamics of Memory-1 Strategies
2.2.1. Zero Selection Gradient
- and
- and
- and
2.2.2. Selection Gradient Perpendicular into the Boundary
- and ;
- and ;
- and simultaneously take extremal values.
2.3. Probability of Reaching a Strategy Class
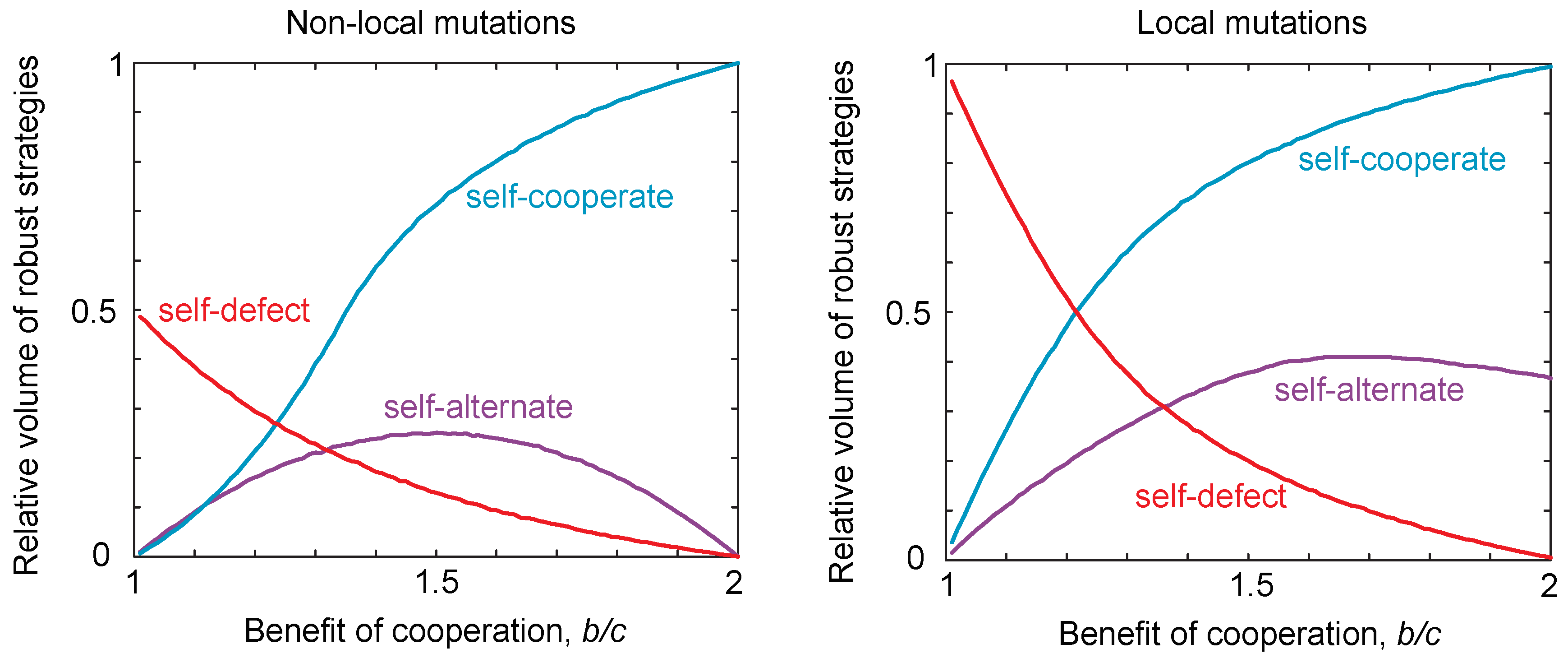
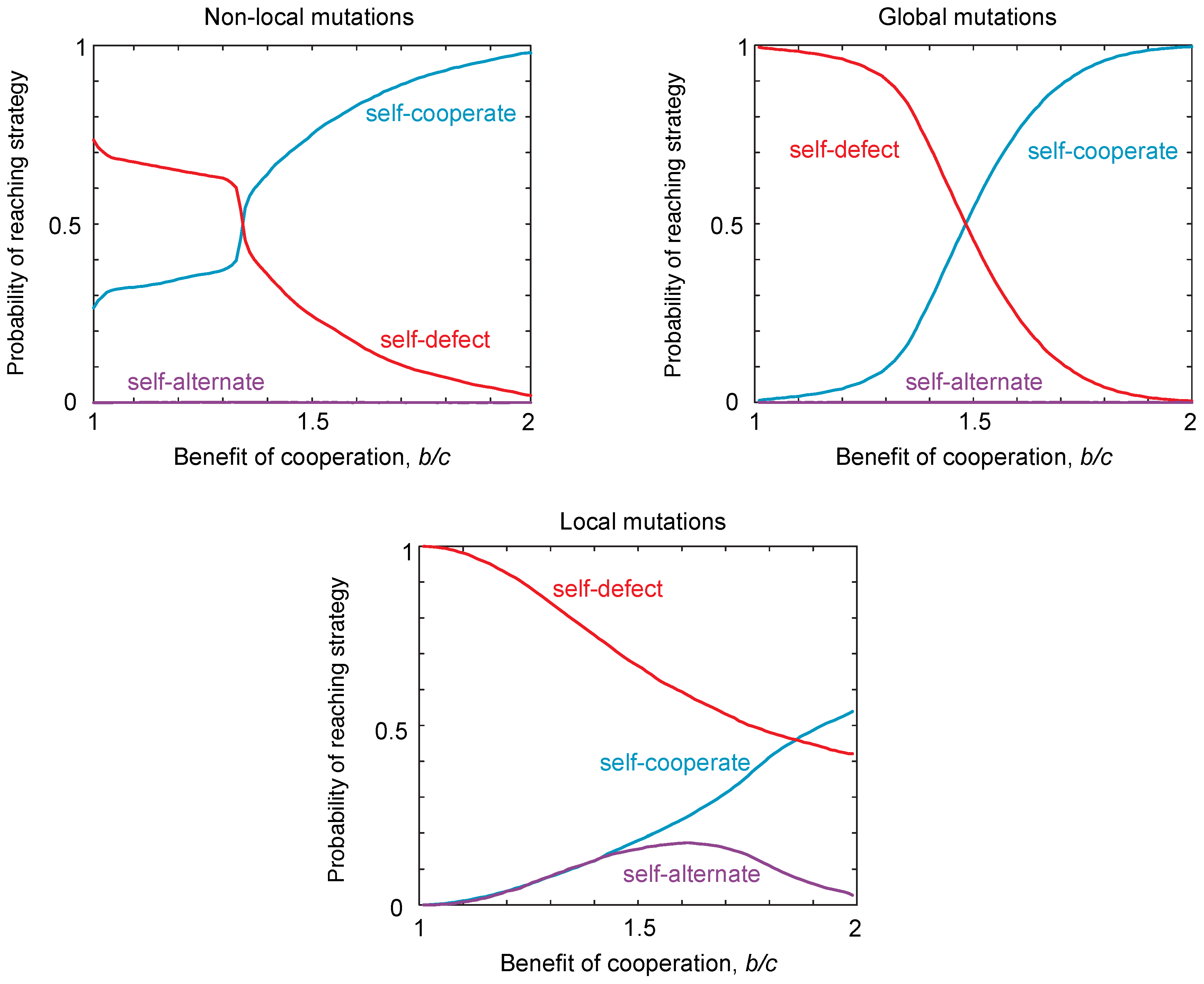
2.4. Neutral Drift
2.5. Evolution of Investment

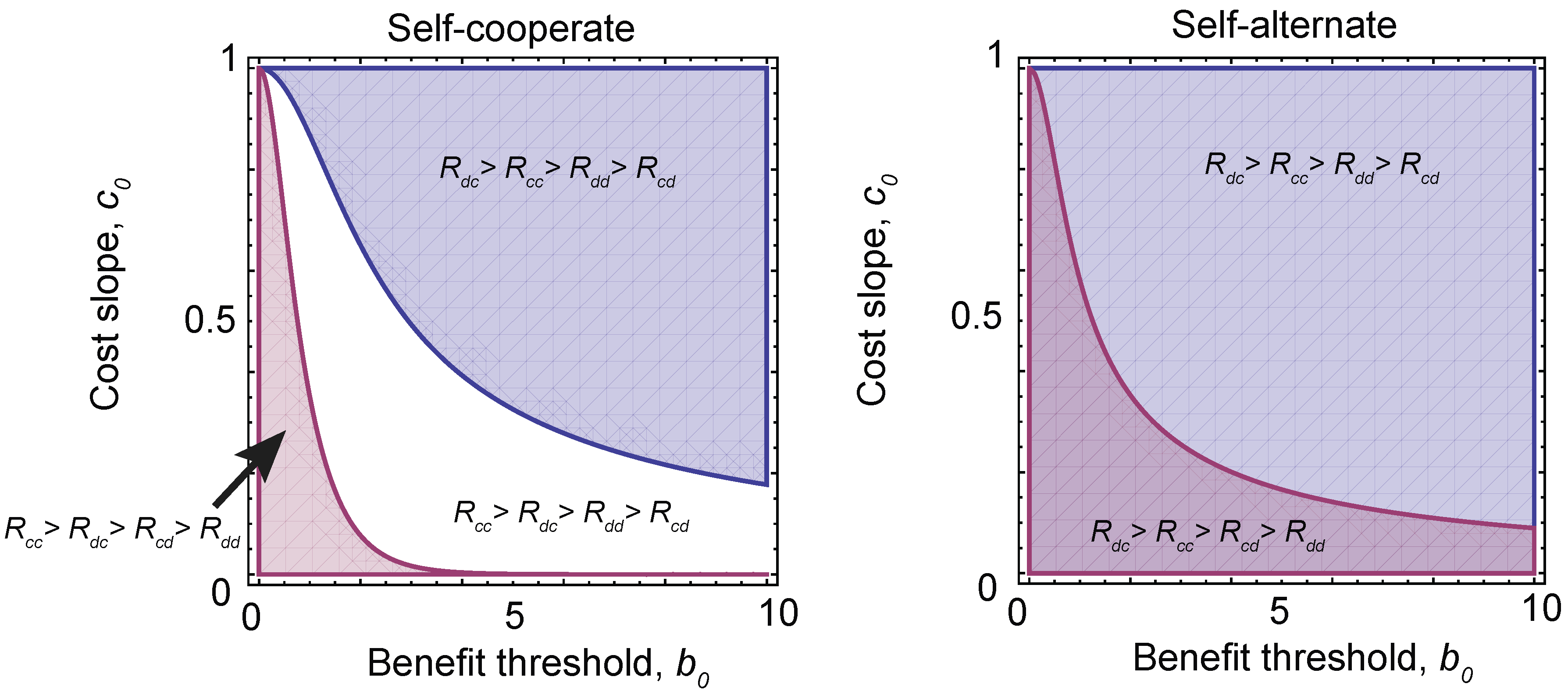
3. Discussion and Conclusions
4. Materials and Methods
4.1. Evolution of Memory-1 Strategies under Local Mutations
4.1.1. Selection Gradient away from the Boundaries
4.1.2. Selection Gradient at the Boundaries
4.1.3. Intersection of Multiple Strategy Classes
4.2. Evolution of Investment
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Axelrod, R.; Axelrod, D.E.; Pienta, K.J. Evolution of cooperation among tumor cells. Proc. Natl. Acad. Sci. USA 2006, 103, 13474–13479. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Boyd, R.; Gintis, H.; Bowles, S. Coordinated punishment of defectors sustains cooperation and can proliferate when rare. Science 2010, 328, 617–620. [Google Scholar] [CrossRef] [PubMed]
- Cordero, O.X.; Ventouras, L.A.; DeLong, E.F.; Polz, M.F. Public good dynamics drive evolution of iron acquisition strategies in natural bacterioplankton populations. Proc. Natl. Acad. Sci. USA 2012, 109, 20059–20064. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Van Dyken, J.D.; Wade, M.J. Detecting the molecular signature of social conflict: Theory and a test with bacterial quorum sensing genes. Am. Nat. 2012, 179, 436–450. [Google Scholar] [CrossRef] [PubMed]
- Waite, A.J.; Shou, W. Adaptation to a new environment allows cooperators to purge cheaters stochastically. Proc. Natl. Acad. Sci. USA 2012, 109, 19079–19086. [Google Scholar] [CrossRef] [PubMed]
- Draghi, J.; Wagner, G.P. The evolutionary dynamics of evolvability in a gene network model. J. Evolut. Biol. 2009, 22, 599–611. [Google Scholar] [CrossRef] [PubMed]
- Masel, J.; Trotter, M. Robustness and evolvability. Trends Genet. 2010, 26, 406–414. [Google Scholar] [CrossRef] [PubMed]
- Draghi, J.; Wagner, G.P. Evolution of evolvability in a developmental model. Evolution 2008, 62, 301–315. [Google Scholar] [CrossRef] [PubMed]
- Draghi, J.; Parsons, T.; Wagner, G.; Plotkin, J. Mutational robustness can facilitate adaptation. Nature 2010, 436, 353–355. [Google Scholar] [CrossRef] [PubMed]
- Stewart, A.; Parsons, T.; Plotkin, J. Environmental robustness and the adaptability of populations. Evolution 2012, 66, 1598–1612. [Google Scholar] [CrossRef] [PubMed]
- Akin, E. Stable Cooperative Solutions for the Iterated Prisoner’s Dilemma. 2012. arXiv:1211.0969. Available online: http://arxiv.org/abs/1211.0969v1 (accessed on 21 July 2015).
- Press, W.H.; Dyson, F.J. Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent. Proc. Natl. Acad. Sci. USA 2012, 109, 10409–10413. [Google Scholar] [CrossRef] [PubMed]
- Stewart, A.J.; Plotkin, J.B. From extortion to generosity, evolution in the Iterated Prisoner’s Dilemma. Proc. Natl. Acad. Sci. USA 2013, 110, 15348–15353. [Google Scholar] [CrossRef] [PubMed]
- Stewart, A.J.; Plotkin, J.B. Collapse of cooperation in evolving games. Proc. Natl. Acad. Sci. USA 2014, 111, 17558–17563. [Google Scholar] [CrossRef] [PubMed]
- Hilbe, C.; Nowak, M.A.; Sigmund, K. Evolution of extortion in Iterated Prisoner’s Dilemma games. Proc. Natl. Acad. Sci. USA 2013, 110, 6913–6918. [Google Scholar] [CrossRef] [PubMed]
- Fudenberg, D.; Maskin, E. Evolution and Cooperation in noisy repeated games. Am. Econ. Rev. 1990, 80, 274–279. [Google Scholar]
- Geritz, S.; Kisdi, E.; Meszéna, G.; Metz, J. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evolut. Ecol. Res. 1998, 12, 35–37. [Google Scholar] [CrossRef]
- Hilbe, C.; Nowak, M.A.; Traulsen, A. Adaptive dynamics of extortion and compliance. PLoS ONE 2013, 8, e77886. [Google Scholar] [CrossRef] [PubMed]
- Imhof, L.A.; Nowak, M.A. Stochastic evolutionary dynamics of direct reciprocity. Proc. Biol. Sci. 2010, 277, 463–468. [Google Scholar] [CrossRef] [PubMed]
- Hilbe, C. Local replicator dynamics: A simple link between deterministic and stochastic models of evolutionary game theory. Bull. Math. Biol. 2011, 73, 2068–2087. [Google Scholar] [CrossRef] [PubMed]
- Boerlijst, M.C.; Nowak, M.A.; Sigmund, K. Equal pay for all prisoners. Am. Math. Month. 1997, 104, 303–307. [Google Scholar] [CrossRef]
- Stewart, A.J.; Plotkin, J.B. Extortion and cooperation in the Prisoner’s Dilemma. Proc. Natl. Acad. Sci. USA 2012, 109, 10134–10135. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Page, K.M.; Nowak, M.A. Unifying evolutionary dynamics. J. Theor. Biol. 2002, 219, 93–98. [Google Scholar] [CrossRef]
- Lieberman, E.; Hauert, C.; Nowak, M.A. Evolutionary dynamics on graphs. Nature 2005, 433, 312–316. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M.A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar] [CrossRef] [PubMed]
- Cabrales, A. Stochastic replicator dynamics. Int. Econ. Rev. 2000, 41, 451–482. [Google Scholar] [CrossRef]
- Foster, D.; Young, P. Stochastic evolutionary game dynamics. Theor. Popul. Biol. 1990, 38, 219–232. [Google Scholar] [CrossRef]
- Fudenberg, D.; Harris, C. Evolutionary dynamics with aggregate shocks. J. Econ. Theory 1992, 57, 420–441. [Google Scholar] [CrossRef]
- Wang, Z.; Szolnoki, A.; Perc, M. Different perceptions of social dilemmas: Evolutionary multigames in structured populations. Phys. Rev. E 2014, 90, 032813. [Google Scholar] [CrossRef]
- Perc, M.; Szolnoki, A. Coevolutionary games—A mini review. Biosystems 2010, 99, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Doebeli, M.; Hauert, C.; Killingback, T. The evolutionary origin of cooperators and defectors. Science 2004, 306, 859–862. [Google Scholar] [CrossRef] [PubMed]
- Traulsen, A.; Nowak, M.A.; Pacheco, J.M. Stochastic dynamics of invasion and fixation. Phys. Rev. E 2006, 74, 011909. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stewart, A.J.; Plotkin, J.B. The Evolvability of Cooperation under Local and Non-Local Mutations. Games 2015, 6, 231-250. https://doi.org/10.3390/g6030231
Stewart AJ, Plotkin JB. The Evolvability of Cooperation under Local and Non-Local Mutations. Games. 2015; 6(3):231-250. https://doi.org/10.3390/g6030231
Chicago/Turabian StyleStewart, Alexander J., and Joshua B. Plotkin. 2015. "The Evolvability of Cooperation under Local and Non-Local Mutations" Games 6, no. 3: 231-250. https://doi.org/10.3390/g6030231




