Reciprocity Effects in the Trust Game
Abstract
:1. Introduction
2. Experimental Section
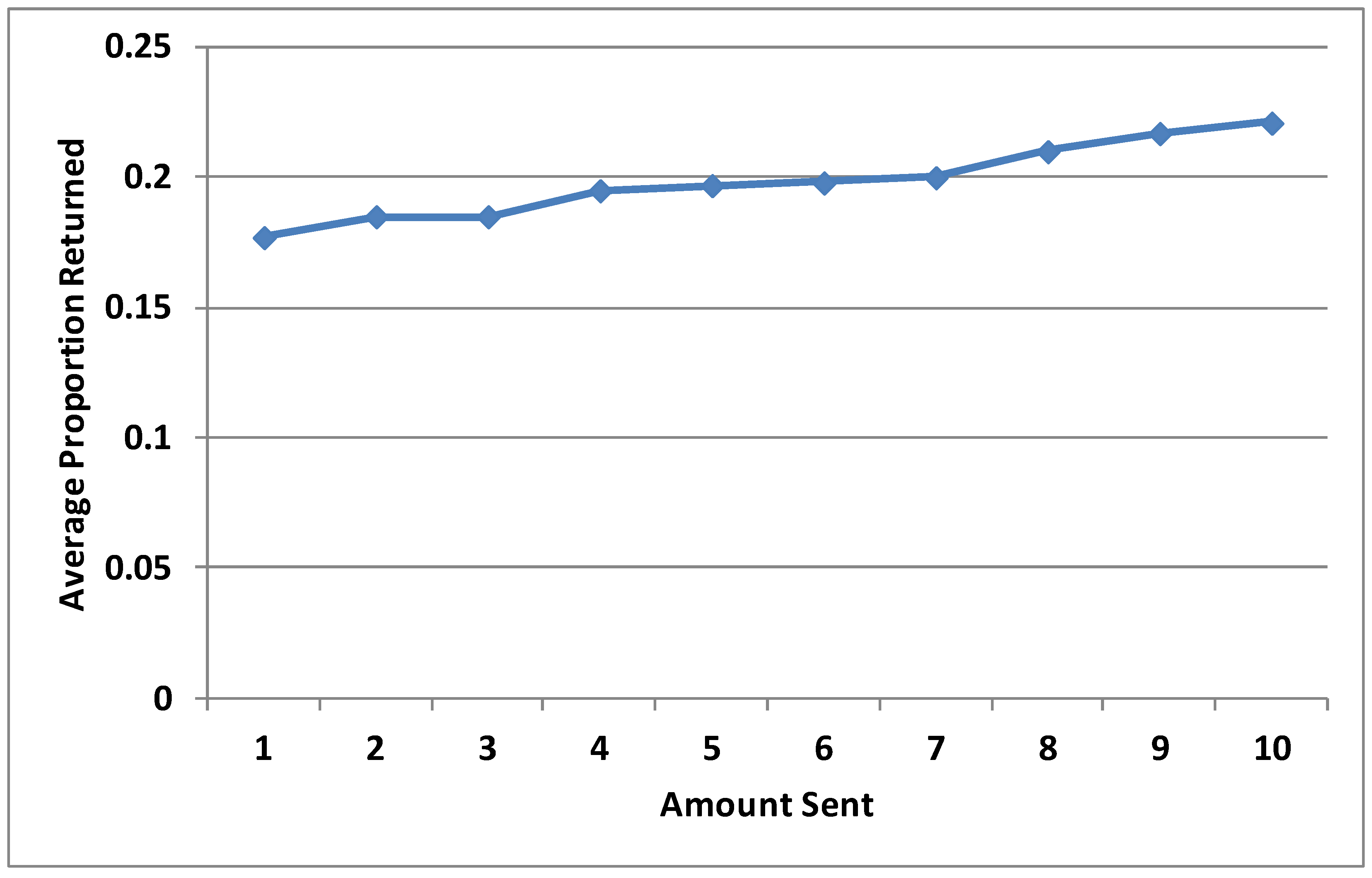
3. Results and Discussion
| Classification | Number | Percentage |
|---|---|---|
| Reciprocator | 10 | 31% |
| neutral | 10 | 31% |
| Anti-Reciprocator | 4 | 13% |
| Free Rider | 8 | 25% |
| Total | 32 | 100% |
| Classification | Number | Percentage |
|---|---|---|
| Reciprocator | 42 | 22% |
| neutral | 87 | 45% |
| Anti-Reciprocator | 13 | 7% |
| Free Rider | 50 | 26% |
| Total | 192 | 100% |
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Berg, J.; Dickhaut, J.; McCabe, K. Trust, reciprocity, and social history. Games Econ. Behav. 1995, 10, 122–142. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Dufwenberg, M.; Kirchsteiger, G. A theory of sequential reciprocity. Games Econ. Behav. 2004, 47, 268–298. [Google Scholar] [CrossRef]
- Cox, J.C. How to identify trust and reciprocity. Games Econ. Behav. 2004, 46, 260–281. [Google Scholar] [CrossRef]
- Cochard, F.; Nguyen-Van, P.; Willinger, M. Trusting behavior in a repeated investment game. J. Econ. Behav. Organ. 2004, 55, 31–44. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gaechter, S.; Fehr, E. Are people conditionally cooperative? Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef]
- Eckel, C.C.; Petrie, R. Face value. Am. Econ. Rev. 2011, 101, 1497–1513. [Google Scholar] [CrossRef]
- Brandts, J.; Charness, G. The strategy versus the direct-response method: A first survey of experimental comparisons. Exp. Econ. 2011, 14, 375–398. [Google Scholar] [CrossRef] [Green Version]
- Amdur, D.; Schmick, E. Does the direct-response method induce guilt aversion in a trust game? Econ. Bull. 2013, 33, 687–693. [Google Scholar]
- Rick, S.; Weber, R.A. Meaningful learning and transfer of learning in repeated games played repeatedly without feedback. Games Econ. Behav. 2010, 68, 716–730. [Google Scholar] [CrossRef]
Appendix
| Subject | Response Function | Average Response Function | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||||||
| ρ | p | type | ρ | p | type | ρ | p | type | ρ | p | type | ρ | p | type | ρ | p | type | ρ | p | type | |
| 1 | 0.89 | 0.00 | R | 0.87 | 0.00 | R | 0.86 | 0.00 | R | 0.80 | 0.01 | R | 0.83 | 0.00 | R | 0.89 | 0.00 | R | 0.94 | 0.00 | R |
| 2 | 0.15 | 0.69 | N | 0.23 | 0.52 | N | 0.16 | 0.66 | N | 0.16 | 0.66 | N | 0.12 | 0.74 | N | 0.13 | 0.72 | N | 0.12 | 0.74 | N |
| 3 | 0.23 | 0.52 | N | 0.64 | 0.04 | R | 0.78 | 0.01 | R | 0.05 | 0.90 | N | 0.87 | 0.00 | R | 0.23 | 0.53 | N | 0.94 | 0.00 | R |
| 4 | 0.78 | 0.01 | R | 0.17 | 0.65 | N | 0.98 | 0.00 | R | 0.87 | 0.00 | R | 0.98 | 0.00 | R | 0.98 | 0.00 | R | 0.96 | 0.00 | R |
| 5 | 0.52 | 0.12 | N | 0.52 | 0.12 | N | 0.52 | 0.12 | N | 0.52 | 0.12 | N | 0.52 | 0.12 | N | 0.52 | 0.12 | N | 0.52 | 0.12 | N |
| 6 | 0.00 | 1.00 | N | −0.52 | 0.12 | N | 0.10 | 0.79 | N | 1.00 | 0.00 | R | 0.00 | 1.00 | N | 0.19 | 0.60 | N | 0.31 | 0.38 | N |
| 7 | 0.52 | 0.12 | N | 0.00 | 1.00 | FR | 0.00 | 1.00 | N | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.52 | 0.12 | FR |
| 8 | −0.80 | 0.01 | AR | −0.48 | 0.16 | N | 0.00 | 1.00 | N | 0.00 | 1.00 | N | −1.00 | 0.00 | AR | 0.20 | 0.57 | N | −0.90 | 0.00 | AR |
| 9 | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR |
| 10 | 0.64 | 0.04 | R | 0.64 | 0.04 | R | 0.64 | 0.04 | R | 0.64 | 0.04 | R | 0.64 | 0.04 | R | 0.64 | 0.04 | R | 0.64 | 0.04 | R |
| 11 | 0.63 | 0.05 | R | 0.63 | 0.05 | R | 0.00 | 1.00 | FR | 0.75 | 0.01 | R | 0.68 | 0.03 | R | 0.70 | 0.02 | R | 0.94 | 0.00 | R |
| 12 | −0.40 | 0.25 | N | 0.16 | 0.65 | N | −0.19 | 0.60 | N | −0.44 | 0.20 | N | 0.05 | 0.90 | N | −0.14 | 0.70 | N | −0.10 | 0.79 | N |
| 13 | 0.42 | 0.23 | N | 0.42 | 0.23 | N | 0.42 | 0.23 | N | 0.42 | 0.23 | N | 0.42 | 0.23 | N | 0.42 | 0.23 | N | 0.42 | 0.23 | N |
| 14 | −0.52 | 0.12 | N | 0.12 | 0.74 | N | −0.27 | 0.44 | N | 0.20 | 0.58 | N | 0.05 | 0.89 | N | −0.74 | 0.02 | AR | −0.43 | 0.22 | N |
| 15 | −0.90 | 0.00 | AR | −0.98 | 0.00 | AR | −0.66 | 0.04 | AR | −0.98 | 0.00 | AR | −0.99 | 0.00 | AR | 0.68 | 0.03 | R | −0.89 | 0.00 | AR |
| 16 | 0.66 | 0.04 | R | 1.00 | 0.00 | R | 0.00 | 1.00 | N | 0.03 | 0.93 | N | 0.94 | 0.00 | R | 0.00 | 1.00 | N | 0.87 | 0.00 | R |
| 17 | 0.40 | 0.26 | N | 0.45 | 0.19 | N | 1.00 | 0.00 | R | −0.49 | 0.15 | N | 0.46 | 0.18 | N | 0.58 | 0.08 | N | 0.65 | 0.04 | R |
| 18 | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR |
| 19 | 0.00 | 1.00 | N | 0.00 | 1.00 | N | 0.00 | 1.00 | N | 0.00 | 1.00 | N | 0.00 | 1.00 | N | 0.00 | 1.00 | N | 0.00 | 1.00 | N |
| 20 | −0.89 | 0.00 | AR | 0.01 | 0.99 | N | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | −0.83 | 0.00 | FR |
| 21 | 0.83 | 0.00 | R | 0.92 | 0.00 | R | 0.55 | 0.10 | N | 0.07 | 0.85 | N | 0.81 | 0.00 | R | 0.67 | 0.03 | R | 0.87 | 0.00 | R |
| 22 | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR |
| 23 | 0.81 | 0.00 | R | 0.80 | 0.01 | R | 0.35 | 0.32 | N | 0.30 | 0.40 | N | −1.00 | 0.00 | AR | 0.52 | 0.12 | N | 0.76 | 0.01 | R |
| 24 | −1.00 | 0.00 | AR | 0.53 | 0.11 | N | 0.66 | 0.04 | R | 0.20 | 0.57 | N | 0.24 | 0.50 | N | 0.53 | 0.12 | N | −0.06 | 0.87 | N |
| 25 | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR |
| 26 | −0.13 | 0.72 | N | −0.44 | 0.21 | N | −0.53 | 0.12 | N | 0.00 | 1.00 | FR | −0.51 | 0.13 | N | 0.00 | 1.00 | FR | −0.41 | 0.24 | N |
| 27 | −0.55 | 0.10 | N | −0.32 | 0.37 | N | 0.28 | 0.44 | N | 0.00 | 1.00 | N | 0.00 | 1.00 | N | −0.70 | 0.02 | AR | −0.54 | 0.11 | N |
| 28 | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR |
| 29 | −1.00 | 0.00 | AR | −0.45 | 0.19 | N | −0.45 | 0.19 | N | −0.45 | 0.19 | N | −0.45 | 0.19 | N | −0.45 | 0.19 | N | −0.85 | 0.00 | AR |
| 30 | −0.52 | 0.12 | N | −0.41 | 0.24 | N | −0.29 | 0.42 | N | −0.17 | 0.63 | N | −0.06 | 0.87 | N | 0.06 | 0.87 | N | −0.97 | 0.00 | AR |
| 31 | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR | 0.00 | 1.00 | FR |
| 32 | 0.00 | 1.00 | FR | 0.75 | 0.01 | R | 0.68 | 0.03 | R | 0.00 | 1.00 | FR | 0.68 | 0.03 | R | 0.75 | 0.01 | R | 0.91 | 0.00 | R |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Smith, A. Reciprocity Effects in the Trust Game. Games 2013, 4, 367-374. https://doi.org/10.3390/g4030367
Smith A. Reciprocity Effects in the Trust Game. Games. 2013; 4(3):367-374. https://doi.org/10.3390/g4030367
Chicago/Turabian StyleSmith, Alexander. 2013. "Reciprocity Effects in the Trust Game" Games 4, no. 3: 367-374. https://doi.org/10.3390/g4030367




