The Minority of Three-Game: An Experimental and Theoretical Analysis
Abstract
: We report experimental results on the minority of three-game, where three players choose one of two alternatives and the most rewarding alternative is the one chosen by a single player. This coordination game has many asymmetric equilibria in pure strategies that are non-strict and payoff-asymmetric and a unique symmetric mixed strategy equilibrium in which each player's behavior is based on the toss of a fair coin. This straightforward behavior is predicted by equilibrium selection, impulse-balance equilibrium, and payoff-sampling equilibrium. Experimental participants rely on various decision rules, and only a quarter of them perfectly randomize.1. Introduction
Many games have multiple (perfect) equilibria so that the equilibrium concept alone does not answer or explain how the game will be played. One such class of games are market entry games (Selten and Güth [1]) capturing the coordination problem when a newly emergent profit opportunity can be exploited only by a limited number of agents. In a market entry game each player enters one of several markets. For at least one of the markets, the payoff upon entering that market decreases with the number of entrants. Market entry games thus share two essential characteristics: First, players have a common interest in selecting different actions, and, second, players face the same set of choices and similar incentives. Due to their common interest in selecting different actions, players would like to have or would appreciate some external clues to determine how different players are going to (should) act. But especially in the case of symmetry, the game does not offer any such clues when more than two players are involved. There are typically multiple asymmetric equilibria in pure strategies, each of them maximizing joint payoffs, and a unique inefficient mixed strategy equilibrium. Market entry game experiments have shown that behavior is consistent with reinforcement learning and that information about others' choices shapes behavioral adjustment over time (see Ochs [2] and Camerer [3] (chapter 7, section 3) for reviews).
In this paper, we present experimental evidence on the minority of three-game, which in one important aspect differs from previously studied market entry games: all its asymmetric equilibria in pure strategies are non-strict and imply earning discrepancies. Thus, the unique symmetric mixed strategy equilibrium appears the natural benchmark to which we will compare observed behavior. According to the unique symmetry invariant equilibrium of the minority of three-game, each player's behavior is based on the toss of a fair coin. Such straightforward behavior is also predicted by alternative solution concepts such as the impulse-balance equilibrium and the payoff-sampling equilibrium. Thus, deviations from the mixed strategy hypothesis result most likely from heterogeneous decision rules.
Our experimental setup provides an adequate environment to identify alternative decision rules. First, we endow experimental subjects with a mixing device to directly elicit mixed strategies and to generate i.i.d choice sequences. Indeed, unlike in games with many interacting parties where (population) shares of different strategies may be interpreted as a mixed population strategy, triadic interaction is better studied by directly eliciting individual mixing. Of course, mixing may be due to ambiguous expectations rather than indifference. Controlling for information retrieval could allow to disentangle the hypotheses of ambiguous expectations (to be correlated with more retrievals) and of indifference (previous choices of others render both choices equally good).
Eliciting individual mixing is not new (see, e.g., Ochs [2]), but the focus has been mainly on games with a unique (mixed strategy) equilibrium. The use of mixed equilibrium strategies could only partly be confirmed, which still does not exclude that using them can be learned. Furthermore, the coexistence of mixed and pure strategy equilibria could suggest another reason for mixing, namely an attempt to cope with the multiplicity of equilibria. Although the minority of three-game belongs to the class of market entry games, of which this is the simplest one, market entry game experiments typically differ from our experiment. In a prototypical market entry experiment, the number of potential entrants is kept constant, whereas the so-called “capacity” of the market varies over the progress of the session. Thus, participants learn to play a specific class of market entry games, whereas in our study they learn to play just the minority of three-game.
Second, we implement a strangers design which increases the difficulty to adapt to others' past play. Such changes may, of course, question the findings of former experiments that employed market entry games such as convergence to equilibrium play via reinforcement learning and the effects of information feedback. In this sense, our study appears to be a stress test of how robust the former findings are.
In Section 2 we provide a thorough theoretical analysis of the minority of three-game. Section 3 describes the experimental protocol and Section 4 presents the experimental results. Section 5 discusses previous related research and Section 6 concludes.
2. Theory
In this section, we first introduce the minority of three-game and derive its standard game-theoretical predictions. Second, we theoretically analyze a uniformly and an asymmetrically perturbed version of the game, and we discuss the implications of Harsanyi and Selten's [4] equilibrium selection theory. Finally, we derive alternative predictions for the minority of three-game. Proofs can be found in the appendix.
2.1. The Minority of Three-Game
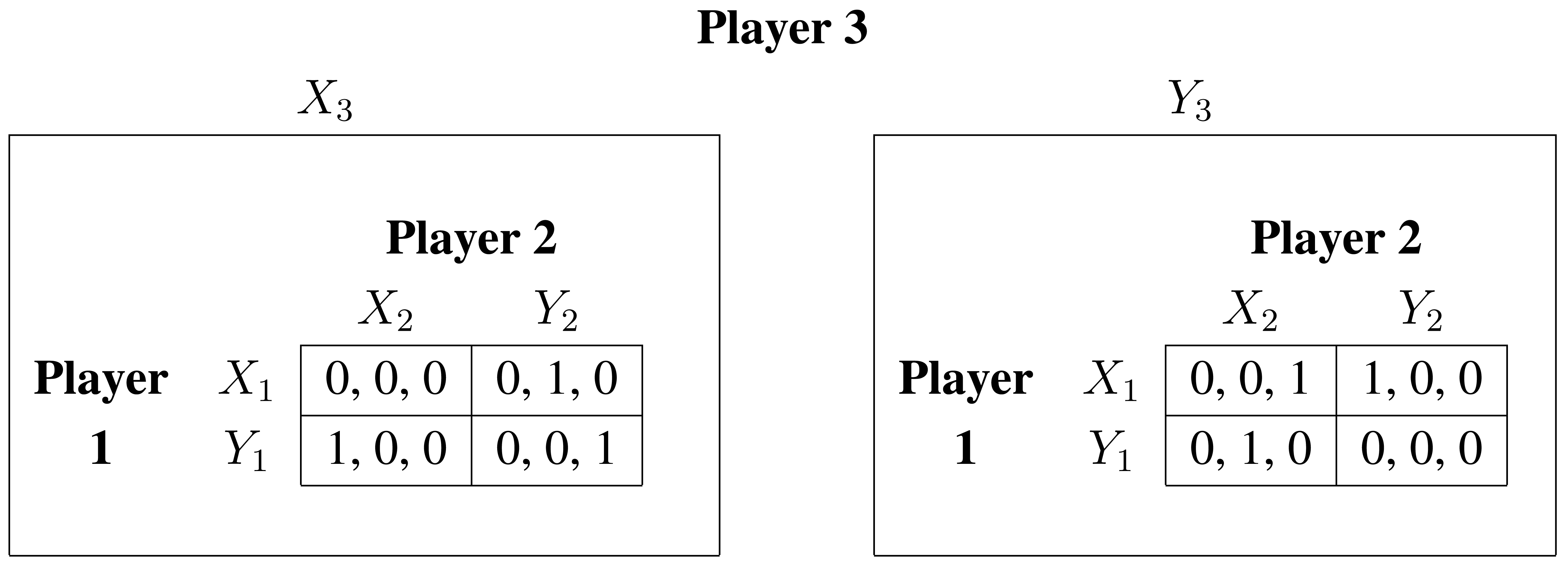
Three players have to choose one of two alternatives independently, and the most rewarding alternative is the one chosen by a single player. Hence the two alternatives are perfectly symmetric and players' payoffs are solely based on how players distribute the payoffs between them. Formally, we denote the minority of three-game by M3G = 〈N, (Ai)i∈N, (ui) i∈N〉 where N = {1, 2, 3} is the set of players, Ai = {Xi, Yi} for each i ∈ N is the set of alternatives, and ui : A → ℝ with A = ×i∈N Ai is player i's (vNM) utility function such that
There exist 6 pure strategy equilibria: (X1, Y2, X3), (X1, X2, Y3), (X1, Y2, Y3), (Y1, X2, X3), (Y1, Y2, X3), and (Y1, X2, Y3). These pure strategy equilibria are Pareto efficient and non-strict since each of the two players with 0 payoff can deviate unilaterally without affecting her own payoff. Actually, the best reply structure of the game is rather simple since each player i ∈ N should choose alternative Xi (resp. Yi) if the sum of the probabilities for alternative X (resp. Y ) by her opponents is strictly lower than 1. Indeed, for each player i ∈ N, Ui (Xi, σ−i) = Π j∈Nσj(Yj) > Ui (Yi, σ−i) = Πj∈Nσj(Xj) is equivalent to 1 > Σj∈N σj(Xj) where i ≠ j and σ−i ∈ ×j∈N Δ(Aj). Moreover, a player is indifferent between alternative X and alternative Y whenever her opponents' probabilities for one of the two alternatives sum to 1. This justifies the (continuum of) equilibria where σi(Xi) ∈ [0, 1] and σj(Xj) = 1 − σk(Xk) = 1 with i, j, k ∈ N and i ≠ j ≠ k. In such a case, player i ∈ N can induce either one of the two pure strategy equilibria. It also justifies the completely mixed equilibrium with σi(Xi) = 1/2 ∀ i ∈ N, which is the only symmetry invariant equilibrium of the minority of three-game and which we consider as the natural benchmark equilibrium to which we will compare the experimentally observed behavior. To summarize, the Nash equilibria of the minority of three-game are (1/2, 1/2, 1/2) and all permutations of (σ(X), 1, 0) where σ(X) ∈ [0, 1].
Interestingly enough, the standard game-theoretical predictions remain unchanged if one considers a slightly modified version of the minority of three-game where player i's utility function is given by
2.2. Equilibrium selection
In view of the theories of equilibrium selection, the minority of three-game is quite pathologic since it is one of the rare applications where one encounters a minimal formation containing multiple equilibria (see Harsanyi and Selten [4] and Güth and Kalkofen [7] for other applications of equilibrium selection theory).
Lemma 1
The minority of three-game M3G has no proper subformation and is therefore a minimal formation.
We now demonstrate that this pathology is fundamental in the sense that (i) it is noise persistent; and (ii) asymmetries will not question the solution. The idea of “noise” is to solve the unperturbed game as an idealization. Asymmetry of “noise” appears to be realistic but is rather arbitrary from a normative perspective.
If we neglect that pure strategy equilibria are represented by equilibria in extreme mixed strategies (all freely disposable probability is put on one choice), the same multiplicity of equilibria exists also in the ε-uniformly perturbed minority of three-game with the restrictions σi(Xi) ∈ [ε, 1 − ε] for i = 1, 2, 3 where ε ∈ (0, 1/2) is supposed to be small.
Lemma 2
For all ε ∈ (0, 1/2), the ε -uniformly perturbed minority of three-game has no proper subformation and is therefore a minimal formation.
Instead of assuming uniform trembles, one can consider asymmetric trembles. More precisely, let us introduce a minor asymmetry in the sense that no two players have the same minimal choice probabilities, which we assume to be the same for both their pure strategies. Let ε ∈ (0, 1/6) and assume, for the sake of specificity, σ1(X1) ∈ [ε, 1 − ε], σ2(X2) ∈ [2ε, 1 − 2ε], and σ3 (X3) ∈ [3ε, 1 − 3ε]. We refer to the extreme mixtures by , which are and for player 1, and for player 2, and and for player 3. We can establish the following result:
Lemma 3
The minority of three-game with the asymmetric trembles ε for player 1, 2ε for player 2, and 3ε for player 3, where ε ∈ (0, 1/6) has only two “pure strategy equilibria” (in the sense of using one choice with maximal probability), namely and .
When one tries to select a unique solution for the (ε-uniformly perturbed) minority of three-game, the fact that this game has no proper subformation becomes crucial. According to the theory of Harsanyi and Selten [4], one therefore has to apply the tracing procedure directly to the (ε-uniformly perturbed) minority of three-game to select a unique equilibrium. In view of the complete symmetry of the (ε-uniformly perturbed) minority of three-game as well as of the tracing procedure, this means selecting the completely mixed equilibrium according to which all three players use both choices with equal probability. Thus, to avoid the only symmetry invariant solution of the unperturbed game, it does not suffice to assume different trembles for different players [8].
In the asymmetric (trembles) case, the two “pure strategy equilibria” qualify as primitive formations since both equilibria are strict. Since neither of these two solution candidates can (payoff or) risk dominate the other, the theory of Harsanyi and Selten [4] suggests to neglect them, which essentially means to apply the tracing procedure to the full minority of three-games with asymmetric trembles. The degenerate nature of these games implies that the linear tracing procedure yields no unique result so that one has to apply its logarithmic version, something that is hardly ever needed in (economic) applications. The symmetry of the two “pure strategy” equilibria (in the sense of using one choice with maximal probability) as well as of the logarithmic tracing procedure implies that the solution for ε → 0 prescribes that all three players should use both choices (X and Y ) with equal probability. (It is obvious that the sum of expected payoffs over all three players, implied by the solution, is less than that of any of its pure strategy equilibria [9].
2.3. Alternative Equilibrium Concepts
Below, we establish that the completely mixed equilibrium is also predicted by alternative solution concepts which, arguably, rely on less stringent assumptions regarding the knowledge and understanding of players.
2.3.1. Payoff-Sampling Equilibrium
Contrary to the common approach, which is based on the dynamics of evolution and learning, Osborne and Rubinstein [10] have recently developed a static and equilibrium-based approach to the modeling of bounded rationality in games. Needless to say, this approach relies on less stringent assumptions regarding the knowledge and understanding of players than does the standard theory of Nash equilibrium [11]. Indeed, each player, rather than optimizing, given a belief about the other players' behavior, first associates one consequence with each of her actions by sampling each of her actions K times, K ∈ ℕ*, and then chooses the action that yields the best consequence. In a symmetric game, a payoff-sampling(K) equilibrium (S(K)-equilibrium) is a mixed strategy such that if all other players adopt this strategy throughout the sampling procedure, then the probability that a given action is best under the sampling procedure is precisely the probability with which it is chosen. One interpretation of payoff-sampling equilibria advanced by Osborne and Rubinstein is that it is the steady state of a dynamic process involving a large population of individuals who are randomly matched to play the game. Each member of the population adopts the same action throughout her stay in the population, and the population composition changes as a result of new entrants and departures. When entering, a player samples each action K times and selects that which yields the best outcome according to the procedure described above. In this case, an S(K)-equilibrium is a distribution of actions in the incumbent population,inducing the same distribution of actions in the flow of entrants. Sethi [12] formalizes this dynamic process and uses the criterion of dynamic stability as an equilibrium refinement.
In the minority of three-game, if player i ∈ N samples both available actions (Xi and Yi) K times, the probability that action Xi yields the best outcome is given by
As already mentioned, a payoff-sampling equilibrium of a symmetric game corresponds to the steady state of a dynamic process involving a large single population of individuals who are randomly matched to play the game. An S(K)-equilibrium of the minority of three-game is a probability distribution (σ(X), σ(X), σ(X)) ∈ [0, 1]3 such that
According to Osborne and Rubinstein's [10] corollary (p. 844), the equilibrium mixed strategy of the minority of three-game is the unique limit of S(K)-equilibria as K → ∞. In fact, this equivalence holds for every level of sampling, not only in the limit.
Lemma 4
For each K ∈ ℕ*, the unique S(K)-equilibrium of the minority of three-game is given by (1/2, 1/2,1/2).
2.3.2. Impulse-Balance Equilibrium
Impulse-balance equilibrium is based on a simple principle of ex post rationality. It applies to all games in which players repeatedly decide on one parameter and in which the feedback environment allows conclusions about what would have been the better choice in the last interaction. Ockenfels and Selten [13] show that the impulse-equilibrium concept captures the experimental data of sealed-bid first-price auctions with private values. In the minority of three-game, the parameter is the probability of choosing one of the two alternatives, which can be adjusted upward or downward. Expected upward and downward impulses are equal for each of the three players simultaneously in impulse-balance equilibrium.
Note that to incorporate loss aversion, the impulses are calculated with respect to transformed payoffs. Impulse-balance equilibrium weights losses are doubled, i.e., gains are halved, where losses are defined as values below the pure strategy maximin value. Due to binary payoffs, this transformation has no bite in the minority of three-game.
Lemma 5
The set of impulse-balance equilibria is identical to the set of Nash equilibria of the minority of three-game: it consists of (1/2,1/2,1/2) and all permutations of (σ (X), 1, 0) where σ(X) ∈ [0, 1].
2.4. Learning models
In addition to the prediction of the stationary concepts described above, we test the predictions of a series of learning models against our experimental data at the individual level. We consider the two varieties of learning which have received the most scrutiny in experiments, belief learning models and reinforcement learning models, as well as learning models which formalize the dynamic processes that might lead to the alternative equilibrium concepts. Partly, the studies not only suggest learning models but also test them.
2.4.1. Belief-Based Learning
One widely used model of learning is the process of fictitious play (FP), see Fudenberg and Levine [14] for details. In this process, players behave as if they think they are facing a stationary, but unknown, distribution of opponents? Strategies. Initially, each opponent's alternative is equally likely to be chosen. In each repetition of the game, players choose a pure strategy that is a best response to the belief formed from a weighted average of the immediate past and the history before that, and they randomize when it is indifferent. In repetition t + 1, the weight associated with the immediate past equals 1/t.
As a special case, we also consider the Cournot adjustment model (Cournot), where players choose a pure strategy that is a best response to the belief formed from the immediate past.
2.4.2. Reinforcement Learning
An alternative, very elementary type of learning, is reinforcement learning (RL), which has recently become the subject of ongoing experimental research in economics (see, Erev and Roth [15]). Players associate a propensity with each alternative, and the two propensities are set equal to one in the first play of the game. After each play, actual payoffs are added to propensities (clearly, for a given player nothing is added to the propensity which corresponds to the alternative not chosen). Players choose an alternative according to the mixed strategy given by the ratios of the two propensities to their sum.
2.4.3. Self-Tuning Experience-Weighted Attraction Learning
Camerer and Ho's [16] experience-weighted attraction learning model is a hybrid model that encompasses several belief-based and reinforcement learning models as special cases. Unfortunately, this learning model has many parameters which makes it difficult to compare with other (simpler) learning models. We consider the one-parameter version of this learning model, named the self-tuning experience-weighted attraction learning model (STEWAL), and we refer the reader to Ho, Camerer, and Chong [17] for full details.
The response sensitivity is a parameter which needs to be calibrated before predictions can be compared to individual behavior. We allow the response sensitivity to take any value in the interval [0, ∞].
2.4.4. Impulse-Balance Learning
Impulse-balance learning (IBL) relates to the concepts of impulse-balance equilibrium and learning direction theory (Selten [18]). The Concept of IBL was introduced by (Chmura, Selten, and Goerg [19]). As in reinforcement learning, players associate a propensity with each alternative (a propensity) (initially, the two propensities are set equal to one), and alternatives are chosen according to the mixed strategy given by the ratios of the two propensities to their sum. However, propensities are updated differently than in reinforcement learning. In particular, only the propensity of the non-chosen alternative might be updated. Suppose that the alternative chosen by the player in a given play of the game is not the best reply to the pair of alternatives chosen by (the) his opponents. Then the difference between the best-reply payoff and the actual payoff is added to the propensity of the non-chosen alternative. There is no updating of propensities whenever the alternative chosen is the best reply. More recent studies of impulse-balance equilibrium account for the equilibrium predictions in comparison with other equilibrium concepts, see (Ockenfels and Selten [13]), (Selten and Chmura [20]), (Selten, Chmura and Goerg [21]), (Brunner, Camerer, and Goeree [22]), and (Goerg and Selten [23]).
2.4.5. Impulse-Matching Learning
Impulse-matching learning (IML) is identical to impulse-balance learning except that the difference between the best-reply payoff and the actual payoff is always added to the propensity of the optimal alternative (see originally Chmura, Selten, and Goerg [19]).
2.4.6. Payoff-Sampling Learning
Payoff-sampling learning (PSL) (see originally Chmura, Selten, and Goerg [19]) relates to the concept of payoff-sampling equilibrium exposed above. In each play of the game, players first draw one sample of earlier payoffs for each alternative where the samples are randomly drawn with replacement. Second, the cumulated payoffs of each sample are computed, and the alternative with the largest payoffs is chosen (if cumulated payoffs are identical, players randomize). Initially, and until positive payoffs for each alternative have been obtained at least once, players randomize.
The sample size is a parameter which needs to be calibrated before predictions can be compared to individual behavior. We allow the sample size to take any value between 2 and 7. Allowing for wider ranges of sample sizes as in (Selten and Chmura [20]), or (Brunner, Camerer, and Goeree [22]) does not question our conclusions.
3. Experimental Design
The experiment consisted of four sessions, with 27 subjects in each session, i.e., a total of 108 subjects. Subjects played the minority of three-game for 50 rounds, they were randomly rematched after each play, and earnings, derived from the payoff numbers in the previous section, were recorded in points (the experimental currency).
In each round, subjects were asked to give a probability distribution over the two alternatives (X and Y ) instead of picking an alternative. A single random draw was made from this distribution, and the realization became the subject's alternative. This mixed strategy device allowed subjects to generate random play through a probability experiment that they controlled and conducted on the computer. Each subject had the option to fill an urn of 100 balls with any composition of alternatives (balls) he or she desired. Once the urn was filled, the computer randomly selected one of the 100 balls as the chosen alternative. However, opponents were only shown the chosen alternative (ball), not the mixed strategy (i.e., the composition of the urn). This generation of a random outcome is in the spirit of how mixed strategies are motivated in the classical treatments of game theory; namely, players choose a probability distribution over the set of alternatives, and then draw a realization. The mixed strategy device provides benefits to both the experimenter and the subjects. First, this device allows subjects to easily generate i.i.d. sequences of alternatives across stage games or, in other words, successfully execute intended mixed strategies. Second, the device also provides the researcher with a new view of how subjects may actually be playing the game.
In each round, subjects had the possibility to collect some information about the five previous rounds. Concretely, subjects had access to: (i) their choice and their earnings; (ii) the percentage of their interacting opponents who chose alternative “X” and the percentage of their interacting opponents who chose alternative “Y”; and (iii) the average earnings of their interacting opponents who chose “X” and the average earnings of their interacting opponents who chose “Y”. These information-gathering data will illuminate the behavioral rules subjects used and enable an indirect test of whether they are best-replying (belief-based learning).
3.1. Practical Procedures
The four sessions of the computerized experiment were conducted at the Experimental Laboratory of the Max Planck Institute of Economics in Jena, Germany. The experiment was programmed and conducted with the software z-Tree (Fischbacher [24]). Subjects were invited using an Online Recruitment System (Greiner [25]). All 108 subjects were undergraduate students from various disciplines at the University of Jena. In each session the gender composition was approximately balanced, and no subject participated in more than one session. Some subjects had participated in earlier economics experiments, but all were inexperienced in the sense that they had never taken part in an earlier session or experiment? of this type. Each session lasted on average slightly less than 2 hours, and the average earnings per subject were about 15 euros (about $22), including a 2.50 euros show-up fee [26].
At the beginning of each session, subjects randomly drew a cubicle number. Once all subjects were seated in their cubicles, instructions were distributed. Cubicles were visually isolated from each other and communication between the subjects was strictly prohibited. Subjects first read the instructions silently and then listened as the monitor read them aloud (the monitor was a native German speaker). Questions were answered privately. A short control questionnaire and two training rounds followed [27]. After all subjects had correctly answered the control questionnaire, subjects played the minority of three-game for 50 rounds. Subjects were told that they would interact with randomly changing opponents. Actually, in each session there were three independent matching groups with nine players. Subjects played against randomly chosen opponents but only within their independent group. They were not informed about the fact that there were three groups. We did not lie to them but conveyed the impression that they interacted with 26 other players. After each repetition of the minority of three-game, the computer screen displayed the alternative chosen by each of the three players as well as the three earnings. Subjects were not permitted to take notes of any kind about their playing experience. At the end of the 50 rounds, subjects' payoffs were displayed on their screens, and subjects privately received their final earnings (including the show-up fee).
4. Results
In this section, we attempt to characterize the decision rules used by participants. First, we provide some aggregate statistics of our experimental data. At the aggregate level, participants? Behavior seems based on the toss of a fair coin. Second, we investigate individual behavior. Our individual-data analysis strongly indicates the existence of heterogeneous decision rules among participants.
4.1. Aggregate Statistics
Table 2 reports the matching group-level means and standard deviations in per round payoffs and the chosen number of X-balls. In a given round, the number of X-balls chosen by the subject might be interpreted as her mixed strategy. Clearly, observed behavior is very much in line with the predictions of the completely mixed equilibrium at the aggregate level.
Figure 1 shows the distribution of the changes of X-balls in successive rounds. Five peaks are worth noticing. The by far highest peak at 0 reveals that in more than 50 percent of the cases there is no change toward the next round. Of these only 5 percent are sticking to pure strategies, whereas all others repeat the former completely mixed strategies. The other peaks, at –100 and 100, reveal that switches between the pure strategies occur in slightly more than 10 percent of the cases. The peaks at –50 and 50 reveal switches from the symmetric equilibrium to one of the pure strategies or vice versa. Those switches occur in less than 10 percent of the cases.
Finally, Figure 2 illustrates the temporal paths of X-balls choices for three different participants in the first matching group. Participant 4 chose 50 X-balls in every round, whereas participant 9 quite regularly alternated her choice of X-balls between 100 and 0. Participant 6 is an example of a player who avoided the extrema. This illustration suggests the existence of heterogeneous decision rules, which is confirmed in our individual-data analysis below. Distinguishing participants with constant or alternative play, such as participant 4, respectively 9, can be easily accomplished by a median split via computing the average change in the number of X-balls from one round to the next. Doing so neither reveals nor clears out differences in choice probabilities, payoffs, or information retrieval.
4.2. Individual Decision Rules
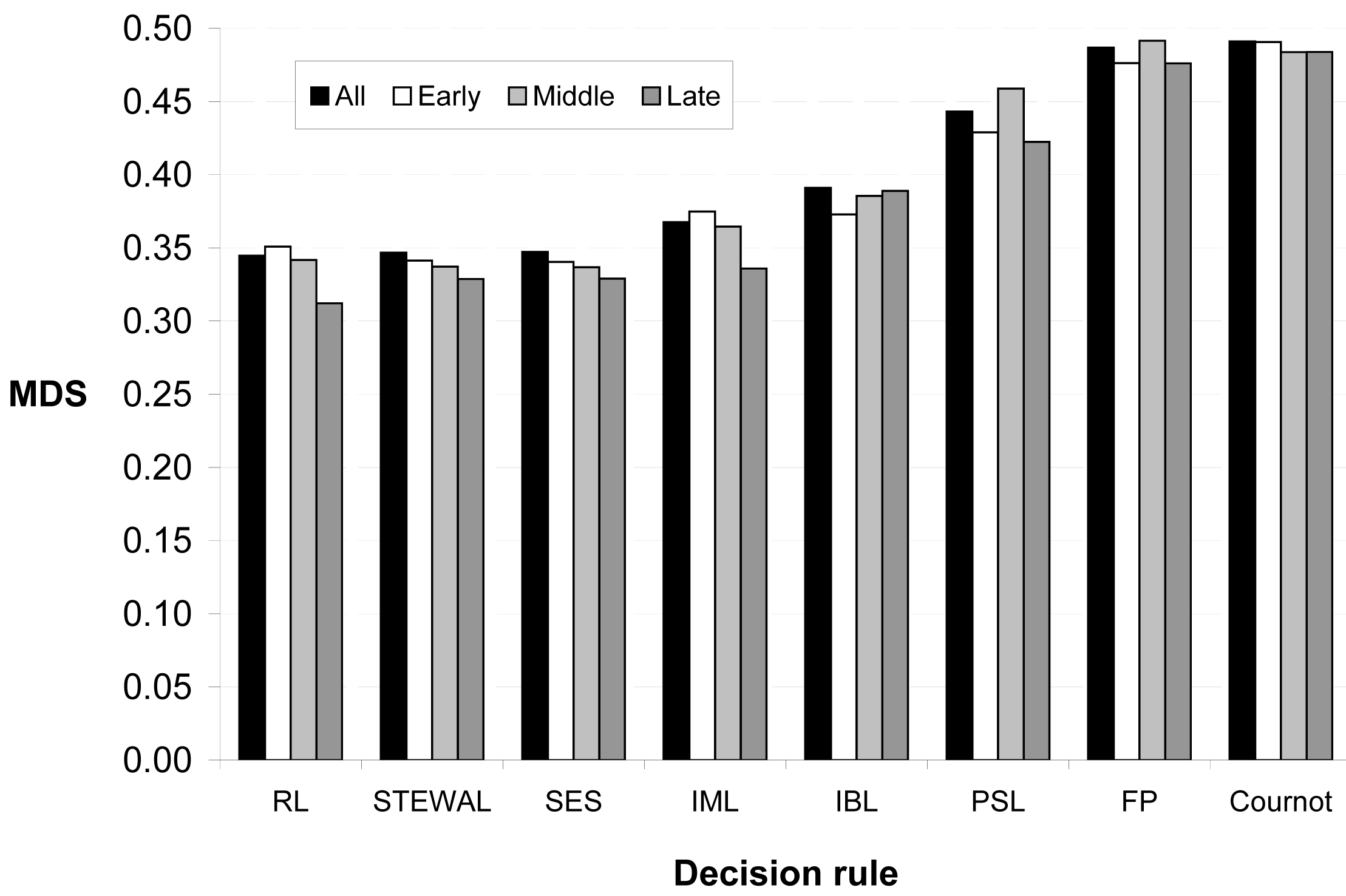
To assess the descriptive power of a given learning model LM, we compute for each subject i and in each round t ∈ {1,…, 50} the mean-squared deviation
Figure 3 reports the mean deviations scores averaged over all 108 subjects. For most learning models as well as for the symmetric equilibrium strategy, minor differences are observed between the predictive power of early, middle, and late play. Still, in the case of reinforcement learning, self-tuning experience-weighted attraction learning, impulse-matching learning, and the symmetric equilibrium strategy, the predictive power clearly increases during the course of the session. We performed pairwise comparisons of these scores with the help of Fisher–Pitman permutation tests for paired samples. As summarized in Table 3, these statistical comparisons confirm the existence of heterogeneous decision rules among our participants. The three best learning models are self-tuning experience-weighted attraction learning, impulse-matching learning, and reinforcement learning, and their predictive power is comparable to that (the one) achieved by the symmetric equilibrium strategy. Note that the mean deviation score of self-tuning experience-weighted attraction learning is minimized when the response sensitivity equals 0.32, whereas the mean deviation score of payoff-sampling learning is minimized when the sample size equals 2.
4.3. Information Retrieval
Our analysis of the goodness of fit indicates heterogeneity of decision rules and low predictive power of belief learning models. The latter result is confirmed by the analysis of participants' information retrieval. Participants mainly retrieved information about their own payoff as well as their opponents' payoffs in the previous round. Few information retrievals were made concerning earlier rounds than the previous round. Thus, any attempt to account for the heterogeneity of decision rules by different kinds of information retrieval would have been futile due to no, or very minor, differences in retrieving information.
5. Related Literature
Though the minority game is related to market entry games, its equilibrium structure is different and favors the completely mixed equilibrium as a natural benchmark. Thus, the numerous evidence gathered by experimental economists on behavior in market entry games [29] might not be transferable to minority games. Another related game is the route-choice game, experimentally studied by Selten, Chmura, Pitz, Kube, and Schreckenberg [30]. Again, the likelihood of observing convergence to a pure strategy equilibrium is larger than in the minority game since pure strategy equilibria induce the same payoff for all players.
Few experimental studies have been conducted by economists on the minority game. Chmura and Pitz [31] report on two experimental treatments that differ in the amount of information given to participants. The more information participants receive, the more often they stick to their choice in the next round. Chmura and Pitz [32] compare the behavior of Chinese and German participants and show that Chinese participants exhibit a stronger tendency to stick to their choice. Bottazzi and Devetag [33] investigate the extent to which stationary groups of five participants are able to coordinate efficiently in a repeated minority game as well as the impact of information on the resulting efficiency. Groups achieve a payoff level equal to, or higher than, the one associated with the completely mixed equilibrium, and participants use public information as a coordination device. At the individual level, while little evidence of behavioral consistency with the completely mixed equilibrium is found, there is strong evidence of dynamic adaptation. Our experimental study confirms the finding of (that there is) considerable heterogeneity in participants' behavior. However, by implementing a strangers design and endowing participants with a mixing device, we give the predictions of the completely mixed equilibrium their “best shot”. Our results question that participants constantly play the symmetric equilibrium strategy. Since this cannot be due to their inability to generate random sequences of actions and is unlikely to have resulted from repeated game effects, the implication is that participants are more influenced by path dependence than by static equilibrium notions.
6. Conclusions
Market entry games are prototypical of coordination problems arising from a newly emergent profit opportunity that can be exploited only by a limited number of individuals. Many experimental studies have been conducted in an effort to find out which type of equilibrium participants are likely to coordinate upon. However, none of these experimental studies has yielded evidence to suggest that participants consistently play equilibrium strategies. Pursuing this line of research, we have conducted an experiment on the minority of three-game.
While this game has multiple asymmetric equilibria in pure strategies that are non-strict and payoff-asymmetric, it also has a unique symmetric mixed strategy equilibrium, in which each player selects the two actions with equal probability. We show that such straightforward behavior is predicted by Harsanyi and Selten's [4] equilibrium selection theory as well as alternative solution concepts such as impulse-balance equilibrium and payoff-sampling equilibrium. We give the predictions of the completely mixed equilibrium their “best shot” by implementing a strangers design and endowing participants with a mixing device. We also allow to collect information about previous play.
Our results indicate that participants rely on various decision rules and that a quarter of them [34] decide according to the toss of a fair coin. See Dittrich, Güth, Kocher and Pezanis-Christou [35] for an experiment also allowing for explicit individual mixing but for games with unique strict equilibria and nevertheless quite similar shares of mixing. Reinforcement learning is the most successful decision rule as it describes best the behavior of about a third of our participants. Belief learning models have low predictive success, which is line with the fact that participants mainly collect information about past payoffs.
In conclusion, heterogeneity of behavioral rules seems a persistent fact of games with many equilibrium outcomes, and this considerable heterogeneity in behavior does not result only from participants' inability to generate random sequences of actions or from repeated game considerations.


 |
| Matching | Payoff | Number of X-balls | ||
|---|---|---|---|---|
| group | Mean | Std. Dev. | Mean | Std. Dev. |
| 1 | 0.258 | 0.438 | 49.042 | 31.081 |
| 2 | 0.256 | 0.437 | 49.769 | 33.050 |
| 3 | 0.247 | 0.432 | 52.900 | 37.387 |
| 4 | 0.229 | 0.421 | 48.049 | 32.430 |
| 5 | 0.242 | 0.429 | 47.958 | 40.439 |
| 6 | 0.253 | 0.435 | 49.573 | 36.756 |
| 7 | 0.269 | 0.444 | 49.613 | 41.347 |
| 8 | 0.251 | 0.434 | 48.776 | 36.404 |
| 9 | 0.264 | 0.441 | 53.271 | 38.950 |
| 10 | 0.255 | 0.437 | 44.042 | 37.381 |
| 11 | 0.260 | 0.439 | 47.380 | 42.629 |
| 12 | 0.260 | 0.439 | 50.198 | 33.481 |
| Mean | 0.254 | 0.435 | 49.214 | 36.778 |
| RL | STEWAL | SES | IML | IBL | PSL | FP | |
|---|---|---|---|---|---|---|---|
| STEWAL | n.s. | ||||||
| SES | n.s. | n.s. | |||||
| IML | n.s. | n.s. | n.s. | ||||
| IBL | < 0.01 | < 0.05 | < 0.05 | n.s. | |||
| PSL | < 0.01 | < 0.01 | < 0.01 | < 0.01 | < 0.01 | ||
| FP | < 0.01 | < 0.01 | < 0.01 | < 0.01 | < 0.01 | < 0.05 | |
| Cournot | < 0.01 | < 0.01 | < 0.01 | < 0.01 | < 0.01 | < 0.01 | n.s. |
 |
 |
Acknowledgments
We thank two anonymous referees for useful comments and suggestions. Sebastian Goerg, Ming Jiang, and Christoph Göring provided valuable research assistance. We especially thank Anthony Ziegelmeyer and Thomas Pitz for their massive contribution to this paper.
Appendix: Proofs
Proof of Lemma 1
A formation of M3G is a substructure F = (F1, F2, F3, u1 (·) |F, u2 (·) |F, u3 (·)|F) with ∅ ≠ Fi ⊆ Ai for i = 1, 2, 3 and ui (·) |F denoting the restriction of ui (·) to strategy vectors a ∈ ×j∈NFj, which is closed with respect to best replies. Such a formation F of M3G is minimal when there exists no proper subformation F' of F.
If F is a proper substructure of M3G then there exists a player i ∈ {1, 2, 3} with either Fi = {Xi} or Fi = {Yi}. Without loss of generality, we assume that Fi = {Xi}. To show that such a substructure is no formation, we simply distinguish the possible cases where we denote by j and k the two opponents of player i.
If |Fj| = |Fk| = 1, i.e., all three players have only one strategy, then the two possibilities are:
Fj and Fk contain the same choice (X or Y ): If Fi also contains the same choice then player i's best reply is not contained in Fi. If Fi contains a different choice then both pure strategies are best replies for player j and player k. In both cases, F does not qualify as a formation.
Fj and Fk contain different choices: Without loss of generality, we assume that Fi and Fj contain the same choice. Clearly, both pure strategies are best replies for player i and player j. F does not qualify as a formation.
At least one of the two sets Fj or Fk contains two strategies where, without loss of generality, we assume that this is Fj.
If Fi and Fk contain the same choice, player i will want to use his strategy, not contained in Fi, when j uses the same choice as k. Thus, F is no formation.
If Fi and Fk contain different choices, for both of them their in F non-feasible action is a best reply if j chooses the same alternative as the other (the choice in Fi, respectively Fk, when considering player i, respectively k). Again, F cannot be closed with respect to best replies.
Proof of Lemma 2
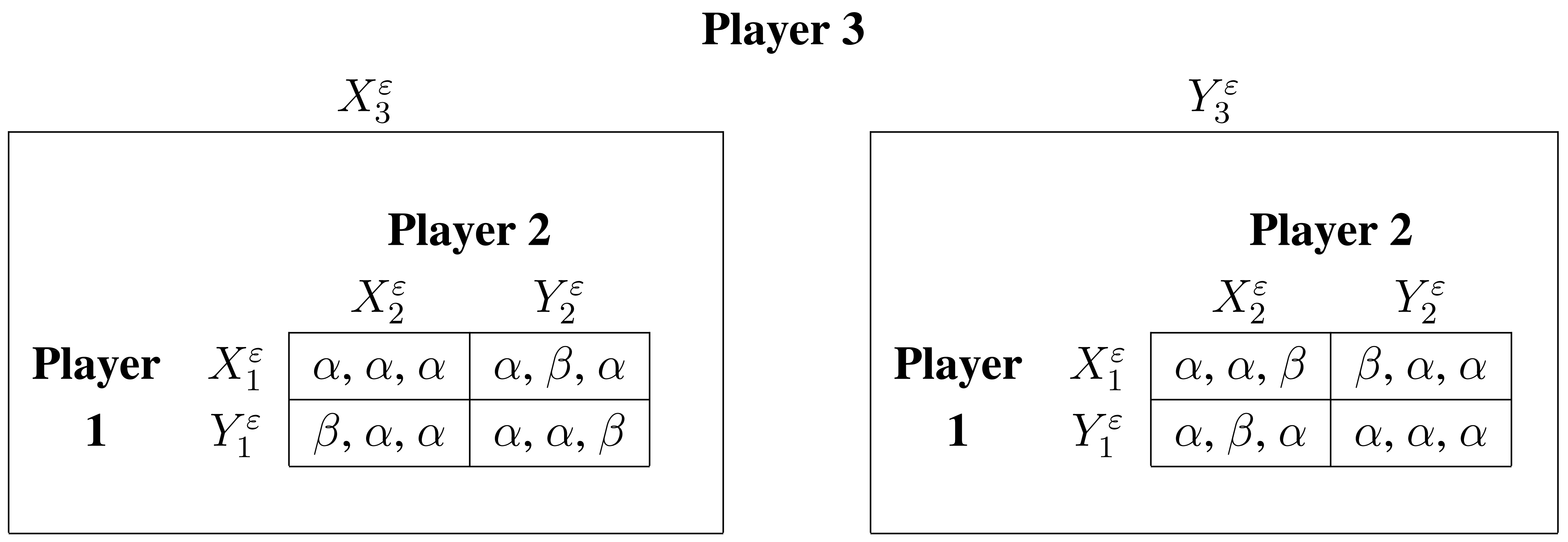
For a given ε ∈ (0, 1/2), we denote by , ai ∈ Ai = {Xi, Yi}, the extreme mixed strategy with σi(ai) = 1 − ε (σi(bi) = ε where bi ∈ Ai = {Xi, Yi} and bi ≠ ai). The normal-form representation of the ε-uniformly perturbed minority of three-game is given by
where α = ε(1 ‒ ε) and β = (1 − ε)3 +ε3. As (1 − ε)3 +ε3 −ε(1 − ε) = (1 −2ε)2 > 0, we can transform this bimatrix by the positively affine utility transformation ũi(·) = (ui(·) − ε(1 − ε))/((1 − 2ε)2) for i = 1, 2, 3 to obtain the same bimatrix representation as for the non-perturbed minority of three-game, shown in Table 4.
Proof of Lemma 3
The payoff structure of the minority of three-game with the considered asymmetric trembles is given by
Proof of Lemma 4
As already mentioned, an S(K)-equilibrium of the minority of three-game is a probability distribution (σ(X), σ(X), σ(X)) ∈ [0, 1]3 such that
Below, we rewrite this equality. First,
Second, σ(X)2 + (1 − σ(X)2) = 1 implies that
Finally, (1 − σ(X))2 + (σ(X) (2 − σ(X))) = 1 implies that
With
and . A final simplification leads to
Clearly, for a given K ∈ ℕ*, (σ(X), σ(X), σ(X)) ∈ [0, 1]3 is an S(K)-equilibrium of the minority of three-game if and only if σ(X) ∈[0, 1] is a fixed point of f(σ(X), K) where f(σ(X), K) is the right-hand side of the above equality.
We now show by induction that for each K ∈ ℕ*, 1/2 is indeed a fixed point of f(·,K). For K = 1, one can easily check that f(1/2, 1) = 1/2. Additionally, one can show that (details are available from the authors upon request)
Assuming that, for each K ∈ ℕ*, f (1/2, K) = 1/2 the above equality simplifies to f (1/2, K+1) = 1/2.
Finally, we show that for each K ∈ ℕ*, f (σ(X),K) decreases on the interval [0, 1]. Remember that
First, for each K ∈ ℕ*, the second term of the function decreases on the interval [0, 1] because: (i) (σ(X) (2 − σ(X)))K increases on the interval [0, 1] (ii) σ(X)2 clearly increases on the interval [0, 1] which implies that (1 − σ(X)2)K decreases on the interval [0, 1] and therefore (1 − (1 − σ(X)2)K) increases on the interval [0, 1].
Second, we show that the third term of the function also decreases on the interval [0, 1]. Let b̃1 be a binomially distributed random variable whose probability distribution is given by B(K, σ(X)2). corresponds to Pr(b̃1 ≤ k − 1) and corresponds to P(b̃1 ≥ k + 1). When σ(X) (and therefore σ(X)2) increases, the probability of success increases, so K independent trials lead to more successes. Accordingly, for each k1 ∈ {1,…, K}, g(σ(X), K) − h(σ(X), K) decreases when σ(X) increases. Let b̃2 be a binomially distributed random variable whose probability distribution is given by B(K, (1 − σ(X))2). corresponds to Pr(b̃2 = k1). When σ(X) increases, (1 − σ(X))2 decreases, so Pr(b̃2 = k1) increases for small values of k1 and decreases for large values of k1. Hence for each k1 ∈ {1,…,K}, decreases when σ(X) increases and thus the sum decreases.
To summarize, for each K ∈ ℕ*, f(σ(X), K) decreases on the interval [0, 1] which implies that 1/2 is the only fixed point of f(σ(X), K) on the interval [0, 1]. This completes the proof.
Proof of Lemma 5
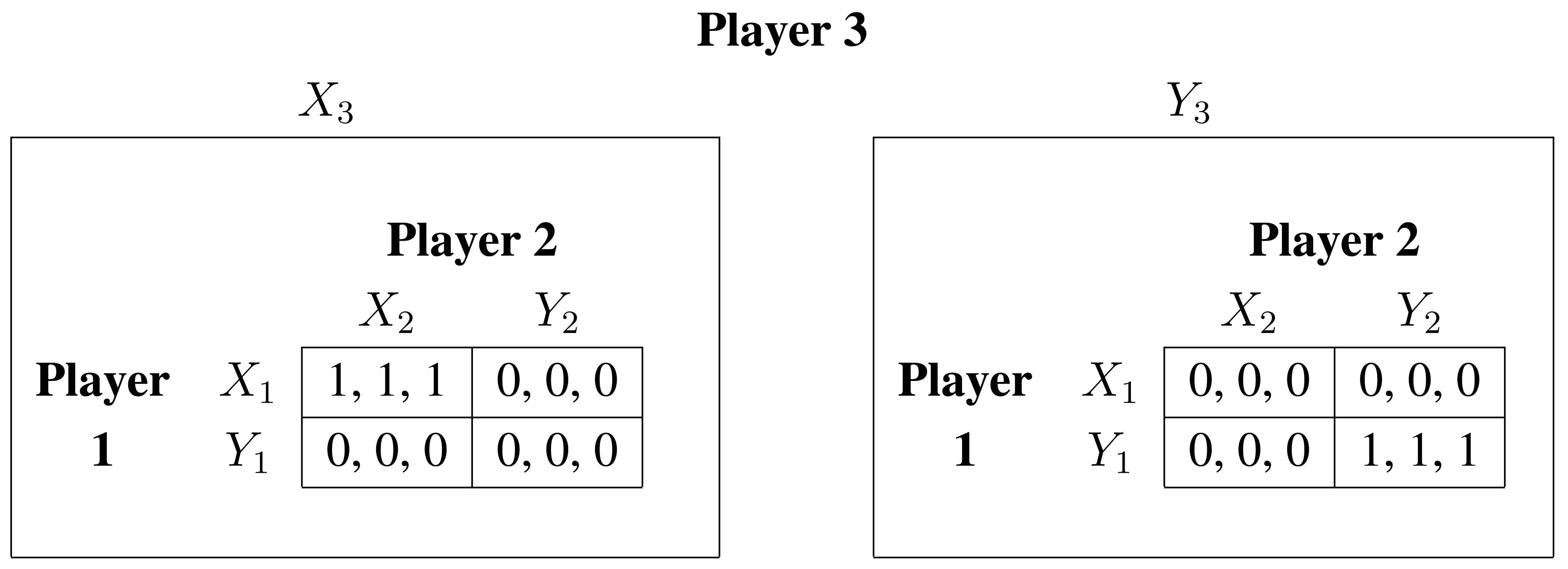
Table 5 shows the impulses obtained to the alternative not chosen, similar to a payoff table.
Impulse-balance equilibrium requires that player i's expected impulse from Xi to Yi is equal to his expected impulse from Yi to Xi, i ∈ N. This yields to the following impulse-balance equation: Πi∈Nσi(Xi) = Πi∈N (1− σi(Xi)) which completes the proof.
References
- Selten, R.; Güth, W. Equilibrium Point Selection in a Class of Market Entry Games. In Games, Economic Dynamics, and Time Series Analysis; Diestler, M., Fürst, E., Schwödiauer, G., Eds.; Physica-Verlag: Wien-Würzburg, Austria, 1982. [Google Scholar]
- Ochs, J. Coordination in Market Entry Games. In Games and Human Behavior: Essays in Honor of Amnon Rapoport; Budescu, D., Erev, I., Zwick, R., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA, 1999. [Google Scholar]
- Camerer, C. Behavioral Game Theory; Russell Sage Foundation, Princeton University Press: New York, NY, USA, 2003. [Google Scholar]
- Harsanyi, J.; Selten, R. A General Theory of Equilibrium Selection in Games; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- The minority of three-game belongs to the class of win-loss games. For the sake of completeness, one can denote by π the monetary payoff associated with the less rewarding alternative, i.e., the one chosen by two or more players, and by Π > π the monetary payoff associated with the most rewarding alternative, i.e., the one chosen by a single player. Obviously, because each player can receive only one of two possible payoffs, there is no opportunity for choices by expected-utility maximizers to be influenced by nonlinearities (risk preferences) in their utility functions. In particular, when players play mixed strategies, all of the induced lotteries are binary lotteries.
- This payoff structure is the one underlying a three-player market entry game with two markets, each market having a unitary capacity, and a payoff function decreasing in a linear way.
- Güth, W.; Kalkofen, B. Unique Solutions for Strategic Games: Equilibrium Selection based on Resistance Avoidance (Lecture Notes in Economics and Mathematical Systems); Springer: Berlin, Germany, 1989. [Google Scholar]
- One might assume different trembles also for different choices, which appears even more arbitrary, however.
- Each player's expected payoff at the symmetric equilibrium equals 1/4 which leads to an expected total payoff of 3/4 for the three players.
- Osborne, M.; Rubinstein, A. Games with procedurally rational players. Am. Econ. Rev. 1998, 88, 834–847. [Google Scholar]
- Actually, each player needs to know only her own set of actions.
- Sethi, R. Stability of equilibria in games with procedurally rational players. Games Econ. Behav. 2000, 32, 85–104. [Google Scholar]
- Ockenfels, A.; Selten, R. Impulse balance equilibrium and feedback in first price auctions. Games Econ. Behav. 2005, 51, 155–170. [Google Scholar]
- Fudenberg, D.; Levine, D. The Theory of Learning in Games; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Erev, I.; Roth, A. Predicting how people play games: reinforcement learning in experimental games with unique, mixed strategy equilibria. Am. Econ. Rev. 1998, 88, 848–881. [Google Scholar]
- Camerer, C.F.; Ho, T.H. Experience-weighted attraction learning in normal-form games. Econometrica 1999, 67, 827–874. [Google Scholar]
- Ho, T.H.; Camerer, C.F.; Chong, J.K. Self-tuning experience weighted attraction learning in games. J. Econ. Theory 2007, 133, 177–198. [Google Scholar]
- Selten, R. Features ofexperimentally observed bounded rationality. presidential address. Eur. Econ. Rev. 1998, 42, 413–436. [Google Scholar]
- Chmura, T.; Sebastian, G.; Reinhard, S. Learning in Experimental 2 × 2 Games; Bonn Discussion Paper; University of Bonn: Bonn, Germany, 2008. [Google Scholar]
- Selten, R.; Chmura, T. Stationary concepts in experimental 2 × 2 games. Am. Econ. Rev. 2008, 98, 938–966. [Google Scholar]
- Selten, R.; Chmura, T.; Goerg, S. Correction and re-examination of stationary concepts for experimental 2 × 2 games: A reply. Am. Econ. Rev. 2011. in press. [Google Scholar]
- Brunner, C.; Camerer, C.; Goeree, J. Correction and re-examination of stationary concepts for experimental 2 × 2 games. Am. Econ. Rev. 2011, 437, 1–15. [Google Scholar]
- Goerg, S.; Selten, R. Experimental investigation of a cyclic duopoly game. Exp. Econ. 2009, 12, 253–271. [Google Scholar]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar]
- Greiner, B. An Online Recruitment System for Economic Experiments. In Forschung und Wissenschaftliches Rechnen 2003; Kremer, K., Macho, V., Eds.; GWDG Bericht 63. Ges. für Wiss. Datenverarbeitung: Göttingen, Germany, 2004; pp. 79–93. [Google Scholar]
- Points were converted to euros in the calculation of subjects' final earnings at a conversion rate of 1 point to 1 euro.
- We took subjects through two training rounds to familiarize them with the software, especially the mixed strategy device. During the two trial rounds, subjects were not able to freely choose the composition of the urn. Indeed, in the first trial round the urn had to consist of 99 “X” balls and 1 “Y” ball, whereas in the second trial round the urn had to consist of 1 “X” ball and 99 “Y” balls. Subjects whose questionnaire results indicated that they had not sufficiently understood the rules of the game were replaced and paid 5 euros for answering the questionnaire (35 subjects were invited for each session).
- Cheung, Y.W.; Friedman, D. Individual learning in normal form games: some laboratory results. Games Econ. Behav. 1997, 19, 46–76. [Google Scholar]
- Duffy, J.; Hopkins, E. Learning, information, and sorting in market entry games: Theory and evidence. Games Econ. Behav. 2005, 51, 31–62. [Google Scholar]
- Selten, R.; Chmura, T.; Pitz, T.; Kube, S.; Schreckenberg, M. Commuters route choice behavior. Games Econ. Behav. 2007, 58, 394–406. [Google Scholar]
- Chmura, T.; Pitz, T. Successful Strategies in Repeated Minority Games. Phys. Stat. Mech. Appl. 2006, 363, 477–480. [Google Scholar]
- Chmura, T.; Pitz, T. Response Modes and Coordination in a Traffic Context: An Experimental Comparison of Chinese and German Participants; Bonn Discussion Paper; University of Bonn: Bonn, Germany, 2010. [Google Scholar]
- Bottazzi, G.; Devetag, G. Competition and coordination in experimental minority games. J. Evol. Econ. 2007, 17, 241–275. [Google Scholar]
- Since the minority of three-game is an exceptional case, this share is hardly comparable to experimental games with unique pure or mixed strategy equilibria.
- Dennis, D.; Güth, W.; Kocher, M.; Pezanis-Christou, P. Loss Aversion and Learning to Bid; Papers on Strategic Interaction 2005-03; Max Planck Institute of Economics, Strategic Interaction Group: Jena Germany, 2005. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chmura, T.; Güth, W. The Minority of Three-Game: An Experimental and Theoretical Analysis. Games 2011, 2, 333-354. https://doi.org/10.3390/g2030333
Chmura T, Güth W. The Minority of Three-Game: An Experimental and Theoretical Analysis. Games. 2011; 2(3):333-354. https://doi.org/10.3390/g2030333
Chicago/Turabian StyleChmura, Thorsten, and Werner Güth. 2011. "The Minority of Three-Game: An Experimental and Theoretical Analysis" Games 2, no. 3: 333-354. https://doi.org/10.3390/g2030333




