Robust Satisfaction of Metric Interval Temporal Logic Objectives in Adversarial Environments
Abstract
1. Introduction
- We introduce durational stochastic games (DSGs) to model the interaction between the CPS that has to satisfy a time-critical objective and an adversary who can initiate actuator and timing attacks.
- We define notions of spatial, temporal, and spatio-temporal robustness, which quantify the robustness of system trajectories to spatial, temporal, and spatio-temporal perturbations, respectively, and present computational procedures to estimate them. We design an algorithm to compute a policy for the CPS (defender) with a robustness guarantee when the adversary is limited to effecting only actuator attacks.
- We demonstrate that the defender cannot correctly estimate the spatio-temporal robustness when the adversary can initiate both actuator and timing attacks. We relax the robustness constraints in such cases and present a value iteration-based procedure to compute the defender’s policy, represented as a finite-state controller, to maximize the probability of satisfying the MITL objective.
- We evaluate our approach on a signalized traffic network. We compare our approach with two baselines and show that it outperforms both baselines.
2. Related Work
3. MITL and Timed Automata
- 1.
- if and only if (iff) is true;
- 2.
- iff ;
- 3.
- iff does not satisfy φ;
- 4.
- iff and ;
- 5.
- iff such that , and holds for all .
4. Problem Setup and Formulation
4.1. Environment, Defender, and Adversary Models
4.2. Definitions of Robustness Degree
4.2.1. Spatial Robustness
4.2.2. Temporal Robustness
4.2.3. Spatio-Temporal Robustness
4.2.4. Robust MITL Semantics
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- .
4.3. Problem Statement
5. Solution: Only Actuator Attack
5.1. Product DSG
| Algorithm 1 Computing the set of GAMECs . |
|
5.2. Evaluating Spatial Robustness
5.3. Evaluating Temporal Robustness
| Algorithm 2 Evaluate temporal robustness. |
|
5.4. Evaluating Spatio-Temporal Robustness
| Algorithm 3 Evaluate spatio-temporal robustness. |
|
5.5. Control Policy Synthesis
| Algorithm 4 Robust control policy synthesis for defender. |
|
6. Solution: Actuator and Timing Attacks
| Algorithm 5 Computing an optimal control policy. |
|
7. Case Study
7.1. Signalized Traffic Network Model
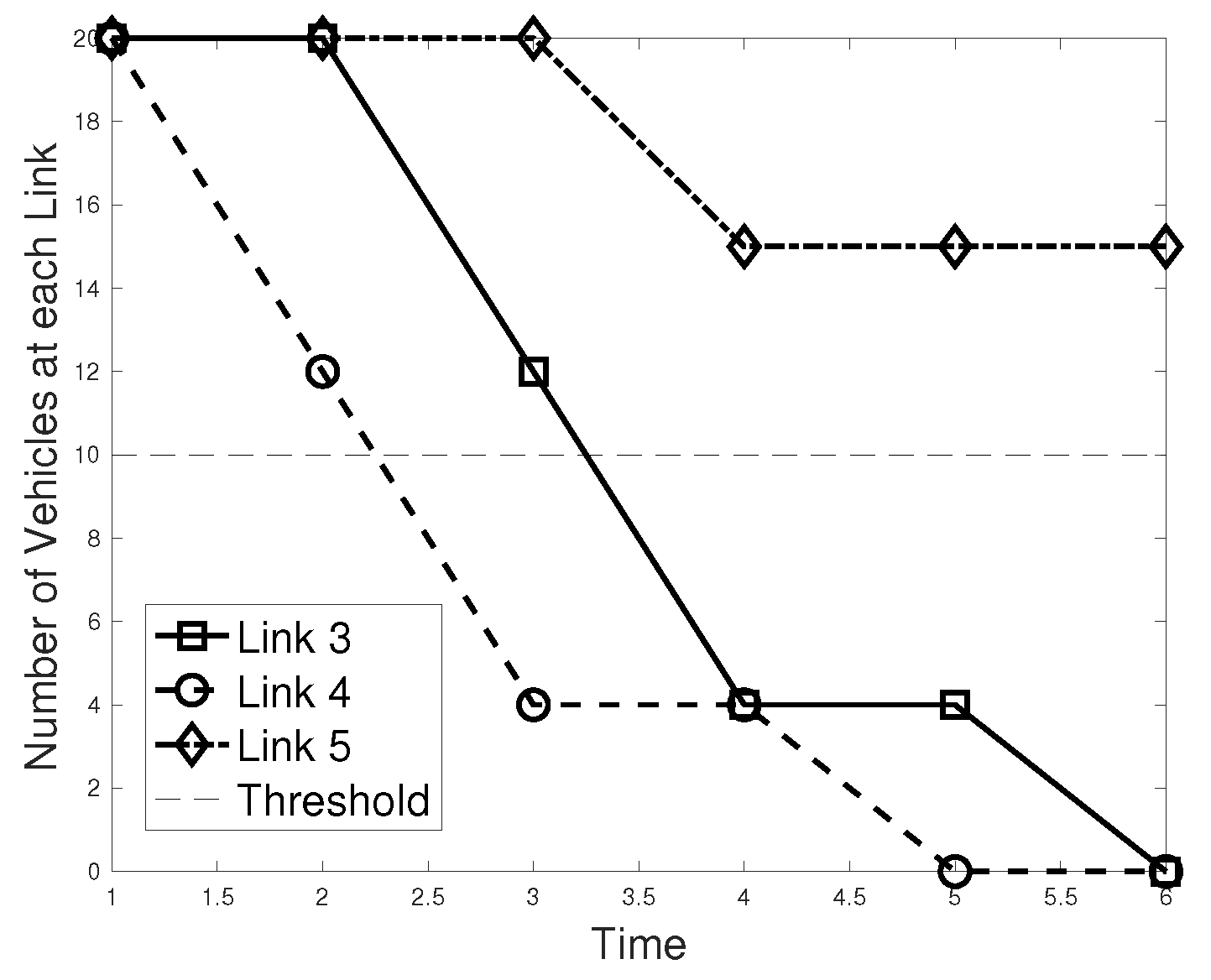
7.2. Numerical Results
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Summary of Notations
| Variable Notation | Interpretation |
|---|---|
| MITL formula | |
| Timed word | |
| Deterministic timed Büchi automaton (DTBA) | |
| Clock valuation | |
| Run of DTBA | |
| Durational stochastic game (DSG) | |
| Defender’s policy | |
| Actuator attack policy by the adversary | |
| Timing attack policy by the adversary | |
| Spatial robustness | |
| Temporal robustness | |
| Spatio-temporal robustness | |
| Product durational stochastic game | |
| Finite-state controller (FSC) | |
| Global durational stochastic game (GDSG) | |
| Set of generalized accepting maximal end components (GAMECs) |
Appendix B. Proofs of Technical Results
- 1.
- Suppose . In this case, state is included in set . If adding to makes states in GAMEC not reachable from , then Algorithm 4 executes Lines 26–29 and terminates by reporting failure.
- 2.
- Suppose . However, the remaining control actions cannot make GAMEC reachable from the initial state . In this case, Algorithm 4 will execute Lines 26–29 and terminates.
- 3.
- Suppose , and GAMEC is reachable from . We further assume that all actions that are admissible by the policy generated at Line 25 result in a robustness greater than or equal to . As a consequence, the remaining control actions in must steer the system into some neighboring state of such that . Therefore, Algorithm 4 will execute Scenario I at iteration and thus terminates.
- 4.
- Suppose and GAMEC is reachable from the initial state . Now assume that there exists some action such that it is admissible by the policy generated at Line 25 and results in the robustness below for some neighboring state of . In this case, this will be removed according to Line 12 at iteration . As there are only finitely many states and control actions, this case will converge to one of the cases discussed in (1), (2), or (3) in a finite number of iterations.
- 1.
- Suppose . From Line 18, is included in set . If adding to makes states in GAMEC not reachable from , then Algorithm 4 executes Lines 26–29 and terminates by reporting failure.
- 2.
- Suppose and GAMEC is not reachable from the for all . In this case, Algorithm 4 will execute Lines 26–29 and terminate.
- 3.
- Suppose , and GAMEC is reachable from . Assume that all actions that are admissible by the policy generated at Line 25 result in robustness . In this case, the game must be steered to a neighboring state of such that . Then, Algorithm 4 will execute Scenario I at iteration and terminate.
- 4.
- Suppose , and GAMEC is reachable from . Now assume that the policy generated at Line 25 results in robustness below for some neighboring state of . In this case, the control action will be removed according to Lines 12 and 20 at iteration . As there are only finitely many states and control actions, this case will converge to one of the cases discussed in (1), (2), or (3) in a finite number of iterations.
References
- Baheti, R.; Gill, H. Cyber-physical systems. Impact Control. Technol. 2011, 12, 161–166. [Google Scholar] [CrossRef]
- Baier, C.; Katoen, J.P.; Larsen, K.G. Principles of Model Checking; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Alur, R.; Dill, D.L. A theory of timed automata. Theor. Comput. Sci. 1994, 126, 183–235. [Google Scholar] [CrossRef]
- Kress-Gazit, H.; Fainekos, G.E.; Pappas, G.J. Temporal-logic-based reactive mission and motion planning. IEEE Trans. Robot. 2009, 25, 1370–1381. [Google Scholar] [CrossRef]
- Ding, X.; Smith, S.L.; Belta, C.; Rus, D. Optimal control of Markov decision processes with linear temporal logic constraints. IEEE Trans. Autom. Control. 2014, 59, 1244–1257. [Google Scholar] [CrossRef]
- Zhou, Y.; Maity, D.; Baras, J.S. Timed automata approach for motion planning using metric interval temporal logic. In Proceedings of the European Control Conference, Aalborg, Denmark, 29 June–1 July 2016; pp. 690–695. [Google Scholar] [CrossRef]
- Fu, J.; Topcu, U. Computational methods for stochastic control with metric interval temporal logic specifications. In Proceedings of the Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 7440–7447. [Google Scholar] [CrossRef]
- Fainekos, G.E.; Pappas, G.J. Robustness of temporal logic specifications for continuous-time signals. Theor. Comput. Sci. 2009, 410, 4262–4291. [Google Scholar] [CrossRef]
- Donzé, A.; Maler, O. Robust satisfaction of temporal logic over real-valued signals. In Proceedings of the International Conference on Formal Modeling and Analysis of Timed Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 92–106. [Google Scholar] [CrossRef]
- Niu, L.; Clark, A. Optimal Secure Control with Linear Temporal Logic Constraints. IEEE Trans. Autom. Control. 2020, 65. [Google Scholar] [CrossRef]
- Zhu, M.; Martinez, S. Stackelberg-game analysis of correlated attacks in cyber-physical systems. In Proceedings of the American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 4063–4068. [Google Scholar] [CrossRef]
- Wang, J.; Tu, W.; Hui, L.C.; Yiu, S.M.; Wang, E.K. Detecting time synchronization attacks in cyber-physical systems with machine learning techniques. In Proceedings of the International Conference on Distributed Computing Systems, Atlanta, GA, USA, 5–8 June 2017; pp. 2246–2251. [Google Scholar] [CrossRef]
- Jewell, W.S. Markov-renewal programming: Formulation, finite return models. Oper. Res. 1963, 11, 938. [Google Scholar] [CrossRef]
- Ross, S.M. Introduction to Stochastic Dynamic Programming; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Stidham, S.; Weber, R. A survey of Markov decision models for control of networks of queues. Queueing Syst. 1993, 13, 291–314. [Google Scholar] [CrossRef]
- Leitmann, G. On generalized Stackelberg strategies. J. Optim. Theory Appl. 1978, 26, 637–643. [Google Scholar] [CrossRef]
- Wei, L.; Sarwat, A.I.; Saad, W.; Biswas, S. Stochastic games for power grid protection against coordinated cyber-physical attacks. IEEE Trans. Smart Grid 2016, 9, 684–694. [Google Scholar] [CrossRef]
- Garnaev, A.; Baykal-Gursoy, M.; Poor, H.V. A game theoretic analysis of secret and reliable communication with active and passive adversarial modes. IEEE Trans. Wirel. Commun. 2015, 15, 2155–2163. [Google Scholar] [CrossRef]
- Bouyer, P.; Laroussinie, F.; Markey, N.; Ouaknine, J.; Worrell, J. Timed temporal logics. In Models, Algorithms, Logics and Tools; Springer: Berlin/Heidelberg, Germany, 2017; pp. 211–230. [Google Scholar] [CrossRef]
- Alur, R.; Feder, T.; Henzinger, T.A. The benefits of relaxing punctuality. J. ACM 1996, 43, 116–146. [Google Scholar] [CrossRef]
- Maler, O.; Nickovic, D.; Pnueli, A. From MITL to timed automata. In Proceedings of the International Conference on Formal Modeling and Analysis of Timed Systems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 274–289. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Vehicle routing problem with metric temporal logic specifications. In Proceedings of the Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 3953–3958. [Google Scholar] [CrossRef]
- Liu, J.; Prabhakar, P. Switching control of dynamical systems from metric temporal logic specifications. In Proceedings of the International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 5333–5338. [Google Scholar] [CrossRef]
- Nikou, A.; Tumova, J.; Dimarogonas, D.V. Cooperative task planning of multi-agent systems under timed temporal specifications. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 7104–7109. [Google Scholar] [CrossRef]
- Hansen, E.A. Solving POMDPs by searching in policy space. In Proceedings of the Conference on Uncertainty in Artificial Intelligence, Madison, WI, USA, 24–26 July 1998; pp. 211–219. [Google Scholar]
- Sharan, R.; Burdick, J. Finite state control of POMDPs with LTL specifications. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; p. 501. [Google Scholar] [CrossRef]
- Ramasubramanian, B.; Clark, A.; Bushnell, L.; Poovendran, R. Secure control under partial observability with temporal logic constraints. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 10–12 July 2019; pp. 1181–1188. [Google Scholar] [CrossRef]
- Ramasubramanian, B.; Niu, L.; Clark, A.; Bushnell, L.; Poovendran, R. Secure control in partially observable environments to satisfy LTL specifications. IEEE Trans. Autom. Control 2021, 66, 5665–5679. [Google Scholar] [CrossRef]
- Zhao, G.; Li, H.; Hou, T. Input–output dynamical stability analysis for cyber-physical systems via logical networks. IET Control Theory Appl. 2020, 14, 2566–2572. [Google Scholar] [CrossRef]
- Zhao, G.; Li, H. Robustness analysis of logical networks and its application in infinite systems. J. Frankl. Inst. 2020, 357, 2882–2891. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Angeli, D. A Lyapunov approach to incremental stability properties. IEEE Trans. Autom. Control 2002, 47, 410–421. [Google Scholar] [CrossRef]
- Rizk, A.; Batt, G.; Fages, F.; Soliman, S. A general computational method for robustness analysis with applications to synthetic gene networks. Bioinformatics 2009, 25, i169–i178. [Google Scholar] [CrossRef]
- Jakšić, S.; Bartocci, E.; Grosu, R.; Nguyen, T.; Ničković, D. Quantitative monitoring of STL with edit distance. Form. Methods Syst. Des. 2018, 53, 83–112. [Google Scholar] [CrossRef]
- Aksaray, D.; Jones, A.; Kong, Z.; Schwager, M.; Belta, C. Q-learning for robust satisfaction of signal temporal logic specifications. In Proceedings of the Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 2016; pp. 6565–6570. [Google Scholar] [CrossRef]
- Lindemann, L.; Dimarogonas, D.V. Robust control for signal temporal logic specifications using discrete average space robustness. Automatica 2019, 101, 377–387. [Google Scholar] [CrossRef]
- Rodionova, A.; Lindemann, L.; Morari, M.; Pappas, G. Temporal robustness of temporal logic specifications: Analysis and control design. ACM Trans. Embed. Comput. Syst. 2022, 22, 1–44. [Google Scholar] [CrossRef]
- Rodionova, A.; Lindemann, L.; Morari, M.; Pappas, G.J. Combined left and right temporal robustness for control under STL specifications. IEEE Control Syst. Lett. 2022, 7, 619–624. [Google Scholar] [CrossRef]
- Niu, L.; Ramasubramanian, B.; Clark, A.; Bushnell, L.; Poovendran, R. Control Synthesis for Cyber-Physical Systems to Satisfy Metric Interval Temporal Logic Objectives under Timing and Actuator Attacks. In Proceedings of the International Conference on Cyber-Physical Systems, Sydney, Australia, 21–25 April 2020; pp. 162–173. [Google Scholar] [CrossRef]
- Ouaknine, J.; Worrell, J. Some recent results in metric temporal logic. In Proceedings of the International Conference on Formal Modeling and Analysis of Timed Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–13. [Google Scholar] [CrossRef]
- Levenshtein, V.I. Binary codes capable of correcting deletions, insertions, and reversals. In Proceedings of the Soviet Physics Doklady; The American Institute of Physics: New York, NY, USA, 1966; Volume 10, pp. 707–710. [Google Scholar]
- Mohri, M. Edit-distance of weighted automata: General definitions and algorithms. Int. J. Found. Comput. Sci. 2003, 14, 957–982. [Google Scholar] [CrossRef]
- Coogan, S.; Gol, E.A.; Arcak, M.; Belta, C. Traffic network control from temporal logic specifications. IEEE Trans. Control Netw. Syst. 2015, 3, 162–172. [Google Scholar] [CrossRef]
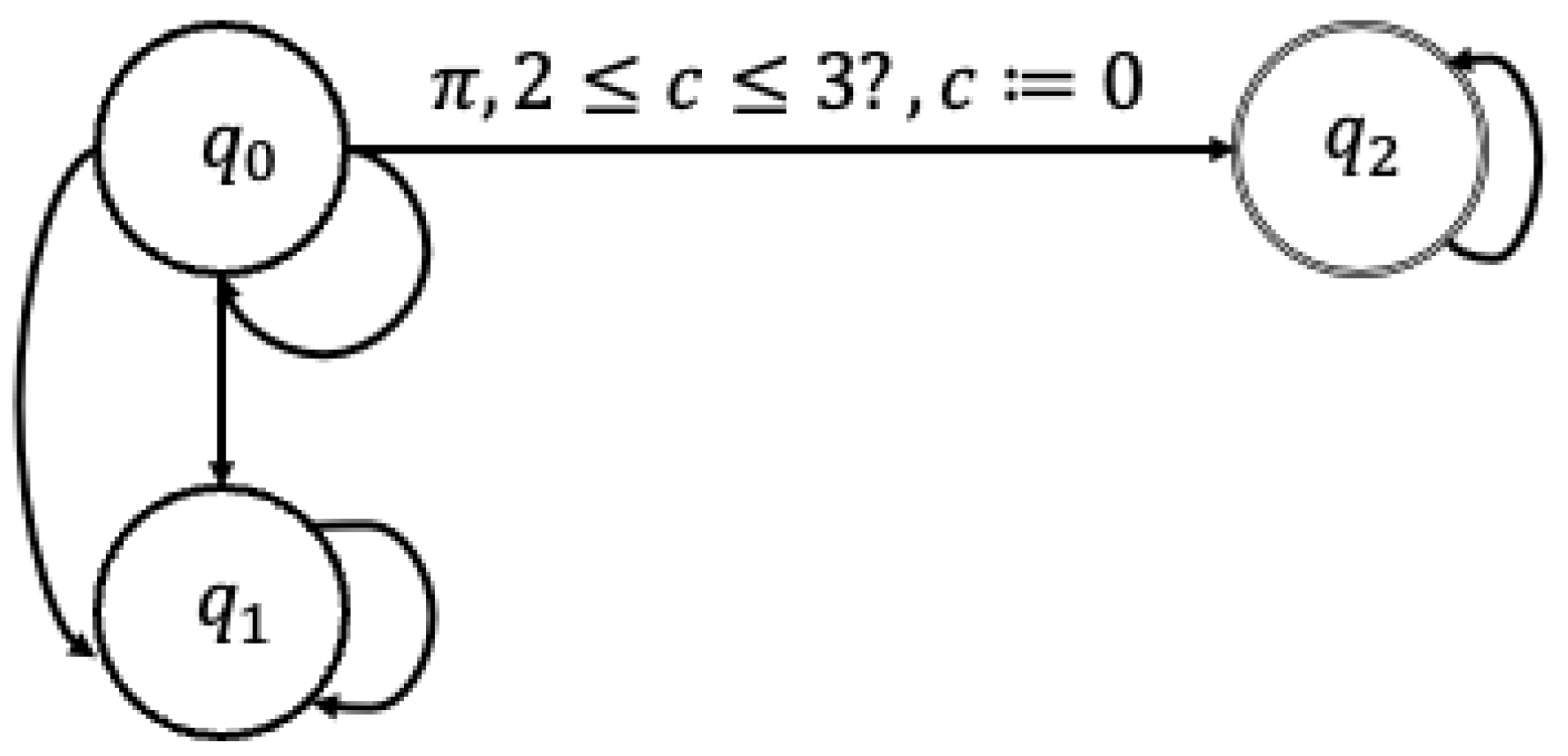
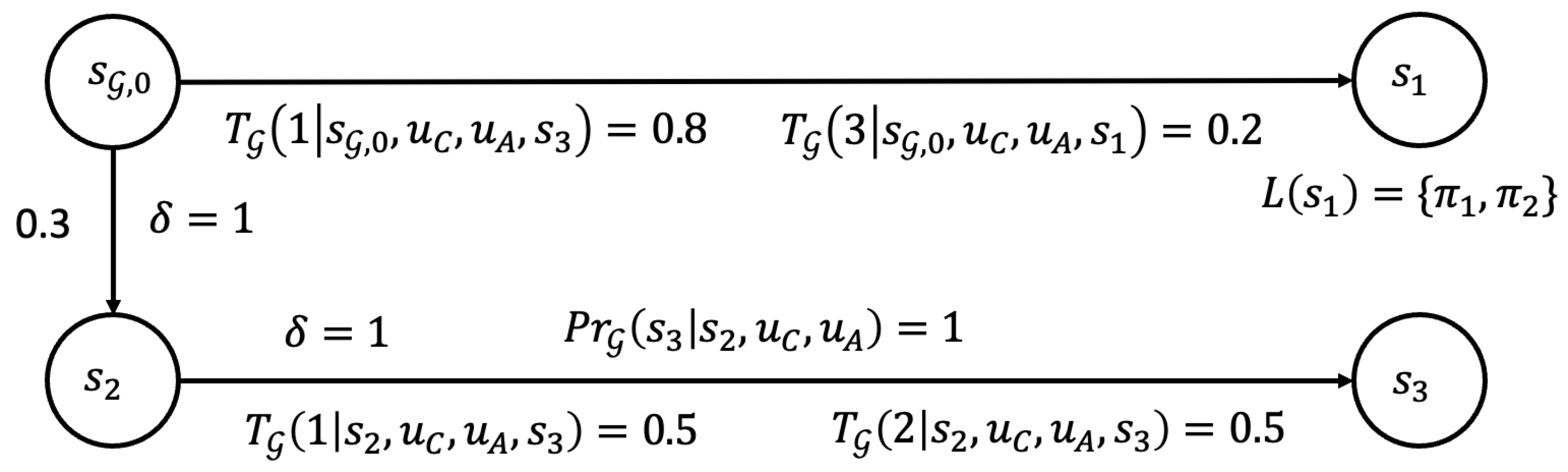

| Robustness | Complexity |
|---|---|
| Spatial (S) | |
| Temporal (T) |
| Intersection | |||||
|---|---|---|---|---|---|
| Time | 1 | 2 | 3 | 4 | 5 |
| 1 | G | R | R | G | R |
| 2 | R | R | G | G | R |
| 3 | R | G | G | G | R |
| 4 | R | R | R | R | G |
| 5 | R | G | G | G | R |
| 6 | G | G | G | R | G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, L.; Ramasubramanian, B.; Clark, A.; Poovendran, R. Robust Satisfaction of Metric Interval Temporal Logic Objectives in Adversarial Environments. Games 2023, 14, 30. https://doi.org/10.3390/g14020030
Niu L, Ramasubramanian B, Clark A, Poovendran R. Robust Satisfaction of Metric Interval Temporal Logic Objectives in Adversarial Environments. Games. 2023; 14(2):30. https://doi.org/10.3390/g14020030
Chicago/Turabian StyleNiu, Luyao, Bhaskar Ramasubramanian, Andrew Clark, and Radha Poovendran. 2023. "Robust Satisfaction of Metric Interval Temporal Logic Objectives in Adversarial Environments" Games 14, no. 2: 30. https://doi.org/10.3390/g14020030
APA StyleNiu, L., Ramasubramanian, B., Clark, A., & Poovendran, R. (2023). Robust Satisfaction of Metric Interval Temporal Logic Objectives in Adversarial Environments. Games, 14(2), 30. https://doi.org/10.3390/g14020030






