Air Condition’s PID Controller Fine-Tuning Using Artificial Neural Networks and Genetic Algorithms
Abstract
1. Introduction
2. Related Work
3. The Proposed Methodology
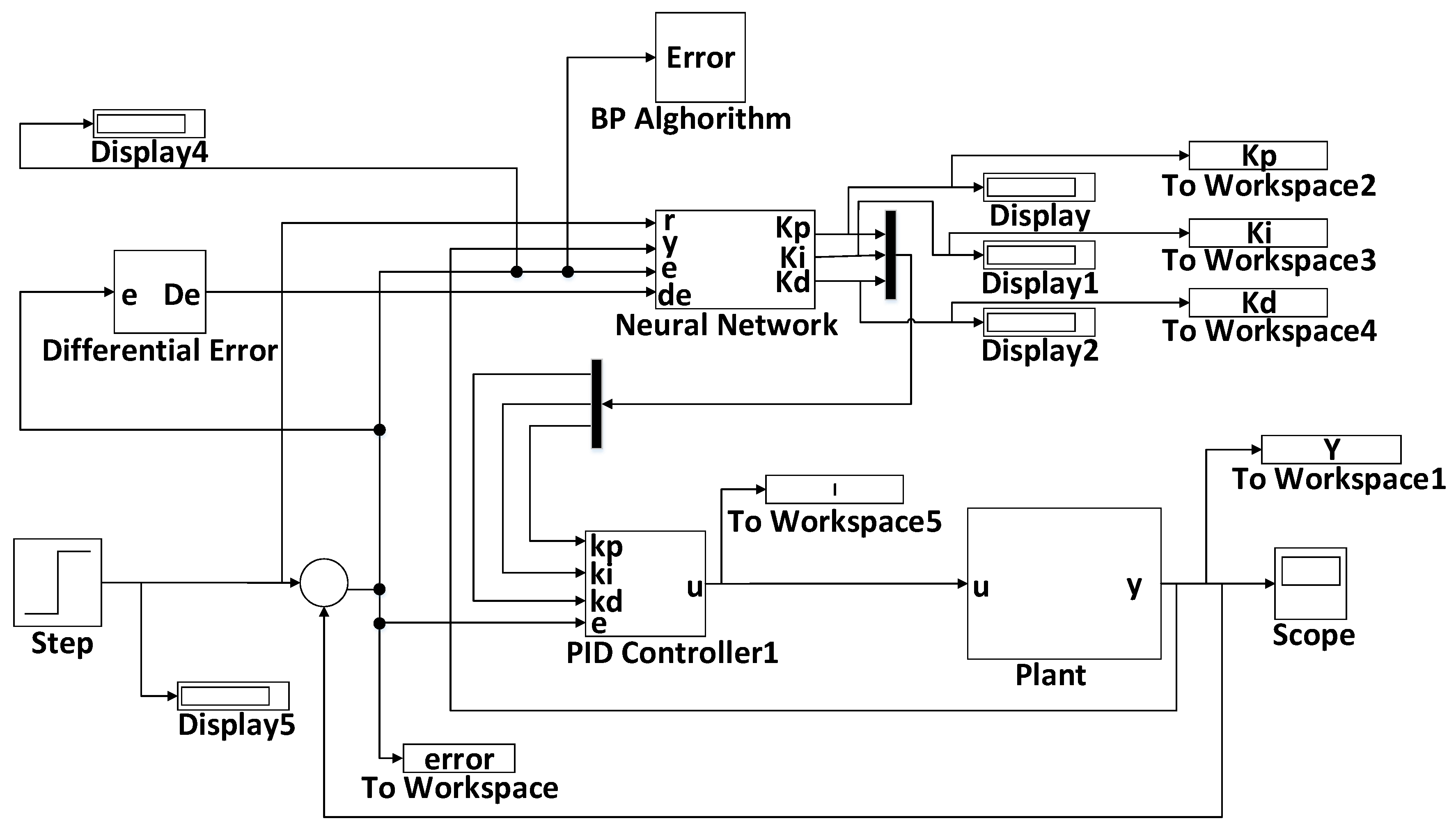
- The input data to networks is designed to train the neural network error, an error derived from the input and output.
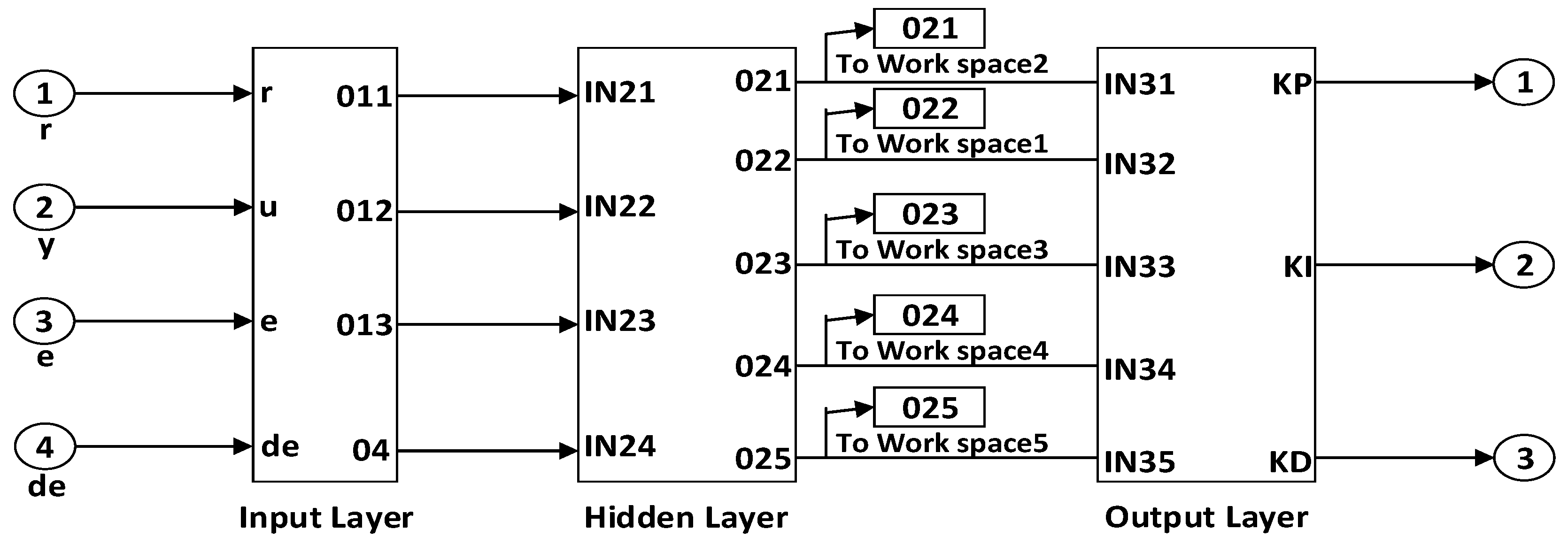
- The designed network has four inputs and three outputs.
- Simulations were executed using MatLab software and the neural network toolbox.
- Comparison performance of the neural network system is the squared square of system error displayed as Equation (3):
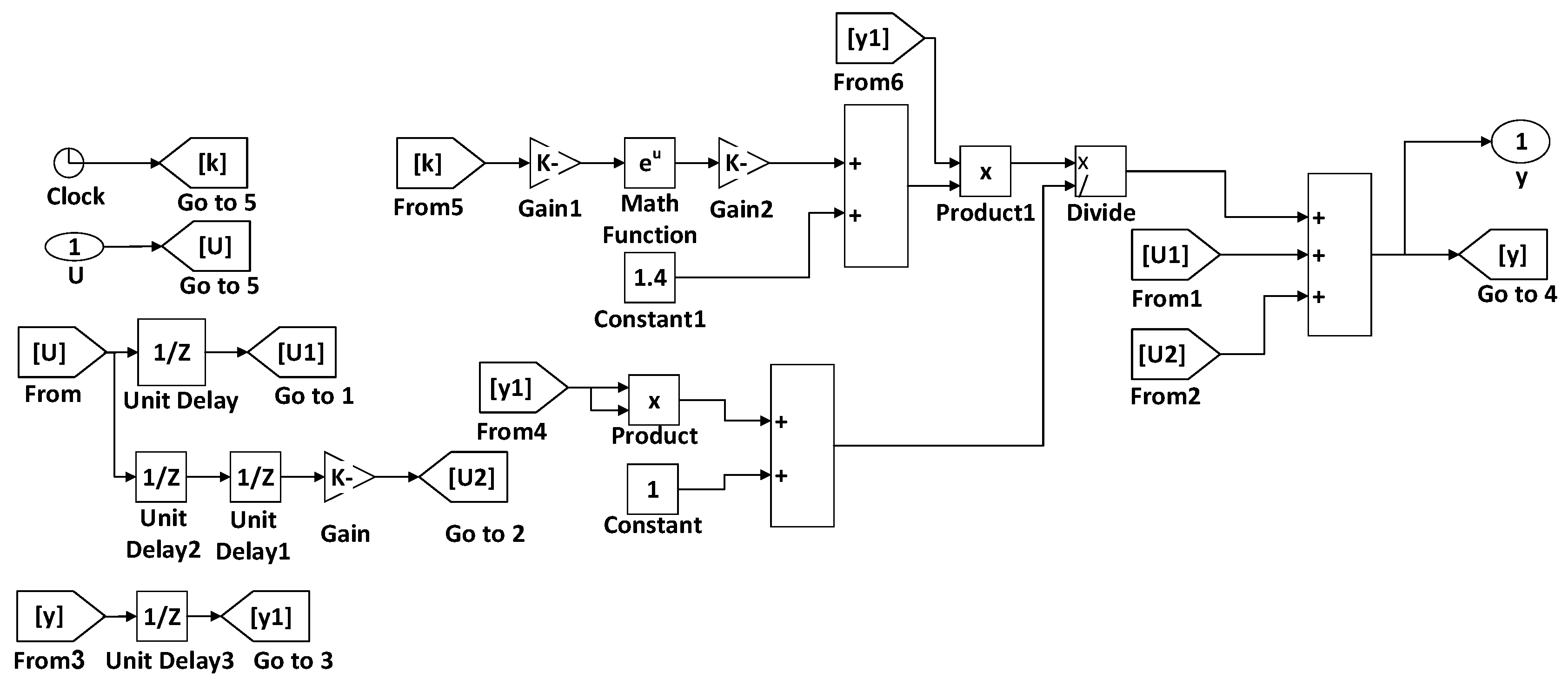
3.1. Control Systems
3.1.1. Expression of the Performance of Classical PID Controllers
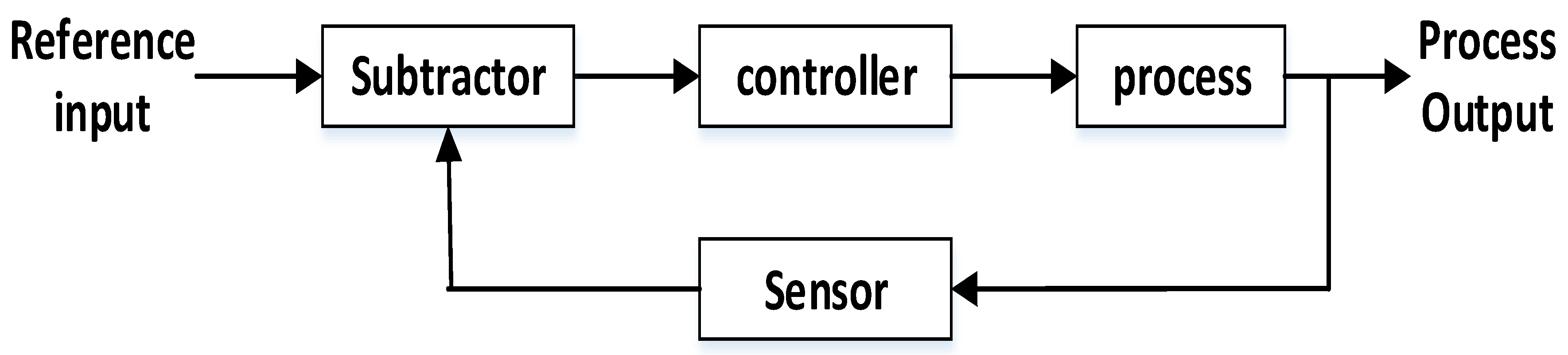
Open-Loop Control Systems
Closed Loop Control Systems
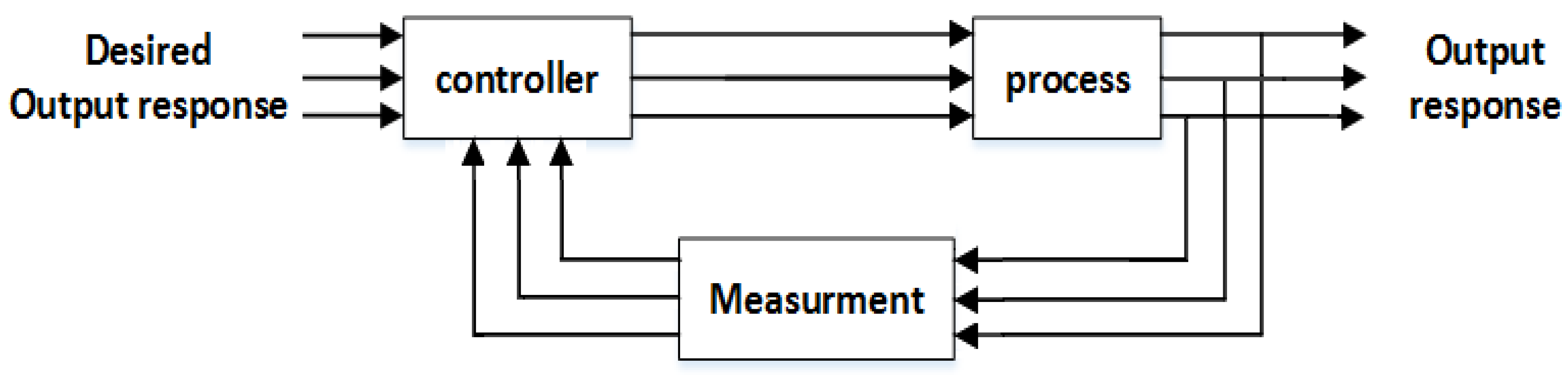
Multi-Input, Multi-Output Control Systems
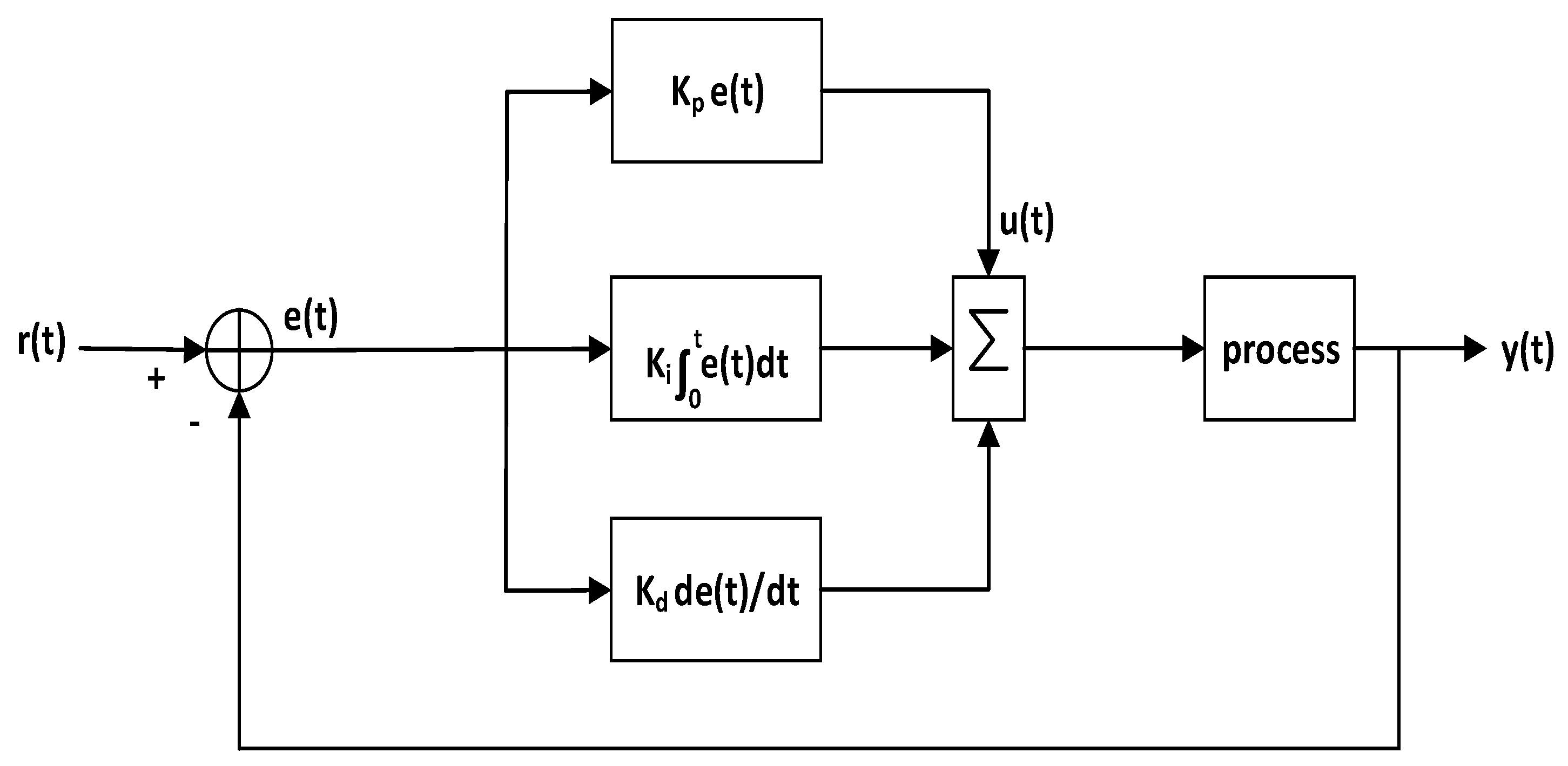
Proportional–Integral–Derivative Control (PID)
3.2. Neural Network
- (A)
- Perceptron training
- Assigning random values to weights
- Applying the perceptron to each training example
- Ensuring that all training examples have been evaluated correctly [Yes: the end of the algorithm, No: go back to step 2]
- (B)
- Back propagation algorithm
- (C)
- Back-propagation algorithm
3.3. Genetic Algorithms
3.3.1. Genetic Algorithm Optimization Method
- Individual: In genetics, each individual is referred to as a member of the population who can participate in the reproduction process and create a new member population that will create an increased population of these individuals.
- Population and production: In genetics, the population is a collection of all individuals that are present in the population, are capable of generating a generation and creating a new one and, consequently, producing a new population.
- Parents: This refers to individuals that intend to participate in the reproduction process and produce a new individual.
3.3.2. The Mathematical Structure of the Genetic Algorithm
4. Experimental Result
4.1. Dataset Description
4.2. Optimal Networks Topology
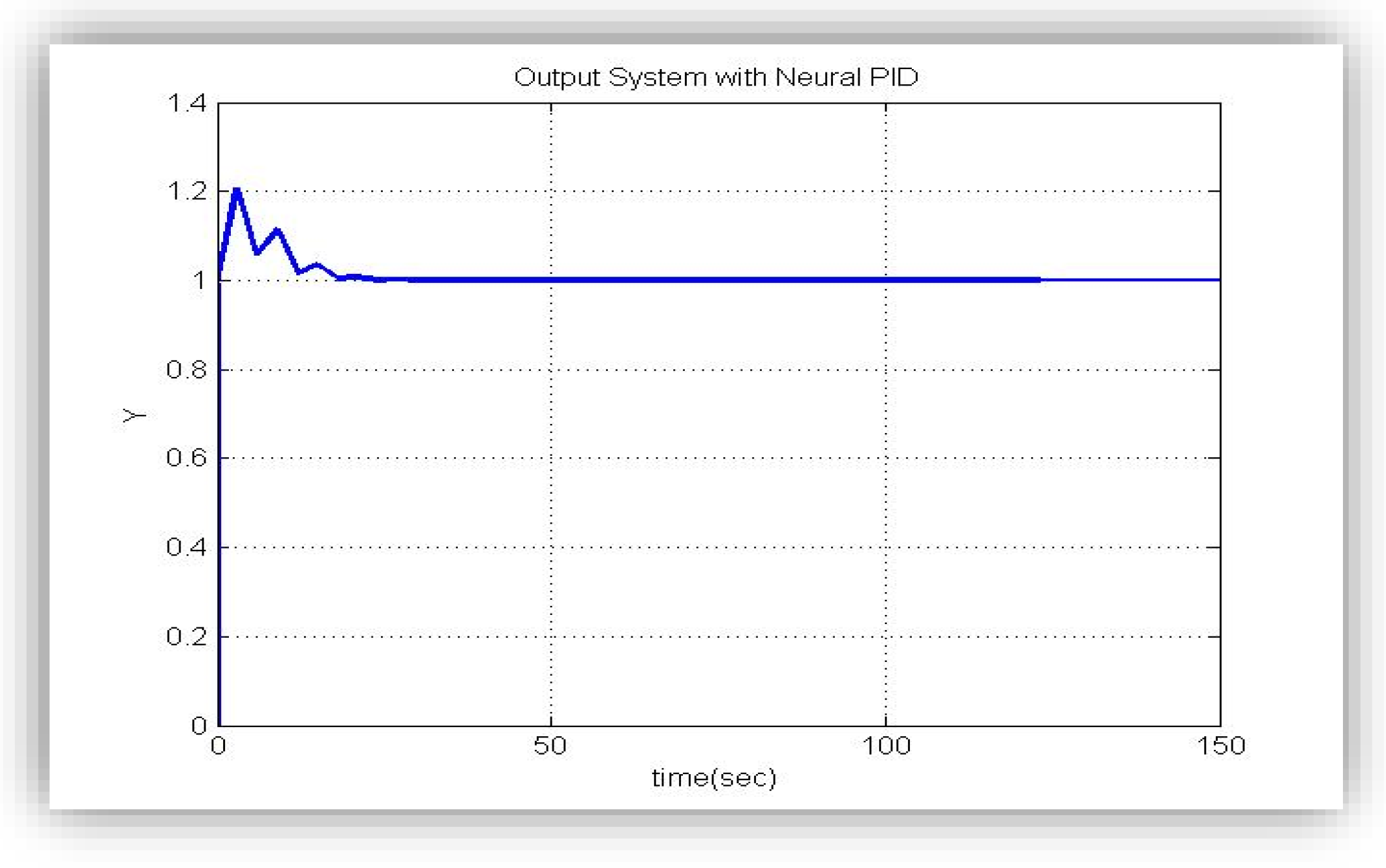
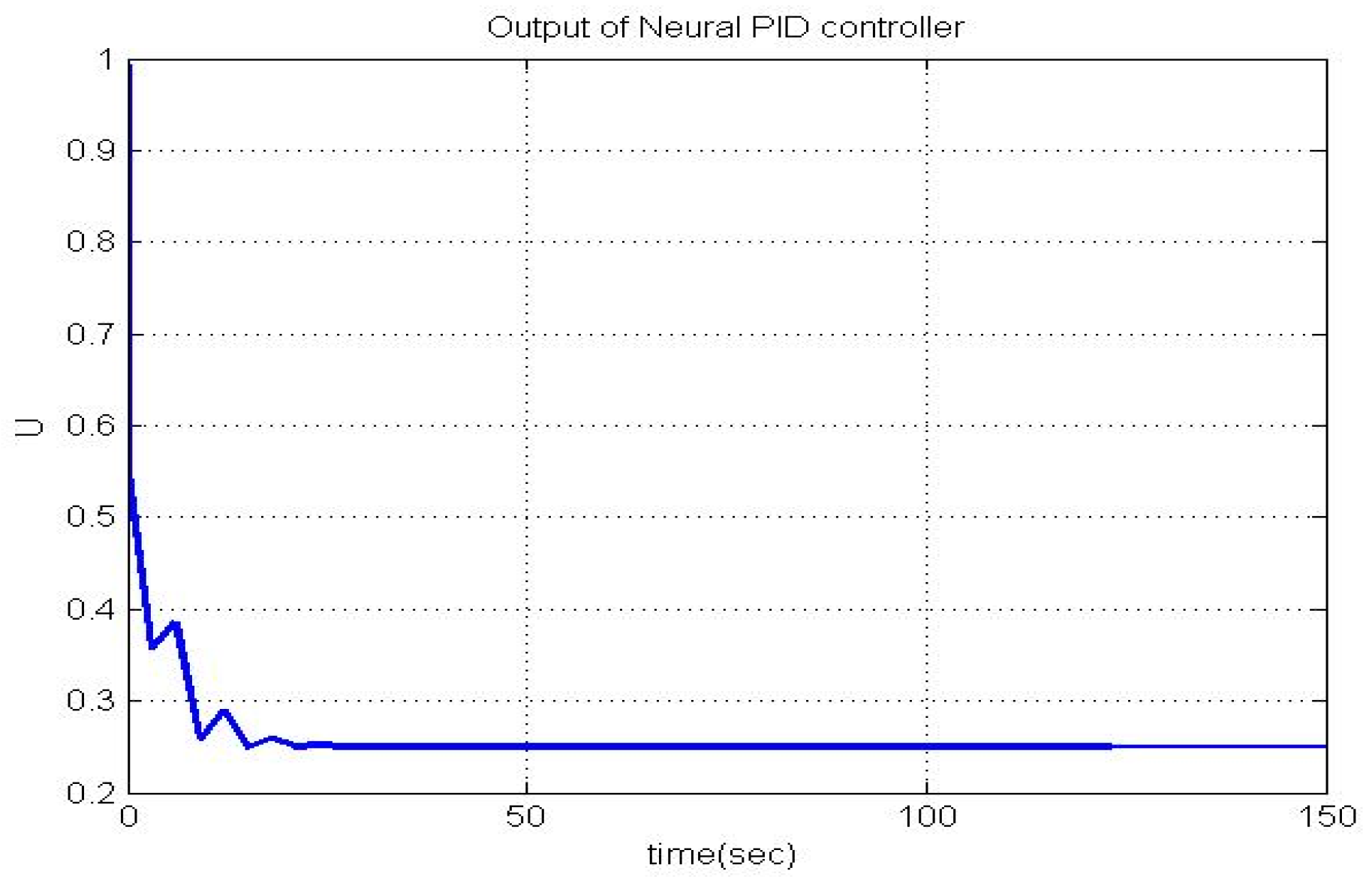
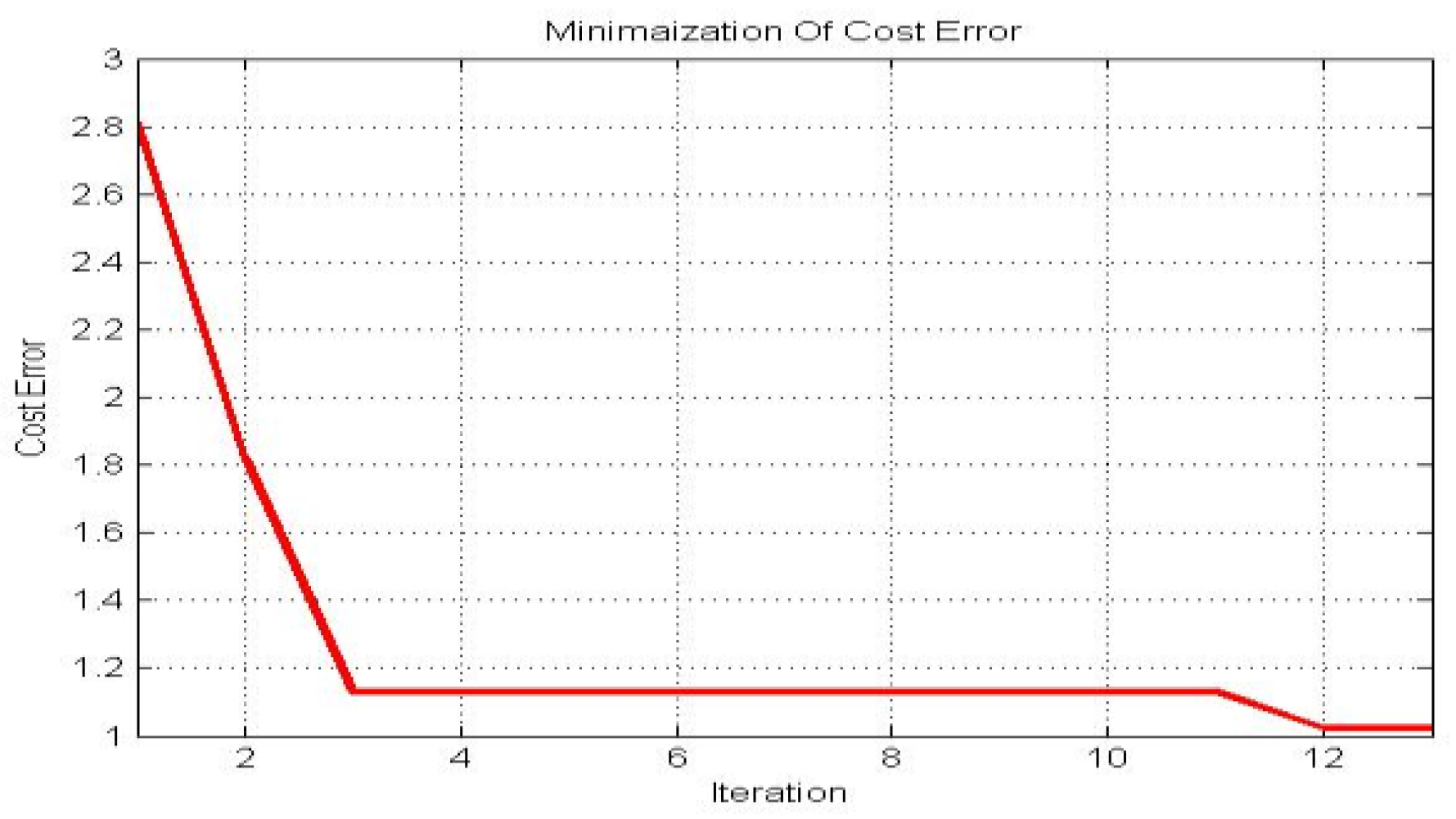
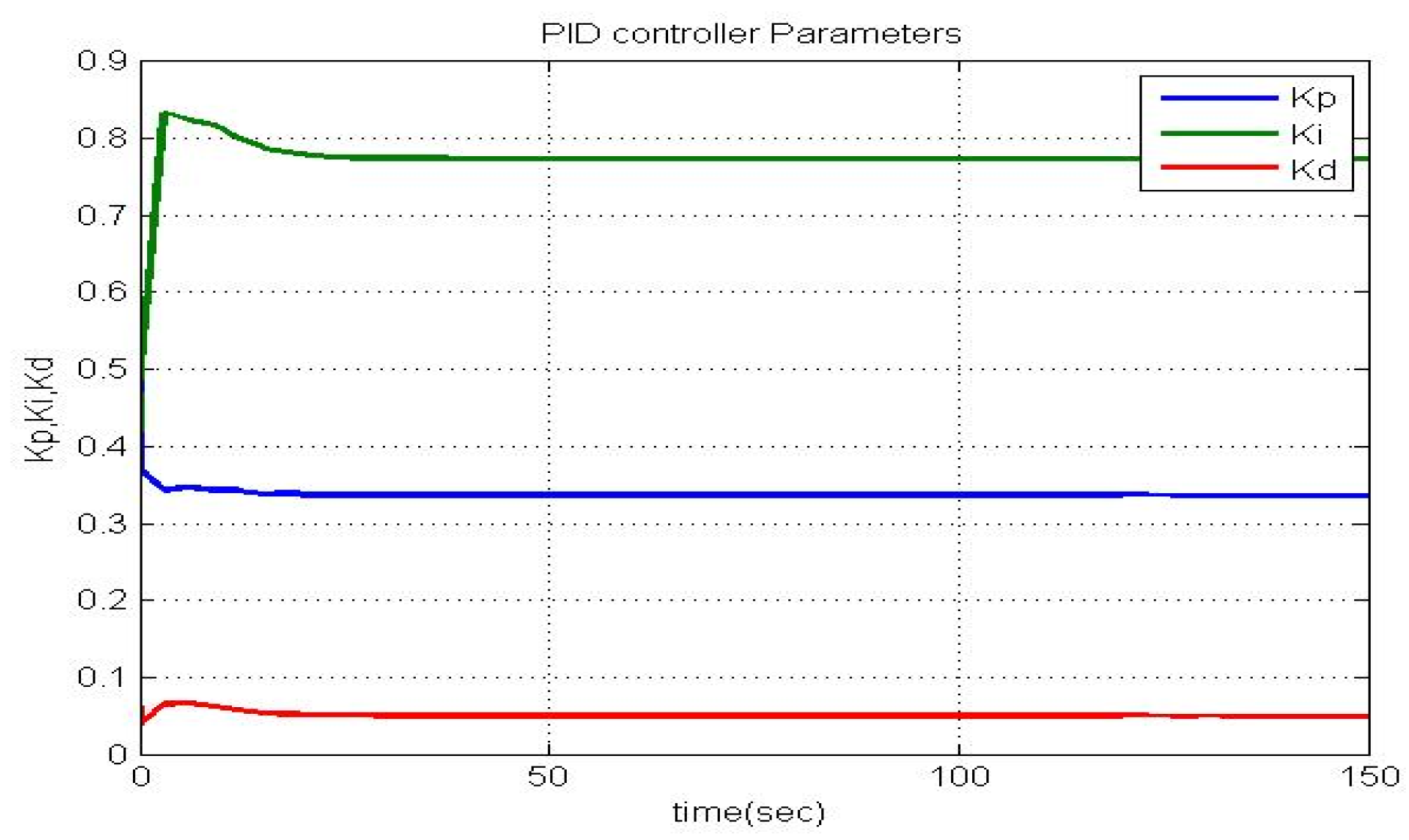
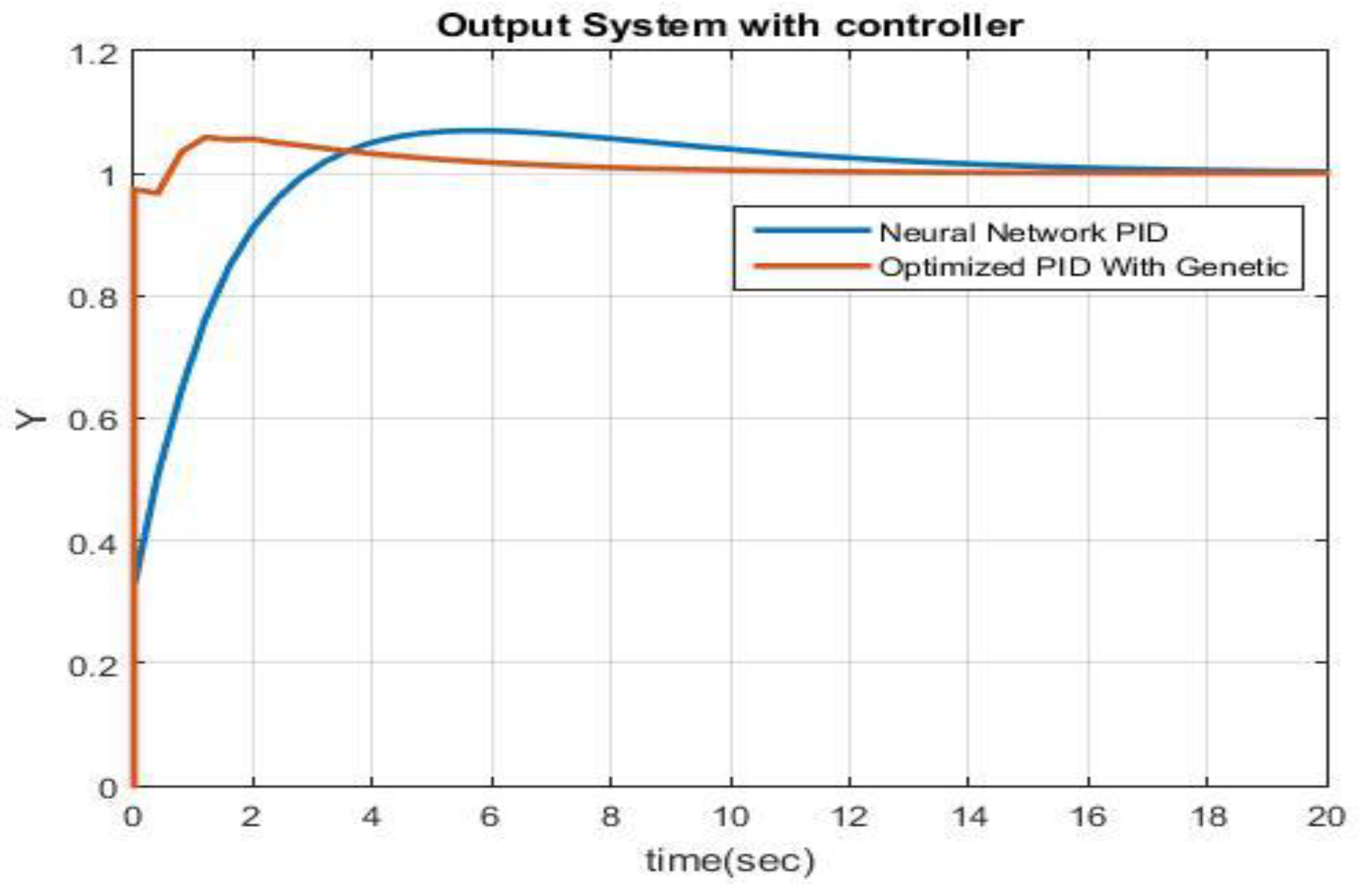
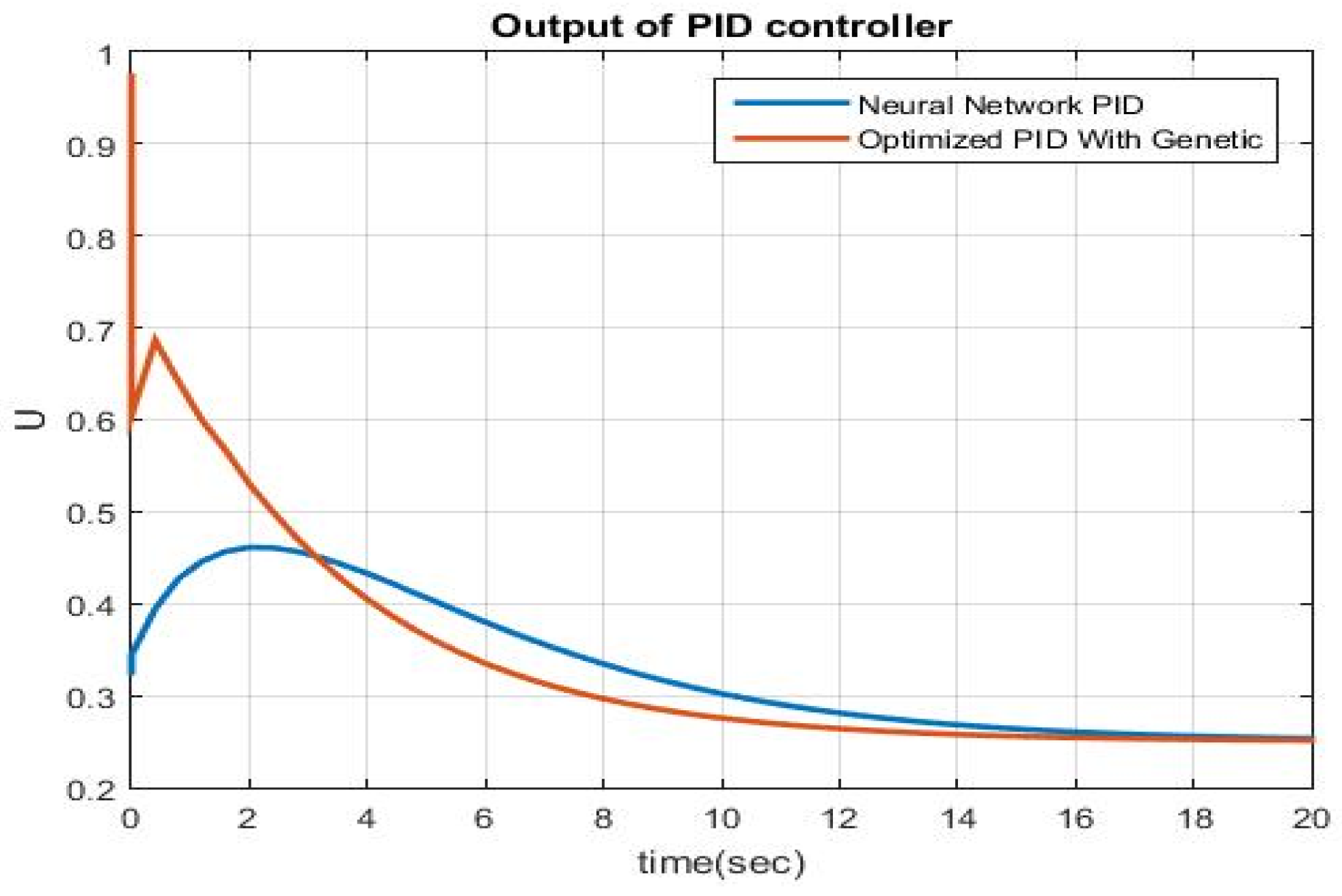
4.3. Optimal PID Outputs
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Winter, R.; Widrow, B. MADALINE RULE II: A training algorithm for neural networks (PDF). In Proceedings of the IEEE International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; pp. 401–408. [Google Scholar]
- Waibel, A.; Hanazawa, T.; Hinton, G.; Shikano, K.; Lang, K.J. Phoneme Recognition Using Time-Delay Neural Networks. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 328–339. [Google Scholar] [CrossRef]
- Krauth, W.; Mezard, M. Learning algorithms with optimal stabilty in neural networks. J. Phys. A Math. Gen. 2008, 20, L745–L752. [Google Scholar] [CrossRef]
- Guimarães, J.G.; Nóbrega, L.M.; da Costa, J.C. Design of a Hamming neural network based on single-electron tunneling devices. Microelectron. J. 2006, 37, 510–518. [Google Scholar] [CrossRef]
- Mui, K.W.; Wong, L.T. Evaluation of neutral criterion of indoor air quality for air-conditioned offices in subtropical climates. Build. Serv. Eng. Res. Technol. 2007, 28, 23–33. [Google Scholar] [CrossRef]
- ASHRAE. Design for Acceptable Indoor Air Quality; ANSI/ASHRAE Standard 62-2007; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2007. [Google Scholar]
- Levermore, G.J. Building Energy Management Systems: An Application to Heating and Control; E & FN Spon: London, UK; New York, NY, USA, 1992. [Google Scholar]
- Rahmati, V.; Ghorbani, A. A Novel Low Complexity Fast Response Time Fuzzy PID Controller for Antenna Adjusting Using Two Direct Current Motors. Indian J. Sci. Technol. 2018, 11. [Google Scholar] [CrossRef]
- Dounis, A.I.; Bruant, M.; Santamouris, M.J.; Guarracino, G.; Michel, P. Comparison of conventional and fuzzy control of indoor air quality in buildings. J. Intell. Fuzzy Syst. 1996, 4, 131–140. [Google Scholar]
- Tan, W. Unified tuning of PID load frequency controller for power systems via IMC. IEEE Trans. Power Syst. 2010, 25, 341–350. [Google Scholar] [CrossRef]
- Howell, M.N.; Best, M.C. On-line PID tuning for engine idle-speed control using continuous action reinforcement learning automata. Control Eng. Pract. 2000, 8, 147–154. [Google Scholar] [CrossRef]
- European Union. The New Directive on the Energy Performance of Buildings, 3rd ed.; European Union: Brussels, Belgium, 2002. [Google Scholar]
- Tian, L.; Lin, Z.; Liu, J.; Yao, T.; Wang, Q. The impact of temperature on mean local air age and thermal comfort in a stratum ventilated office. Build. Environ. 2011, 46, 501–510. [Google Scholar] [CrossRef]
- Hui, P.S.; Wong, L.T.; Mui, K.W. Feasibility study of an express assessment protocol for the indoor air quality of air conditioned offices. Indoor Built Environ. 2006, 15, 373–378. [Google Scholar] [CrossRef]
- The American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). Thermal Environment Conditions for Human Occupancy; ASHRAE Standard 55: Atlanta, GA, USA, 2004. [Google Scholar]
- Wyon, D.P. The effects of indoor air quality on performance and productivity. Indoor Air 2004, 14, 92–101. [Google Scholar] [CrossRef] [PubMed]
- Fanger, P.O. What is IAQ. Indoor Air 2006, 16, 328–334. [Google Scholar] [CrossRef] [PubMed]
- Lundgren, K.; Kjellstrom, T. Sustainability Challenges from Climate Change and Air Conditioning Use in Urban Areas. Sustainability 2013, 5, 3116–3128. [Google Scholar] [CrossRef]
- Maerefat, M.; Omidvar, A. Thermal Comfort; Kelid Amoozesh: Tehran, Iran, 2008; pp. 1–10. [Google Scholar]
- Tian, L.; Lin, Z.; Liu, J.; Wang, Q. Experimental investigation of thermal and ventilation performances of stratum ventilation. Build. Environ. 2011, 46, 1309–1320. [Google Scholar] [CrossRef]
- Morovat, N. Analysis of Thermal Comfort, Air Quality and Energy Consumption in a Hybrid System of the Hydronic Radiant Cooling and Stratum Ventilation. Master’s Thesis, Department of Mechanical Engineering, Tarbiat Modares University, Tehran, Iran, 2013. [Google Scholar]
- Protopapadakis, E.; Schauer, M.; Pierri, E.; Doulamis, A.D.; Stavroulakis, G.E.; Böhrnsen, J.; Langer, S. A genetically optimized neural classifier applied to numerical pile integrity tests considering concrete piles. Comput. Struct. 2016, 162, 68–79. [Google Scholar] [CrossRef]
- Oreski, S.; Oreski, G. Genetic algorithm-based heuristic for feature selection in credit risk assessment. Expert Syst. Appl. 2014, 41, 2052–2064. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization. IEEE Geosci. Remote Sens. Lett. 2015, 12, 309–313. [Google Scholar] [CrossRef]
- Wang, S.; Jin, X. Model-based optimal control of VAV air-conditioning system using genetic algorithms. Build. Environ. 2000, 35, 471–487. [Google Scholar] [CrossRef]
- Maerefat, M.; Morovat, N. Analysis of thermal comfort in space equipped with stratum ventilation and radiant cooling ceiling. Modares Mech. Eng. 2013, 13, 41–54. [Google Scholar]
- Yu, B.F.; Hu, Z.B.; Liu, M. Review of research on air conditioning systems and indoor air quality control for human health. Int. J. Refrig. 2009, 32, 3–20. [Google Scholar] [CrossRef]
- Yang, S.; Wu, S.; Yan, Y.Y. Control strategies for indoor environment quality and energy efficiency—A review. Int. J. Low-Carbon Technol. 2015, 10, 305–312. [Google Scholar]
- Mui, K.W.; Wong, L.T.; Hui, P.S.; Law, K.Y. Epistemic evaluation of policy influence on workplace indoor air quality of Hong Kong in 1996–2005. Build. Serv. Eng. Res. Technol. 2008, 29, 157–164. [Google Scholar] [CrossRef]
- Chen, S.; Cowan, C.F.N.; Grant, P.M. Orthogonal Least Squares Learning Algorithm for Radial Basis Function Networks. IEEE Trans. Neural Netw. 2010, 2, 302–309. [Google Scholar] [CrossRef] [PubMed]

| Neural Network of Performance Criterion | The Number of Hidden |
|---|---|
| Layer Neural Network | |
| 21.56 | No hidden layer |
| 1.34 | A hidden layer |
| 14.38 | Two hidden layers |
| 7.66 | Three hidden layers |
| 5.21 | Four hidden layers |
| Training Algorithm | Neural Network of Performance Criterion |
|---|---|
| Trainlm | 1.384 |
| Trainbfg | 2.214 |
| Trainrp | 2.562 |
| Trainscg | 4.651 |
| Traincgb | 3.563 |
| Traincgf | 2.201 |
| Traincgp | 1.493 |
| Traionoss | 3.452 |
| Traingdx | 2.856 |
| Traingd | 1.132 |
| Traingdm | 1.081 |
| Traingda | 2/342 |
| Genetic algorithm | 0.596 |
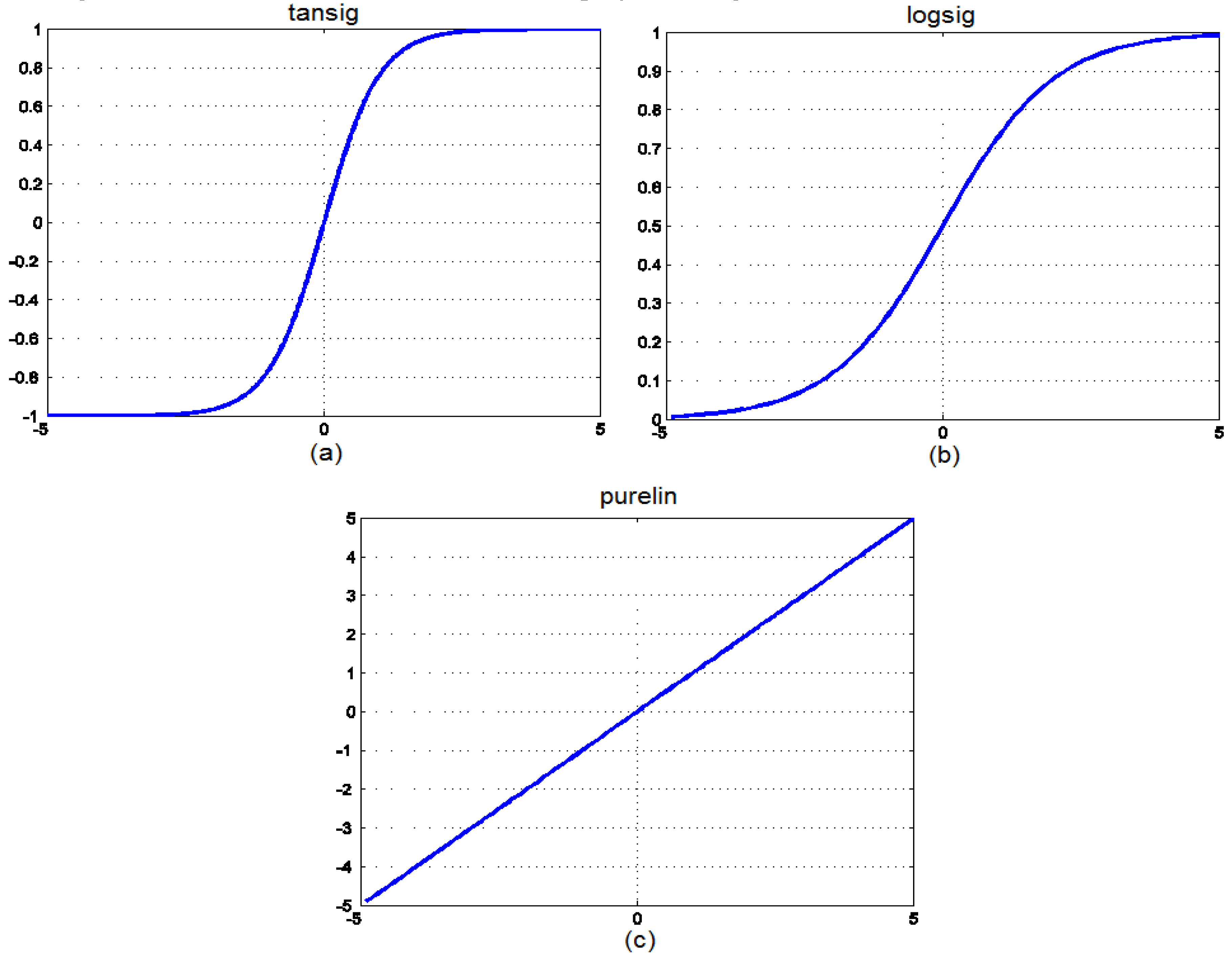
| Neural Network of Performance Criterion | Activator Functions | |
|---|---|---|
| Output Layer | Hidden Layer | |
| 6.371 | purelin | Purelin |
| 6.526 | logsig | Purelin |
| 4.411 | tansig | Purelin |
| 2.321 | purelin | Logsig |
| 0.931 | logsig | Logsig |
| 2.504 | tansig | logsig |
| 0.956 | purelin | tansig |
| 1.732 | logsig | tansig |
| 3.043 | tansig | tansig |
| Neural Network of Performance Criterion | Hidden Layer Size | Neural Network of Performance Criterion | Hidden Layer Size |
|---|---|---|---|
| 0.932 | 1 | 2.788 | 6 |
| 1.215 | 2 | 1.546 | 7 |
| 1.368 | 3 | 1.012 | 8 |
| 1.116 | 4 | 0.994 | 9 |
| 0.874 | 5 | 1.016 | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malekabadi, M.; Haghparast, M.; Nasiri, F. Air Condition’s PID Controller Fine-Tuning Using Artificial Neural Networks and Genetic Algorithms. Computers 2018, 7, 32. https://doi.org/10.3390/computers7020032
Malekabadi M, Haghparast M, Nasiri F. Air Condition’s PID Controller Fine-Tuning Using Artificial Neural Networks and Genetic Algorithms. Computers. 2018; 7(2):32. https://doi.org/10.3390/computers7020032
Chicago/Turabian StyleMalekabadi, Maryam, Majid Haghparast, and Fatemeh Nasiri. 2018. "Air Condition’s PID Controller Fine-Tuning Using Artificial Neural Networks and Genetic Algorithms" Computers 7, no. 2: 32. https://doi.org/10.3390/computers7020032
APA StyleMalekabadi, M., Haghparast, M., & Nasiri, F. (2018). Air Condition’s PID Controller Fine-Tuning Using Artificial Neural Networks and Genetic Algorithms. Computers, 7(2), 32. https://doi.org/10.3390/computers7020032





