Mapping Smallholder Yield Heterogeneity at Multiple Scales in Eastern Africa
Abstract
:1. Introduction
2. Materials and Methods
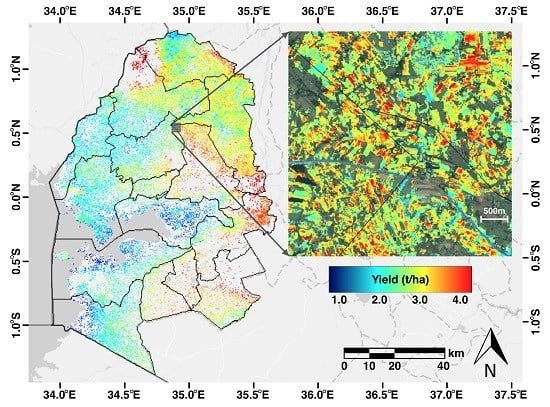
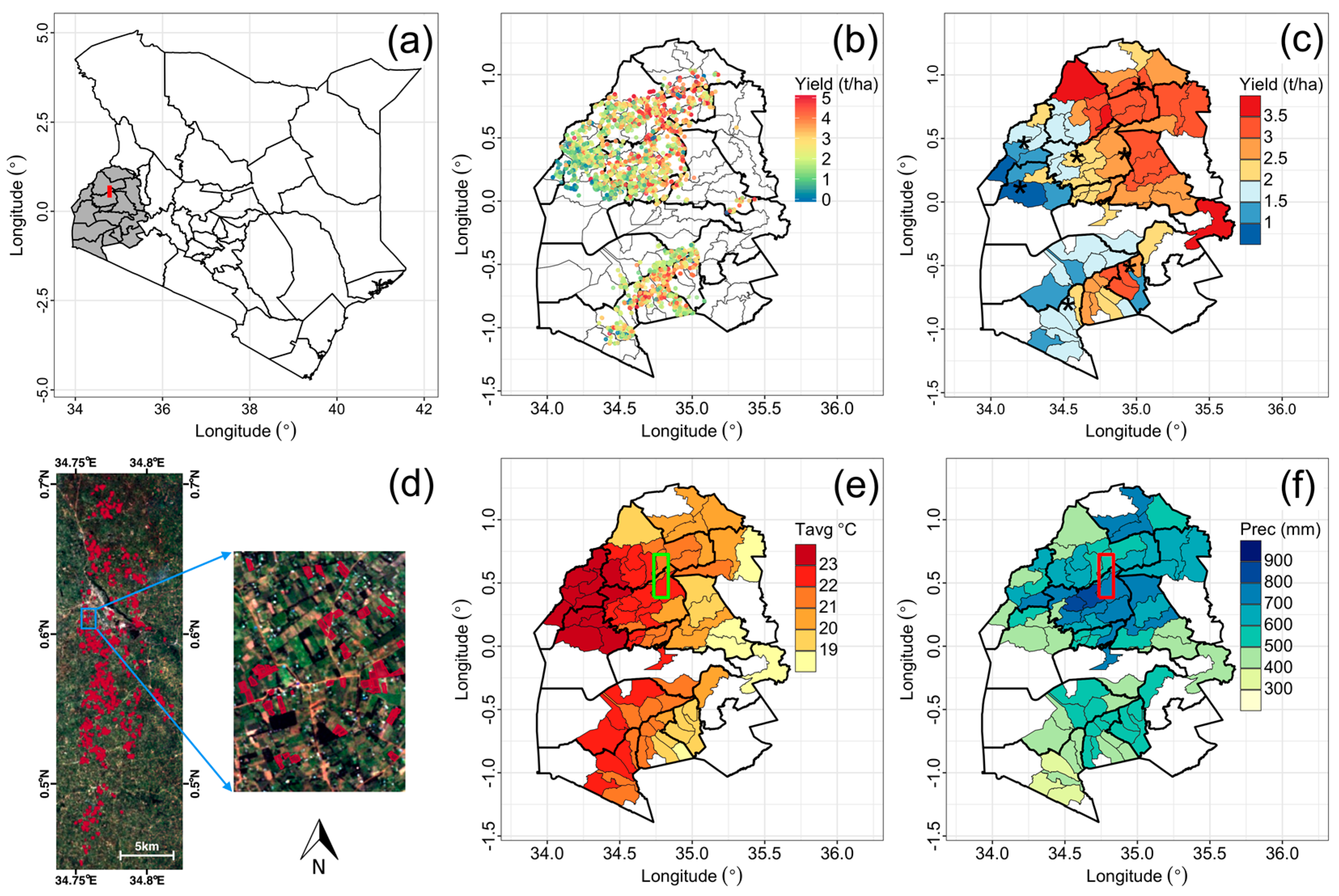
2.1. Study Area and Field Data Collection
2.2. Satellite Image Processing
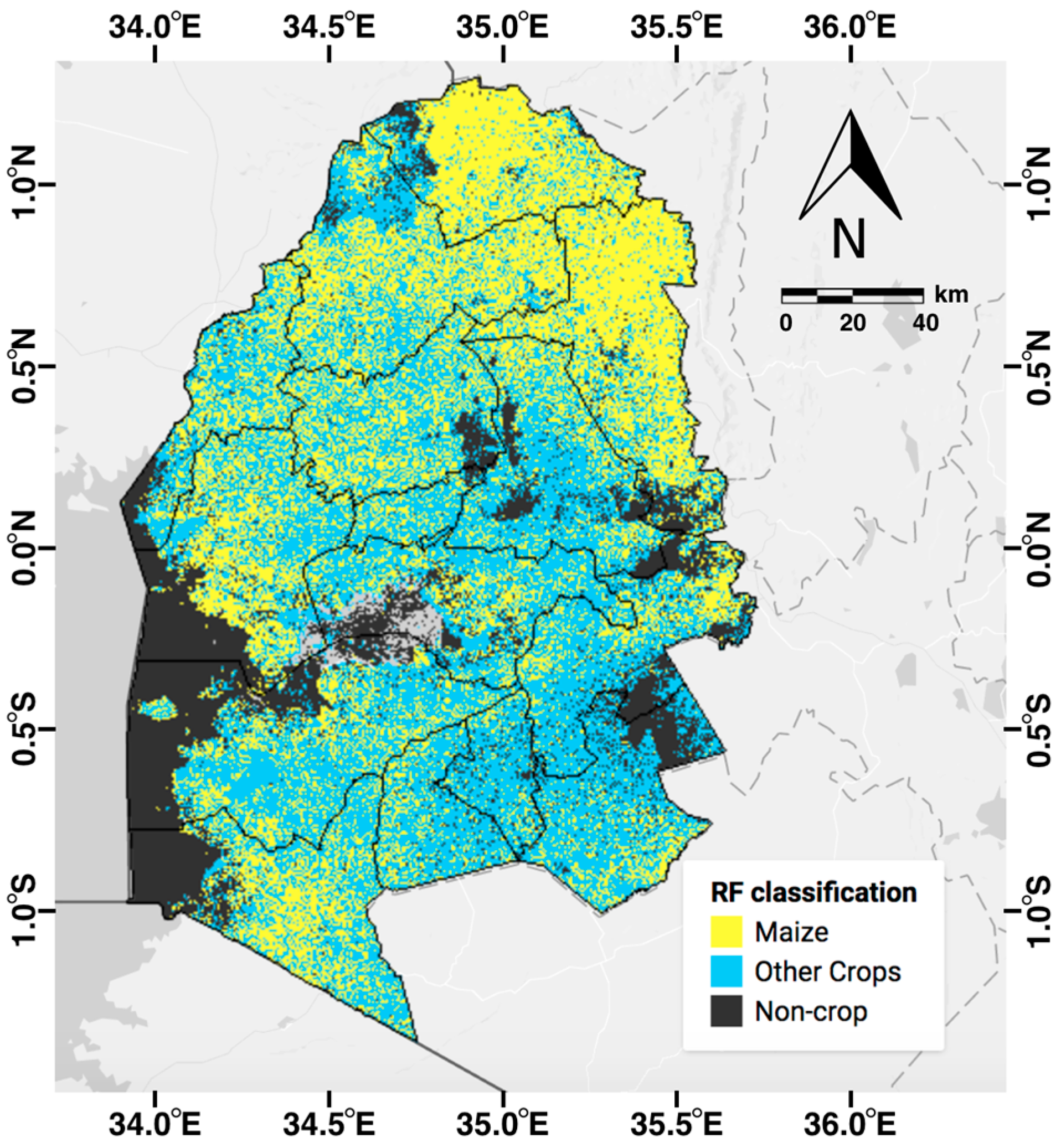
2.3. Land Cover Classification
2.4. Satellite Based Yield Estimation
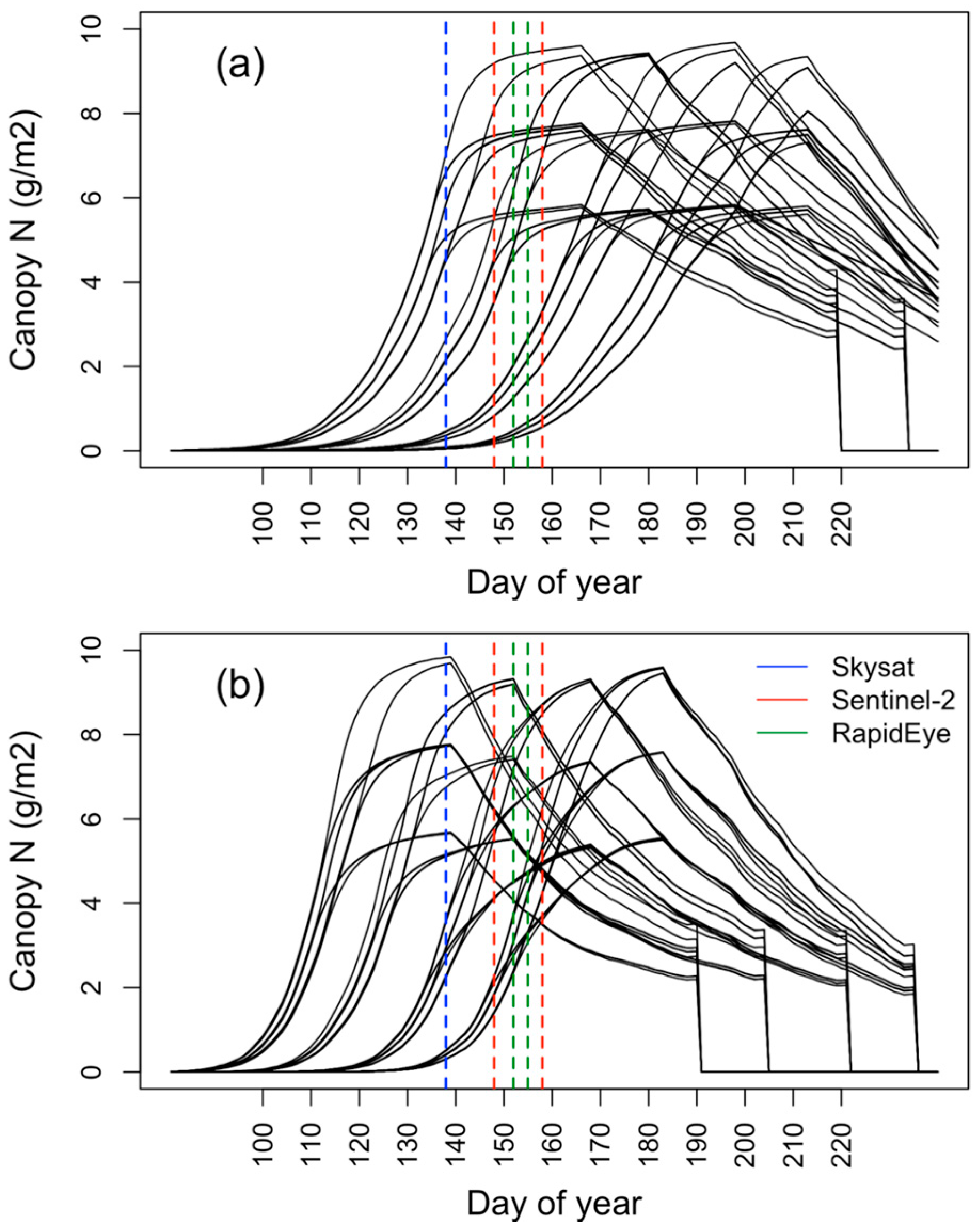
2.4.1. Agricultural Production Systems Simulator (APSIM) Simulation
2.4.2 Multiple Avenues to Improve Performance
3. Results
3.1. 1AF-Measured Yield
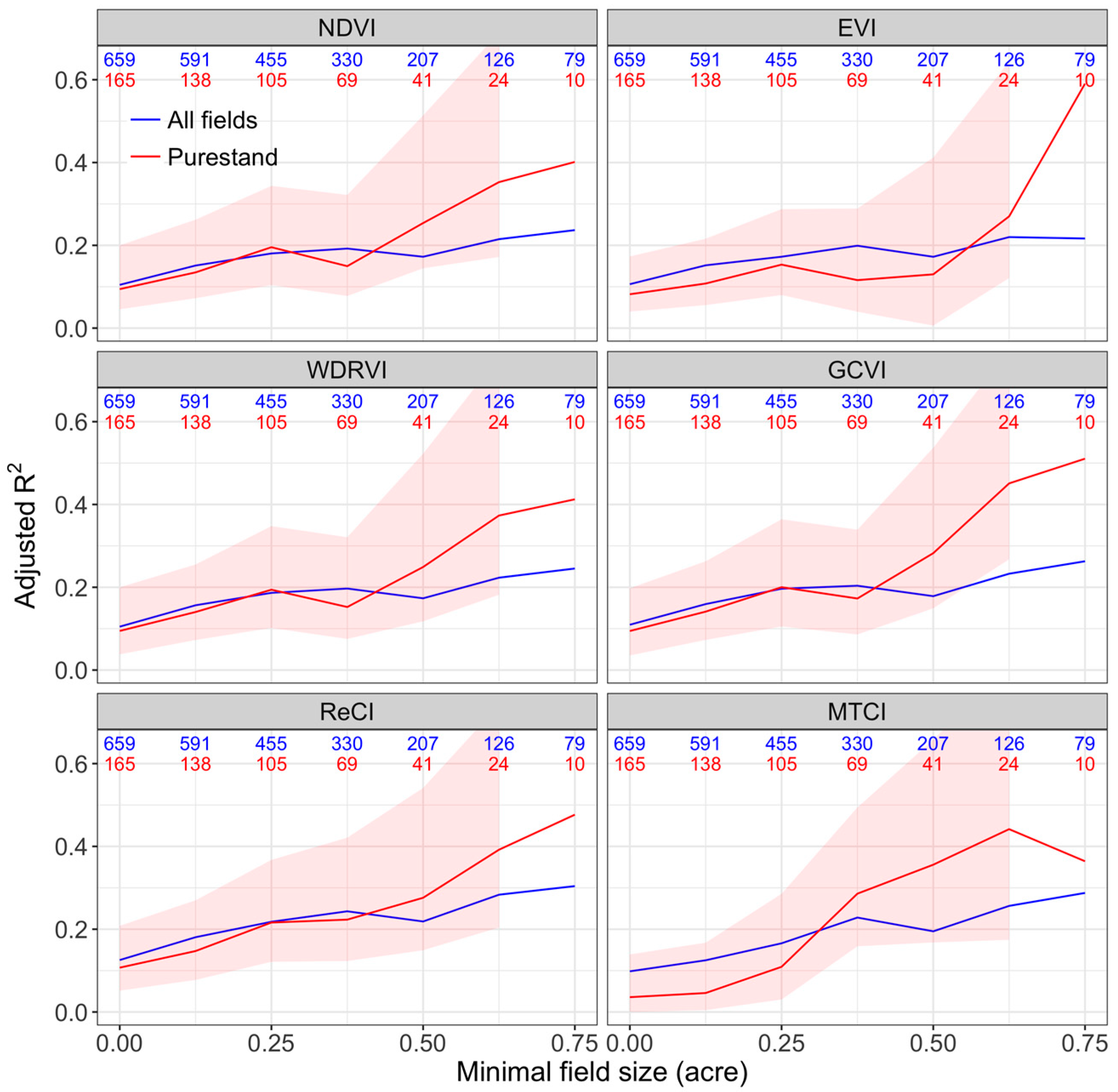
3.2. Performance of Multiple VIs at Bungoma
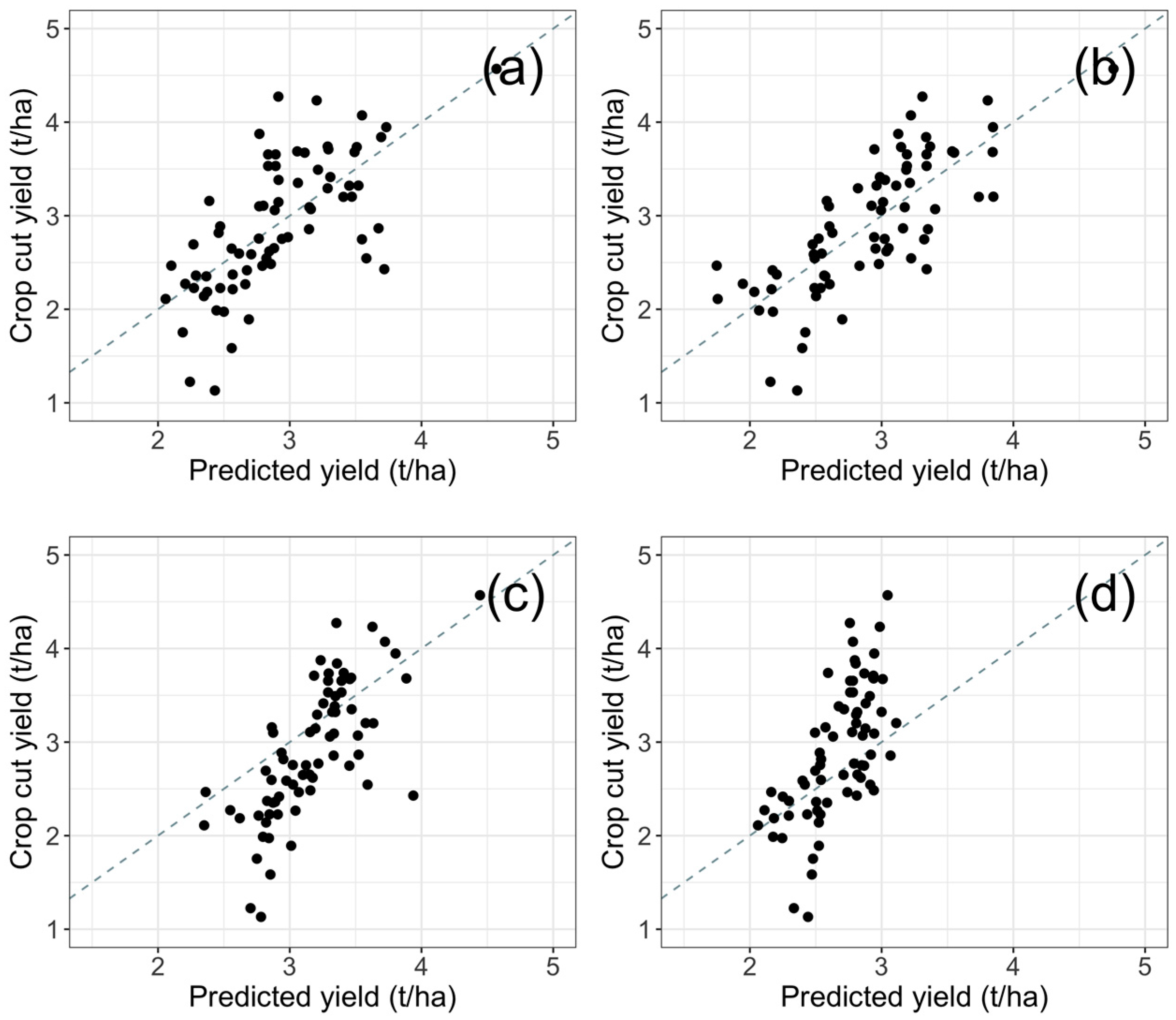
3.3. Performance of the Calibrated Model
3.4. Performance of the Uncalibrated Model
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- World Bank World Development Report 2008—Agriculture for Development. Available online: https://openknowledge.worldbank.org/handle/10986/5990 (accessed on 5 September 2017).
- Morton, J.F. The impact of climate change on smallholder and subsistence agriculture. Proc. Natl. Acad. Sci. USA 2007, 104, 19680–19685. [Google Scholar] [CrossRef] [PubMed]
- Carletto, C.; Jolliffe, D.; Banerjee, R. From Tragedy to Renaissance: Improving Agricultural Data for Better Policies. J. Dev. Stud. 2015, 51, 133–148. [Google Scholar] [CrossRef]
- Lobell, D.B. The use of satellite data for crop yield gap analysis. Field Crop. Res. 2013, 143, 56–64. [Google Scholar] [CrossRef]
- Shelestov, A.; Lavreniuk, M.; Kussul, N.; Novikov, A.; Skakun, S. Exploring Google Earth Engine Platform for Big Data Processing: Classification of Multi-Temporal Satellite Imagery for Crop Mapping. Front. Earth Sci. 2017, 5, 1–10. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Burke, M.; Lobell, D.B. Satellite-based assessment of yield variation and its determinants in smallholder African systems. Proc. Natl. Acad. Sci. USA 2017, 114, 2189–2194. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Azzari, G.; Lobell, D.B. Improving the accuracy of satellite-based high-resolution yield estimation: A test of multiple scalable approaches. Agric. For. Meteorol. 2017, 247, 207–220. [Google Scholar]
- Carletto, C.; Gourlay, S.; Winters, P. From guesstimates to GPStimates: Land area measurement and implications for agricultural analysis. J. Afr. Econ. 2015, 24, 593–628. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Okains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973; Freden, S.C., Mercanti, E.P., Eds.; NASA: Washington, DC, USA, 1974. [Google Scholar]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; Van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 2523, 5403–5413. [Google Scholar] [CrossRef]
- Hansen, M.C.; Egorov, A.; Potapov, P.V.; Stehman, S.V.; Tyukavina, A.; Turubanova, S.A.; Roy, D.P.; Goetz, S.J.; Loveland, T.R.; Ju, J.; et al. Monitoring conterminous United States (CONUS) land cover change with Web-Enabled Landsat Data (WELD). Remote Sens. Environ. 2014, 140, 466–484. [Google Scholar] [CrossRef]
- Azzari, G.; Lobell, D.B. Landsat-based classification in the cloud: An opportunity for a paradigm shift in land cover monitoring. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]
- Schlemmera, M.; Gitelson, A.; Schepersa, J.; Fergusona, R.; Peng, Y.; Shanahana, J.; Rundquist, D. Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 47–54. [Google Scholar] [CrossRef]
- Bassu, S.; Brisson, N.; Durand, J.-L.L.; Boote, K.; Lizaso, J.; Jones, J.W.; Rosenzweig, C.; Ruane, A.C.; Adam, M.; Baron, C.; et al. How do various maize crop models vary in their responses to climate change factors? Glob. Chang. Biol. 2014, 20, 2301–2320. [Google Scholar] [CrossRef] [PubMed]
- Kumudini, S.; Andrade, F.H.; Boote, K.J.; Brown, G.A.; Dzotsi, K.A.; Edmeades, G.O.; Gocken, T.; Goodwin, M.; Halter, A.L.; Hammer, G.L.; et al. Predicting maize phenology: Intercomparison of functions for developmental response to temperature. Agron. J. 2014, 106, 2087–2097. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Miguez, F.E.; Moore, K.J. Evaluating APSIM Maize, Soil Water, Soil Nitrogen, Manure, and Soil Temperature Modules in the Midwestern United States. Agron. J. 2014, 106, 1025. [Google Scholar] [CrossRef]
- Jin, Z.; Zhuang, Q.; Tan, Z.; Dukes, J.S.; Zheng, B.; Melillo, J.M. Do maize models capture the impacts of heat and drought stresses on yield? Using algorithm ensembles to identify successful approaches. Glob. Chang. Biol. 2016, 22, 3112–3126. [Google Scholar] [CrossRef] [PubMed]
- Rojas, O. Operational maize yield model development and validation based on remote sensing and agro-meteorological data in Kenya. Int. J. Remote Sens. 2007, 28, 3775–3793. [Google Scholar] [CrossRef]
- Peng, Y.; Nguy-Robertson, A.; Arkebauer, T.; Gitelson, A.A. Assessment of canopy chlorophyll content retrieval in maize and soybean: Implications of hysteresis on the development of generic algorithms. Remote Sens. 2017, 9, 226. [Google Scholar] [CrossRef]

| Band | Use | Spectral Range | Pixel Size |
|---|---|---|---|
| Skysat | |||
| B | Blue | 450–515 nm | 2 m |
| G | Green | 515–595 nm | 2 m |
| R | Red | 605–695 nm | 2 m |
| N | Near Infrared (NIR) | 740–900 nm | 2 m |
| RapidEye | |||
| b1 | Blue | 440–510 nm | 5 m |
| b2 | Green | 520–590 nm | 5 m |
| b3 | Red | 630–685 nm | 5 m |
| b4 | Red Edge (RE) | 690–730 nm | 5 m |
| b5 | NIR | 760–850 nm | 5 m |
| Sentinel-2 | |||
| B2 | Blue | 458–523 nm | 10 m |
| B3 | Green | 543–578 nm | 10 m |
| B4 | Red | 650–680 nm | 10 m |
| B5 | Red Edge (RE) | 698–713 nm | 20 m |
| B8 | NIR | 785–900 nm | 10 m |
| Vegetation Index | Formula | Reference |
|---|---|---|
| Normalized Difference Vegetation Index (NDVI) | (NIR − Red)/(NIR + Red) | Rouse et al., 1973 [11] |
| Enhanced Vegetation Index (EVI) | 2.5 × (NIR − Red)/(NIR + 6 × Red + 7 × Blue − 1) | Huete et al., 1997 [12] |
| Wide Dynamic Range Vegetation Index (WDRVI) | (0.2 × NIR − Red)/(0.2 × NIR + Red) | Gitelson, 2004 [13] |
| Green Chlorophyll Vegetation Index (GCVI) | (NIR/Green − 1) | Gitelson et al., 2003 [14] |
| Red edge Chlorophyll Index (ReCI) | NIR/RE − 1 | Gitelson et al., 2003 [14] |
| MERIS Terrestrial Chlorophyll Index (MTCI) | (NIR − RE)/(RE − Red) | Dash and Curran, 2004 [15] |
| Vegetation Index | B-K Sub-region | 1AF Region | ||
|---|---|---|---|---|
| Full | Purestand | Division | District | |
| GCVI | 0.18 | 0.28 | 0.29 (0.36) | 0.43 (0.49) |
| MTCI | 0.20 | 0.36 | 0.36 (0.44) | 0.57 (0.66) |
| Simulation Settings | B-K Sub-region | 1AF Region | |||||
|---|---|---|---|---|---|---|---|
| Phenology | VI | Yield Estimates | Sowing Window | Full | Purestand | Division | District |
| Default | GCVI | Yields | Wide | 0.018 | 0.038 | 0.277 ** | 0.426 ** |
| Default | GCVI | Yields | Narrow | 0.009 | 0 | 0..279 ** | 0.424 ** |
| Default | GCVI | Biomass×HI | Wide | 0.007 | 0.02 | 0.285 ** | 0.423 ** |
| Default | GCVI | Biomass×HI | Narrow | 0 | 0 | 0.281 ** | 0.42 ** |
| Default | MTCI | Yields | Wide | 0.016 | 0.238 ** | 0.335 ** | 0.525 ** |
| Default | MTCI | Yields | Narrow | 0.013 | 0.208 * | 0.349 ** | 0.531 ** |
| Default | MTCI | Biomass×HI | Wide | 0.007 | 0.204 * | 0.355 ** | 0.51 ** |
| Default | MTCI | Biomass×HI | Narrow | 0 | 0.118 ˙ | 0.349 ** | 0.509 ** |
| Updated | GCVI | Yields | Wide | 0.015 | 0 | 0.116 ** | 0.112 ** |
| Updated | GCVI | Yields | Narrow | 0.11 ˙ | 0.25 ** | 0.21 ** | 0.291 ** |
| Updated | GCVI | Biomass×HI | Wide | 0 | 0 | 0.284 ** | 0.413 ** |
| Updated | GCVI | Biomass×HI | Narrow | 0.172* | 0.169* | 0.289 ** | 0.421 ** |
| Updated | MTCI | Yields | Wide | 0.006 | 0.115 ˙ | 0.109 ** | 0.116 ** |
| Updated | MTCI | Yields | Narrow | 0.06 | 0.222 ** | 0.19 ** | 0.255 ** |
| Updated | MTCI | Biomass×HI | Wide | 0 | 0.102 ˙ | 0.293 ** | 0.404 ** |
| Updated | MTCI | Biomass×HI | Narrow | 0.147 * | 0.363 ** | 0.316 ** | 0.44 ** |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Z.; Azzari, G.; Burke, M.; Aston, S.; Lobell, D.B. Mapping Smallholder Yield Heterogeneity at Multiple Scales in Eastern Africa. Remote Sens. 2017, 9, 931. https://doi.org/10.3390/rs9090931
Jin Z, Azzari G, Burke M, Aston S, Lobell DB. Mapping Smallholder Yield Heterogeneity at Multiple Scales in Eastern Africa. Remote Sensing. 2017; 9(9):931. https://doi.org/10.3390/rs9090931
Chicago/Turabian StyleJin, Zhenong, George Azzari, Marshall Burke, Stephen Aston, and David B. Lobell. 2017. "Mapping Smallholder Yield Heterogeneity at Multiple Scales in Eastern Africa" Remote Sensing 9, no. 9: 931. https://doi.org/10.3390/rs9090931
APA StyleJin, Z., Azzari, G., Burke, M., Aston, S., & Lobell, D. B. (2017). Mapping Smallholder Yield Heterogeneity at Multiple Scales in Eastern Africa. Remote Sensing, 9(9), 931. https://doi.org/10.3390/rs9090931