The Impact of Mapping Error on the Performance of Upscaling Agricultural Maps
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Areas and Materials
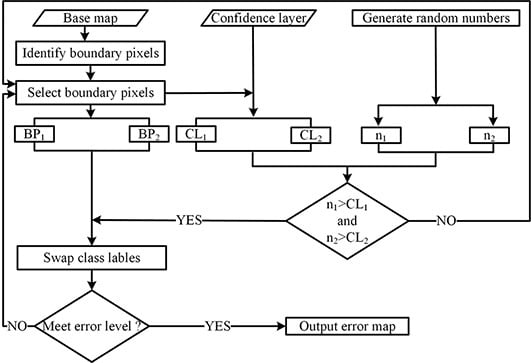
2.2. Error Simulation
2.3. Upscaling Method
2.4. Assessment of MRB
2.5. Landscape Metrics
3. Results
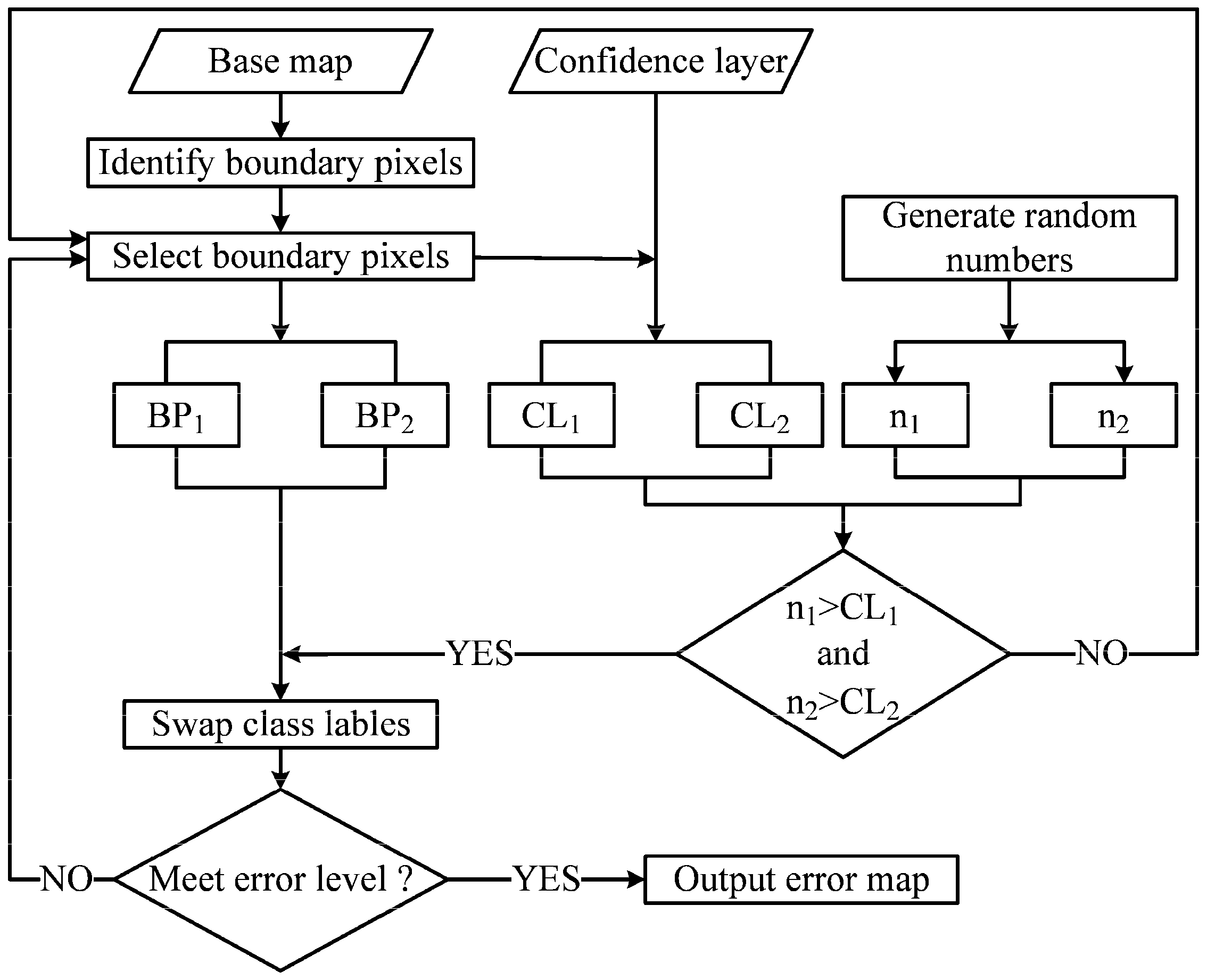
3.1. Error Simulation
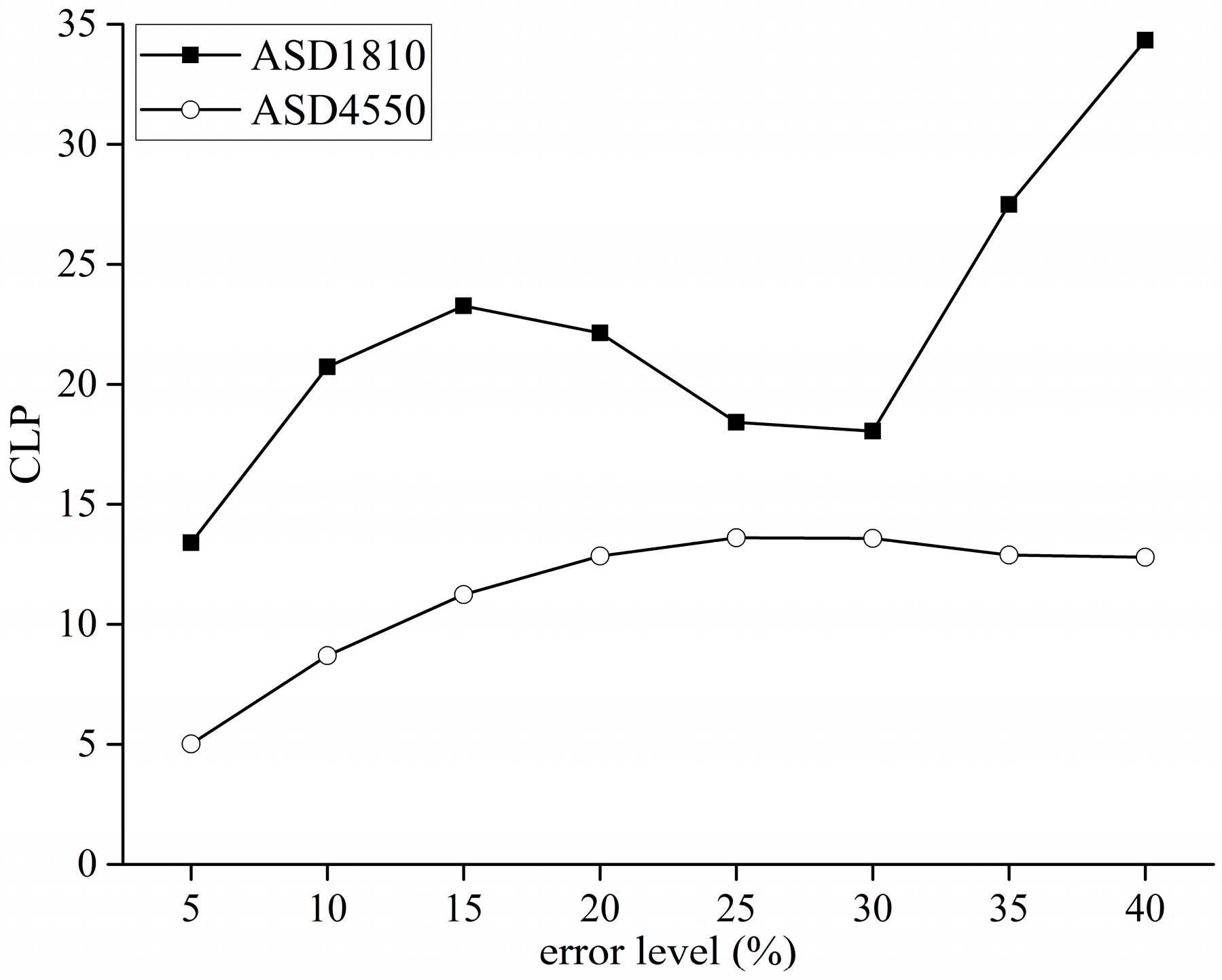
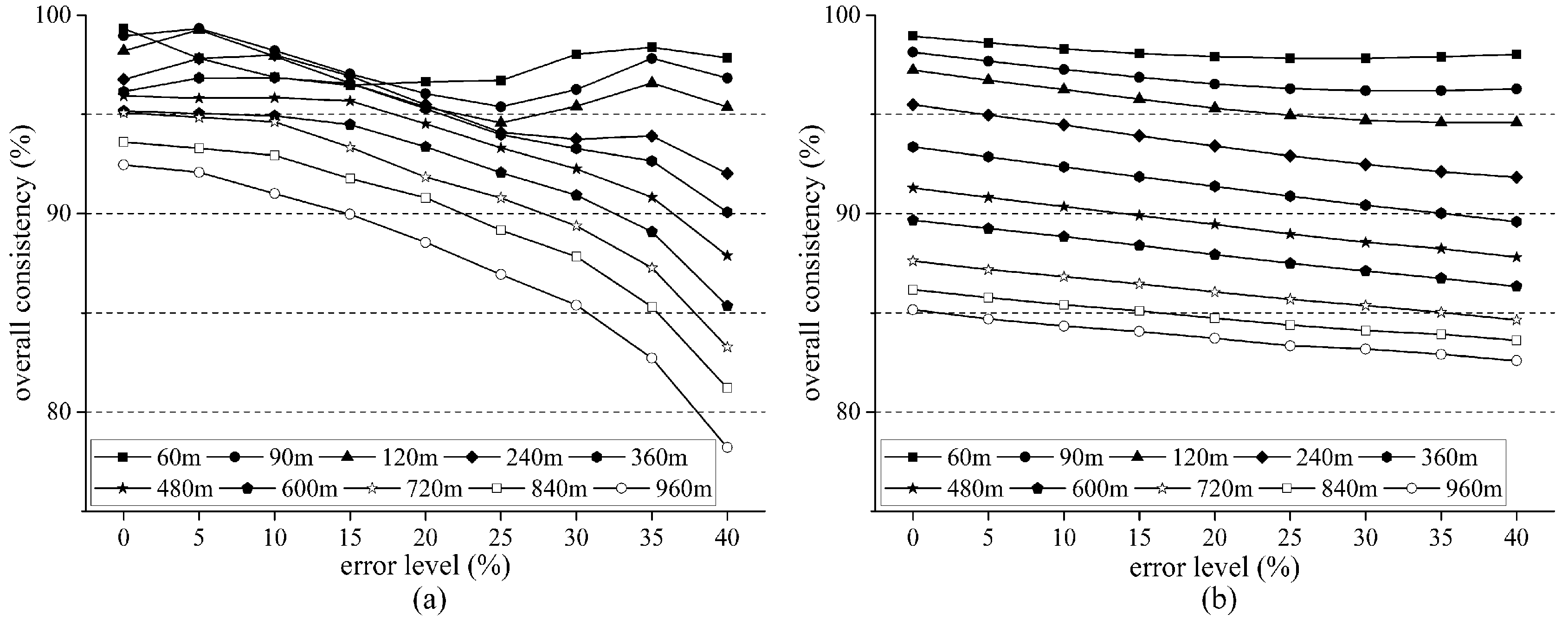
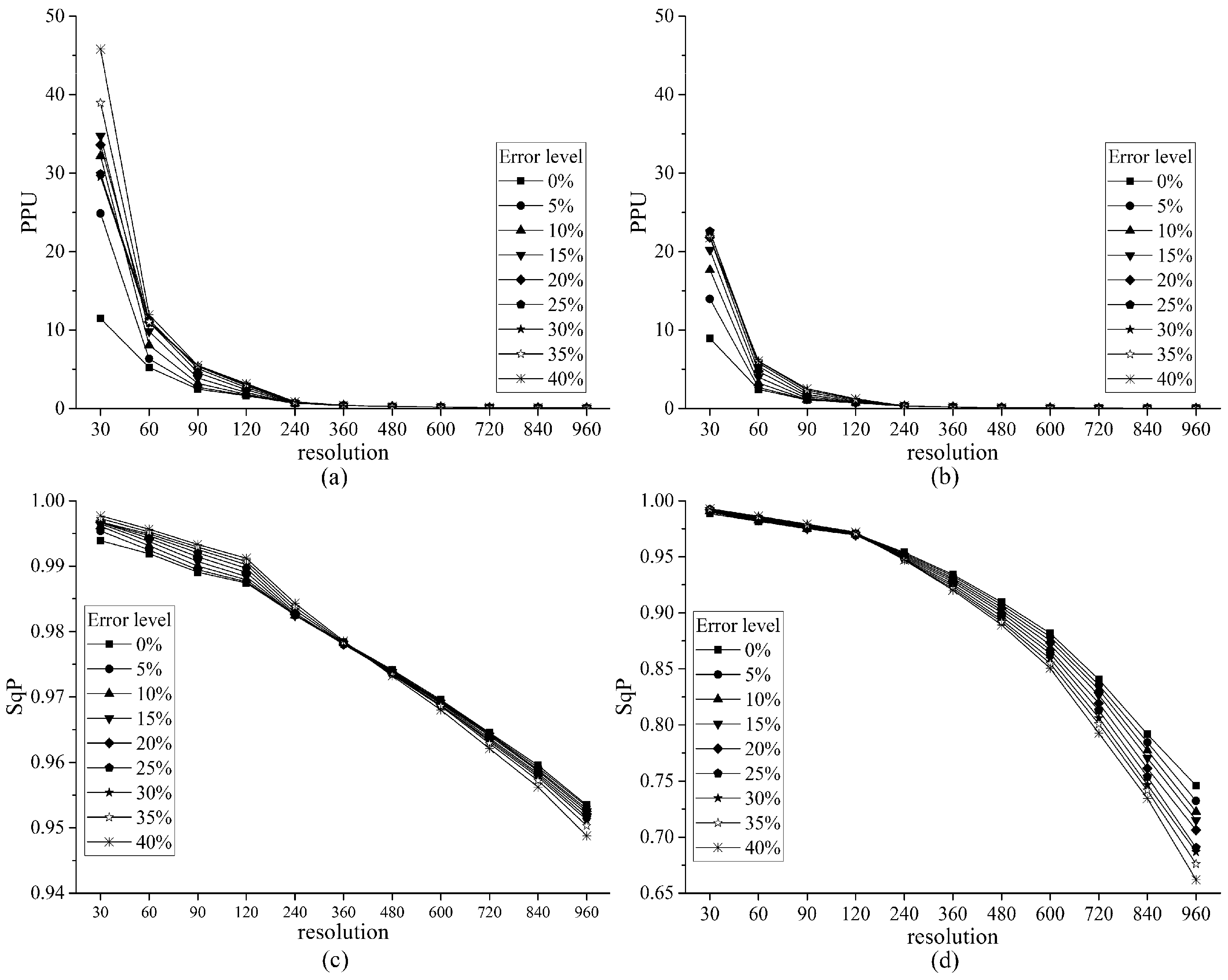
3.2. Impacts of Upscaling and Map Error on PE and OC
3.3. Landscape Changes Based on Different Error Level
4. Discussion
4.1. Error Simulation Issues
4.2. Impacts of Upscaling and Map Error on PE and OC
4.3. Comparison of Landscape Changes Based on Different Error Level
4.4. Comparison of the Performance Based on Different Study Areas
4.5. Limitations and Future Work
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alexander, P.; Prestele, R.; Verburg, P.H.; Arneth, A.; Baranzelli, C.; Batista e Silva, F.; Brown, C.; Butler, A.; Calvin, K.; Dendoncker, N.; et al. Assessing uncertainties in land cover projections. Glob. Chang. Biol. 2017, 23, 767–781. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, R.; Herold, M.; Verburg, P.H.; Clevers, J.G.P.W.; Eberle, J. Gross changes in reconstructions of historic land cover/use for europe between 1900 and 2010. Glob. Chang. Biol. 2015, 21, 299–313. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Jiang, Y.; Chen, Y.; Stein, A.; Jiang, D.; Jia, Y. Designing an experiment to investigate subpixel mapping as an alternative method to obtain land use/land cover maps. Remote Sens. 2016, 8, 360. [Google Scholar] [CrossRef]
- Grafius, D.R.; Corstanje, R.; Warren, P.H.; Evans, K.L.; Hancock, S.; Harris, J.A. The impact of land use/land cover scale on modelling urban ecosystem services. Landsc. Ecol. 2016, 31, 1509–1522. [Google Scholar] [CrossRef]
- Kitron, U.; Clennon, J.A.; Cecere, M.C.; Gürtler, R.E.; King, C.H.; Vazquez-Prokopec, G. Upscale or downscale: Applications of fine scale remotely sensed data to chagas disease in argentina and schistosomiasis in kenya. Geospat. Health 2006, 1, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Poulter, B.; MacBean, N.; Hartley, A.; Khlystova, I.; Arino, O.; Betts, R.; Bontemps, S.; Boettcher, M.; Brockmann, C.; Defourny, P.; et al. Plant functional type classification for earth system models: Results from the european space agency’s land cover climate change initiative. Geosci. Model. Dev. 2015, 8, 2315–2328. [Google Scholar] [CrossRef]
- Dong, M.; Bryan, B.A.; Connor, J.D.; Nolan, M.; Gao, L. Land use mapping error introduces strongly-localised, scale-dependent uncertainty into land use and ecosystem services modelling. Ecosyst. Serv. 2015, 15, 63–74. [Google Scholar] [CrossRef]
- Chen, Y.; Song, X.; Wang, S.; Huang, J.; Mansaray, L.R. Impacts of spatial heterogeneity on crop area mapping in canada using modis data. ISPRS J. Photogramm. Remote Sens. 2016, 119, 451–461. [Google Scholar] [CrossRef]
- Feddema, J.J.; Oleson, K.W.; Bonan, G.B.; Mearns, L.O.; Buja, L.E.; Meehl, G.A.; Washington, W.M. The importance of land-cover change in simulating future climates. Science 2005, 310, 1674–1678. [Google Scholar] [CrossRef] [PubMed]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Feng, M.; Jiang, H.; Wang, J.; Zhu, Y.; Liu, Y. Assessing consistency of five global land cover data sets in china. Remote Sens. 2014, 6, 8739–8759. [Google Scholar] [CrossRef]
- Ju, J.; Gopal, S.; Kolaczyk, E.D. On the choice of spatial and categorical scale in remote sensing land cover classification. Remote Sens. Environ. 2005, 96, 62–77. [Google Scholar] [CrossRef]
- Grekousis, G.; Mountrakis, G.; Kavouras, M. An overview of 21 global and 43 regional land-cover mapping products. Int. J. Remote Sens. 2015, 36, 5309–5335. [Google Scholar] [CrossRef]
- Yu, L.; Wang, J.; Li, X.; Li, C.; Zhao, Y.; Gong, P. A multi-resolution global land cover dataset through multisource data aggregation. Sci. China Earth Sci. 2014, 57, 2317–2329. [Google Scholar] [CrossRef]
- Congalton, R.; Gu, J.; Yadav, K.; Thenkabail, P.; Ozdogan, M. Global land cover mapping: A review and uncertainty analysis. Remote Sens. 2014, 6, 12070–12093. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Pardo-Igúzquiza, E. A new geostatistical solution to remote sensing image downscaling. IEEE Trans. Geosci. Remote Sens. 2016, 54, 386–396. [Google Scholar] [CrossRef]
- Wu, J. Effects of changing scale on landscape pattern analysis: Scaling relations. Landsc. Ecol. 2004, 19, 125–138. [Google Scholar] [CrossRef]
- Yang, W.; Merchant, J.W. Impacts of upscaling techniques on land cover representation in nebraska, U.S.A. Geocarto Int. 1997, 12, 27–39. [Google Scholar] [CrossRef]
- Raj, R.; Hamm, N.A.S.; Kant, Y. Analysing the effect of different aggregation approaches on remotely sensed data. Int. J. Remote Sens. 2013, 34, 4900–4916. [Google Scholar] [CrossRef]
- Bartholomé, E.; Belward, A.S. Glc2000: A new approach to global land cover mapping from earth observation data. Int. J. Remote Sens. 2005, 26, 1959–1977. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. Modis collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Y.; Li, C.; Yu, L.; Liu, D.; Gong, P. Mapping global land cover in 2001 and 2010 with spatial-temporal consistency at 250 m resolution. ISPRS J. Photogramm. Remote Sens. 2015, 103, 38–47. [Google Scholar] [CrossRef]
- Gardner, R.H.; Lookingbill, T.R.; Townsend, P.A.; Ferrari, J. A new approach for rescaling land cover data. Landsc. Ecol. 2008, 23, 513–526. [Google Scholar] [CrossRef]
- Stein, A.; Riley, J.; Halberg, N. Issues of scale for environmental indicators. Agric. Ecosyst. Environ. 2001, 87, 215–232. [Google Scholar] [CrossRef]
- Tang, Y.; Atkinson, P.M.; Zhang, J. Downscaling remotely sensed imagery using area-to-point cokriging and multiple-point geostatistical simulation. ISPRS J. Photogramm. Remote Sens. 2015, 101, 174–185. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Ramirez-Villegas, J.; Jarvis, A. Downscaling global circulation model outputs: The delta method decision and policy analysis working paper no. 1. Policy Anal. 2010, 1, 1–18. [Google Scholar]
- Wilby, R.L.; Wigley, T.M.L. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr. 1997, 21, 530–548. [Google Scholar] [CrossRef]
- Lechner, A.M.; Reinke, K.J.; Wang, Y.; Bastin, L. Interactions between landcover pattern and geospatial processing methods: Effects on landscape metrics and classification accuracy. Ecol. Complex. 2013, 15, 71–82. [Google Scholar] [CrossRef]
- Moody, A.; Woodcock, C.E. Scale-dependent errors in the estimation of land-cover proportions. Implications for global land-cover datasets. Photogramm. Eng. Remote Sens. 1994, 60, 585–594. [Google Scholar]
- He, H.S.; Ventura, S.J.; Mladenoff, D.J. Effects of spatial aggregation approaches on classified satellite imagery. Int. J. Geogr. Inf. Sci. 2002, 16, 93–109. [Google Scholar] [CrossRef]
- Saura, S. Effects of remote sensor spatial resolution and data aggregation on selected fragmentation indices. Landsc. Ecol. 2004, 19, 197–209. [Google Scholar] [CrossRef]
- Moody, A.; Woodcock, C.E. The influence of scale and the spatial characteristics of landscapes on land-cover mapping using remote sensing. Landsc. Ecol. 1995, 10, 363–379. [Google Scholar] [CrossRef]
- Hlavka, C.A.; Dungan, J.L. Areal estimates of fragmented land cover: Effects of pixel size and model-based corrections. Int. J. Remote Sens. 2002, 23, 711–724. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Fritz, S.; See, L.; Rembold, F. Comparison of global and regional land cover maps with statistical information for the agricultural domain in Africa. Int. J. Remote Sens. 2010, 31, 2237–2256. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with landsat tm and etm+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Wickham, J.; Stehman, S.V.; Gass, L.; Dewitz, J.A.; Sorenson, D.G.; Granneman, B.J.; Poss, R.V.; Baer, L.A. Thematic accuracy assessment of the 2011 national land cover database (nlcd). Remote Sens. Environ. 2017, 191, 328–341. [Google Scholar] [CrossRef]
- Larsen, A.E. Agricultural landscape simplification does not consistently drive insecticide use. Proc. Natl. Acad. Sci. USA 2013, 110, 15330–15335. [Google Scholar] [CrossRef] [PubMed]
- USDA. National Agricultural Statistics Service Frequently Asked Questions Related to Quick Stats County Data. Available online: https://www.nass.usda.gov/Data_and_Statistics/County_Data_Files/Frequently_Asked_Questions.htm (accessed on 17 May 2017).
- Boryan, C.; Yang, Z.; Mueller, R.; Craig, M. Monitoring us agriculture: The US department of agriculture, national agricultural statistics service, cropland data layer program. Geocarto Int. 2011, 26, 341–358. [Google Scholar] [CrossRef]
- Wright, C.K.; Wimberly, M.C. Recent land use change in the western corn belt threatens grasslands and wetlands. Proc. Natl. Acad. Sci. USA 2013, 110, 4134–4139. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Anderson, M.C.; Zhang, X.; Yang, Z.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of landsat and modis imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef]
- Gonzales, D.S.; Searcy, S.W. Gis-based allocation of herbaceous biomass in biorefineries and depots. Biomass Bioenergy 2017, 97, 1–10. [Google Scholar] [CrossRef]
- Congalton, R.; Brennan, M. Error in remotely sensed data analysis: Evaluation and reduction. In Proceedings of the Sixty Fifth Annual Meeting of the American Society of Photogrammetry and Remote Sensing, Portland, OR, USA, 17–21 May 1999; Volume 729. [Google Scholar]
- Congalton, R.G.; Green, K. A practical look at the sources of confusion in error matrix generation. Photogramm. Eng. Remote Sens. 1993, 59, 641–644. [Google Scholar]
- Lunetta, R.S.; Congalton, R.G.; Fenstermaker, L.K.; Jensen, J.R.; McGwire, K.C.; Tinney, L.R. Remote sensing and geographic information system data integration: Error sources and research issues. Photogramm. Eng. Remote Sens. 1991, 57, 677–687. [Google Scholar]
- Crosetto, M.; Moreno Ruiz, J.A.; Crippa, B. Uncertainty propagation in models driven by remotely sensed data. Remote Sens. Environ. 2001, 76, 373–385. [Google Scholar] [CrossRef]
- Ligmann-Zielinska, A.; Jankowski, P. Spatially-explicit integrated uncertainty and sensitivity analysis of criteria weights in multicriteria land suitability evaluation. Environ. Model. Softw. 2014, 57, 235–247. [Google Scholar] [CrossRef]
- Matott, L.S.; Babendreier, J.E.; Purucker, S.T. Evaluating uncertainty in integrated environmental models: A review of concepts and tools. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Congalton, R.G. Using spatial autocorrelation analysis to explore the errors in maps generated from remotely sensed data. Photogramm. Eng. Remote Sens. 1988, 54, 587–592. [Google Scholar]
- Riitters, K.H.; O’Neill, R.V.; Hunsaker, C.T.; Wickham, J.D.; Yankee, D.H.; Timmins, S.P.; Jones, K.B.; Jackson, B.L. A factor analysis of landscape pattern and structure metrics. Landsc. Ecol. 1995, 10, 23–39. [Google Scholar] [CrossRef]
- Frohn, R.C. Remote Sensing for Landscape Ecology: New Metric Indicators for Monitoring, Modeling, and Assessment of Ecosystems; Lewis Publishers, CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Frohn, R.C.; Hao, Y. Landscape metric performance in analyzing two decades of deforestation in the amazon basin of rondonia, brazil. Remote Sens. Environ. 2006, 100, 237–251. [Google Scholar] [CrossRef]
- O’Neill, R.V.; Jones, K.B.; Riitters, K.H.; Wickham, J.D.; Goodman, I.A. Landscape Monitoring and Assessment Research Plan; Environmental Protection Agency: Washington, DC, USA, 1994; Volume 620.
- O’Neill, R.V.; Krumme, J.R.R.H.; Gardner, G.; Sugihara, B.; Jackson, D.L.; DeAngelist, B.T.; Milne, M.G.; Turner, B.; Zygmunt, S.W.; Christensen, V.H.; et al. Indicesin landscape pattern. Landsc. Ecol. 1988, 1, 153–162. [Google Scholar] [CrossRef]
- Turner, M.G.; O’Neill, R.V.; Gardner, R.H.; Milne, B.T. Effects of changing spatial scale on the analysis of landscape pattern. Landsc. Ecol. 1989, 3, 153–162. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Ene, E. Fragstats v4: Spatial Pattern Analysis Program for Categorical and Continuous Maps; University of Massachusetts: Amherst, MA, USA; Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 10 March 2017).
- Oguro, Y.; Suga, Y.; Takeuchi, S.; Ogawa, M.; Konishi, T.; Tsuchiya, K. Comparison of sar and optical sensor data for monitoring of rice plant around hiroshima. Adv. Space Res. 2001, 28, 195–200. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, J.; Zhu, X.; Pan, Y.; Liu, H. A highly efficient temporal-spatial probability synthesized model from multi-temporal remote sensing for paddy rice identification. Eur. J. Remote Sens. 2017, 50, 98–110. [Google Scholar] [CrossRef]
- Shao, Y.; Lunetta, R.S. Comparison of support vector machine, neural network, and cart algorithms for the land-cover classification using limited training data points. ISPRS J. Photogramm. Remote Sens. 2012, 70, 78–87. [Google Scholar] [CrossRef]
- Congalton, R.G. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: New York, NY, USA, 2008. [Google Scholar]
- Fortin, M.-J.; James, P.M.A.; MacKenzie, A.; Melles, S.J.; Rayfield, B. Spatial statistics, spatial regression, and graph theory in ecology. Spat. Stat. 2012, 1, 100–109. [Google Scholar] [CrossRef]
- Cockx, K.; Van de Voorde, T.; Canters, F. Quantifying uncertainty in remote sensing-based urban land-use mapping. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 154–166. [Google Scholar] [CrossRef]
- Richards, J.A. Classifier performance and map accuracy. Remote Sens. Environ. 1996, 57, 161–166. [Google Scholar] [CrossRef]
- Momeni, R.; Aplin, P.; Boyd, D. Mapping complex urban land cover from spaceborne imagery: The influence of spatial resolution, spectral band set and classification approach. Remote Sens. 2016, 8, 88. [Google Scholar] [CrossRef]
- Löw, F.; Duveiller, G. Defining the spatial resolution requirements for crop identification using optical remote sensing. Remote Sens. 2014, 6, 9034–9063. [Google Scholar] [CrossRef]




| ASD | TA (ha) | NP | Mean, Median, and Standard Deviation of Parcel Size (ha) | LPI | AI | Dominance | PPU | SqP | |
|---|---|---|---|---|---|---|---|---|---|
| Study Area | 1810 | 1,075,972.68 | 123,233 | 8.73, 0.18, 1102.49 | 35.93 | 90.55 | 0.3568 | 11.45 | 0.99 |
| 4550 | 1,253,235.96 | 30,502 | 11.17, 0.09, 3273.80 | 87.48 | 95.28 | 0.7179 | 8.95 | 0.989 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Congalton, R.G.; Grybas, H.; Pan, Y. The Impact of Mapping Error on the Performance of Upscaling Agricultural Maps. Remote Sens. 2017, 9, 901. https://doi.org/10.3390/rs9090901
Sun P, Congalton RG, Grybas H, Pan Y. The Impact of Mapping Error on the Performance of Upscaling Agricultural Maps. Remote Sensing. 2017; 9(9):901. https://doi.org/10.3390/rs9090901
Chicago/Turabian StyleSun, Peijun, Russell G. Congalton, Heather Grybas, and Yaozhong Pan. 2017. "The Impact of Mapping Error on the Performance of Upscaling Agricultural Maps" Remote Sensing 9, no. 9: 901. https://doi.org/10.3390/rs9090901