First Assessment of Sentinel-1A Data for Surface Soil Moisture Estimations Using a Coupled Water Cloud Model and Advanced Integral Equation Model over the Tibetan Plateau
Abstract
:1. Introduction
2. Study Area and Data
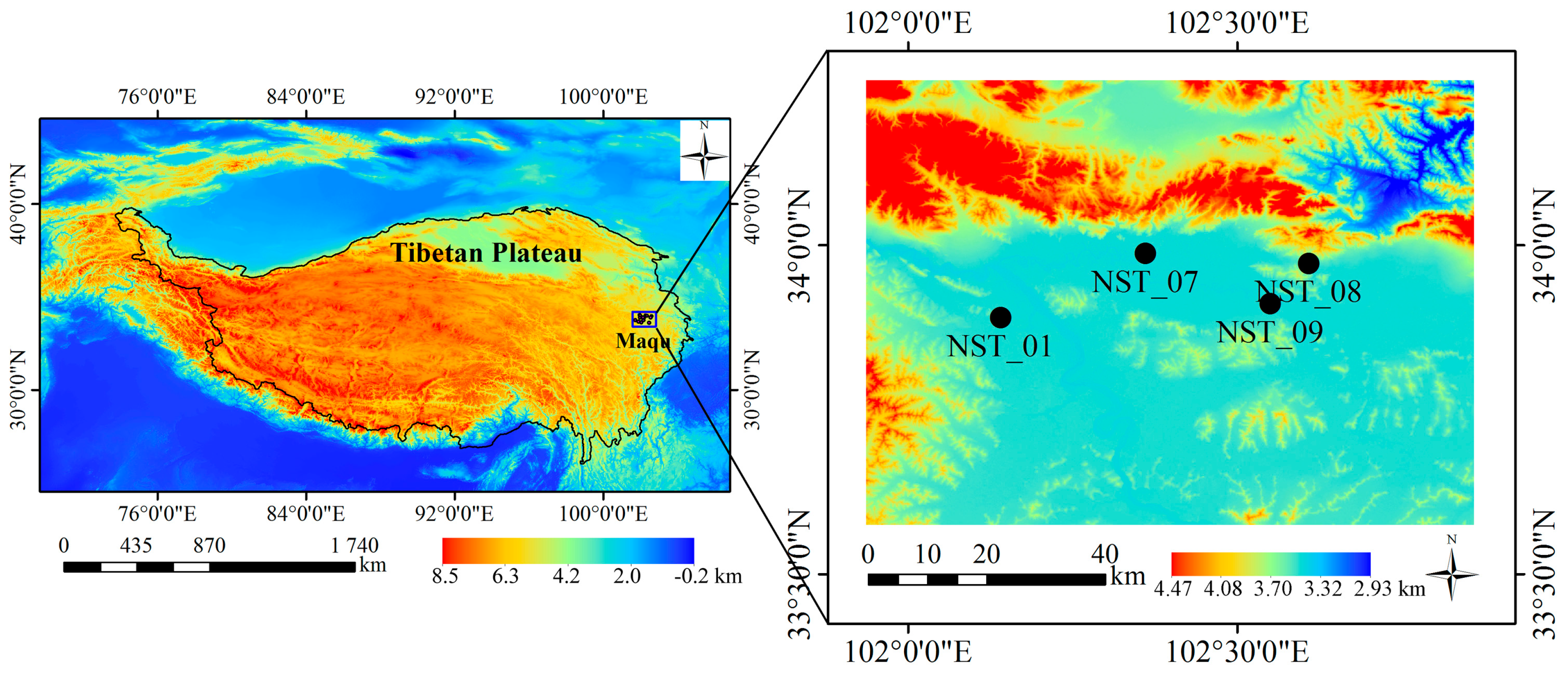
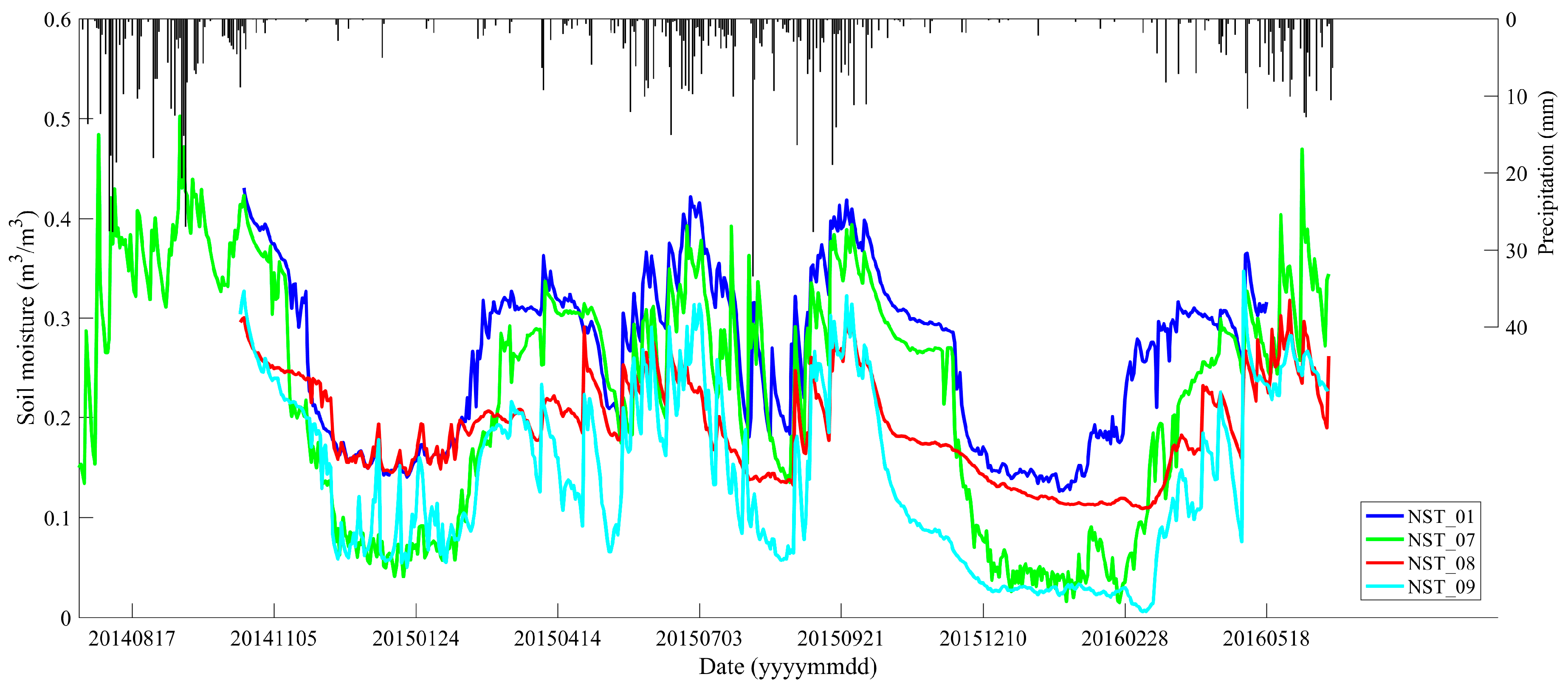
2.1. Study Area and In Situ Measurements
2.2. Sentinel-1A Data
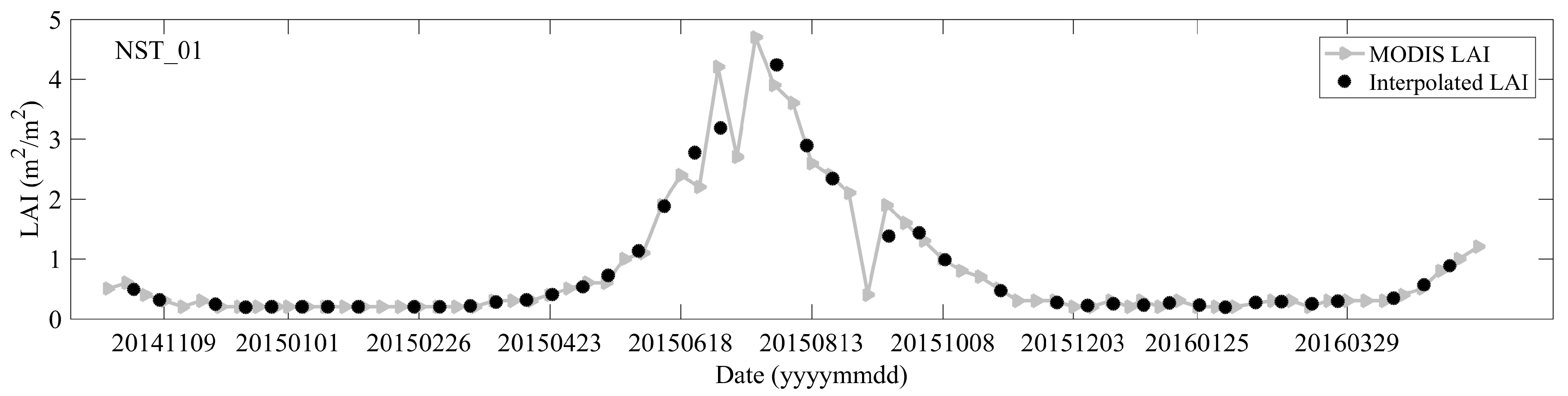
2.3. MODIS Data
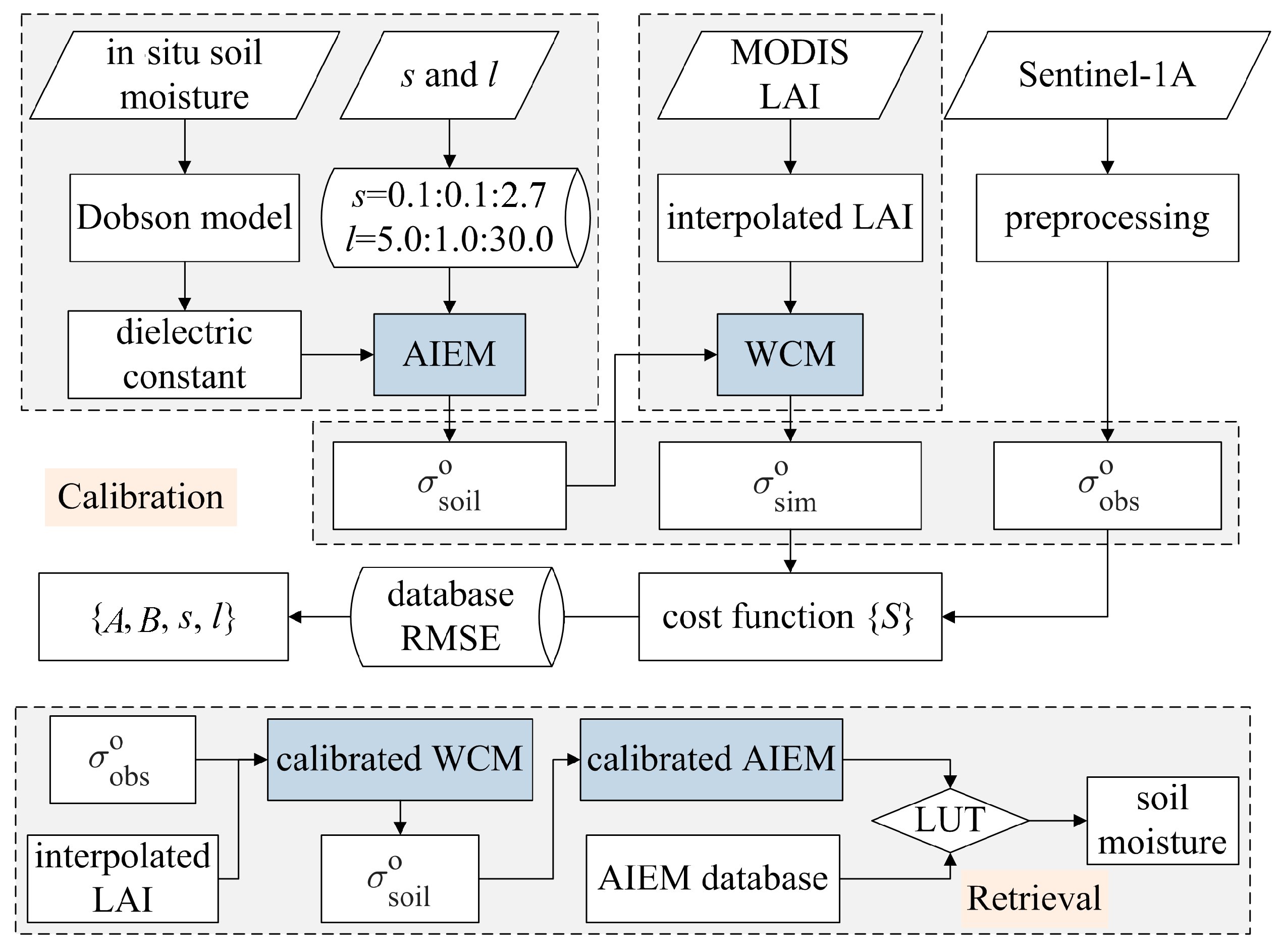
3. Methodology
3.1. Vegetation Backscattering Modelling
3.2. Bare Soil Backscattering Modelling
3.3. Model Calibration and Soil Moisture Estimation
4. Results
4.1. Calibration for the Coupled Model
4.2. Soil Moisture Estimation from the Sentinel-1A Data
5. Discussion
5.1 Impacts of Effective Roughness Parameters
5.2 Impacts of Uncertaines in the LAI on the Soil Moisture Retrieval
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| No. | Date | UTC Time | Incidence (°) | Orbit | Polar | Absolute Orbit |
|---|---|---|---|---|---|---|
| 1 | 2014/10/26 | 23:11:17–23:11:42 | 30.99–46.29 | descending | VV | 3007 |
| 2 | 2014/10/26 | 23:11:42–23:12:07 | 31.16–46.42 | descending | VV | 3007 |
| 3 | 2014/11/07 | 11:09:21–11:09:46 | 31.13–46.41 | ascending | VV | 3175 |
| 4 | 2014/12/01 | 11:09:21–11:09:46 | 31.13–46.41 | ascending | VV | 3525 |
| 5 | 2015/03/07 | 11:09:19–11:09:44 | 31.13–46.41 | ascending | VV | 4925 |
| 6 | 2015/03/19 | 23:11:14–23:11:39 | 30.99–46.29 | descending | VV | 5107 |
| 7 | 2015/03/19 | 23:11:39–23:12:04 | 31.15–46.41 | descending | VV | 5107 |
| 8 | 2015/03/31 | 11:09:19–11:09:44 | 31.13–46.41 | ascending | VV | 5275 |
| 9 | 2015/04/12 | 23:11:15–23:11:40 | 30.99–46.29 | descending | VV | 5457 |
| 10 | 2015/04/12 | 23:11:40–23:12:05 | 31.15–46.41 | descending | VV | 5457 |
| 11 | 2015/04/24 | 11:09:20–11:09:45 | 31.13–46.41 | ascending | VV | 5625 |
| 12 | 2015/05/06 | 23:11:16–23:11:41 | 31.00–46.29 | descending | VV | 5807 |
| 13 | 2015/05/06 | 23:11:41–23:12:06 | 31.15–46.41 | descending | VV | 5807 |
| 14 | 2015/05/18 | 11:09:22–11:09:47 | 31.13–46.41 | ascending | VV | 5975 |
| 15 | 2015/05/30 | 23:11:24–23:11:49 | 31.03–46.41 | descending | VV | 6157 |
| 16 | 2015/05/30 | 23:11:49–23:12:14 | 31.16–46.51 | descending | VV | 6157 |
| 17 | 2015/06/11 | 11:09:23–11:09:48 | 31.13–46.41 | ascending | VV | 6325 |
| 18 | 2015/06/23 | 23:11:31–23:11:56 | 31.07–46.44 | descending | VV | 6507 |
| 19 | 2015/07/05 | 11:09:10–11:09:35 | 31.14–46.43 | ascending | VV | 6675 |
| 20 | 2015/07/29 | 11:09:11–11:09:36 | 31.15–46.44 | ascending | VV | 7027 |
| 21 | 2015/08/10 | 23:11:33–23:11:55 | 31.22–46.40 | descending | VV | 7207 |
| 22 | 2015/08/22 | 11:09:13–11:09:38 | 31.14–46.43 | ascending | VV | 7375 |
| 23 | 2015/09/15 | 11:09:13–11:09:38 | 31.14–46.43 | ascending | VV | 7725 |
| 24 | 2015/09/27 | 23:11:35–23:12:00 | 31.07–46.44 | descending | VV | 7907 |
| 25 | 2015/10/09 | 11:09:14–11:09:39 | 31.14–46.43 | ascending | VV | 8075 |
| 26 | 2015/11/02 | 11:09:14–11:09:39 | 31.14–46.43 | ascending | VV,VH | 8425 |
| 27 | 2015/11/26 | 11:09:08–11:09:33 | 31.19–46.45 | ascending | VV | 8775 |
| 28 | 2015/11/26 | 11:09:33–11:09:58 | 31.11–46.39 | ascending | VV | 8775 |
| 29 | 2016/03/01 | 11:09:06–11:09:31 | 31.19–46.45 | ascending | VV | 10,175 |
| 30 | 2016/03/01 | 11:09:31–11:09:56 | 31.11–46.39 | ascending | VV | 10,175 |
| 31 | 2016/03/13 | 23:11:27–23:11:52 | 31.04–46.40 | descending | VV | 10,357 |
| 32 | 2016/03/13 | 23:11:52–23:12:17 | 31.18–46.51 | descending | VV | 10,357 |
| 33 | 2016/03/25 | 11:09:06–11:09:31 | 31.19–46.45 | ascending | VV | 10,525 |
| 34 | 2016/03/25 | 11:09:31–11:09:56 | 31.11–46.39 | ascending | VV | 10,525 |
| 35 | 2016/04/18 | 11:09:07–11:09:32 | 31.19–46.45 | ascending | VV | 10,875 |
| 36 | 2016/04/18 | 11:09:32–11:09:57 | 31.12–46.39 | ascending | VV | 10,875 |
| 37 | 2016/04/30 | 23:11:28–23:11:53 | 31.04–46.40 | descending | VV | 11,057 |
| 38 | 2016/05/12 | 11:09:08–11:09:33 | 31.19–46.45 | ascending | VV | 11,225 |
| 39 | 2016/05/12 | 11:09:33–11:09:58 | 31.11–46.39 | ascending | VV | 11,225 |
Appendix B
References
- Kornelsen, K.C.; Coulibaly, P. Advances in soil moisture retrieval from synthetic aperture radar and hydrological applications. J. Hydrol. 2013, 476, 460–489. [Google Scholar] [CrossRef]
- Su, Z.; Wen, J.; Dente, L.; van der Velde, R.; Wang, L.; Ma, Y.; Yang, K.; Hu, Z. The Tibetan Plateau observatory of plateau scale soil moisture and soil temperature (Tibet-Obs) for quantifying uncertainties in coarse resolution satellite and model products. Hydrol. Earth Syst. Sci. 2011, 15, 2303–2316. [Google Scholar] [CrossRef]
- Zhong, L.; Ma, Y.; Salama, M.S.; Su, Z. Assessment of vegetation and their response to variations in precipitation and temperature in the Tibetan Plateau. Clim. Chang. 2010, 103, 519–535. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Barrett, B. Surface soil moisture retrievals from remote sensing: Current status products & future trends. Phys. Chem. Earth 2015, 83, 36–56. [Google Scholar]
- Barrett, B.W.; Dwyer, E.; Whelan, P. Soil moisture retrieval from active spaceborne microwave observations: An evaluation of current techniques. Remote Sens. 2009, 1, 210–242. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Scipal, K.; Parinussa, R.M.; Liu, Y.Y.; Wagner, W.; de Jeu, R.A.M.; Naeimi, V. Error characterization of global active and passive microwave soil moisture datasets. Hydrol. Earth Syst. Sci. 2010, 14, 2605–2616. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.P.; Ducharne, A.; Kerr, Y.H.; Wagner, W.; De Lannoy, G.; Reichle, R.; Al Bitar, A.; Dorigo, W.; Richaume, P.; et al. Global-scale comparison of passive (SMOS) and active (ASCAT) satellites based microwave soil moisture retrieval with soil moisture simulations (MERRA-Land). Remote Sens. Environ. 2014, 152, 614–626. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Dubois, P.C.; van Zyl, J.J.; Engman, E.T. Measuring soil moisture with imaging radar. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimating of bare surface soil moisture and surface roughness parameters using L-band SAR images data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Fung, A.K. Microwave Scattering and Emission Models and Their Applications; Artech House: Boston, MA, USA, 1994. [Google Scholar]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Wu, T.D.; Chen, K.S.; Shi, J.C.; Fung, A.K. A transition model for the reflection coefficients in surface scattering. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2040–2050. [Google Scholar]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.C.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Chen, K.S. Simulation and SMAP observation of sun-glint over the land surface at the L-band. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2589–2604. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, K.S.; Liu, Y.; Zeng, J.; Xu, P.; Li, Z.L. On angular features of radar bistatic scattering from rough surface. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3223–3235. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Graham, A.J.; Harris, R. Extracting biophysical parameters from remotely sensed radar data: A review of the water cloud model. Prog. Phys. Geogr. 2003, 27, 217–229. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Sarabandi, K.; McDonald, K.; Whitt, M.; Dobson, M.C. Michigan microwave canopy scattering model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Bracaglia, M.; Ferrazzoli, P.; Guerriero, L. A fully polarimetric multiple scattering model for crops. Remote Sens. Environ. 1995, 54, 170–179. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Guerriero, L. Emissivity of vegetation: Theory and computational aspects. J. Electromagn. Waves Appl. 1996, 10, 609–628. [Google Scholar] [CrossRef]
- He, B.; Xing, M.; Bai, X. A synergistic methodology for soil moisture estimation in an alpine prairie using radar and optical satellite data. Remote Sens. 2014, 6, 10966–10985. [Google Scholar] [CrossRef]
- Wang, S.G.; Li, X.; Han, X.J.; Jin, R. Estimation of surface soil moisture and roughness from multi-angular ASAR imagery in the watershed allied telemetry experimental research (WATER). Hydrol. Earth Syst. Sci. 2011, 15, 1415–1426. [Google Scholar] [CrossRef]
- Joseph, A.T.; van der Velde, R.; O’Neill, P.E.; Lang, R.; Gish, T. Effects of corn on C- and L-band radar backscatter: A correction method for soil moisture retrieval. Remote Sens. Environ. 2010, 114, 2417–2430. [Google Scholar] [CrossRef]
- Lievens, H.; Verhoest, N.E.C. On the retrieval of soil moisture in wheat fields from L-band SAR based on water cloud modeling, the IEM, and effective roughness parameters. IEEE Geosci. Remote Sens. Lett. 2011, 8, 740–744. [Google Scholar] [CrossRef]
- Quan, X.; He, B.; Li, X. A Bayesian network-based method to alleviate the ill-posed inverse problem: A case study on leaf area index and canopy water content retrieval. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6507–6517. [Google Scholar] [CrossRef]
- Wen, J.; Su, Z. A time series based method for estimating relative soil moisture with ERS wind scatterometer data. Geophys. Res. Lett. 2003, 30, 1397. [Google Scholar] [CrossRef]
- Van der Velde, R.; Su, Z. Dynamics in land surface conditions on the Tibetan Plateau observed by Advanced Synthetic Aperture Radar (ASAR). Hydrol. Sci. J. 2009, 54, 1079–1093. [Google Scholar] [CrossRef]
- Van der Velde, R.; Su, Z.; Ma, Y. Impact of soil moisture dynamics on ASAR σ° signatures and its spatial variability observed over the Tibetan Plateau. Sensors 2008, 8, 5479–5491. [Google Scholar] [CrossRef] [PubMed]
- Van der Velde, R.; Su, Z.; van Oevelen, P.; Wen, J.; Ma, Y.; Salama, M.S. Soil moisture mapping over the central part of the Tibetan Plateau using a series of ASAR WS images. Remote Sens. Environ. 2012, 120, 175–187. [Google Scholar] [CrossRef]
- Bai, X.; He, B.; Xing, M.; Li, X. Method for soil moisture retrieval in arid prairie using TerraSAR-X data. J. Appl. Remote Sens. 2015, 9, 096062. [Google Scholar] [CrossRef]
- Bai, X.; He, B. Potential of Dubois model for soil moisture retrieval in prairie areas using SAR and optical data. Int. J. Remote Sens. 2015, 36, 5737–5753. [Google Scholar] [CrossRef]
- Bai, X.; He, B.; Li, X. Optimum surface roughness to parameterize advanced integral equation model for soil moisture retrieval in prairie area using Radarsat-2 data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2437–2449. [Google Scholar] [CrossRef]
- Gherboudj, I.; Magagi, R.; Berg, A.A.; Toth, B. Soil moisture retrieval over agricultural fields from multi-polarized and multi-angular Radarsat-2 SAR data. Remote Sens. Environ. 2011, 115, 33–43. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Sentinel-1 User Handbook. Available online: https://earth.esa.int/documents/247904/685163/Sentinel-1_User_Handbook (accessed on 1 September 2013).
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Budzynska, M.; Tomaszewska, M.; Malinska, A.; Gatkowska, M.; Bartold, M.; Malek, I. Assessment of carbon flux and soil moisture in wetlands applying Sentinel-1 data. Remote Sens. 2016, 8, 756. [Google Scholar] [CrossRef]
- Zeng, Y.; Su, Z.; van der Velde, R.; Wang, L.; Xu, K.; Wang, X.; Wen, J. Blending satellite observed, model simulated, and in situ measured soil moisture over Tibetan Plateau. Remote Sens. 2016, 8, 268. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Chen, Q.; Bi, H. Method for soil moisture and surface temperature estimation in the Tibetan Plateau using spaceborne radiometer observations. IEEE Geosci. Remote Sens. Lett. 2015, 12, 97–101. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Chen, Q.; Bi, H.; Qiu, J.; Zou, P. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Qin, J.; Zhao, L.; Tang, W.; Han, M. Evaluation of AMSR-E retrievals and GLDAS simulations against observations of a soil moisture network on the central Tibetan Plateau. J. Geophys. Res. 2013, 118, 4466–4475. [Google Scholar] [CrossRef]
- Su, Z.; de Rosnay, P.; Wen, J.; Wang, L.; Zeng, Y. Evaluation of ECMWF’s soil moisture analysis using observations on the Tibetan Plateau. J. Geophys. Res. 2013, 118, 5304–5318. [Google Scholar]
- Dente, L.; Vekerdy, Z.; Wen, J.; Su, Z. Maqu network for validation of satellite-derived soil moisture products. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 55–65. [Google Scholar] [CrossRef]
- Guo, D.; Yang, M.; Wang, H. Characteristics of land surface heat and water exchange under different soil freeze/thaw conditions over the central Tibetan Plateau. Hydrol. Process. 2011, 25, 2531–2541. [Google Scholar] [CrossRef]
- Qin, Y.; Lei, H.; Yang, D.; Gao, B.; Wang, Y.; Cong, Z.; Fan, W. Long term change in the depth of seasonally frozen ground and its ecohydrological impacts in the Qilian Mountains, northeastern Tibetan Plateau. J. Hydrol. 2016, 542, 204–221. [Google Scholar] [CrossRef]
- Wang, Q.; van der Velde, R.; Su, Z.; Wen, J. Aquarius L-band scatterometer and radiometer observations over a Tibetan Plateau site. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 165–177. [Google Scholar] [CrossRef]
- SRTM 90m Digital Elevation Database v4.1. Available online: http://www.cgiar-csi.org/data/srtm-90m-digital-elevation-database-v4-1 (accessed on 24 March 2013).
- Lee, J.S.; Grunes, M.R.; De Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least square procedure. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, K.S.; Bi, H.; Zhao, T.; Yang, X. A comprehensive analysis of rough soil surface scattering and emission predicted by AIEM with comparison to numerical simulations and experimental measurements. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1696–1708. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwve dielectric behavior of wet soil part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, 23, 35–46. [Google Scholar] [CrossRef]
- Dente, L.; Ferrazzoli, P.; Su, Z.; van der Velde, R.; Guerriero, L. Combined use of active and passive microwave satellite data to constrain a discrete scattering model. Remote Sens. Environ. 2014, 155, 222–238. [Google Scholar] [CrossRef]
- Su, Z.; Troch, P.A.; De Troch, F.P. Remote sensing of bare surface soil moisture using EMAC/ESAR data. Int. J. Remote Sens. 1997, 18, 2105–2124. [Google Scholar] [CrossRef]
- Lievens, H.; Verhoest, N.E.C.; De Keyser, E.; Vernieuwe, H.; Matgen, P.; Álvarez-Mozos, J.; De Baets, B. Effective roughness modeling as a tool for soil moisture retrieval from C- and L-band SAR. Hydrol. Earth Syst. Sci. 2011, 15, 151–162. [Google Scholar] [CrossRef]
- Verhoest, N.E.C.; Lievens, H.; Wagner, W.; Alvarez-Mozos, J.; Moran, M.S.; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surface from synthetic aperture radar. Sensor 2008, 8, 4213–4248. [Google Scholar] [CrossRef] [PubMed]
- Baghdadi, N.; Zribi, M. Evaluation of radar backscatter models IEM, Oh, and Dubois using experimental observations. Int. J. Remote Sens. 2006, 27, 3831–3852. [Google Scholar] [CrossRef]
- Wu, T.D.; Chen, K.S. A reappraisal of the validity of the IEM model for backscattering from rough surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 743–753. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, Volume II: Radar Remote Sensing and Surface Scattering and Emission Theory; Artech House Publishers: Norwood, MA, USA, 1986. [Google Scholar]
- Lievens, H.; Vernieuwe, H.; Álvarez-Mozos, J.; De Baets, B.; Verhoest, N.E.C. Error in radar derived soil moisture due to roughness parameterization: An analysis based on synthetically surface profiles. Sensors 2009, 9, 1067–1093. [Google Scholar] [CrossRef] [PubMed]
- Baghdadi, N.; Gherboudj, I.; Zribi, M.; Sahebi, M.; King, C.; Bonn, F. Semi-empirical calibration of the IEM backscattering model using radar images and moisture and roughness field measurements. Int. J. Remote Sens. 2004, 25, 3593–3623. [Google Scholar] [CrossRef]
- Callens, M.; Verhoest, N.E.C.; Davidson, M.W.J. Parameterization of tillage-induced single-scale soil roughness from 4-m profiles. IEEE Trans. Geosci. Remote Sens. 2006, 44, 878–888. [Google Scholar] [CrossRef]
- Wagner, W.; Bloschl, G.; Pampaloni, P.; Calvet, J.; Bizzarri, B.; Wigneron, J.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sens. Environ. 2002, 84, 42–52. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M.; Paloscia, S.; Verhoest, N.E.C.; Lievens, H.; Baup, F.; Mattia, F. Semi-empirical calibration of the integral equation model for co-polarized L-band backscattering. Remote Sens. 2015, 7, 13626–13640. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global mapping of foliage clumping index using multi-angular satellite data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Pisek, J.; Schaaf, C.B.; Strahler, A.H. Global clumping index map derived from the MODIS BRDF product. Remote Sens. Environ. 2012, 119, 118–130. [Google Scholar] [CrossRef]
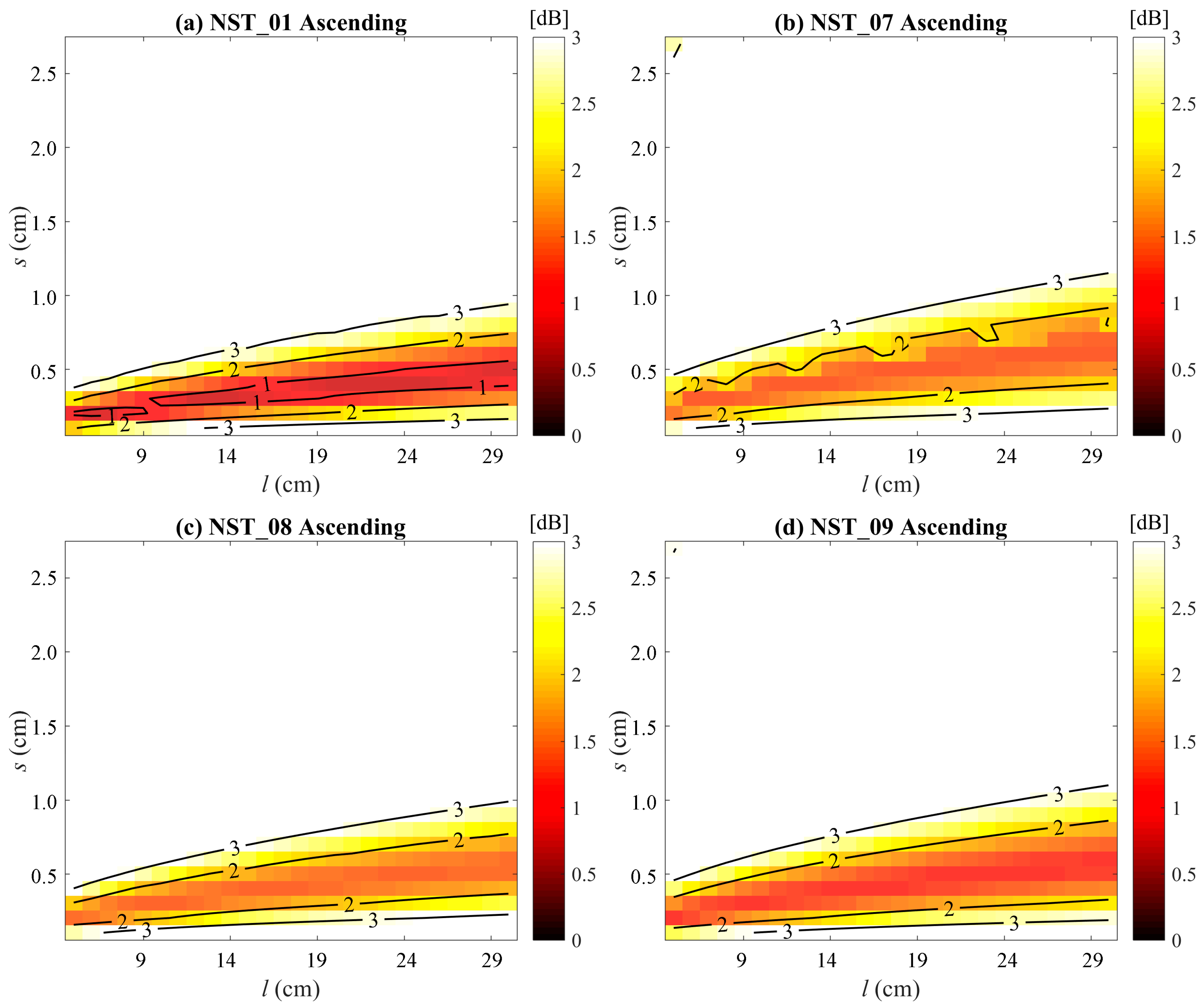
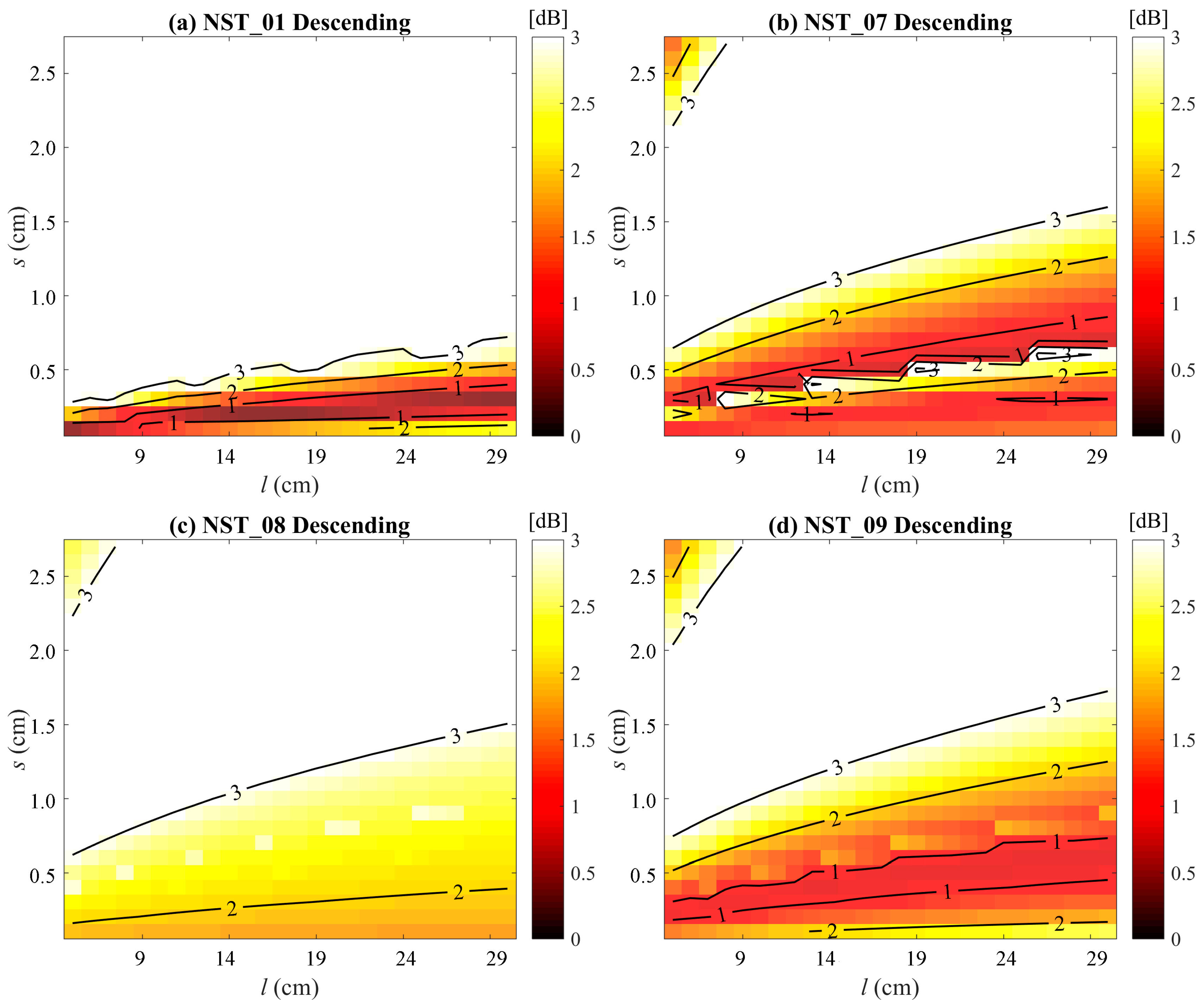
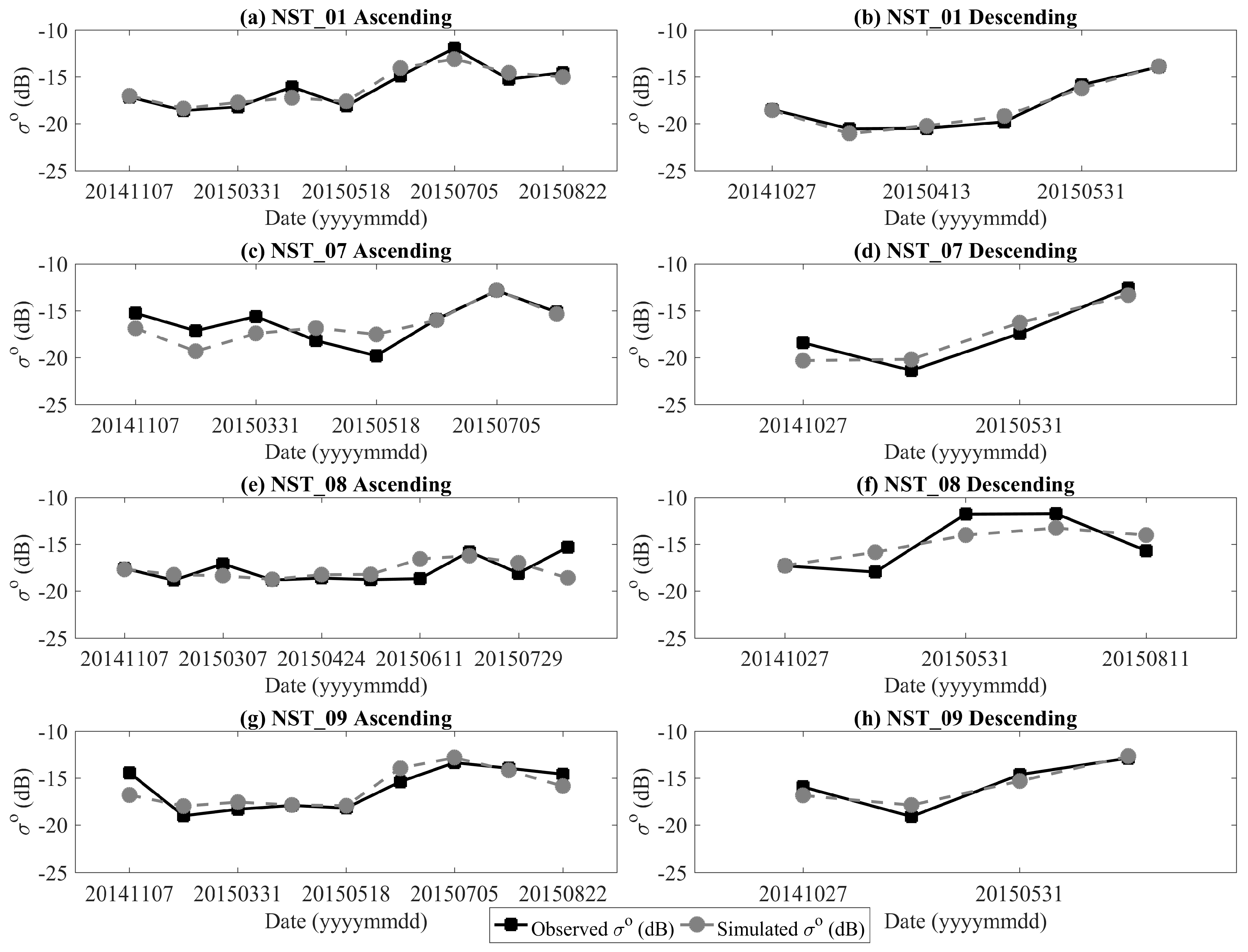
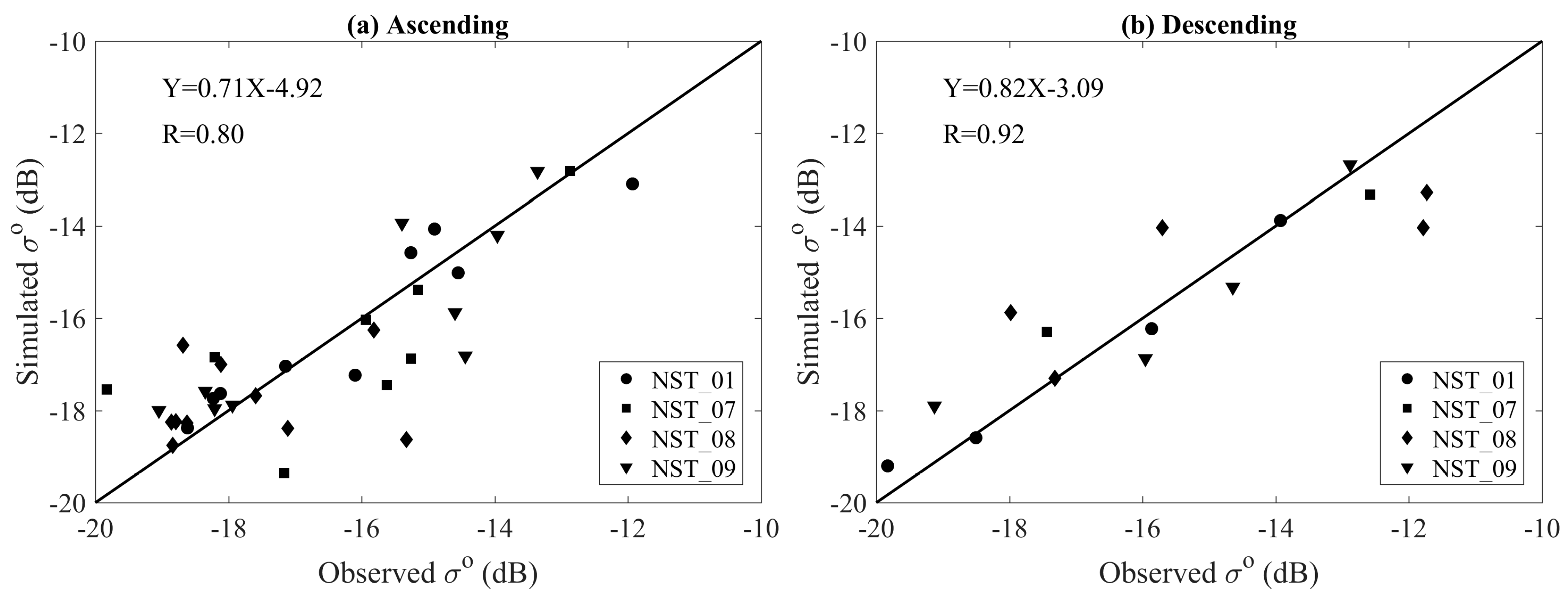
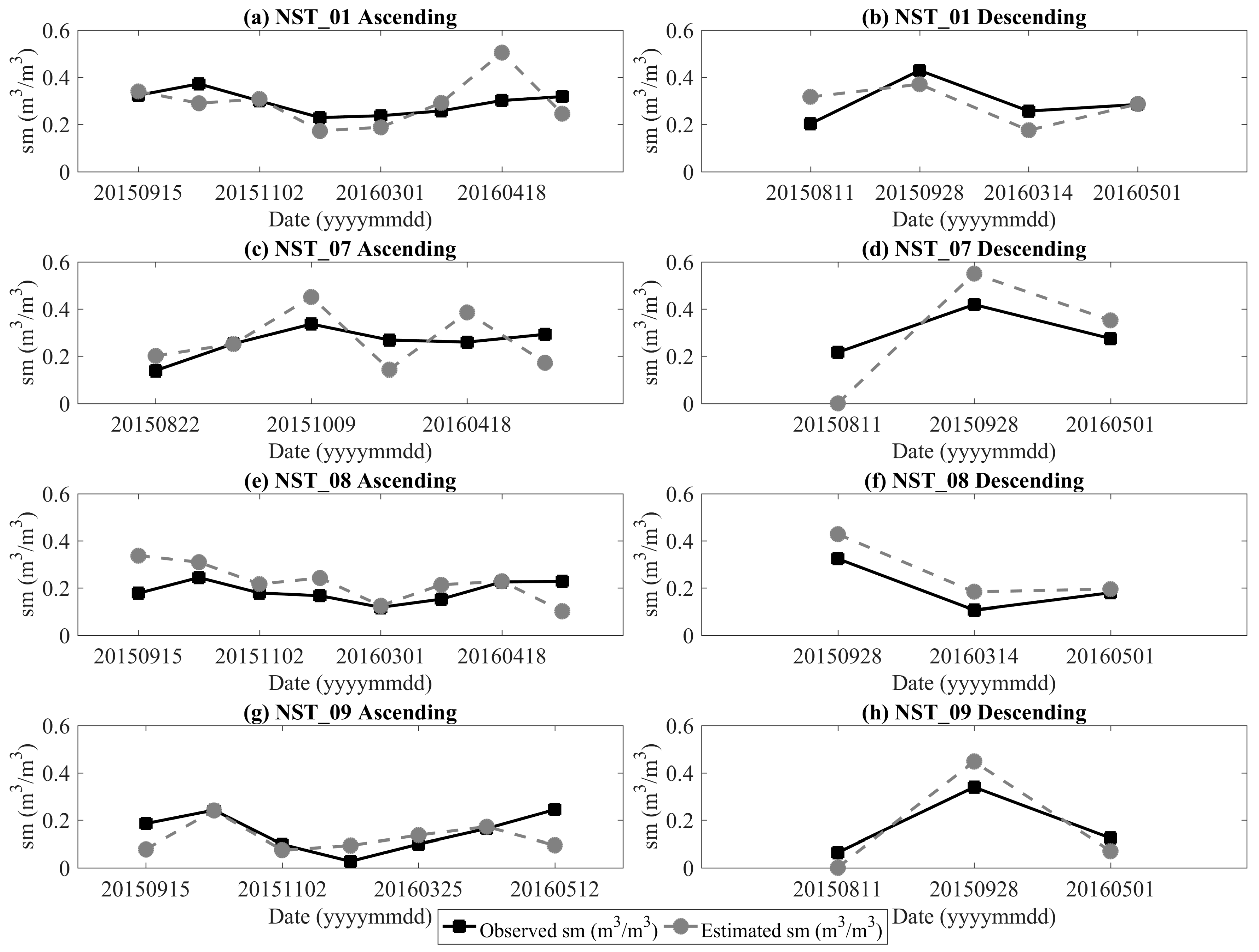
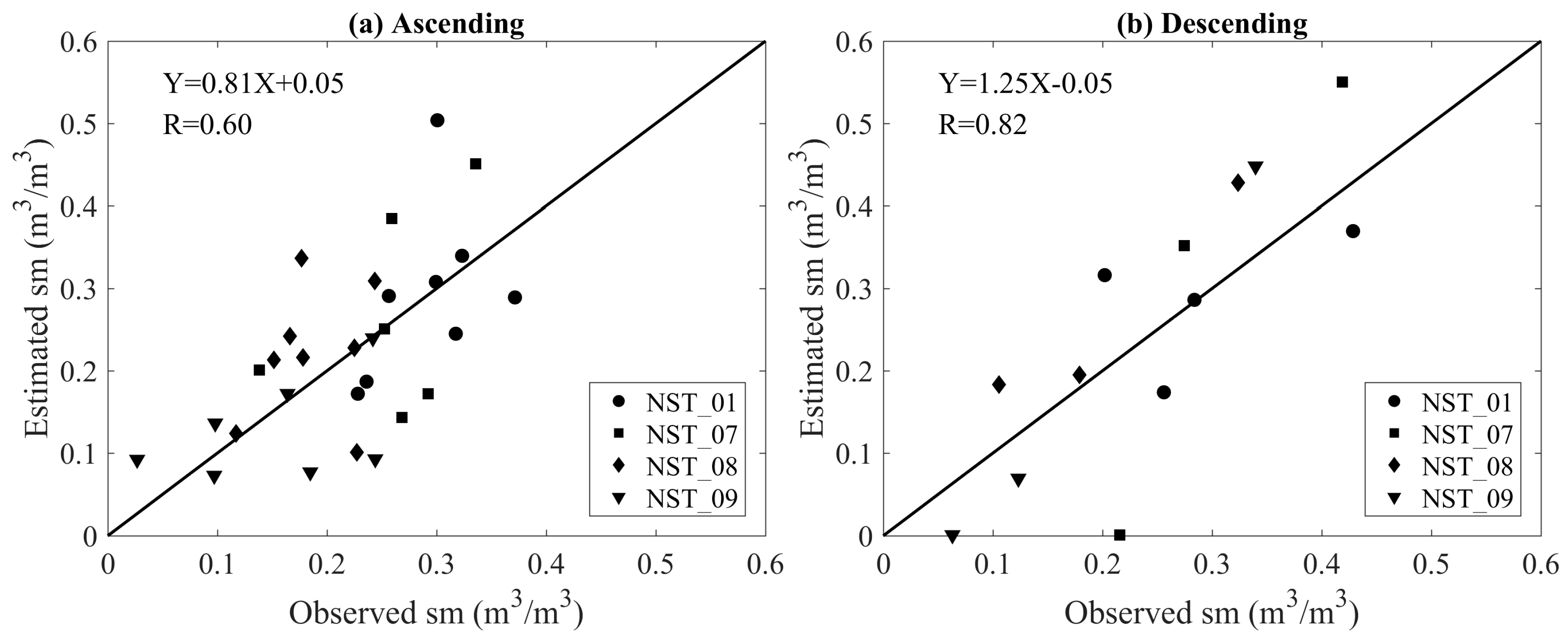
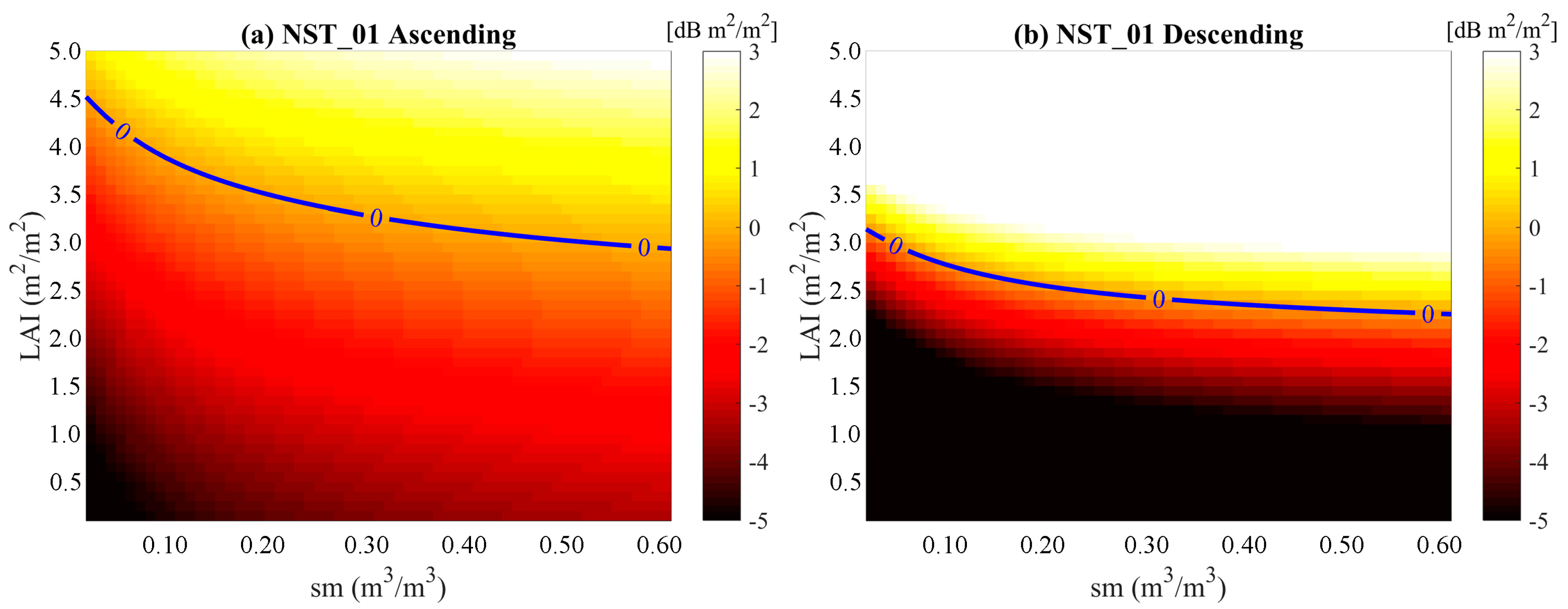
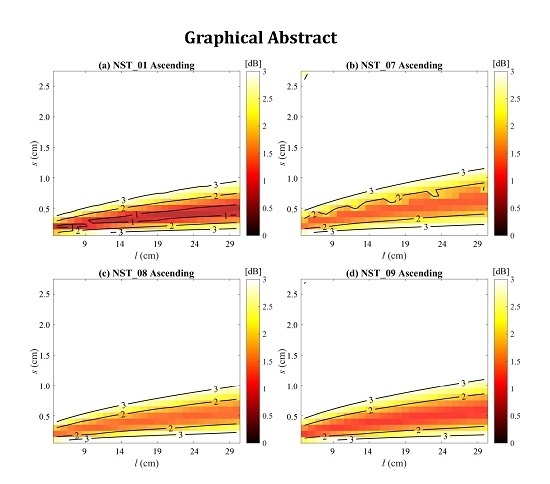
| Stations | Orbits | Model Coefficients | Effective Roughness | Statistical Metrics | ||||
|---|---|---|---|---|---|---|---|---|
| A | B | s (cm) | l (cm) | Bias (dB) | MAE (dB) | RMSE (dB) | ||
| NST_01 | ascending | −3.03 | 0.08 | 0.4 | 22.0 | 0.009 | 0.624 | 0.714 |
| descending | −4.54 | 0.15 | 0.2 | 16.0 | 0.001 | 0.317 | 0.379 | |
| NST_07 | ascending | −0.34 | 0.06 | 0.2 | 5.0 | −0.283 | 1.207 | 1.497 |
| descending | −0.64 | 0.27 | 0.1 | 15.0 | −0.076 | 1.251 | 1.318 | |
| NST_08 | ascending | −5.17 | 0.06 | 0.3 | 10.0 | −0.029 | 0.991 | 1.385 |
| descending | −11.06 | 0.70 | 0.1 | 30.0 | −0.001 | 1.519 | 1.714 | |
| NST_09 | ascending | −5.91 | 0.16 | 0.5 | 23.0 | 0.024 | 0.889 | 1.129 |
| descending | −0.07 | 0.11 | 0.5 | 25.0 | −0.040 | 0.758 | 0.844 | |
| Average | ascending | - | - | - | - | −0.063 | 0.603 | 0.983 |
| descending | - | - | - | - | −0.024 | 0.319 | 0.679 | |
| Stations | Ascending | Descending | ||||
|---|---|---|---|---|---|---|
| Bias (m3/m3) | MAE (m3/m3) | RMSE (m3/m3) | Bias (m3/m3) | MAE (m3/m3) | RMSE (m3/m3) | |
| NST_01 | 0.001 | 0.066 | 0.087 | −0.006 | 0.064 | 0.076 |
| NST_07 | 0.010 | 0.092 | 0.103 | −0.002 | 0.141 | 0.152 |
| NST_08 | 0.035 | 0.067 | 0.084 | 0.066 | 0.066 | 0.076 |
| NST_09 | −0.025 | 0.057 | 0.076 | −0.003 | 0.075 | 0.079 |
| Average | 0.006 | 0.048 | 0.073 | 0.012 | 0.026 | 0.055 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, X.; He, B.; Li, X.; Zeng, J.; Wang, X.; Wang, Z.; Zeng, Y.; Su, Z. First Assessment of Sentinel-1A Data for Surface Soil Moisture Estimations Using a Coupled Water Cloud Model and Advanced Integral Equation Model over the Tibetan Plateau. Remote Sens. 2017, 9, 714. https://doi.org/10.3390/rs9070714
Bai X, He B, Li X, Zeng J, Wang X, Wang Z, Zeng Y, Su Z. First Assessment of Sentinel-1A Data for Surface Soil Moisture Estimations Using a Coupled Water Cloud Model and Advanced Integral Equation Model over the Tibetan Plateau. Remote Sensing. 2017; 9(7):714. https://doi.org/10.3390/rs9070714
Chicago/Turabian StyleBai, Xiaojing, Binbin He, Xing Li, Jiangyuan Zeng, Xin Wang, Zuoliang Wang, Yijian Zeng, and Zhongbo Su. 2017. "First Assessment of Sentinel-1A Data for Surface Soil Moisture Estimations Using a Coupled Water Cloud Model and Advanced Integral Equation Model over the Tibetan Plateau" Remote Sensing 9, no. 7: 714. https://doi.org/10.3390/rs9070714