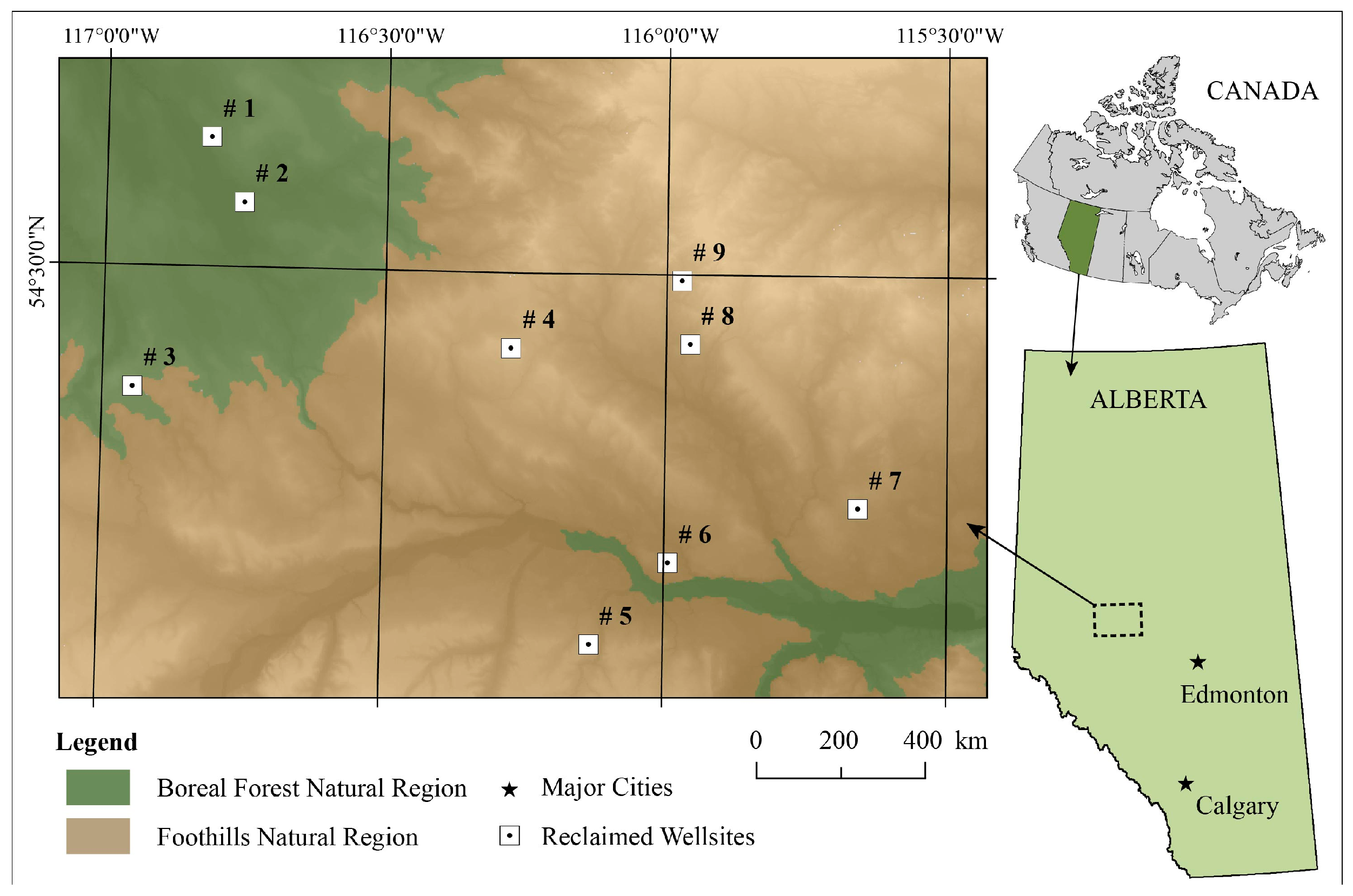
The Foothills Natural Region is a transition zone between the Boreal Forest and Rocky Mountain Natural Regions, with a cool, moist climate, and gently undulating to rolling hills [
37]. Lower elevations are covered by mixed-wood forests where mixtures of trembling aspen (
Populus tremuloides Michx.), lodgepole pine (
Pinus contorta Dougl. var
. latifolia Englem. Ex S. Watson), white spruce (
Picea glauca (Moench) Voss) and balsam poplar (
Populus balsamifera L.) dominate. Higher elevations generally support lodgepole pine stands. Wildlife species include among others woodland caribou (
Rangifer tarandus), elk (
Cervus canadensis), wolverine (
Gulo gulo) and grizzly bear (
Ursus arctos) [
37].
2.1. Field Data Collection and Processing
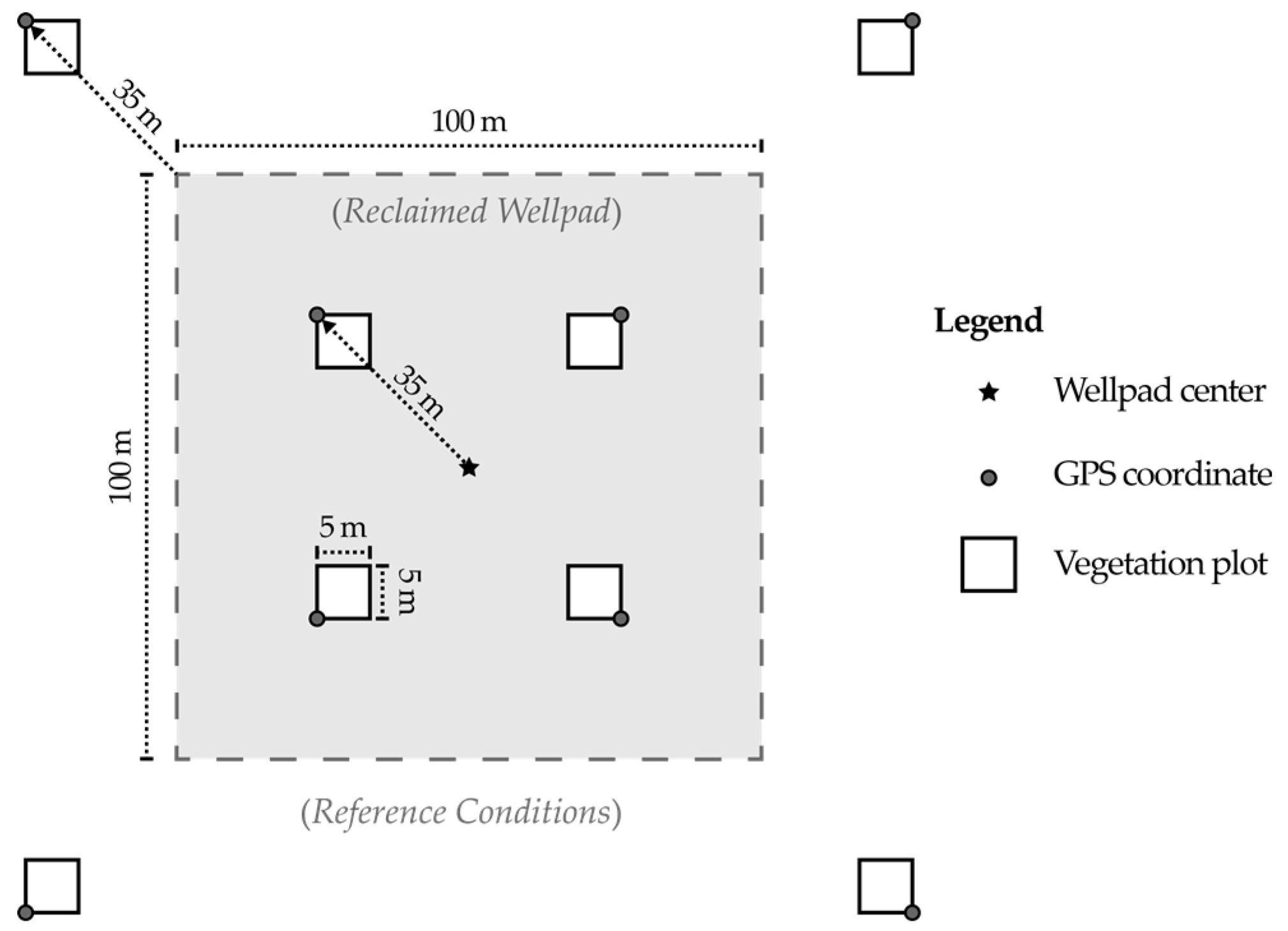
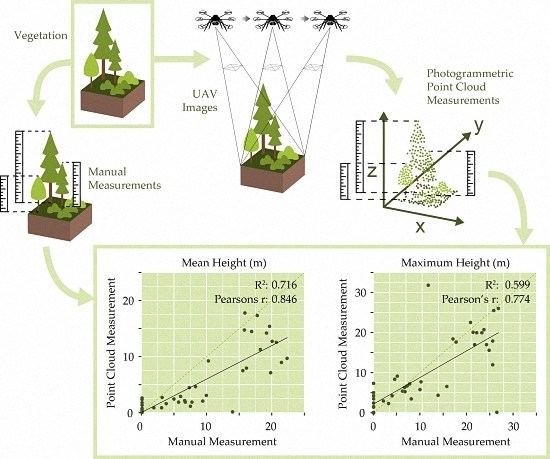
Information on vegetation structure was collected at each of our nine study sites during the summer of 2014, using a systematic sampling protocol. A series of eight 5 m × 5 m vegetation plots were laid out at each well site—four of which were systematically placed on the wellpad itself (i.e., the area cleared for well construction), and four of which were distributed within the nearby, undisturbed (i.e., natural) forested landscape so as to capture the local, natural vegetative state to which the reclaimed, disturbed area would ideally return. This is referred to as the
reference condition. The idealized plot layout is shown in
Figure 2. It should be noted that the four undisturbed vegetation plots were repositioned in the field if their intended location coincided with or were close to any anthropogenic disturbances such as a road.
Table 1 lists the six structural vegetation measurements collected in the field at each 5 m × 5 m plot and used in the study. Measurements were generally focused on a particular type of vegetation growth form (herb and forb vs. shrub vs. tree), as is typical of traditional vegetation surveys for recovery monitoring. Additional information was collected, but is not relevant to the present study and is therefore not presented here. See Alberta Biodiversity Monitoring Institute, 2013 [
39] for a full description of field data collection protocols.
Firstly, two-dimensional herb/forb and shrub vegetation cover was estimated at three separate height strata for each 5 m × 5 m plot: (1) <0.5 m, (2) 0.5 m to 2 m, and (3) 2 m to 5 m. Herbs and forbs were identified as non-woody vascular plants, whereas shrubs were defined as non-tree, vascular plants with woody stems. Small trees <1.3 m in height were included in estimates of shrub cover.
When trees were present at a 5 m × 5 m plot, both top height (m) and diameter at breast height (DBH: 1.3 m above ground; measured in cm) were measured for each individual tree. All live trees ≥1.3 m in height, as well as dead trees ≥1.3 m in height, and not leaning >45° from vertical were measured, with the exception of
Alnus (alder) or
Salix (willow) species. Height was measured using a vertex hypsometer, and DBH was measured using DBH tape. Once again, further detail can be found in [
39].
Given that shrub and herb/forb cover were estimated at the 5 m × 5 m plot level, and individual tree locations were not recorded in the field, we used the plot as the unit of analysis (i.e., our sample unit) in order to maintain consistency in our investigation. Therefore, tree heights and DBH measurements were summarized for each 5 m × 5 m plot using basic descriptive statistics (mean, standard deviation, minimum, maximum, and range) before being included in our statistical analysis (see
Table 1).
Summary statistics for the six field-measured vegetation variables measured at eight of our nine study sites are provided in
Table 2. It must be noted that due to errors in the PPC for one of our study sites (site 3; see
Section 2.2. for details), this site was removed from further analysis and is therefore not included in the summary given in
Table 2, nor in subsequent analysis results.
2.2. UAV Data Collection and Processing
Digital RGB photography was acquired at each study site using a Panasonic Lumix GX1 camera mounted on a Mikrokopter Hexacopter XL—a commercially-available ‘ready-to-fly’ UAV, manually flown over each well site. UAV observations were temporally consistent (within several weeks) with ground vegetation observations, both of which were acquired during summer leaf-on conditions. Specifications of the UAV are provided in
Table 3. Average flying altitude over the nine study sites ranged from 58.1 m to 74.7 m above ground. The mounted, consumer-grade camera possesses a resolution of 4000 × 3000 pixels at a 20-mm focal length. The number of pictures captured at each site ranged from 147 to 986. Forward and side overlap are estimated at 80% to 90%, and 70%, respectively. A series of three ground control points (GCPs) were also recorded at each study site using a Trimble GeoXT handheld Global Positioning System (GPS) unit, which typically provides sub-meter accuracy.
The UAV-acquired images for each study site were converted to JPEG format, and irrelevant photos (e.g., those taken during take-off and landing) were removed. The Agisoft PhotoScan Professional software (
http://www.agisoft.com) was used to generate image-based (i.e., photogrammetric) point clouds for each study site through an automated set of procedures based on structure-from-motion algorithms [
40]. The overall process for point-cloud generation involves image alignment; identification of tie points; and construction of a sparse, and then a dense, point cloud. This is followed by the manual identification and flagging of three, spatially-distributed GCPs at each study site with their recorded x, y and z location coordinates, as a means of georeferencing the final PPCs. We georeferenced our PPCs to the World Geodetic System 1984 Universal Transverse Mercator Zone 11N projection. The process produced a PPC for each of the nine study sites, contained within a LASer (LAS) file format (see
https://www.asprs.org/committee-general/laser-las-file-format-exchange-activities.html for specifications)—the same format typically used to store LiDAR point clouds. A section of one such PPC is shown in
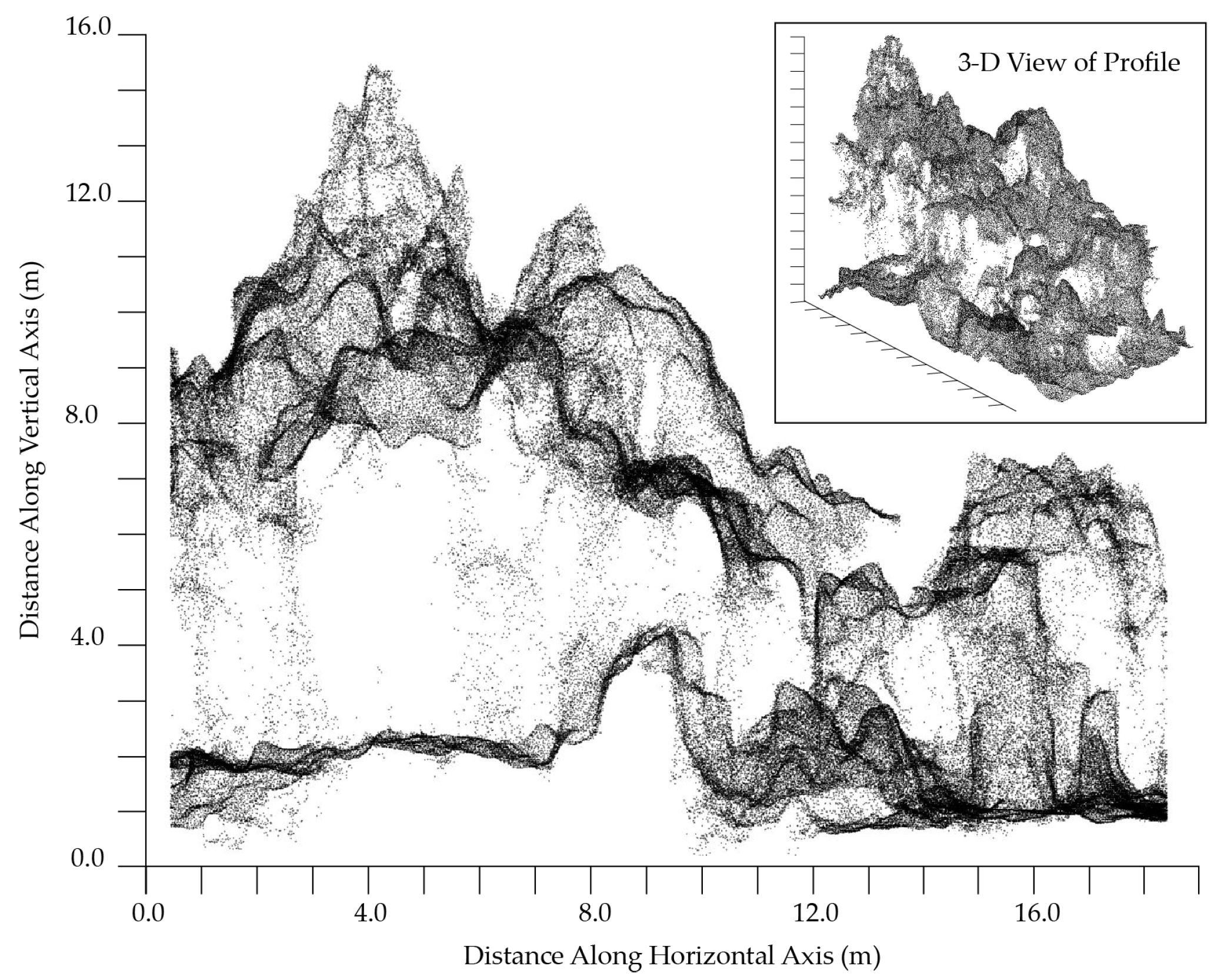
Figure 3.
Given the largely forested environment of our study area and the nature of PPCs—more particularly, their basis in passive optical photography—it is inevitable that where dense forest occurs there is an under-representation of the understory and underlying ground surface. This makes it challenging to extract vegetation height above ground surface in heavily vegetated landscapes using only the information contained in the PPC—a well-recognized limitation of these data [
41,
42]. However, digital terrain models (DTMs) offer an accurate and reliable ‘ground’ surface for normalizing our PPCs to height above ground. This approach has been used successfully by a number of researchers as a means of improving PPC height normalization (e.g., [
13,
22,
43,
44]).
To deal with this limitation in our data, we employed a set of 1-m DTMs derived from spatially coincident LiDAR data sets acquired between 2005 and 2007, with an average point density of 1.65 points per m
2. These data were acquired by Airborne Imaging (
http://airborneimaging.ca/), and accessed through the Government of Alberta. Accuracy estimates provided by Airborne Imaging for these LiDAR point clouds comprise maximum root-mean-square errors (RMSEs) of 0.30 m and 0.45 m for the vertical and horizontal directions, respectively. Unfortunately, because our sites are in remote, mostly natural areas there are no permanent anthropogenic structures or surfaces that can be used to co-register the two data sets as could be done in an urban area. Nevertheless, our sites are geomorphologically stable, are not topographically complex, with no steep slopes present. It was therefore reasonable to assume that the aforementioned LiDAR DTMs would provide an appropriate data source with which to normalize our UAV PPC heights to above ground.
Table 4 presents the coverage, point densities, and other details of the PPCs generated for each of our nine study sites. The number of photos taken and aerial coverage of the point clouds differ considerably at two of our sites (sites 6 and 7), which was the result of technological challenges with the UAV camera payload itself during these two flights. In particular, our camera settings at these two sites led to a longer interval between image captures, which was not discovered until later. Camera settings were adjusted for the remaining sites to permit a shorter interval between subsequent images, which enabled greater numbers of photos to be taken at these remaining sites. Nevertheless, ground resolution and point densities are consistently high across all of the point clouds, indicating that the number of photos captured at each site did not affect the quality of our resulting PPCs.
The PhotoScan software calculates average PPC x, y and z errors based on the RMSEs of the GCP points themselves [
45]. All but one of our PPC x and y errors were below 2 m (
Table 4). The PPC for site 3 possessed high levels of x and y errors (>5 m), which exceed levels appropriate for any further analysis, particularly in view of our 5 m × 5 m plot size. The data from this site was therefore removed from all further analysis.
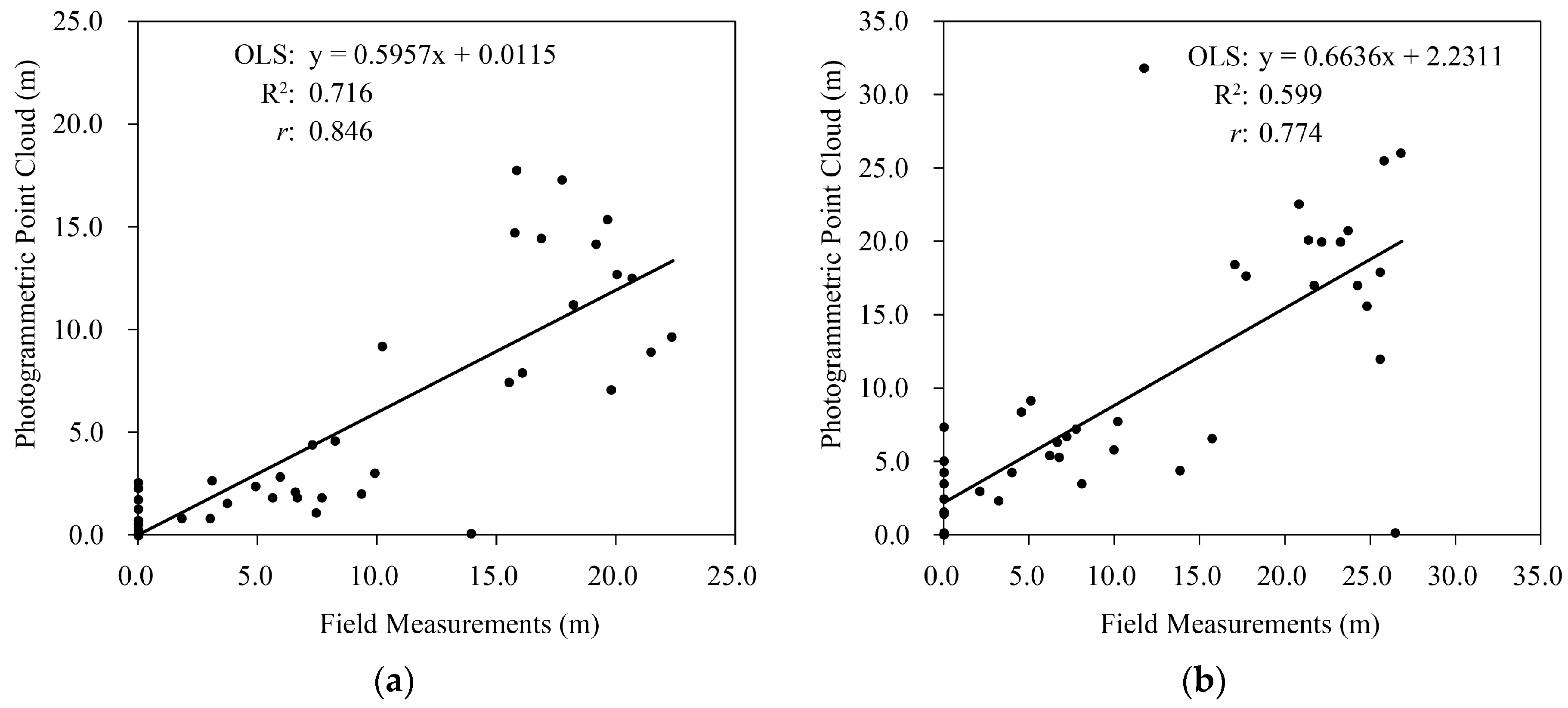
The PPC errors estimated for the remaining eight plots are comparable to PPC errors listed by Dandois and Ellis [
33], and slightly higher than those reported by Wallace et al. [
36] and Zhang et al. [
46]. Our PPC z errors were under 0.10, which are either comparable to or lower than the vertical PPC errors reported in these studies.
We observed a vertical mismatch between the PPCs and the corresponding LiDAR-derived DTMs at our nine study sites. The mismatch ranged from sub-meter differences to greater than 20 m, and may be due at least in part to GCP coordinate data accuracy acquired from the mapping-grade GPS units used in the field. It is unlikely that the temporal offset between the LiDAR acquisition (i.e., 2005–2007) and the UAV data acquisition (2014) is a cause of this vertical mismatch. Our study sites represent remote features that are no longer under active anthropogenic management and are thus unlikely to have changed this drastically over the given time. A lack of clearly identifiable, permanent features with known coordinates at our remote, forested study sites limits our ability to quantify any misalignment between the data sets.
To vertically align our PPCs with the coincident LiDAR DTMs we used an in-house customized software tool. The tool divides each PPC into a set of 50 m × 50 m tiles and normalizes each tile’s height values using the difference between the local height minima within that tile and that within the equivalent 50 m × 50 m section of the LiDAR DTM. We tested several tile sizes from 10 m × 10 m to 100 m × 100 m, evaluating the statistical independence between the tiles for each tile size. Smaller tile sizes led to more tiles and a more customized local adjustment, but less statistical independence between the tiles themselves, while the opposite was true of larger tile sizes. We found the best compromise between number of tiles and statistical independence at the 50 m × 50 m tile size.
Once normalized to height above ground, the PPCs were clipped to the 5 m × 5 m plot areas at each study site, and a series of metrics calculated for each plot.
Table 5 and
Table 6 list the various height, vegetation cover, and spectrally-based metrics that were calculated. We selected a large number and wide variety of metrics in support of an exploratory analysis approach. Our selections were based on metrics and RGB spectral indices commonly used or identified in the literature.
Deriving point cloud plot-level canopy height descriptive statistics (e.g., mean, maximum, standard deviation, etc.) is standard practice in LiDAR applications to forestry, as is the calculation of height percentiles and canopy cover or density measures at varying height strata within an area of interest (e.g., [
8,
10,
47]). These metrics are also now regularly applied to PPC-based studies in forested areas (e.g., [
15,
16,
33,
41,
44,
48,
49,
50]). Our spectrally-based metrics are less commonly used in these types of studies, although Dandois and Ellis [
33] show the utility of PPC spectral information for examining tree phenology on a very local and detailed scale. With the aim of exploring the potential value of spectral metrics from PPCs in estimating forest structural attributes, we derived a number of visible spectral band predictor variables found within the literature (e.g., [
51,
52,
53,
54,
55]) to include in our analysis (
Table 6). In order to ensure the statistical independence between each of the clipped PPCs for the eight 5 m × 5 m vegetation plots at each site, we performed a non-parametric Kruskal–Wallis test [
56] on a random sample of the points’ z coordinates from each plot. Our Kruksal–Wallis test results indicated that seven of the eight plots contained at least one clipped 5 m × 5 m plot PPC that was not a statistically independent sample, to an alpha of 0.05, when compared to one or more of the other 5 m × 5 m plot point clouds within the same study site. As a result, a total of eight plot point clouds were removed from our analysis. It should also be noted that 11 of the vegetation plots were not adequately represented by our PPCs due to insufficient photographic coverage resulting in gaps in our PPCs over these plots; these ‘no data’ plots were also not included in the analysis. The remaining 46 vegetation plots comprised our analysis (i.e.,
n = 46).
We followed three statistical approaches commonly found in the literature to test the reliability and accuracy of PPC-based vegetation structure information: (1) correlation analysis, (2) statistical error calculations, and (3) linear regression. These analyses were performed within the Microsoft Excel 2010 (
www.microsoft.com) and IBM SPSS Statistics 20.0 (
www.ibm.com/software/analytics/spss/products/statistics/) software.
Both correlation analysis and statistical error calculations (e.g., RMSE) are used in the literature to examine attributes that are directly comparable, such as mean tree height or canopy cover, as estimated from point clouds versus field measurements (e.g., [
41,
50,
57]). We calculated a traditional Pearson correlation statistic (
r) using a significance level of 0.05. We recognize that our sample size is not large and our data not likely to be normally distributed, but note that the literature has shown the Pearson statistic to be quite robust under both conditions [
58,
59]. With regard to statistical error tests, we calculated both RMSE and relative RMSE (RMSE %). The latter is simply RMSE normalized by the mean of the observed (e.g., field-measured) values [
50], and provides a relative measure of error that is more intuitive than the more traditional RMSE. It, too, is used by numerous examinations of PPC data sets within the context of vegetation studies (e.g., [
13,
42,
43,
44,
60]). It should be noted that tree DBH measurements were not derivable from our PPCs, and direct comparisons of these estimates through correlation or RMSE calculations were therefore not part of this analysis.
Our final statistical analysis involved using a forward-stepwise multivariate linear regression as a means of modeling various vegetation structural attributes using a number of PPC-derived vegetation metrics. This regression approach produces multivariate linear models comprising the best set of independent or predictor variables from those provided, based on a selection criterion. In this case, the analysis was done within IBM’s SPSS statistical software package (SPSS 20.0), which uses F-statistics to determine which of the independent variables are the most significant predictors, and adds them to the regression equation in a stepwise manner. Model performance is indicated by an adjusted coefficient of determination (i.e., adjusted R
2); adjusted R
2 values greater than 0.70 indicate a good model fit. Similar analyses are, again, found frequently in the literature (e.g., [
13,
22,
33,
43,
61]).