Assessing a Multi-Platform Data Fusion Technique in Capturing Spatiotemporal Dynamics of Heterogeneous Dryland Ecosystems in Topographically Complex Terrain
Abstract
:1. Introduction
2. Methods
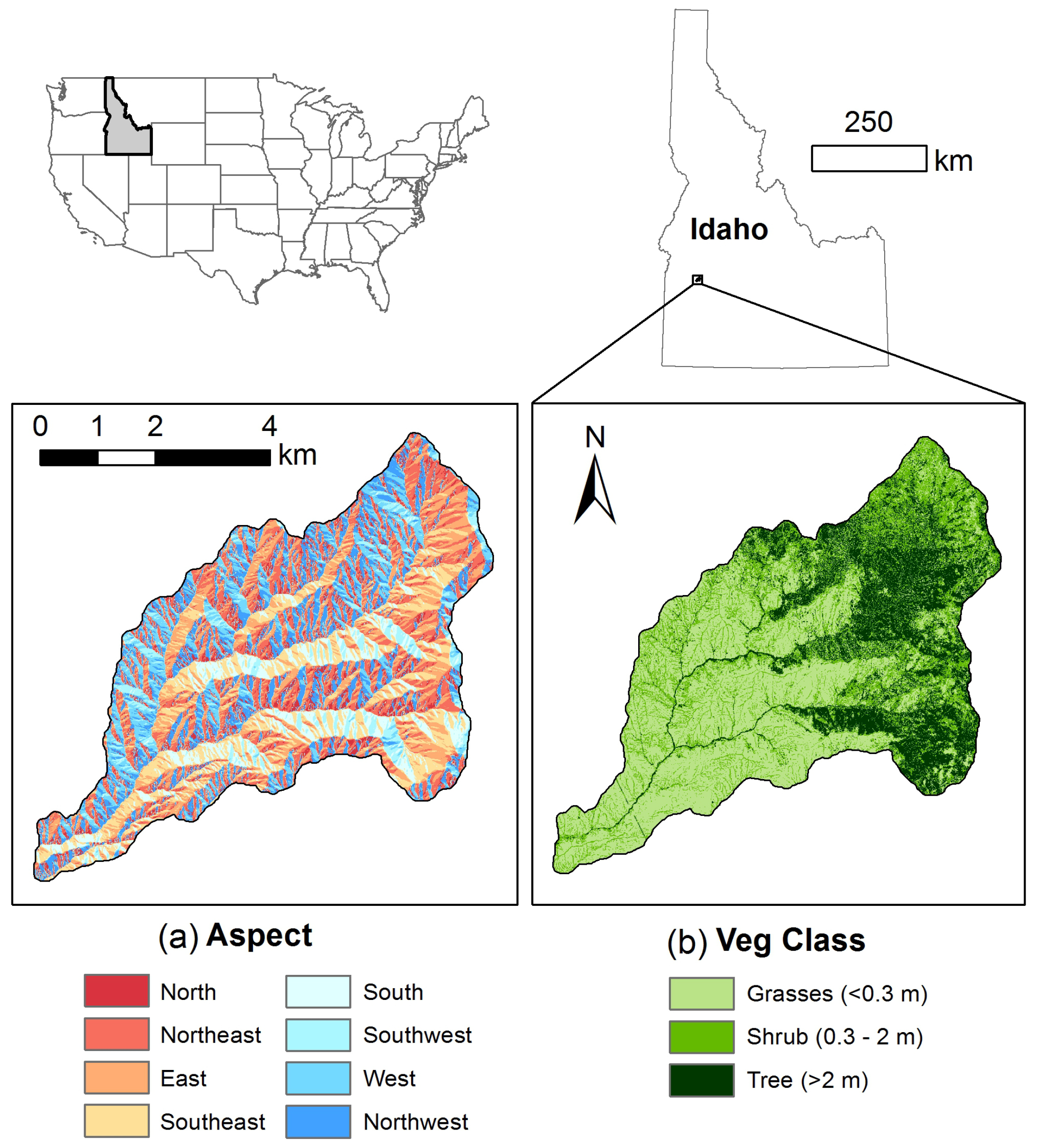
2.1. Study Area
2.2. Remote Sensing Datasets
2.3. STARFM Algorithm
2.4. Error Analysis
3. Results
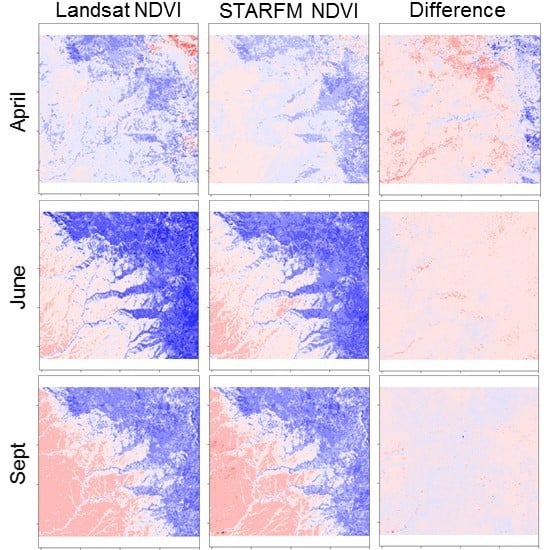
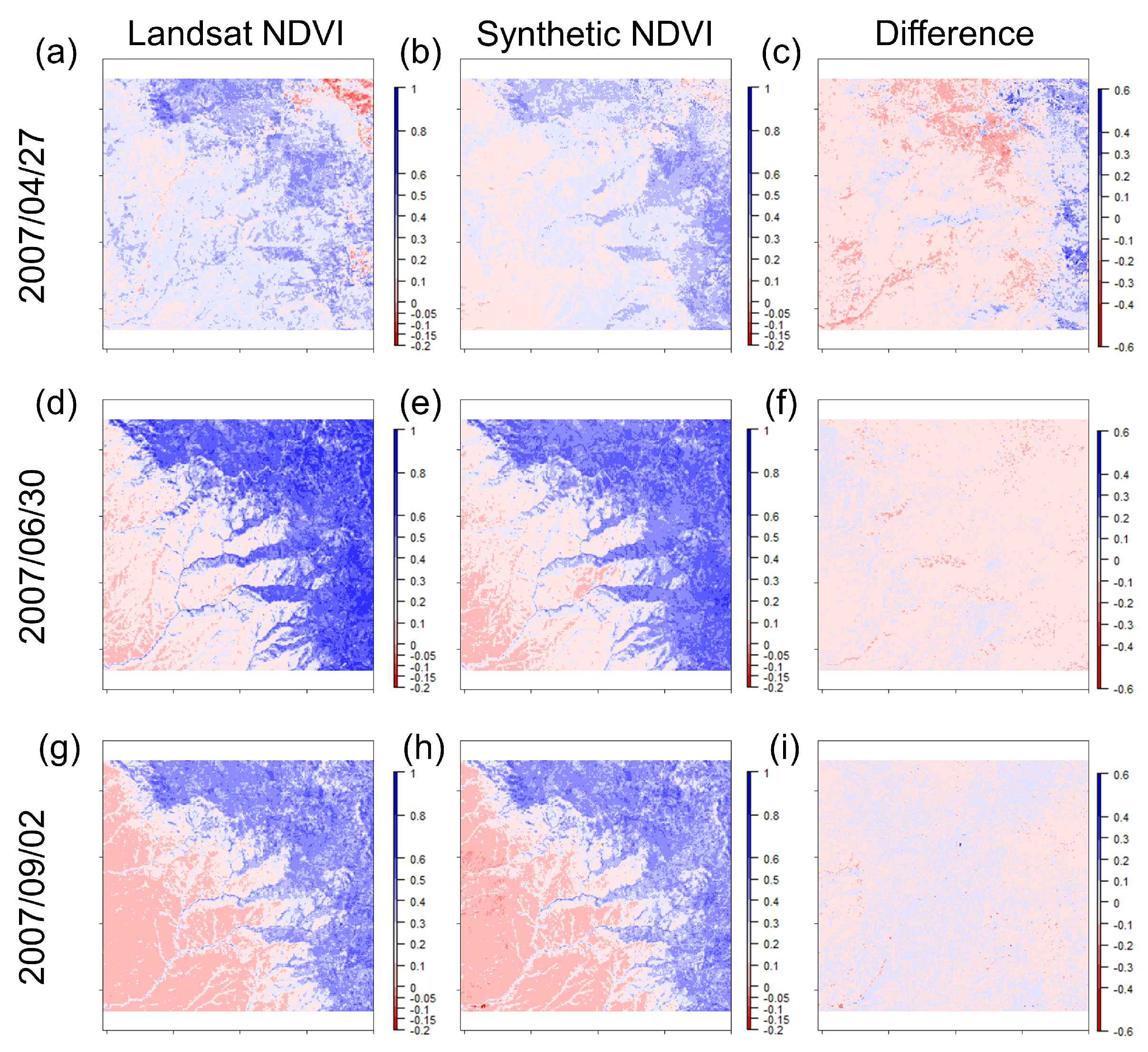
3.1. STARFM Algorithm Performance
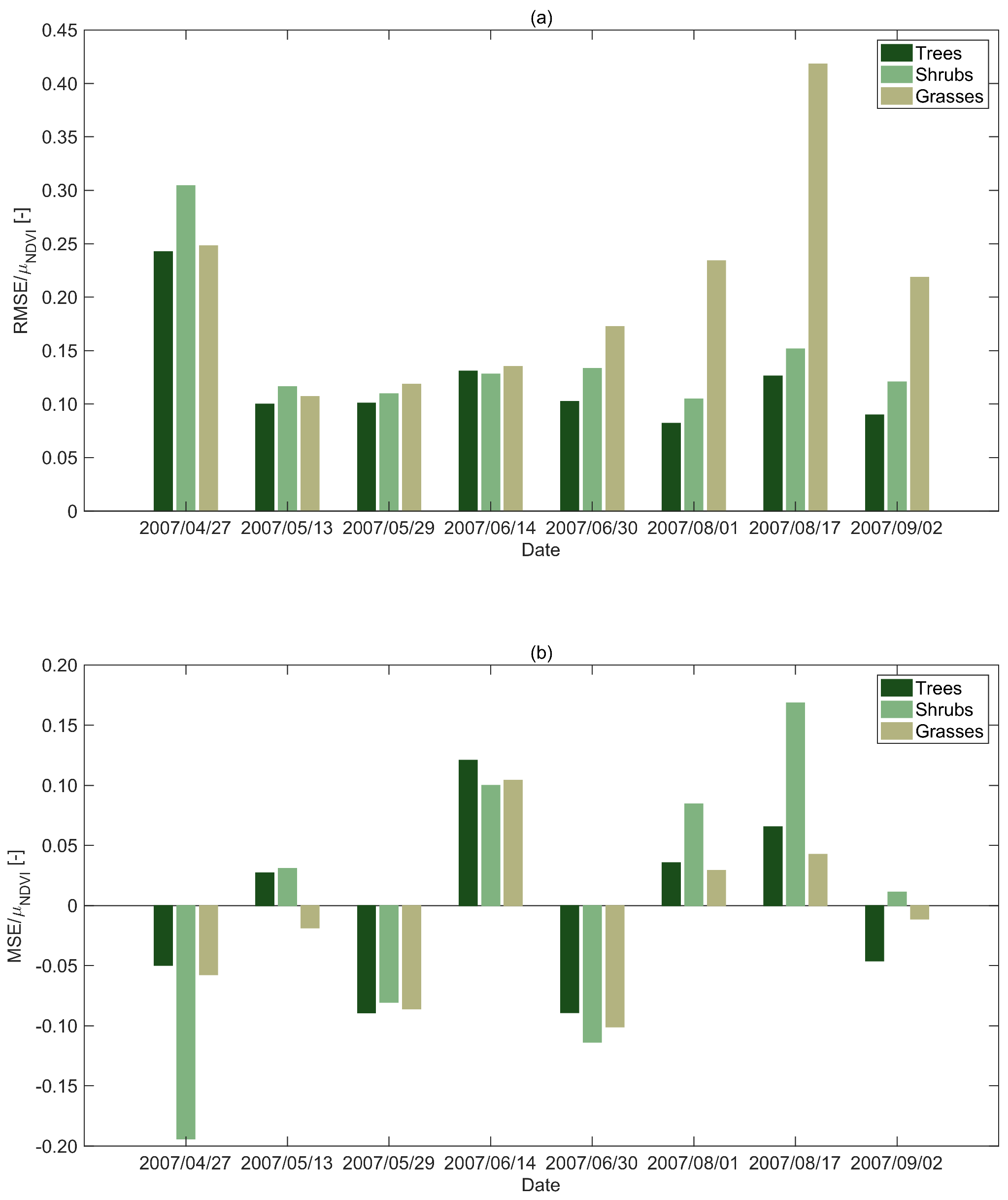
3.2. Sources of Error
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, N.; Bi, J.; Broquet, G.; Canadell, J.G.; Chevallier, F.; Liu, Y.Y.; et al. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Ji, M.; Xie, Y.; Wang, S.; He, Y.; Ran, J. Global semi-arid climate change over last 60 years. Clim. Dyn. 2016, 46, 1131–1150. [Google Scholar] [CrossRef]
- Davies, J.; Poulsen, L.; Schulte-Herbrüggen, B.; MacKinnon, K.; Crawhall, N.; Henwood, W.D.; Dudley, N.; Smith, J.; Gudka, M. Conserving Dryland Biodiversity; IUCN: Nairobi, Kenya, 2012. [Google Scholar]
- Balch, J.K.; Bradley, B.A.; D’Antonio, C.M.; Gómez-Dans, J. Introduced annual grass increases regional fire activity across the arid western USA (1980–2009). Glob. Chang. Biol. 2013, 19, 173–183. [Google Scholar] [CrossRef] [PubMed]
- Adler, P.; Raff, D.; Lauenroth, W. The effect of grazing on the spatial heterogeneity of vegetation. Oecologia 2001, 128, 465–479. [Google Scholar] [CrossRef] [PubMed]
- Van de Koppel, J.; Rietkerk, M.; van Langevelde, F.; Kumar, L.; Klausmeier, C.A.; Fryxell, J.M.; Hearne, J.W.; van Andel, J.; de Ridder, N.; Skidmore, A.; et al. Spatial heterogeneity and irreversible vegetation change in semiarid grazing systems. Am. Nat. 2002, 159, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Backlund, P.; Janetos, A.C.; Schimel, D.S. The Effects of Climate Change on Agriculture, Land Resources, Water Resources, and Biodiversity in the United States; Nova Science Pub Incorporated: New York, NY, USA, 2008. [Google Scholar]
- Puigdefábregas, J. The role of vegetation patterns in structuring runoff and sediment fluxes in drylands. Earth Surf. Process. Landf. 2005, 30, 133–147. [Google Scholar] [CrossRef]
- Foti, R.; Ramírez, J.A. A mechanistic description of the formation and evolution of vegetation patterns. Hydrol. Earth Syst. Sci. 2013, 17, 63–84. [Google Scholar] [CrossRef]
- Zou, C.B.; Barron-Gafford, G.A.; Breshears, D.D. Effects of topography and woody plant canopy cover on near-ground solar radiation: Relevant energy inputs for ecohydrology and hydropedology. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Schlaepfer, D.R.; Lauenroth, W.K.; Bradford, J.B. Ecohydrological niche of sagebrush ecosystems. Ecohydrology 2012, 5, 453–466. [Google Scholar] [CrossRef]
- Asner, G.P.; Levick, S.R.; Kennedy-Bowdoin, T.; Knapp, D.E.; Emerson, R.; Jacobson, J.; Colgan, M.S.; Martin, R.E. Large-scale impacts of herbivores on the structural diversity of African savannas. Proc. Nat. Acad. Sci. USA 2009, 106, 4947–4952. [Google Scholar] [CrossRef] [PubMed]
- D’Odorico, P.; Okin, G.S.; Bestelmeyer, B.T. A synthetic review of feedbacks and drivers of shrub encroachment in arid grasslands. Ecohydrology 2012, 5, 520–530. [Google Scholar]
- Kurz, W.A.; Dymond, C.C.; Stinson, G.; Rampley, G.J.; Neilson, E.T.; Carroll, A.L.; Ebata, T.; Safranyik, L. Mountain pine beetle and forest carbon feedback to climate change. Nature 2008, 452, 987–990. [Google Scholar] [CrossRef] [PubMed]
- Stark, S.C.; Breshears, D.D.; Garcia, E.S.; Law, D.J.; Minor, D.M.; Saleska, S.R.; Swann, A.L.S.; Villegas, J.C.; Aragão, L.E.O.C.; Bella, E.M.; et al. Toward accounting for ecoclimate teleconnections: Intra- and inter- continental consequences of altered energy balance after vegetation change. Landsc. Ecol. 2016, 31, 181–194. [Google Scholar]
- Moorcroft, P.R.; Hurtt, G.C.; Pacala, S.W. A method for scaling vegetation dynamics: The ecosystem demography model (ED). Ecol. Monogr. 2001, 71, 557–585. [Google Scholar] [CrossRef]
- Best, M.J.; Pryor, M.; Clark, D.B.; Rooney, G.G.; Essery, R.L.H.; Ménard, C.B.; Edwards, J.M.; Hendry, M.A.; Porson, A.; Gedney, N.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 1: Energy and water fluxes. Geosci. Model Dev. 2011, 4, 677–699. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in Version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Medvigy, D.; Wofsy, S.C.; Munger, J.W.; Hollinger, D.Y.; Moorcroft, P.R. Mechanistic scaling of ecosystem function and dynamics in space and time: Ecosystem Demography model version 2. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef]
- Tague, C.; McMichael, C.; Hope, A.; Choate, J.; Clark, R. Application of the RHESSys model to a California semiarid shrubland watershed. JAWRA J. Am. Water Resour. Assoc. 2004, 40, 575–589. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Bras, R.L.; Vivoni, E.R. Vegetation-hydrology dynamics in complex terrain of semiarid areas: 1. A mechanistic approach to modeling dynamic feedbacks. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS–Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Walker, J.J.; de Beurs, K.M.; Wynne, R.H.; Gao, F. Evaluation of Landsat and MODIS data fusion products for analysis of dryland forest phenology. Remote Sens. Environ. 2012, 117, 381–393. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Y.; Onojeghuo, A.O.; Zhu, X.; Atkinson, P.M. Enhancing Spatio-Temporal Fusion of MODIS and Landsat Data by Incorporating 250 m MODIS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Bradley, B.A.; Mustard, J.F. Characterizing the landscape dynamics of an invasive plant and risk of invasion using remote sensing. Ecol. Appl. 2006, 16, 1132–1147. [Google Scholar] [CrossRef]
- Okin, G.S.; Roberts, D.A.; Murray, B.; Okin, W.J. Practical limits on hyperspectral vegetation discrimination in arid and semiarid environments. Remote Sens. Environ. 2001, 77, 212–225. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Fu, D.; Chen, B.; Wang, J.; Zhu, X.; Hilker, T. An improved image fusion approach based on enhanced spatial and temporal the adaptive reflectance fusion model. Remote Sens. 2013, 5, 6346–6360. [Google Scholar] [CrossRef]
- Emelyanova, I.V.; McVicar, T.R.; Van Niel, T.G.; Li, L.T.; van Dijk, A.I.J.M. Assessing the accuracy of blending Landsat–MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sens. Environ. 2013, 133, 193–209. [Google Scholar] [CrossRef]
- Schmidt, M.; Udelhoven, T.; Gill, T.; Röder, A. Long term data fusion for a dense time series analysis with MODIS and Landsat imagery in an Australian Savanna. J. Appl. Remote Sens. 2012, 6. [Google Scholar] [CrossRef]
- Olexa, E.M.; Lawrence, R.L. Performance and effects of land cover type on synthetic surface reflectance data and NDVI estimates for assessment and monitoring of semi-arid rangeland. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 30–41. [Google Scholar] [CrossRef]
- Yenko, M.K. Hydrometric and Geochemical Evidence of Streamflow Sources in the Upper Dry Creek Experimental Watershed, Southwestern Idaho, Ph.D. Thesis, Boise State University, Boise, ID, USA, 2003. [Google Scholar]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Streutker, D.R.; Glenn, N.F. LiDAR measurement of sagebrush steppe vegetation heights. Remote Sens. Environ. 2006, 102, 135–145. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe efficiency index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Jain, S.K.; Sudheer, K.P. Fitting of hydrologic models: A close look at the Nash–Sutcliffe index. J. Hydrol. Eng. 2008, 13, 981–986. [Google Scholar] [CrossRef]
- Hall, D.K.; Frei, A.; Drey, S.J. Remote Sensing of Snow Cover. Section: Snow Extent; NASA: Washington, DC, USA, 2012.
- Geroy, I.J.; Gribb, M.M.; Marshall, H.P.; Chandler, D.G.; Benner, S.G.; McNamara, J.P. Aspect influences on soil water retention and storage. Hydrol. Process. 2011, 25, 3836–3842. [Google Scholar] [CrossRef]
- Kunkel, M.L.; Flores, A.N.; Smith, T.J.; McNamara, J.P. A simplified approach for estimating soil carbon and nitrogen stocks in semi-arid complex terrain. Geoderma 2011, 165, 1–11. [Google Scholar] [CrossRef]
- Smith, T.J.; McNamara, J.P.; Flores, A.N.; Gribb, M.M.; Aishlin, P.S.; Benner, S.G. Small soil storage capacity limits benefit of winter snowpack to upland vegetation. Hydrol. Process. 2011, 25, 3858–3865. [Google Scholar] [CrossRef]
- Yetemen, O.; Istanbulluoglu, E.; Vivoni, E.R. The implications of geology, soils, and vegetation on landscape morphology: Inferences from semi-arid basins with complex vegetation patterns in Central New Mexico, USA. Geomorphology 2010, 116, 246–263. [Google Scholar] [CrossRef]
- Gutiérrez-Jurado, H.A.; Vivoni, E.R.; Cikoski, C.; Harrison, J.B.J.; Bras, R.L.; Istanbulluoglu, E. On the observed ecohydrologic dynamics of a semiarid basin with aspect-delimited ecosystems. Water Resour. Res. 2013, 49, 8263–8284. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Barron-Gafford, G.A.; Breshears, D.D.; Brooks, P.D.; Chorover, J.; Durcik, M.; Harman, C.J.; Huxman, T.E.; Lohse, K.A.; Lybrand, R.; et al. Coevolution of nonlinear trends in vegetation, soils, and topography with elevation and slope aspect: A case study in the sky islands of southern Arizona. J. Geophys. Res. Earth Surf. 2013, 118, 741–758. [Google Scholar] [CrossRef]
- Zhou, X.; Istanbulluoglu, E.; Vivoni, E.R. Modeling the ecohydrological role of aspect-controlled radiation on tree-grass-shrub coexistence in a semiarid climate. Water Resour. Res. 2013, 49, 2872–2895. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Seitz, N.; White, J.C.; Gao, F.; Masek, J.G.; Stenhouse, G. Generation of dense time series synthetic Landsat data through data blending with MODIS using a spatial and temporal adaptive reflectance fusion model. Remote Sens. Environ. 2009, 113, 1988–1999. [Google Scholar] [CrossRef]
- Watts, J.D.; Powell, S.L.; Lawrence, R.L.; Hilker, T. Improved classification of conservation tillage adoption using high temporal and synthetic satellite imagery. Remote Sens. Environ. 2011, 115, 66–75. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q. Enhancing temporal resolution of satellite imagery for public health studies: A case study of West Nile Virus outbreak in Los Angeles in 2007. Remote Sens. Environ. 2012, 117, 57–71. [Google Scholar] [CrossRef]
- Tewes, A.; Thonfeld, F.; Schmidt, M.; Oomen, R.J.; Zhu, X.; Dubovyk, O.; Menz, G.; Schellberg, J. Using RapidEye and MODIS data fusion to monitor vegetation dynamics in semi-arid rangelands in South Africa. Remote Sens. 2015, 7, 6510–6534. [Google Scholar] [CrossRef]
- Wu, M.; Li, H.; Huang, W.; Niu, Z.; Wang, C. Generating daily high spatial land surface temperatures by combining ASTER and MODIS land surface temperature products for environmental process monitoring. Environ. Sci. Process. Impacts 2015, 17, 1396–1404. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Zhang, M.; Zhang, X.; Zeng, H.; Wu, B. Mapping winter wheat biomass and yield using time series data blended from PROBA-V 100- and 300-m S1 products. Remote Sens. 2016, 8, 824. [Google Scholar] [CrossRef]
- Wang, Q.; Blackburn, G.A.; Onojeghuo, A.O.; Dash, J.; Zhou, L.; Zhang, Y.; Atkinson, P.M. Fusion of Landsat 8 OLI and Sentinel-2 MSI data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3885–3899. [Google Scholar] [CrossRef]

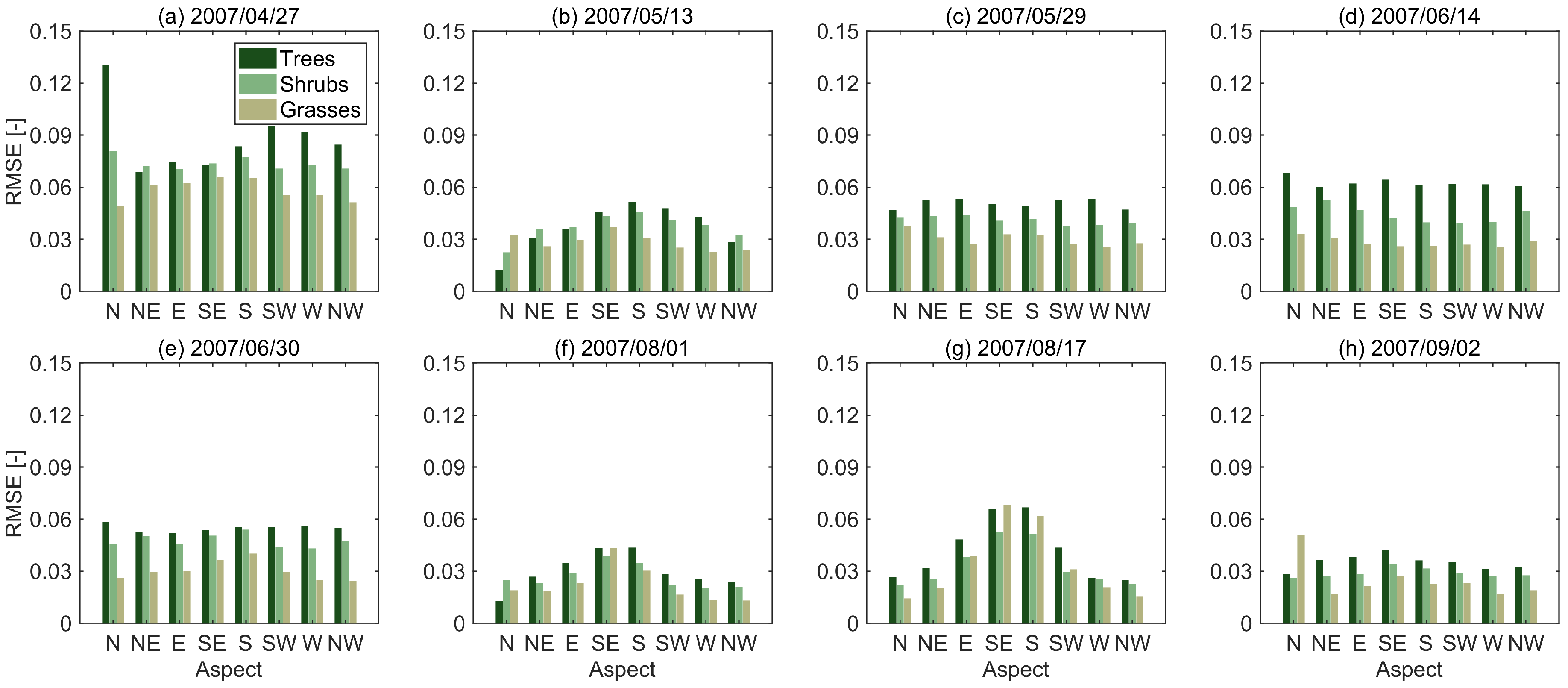

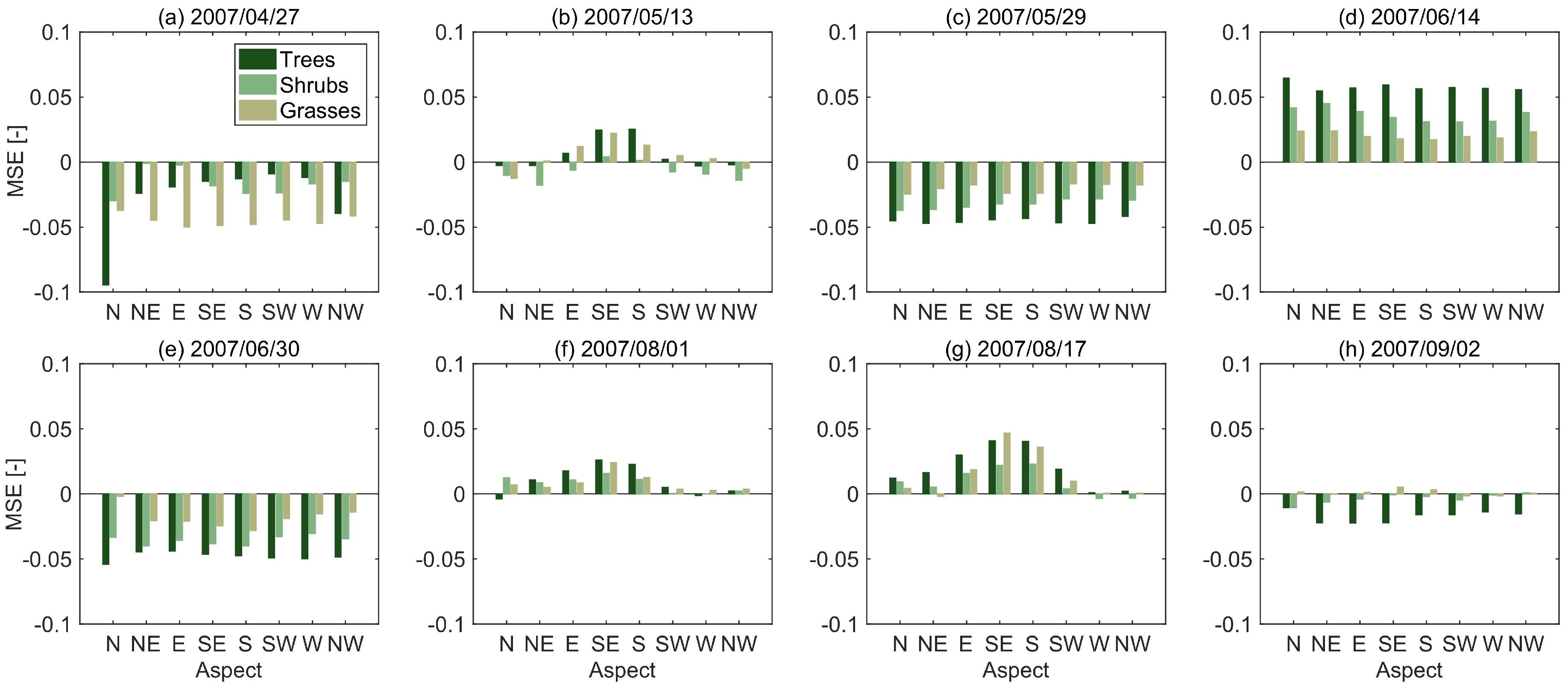
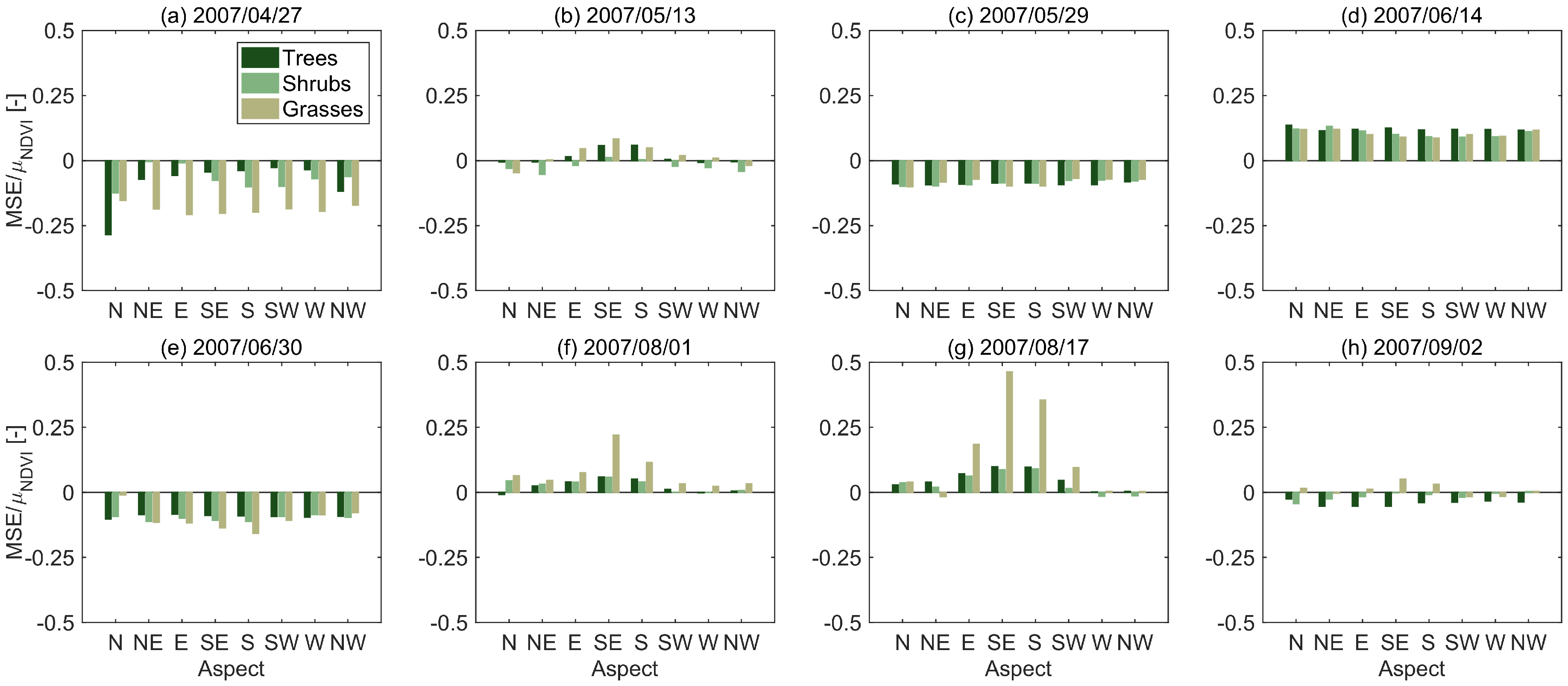

| Date | Trees | Shrubs | Grasses |
|---|---|---|---|
| 27 April 2007 | 0.3317 | 0.2380 | 0.2406 |
| 13 May 2007 | 0.4281 | 0.3374 | 0.2654 |
| 29 May 2007 | 0.5068 | 0.3728 | 0.2436 |
| 14 June 2007 | 0.4734 | 0.3417 | 0.1983 |
| 30 June 2007 | 0.5255 | 0.3567 | 0.1780 |
| 1 August 2007 | 0.4367 | 0.2714 | 0.1090 |
| 17 August 2007 | 0.4141 | 0.2514 | 0.1009 |
| 2 September 2007 | 0.4110 | 0.2419 | 0.0984 |
| Date | Data Set | MAE | MSE | RMSE | Error SD | NSE | Intercept | Slope | |
|---|---|---|---|---|---|---|---|---|---|
| 27 April 2007 | NDVI | 0.060 | −0.023 | 0.077 | 0.073 | 0.197 | 0.094 | 0.561 | 0.369 |
| 13 May 2007 | NDVI | 0.029 | 0.008 | 0.041 | 0.040 | 0.810 | 0.018 | 0.971 | 0.838 |
| 29 May 2007 | NDVI | 0.036 | −0.032 | 0.044 | 0.030 | 0.909 | 0.023 | 0.851 | 0.973 |
| 14 June 2007 | NDVI | 0.040 | 0.039 | 0.048 | 0.029 | 0.899 | −0.002 | 1.124 | 0.984 |
| 30 June 2007 | NDVI | 0.036 | −0.033 | 0.045 | 0.031 | 0.943 | 0.005 | 0.894 | 0.981 |
| 1 August 2007 | NDVI | 0.021 | 0.009 | 0.029 | 0.028 | 0.971 | 0.012 | 0.991 | 0.974 |
| 17 August 2007 | NDVI | 0.031 | 0.017 | 0.043 | 0.040 | 0.931 | 0.024 | 0.973 | 0.943 |
| 2 September 2007 | NDVI | 0.022 | −0.007 | 0.030 | 0.029 | 0.966 | 0.001 | 0.969 | 0.968 |
| Date | Data Set | MAE | MSE | RMSE | Error SD | NSE | Intercept | Slope | |
|---|---|---|---|---|---|---|---|---|---|
| 27 April 2007 | NDVI | 0.095 | −0.085 | 0.123 | 0.089 | −1.063 | 0.066 | 0.435 | 0.199 |
| 13 May 2007 | NDVI | 0.043 | −0.015 | 0.060 | 0.058 | 0.604 | 0.018 | 0.901 | 0.693 |
| 29 May 2007 | NDVI | 0.037 | −0.016 | 0.048 | 0.045 | 0.892 | 0.064 | 0.784 | 0.927 |
| 14 June 2007 | NDVI | 0.043 | 0.042 | 0.050 | 0.027 | 0.894 | 0.014 | 1.083 | 0.979 |
| 30 June 2007 | NDVI | 0.039 | −0.033 | 0.050 | 0.037 | 0.929 | 0.021 | 0.846 | 0.979 |
| 1 August 2007 | NDVI | 0.041 | 0.037 | 0.052 | 0.036 | 0.912 | 0.023 | 1.053 | 0.966 |
| 17 August 2007 | NDVI | 0.018 | 0.002 | 0.024 | 0.024 | 0.979 | 0.003 | 0.995 | 0.979 |
| 2 September 2007 | NDVI | 0.019 | −0.006 | 0.025 | 0.025 | 0.975 | 0.001 | 0.973 | 0.977 |
| Date | Previous | Data- | MAE | MSE | RMSE | ErrorSD | NSE | Inter- | Slope | |
|---|---|---|---|---|---|---|---|---|---|---|
| Date | Set | cept | ||||||||
| 27 April 2007 | 26 March 2007 | NDVI | 0.142 | −0.142 | 0.152 | 0.056 | −2.180 | −0.012 | 0.515 | 0.586 |
| 13 May 2007 | 27 April 2007 | NDVI | 0.077 | −0.069 | 0.103 | 0.077 | −0.189 | 0.073 | 0.578 | 0.410 |
| 29 May 2007 | 13 May 2007 | NDVI | 0.060 | −0.035 | 0.076 | 0.067 | 0.731 | 0.111 | 0.605 | 0.870 |
| 14 June 2007 | 29 May 2007 | NDVI | 0.042 | 0.038 | 0.047 | 0.027 | 0.905 | 0.057 | 0.942 | 0.968 |
| 30 June 2007 | 14 June 2007 | NDVI | 0.038 | −0.019 | 0.048 | 0.044 | 0.936 | 0.050 | 0.804 | 0.976 |
| 1 August 2007 | 30 June 2007 | NDVI | 0.077 | 0.077 | 0.086 | 0.037 | 0.756 | 0.061 | 1.059 | 0.963 |
| 17 August 2007 | 1 August 2007 | NDVI | 0.023 | 0.017 | 0.030 | 0.025 | 0.966 | 0.004 | 1.051 | 0.982 |
| 2 September 2007 | 17 August 2007 | NDVI | 0.017 | 0.005 | 0.023 | 0.022 | 0.980 | 0.003 | 1.006 | 0.982 |
| Date | Data Set | MAE | MSE | RMSE | Error SD | NSE | Intercept | Slope | |
|---|---|---|---|---|---|---|---|---|---|
| 27 April 2007 | Green | 229.172 | 148.714 | 333.796 | 298.840 | 0.053 | 99.360 | 0.358 | 0.270 |
| Red | 232.321 | 122.325 | 377.638 | 357.280 | 0.329 | 87.230 | 0.474 | 0.410 | |
| NIR | 227.374 | 101.759 | 339.601 | 323.999 | 0.405 | 126.700 | 0.517 | 0.464 | |
| 13 May 2007 | Green | 63.016 | −53.908 | 77.160 | 55.205 | 0.875 | −16.910 | 1.083 | 0.954 |
| Red | 76.917 | −58.629 | 96.561 | 76.725 | 0.929 | −14.560 | 1.060 | 0.964 | |
| NIR | 157.154 | −85.866 | 225.754 | 208.788 | 0.570 | 65.180 | 0.744 | 0.647 | |
| 29 May 2007 | Green | 68.304 | 54.570 | 82.069 | 61.299 | 0.892 | 30.580 | 0.817 | 0.961 |
| Red | 87.665 | 56.253 | 106.767 | 90.747 | 0.947 | 27.110 | 0.854 | 0.977 | |
| NIR | 128.410 | −94.798 | 168.274 | 139.031 | 0.822 | 62.970 | 0.769 | 0.897 | |
| 14 June 2007 | Green | 104.656 | −102.948 | 119.241 | 60.168 | 0.782 | −23.220 | 1.086 | 0.961 |
| Red | 117.969 | −107.972 | 141.261 | 91.087 | 0.907 | −27.540 | 1.104 | 0.978 | |
| NIR | 107.866 | 42.687 | 139.203 | 132.498 | 0.878 | −37.650 | 1.133 | 0.932 | |
| 30 June 2007 | Green | 71.448 | 60.893 | 85.524 | 60.054 | 0.932 | 22.670 | 0.885 | 0.975 |
| Red | 91.783 | 63.634 | 111.525 | 91.589 | 0.964 | 22.670 | 0.897 | 0.983 | |
| NIR | 133.999 | −92.914 | 176.863 | 150.493 | 0.867 | 57.930 | 0.790 | 0.923 | |
| 1 August 2007 | Green | 71.702 | −69.025 | 83.267 | 46.572 | 0.939 | −6.799 | 0.999 | 0.981 |
| Red | 83.710 | −77.200 | 101.627 | 66.093 | 0.971 | −47.127 | 0.982 | 0.988 | |
| NIR | 125.724 | −91.562 | 159.062 | 130.067 | 0.842 | 35.800 | 0.841 | 0.898 | |
| 17 August 2007 | Green | 44.814 | −14.633 | 58.288 | 56.421 | 0.971 | 1.951 | 0.976 | 0.973 |
| Red | 72.434 | −55.137 | 91.863 | 73.476 | 0.976 | −4.255 | 0.992 | 0.985 | |
| NIR | 119.299 | −13.138 | 152.453 | 151.887 | 0.854 | 52.380 | 0.796 | 0.859 | |
| 2 September 2007 | Green | 106.265 | 86.322 | 121.152 | 85.008 | 0.871 | 16.870 | 0.935 | 0.936 |
| Red | 109.260 | 97.836 | 128.196 | 82.839 | 0.951 | 11.960 | 0.986 | 0.980 | |
| NIR | 164.839 | 131.660 | 197.753 | 147.554 | 0.785 | 44.210 | 0.871 | 0.880 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olsoy, P.J.; Mitchell, J.; Glenn, N.F.; Flores, A.N. Assessing a Multi-Platform Data Fusion Technique in Capturing Spatiotemporal Dynamics of Heterogeneous Dryland Ecosystems in Topographically Complex Terrain. Remote Sens. 2017, 9, 981. https://doi.org/10.3390/rs9100981
Olsoy PJ, Mitchell J, Glenn NF, Flores AN. Assessing a Multi-Platform Data Fusion Technique in Capturing Spatiotemporal Dynamics of Heterogeneous Dryland Ecosystems in Topographically Complex Terrain. Remote Sensing. 2017; 9(10):981. https://doi.org/10.3390/rs9100981
Chicago/Turabian StyleOlsoy, Peter J., Jessica Mitchell, Nancy F. Glenn, and Alejandro N. Flores. 2017. "Assessing a Multi-Platform Data Fusion Technique in Capturing Spatiotemporal Dynamics of Heterogeneous Dryland Ecosystems in Topographically Complex Terrain" Remote Sensing 9, no. 10: 981. https://doi.org/10.3390/rs9100981