Mapping Extent Dynamics of Small Lakes Using Downscaling MODIS Surface Reflectance
Abstract
:1. Introduction
2. Study Area and Data Source
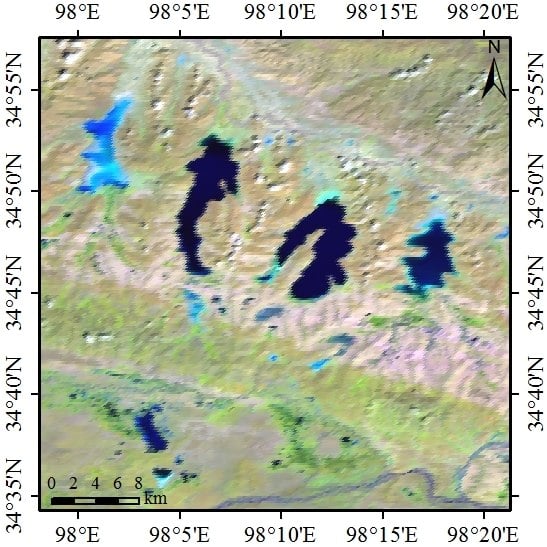
2.1. Study Area
2.2. Data Sources
3. Methods
3.1. Downscaling Method
3.1.1. Regression between Finer and Coarser Bands
3.1.2. Optimal Window (OW) Selection
3.1.3. Residuals Interpolation using PSF
3.2. Water Detection Method
3.3. Trend and Season Decomposition Model
3.4. Accuracy Assessment
3.4.1. MODIS–Landsat-7 ETM+ SR Comparison
- (1)
- To be comparable between Landsat and MODIS pixels, the image was aggregated to MODIS projection and pixel footprint.
- (2)
- Homogeneous regions at the Landsat and the MODIS resolutions were identified. Specifically, for the MODIS pixel, a value range is calculated as the difference between the maximum and the minimum values of the 9 MODIS pixels in the 3 × 3 window centered at that MODIS pixel. Similarly, the value range of all Landsat pixels located within a MODIS pixel coverage is also calculated. The MODIS pixels with two value ranges less than 0.03 were considered to be homogeneous.
- (3)
- To avoid the potential impact of different view zenith angles on the reflectance values (BRDF effect), only MODIS pixels having view zenith angles within the view zenith angle range of the Landsat (i.e., ±7.5° from nadir) were used in the comparison.
- (4)
- To minimize the impact due to cloud movement on the comparison results, both cloud and shadow pixels from MODIS and Landsat were excluded using MODIS QA band.
3.4.2. Spectral Fidelity Assessment
3.4.3. Water Classification Test on Fused Images
4. Results
4.1. Comparison of MODIS–Landsat-7 ETM+ SR
4.2. Fidelity of Downscaled MODIS SR
4.3. Improvement of Water Classification on Fused Image
4.4. Lake Dynamics Trend
5. Discussion
5.1. Usability of CC, OW, PSF for Downscaling Method
5.2. Analysis of Lake Dynamics
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated water extraction index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Downing, J.A. Emerging global role of small lakes and ponds: Little things mean a lot. Limnetica 2010, 29, 9–24. [Google Scholar]
- Liu, C.; Xian, D.; Quan, J. The change of effectively irrigated land area in China during the past 20 years. Resour. Sci. 2006, 28, 8–12. [Google Scholar]
- Huang, Z.; Xue, B.; Yao, S.; Pang, Y. Lake evolution and its implication for environmental changes in China during 1950–2000. J. Geogr. Sci. 2008, 18, 131–141. [Google Scholar] [CrossRef]
- Cammalleri, C.; Ciraolo, G.; Minacapilli, M.; Rallo, G. Evapotranspiration from an olive orchard using remote sensing-based dual crop coefficient approach. Water Resour. Manag. 2013, 27, 4877–4895. [Google Scholar] [CrossRef]
- Che, X.; Feng, M.; Jiang, H.; Song, J.; Jia, B. Downscaling MODIS surface reflectance to improve water body extraction. Adv. Meteorol. 2015. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, R.; Jain, M.; Lohani, A. Delineation of flood-prone areas using remote sensing techniques. Water Resour. Manag. 2005, 19, 333–347. [Google Scholar] [CrossRef]
- Frazier, P.S.; Page, K.J. Water body detection and delineation with Landsat TM data. Photogramm. Eng. Remote Sens. 2000, 66, 1461–1468. [Google Scholar]
- Smith, L.C. Satellite remote sensing of river inundation area, stage, and discharge: A review. Hydrol. Process. 1997, 11, 1427–1439. [Google Scholar] [CrossRef]
- Sun, F.; Zhao, Y.; Gong, P.; Ma, R.; Dai, Y. Monitoring dynamic changes of global land cover types: Fluctuations of major lakes in China every 8 days during 2000–2010. Chin. Sci. Bull. 2014, 59, 171–189. [Google Scholar] [CrossRef]
- Vikhamar, D.; Solberg, R. Snow-cover mapping in forests by constrained linear spectral unmixing of MODIS data. Remote Sens. Environ. 2003, 88, 309–323. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Kim, S.-H.; Kang, S.-J.; Lee, K.-S. Comparison of fusion methods for generating 250 m MODIS image. Korean J. Remote Sens. 2010, 26, 305–316. [Google Scholar]
- Ribeiro Sales, M.H.; Souza, C.M.; Kyriakidis, P.C. Fusion of MODIS images using kriging with external drift. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2250–2259. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Zhao, Y. Downscaling MODIS images with area-to-point regression kriging. Remote Sens. Environ. 2015, 166, 191–204. [Google Scholar] [CrossRef]
- Ma, R.; Yang, G.; Duan, H.; Jiang, J.; Wang, S.; Feng, X.; Li, A.; Kong, F.; Xue, B.; Wu, J. China’s lakes at present: Number, area and spatial distribution. Sci. China Earth Sci. 2011, 54, 283–289. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Zhang, S.; Shao, Q.; Liu, J.; Xu, X. Land use and landscape pattern change in Madoi County, the source region of Yellow River. Geo-Inf. Sci. 2007, 4, 021. [Google Scholar]
- Wang, S.; Dou, H. Chinese Lakes; Science Press: Beijing, China, 1998; p. 5. [Google Scholar]
- Wan, L.; Cao, W.; Zhou, X.; Hu, F.; Li, Z.; Xu, W. Changes of the water environment in the headwater area of the Yellow River and the cause for the zero-flow of the river occurring in winter. Geol. Bull. China 2003, 22, 521–526. (In Chinese) [Google Scholar]
- The National Disaster Monthly Report. Disaster Reduction in China; National Disaster Reduction Center: Beijing, China, 2007; pp. 54–63.
- Salomonson, V.V.; Barnes, W.; Maymon, P.W.; Montgomery, H.E.; Ostrow, H. Modis: Advanced facility instrument for studies of the earth as a system. IEEE Trans. Geosci. Remote Sens. 1989, 27, 145–153. [Google Scholar] [CrossRef]
- Vermote, E.; Kotchenova, S.; Ray, J. Modis Surface Reflectance User’s Guide; MODIS Land Surface Reflectance Science Computing Facility; Terrestrial Information Systems Laboratory: Maryland, MD, USA, 2008; p. 1. [Google Scholar]
- MODIS. Available online: http://modis.gsfc.nasa.gov (accessed on 7 October 2016).
- Vermote, E.F.; El Saleous, N.Z.; Justice, C.O. Atmospheric correction of MODIS data in the visible to middle infrared: First results. Remote Sens. Environ. 2002, 83, 97–111. [Google Scholar] [CrossRef]
- Global Land Cover Facility. Available online: http://www.landcover.org/data/gls_SR (accessed on 10 October 2016).
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.G.; Wolfe, R.E.; Huang, C. Building a consistent medium resolution satellite data set using moderate resolution imaging spectroradiometer products as reference. J. Appl. Remote Sens. 2010, 4, 043526. [Google Scholar]
- Zheng, W.; Shao, J.; Wang, M.; Huang, D. A thin cloud removal method from remote sensing image for water body identification. Chin. Geogr. Sci. 2013, 23, 460–469. [Google Scholar] [CrossRef]
- Lu, J.; Li, S. Improvement of the techniques for distinguishing water bodies from TM data. Remote Sens. Environ. 1992, 7, 17–23. [Google Scholar]
- Ovakoglou, G.; Alexandridis, T.K.; Crisman, T.L.; Skoulikaris, C.; Vergos, G.S. Use of MODIS satellite images for detailed lake morphometry: Application to basins with large water level fluctuations. Int. J. Appl. Earth Obs. Geo-Inf. 2016, 51, 37–46. [Google Scholar] [CrossRef]
- Li, X.-M.; Wang, G.; Tian, J. Study of the method of picking-up small water-bodies in Landsat TM remote sensing image. J. Southwest Agric. Univ. 2006, 4, 15. [Google Scholar]
- Ding, L.; Wu, H.; Wang, C.; Qin, Z.; Zhang, Q. Study of the water body extracting from MODIS images based on spectrum-photometric method. Geomat. Spat. Inf. Technol. 2006, 29, 25–27. [Google Scholar]
- Zhou, C.; Luo, J.; Yang, X.; Yang, C. Geo-Understanding and Analysis in Remote Sensing Image; Science Press: Beijing, China, 2003. [Google Scholar]
- Xu, H. A study on information extraction of water body with the modified normalized difference water index (MNDWI). J. Remote Sens. 2005, 5, 589–595. [Google Scholar]
- Hu, C.; Lee, Z.; Ma, R.; Yu, K.; Li, D.; Shang, S. Moderate resolution imaging spectroradiometer (MODIS) observations of cyanobacteria blooms in Taihu Lake, China. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Jiang, H.; Feng, M.; Zhu, Y.; Lu, N.; Huang, J.; Xiao, T. An automated method for extracting rivers and lakes from Landsat imagery. Remote Sens. 2014, 6, 5067–5089. [Google Scholar] [CrossRef]
- Verbesselt, J.; Zeileis, A.; Hyndman, R.; Verbesselt, M.J. Package ‘bfast’. 2012. Available online: https://cran.r-project.org/web/packages/bfast/bfast.pdf (accessed on 16 January 2017).
- Quan, J.; Zhan, W.; Chen, Y.; Wang, M.; Wang, J. Time series decomposition of remotely sensed land surface temperature and investigation of trends and seasonal variations in surface urban heat islands. J. Geophys. Res. Atmos. 2016, 121, 2638–2657. [Google Scholar] [CrossRef]
- Zeileis, A.; Kleiber, C.; Krämer, W.; Hornik, K. Testing and dating of structural changes in practice. Comput. Stat. Data Anal. 2003, 44, 109–123. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.S. Modelling of diurnal cycles of brightness temperature extracted from METEOSAT data. Remote Sens. Environ. 2001, 76, 337–348. [Google Scholar] [CrossRef]
- Zeileis, A.; Leisch, F.; Hornik, K.; Kleiber, C. Strucchange. An R Package for Testing for Structural Change in Linear Regression Models; WU Vienna University of Economics and Business: Vienna, Austria, 2001. [Google Scholar]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS–Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Feng, M.; Huang, C.; Channan, S.; Vermote, E.F.; Masek, J.G.; Townshend, J.R. Quality assessment of Landsat surface reflectance products using MODIS data. Comput. Geosci. 2012, 38, 9–22. [Google Scholar] [CrossRef]
- Hakanson, L. A Manual of Lake Morphometry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Thomas, I.; Frankhauser, P.; Biernacki, C. The morphology of built-up landscapes in Wallonia (Belgium): A classification using fractal indices. Landsc. Urban Plan. 2008, 84, 99–115. [Google Scholar] [CrossRef]
- Sun, W.; Xu, G.; Gong, P.; Liang, S. Fractal analysis of remotely sensed images: A review of methods and applications. Int. J. Remote Sens. 2006, 27, 4963–4990. [Google Scholar] [CrossRef]
- Sirguey, P.; Mathieu, R.; Arnaud, Y.; Khan, M.M.; Chanussot, J. Improving MODIS spatial resolution for snow mapping using wavelet fusion and ARSIS concept. IEEE Geosci. Remote Sens. Lett. 2008, 5, 78–82. [Google Scholar] [CrossRef]
- Trishchenko, A.P.; Luo, Y.; Khlopenkov, K.V. A Method for Downscaling Modis Land Channels to 250 m Spatial Resolution Using Adaptive Regression and Normalization Alexander; SPIE: Bellingham, WA, USA, 2006; Volume 6366. [Google Scholar]
- Van der Meer, F. Remote-sensing image analysis and geostatistics. Int. J. Remote Sens. 2012, 33, 5644–5676. [Google Scholar] [CrossRef]
- Trishchenko, A.P.; Luo, Y.; Khlopenkov, K.V.; Wang, S. A method to derive the multispectral surface albedo consistent with MODIS from historical ANHRR and VGT satellite data. J. Appl. Meteorol. Climatol. 2008, 47, 1199–1221. [Google Scholar] [CrossRef]
- Duan, S.; Fan, S.; Cao, G.; Liu, X.; Sun, Y. The changing features and cause analysis of the lakes in the source regions of the Yellow River from 1976 to 2014. J. Glaciol. Geocryol. 2015, 37, 745–756. [Google Scholar]
- Che, X.; Feng, M.; Jiang, H. Detection and Analysis of Qinghai-Tibet Plateau Lake Areas from 2000 to 2013. J. Geo-Inf. Sci. 2015, 17, 99–107. [Google Scholar]
- Qin, B.; Shi, Y.; Yu, G. Lake level fluctuations of Asia inland lakes during 18 kaBP and 6 kaBP with their significance. Chin. Sci. Bull. 1997, 42, 2586–2595. [Google Scholar]
- Zou, K.H.; Tuncali, K.; Silverman, S.G. Correlation and simple linear regression 1. Radiology 2003, 227, 617–628. [Google Scholar] [CrossRef] [PubMed]
- Berry, P.; Garlick, J.; Freeman, J.; Mathers, E. Global inland water monitoring from multi-mission altimetry. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]







 indicates the location of the breakpoints; (a) is the area dynamics for Lake I; (b) is for Lake II; (c) is for Lake III; (d) is for Lake IV.
indicates the location of the breakpoints; (a) is the area dynamics for Lake I; (b) is for Lake II; (c) is for Lake III; (d) is for Lake IV.
 indicates the location of the breakpoints; (a) is the area dynamics for Lake I; (b) is for Lake II; (c) is for Lake III; (d) is for Lake IV.
indicates the location of the breakpoints; (a) is the area dynamics for Lake I; (b) is for Lake II; (c) is for Lake III; (d) is for Lake IV.

| Band | Band ID | Resolution (m) | Bandwidth (nm) |
|---|---|---|---|
| R | 1 (B1) | 250 | 620–670 |
| NIR | 2 (B2) | 250 | 841–876 |
| B | 3 (B3) | 500 | 459–479 |
| G | 4 (B4) | 500 | 545–565 |
| SWIR1 | 6 (B6) | 500 | 1628–1652 |
| SWIR2 | 7 (B7) | 500 | 2105–2155 |
| Index | IMAR | MAR | Wavelet | |||
|---|---|---|---|---|---|---|
| Metrics | R2 | RMSD | R2 | RMSD | R2 | RMSD |
| Band 3 (Blue) | 0.9 | 3.225 | 0.838 | 4.508 | 0.914 | 3.519 |
| Band 4 (Green) | 0.899 | 3.227 | 0.83 | 4.673 | 0.916 | 3.408 |
| Band 6 (SWIR1) | 0.92 | 2.098 | 0.907 | 2.301 | 0.887 | 4.46 |
| Band 7 (SWIR2) | 0.957 | 1.79 | 0.646 | 4.737 | 0.91 | 6.339 |
| overall | 0.919 | 2.585 | 0.805 | 4.055 | 0.908 | 4.4315 |
| Lakes | Type | OCA (%) | Ec (%) | Eo (%) | Lake Area (km2) | Reference Area (km2) |
|---|---|---|---|---|---|---|
| I | 500 m | 86.16 | 19.76 | 13.83 | 14.382 | 13.577 |
| MAR | 88.54 | 17 | 11.46 | 14.328 | ||
| IMAR | 90.12 | 13.04 | 9.88 | 14.006 | ||
| Wavelet | 88.54 | 13.04 | 11.46 | 13.79 | ||
| II | 500 m | 84.11 | 7.02 | 15.29 | 23.827 | 25.973 |
| MAR | 92.15 | 7.64 | 7.85 | 25.92 | ||
| IMAR | 94.42 | 4.54 | 5.57 | 25.705 | ||
| Wavelet | 90.91 | 4.55 | 9.09 | 24.793 | ||
| III | 500 m | 90.09 | 11.53 | 9.91 | 30.267 | 29.783 |
| MAR | 93.51 | 9.91 | 6.49 | 30.804 | ||
| IMAR | 94.95 | 4.86 | 5.04 | 29.73 | ||
| Wavelet | 93.15 | 5.59 | 6.85 | 29.408 | ||
| IV | 500 m | 78.23 | 7.57 | 7.21 | 17.602 | 17.495 |
| MAR | 88.65 | 8.28 | 11.34 | 16.26 | ||
| IMAR | 91.72 | 6.09 | 6.09 | 17.495 | ||
| Wavelet | 87.42 | 3.68 | 12.58 | 15.938 |
| Lakes | Lake I | Lake II | Lake III | Lake IV | ||||
|---|---|---|---|---|---|---|---|---|
| Variables | AMT | AMP | AMT | AMP | AMT | AMP | AMT | AMP |
| Trend | 0.955 | 0.955 | 0.999 | 0.999 | 0.604 | 0.604 | 0.767 | 0.767 |
| Season | 0.425 | 0.447 | 0.457 | 0.471 | 0.605 | 0.636 | 0.428 | 0.452 |
| Fitted_overall | 0.69 | 0.701 | 0.728 | 0.735 | 0.605 | 0.62 | 0.598 | 0.61 |
| Unfitted_overall | 0.159 | 0.251 | 0.234 | 0.248 | 0.295 | 0.265 | 0.166 | 0.194 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, X.; Yang, Y.; Feng, M.; Xiao, T.; Huang, S.; Xiang, Y.; Chen, Z. Mapping Extent Dynamics of Small Lakes Using Downscaling MODIS Surface Reflectance. Remote Sens. 2017, 9, 82. https://doi.org/10.3390/rs9010082
Che X, Yang Y, Feng M, Xiao T, Huang S, Xiang Y, Chen Z. Mapping Extent Dynamics of Small Lakes Using Downscaling MODIS Surface Reflectance. Remote Sensing. 2017; 9(1):82. https://doi.org/10.3390/rs9010082
Chicago/Turabian StyleChe, Xianghong, Yaping Yang, Min Feng, Tong Xiao, Shengli Huang, Yang Xiang, and Zugang Chen. 2017. "Mapping Extent Dynamics of Small Lakes Using Downscaling MODIS Surface Reflectance" Remote Sensing 9, no. 1: 82. https://doi.org/10.3390/rs9010082
APA StyleChe, X., Yang, Y., Feng, M., Xiao, T., Huang, S., Xiang, Y., & Chen, Z. (2017). Mapping Extent Dynamics of Small Lakes Using Downscaling MODIS Surface Reflectance. Remote Sensing, 9(1), 82. https://doi.org/10.3390/rs9010082