In this section, we explain the basic operations of our 3D-CNN-based classification method in detail, elaborate on how to train this network, and analyze what the 3D-CNN model extracts from HSI.
2.1. 3D Convolution Operation
2D-CNN has been demonstrated with great promise in the field of computer vision and image processing, with applications such as image classification [
38,
39,
40], object detection [
41,
42], and depth estimation from a single image [
43]. The most significant advantage of 2D-CNN is that it offers a principled way to extract features directly from the raw input imagery. However, directly applying 2D-CNN to HSI requires the convolution of every one of the network’s 2D inputs, and each with a set of learnable kernels. The hundreds of channels along the spectral dimension (network inputs) of HSI require a large number of kernels (parameters), which can be prone to over-fitting with increased computational costs.
In order to deal with this problem, DR methods are usually applied to reduce the spectral dimensionality prior to 2D-CNN being employed for feature extraction and classification [
33,
34,
35]. For instance, in [
33], the first three principal components (PCs) are extracted from HSI by PCA, and then a 2D-CNN is used to extract deep features from condensed HSI with a window size of 42 × 42 in order to predict the label of each pixel. Randomized PCA (R-PCA) was also introduced along the spectral dimension to compress the entire HSI in [
34], with the first 10 or 30 PCs being retained. This was carried out prior to the 2D-CNN being used to extract deep features from the compressed HIS (with a window size of 5 × 5), and subsequently to complete the classification task. Furthermore, the approach presented in [
35] requires three computational steps: The high-level features are first extracted by a 2D-CNN, where the entire HSI is whitened with the PCA algorithm, retaining the several top bands; the sparse representation technique is then applied to further reduce the high level spatial features generated by the first step. Only after these two steps are classification results obtained based on learned sparse dictionary. A clear disadvantage of these approaches is that they do not preserve the spectral information well. To address this important issue, a more sophisticated procedure for additional spectral feature extraction can be employed as reported in [
32].
To take the advantage of the capability of automatically learning features in deep learning, we herein introduce 3D-CNN into HSI processing. 3D-CNN uses 3D kernels for the 3D convolution operation, and can extract spatial features and spectral features simultaneously.
Figure 1 illustrates the key difference between the 2D convolution operation and the 3D convolution operation.
In the 2D convolution operation, input data is convolved with 2D kernels (see
Figure 1a), before going through the activation function to form the output data (i.e., feature maps). This operation can be formulated as
where
indicates the layer that is considered,
is the number of feature maps in this layer,
stands for the output at position
on the
th feature map in the
th layer,
is the bias, and
is the activation function,
indexes over the set of feature maps in the
th layer connected to the current feature map, and finally,
is the value at position
of the kernel connected to the
th feature map, with
and
being the height and width of the kernel, respectively.
In conventional 2D-CNN, convolution operations are applied to the 2D feature maps that capture features from the spatial dimension only. When applied to 3D data (e.g., for video analysis [
36]), it is desirable to capture features from both the spatial and temporal dimensions. To this end, 3D-CNN was proposed [
36], where 3D convolution operations are applied to the 3D feature cubes in an effort to compute spatiotemporal features from the 3D input data. Formally, the value at position
on the
th feature cube in the
th layer is given by:
where
is the size of the 3D kernel along the spectral dimension,
is the number of kernels in this layer, and
is the
th value of the kernel connected to the
th feature cube in the preceding layer.
In our 3D-CNN-based HSI classification model, each feature cube is treated independently. Thus,
is set to 1 in Equation (2), and the 3D convolution operation can be (re-)formulated as
where
is the spectral depth of the 3D kernel,
is the number of feature cubes in the previous layer,
is the number of kernels in this layer,
is the output at the position
that is calculated by convolving the
th feature cube of the preceding layer with the
th kernel of the
th layer, and
is the
th value of the kernel connected to the
th feature cube in the preceding layer. As such, the output data of the
th convolution layer contains
3D feature cubes.
The non-saturating activation function Rectified Linear Units (ReLUs) (as proposed by Krizhevsky et al. [
38]) form a type of the most popular choice for activation functions. In particular, in terms of training time with gradient decent, ReLUs tend to be faster than other saturating activation functions. Here we also adopt ReLUs as the activation function. Its formula is shown below:
In summary, for HSI classification, the 2D convolution operation convolves the input data in the spatial dimension, while the 3D convolution operation convolves the input data in both the spatial dimension and the spectral dimension simultaneously. For the 2D convolution operation, regardless of whether it is applied to 2D data or 3D data, its output is 2D. If 2D convolution operations were applied to HSI, substantial spectral information would be lost, while 3D convolution can preserve the spectral information of the input HSI data, resulting in an output volume. This is very important for HSI, which contains rich spectral information.
2.2. 3D-CNN-Based HSI Classification
A conventional 2D-CNN is usually composed of convolutional layers, pooling layers, and fully connected layers. Being different from 2D-CNN, the 3D-CNN used here for HSI classification consists of only convolution layers and a fully connected layer. We do not apply pooling operations, which are known for reducing the spatial resolution in HSI. Compared to the image-level classification models of [
36,
37], our 3D-CNN model is utilized for pixel-level HSI classification. It extracts image cubes consisting of pixels in a small spatial neighborhood (not the whole image) along the entire spectral bands as input data, to convolve with 3D kernels in order to learn the spectral–spatial features. Thus, the resolution of the feature maps is further reduced via the pooling operations. The reason for utilizing the neighboring pixels is based on the observation that pixels inside a small spatial neighborhood often reflect the same underlying material [
24] (as with the smoothness assumption adopted in Markov random fields).
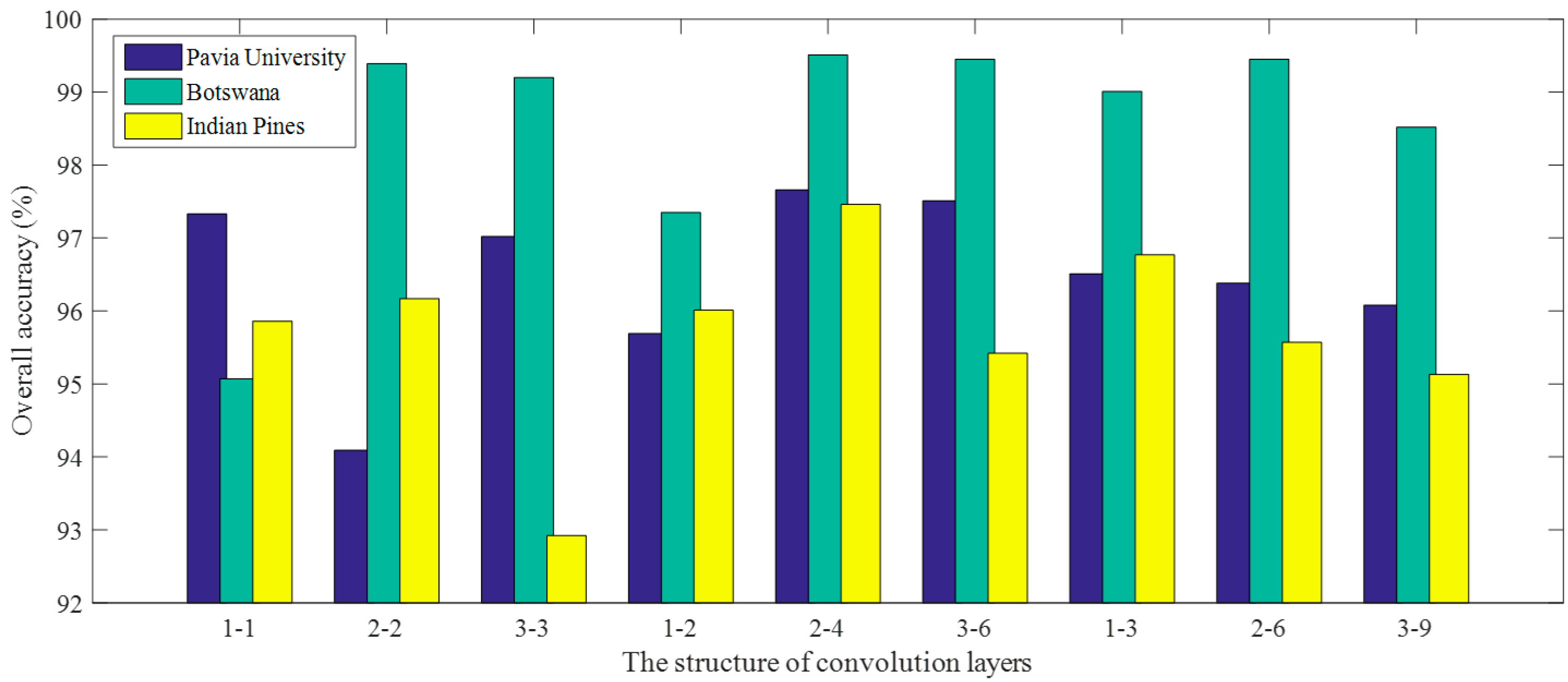
The proposed 3D-CNN model has two 3D convolution layers (C1 and C2) and a fully-connected layer (F1). According to the findings in 2D CNN [
44], small receptive fields of 3 × 3 convolution kernels with deeper architectures generally yield better results. Tran et al. have also demonstrated that small 3 × 3 × 3 kernels are the best choice for 3D CNN in spatiotemporal feature learning [
37]. Inspired by this, we fix the spatial size of the 3D convolution kernels to 3 × 3 while only slightly varying the spectral depth of the kernels. The number of convolution layers is limited by the space size of the input samples (or image cubes), with the window is empirically set to 5 × 5 in this work. Performing the convolution operation twice with a space size of 3 × 3 reduces the size of the samples to 1 × 1. Therefore, it is sufficient for the proposed 3D-CNN to contain only two convolution layers. In addition, the number of kernels in the second convolution layer is set to be twice as many as that in the first convolution layer. Such a ratio is commonly adopted by many CNN models (e.g., those reported in [
37,
38]). The input data is convolved with the learnable 3D kernels at each 3D convolution layer; the convolved results are then run through the selected activation function. The output of the F1 layer is fed to a simple linear classifier (e.g., softmax) to generate the required classification result. Note that the network is trained using the standard back propagation (BP) algorithm [
44]. In this paper, we take softmax loss [
44] as the loss function to train the classifiers. Hence, the framework is named as 3D-CNN. In this section, we explain in detail how to use 3D-CNN to effectively and efficiently classify HSI data.
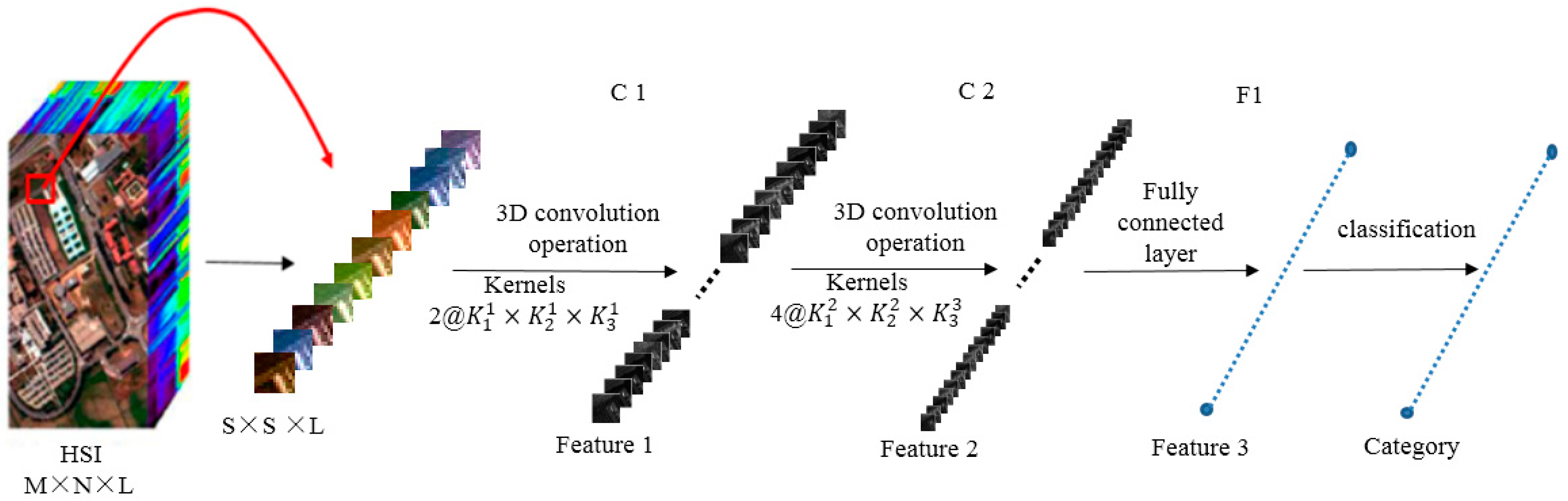
To classify a pixel, relevant information of that pixel is extracted by running the 3D-CNN model.
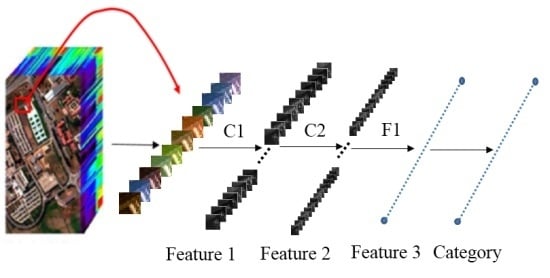
Figure 2 outlines the computational process. For illustration purposes, we divide the 3D-CNN into three steps:
Step 1: Training sample (image cube) extraction. S × S × L image cubes are extracted together with the category labels of the central pixels of these cubes as the training samples. S × S is the spatial size (window size), and L denotes the number of spectral bands.
Step 2: 3D-CNN-based deep spectral–spatial feature extraction. A sample with size S × S × L is used as the input data. The first 3D convolution layer C1 contains two 3D kernels, each of a size
producing two 3D data cubes with size
(according to 3D convolution formula Equation (3)). Each 3D kernel results in one 3D data cube. Taking the two
3D data cubes of the first C1 as input, the second 3D convolution layer C2 involves four 3D kernels (size of
), and produces eight 3D data cubes each with a size of
. The eight 3D data cubes are flattened into a feature vector and fit forward to a fully-connected layer F1, of which the output feature vector (named as Feature 3 in
Figure 2) contains the final learned deep spectral–spatial features.
Step 3: Deep spectral–spatial feature-based classification. We use the softmax loss [
44] to train the deep classifier. As in the case of 2D-CNN, the loss of the network is minimized using stochastic gradient descent with back propagation [
44]. The kernels are updated as:
where
is the iteration index,
is the momentum variable,
is the learning rate,
is the average over the
th batch
of the derivative of the objective with respect to
, and
is the parameters of 3D-CNN, including 3D kernels and biases.
2.3. Feature Analysis
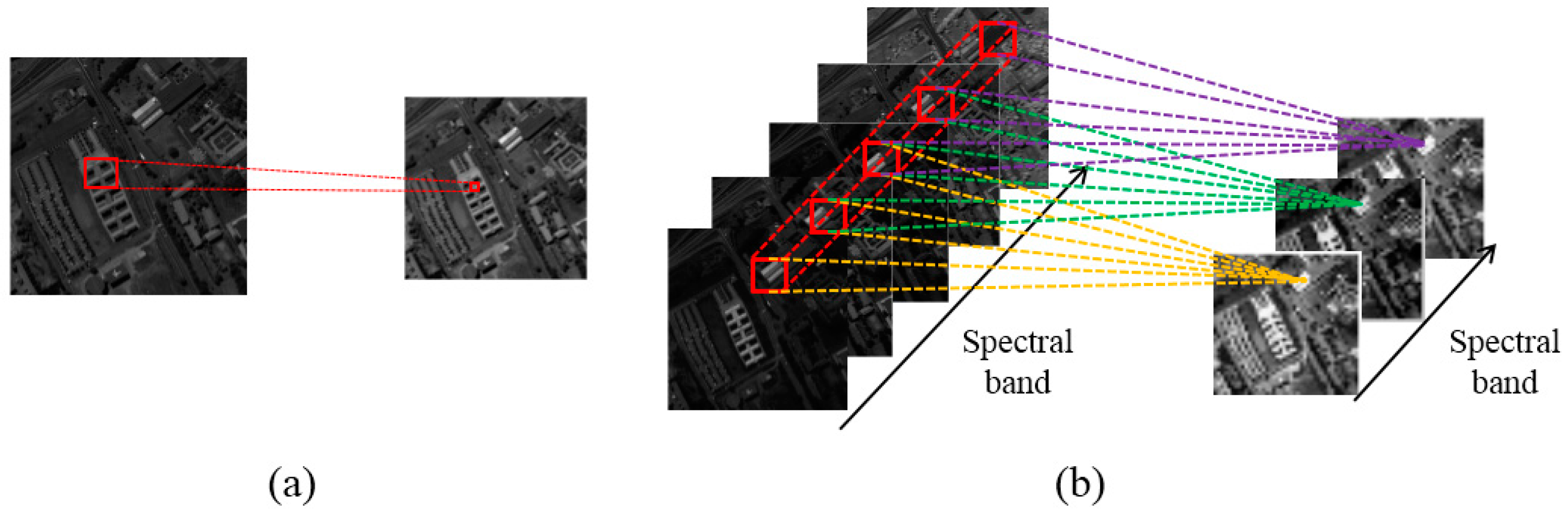
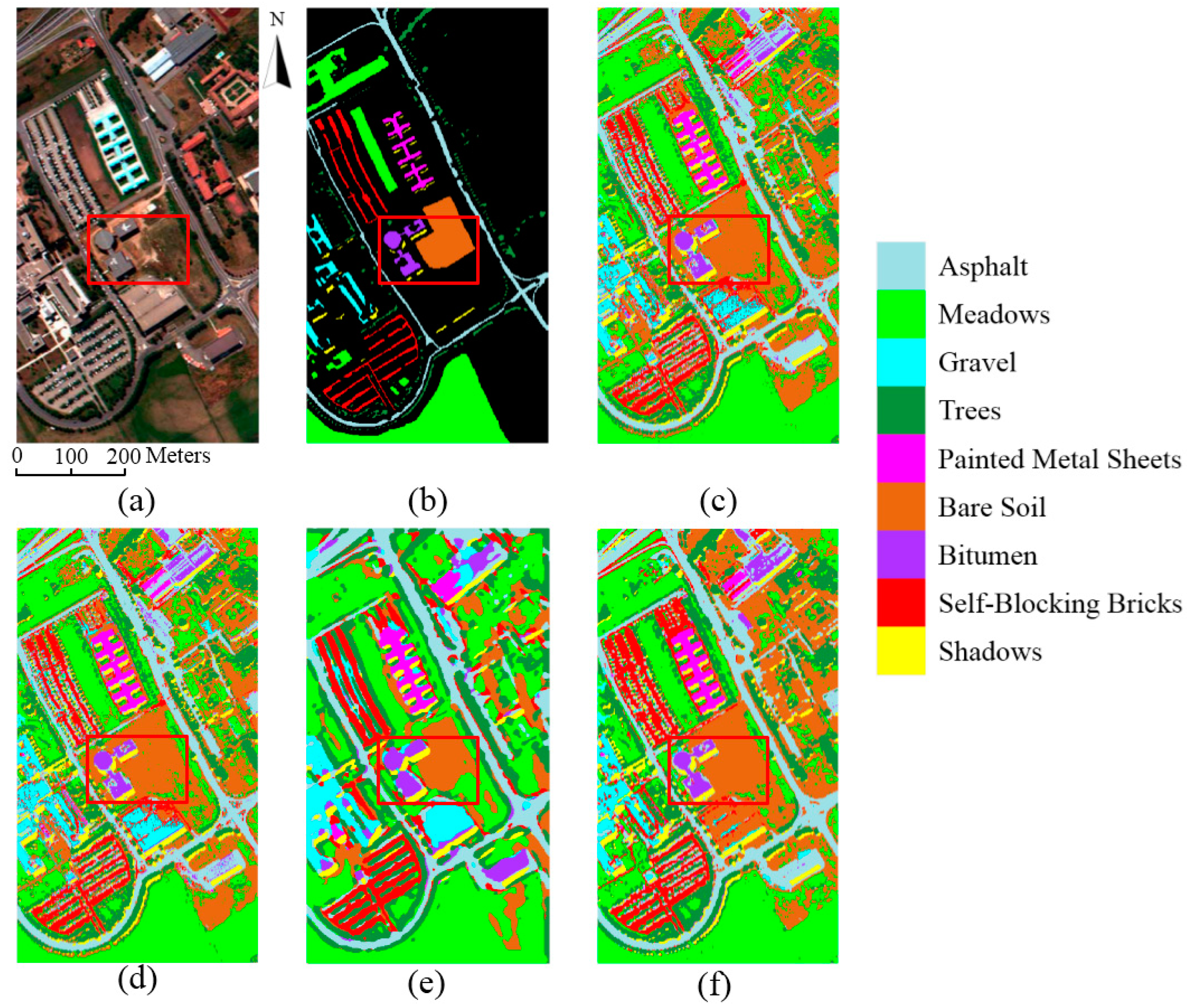
Feature analysis is important to understand the mechanism of deep learning. In this section, we illustrate what features are extracted by the proposed 3D-CNN. Taking the HSI Pavia University Scene as an example, the learned features are visualized with respect to different layers of the 3D-CNN.
The HSI Pavia University Scene contains 103 bands. One data cube was extracted with size 50 × 50 × 103 from the original HSI, and then four bands of this data cube were randomly selected and are shown in
Figure 3a. After 3D convolution operation with the first convolution layer, the data cube was converted into two data cubes, each with a spatial size of 48 × 48, eight bands of which were selected and are shown in
Figure 3b. Taking the output of the first convolution layer as the input to the second convolution layer, we extracted eight bands from the output of the second convolution layer and present them in
Figure 3c. Together, the feature images in
Figure 3 suggest the following:
- (1)
Different feature images are activated by different object types. For example, the eight feature images in
Figure 3c are basically activated by eight different contents.
- (2)
Different layers encode different feature types. At higher layers, the computed features are more abstract and distinguishable.
In general, the number of feature images produced may be very large, and a feature image can be seen as a high-level representation of the input image. A certain representation is hardly complete in capturing the underlying image information, and a large number of feature images are often necessary to represent the image well.