Maximum Likelihood Deconvolution of Beamformed Images with Signal-Dependent Speckle Fluctuations from Gaussian Random Fields: With Application to Ocean Acoustic Waveguide Remote Sensing (OAWRS)
Abstract
:1. Introduction
2. Methods: Theoretical Formulation
2.1. Beamformed Intensity Measurement on a Receiver Array
2.2. Deconvolution of Beamformed Intensity from a Line Array: Maximum Likelihood Estimate of Expected Source Intensity
2.3. Statistics of the Maximum Likelihood Estimator
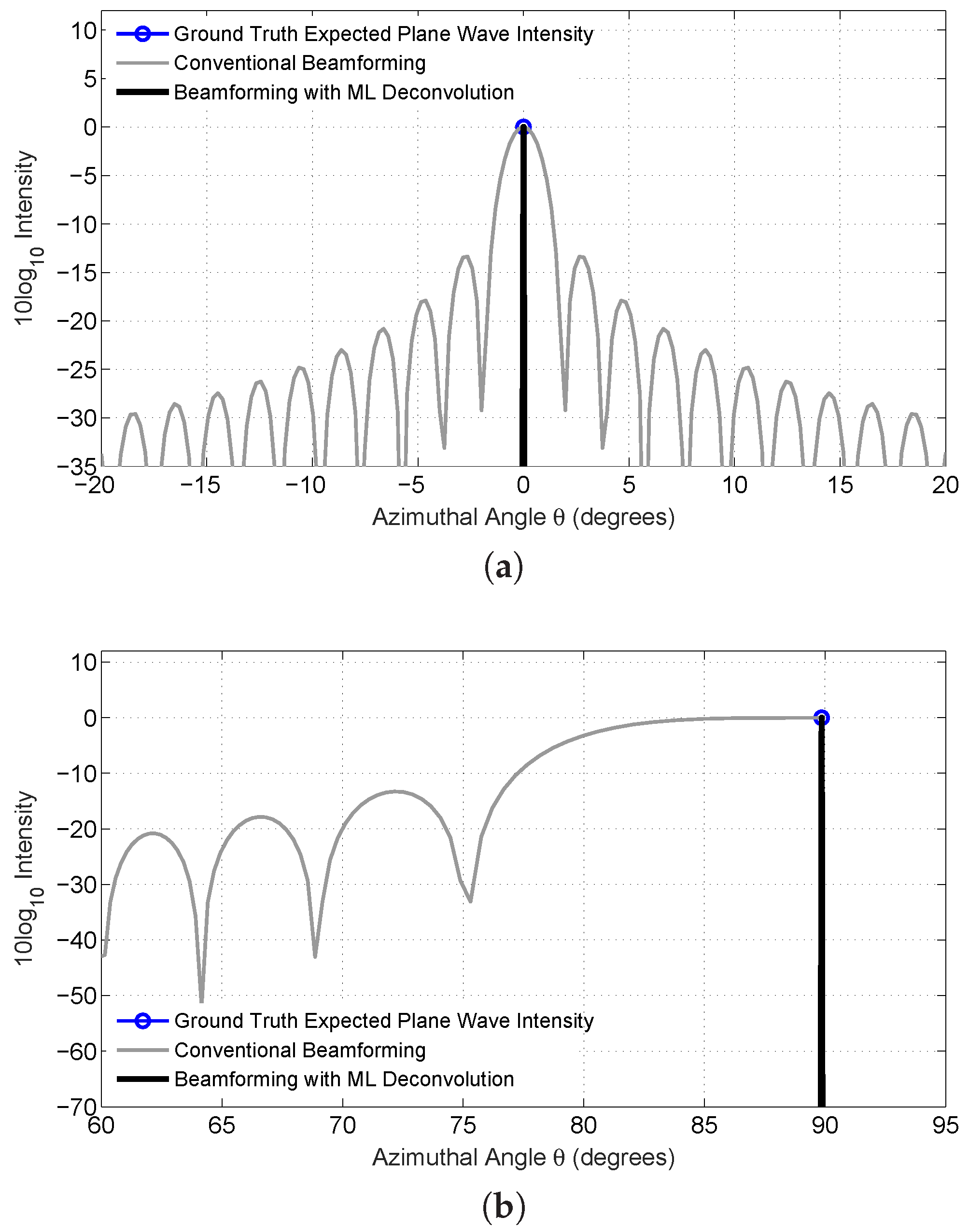
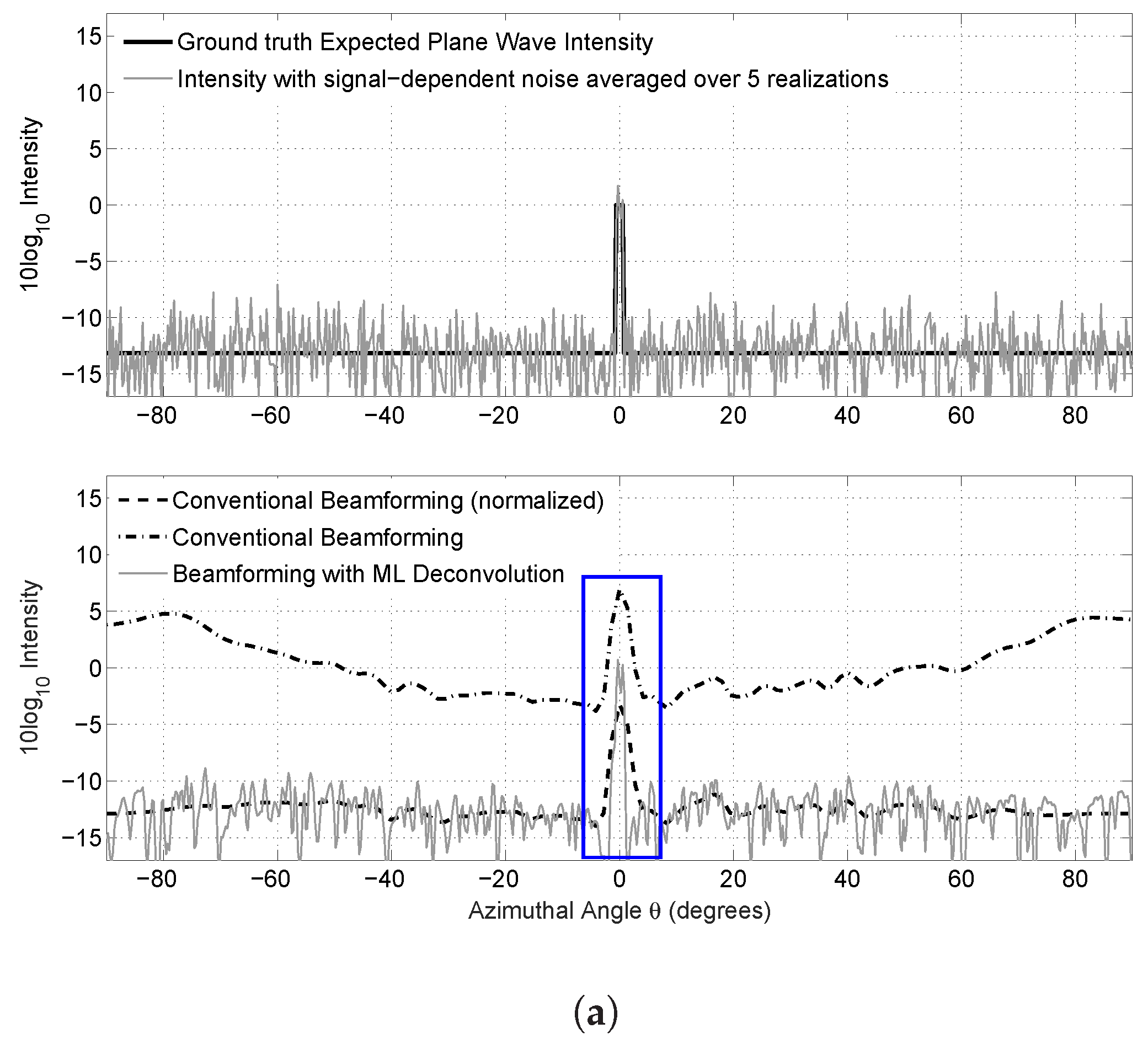
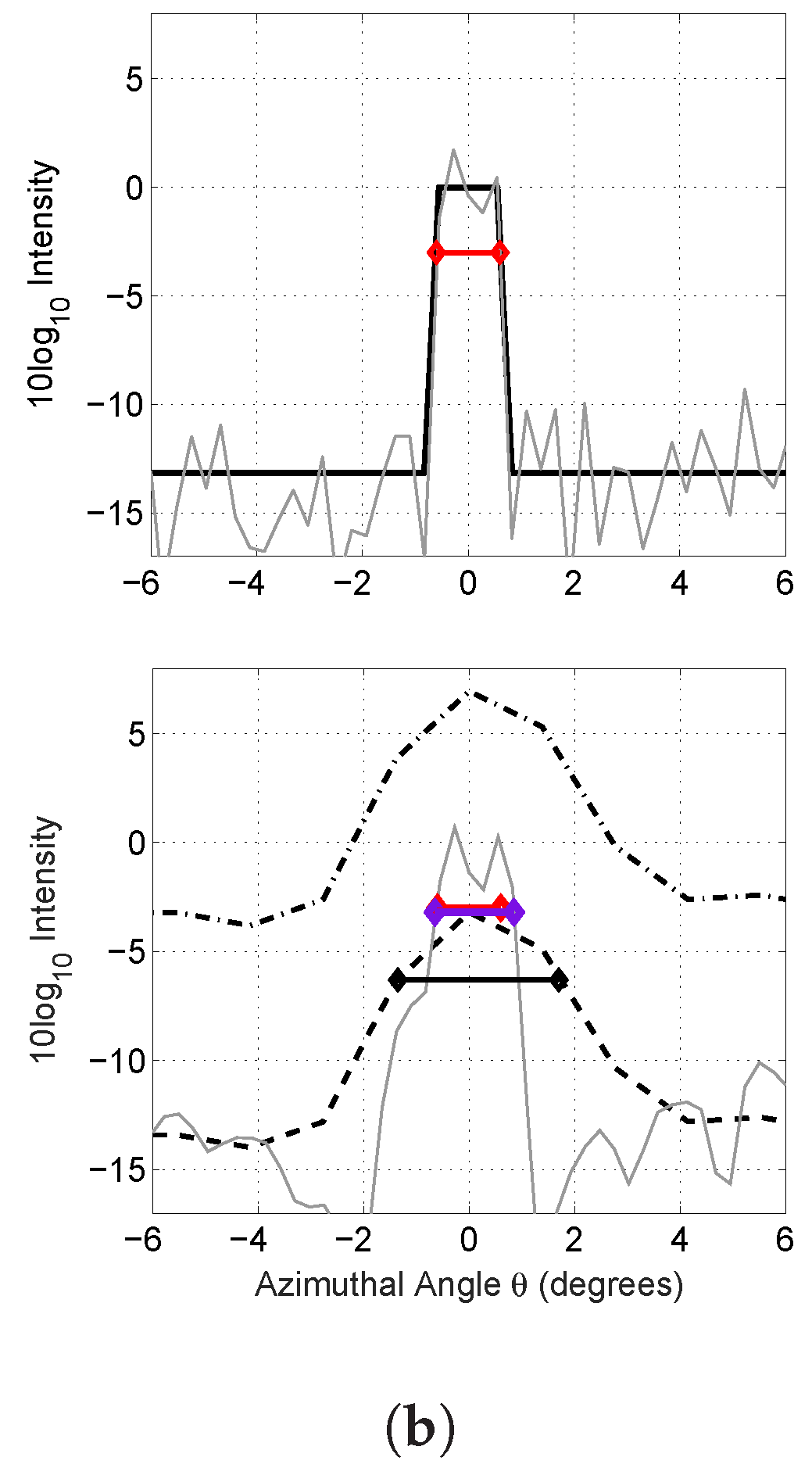
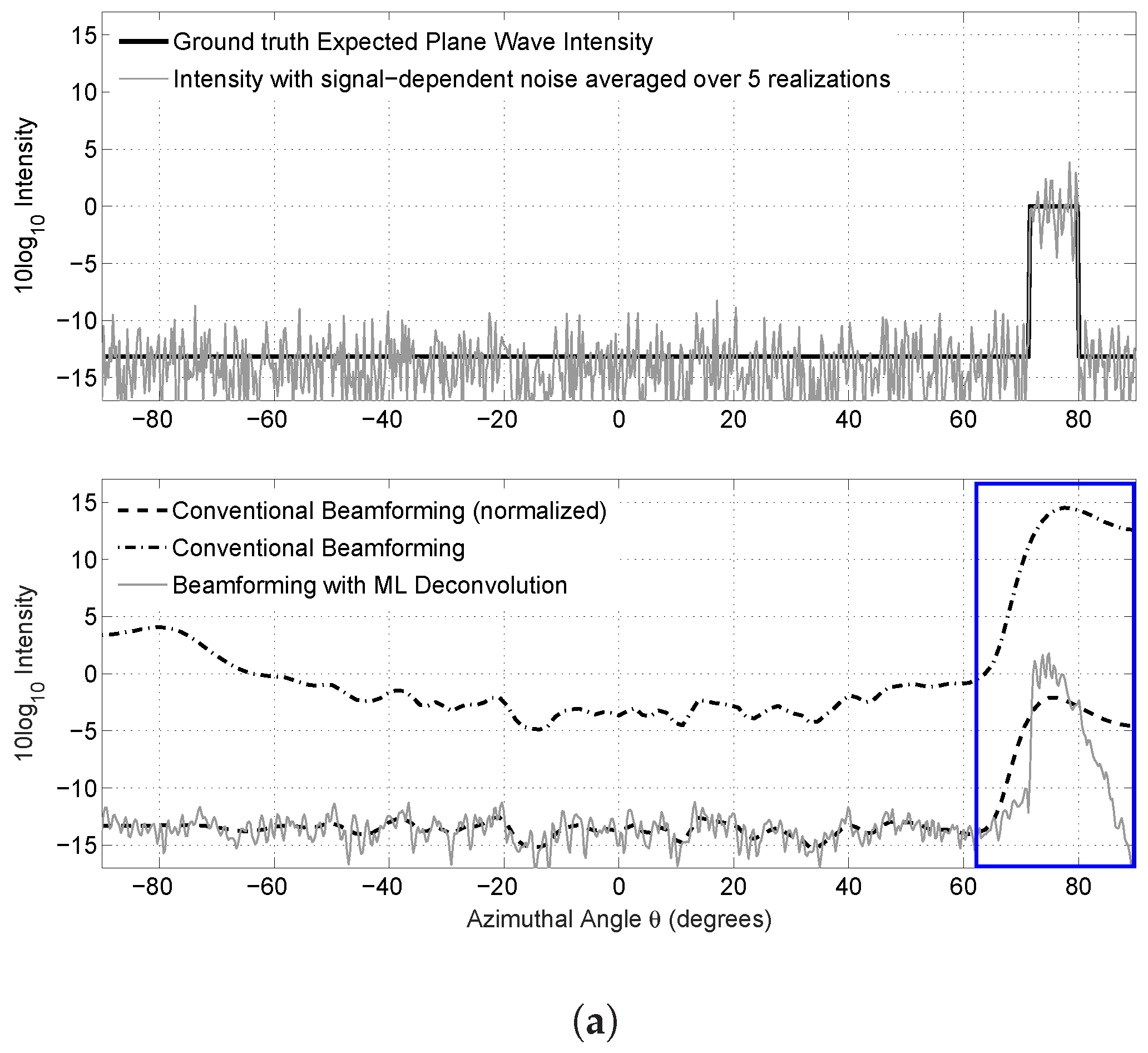
3. Results: Illustrative Examples
3.1. Analytic Solutions
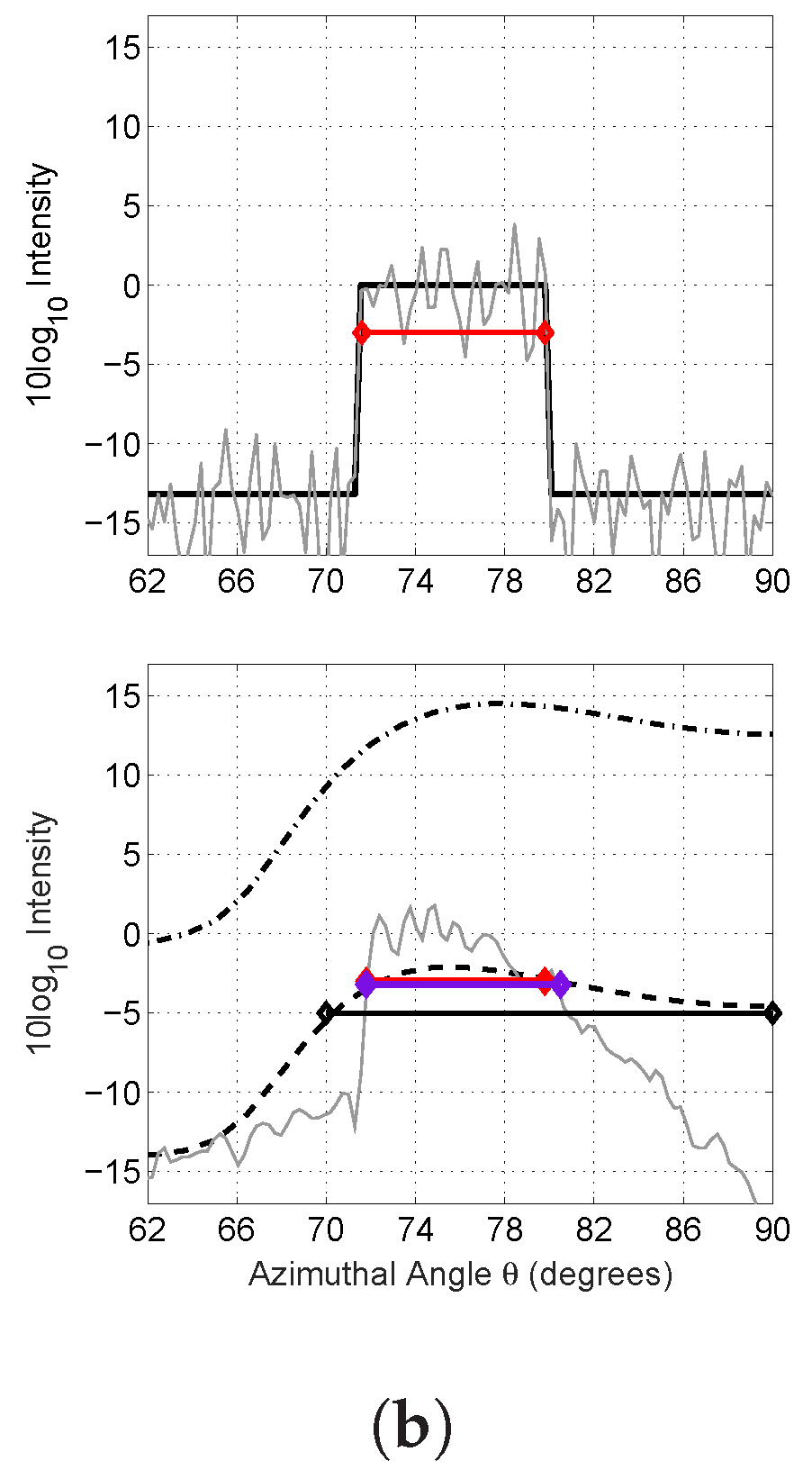
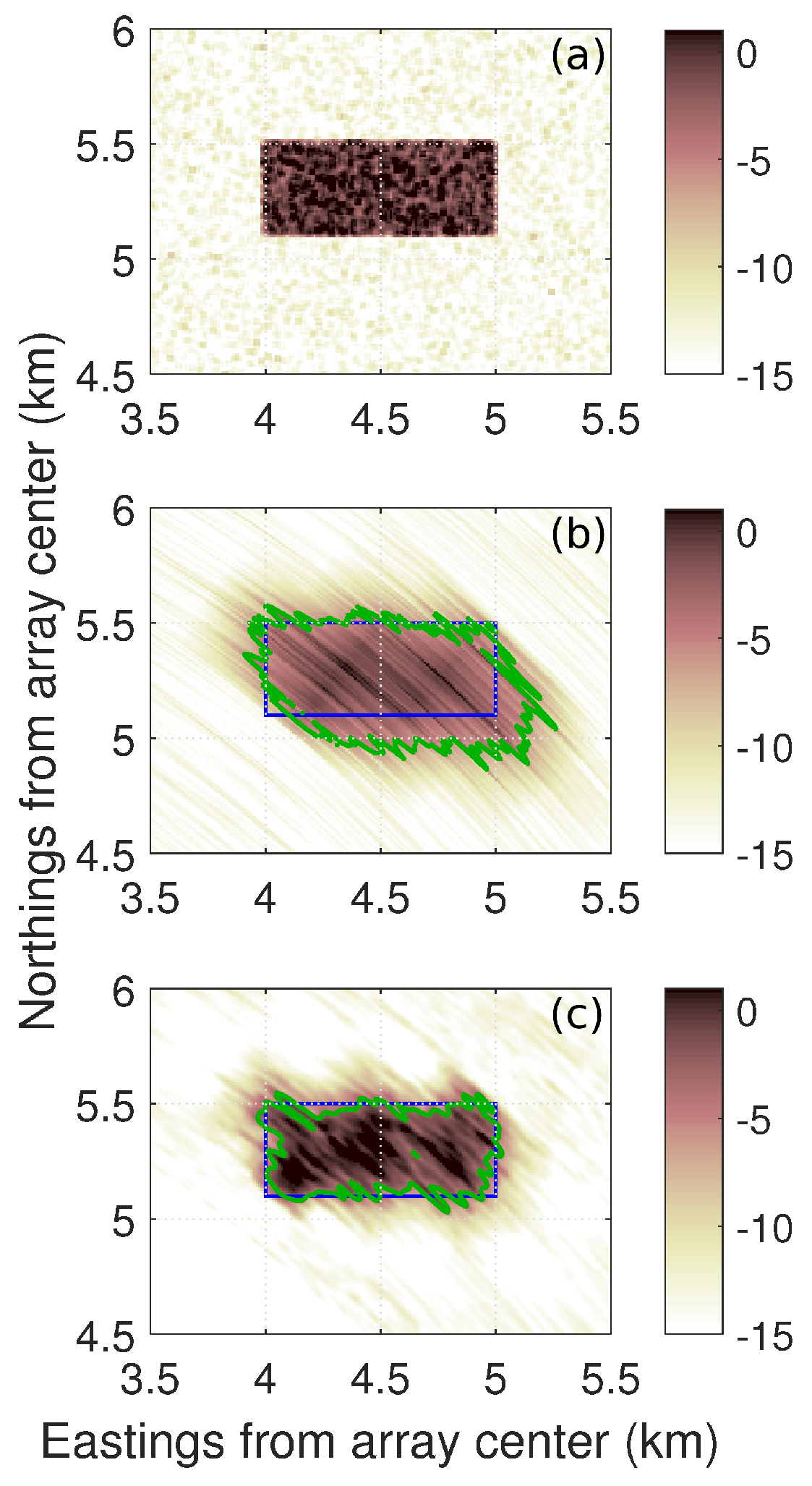
3.2. Synthetic Data
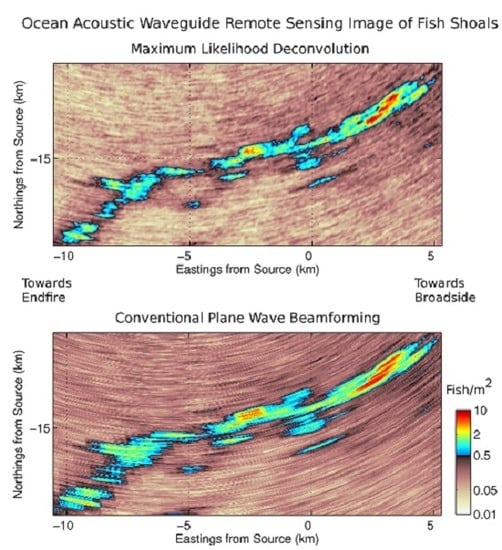
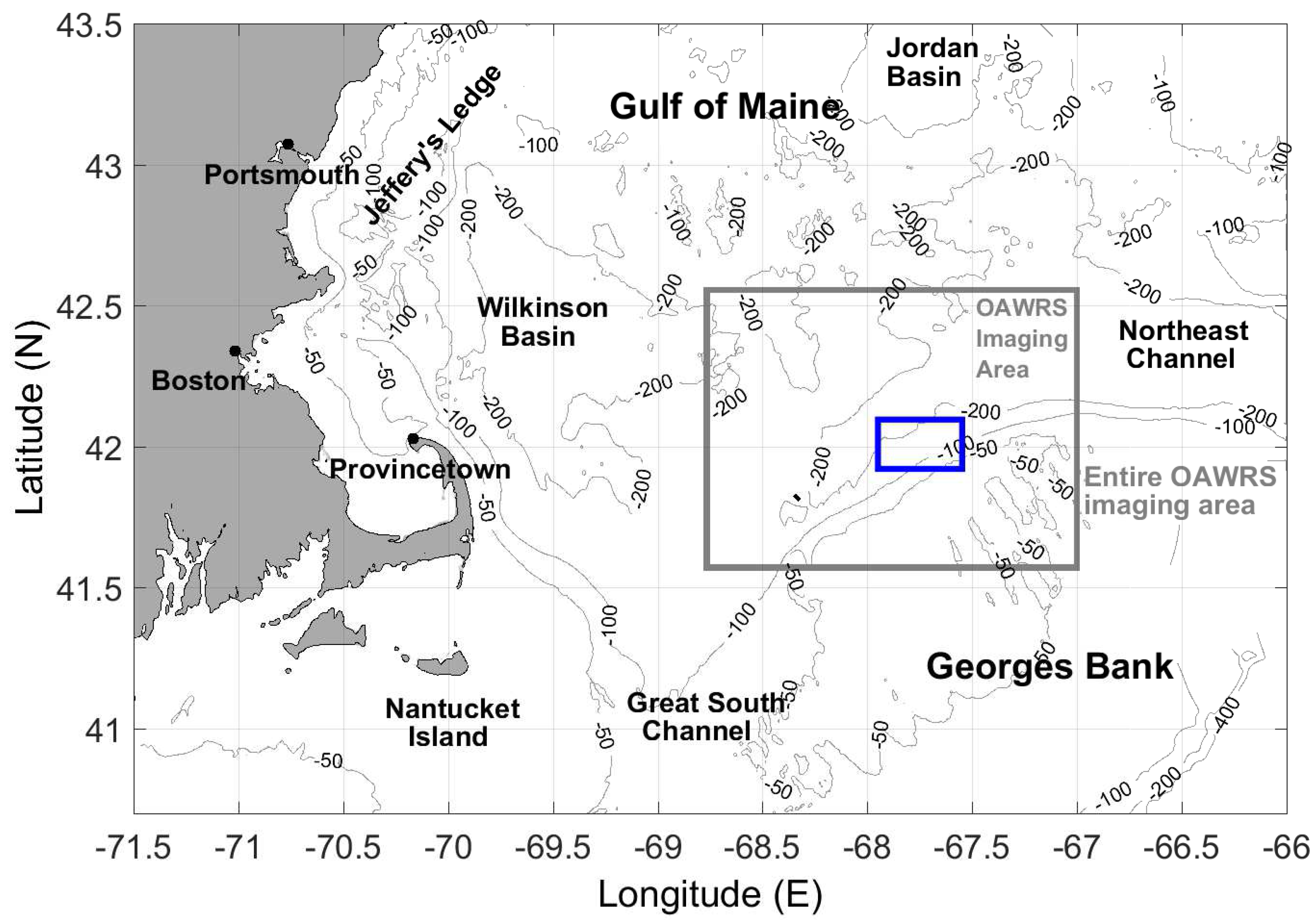
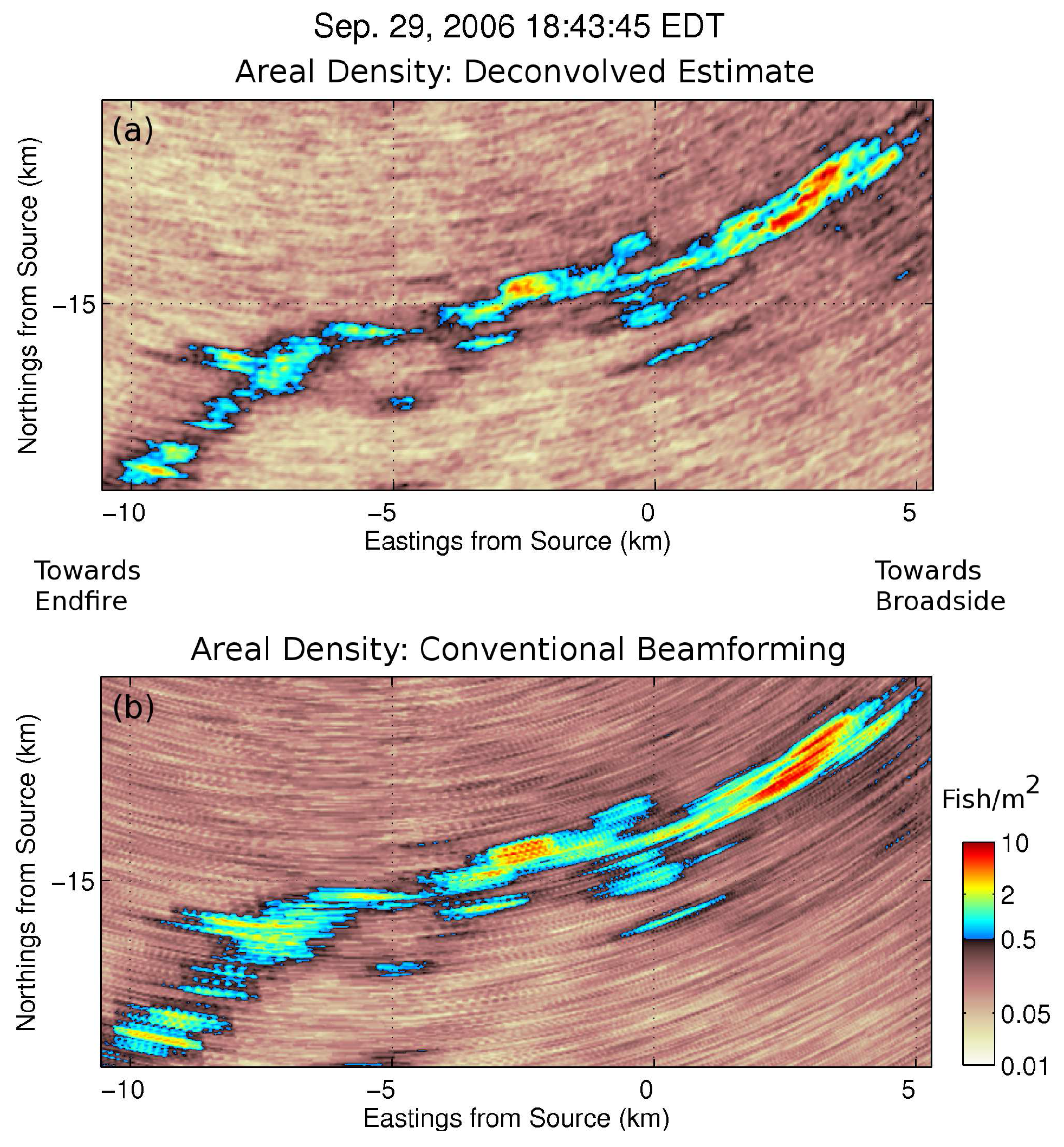
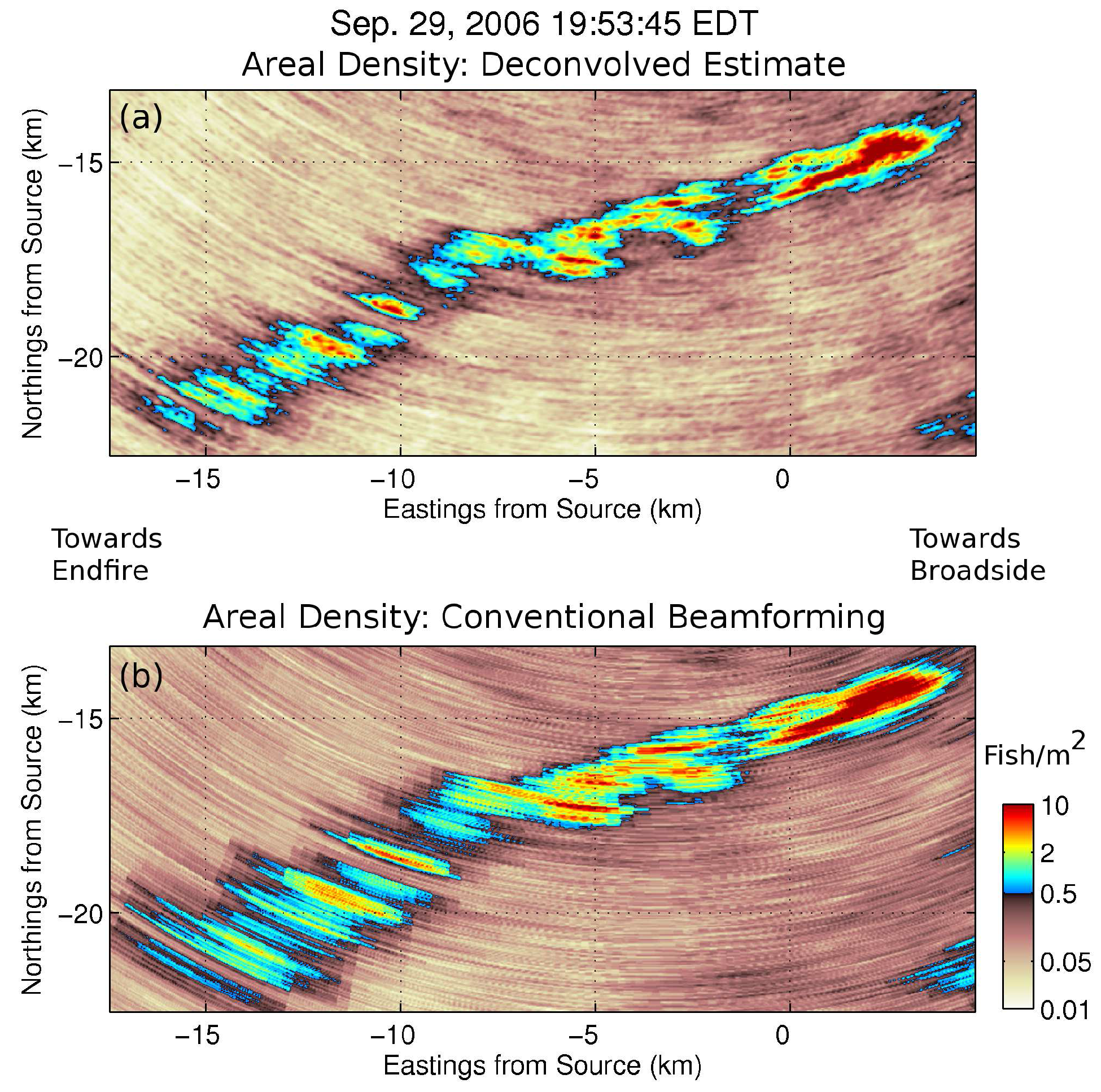
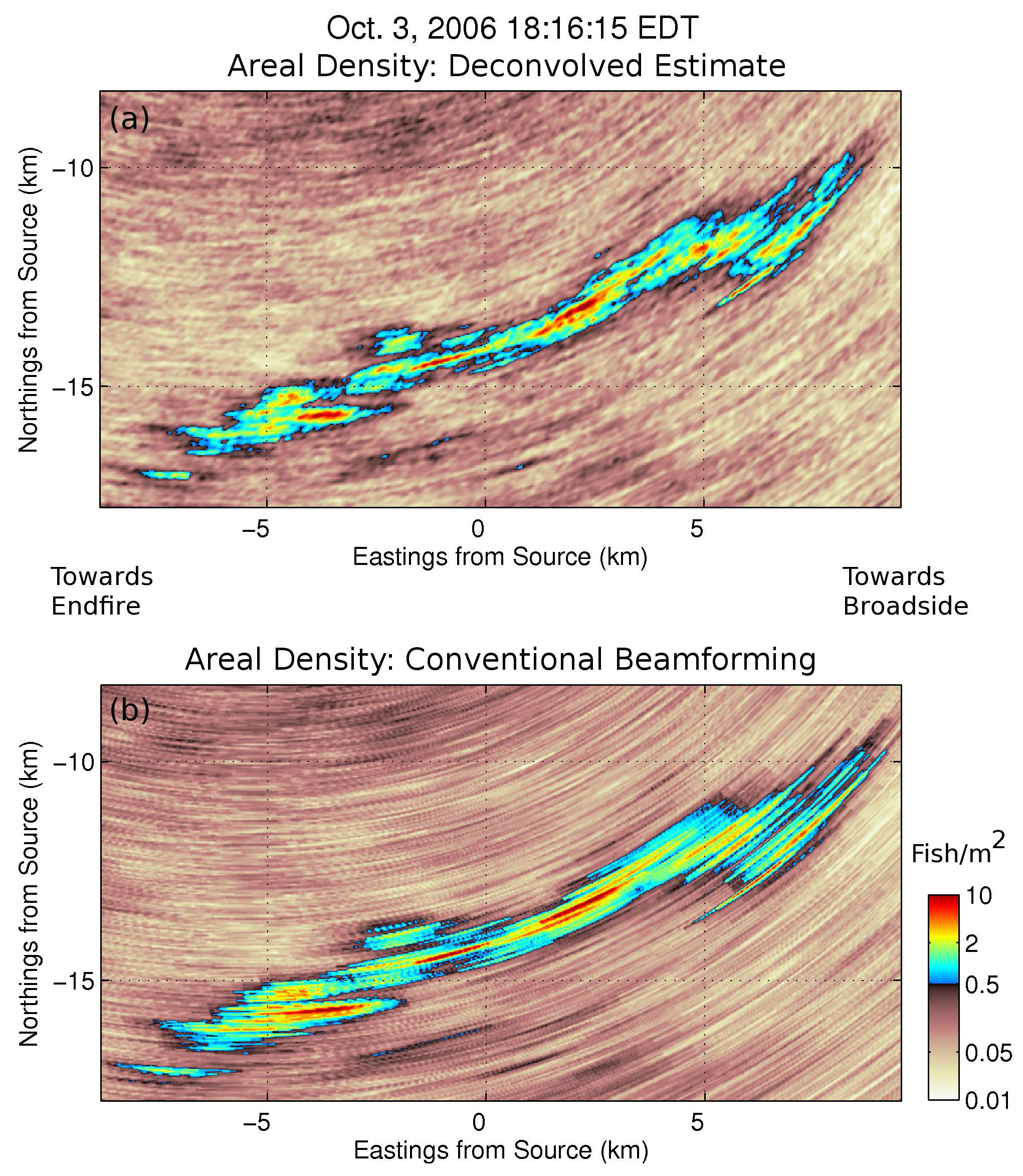
3.3. Ocean Acoustic Waveguide Remote Sensing Images of Fish Shoals
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A.
Appendix A.1 Beamformed Pressure Field for a Single Plane Wave
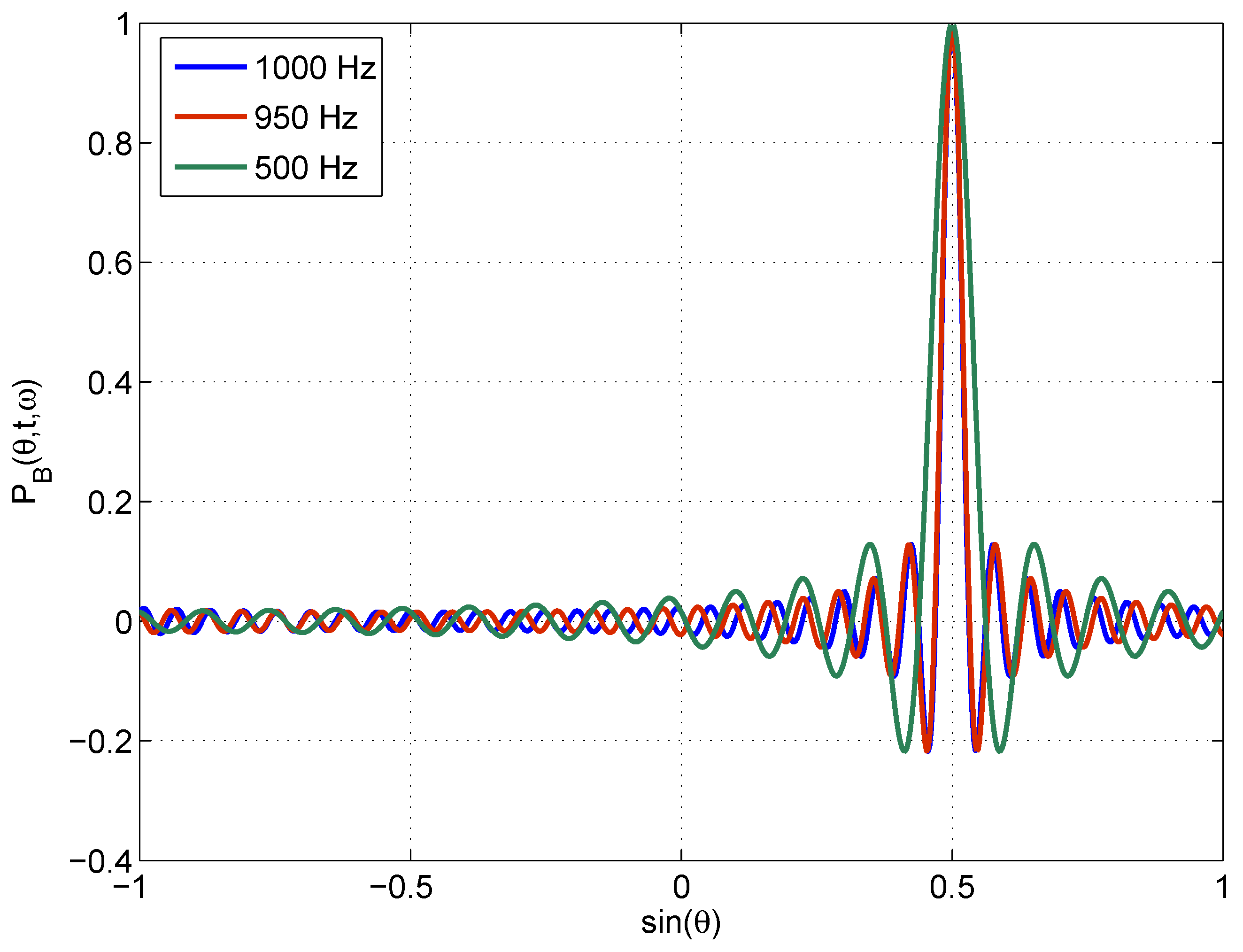
Appendix A.2 Derivation of the Matrix form of MLE of Deconvolved Plane Wave Intensity
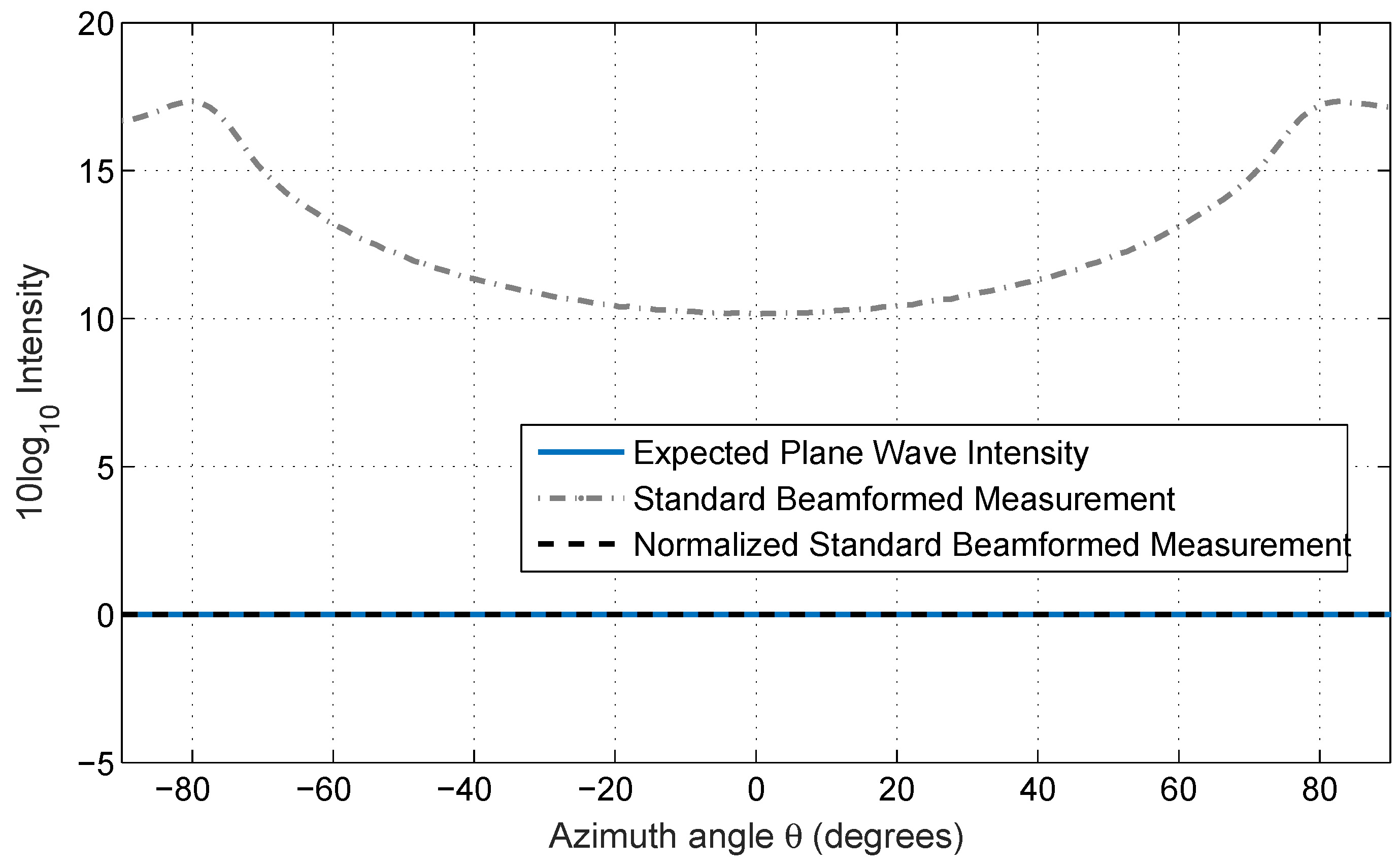
Appendix A.3 A Conventional Beamformer Normalization Useful for Continuous and Relatively Uniform Incident Plane-Wave Distributions
Appendix A.4 Numerical Simulation of Synthetic Beamformed Data
Appendix A.5 Numerical Implementation of the Deconvolution Algorithm
- Step 1.
- The beamformed intensity vector is given by for scanning directions. Select starting solution vectors:for pressure field and intensity vectors, respectively, of length M for M azimuthal directions. A CCGR field with variance equal to the background signal-independent noise intensity is a reasonable starting point for .
- Step 2.
- Every iteration vector attempts to move the log-likelihood function in Equation (10) to its global maximum. Specifically, at the q-th iteration, determine the log likelihood function for the trial solution matrix:containing trial solutions. The matrix is of size where the rows represent a given trial solution vector for M azimuthal directions and columns represent trial solutions. Each trial solution contains a positive or negative increment to the trial solution of the ()-th iteration in only one azimuthal direction, which makes the increment vectors in the trial solutions orthogonal to each other. Specifically, the pressure field at the jth azimuthal direction of the ith trial solution is given by:and the corresponding intensity is given by:where for and for , for M azimuthal directions. At every step, a single trial solution is updated. Once all trial solutions are updated sequentially, that is the end of the q-th iteration. Here, is the Kronecker delta function and, so, takes the value of one if and is zero otherwise, and α is the step size. To move a solution that is stuck in a local minimum, randomly generated noise β, which is drawn from CCGR distribution, is added at every iteration.
- Step 3.
- Find the i-th vector that maximizes the log-likelihood function:The updated solution vector for the q-th iteration then is:This is the end of the q-th iteration. Repeat Steps 2–3 until the value of the maximum likelihood function converges. The maximum likelihood estimate is the one for which is the maximum over all iterations. At this value, the estimated beamformed intensity also converges to in the least square sense [22,23].
References
- Urick, R.J. Principles of Underwater Sound; McGraw Hill: New York, NY, USA, 1983. [Google Scholar]
- Tolstoy, I.; Clay, C. Ocean Acoustics: Theory and Experiment in Underwater Sound; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Van Trees, H.L. Detection, Estimation, and Modulation Theory, Part I; Wiley-Interscience: New York, NY, USA, 2001. [Google Scholar]
- Makris, N.C.; Ratilal, P.; Symonds, D.T.; Jagannathan, S.; Lee, S.; Nero, R.W. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science 2006, 311, 660–663. [Google Scholar] [CrossRef] [PubMed]
- Makris, N.C.; Ratilal, P.; Jagannathan, S.; Gong, Z.; Andrews, M.; Bertsatos, I.; Godø, O.R.; Nero, R.W.; Jech, J.M. Critical population density triggers rapid formation of vast oceanic fish shoals. Science 2009, 323, 1734–1737. [Google Scholar] [CrossRef] [PubMed]
- Gong, Z.; Andrews, M.; Jagannathan, S.; Patel, R.; Jech, J.M.; Makris, N.C.; Ratilal, P. Low-frequency target strength and abundance of shoaling Atlantic herring (Clupea harengus) in the Gulf of Maine during the Ocean Acoustic Waveguide Remote Sensing 2006 Experiment. J. Acoust. Soc. Am. 2010, 127, 104–123. [Google Scholar] [CrossRef] [PubMed]
- Ratilal, P.; Lai, Y.; Symonds, D.T.; Ruhlmann, L.A.; Preston, J.R.; Scheer, E.K.; Garr, M.T.; Holland, C.W.; Goff, J.A.; Makris, N.C. Long range acoustic imaging of the continental shelf environment: The Acoustic Clutter Reconnaissance Experiment 2001. J. Acoust. Soc. Am. 2005, 117, 1977–1998. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, P.G. The Physics of Sound in the Sea; Research Analysis Group: Wakefield, MA, USA, 1946. [Google Scholar]
- Goodman, J.W. Statistical Optics; Wiley-Interscience: New York, NY, USA, 1985. [Google Scholar]
- DiFranco, J.V.; Rubin, W.L. Radar Detection; Prentice-Hall: Englewood Cliffs, NJ, USA, 2004. [Google Scholar]
- Makris, N.C. The effect of saturated transmission scintillation on ocean acoustic intensity measurements. J. Acoust. Soc. Am. 1996, 100, 769–783. [Google Scholar] [CrossRef]
- Makris, N.C. Parameter resolution bounds that depend on sample size. J. Acoust. Soc. Am. 1996, 99, 2851–2861. [Google Scholar] [CrossRef]
- Jagannathan, S.; Küsel, E.T.; Ratilal, P.; Makris, N.C. Scattering from extended targets in range-dependent fluctuating ocean-waveguides with clutter from theory and experiments. J. Acoust. Soc. Am. 2012, 132, 680–693. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.; Andrews, M.; Ratilal, P. Probability distribution for energy of saturated broadband ocean acoustic transmission: Results from Gulf of Maine 2006 experiment. J. Acoust. Soc. Am. 2012, 132, 3659–3672. [Google Scholar] [CrossRef] [PubMed]
- Makris, N.C. A foundation for logarithmic measures of fluctuating intensity in pattern recognition. Opt. Lett. 1995, 20, 2012–2014. [Google Scholar] [CrossRef] [PubMed]
- Hinich, M.J. Maximum-likelihood signal processing for a vertical array. J. Acoust. Soc. Am. 1973, 54, 499–503. [Google Scholar] [CrossRef]
- Zhang, C.; Florêncio, D.; Ba, D.E.; Zhang, Z. Maximum likelihood sound source localization and beamforming for directional microphone arrays in distributed meetings. IEEE Trans. Multimed. 2008, 10, 538–548. [Google Scholar] [CrossRef]
- Baggeroer, A.B.; Kuperman, W.A.; Mikhalevsky, P.N. An overview of matched field methods in ocean acoustics. IEEE J. Ocean. Eng. 1993, 18. [Google Scholar] [CrossRef]
- Johnson, D.H. The application of spectral estimation methods to bearing estimation problems. Proc. IEEE 1982, 70, 1018–1028. [Google Scholar] [CrossRef]
- Baggeroer, A.; Kuperman, W.; Schmidt, H. Matched field processing: Source localization in correlated noise as an optimum parameter estimation problem. J. Acoust. Soc. Am. 1988, 83, 571–587. [Google Scholar] [CrossRef]
- Kuperman, W.A.; Collins, M.D.; Perkins, J.S.; Davis, N. Optimal time-domain beamforming with simulated annealing including application of apriori information. J. Acoust. Soc. Am. 1990, 88, 1802–1810. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Volumes I and II; Pearson Education: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Rao, C.R. Linear Statistical Inference and Its Applications; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Goodman, J.W. Statistical Optics; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Haykin, S. Advances in Spectrum Analysis and Array Processing (Vol. III); Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Kelley, C.T. Iterative Methods for Optimization; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
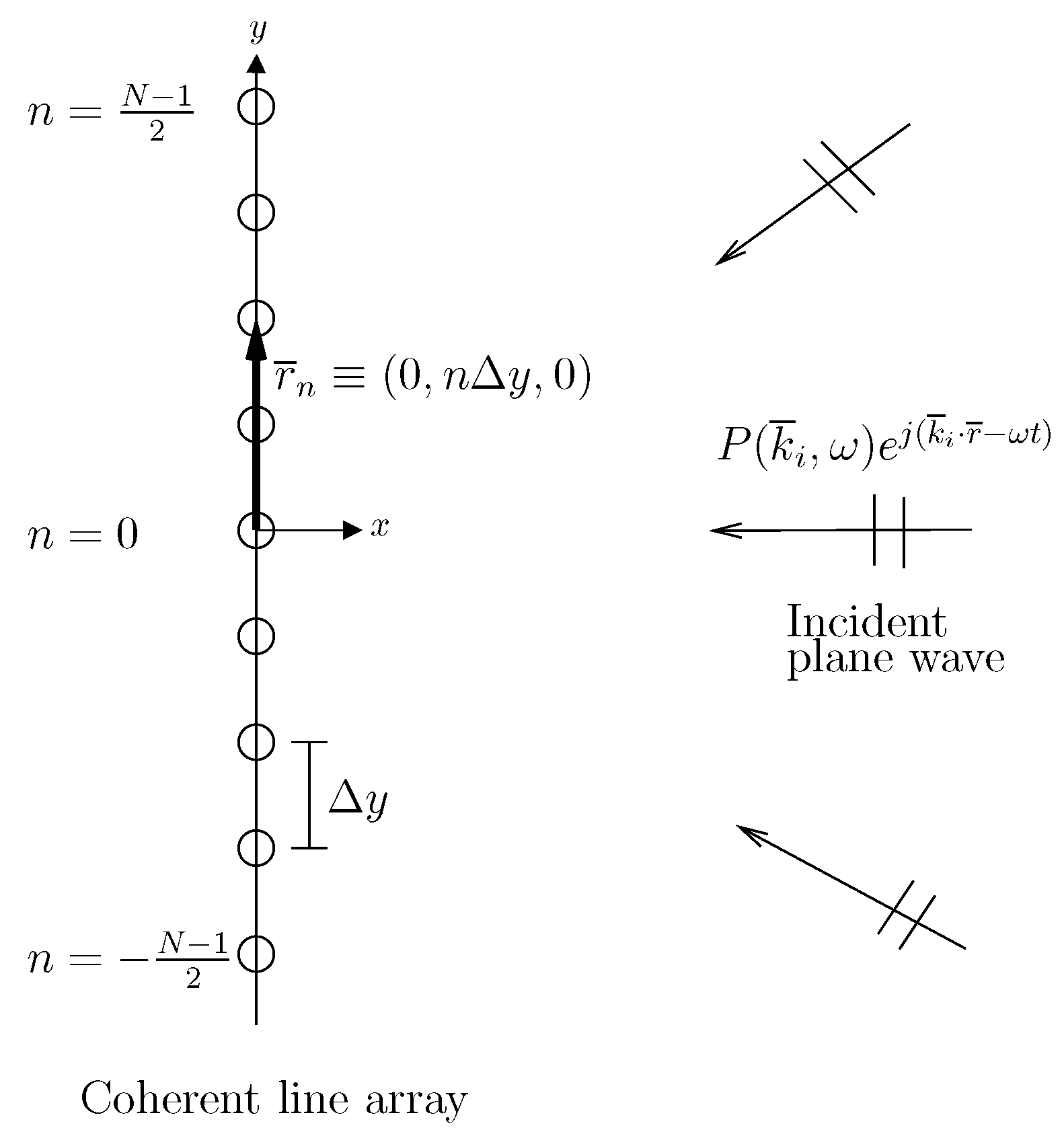
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jain, A.D.; Makris, N.C. Maximum Likelihood Deconvolution of Beamformed Images with Signal-Dependent Speckle Fluctuations from Gaussian Random Fields: With Application to Ocean Acoustic Waveguide Remote Sensing (OAWRS). Remote Sens. 2016, 8, 694. https://doi.org/10.3390/rs8090694
Jain AD, Makris NC. Maximum Likelihood Deconvolution of Beamformed Images with Signal-Dependent Speckle Fluctuations from Gaussian Random Fields: With Application to Ocean Acoustic Waveguide Remote Sensing (OAWRS). Remote Sensing. 2016; 8(9):694. https://doi.org/10.3390/rs8090694
Chicago/Turabian StyleJain, Ankita D., and Nicholas C. Makris. 2016. "Maximum Likelihood Deconvolution of Beamformed Images with Signal-Dependent Speckle Fluctuations from Gaussian Random Fields: With Application to Ocean Acoustic Waveguide Remote Sensing (OAWRS)" Remote Sensing 8, no. 9: 694. https://doi.org/10.3390/rs8090694
APA StyleJain, A. D., & Makris, N. C. (2016). Maximum Likelihood Deconvolution of Beamformed Images with Signal-Dependent Speckle Fluctuations from Gaussian Random Fields: With Application to Ocean Acoustic Waveguide Remote Sensing (OAWRS). Remote Sensing, 8(9), 694. https://doi.org/10.3390/rs8090694