A Sparsity-Based Regularization Approach for Deconvolution of Full-Waveform Airborne Lidar Data
Abstract
:1. Introduction
2. Review of Related Research
2.1. Decomposition Methods
2.2. Deconvolution Methods
3. Methodology
3.1. Deconvolution for Cross-Section Retrieval
3.1.1. Target Cross-Section Retrieval
3.1.2. Sparsity-Constrained Regularization
3.1.3. Optimization with SOCP
3.1.4. Blur Matrix Structure
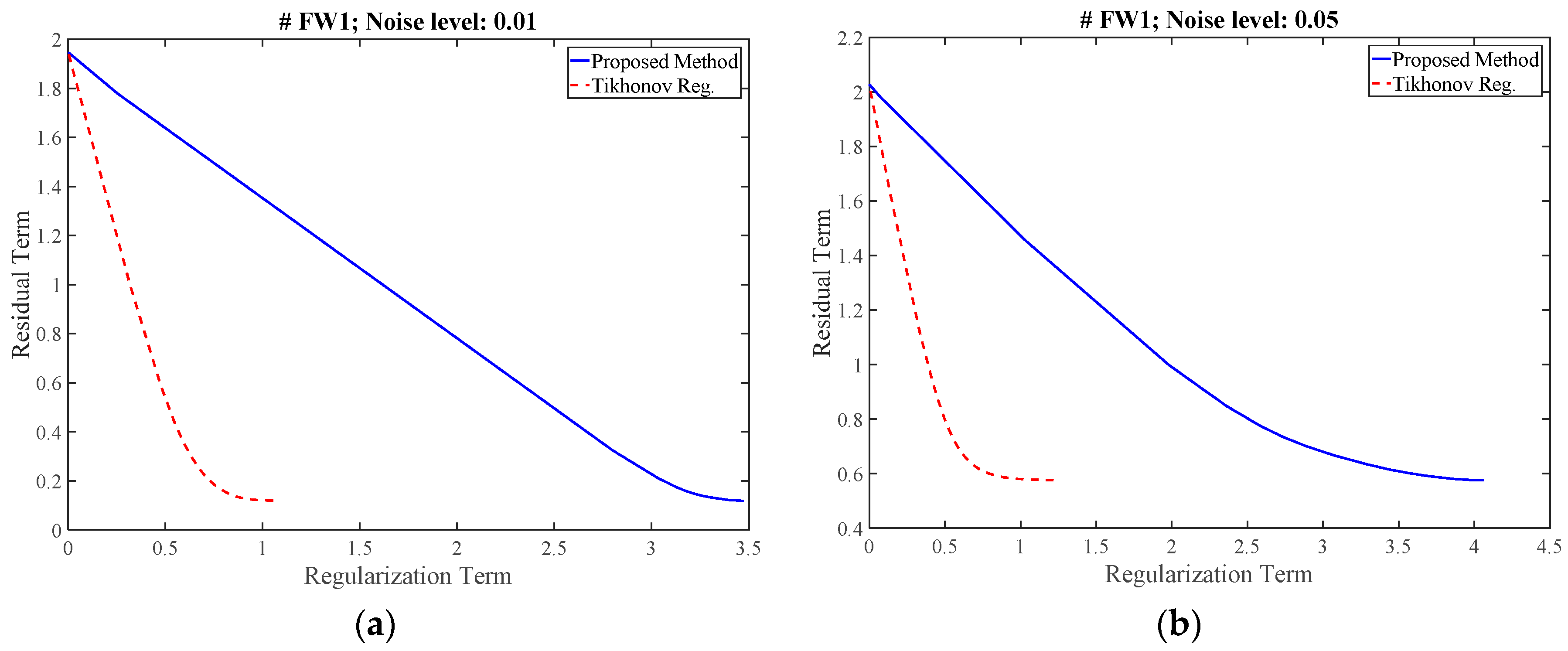
3.2. Determination of the Regularization Parameter
3.3. System Waveform Estimation
3.4. Quantitative Assessment of the Retrieved Waveform
4. Experiments and Discussion
4.1. Experimental Data
4.1.1. Synthetic Data
4.1.2. Real LiDAR Datasets
4.2. Preprocessing
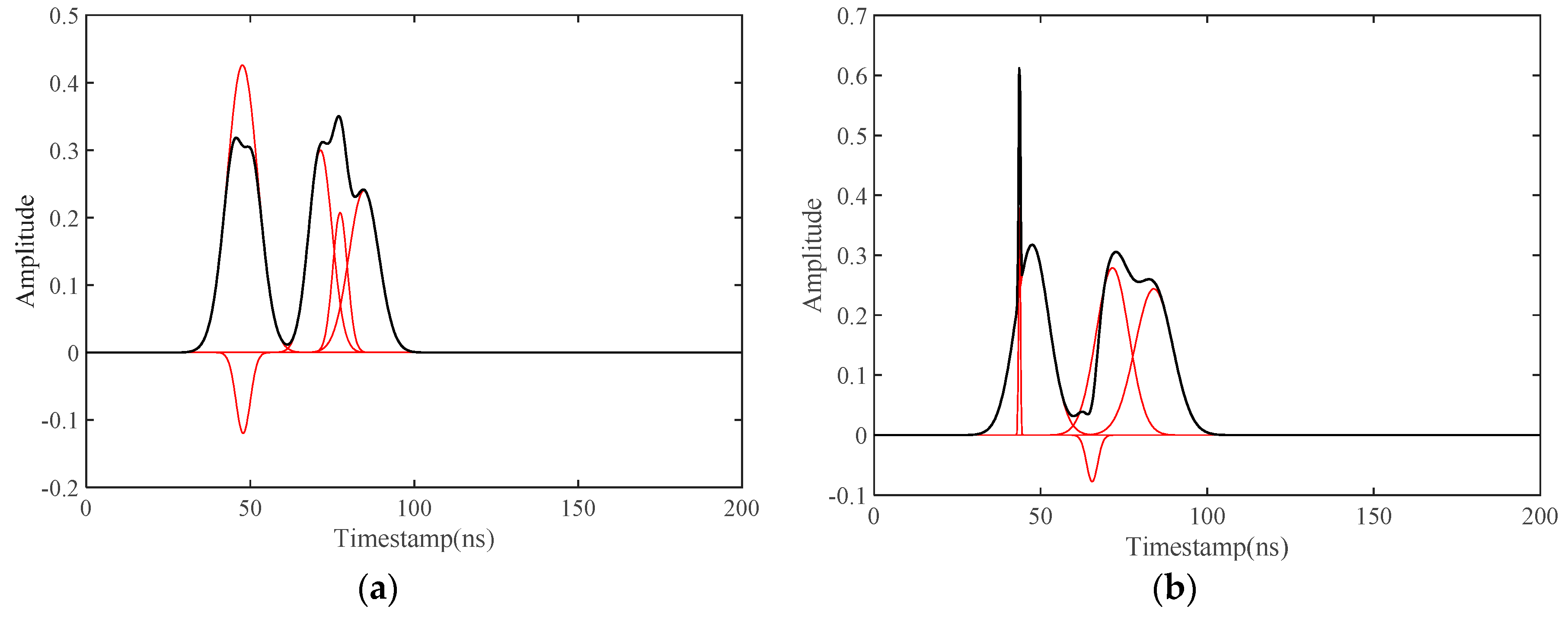
4.3. Deconvolution Results for Synthetic Waveforms
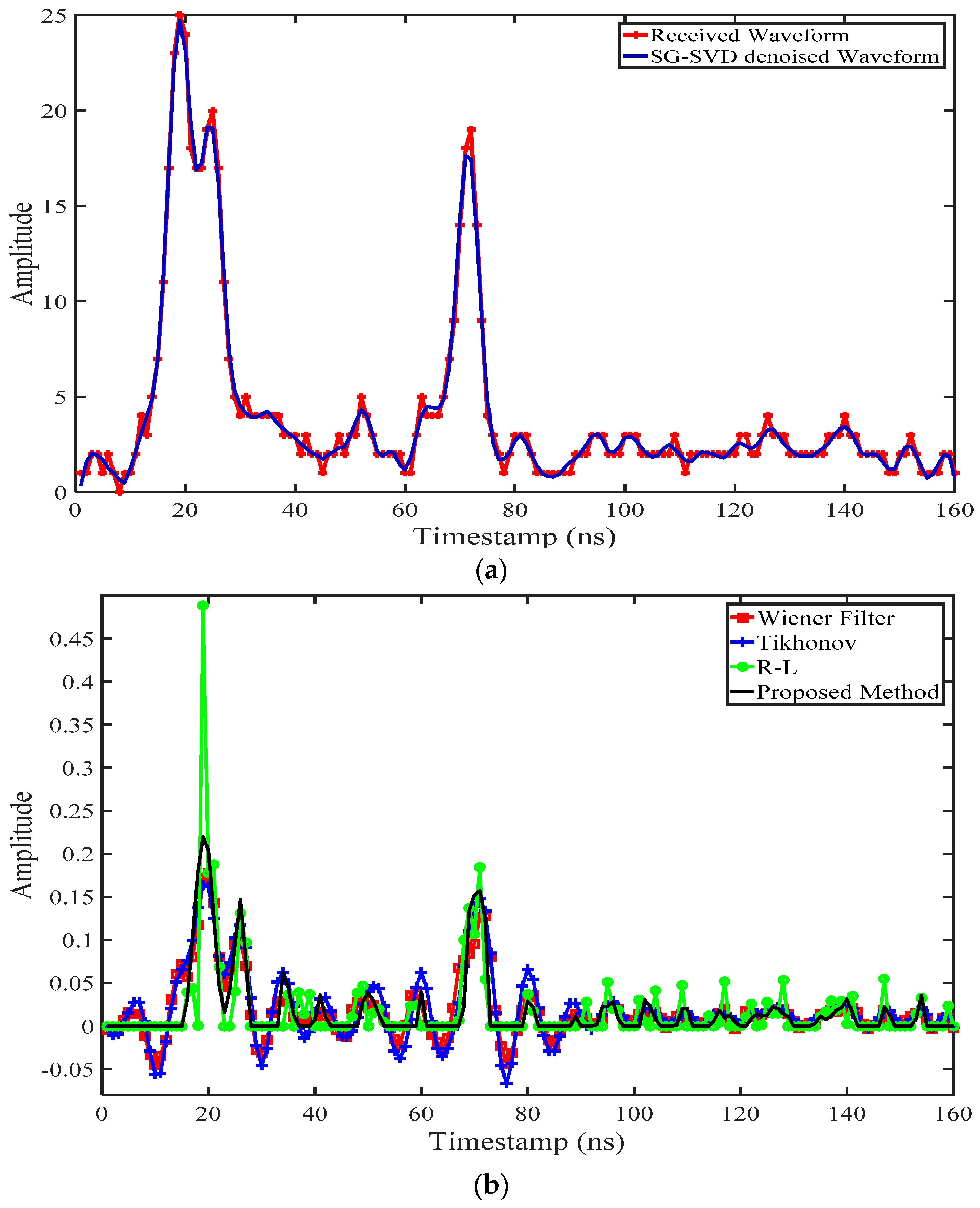
4.4. QLD Dataset
4.5. NSW Dataset
4.5.1. Evaluation of Blind Deconvolution for System Waveform Estimation
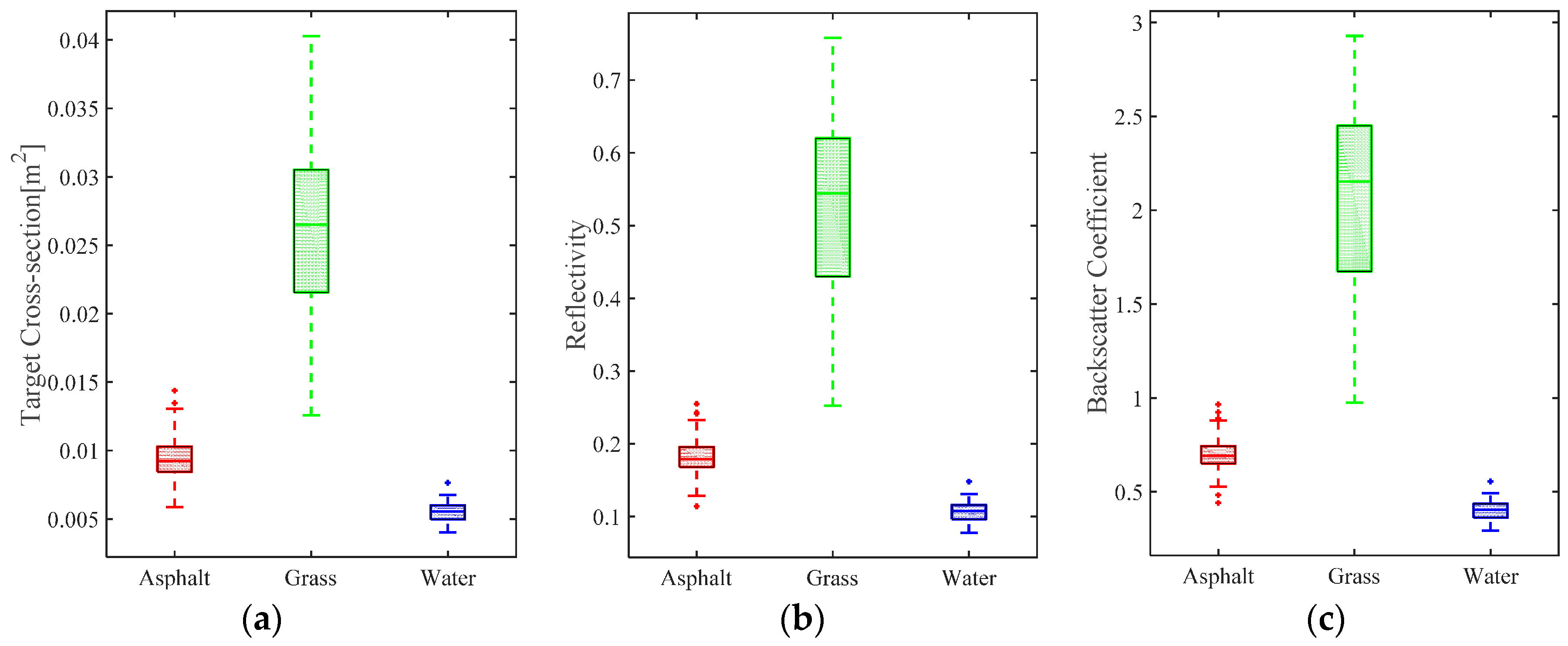
4.5.2. Target Cross-Section Recovery
4.6. Karawatha Dataset
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mallet, C.; Bretar, F.; Roux, M.; Soergel, U.; Heipke, C. Relevance assessment of full-waveform lidar data for urban area classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, S71–S84. [Google Scholar] [CrossRef]
- Bretar, F.; Chauve, A.; Mallet, C.; Jacome, A. Terrain surfaces and 3-D landcover classification from small footprint full-waveform lidar data: Application to badlands. Hydrol. Earth Syst. Sci. 2009, 13, 1531–1545. [Google Scholar] [CrossRef]
- Jutzi, B.; Stilla, U. Extraction of features from objects in urban areas using spacetime analysis of recorded laser pulses. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 1–6. [Google Scholar]
- Hovi, A.; Korpela, I. Real and simulated waveform-recording LiDAR data in juvenile boreal forest vegetation. Remote Sens. Environ. 2014, 140, 665–678. [Google Scholar] [CrossRef]
- Adams, T.; Beets, P.; Parrish, C. Extracting more data from lidar in forested areas by analyzing waveform shape. Remote Sens. 2012, 4, 682–702. [Google Scholar] [CrossRef]
- Hollaus, M.; Aubrecht, C.; Höfle, B.; Steinnocher, K.; Wagner, W. Roughness mapping on various vertical scales based on full-waveform airborne laser scanning data. Remote Sens. 2011, 3, 503–523. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-waveform topographic lidar: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Höfle, B.; Pfeifer, N. Correction of laser scanning intensity data: Data and model-driven approaches. ISPRS J. Photogramm. Remote Sens. 2007, 62, 415–433. [Google Scholar] [CrossRef]
- Jutzi, B.; Stilla, U. Laser pulse analysis for reconstruction and classification of urban objects. In Proceedings of the International Society Photogrammetry and Remote Sensing (ISPRS) Archives, Munich, Germany, 17–19 September 2003.
- Wagner, W.; Ullrich, A.; Melzer, T.; Briese, C.; Kraus, K. From single-pulse to full-waveform airborne laser scanners: Potential and practical challenges. Int. Arch. Photogram. Remote Sens. 2004, 35, 201–206. [Google Scholar]
- Roncat, A.; Bergauer, G.; Pfeifer, N. B-spline deconvolution for differential target cross-section determination in full-waveform laser scanning data. ISPRS J. Photogramm. Remote Sens. 2011, 66, 418–428. [Google Scholar] [CrossRef]
- Jutzi, B.; Stilla, U. Range determination with waveform recording laser systems using a Wiener Filter. ISPRS J. Photogramm. Remote Sens. 2006, 61, 95–107. [Google Scholar] [CrossRef]
- Jelalian, A.V. Laser Radar Systems; Artech House: Boston, MA, USA; London, UK, 1992. [Google Scholar]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Wagner, W. Radiometric calibration of small-footprint full-waveform airborne laser scanner measurements: Basic physical concepts. ISPRS J. Photogramm. Remote Sens. 2010, 65, 505–513. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Roncat, A.; Künzer, C.; Wagner, W. Regularizing method for the determination of the backscatter cross section in lidar data signals. Opt. Soc. Am. 2009, 26, 1071–1079. [Google Scholar] [CrossRef]
- Chauve, A.; Vega, C.; Durrieu, S.; Bretar, F.; Allouis, T.; Deseilligny, M.P.; Puech, W. Advanced full-waveform lidar data echo detection: Assessing quality of derived terrain and tree height models in an alpine coniferous forest. Int. J. Remote Sens. 2009, 30, 5211–5228. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Mills, J.P.; Smith-Voysey, S. Rigorous pulse detection from full-waveform airborne laser scanning data. Int. J. Remote Sens. 2010, 31, 1303–1324. [Google Scholar] [CrossRef]
- Parrish, C.E.; Jeong, I.; Nowak, R.D.; Smith, R.B. Empirical Comparison of Full-Waveform Lidar Algorithms: Range Extraction and Discrimination Performance. Photogram. Eng. Remote Sens. 2011, 77, 825–838. [Google Scholar] [CrossRef]
- Wu, J.; Aardt, J.A.N.V.; Asner, G.P. A comparison of signal deconvolution algorithms based on small-footprint lidar waveform simulation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2402–2414. [Google Scholar] [CrossRef]
- Hofton, M.A.; Minster, J.B.; Blair, J.B. Decomposition of Laser Altimeter Waveforms. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1989–1996. [Google Scholar] [CrossRef]
- Persson, A.; Söderman, U.; Töpel, J.; Ahlberg, S. Visualization and analysis of full-waveform airborne laser scanner data. In Proceedings of the ISPRS Workshop Laser Scanning, Enschede, The Netherlands, 12–14 September 2005; pp. 103–108.
- Mallet, C.; Lafarge, F.; Roux, M.; Soergel, U.; Bretar, F.; Heipke, C. A marked point process for modeling lidar waveforms. IEEE Trans. Image Process. 2010, 19, 3204–3221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jutzi, B.; Stilla, U. Characteristics of the measurement unit of a full-waveform laser system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 17–22. [Google Scholar]
- Alexander, C.; Tansey, K.; Kaduk, J.; Holland, D.; Tate, N.J. Backscatter coefficient as an attribute for the classification of full-waveform airborne laser scanning data in urban areas. ISPRS J. Photogramm. Remote Sens. 2010, 65, 423–432. [Google Scholar] [CrossRef]
- Zhu, R.; Pang, Y.; Zhang, Z.; Xu, G. Application of the deconvolution method in the processing of full-waveform LiDAR data. In Proceedings of the 3rd International Congress on Image and Signal Processing (CISP2010), Yantai, China, 16–18 October 2010; pp. 2975–2979.
- Chauve, A.; Mallet, C.; Bretar, F.; Durrieu, S.; Deseilligny, M.P.; Puech, W. Processing full-waveform lidar data: Modelling raw signals. In Proceedings of the ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; pp. 102–107.
- Wu, J.; van Aardt, J.A.N.; McGlinchy, J.; Asner, G.P. A robust signal preprocessing chain for small-footprint waveform lidar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3242–3255. [Google Scholar] [CrossRef]
- Reeves, S. Generalized cross-validation as a stopping rule for the Richardson-Lucy algorithm. Int. J. Imaging Syst. Technol. 1995, 6, 387–391. [Google Scholar] [CrossRef]
- Khan, M.K.; Morigi, S.; Reichel, L.; Sgallari, F. Iterative methods of richardson-lucy-type for image debluring. Numer. Math. Theory Methods Appl. 2013, 6, 262–275. [Google Scholar]
- Neilsen, K.D. Signal Processing on Digitized LADAR Waveforms for Enhanced Resolution on Surface Edges. Master’s Thesis, Utah State University, Logan, UT, USA, 2011. [Google Scholar]
- Morháč, M.; Matoušek, V. High-resolution boosted deconvolution of spectroscopic data. J. Comput. Appl. Math. 2011, 235, 1629–1640. [Google Scholar] [CrossRef]
- Castorena, J.; Creusere, C.D.; Voelz, D. Modeling LiDAR scene sparsity using compressicve sensing. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010.
- Verdin, B.; von Borries, R. Lidar compressive sensing using chaotic waveform. Proc. SPIE Radar Sens. Technol. 2014. [Google Scholar] [CrossRef]
- Gunturk, B.K. Fundamentals of image restoration. In Image Restoration: Fundamentals and Advances; Gunturk, B.K., Li, X., Eds.; CRC Press: Boca Raton, FL, USA, 2012; pp. 25–61. [Google Scholar]
- Gold, R. An Iterative Unfolding Method for Response Matrices; Argonne National Laboratory: Argonne, IL, USA, 1964. [Google Scholar]
- Richardson, W.H. Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative method for the rectification of the observed distributions. Astron. J. 1974, 79, 745–754. [Google Scholar] [CrossRef]
- Vogel, C.R. Computational Methods for Inverse Problems; Frontiers in Applied Mathematics Series; Society of Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2002; p. 183. [Google Scholar]
- Stefan, W. Total Variation Regularization for Linear Ill-Posed Inverse Problems Extensions and Applications. Ph.D. Thesis, Arizona State University, Phoneix, AZ, USA, 2008. [Google Scholar]
- Hansen, P.C. The discrete picard condition for discrete ill-posed problems. BIT Numer. Math. 1990, 30, 658–672. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004; p. 727. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.I.A. Solutions of Ill-Posed Problems; Winston & Sons: Washington, DC, USA, 1977; p. 258. [Google Scholar]
- Elad, M.; Figueiredo, A.T.; Ma, Y. On the role of sparse and redundant representations in image processing. IEEE Proc. 2010, 98, 972–982. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Pan, T.C. Signal and Image Deconvolution: Algorithms and Applications. Ph.D. Thesis, Hong Kong Baptist University, Hong Kong, China, 2010. [Google Scholar]
- Figueiredo, M.A.T.; Bioucas-Dias, J.M. Algorithms for imaging inverse problems under sparsity regularization. In Proceedings of the 3rd International Workshop on Cognitive Information Processing (CIP), Baiona, Spain, 28–30 May 2012; pp. 1–6.
- Tropp, J.A.; Wright, S.J. Computational methods for sparse solution of linear inverse problems. IEEE Proc. 2010, 98, 948–958. [Google Scholar] [CrossRef]
- Schmidt, M.; Fung, G.; Rosales, R. Fast optimization methods for L1 regularization: A comparative study and two new approaches. In Machine Learning: ECML 2007; Springer: Berlin, Germany; Heidelberg, Germany, 2007; pp. 286–297. [Google Scholar]
- Kim, S.-J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale l1-regularized least squares. IEEE J. Sel. Top. Signal Proc. 2007, 1, 606–617. [Google Scholar]
- Palomar, D.P.; Eldar, Y.C. Convex Optimization in Signal Processing and Communications; Cambridge University Press: New York, NY, USA, 2010; p. 498. [Google Scholar]
- Alizadeh, F.; Goldfarb, D. Second-order cone programming. Math. Program. 2003, 95, 3–51. [Google Scholar] [CrossRef]
- Sousa, M.; Vandenberghe, L.; Boyd, S.; Lebret, H. Applications of second-order cone programming. Linear Algebra Appl. 1998, 284, 193–228. [Google Scholar]
- Hansen, P.C.; Nagy, J.G.; O’Leary, D.P. Deblurring Images: Matrices, Spectra, and Filtering; Society of Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2006; p. 130. [Google Scholar]
- Orfanidis, S.J. Introduction to Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2010; p. 783. [Google Scholar]
- Morozov, V.A. On the solution of functional equations by the method of regularization. Sov. Math. Dokl. 1966, 7, 414–417. [Google Scholar]
- Golub, G.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Correia, T.; Gibson, A.; Schweiger, M.; Hebden, J. Selection of regularization parameter for optical topography. J. Biomed. Opt. 2009, 14. [Google Scholar] [CrossRef] [PubMed]
- White, R.L. Image restoration using the damped Richardson-Lucy method. In Proceedings of the SPIE 2198, Instrumentation in Astronomy VIII, Kailua-Kona, HI, USA, 13 March 1994; pp. 1342–1348.
- Rote, G. Computing the Fréchet distance between piecewise smooth curves. Comput. Geom. 2007, 37, 162–174. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Azadbakht, M.; Fraser, C.S.; Zhang, C.; Leach, J. A signal denoising method for full-waveform LiDAR data. In Proceedings of the ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, Antalya, Turkey, 11–13 November 2013; pp. 31–36.
- Roncat, A. Backscatter Signal Analysis of Small-Footprint Full-Waveform Lidar Data. Ph.D. Thesis, Vienna University of Technology, Vienna, Austria, 2014. [Google Scholar]
- Grant, M.; Boyd, S. Graph implementations for nonsmooth convex programs. In Recent Advances in Learning and Control; Blondel, V.D., Boyd, S., Kimura, H., Eds.; Springer: London, UK, 2008; pp. 95–110. [Google Scholar]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming. Available online: http://cvxr.com/cvx (accessed on 30 May 2016).
- Clark, R.N.; Swayze, G.A.; Wise, R.A.; Livo, K.E.; Hoefen, T.M.; Kokaly, R.F.; Sutley, S.J. USGS Digital Spectral Library Splib06a. Available online: http://speclab.cr.usgs.gov/spectral.lib06/ds231/ (accessed on 20 September 2007).
- Azadbakht, M.; Fraser, C.S.; Zhang, C. Separability of targets in urban areas using features from full-waveform LiDAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5367–5370.

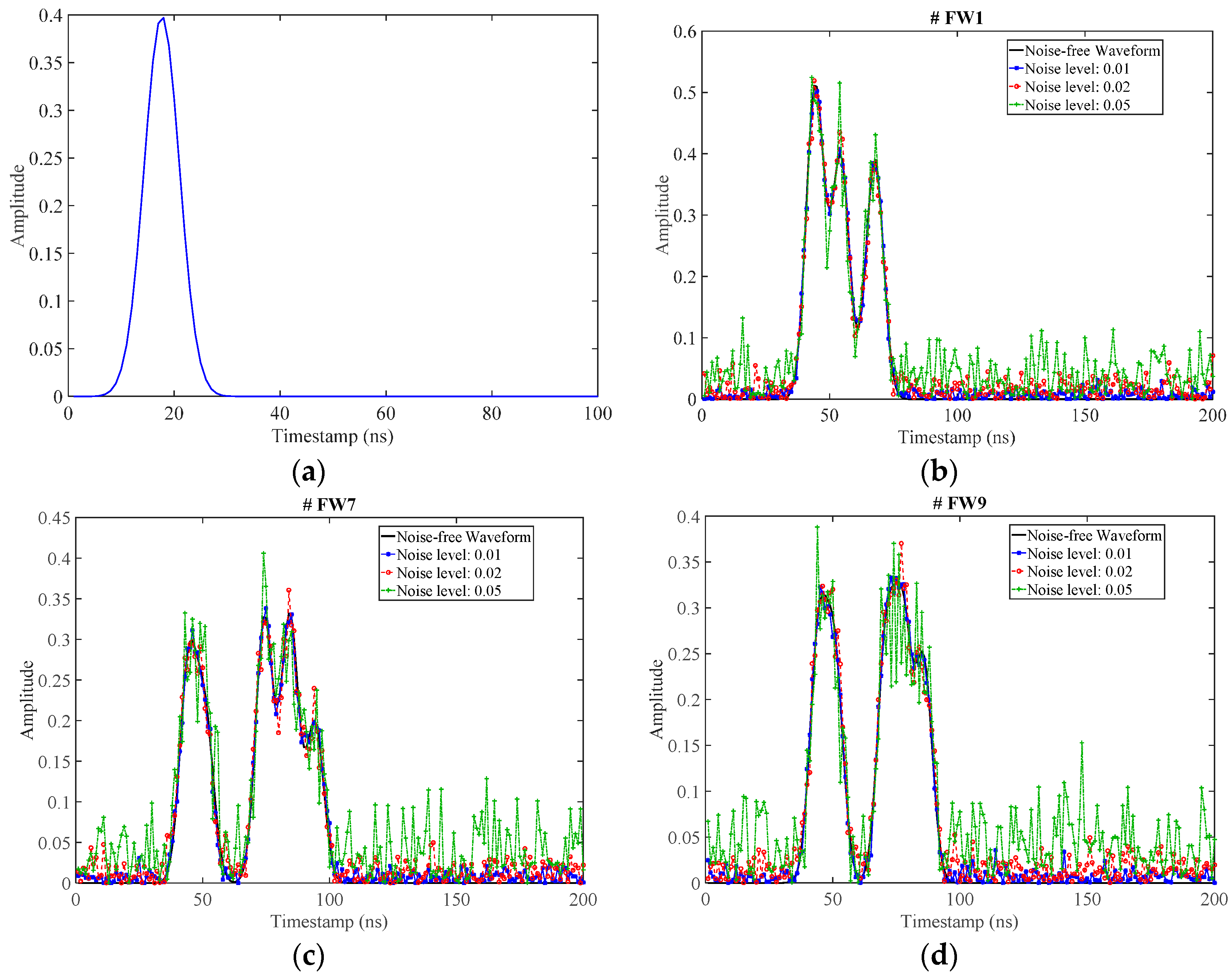

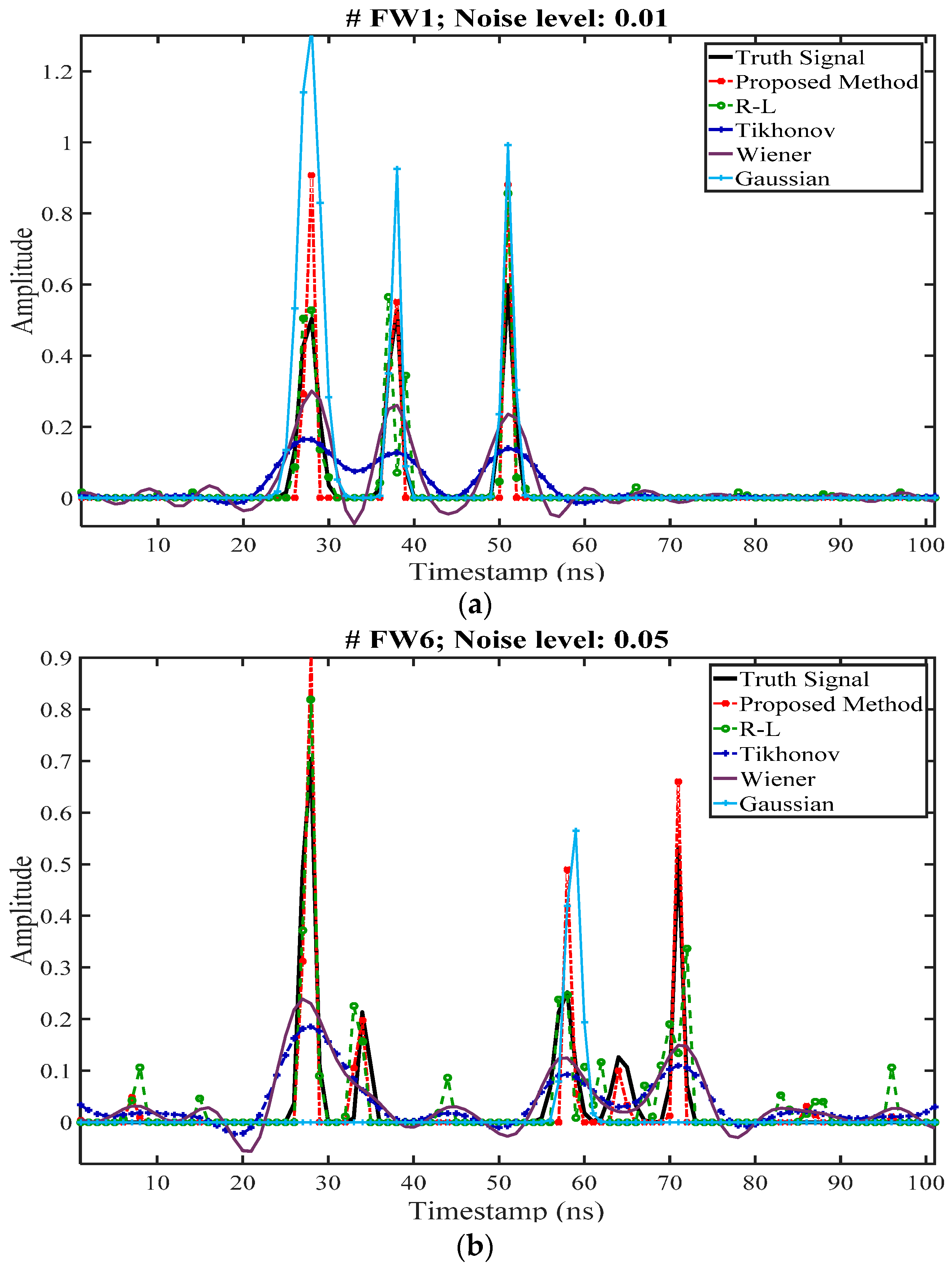
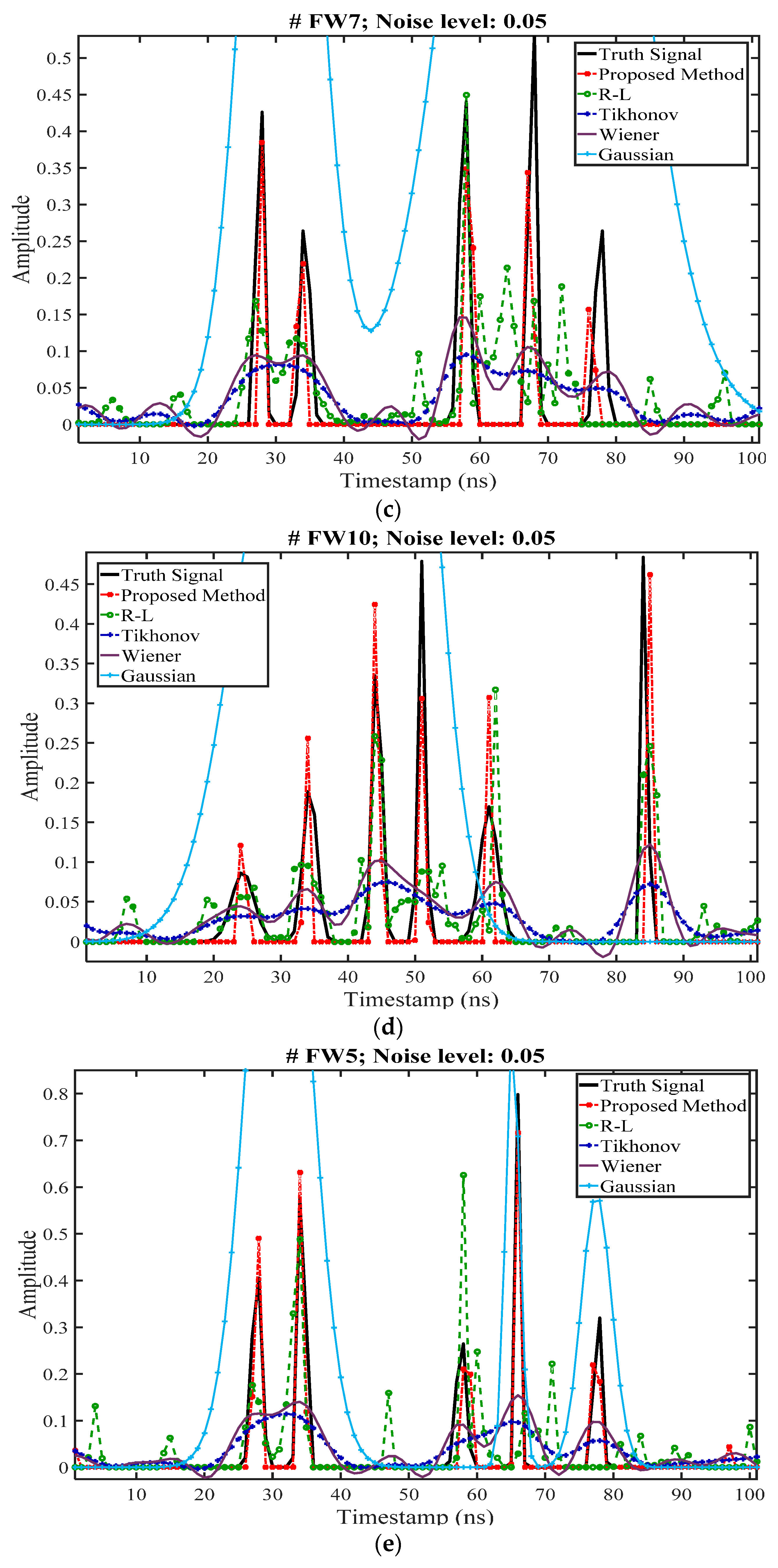

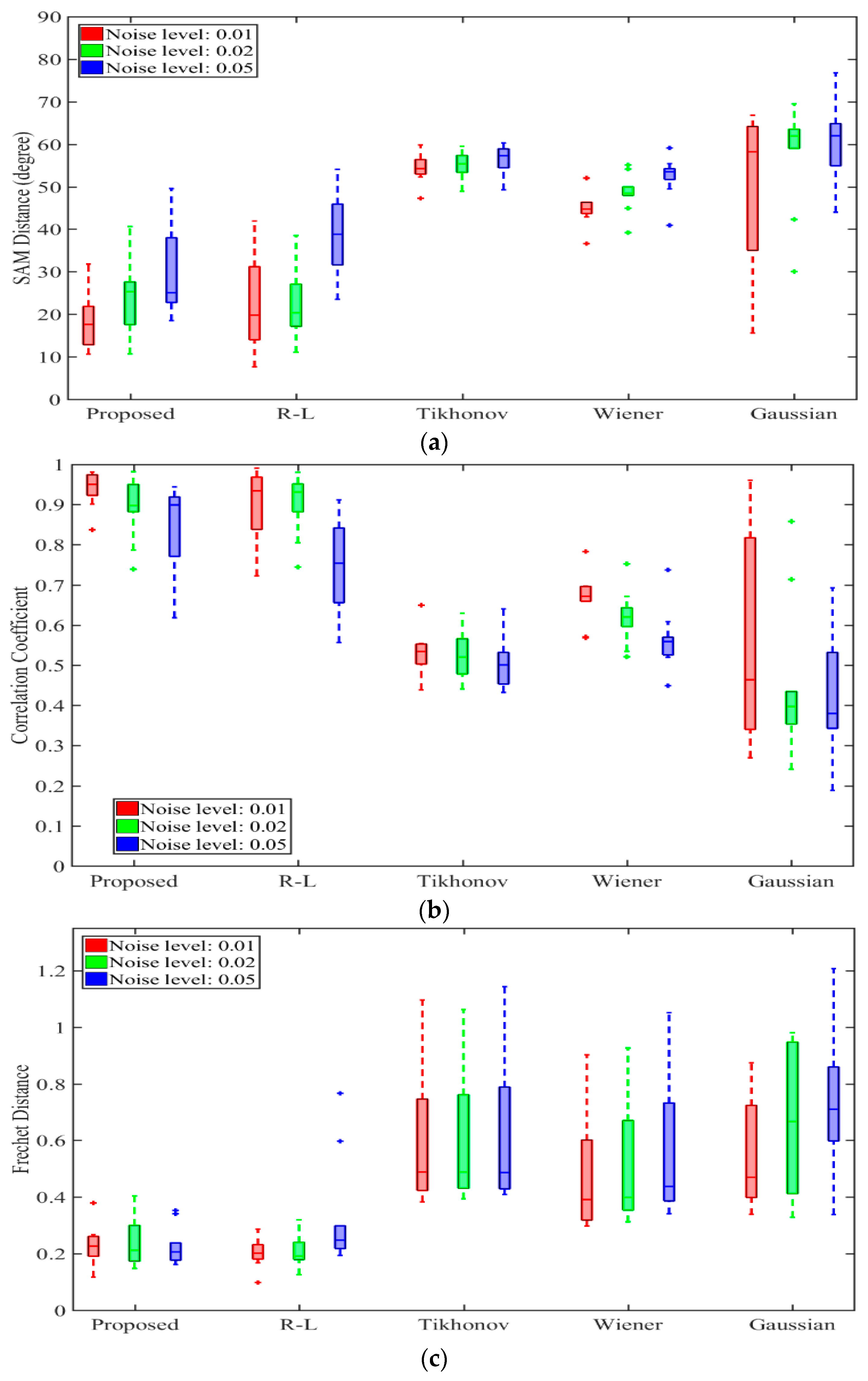



| Parameter | QLD Dataset | NSW Dataset | Karawatha Dataset |
|---|---|---|---|
| Flying altitude (AGL-m) | 600 | 1000 | 300 |
| Pulse rate (kHz) | 150 | 240 | 240 |
| Maximal scan angle (°) | 30 | 40 | 25 |
| Method | Algorithm | Parameter Tuning | Reference(s) |
|---|---|---|---|
| Gaussian decomposition | Levenberg-Marquardt/Thrust region (curve fitting in Matlab) | Visual inspection to specify the number of pulses | [14,64] |
| R-L deconvolution | deconvlucy function in Matlab | RMSE criterion to select optimal iteration numbers | - |
| Wiener filtering | deconvwnr function in Matlab | - | |
| Tikhonov regularization | CVX package | L-curve | [65,66] |
| Sparsity-based regularization | CVX package | L-curve | [65,66] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azadbakht, M.; Fraser, C.S.; Khoshelham, K. A Sparsity-Based Regularization Approach for Deconvolution of Full-Waveform Airborne Lidar Data. Remote Sens. 2016, 8, 648. https://doi.org/10.3390/rs8080648
Azadbakht M, Fraser CS, Khoshelham K. A Sparsity-Based Regularization Approach for Deconvolution of Full-Waveform Airborne Lidar Data. Remote Sensing. 2016; 8(8):648. https://doi.org/10.3390/rs8080648
Chicago/Turabian StyleAzadbakht, Mohsen, Clive S. Fraser, and Kourosh Khoshelham. 2016. "A Sparsity-Based Regularization Approach for Deconvolution of Full-Waveform Airborne Lidar Data" Remote Sensing 8, no. 8: 648. https://doi.org/10.3390/rs8080648







