Comparison of Canopy Volume Measurements of Scattered Eucalypt Farm Trees Derived from High Spatial Resolution Imagery and LiDAR
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
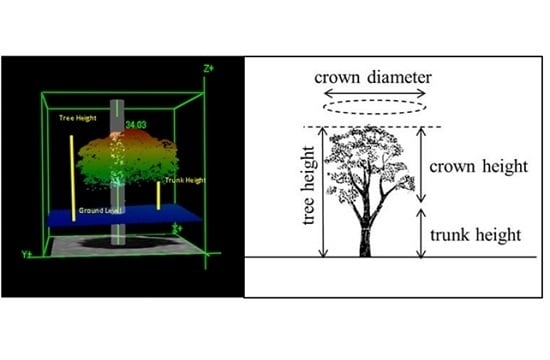
2.2. Field Measurements of Canopy Volume
2.3. LiDAR Data Acquisition and Post-Processing
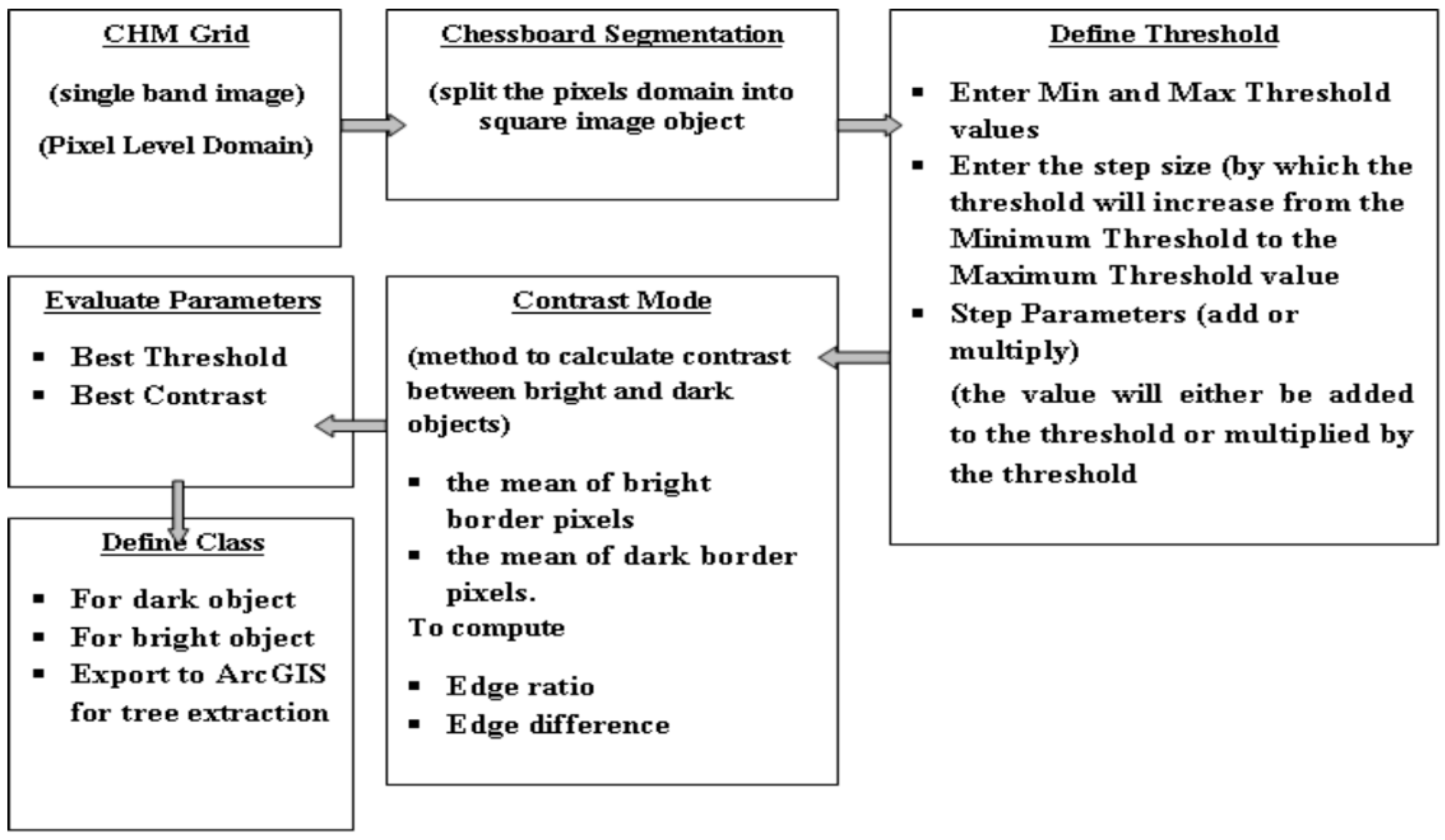
2.4. Delineation of Tree Attributes from WorldView2 Data
2.5. Evaluating the Performance of the Two Techniques
3. Results
3.1. Field Measurements of Tree Parameters
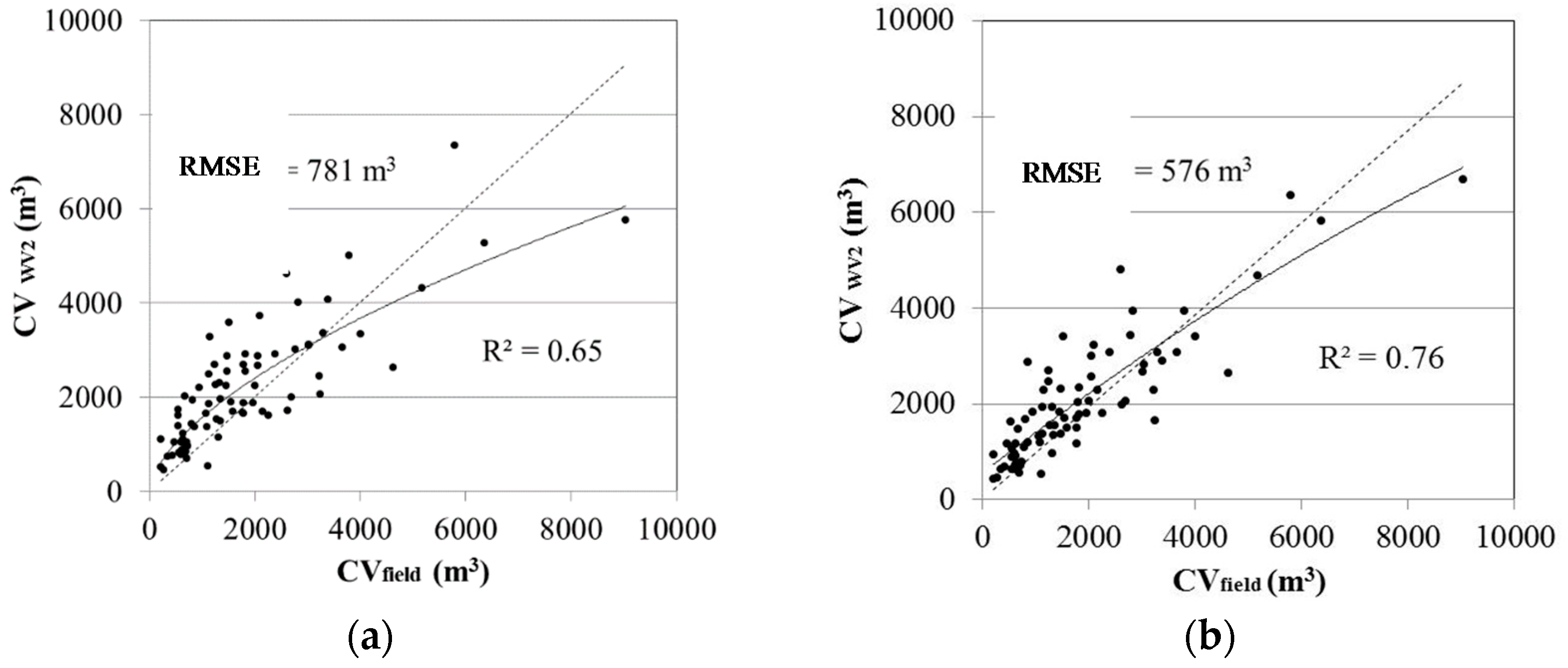
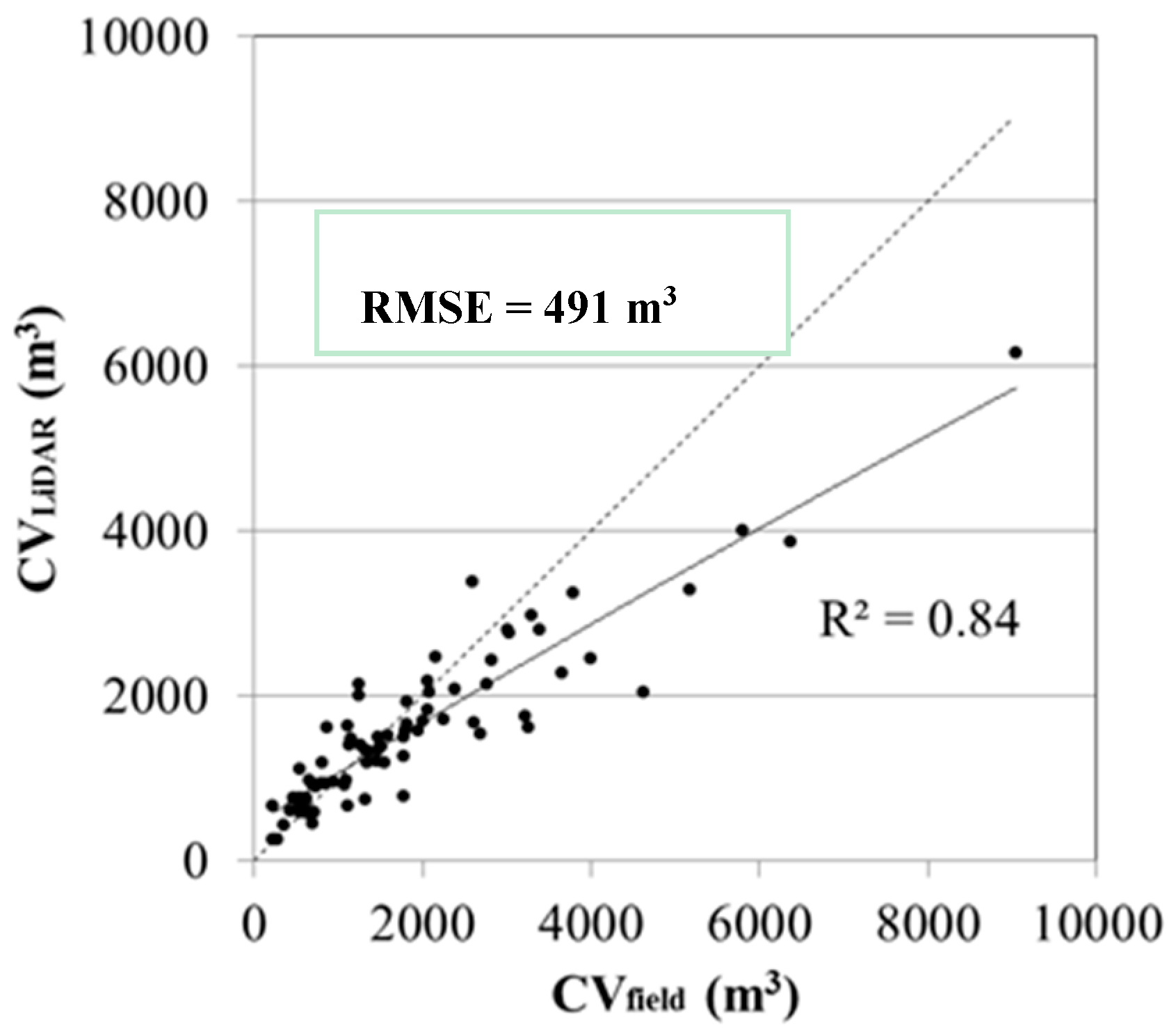
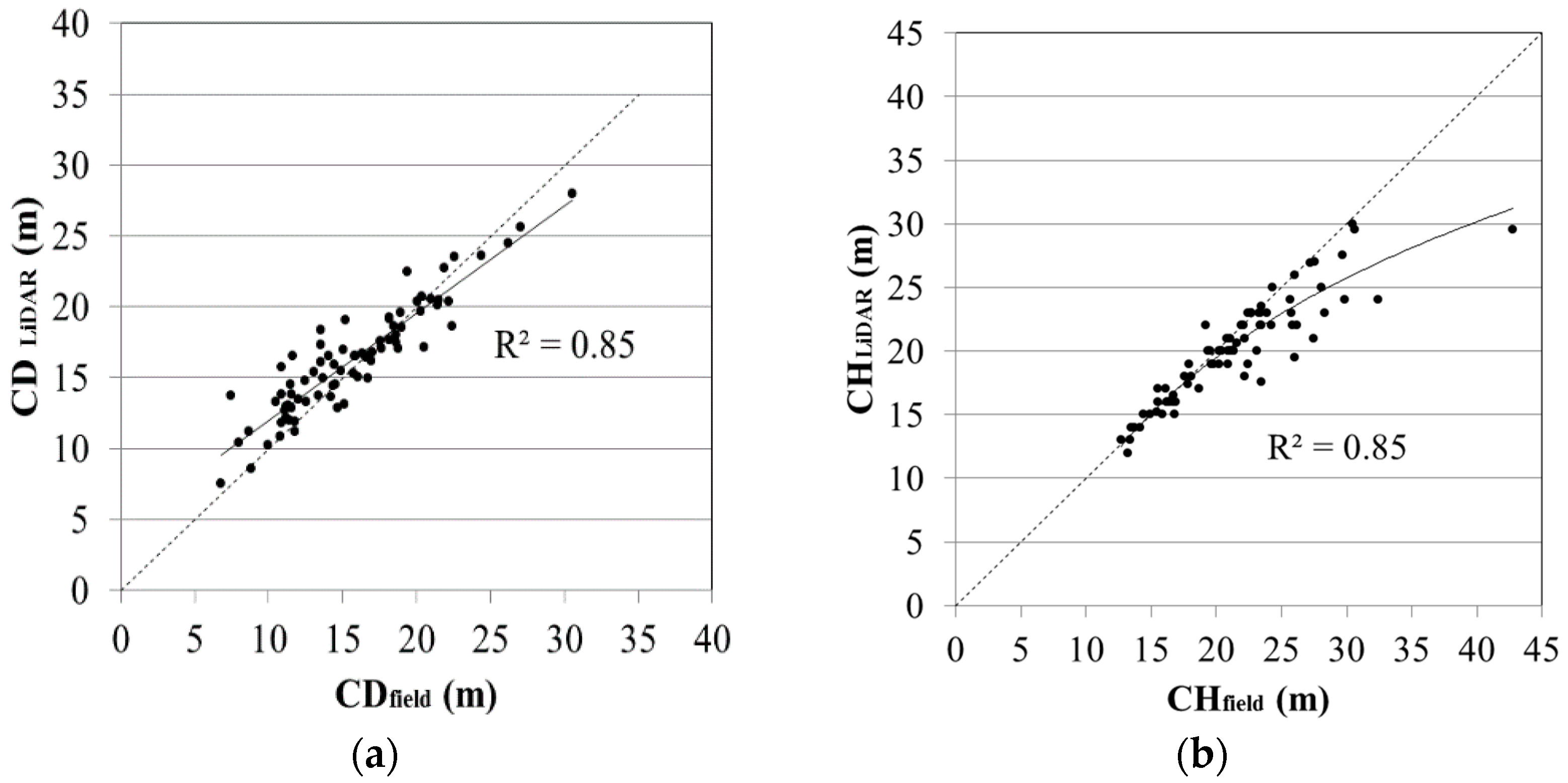
3.2. Canopy Volume Estimations
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zaman, Q.; Schuman, A.W. Performance of an ultrasonic tree volume measurement system in commercial citrus groves. Precis. Agric. 2005, 6, 467–480. [Google Scholar] [CrossRef]
- Usha, K.; Singh, B. Potential applications of remote sensing in horticulture—A review. Sci. Hortic. 2013, 153, 71–83. [Google Scholar] [CrossRef]
- Dubrasich, M.E.; Hann, D.W.; Tappeineer, J.C., II. Methods for evaluating crown area profiles of forest stands. Can. J. For. Res. 1997, 27, 385–392. [Google Scholar] [CrossRef]
- Coder, K.D. Tree Biomechanics Series: Crown Shape Factors & Volumes. Available online: http://www.forestry.uga.edu/warnell/service/library/for00–032/2000 (accessed on 27 January 2014).
- Troxel, B.; Piana, M.; Ashton, M.S.; Dunning, C.M. Relationships between bole and crown size for young urban trees in the northeastern USA. Urban For. Urban Green. 2013, 12, 144–153. [Google Scholar] [CrossRef]
- Rautiainen, M.; Mõttus, M.; Stenberg, P.; Ervasti, S. Crown envelope shape measurements and models. Silv. Fenn. 2007, 42, 19–33. [Google Scholar] [CrossRef]
- Tumbo, S.D.; Salyani, M.; Whitney, J.D.; Wheaton, T.A.; Miller, W.M. Investigation of laser and ultrasonic ranging sensors for measurements of citrus canopy volume. Appl. Eng. Agric. 2002, 18, 367–372. [Google Scholar] [CrossRef]
- Ross, N. Modeling forest canopy heights: The effects of canopy shape. Remote Sens. Environ. 1997, 60, 327–334. [Google Scholar]
- Eamus, D.; McGuinness, K.; Burrows, W. Review of Allometric Relationships for Estimating Woody Biomass for Queensland, the Northern Territory and Western Australia; National Carbon Accounting System Technical Report No. 5A; Australian Greenhouse Office: Canberra, Australia, 2000.
- Keith, H.; Barrett, D.; Keenan, R. Review of Allometric Relationships for Estimating Woody Biomass for New South Wales, The Australian Capital Territory, Victoria, Tasmania and South Australia; National Carbon Accounting System Technical Report No. 5B; Australian Greenhouse Office: Canberra, Australia, 2000.
- Kini, A.U.; Popescu, S.C. TreeVaW: A versatile tool for Analysing Forest Canopy LiDAR Data—A preview with an eye towards the future. In Proceedings of the ASPRS Fall Conference, Kansas City, MO, USA, 12–16 September 2004; pp. 1–10.
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. LiDAR remote sensing for ecosystem studies. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Naesset, E.; Okland, T. Estimating tree height and tree crown properties using airborne scanning laser in a Boreat nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with LiDAR and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- Hemery, G.E.; Savill, P.S.; Pryor, S.N. Applications of the crown diameter–stem diameter relationship for different species of broadleaved trees. For. Ecol. Manag. 2005, 215, 285–294. [Google Scholar] [CrossRef]
- Hyyppa, J.; Hyyppa, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Lim, K.; Hopkinson, C.; Treitz, P. Examining the effects of sampling point densities on laser canopy height and density metrics. For. Cron. 2008, 84, 876–885. [Google Scholar] [CrossRef]
- Segura, M.; Kanninen, M. Allometric models for tree volume and total aboveground biomass in a tropical humid forest in Costa Rica. Biotropica 2005, 37, 2–8. [Google Scholar] [CrossRef]
- Brandtberg, T.; Warner, T.; Landenberg, R.; McGraw, J. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density LiDAR data from the eastern deciduous forest in North America. Remote Sens. Environ. 2003, 85, 290–303. [Google Scholar] [CrossRef]
- Holmgren, J.; Nilsson, M.; Olsson, H. Estimation of tree height and stem volume on plots using airborne laser scanning. For. Sci. 2003, 49, 419–428. [Google Scholar]
- McComb, J.W.; Roberts, S.D.; Evans, D.L. Influence of fusing LiDAR and multispectral imagery on remotely sensed estimates of stand density and mean tree height in a managed loblolly pine plantation. For. Sci. 2003, 49, 457–466. [Google Scholar]
- Holmgren, J.; Persson, A. Identifying species of individual trees using airborne laser scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest: Using LiDAR and multispectral data fusion with local filtering and variable window size for estimating tree height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kaartinen, H.; Maltamo, M. Automatic detection of harvested trees and determination of forest growth using airborne laser scanning. Remote Sens. Environ. 2004, 90, 451–462. [Google Scholar] [CrossRef]
- Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manag. 2005, 213, 54–70. [Google Scholar] [CrossRef]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning LiDAR. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1371. [Google Scholar]
- Næsset, E.; Bjerknes, K.-O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner data. Remote Sens. Environ. 2001, 78, 328–340. [Google Scholar] [CrossRef]
- Rönnholm, P.; Hyyppä, J.; Hyyppä, H.; Haggrén, H.; Yu, X.; Kaartinen, H. Calibration of laser-derived tree height estimates by means of photogrammetric techniques. Scand. J. For. Res. 2004, 19, 524–528. [Google Scholar] [CrossRef]
- Huang, S.; Price, D.; Titus, S.J. Development of ecoregion-based height–diameter models for white spruce in boreal forests. For. Ecol. Manag. 2000, 129, 125–141. [Google Scholar] [CrossRef]
- Hunter, M.O.; Keller, M.; Victoria, D.; Morton, D.C. Tree height and tropical forest biomass estimation. Biogeosciences 2013, 10, 8385–8399. [Google Scholar] [CrossRef]
- Hyyppa, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Persson, A.; Holmgren, J.; Söderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sens. 2002, 68, 925–932. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. LiDAR remote sensing of the canopy structure and biophysical properties of Douglas-fir western hemlock forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Dowling, R.; Accad, A. Vegetation classification of the riparian zone along the Brisbane River, Queensland, Australia using Light Detection and Ranging (LiDAR) data and forward looking digital video. Can. J. Remote Sens. 2003, 29, 556–563. [Google Scholar] [CrossRef]
- Lovell, J.L.; Jupp, D.L.B.; Culvenor, D.S.; Coops, N.C. Using airborne and ground-based ranging LIDAR to measure canopy structure in Australian forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Lucas, R.M.; Cronin, N.; Lee, A.; Moghaddam, M.; Witte, C.; Tickle, P. Empirical relationships between AIRSAR backscatter and LiDAR-derived forest biomass, Queensland, Australia. Remote Sens. Environ. 2006, 100, 407–425. [Google Scholar] [CrossRef]
- Moffiet, T.; Mengersen, K.; Witte, C.; Kinga, R.; Denham, R. Airborne laser scanning: Exploratory data analysis indicates potential variables for classification of individual trees or forest stands according to species. ISPRS J. Photogramm. Remote Sens. 2005, 59, 289–309. [Google Scholar]
- Witte, C.; Denham, R.; Turton, D.; Jonas, D.; Tickle, P.; Norman, P. Airborne laser scanning: A tool for monitoring and assessing the forests and woodlands of Australia. In Proceedings of the 10th Australasian Remote Sensing Conference, Adelaide, Australia, 21–25 August 2000; pp. 348–362.
- Weller, D.; Denham, R.; Witte, C.; Mackie, C.; Smith, D. Assessment and monitoring of foliage projected cover and canopy height across native vegetation in Queensland, Australia, using laser profiler data. Can. J. Remote Sens. 2003, 29, 578–591. [Google Scholar]
- Bunting, P.; Lucas, R.M. The delineation of tree crowns within CASI data of Australian mixed species woodlands. Remote Sens. Environ. 2006, 101, 230–248. [Google Scholar]
- Held, A.; Phinn, S.; Scarth, P.; Stanford, M.; Ticehurst, C.; Hartini, S.; Lymburnber, L. Hyperspectral mapping of rainforests and mangroves. In Proceedings of the International Geosciences and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001.
- Tickle, P.K.; Lee, A.; Lucas, R.M.; Austin, J.; Witte, C. Quantifying Australian forest floristics and structure using small footprint LiDAR and large scale aerial photography. For. Ecol. Manag. 2006, 223, 379–394. [Google Scholar]
- Lee, A.C.; Lucas, R.M. A LiDAR-derived canopy density model for tree stem and crown mapping in Australian forests. Remote Sens. Environ. 2007, 111, 493–518. [Google Scholar] [CrossRef]
- Ozdemir, I. Estimating stem volume by tree crown area and tree shadow area extracted from pan-sharpened Quickbird imagery in open Crimean juniper forests. Int. J Remote Sens. 2008, 29, 5643–5655. [Google Scholar] [CrossRef]
- Greenberg, J.A.; Dobrowski, S.Z.; Ustin, S.L. Shadow allometry: Estimating tree structural parameters using hyperspatial image analysis. Remote Sens. Environ. 2005, 97, 15–25. [Google Scholar] [CrossRef]
- Verma, N.K.; Lamb, D.W.; Reid, N.; Wilson, B. An allometric model for estimating DBH of isolated and clustered Eucalyptus trees from measurements of crown projection area. For. Manag. 2014, 326, 125–132. [Google Scholar] [CrossRef]
- Verma, N.; Lamb, D.W.; Reid, N.; Wilson, B. A comparative study of land cover classification techniques for ‘farmscapes’ using very high-resolution remotely sensed data. Photogramm. Eng. Remote Sens. 2014, 80, 461–470. [Google Scholar]
- Lamb, D.W.; Trotter, M.; Murphy, A.; Young, I. UNE SMART Farm: Showcasing the value of broadband connectivity in the business and lifestyle of farming. In Proceedings of the Digital Rural Futures Conference, University of New England, Australia, 26–28 June 2013.
- Sumida, A.; Komiyama, A. Crown spread patterns for five deciduous broad-leaved woody species: Ecological significance of the retention patterns of larger branches. Ann. Biol. 1997, 80, 759–766. [Google Scholar] [CrossRef]
- Dash, J.; Steinle, E.; Singh, R.P.; Bahr, H.P. Automatic building extraction from laser scanning data: An input tool for disaster management. Adv. Space Res. 2004, 33, 317–322. [Google Scholar] [CrossRef]
- Ryherd, S.; Woodcock, C. Combining spectral and texture data in the segmentation of remotely sensed images. Photogramm. Eng. Remote Sens. 1996, 62, 181–194. [Google Scholar]
- Baatz, M.; Schape, A. Multiresolution segmentation—An optimization approach for high quality multi-scale image segmentation. In Angewandte Geographische Informationsverarbeitung XII, Beitra¨ge zum AGIT-Symposium Salzburg; Wichmann: Heidelberg, Germany, 2000; pp. 12–23. [Google Scholar]
- Benz, U.C.; Hoffmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar]
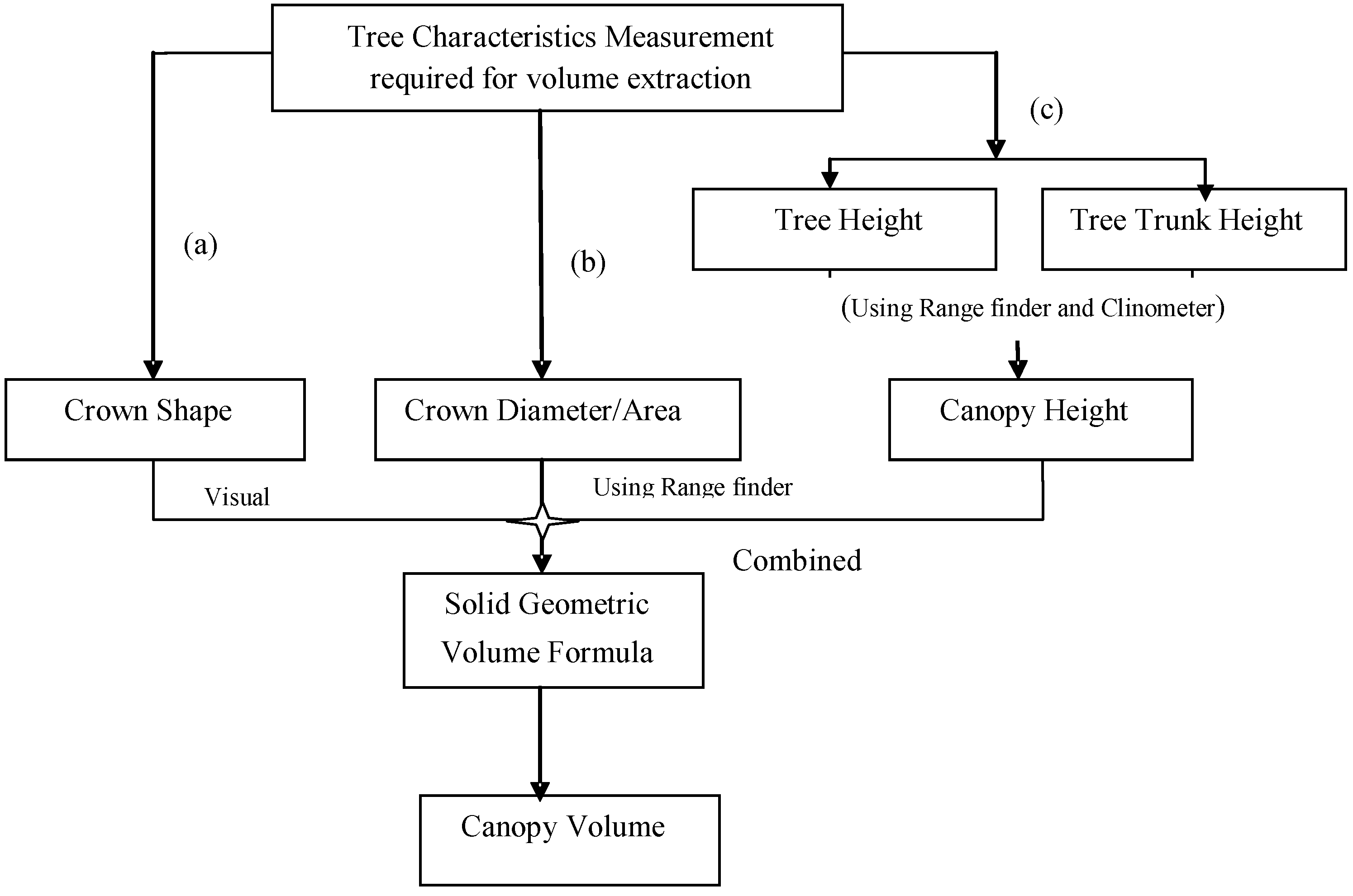
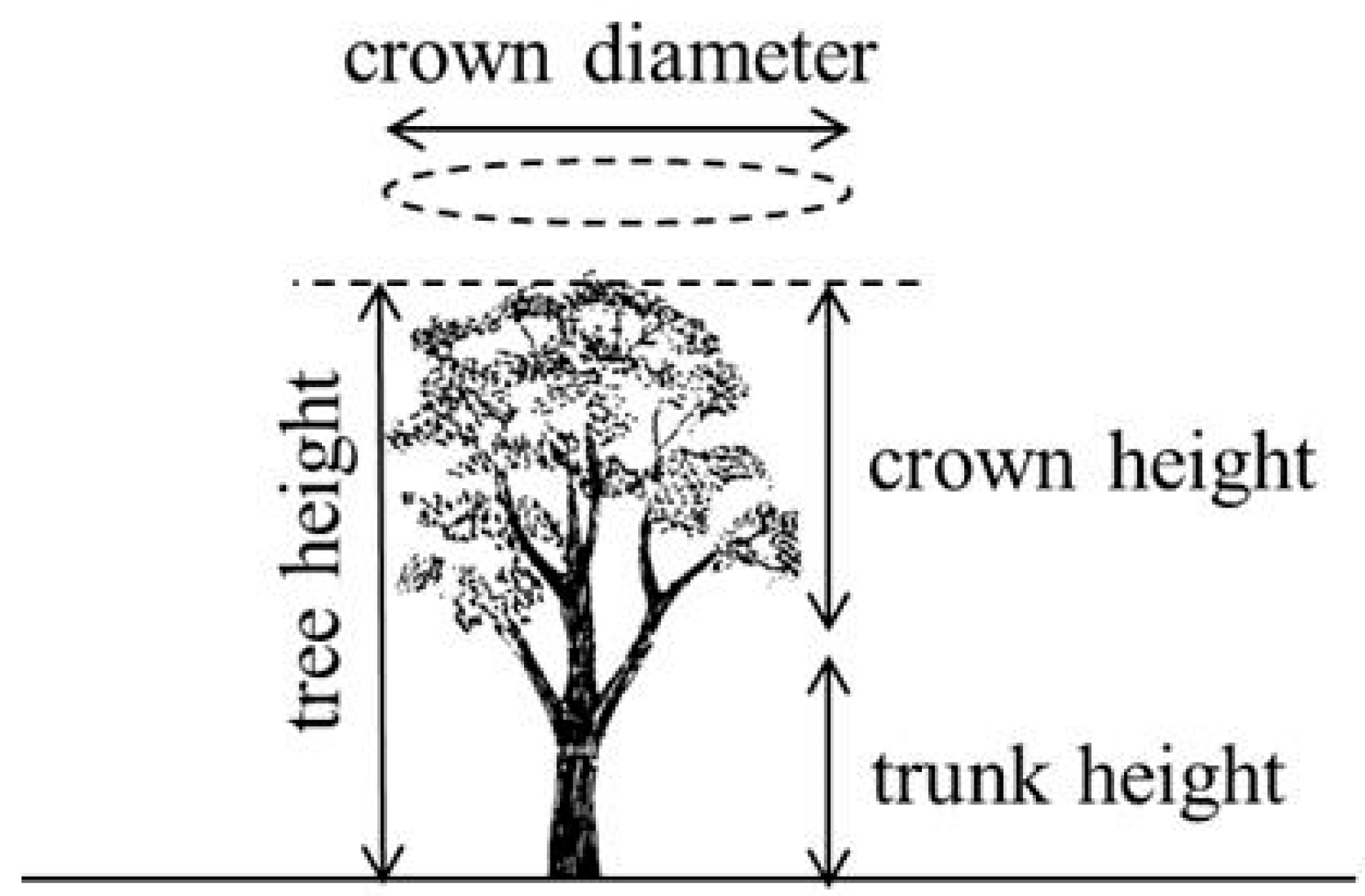

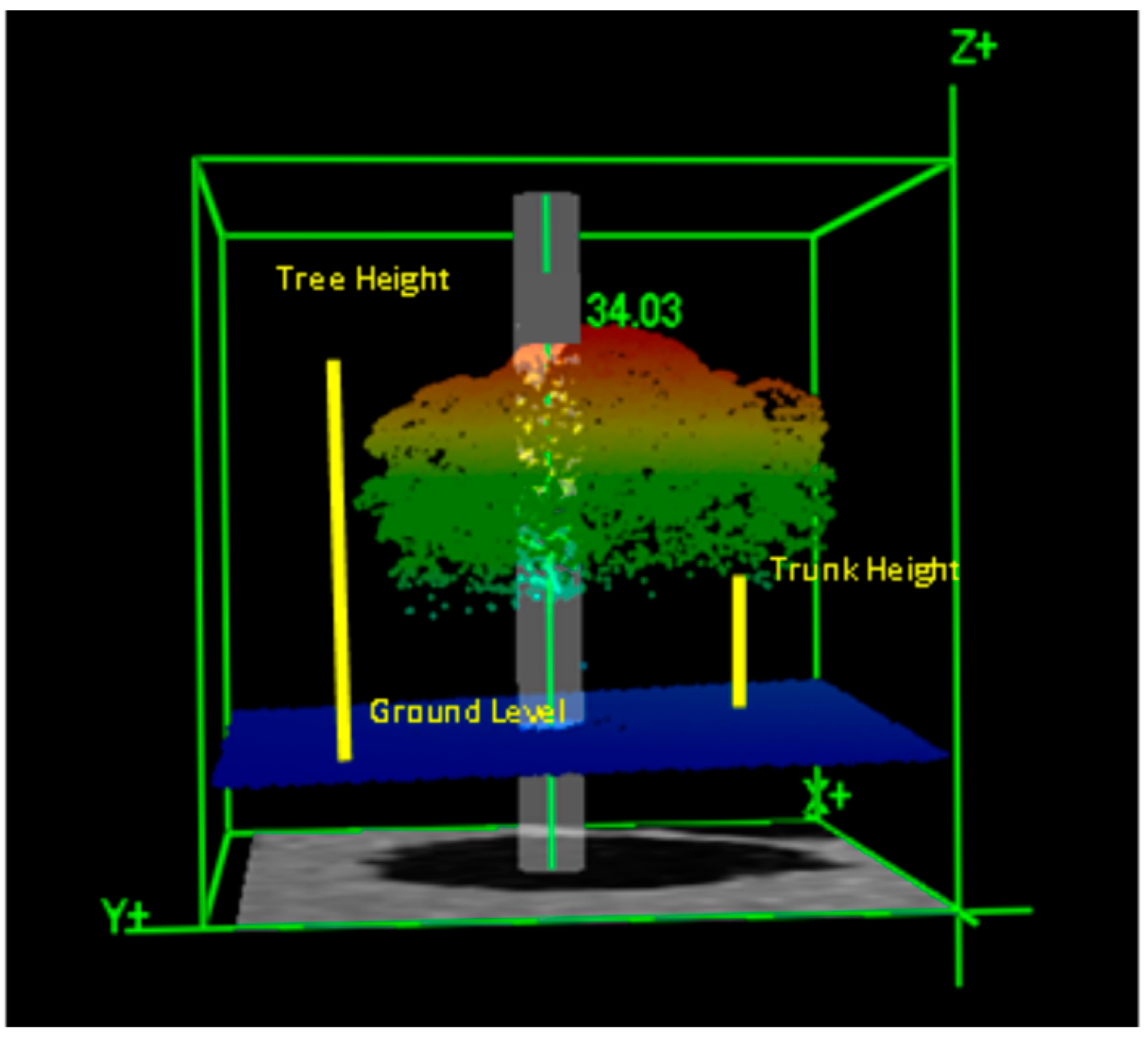

| Parameter | Value | Unit |
|---|---|---|
| Scanning angle | 60 | degrees |
| Flight speed | 216 | km∙h−1 |
| Flight height | 375 | m |
| Scan rate | 192 | Hz |
| Pulse rate | 400 | kHz |
| Swath width | 433 | m |
| Swath overlap | 37 | % |
| Along track point spacing | 0.31 | m (along track) |
| Across track point spacing | 0.31 | m (across track) |
| Outgoing pulse density | 10.26 | m−2 |
| Calculated spot footprint | 0.19 | metres |
| Tree Characteristics | Min | Max | Mean | Std.Dev. |
|---|---|---|---|---|
| Crown diameter (CDfield, m) | 6.8 | 30.5 | 15.2 | 4.9 |
| Crown projected area (CAfield, m2) | 36.3 | 731.8 | 210.4 | 129.1 |
| Tree height (m) | 12.7 | 42.8 | 21.3 | 5.3 |
| Canopy height (m) | 8.8 | 30.6 | 16.1 | 4.1 |
| Trunk Height (m) | 3.6 | 16.2 | 5.2 | 2.6 |
| Canopy vol. (CVfield, m3) (Equation (1)) | 217.9 | 9040.8 | 1840.2 | 1533.1 |
| Equation | R2 | F-stat | p |
|---|---|---|---|
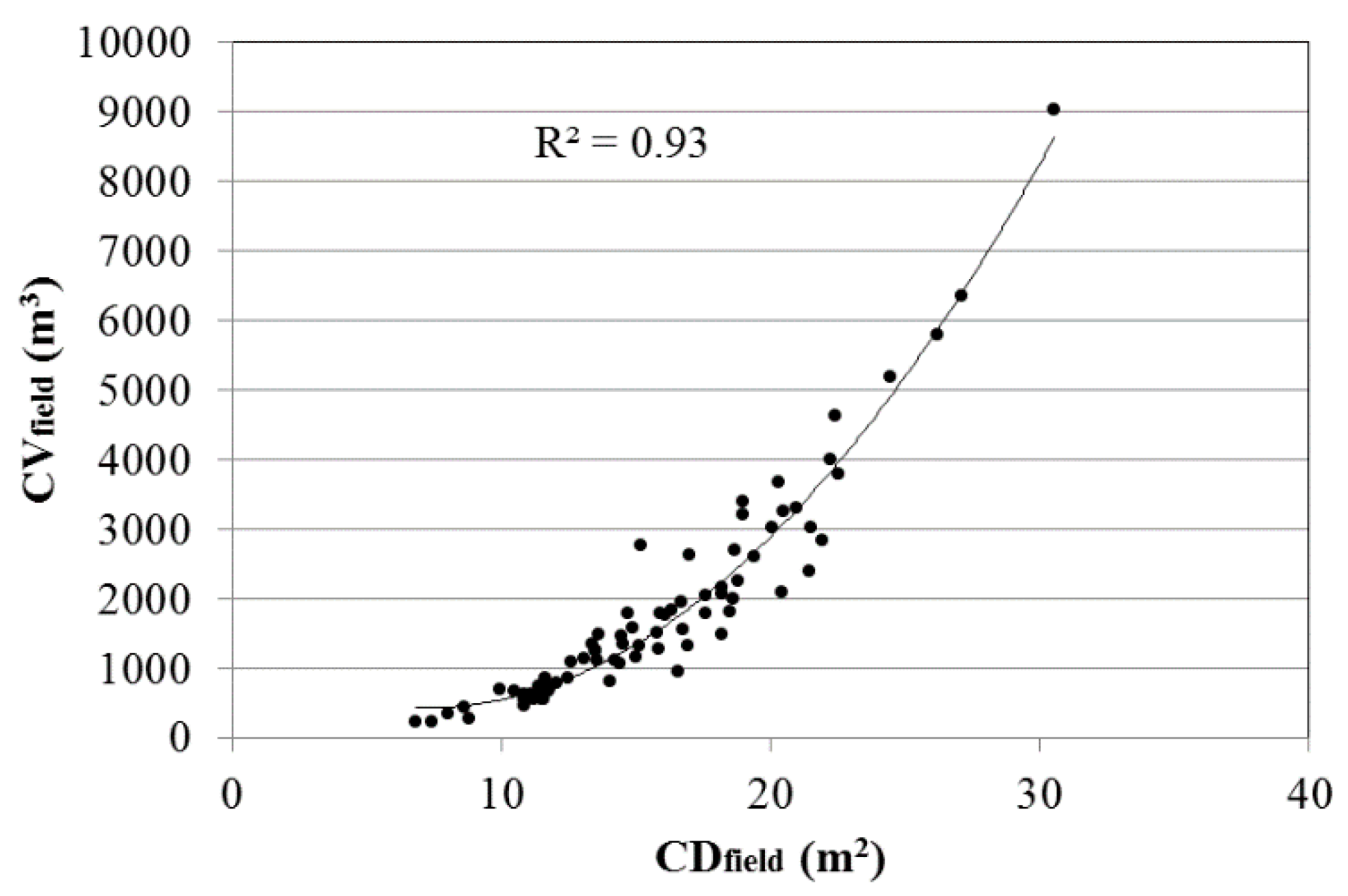
| CVfield = 0.008 × (CAfield)2 + 6.5673 × CAfield – 25.199 | 0.93 | 993.0 | <0.0001 |
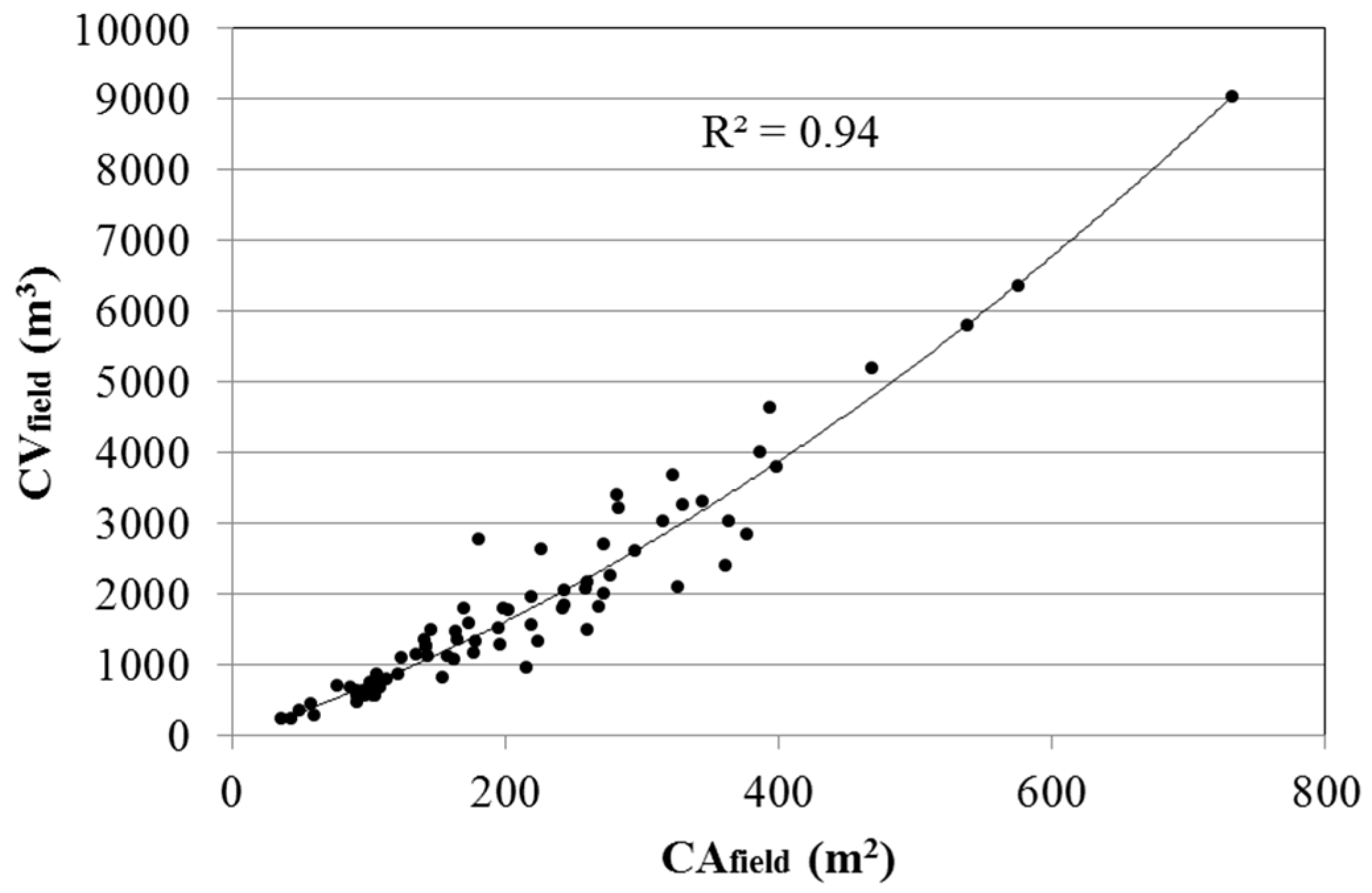
| CVfield = 15.11 × (CDfield)2 – 218.58 × CDfield + 1222.6 | 0.94 | 415.6 | <0.0001 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, N.K.; Lamb, D.W.; Reid, N.; Wilson, B. Comparison of Canopy Volume Measurements of Scattered Eucalypt Farm Trees Derived from High Spatial Resolution Imagery and LiDAR. Remote Sens. 2016, 8, 388. https://doi.org/10.3390/rs8050388
Verma NK, Lamb DW, Reid N, Wilson B. Comparison of Canopy Volume Measurements of Scattered Eucalypt Farm Trees Derived from High Spatial Resolution Imagery and LiDAR. Remote Sensing. 2016; 8(5):388. https://doi.org/10.3390/rs8050388
Chicago/Turabian StyleVerma, Niva Kiran, David W. Lamb, Nick Reid, and Brian Wilson. 2016. "Comparison of Canopy Volume Measurements of Scattered Eucalypt Farm Trees Derived from High Spatial Resolution Imagery and LiDAR" Remote Sensing 8, no. 5: 388. https://doi.org/10.3390/rs8050388
APA StyleVerma, N. K., Lamb, D. W., Reid, N., & Wilson, B. (2016). Comparison of Canopy Volume Measurements of Scattered Eucalypt Farm Trees Derived from High Spatial Resolution Imagery and LiDAR. Remote Sensing, 8(5), 388. https://doi.org/10.3390/rs8050388