1. Introduction
The Doñana National Park holds a system of ponds on aeolian sands that is considered one of the best examples of Mediterranean temporary ponds in Europe [
1,
2]. The aeolian sands extend out of the protected area and with it also the system of temporary ponds. Ponds start flooding with autumn and winter rains and dry-up during spring and summer [
3]. Groundwater seepage feeds the ponds, and the oscillation of the water table level is also responsible for ponds flooding and drying up [
1,
3,
4]. Ponds differ in size and also in the length of time they get flooded every year. They go from rain puddles that remain flooded for a few days -or weeks on rainy winters- to some ponds, up to 187 ha in size, that keep permanent water in part of their basin most of the years. On the other hand, there is a large variability among years on when each pond gets flooded and how long it keeps the water [
1]. We denominate hydroperiod the duration of the flooding period of a pond in an annual cycle [
5]. This is an important ecological parameter as it determines which plants and animals can use the pond for breeding and to complete their life cycles [
2]. Some species have short breeding cycles and require ponds with short hydroperiods where they can out-compete other species with longer cycles. In general, temporary ponds, that dry up completely at some time in their annual cycle do not allow the colonization of species that require permanent water, like fish, and are comparatively free of predators [
2].
The aeolian sands system rests on top of a single, partially confined, aquifer known as the “Almonte-Marismas” aquifer [
6]. It is considered a single aquifer from the perspective of groundwater dynamic although it has been recently divided in 5 sections from a water management point of view [
7]. The Doñana’s system of Mediterranean temporary ponds on the aeolian sands has received substantial attention from the perspective of its hydrology [
8,
9], geomorphology [
10,
11,
12], relation to groundwater [
4,
13,
14], water chemistry [
15,
16], biodiversity [
17,
18,
19,
20] but most studies have been conducted in a few ponds and only for a few years.
Remote sensing is a cost-effective technique to study the temporal dynamic of wetlands. It has the capacity to study simultaneously numerous water bodies over a large area, has the potential to scale-up in-situ data, and can provide retrospective information on wetland evolution using time series of medium resolution sensors [
21,
22,
23,
24]. The Landsat satellites have been acquiring images with comparable sensors from 1972 to the present [
25]. In the case of Doñana’s aeolian sands more than 400 Landsat satellite images have been acquired during the last 35 years.
Optical images are an adequate tool to discriminate flooded areas and can delineate continental water bodies taking advantage of the low reflectance of water in the Near Infrared (NIR) and Short Wave Infrared (SWIR) regions [
26,
27]. They have been used to monitor inland water characteristics [
28,
29], but its use is less frequent for shallow and small waters bodies [
30,
31]. In particular, turbid waters or waters covered by aquatic vegetation may be more difficult to map due to the reflectance peaks between 700 and 900 nm related to the presence of phytoplankton and/or suspended sediments [
29,
32], and the reflectance of vegetation in the NIR region. So small, shallow temporary ponds sometimes turbid or covered by vegetation can be challenging to map accurately [
33].
Optical sensors on board of Landsat satellites have a medium resolution, 60 m pixels in the MSS and 30 m pixels in TM, ETM+ and OLI multispectral bands. They overpass the area every 16 days and, as it is possible to have a long time series of comparable images, we think it is possible to study the hydrological behavior and temporal trends of relatively small temporary ponds on the Doñana’s aeolian sands. The medium resolution of Landsat sensors do not allow to distinguish by their shape small artificial ponds that have been built for irrigation or recreational purposes from natural temporary ponds. Also, some natural ponds in the area may have been transformed and be suffering an artificial flooding regime. For that reason we use the term “temporary water body” to refer to all areas identified by remote sensing that show some kind of periodic flooding regime on the aeolian sands, and we limit the use of the term “temporary pond” to those that have a natural flooding regime.
There are areas in the Doñana’s aeolian sands that have received different levels of legal protection. We expected that the areas that have had a higher level of protection and have been protected for a longer time will have a better preserved system of temporary ponds with a temporal dynamic that is less affected by water use, and more dependent on precipitation. As water use for irrigated agriculture and water consumption by residential areas are the main pressures for groundwater abstraction or surface water diversion in the area [
9,
13,
14,
34], we expected that ponds close to irrigated agriculture or residential areas would be the ones more affected in their hydroperiods and would show a sharper declining trend with time. As agriculture and people “compete” for water with the ponds, we expected that ponds that were close to irrigated agriculture and residential areas would have shorter hydroperiods. Also, as water demand by agriculture and people increase, the mean hydroperiod and total surface flooded would show a stronger declining trend with time in areas with a higher surface of irrigated agriculture or residential areas.
2. Study Area
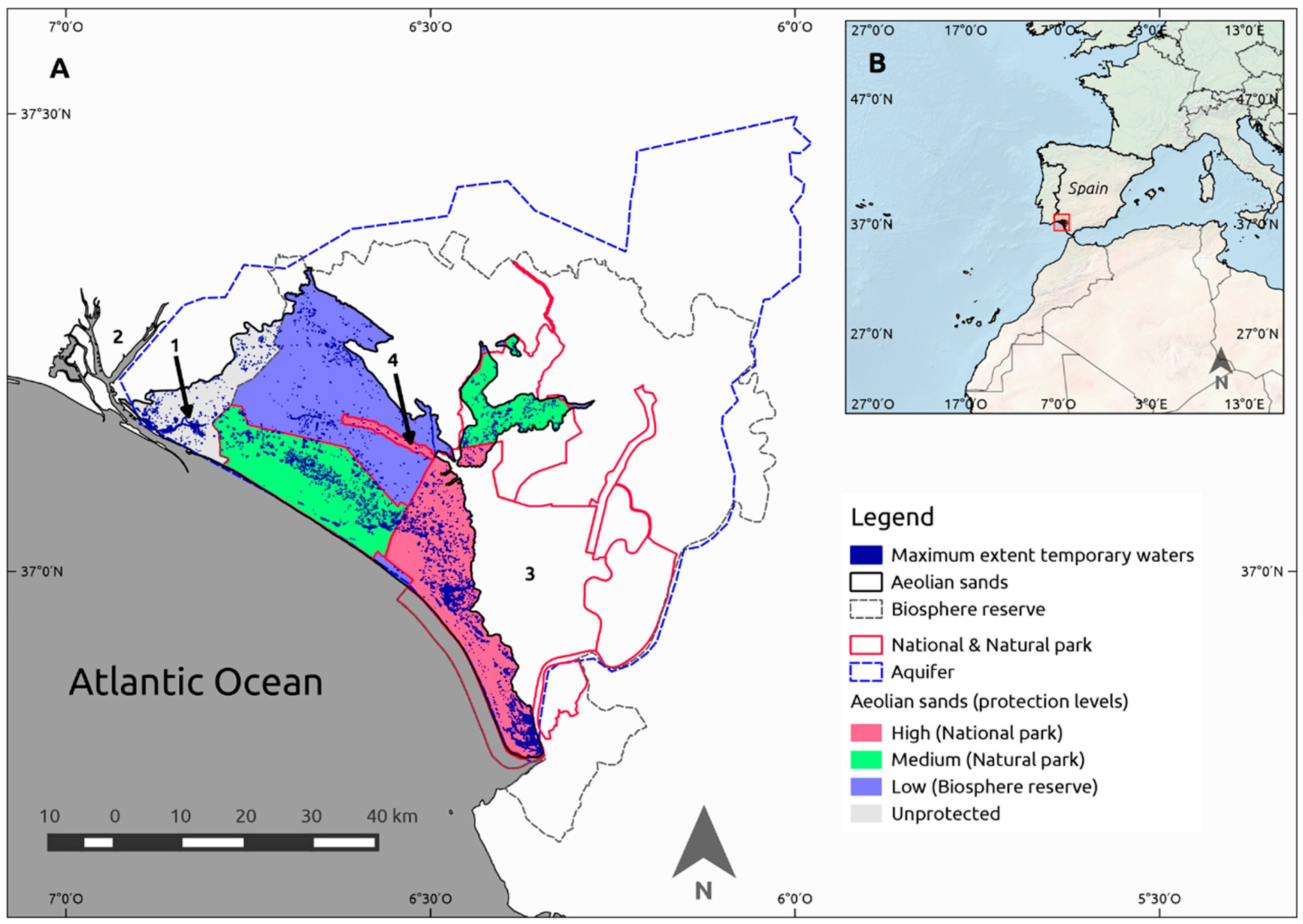
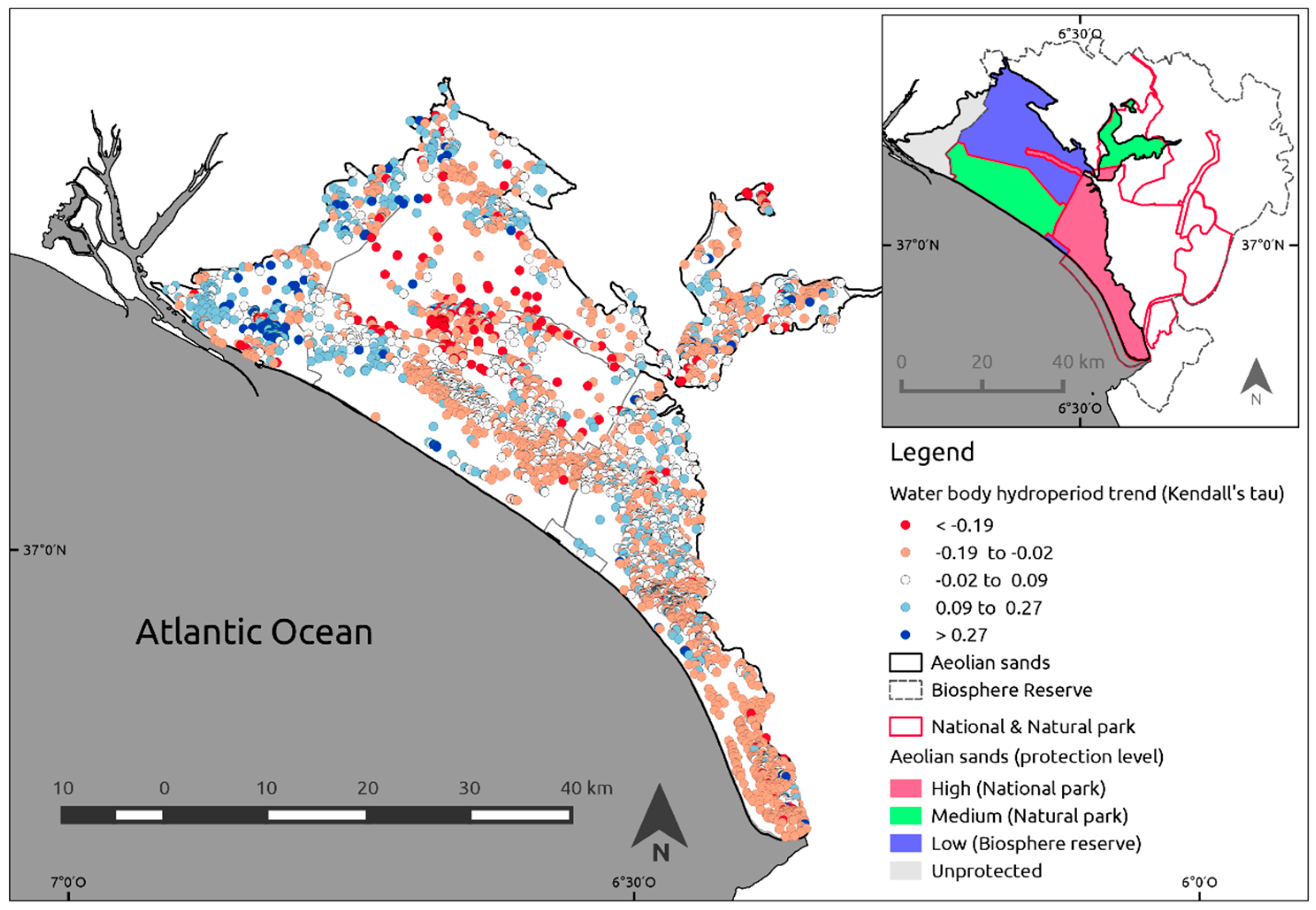
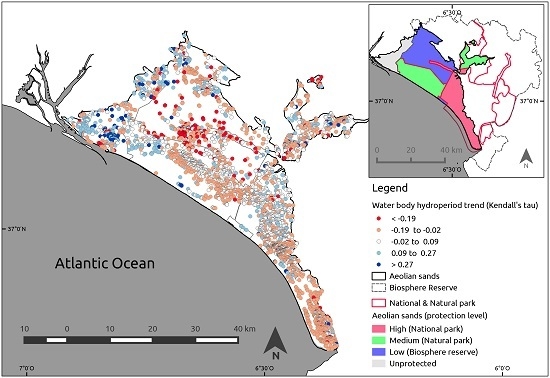
The study area is the Doñana’s aeolian sands, also known as the coastal aeolian mantle (“
Manto Eólico Litoral de Doñana”) in the province of Huelva, Spain (
Figure 1). The area is delimited by the aeolian sand deposits as extracted from the REDIAM geomorphological map of Andalusia 1:400,000 [
35]. These are coastal aeolian sand deposits of Quaternary age on top of Miocene marine marls. Part of the aeolian sands are included in Doñana National Park that was created in 1969 with an extension of 507.2 km
2. The protected area was expanded in 1980 with the creation of a buffer zone the “Preparque Doñana” (542.5 km
2), that was later transformed into the Doñana Natural Park by the Andalusian regional government in 1989. UNESCO recognized Doñana National Park as a Biosphere Reserve with an extent of 772.6 km
2 in 1980. In 1982 Doñana wetlands were included in the list of the Ramsar Convention. In July 2012, UNESCO approved the extension of the biosphere reserve to the present limits covering an area of 2550 km
2. The aeolian sands are affected by these different levels of protection. An area of 239 km
2 has been included within the National Park since 1969. A total of 255 km
2 were included in the buffer zone in 1980 and, currently, are part of the Doñana Natural Park. An extent of 316 km
2 were included in the 2012 expansion of Doñana Biosphere Reserve. The rest of the aeolian sands (108 km
2) have no legal protection, with the exception of some water-table lakes that are included in the “
Paraje Natural Lagunas de Palos y Las Madres” (1989), and have an extent of 6.9 km
2 (
Figure 1). We consider in this paper four sections of the aeolian sands that have been receiving different levels of legal protection considering both the time since they were legally protected and the different legal protection forms. They go, from more to less protection: National Park > Natural Park > Biosphere reserve > Unprotected area.
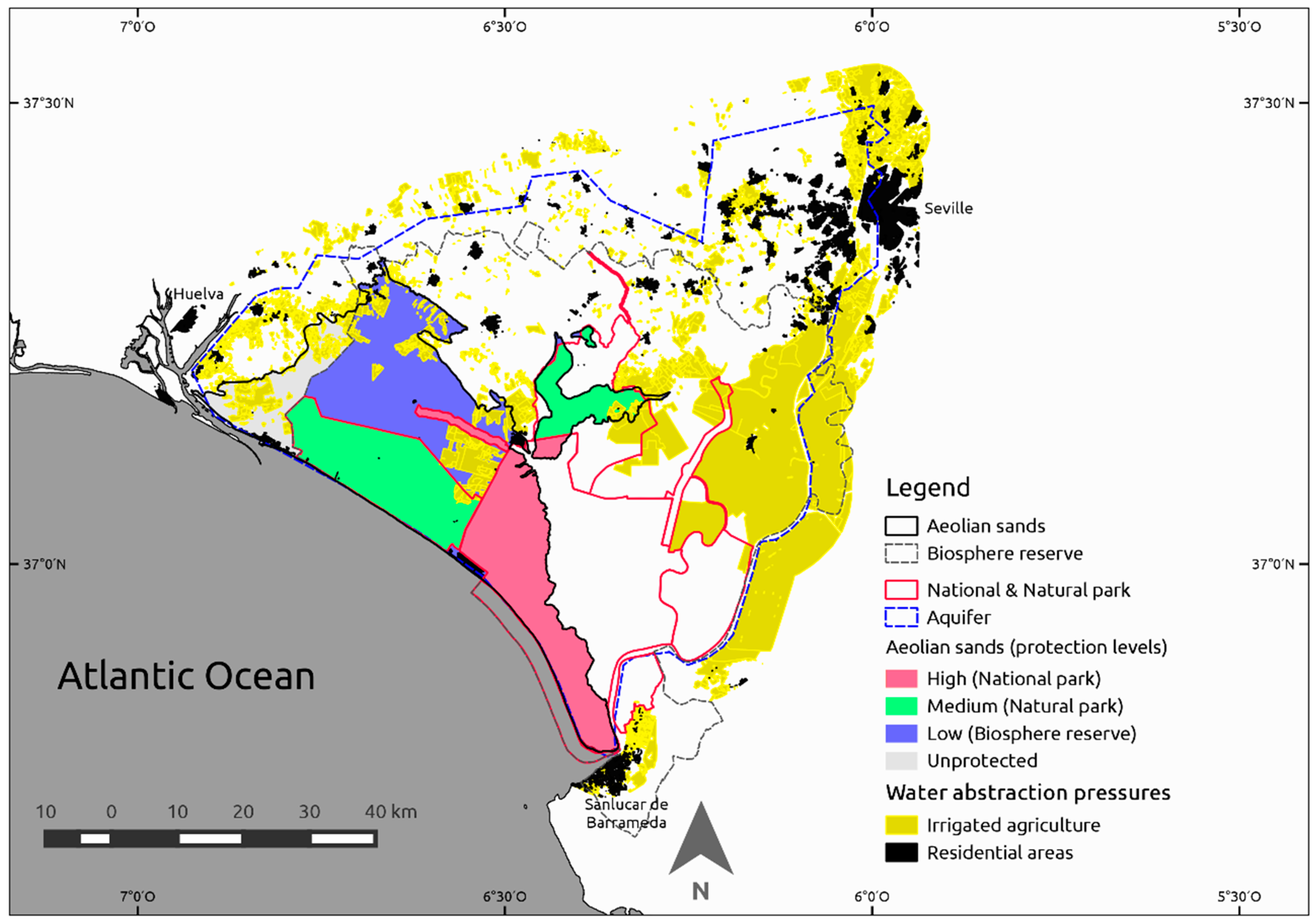
The main transformations in the area that affect water use are residential areas and agriculture. In 2007 residential areas were occupying 8.8 km
2, outside the National and Natural Park, but extended close to their limits. Irrigated agriculture had been increasing during the last three decades, mainly in the area that is unprotected but also within the Doñana Biosphere Reserve, and was covering an extent of 101 km
2 [
36]. The “Almonte-Marismas” aquifer extends over an area of 3290 km
2 and includes 88.6 km
2 of residential use and 617 km
2 of irrigated agriculture (
Figure 2).
3. Material and Methods
3.1. Satellite Imagery
We acquired every available Landsat TM, and ETM+ image for the Doñana’s aeolian sands (Path: 202, Row: 34) from 1985 to 2014. We decided to exclude the images from the Landsat MSS sensor because most temporary ponds in the aeolian sands are shallow and small in size, the MSS pixel size (79 × 57 m
2) is too coarse to identify them, MSS has no SWIR band that is the most adequate for identification of shallow waters, and from 1975 to 1984 the number of satellite images per year was small (0–8 images) so hydroperiod estimation of temporary ponds had too much error. We used 325 valid satellite images from 1985 to 2014 providing 30 years of continuous observation using the TM and ETM+ sensor from Landsat 4 to 7. Some images were discarded due to acquisition problems such as missing lines and columns, radiometric incoherence or lines shifts, and cloud cover. Number of valid scenes per year ranged from 4 to 22 with a median of 11 scenes (
Table S1).
In order to make the time series comparable, a semi-automatic robust and coherent pre-processing was applied. The complete procedure is detailed by Díaz-Delgado et al. [
37] but in short it included metadata retrieval from raw 1 G data images, geometric and atmospheric corrections followed by time series radiometric normalization using ordinary least squares regression towards a reference cloud-free and clear atmosphere image (18 July 2002) using in pseudo-invariant areas [
38,
39].
3.2. Hydroperiod Estimation
We extracted the SWIR band, b5 (1.550–1.750 in TM μm) of the TM and ETM+ images, and obtained a flood mask by considering as flooded any pixel with a normalized reflectance <0.186 (Kappa = 0.66, global accuracy = 94% [
37]). This procedure has been successfully tested to classify flooded areas in shallow waters affected by turbidity and aquatic vegetation [
29,
30,
37], and was employed by Gómez-Rodríguez et al. [
33] to map small temporary ponds in the same area.
We call pixel annual hydroperiod the number of days a 30 m pixel remains flooded in an annual hydrological cycle. As rains in the area start after the northern hemisphere summer our cycles go from 1 September to 31 August of the next year. By convention we name the cycles with the end year, so the cycle from 1 September 1984 to 31 August 1985 is the “1985 cycle”. To calculate the pixel annual hydroperiod we reclassified all flooded pixels in image
i to the number of days spanned from the previous image (
I − 1), provided the pixel was flooded in the previous image, and added up all the reclassified flood masks in the cycle. So pixel annual hydroperiod (H) can be computed according to Equation (1).
where DoC stands for Day of Cycle. For every annual cycle, the
i-th image corresponds to the first date the pixel was classified as flooded while the
n image is the last date when the pixel was classified as flooded. The
n value may eventually be equal the total number of flooding masks per cycle if the pixel is classified as flooded at every flooding mask for that annual cycle. The procedure assumes that a pixel classified as flooded between two consecutive dates has not dried-up in between. If a pixel is dry at an intermediate date the formula discounts the days lapsed from the previous flooded image.
This method to calculate the pixel annual hydroperiod tends to underestimate the true value, because the pixel should flood before the first image in the cycle we classify it as flooded, and should dry-up after the last image in the cycle we classify it as flooded. As this underestimation is influenced by the number and the dates of valid images in a cycle, this tends to create an underestimation in the initial cycles that have a smaller number of images. The existence of this bias is clear by calculating the temporal trend of hydroperiod (
H) in pixels in the Atlantic Ocean that show a positive, although not significant, temporal trend (slope b = 0.87, Student-
t = 0.875,
p = 0.4). To correct this bias we performed a linear stretch to the hydroperiod estimate multiplying Hi by 365/Hmax. Being Hi the value of the pixel, Hmax the maximum value of H in the annual cycle that correspond to pixels extracted from the ocean, and 365 days the expected maximum value of hydroperiod in the cycle. Correction factors for each cycle (C) are provided in
Table S1.
3.3. Study Area Limits
We created a mask of the Doñana’s aeolian sands by reclassifying all the geomorphological units on the Geological map of Andalusia [
35] on top of the “Almonte-Marismas” aquifer that are classified as active dunes, vegetated dunes, aeolian sand mantles, and sand deposits, including the small geomorphological units in-between classified as creeks or lakes, but excluding the impermeable clay deposits that form the Doñana and the Tinto and Odiel marshes (
Figure 1).
Protected area limits were taken from the official published limits of the Doñana Natural Space that include the National and the Natural Park and the Doñana Biosphere Reserve as of 2016. The “Rocina protection area” of Doñana National Park is considered with the same level of protection as the Doñana National Park.
The official limits of the “Almonte-Marismas” aquifer were extracted from the web map services from the Ministry of Agriculture and Environment from Spain [
40] considering all the aquifer sections below the Doñana’s aeolian sands.
3.4. Potential Temporary Waters and Temporary Water Bodies Definitions
Any pixel on the aeolian sands that was classified as flooded once during the study period is considered as potentially holding temporary water ponds, and we denominate this as potential temporary waters. Temporary ponds can be small in size and the spatial resolution of TM and ETM+ (30 m pixels) suggests that water bodies bellow 900 m
2 in area can be overlooked and will be omission errors [
17,
33]. The procedure is also prone to errors of commission caused by cloud, topographic, and tree shadows, specially during winter when the sun is low. All pixels that were classified as potential temporary waters in any annual cycle were overlaid to create a mask of total potential temporary water that was used to define the maximum extent of potential temporary waters on the aeolian sands (
Figure 1) to estimate mean pixel hydroperiod values, temporal trends, and number of temporary water bodies.
We consider as a single temporary water body the one formed by all pixels from the maximum extent of temporary waters that are spatially connected and separated from other water bodies. Pixels that are connected are probably not independent water bodies and analyzing the data on a pixel by pixel basis would be pseudoreplication. This definition of water body we use implies that ponds that are considered as independent ponds in other studies may have been considered as a single water body in our analyses if they are connected at high water levels. This, together with the lower size limit of 900 m
2 to identify a temporary water body, should be taken into account when using the number of water bodies estimated with our methods to compare them with those provided by other studies in the area [
41]. Initial vectorization of the potential temporary waters mask without correcting for topographic shadows or pine woods identified a total of 3638 water bodies.
3.5. Correction of Potential Temporary Waters for Topographic Shadows and Pine Woods
Preliminary exploration of the data suggested that topographic shadows and dense pine woods could be the cause of commission errors in the maximum extent of temporary waters.
To correct for topographic shadows we created a mask of mean topographic shadows in December, when solar elevation is lowest. We calculated a topographic hill-shading image on 21 December, at the time of Landsat overpass, using the 5-m DEM from CNIG [
42] and resampled it at 30 m (with ArcGis). We considered as shadows all pixels with relative illumination below 80 (less that 2% of the lowest values of the hill-shading image). Shadows did not seem to be a general a source of commission errors as could be observed overlaying a vector file of potential temporary waters pixels on top of the hill-shading image. To evaluate the extent of commission errors caused by shadows we extracted the pixels under shadows and only a few temporary water bodies had 100% of the pixels in shadows (33 out of 3638 temporary water bodies, less than 1%).
To correct for errors caused by dense pine woods we reclassified two Landsat images, one from December 2013 and one from December 2010, using a density slice of NDVI values. We selected a time of the year when pine woods show maximum NDVI values [
43]. The cut-point in NDVI was chosen in each case to select dense pine woods, avoiding selecting shrubland or pastures, using as reference well known areas in the Doñana Biological Reserve. A potential temporary waters vector file was overlaid on the Landsat pine maps. Some large areas of pine woods in the south of Doñana tended to be classified as potential temporary waters. It has to be taken into account that if a pixel covered by pines is identified as water in a single mask it will appear in this maximum extent of temporary waters. Out of 3638 water bodies a total of 173 had 100% of pixels covered by pines in both dates, 69 were covered by pines in 2010, and another 176 were covered by pines in 2013. So a total of 418 (11%) temporary water bodies could be commission errors caused by pine woods.
To reduce commission errors caused by pine woods, and by topographic shadows, we excluded from the maximum extent of temporary waters all pixels covered by pine woods or affected by shadows using these masks.
After masking the coverage was vectorized to obtain a total 3939 temporary water bodies. After this we corrected the coverage by eliminating water bodies that corresponded to tidal zones (variations in tide level on the coast) and those that were connected to the marsh, to the river, or to the sea. The final number of temporary water bodies on the aeolian sands was reduced to 3678.
3.6. Environmental Predictors
3.6.1. Precipitation
We obtained the mean accumulated precipitation on top of the “Almonte-Marismas” aquifer for each annual cycle (1 September to 31 August) summing monthly precipitation surfaces obtained from REDIAM [
44]. Surfaces have been calculated by REDIAM by interpolating from all available automatic meteorological station using the inverse distance algorithm in ArcGis. From this gis raster cover we extracted the mean precipitation for each hydroperiod cycle from September 1984 to August 2012 and calculated the mean for the aquifer polygon using SAGA 2.1.4 Statistics for Grids [
45]. The data from 1984 to 2009 are from the “
serie consolidada” [
44] and from 2010 to 2012 from “
serie provisional” [
46]. To complete the series we obtained the monthly precipitation data from 1 September to 31 August from the I.F.A.P.A. automatic agroclimatic stations [
47] inside the aquifer polygon for the cycles 2013 and 2014 that had no interpolated data by REDIAM.
3.6.2. Distance to Irrigated Agriculture and Residential Areas
We assume that distance to irrigated agriculture and distance to residential areas are the best predictors for the main sources for groundwater abstraction and surface water diversion for agriculture and human consumption respectively. Not all wells used for groundwater pumping are known, volumes pumped are not well documented, and many wells are illegal. The distribution of irrigated agriculture and residential areas has been done by photo-interpretation and so less prone to error. We used as source for irrigated agriculture and residential areas the 2007 1:25,000 Land use-land cover coverage from Andalusia from REDIAM [
36]. The area was clipped with a polygon defined calculating a 5 km buffer on the “Almonte-Marismas” aquifer limits (
Figure 2). We reclassified all polygons representative of irrigated agriculture and calculated distance in meters to the closest polygon with IDRISI Selva module DISTANCE [
48]. In a similar way we reclassified all land uses representative of residential areas, including gardens and golf courses and calculated distance in m to the closest residential area pixel. Reclassification criteria are provided in
Tables S2 and S3. Pixels included in irrigated agriculture polygons have a distance value of 0 m to irrigated agriculture and pixels included in residential polygons have a distance value of 0 m to residential areas.
3.6.3. Altitude above Sea Level
Altitude above sea level can be an important characteristics of a temporary pond as it can determine the elevation in relation to the groundwater table and in relation to the surface drainage network, and explain differences in flooding behavior. We used the 5 m DEM from GNIG [
42] resampled to 30 m to calculate the mean altitude above sea level for each water body.
3.6.4. Spatial Location of Water Bodies
Trends in hydroperiod or in the correlation of hydroperiod with precipitation could be due to other spatial trends that are not explained by the environmental predictors we selected (e.g., distance to irrigation cultures or to residential areas). We calculated the X and Y coordinates of the centroid for each temporary water body and tested for a significant spatial trend in the data. Spatial trends can be tested, or corrected, in statistical models in several ways. For example, testing for a linear or polynomial trend in X or in Y. In our models we used smoothing splines surfaces, that is a method of fitting a smooth surface to noisy data using splines, that are piece-wise polynomial functions. The degrees of freedom (d.f.) of the spline surface indicate how much flexibility the model is allowed to follow the spatial pattern in the data. We tested in each model a smoothing spline surface of the spatial coordinates with up to 3 d.f. [
49,
50]. This is a way of testing if the trends observed in relation to distance to threats or protection level are still significant when correcting for more general spatial trends.
3.7. Photo-Interpretation of Randomly Selected Temporary Water Bodies
Not all water bodies identified with this procedure are temporary ponds. To estimate the proportion of different types of water bodies in our coverage we photo-interpreted a random selection of water bodies. We selected at random 100 water bodies from each of the four levels of protection (National Park, Natural Park, Biosphere reserve and Unprotected area). A random number was generated for each water body and the first 100 from each level were selected for photo-interpretation. One of us (DA) blindly photo-interpreted the water body vector limit using Bing and Google Earth images and classified them in the following categories: (1) natural pond; (2) stream; (3) irrigation pond; (4) artificial pond; (5) dense pine wood; (6) other dense vegetation; (7) disperse vegetation; (8) non vegetated, and also classified the water body neighborhood as: (1) natural vegetation; (2) cereal agriculture; (3) irrigated agriculture; (4) greenhouses; (5) industrial; (6) urban; (7) beach-tidal; and (8) other. The criteria used by the photo-interpreter are provided in
Tables S4 and S5.
3.8. Statistical Analyses
We calculated the mean hydroperiod for each pixel included in the coverage of maximum extent of temporary waters on the aeolian sands (excluding topographic shadows, pine woods and tidal areas) for the whole time series (1985–2014) by adding the annual hydroperiod images and dividing by the number of years with IDRISI Selva Image Calculator [
48].
With the module PROFILE of IDRISI Selva [
48] we extracted a temporal profile of the maximum surface flooded, mean hydroperiod, and standard deviation of the hydroperiod for each annual cycle for pixels in each of the four protection levels, using only the pixels included in the mask of maximum extent of temporary waters.
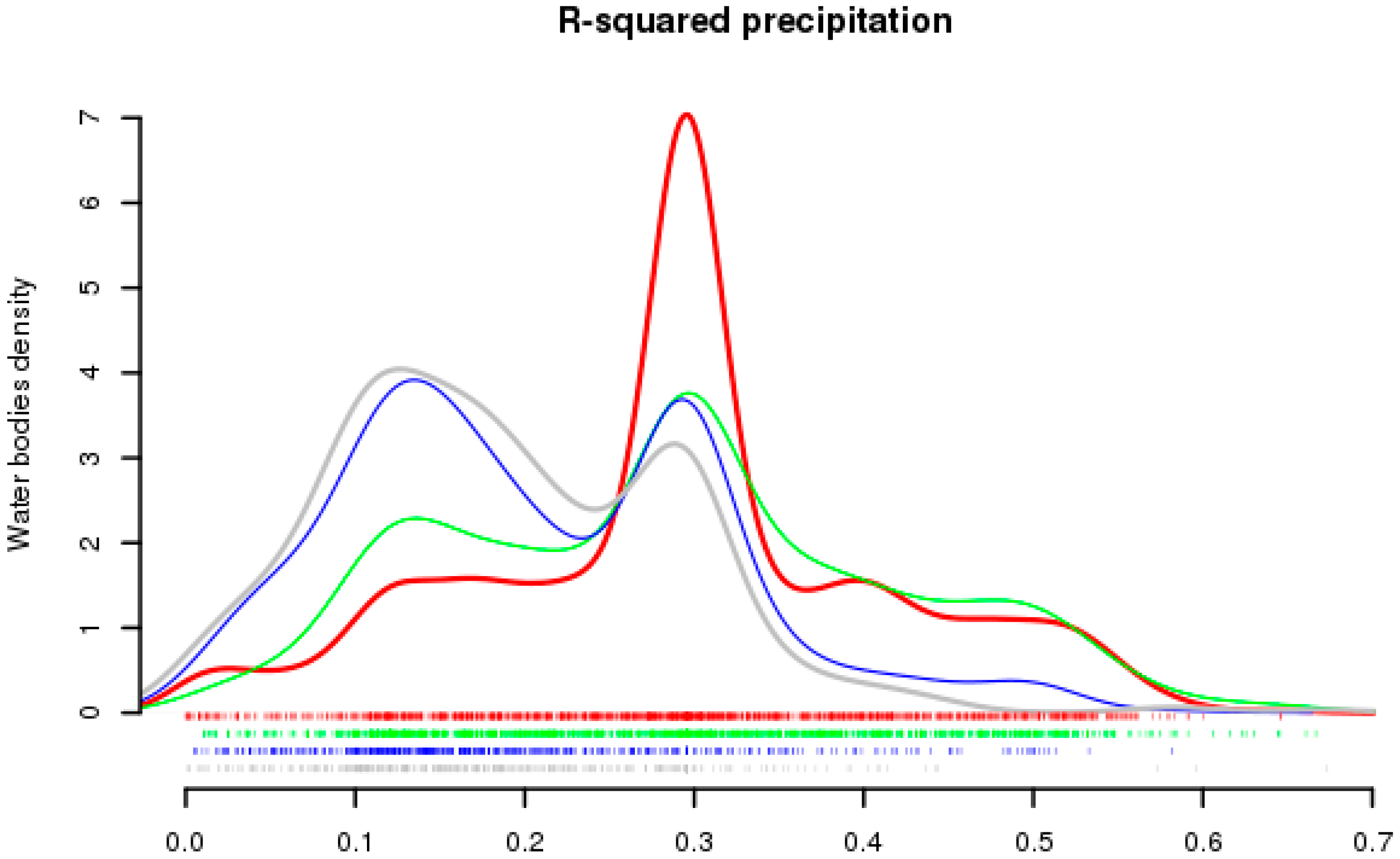
The annual hydroperiod of temporary ponds in the aeolian sands is heavily dependent on accumulated precipitation [
33]. To reduce the noise in pixel hydroperiod temporal trend caused by variable precipitation in each annual cycle we calculated for each pixel an ordinary least squares regression using as response the annual hydroperiod and as predictor the mean accumulated precipitation. From this regression we calculated R-squared at the pixel level, and obtained the residual images of the linear regression using IDRISI Selva module CORRELATE [
48]. With the residual images we calculated the Mann-Kendall rank correlation (or Kendall’s tau) and Theil-Sen slope with IDRISI Selva module KENDALL. Positive Kendall’s tau indicate pixels that have positive trends in hydroperiod once corrected for precipitation (water bodies that did not exist previously or that are increasing in hydroperiod more than it could be expected from precipitation alone) while negative values indicate declining temporal trends in hydroperiod (that cannot be explained by a decline in precipitation). The Theil-Sen slope is a robust method for fitting a linear trend to a set of points that chooses the median slope among all lines through pairs of two points. It is much less sensitive to outliers and in our case indicates how fast is hydroperiod declining or increasing once corrected for precipitation.
All statistical models were fitted in R (version 3.2.5) [
51]. We used linear models and generalized additive models (GAMs), fitted with stats and gam 1.12 R packages respectively, to test which environmental predictors could explain the relationship between precipitation and hydroperiod, and the temporal trends in hydroperiod using all temporary water bodies. For each water body and year we extracted the mean value of the R-squared of the regression with precipitation, mean Mann-Kendall rank correlation (Kendall’s tau), and mean Theil-Sen slope, using all pixels included in the water body. These were used as response variables in the models. The R-squared value (range 0–1) was arcsine transformed, calculating the arcsine of the square root, as this transformation normalized the distribution of errors. For each water body we extracted the protection level (National Park, Natural Park, Biosphere Reserve, Unprotected area), mean distance to irrigated agriculture, mean distance to residential areas, mean altitude above sea level, and X and Y coordinates of the centroid (in m), to be used as predictors. Distances were log transformed (distance + 1).
We started fitting a linear model that included as predictors: protection level as a factor, and distance to irrigated agriculture and distance to residential areas as a linear terms using normal errors. This is the model defined by our a priori hypothesis, that water abstraction pressures and protection level are the main factors influencing hydroperiod behavior in temporary ponds. The model was tested in stepwise fashion using step.gam (gam 1.12 package) for simplification or for increased complexity (backwards-forward procedure) by removing terms or by substitution of the linear term with 2 d.f. and 3 d.f. smoothing splines of the distance to irrigated agriculture or distance to residential areas, a linear term of the altitude above sea level, or a smoothing spline surface of the spatial coordinates (2 d.f. and 3 d.f). The best model obtained in this procedure, the one with minimum AIC, was selected. Δ AIC values for each predictor in each model are given in
Tables S6–S9.
We expected that water bodies could show a different temporal trend depending on their natural or artificial origin. To test if natural or artificial water bodies could be showing different temporal trends in hydroperiod we fitted a full linear model with protection level, type of flooding (natural or artificial), distance to irrigated agriculture and distance to residential areas with all interaction terms, and performed a backward simplification until all remaining terms and interactions were significant according an F-test. Then we refitted the models using a random sample of water bodies that had been photo-interpreted as with natural flooding (natural ponds, streams, and open vegetation far from agricultural or residential areas) to test if the models found using all data were representative of natural temporary ponds or were mainly caused by artificial water bodies.
3.9. Structure of Statistical Analyses
First, we analyze, within each level of protection, the trends from 1985 to 2014 in: mean hydroperiod, coefficient of variation of hydroperiod, and maximum surface flooded, for the pixels that were included in the maximum extent of temporary waters (
Figure 1), and we compare these trends with the trend in precipitation. Then we correlate precipitation with mean hydroperiod and surface flooded for each level of protection to test to what extent precipitation explains the differences in trends.
Second, we fit models at the level of water body to test if distances to threats (irrigation and residential areas) and protection level statistically explain the differences in correlation between hydroperiod an precipitation, and the differences in hydroperiod trend once corrected by precipitation.
Third, from all water bodies we select a random sample from each protection level that are photo-interpreted and classified into natural water bodies, artificial water bodies and errors. They allow us to calculate commission errors, and to estimate proportions of natural ponds and artificial ponds in each protection level.
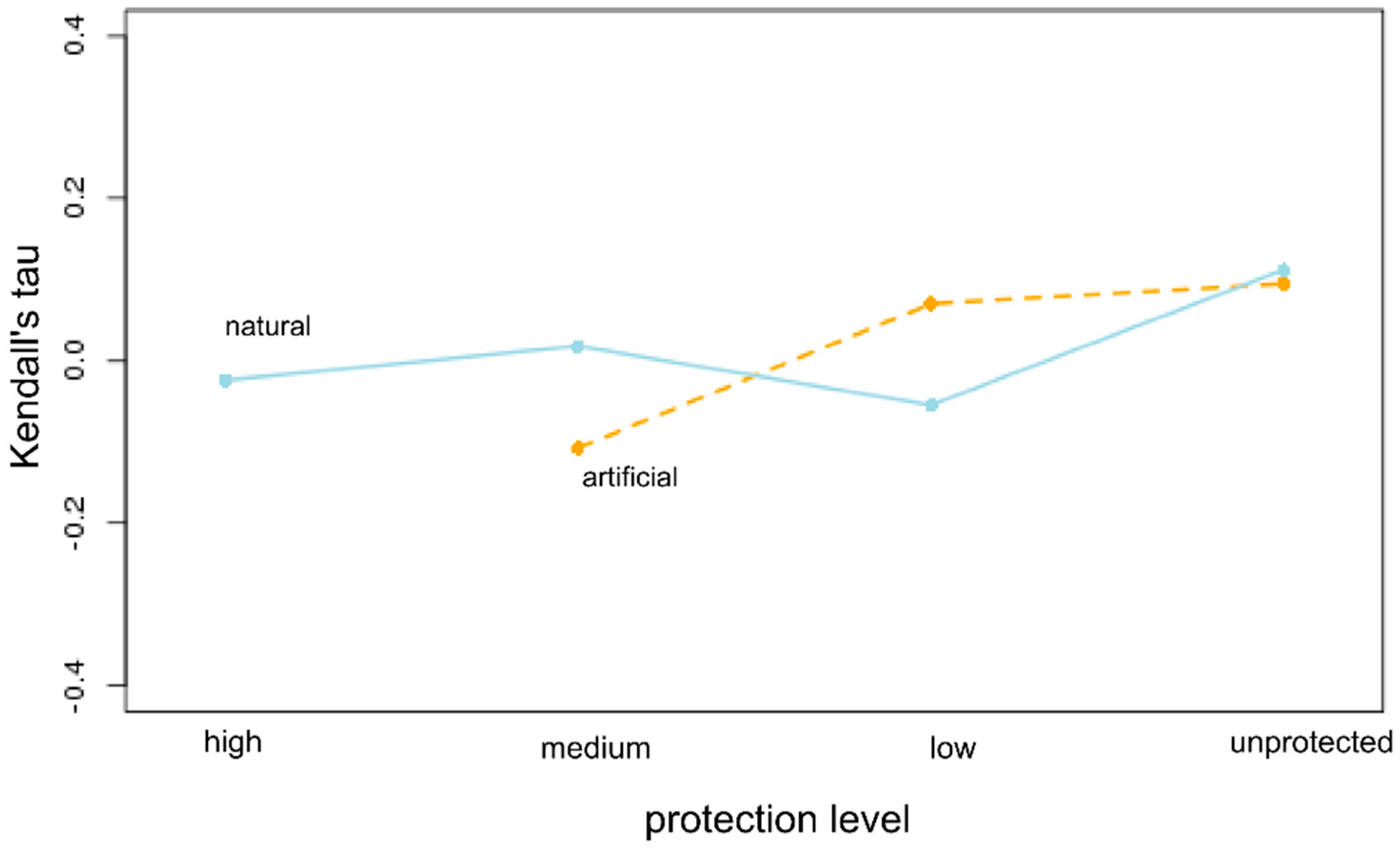
Fourth, with the sample of photo-interpreted water bodies, using as response variable hydroperiod trend (Kendall’s tau) we test for an interaction between flooding regime (natural or artificial) and protection level, under the hypothesis that natural ponds may be showing different trends in hydroperiod depending on the protection level of the area.
Fifth, we refit models to the natural ponds identified in the random sample to test to what extent correlation models developed for all water bodies are representative of the hydroperiod behavior of natural temporary ponds.
5. Discussion
Mediterranean temporary ponds are a priority habitat in the European Union (Code 3170, Habitats Directive 92/43/ECC). They are of great conservation importance because they harbor a large part of the aquatic biodiversity at the landscape scale, and are home to rare and endangered species [
1,
19,
52]. Climate change, together with impacts by urbanization and agriculture are threatening these habitats at the global scale [
52]. The system of ponds on Doñana’s aeolian sands is a good example of Mediterranean temporary ponds. They have been declining with climate change by an increased aridification since the “Little Ice Age” [
10,
11,
12,
53,
54] but have also been suffering an increased anthropogenic pressure [
1,
55]. It has been documented how groundwater abstraction for agriculture [
13] or for tourism resorts has negatively influenced or dessicated certain ponds in the system [
34].
In this paper we show that the time series of Landsat satellite images is a great source of information for surface water variability and temporal trends. It can be used to study temporal trends in the system of temporary ponds on Doñana’s aeolian sands, its hydrological evolution, and to monitor the landscape effect of different conservation actions. Even in a system where many temporary ponds can be smaller than a Landsat pixel [
41] the high number of images allows to detects trends and evaluate changes in the flooding regime. Remote sensing has the advantage of being able to study the system as a whole providing a synoptic view, and the length of the Landsat time series allows to study the hydrological dynamic for a period of 30 years.
Of course, our study has some limitations. The 30 m pixel size of Landsat precludes a clear identification of many ponds that are below this pixel size, also the mean interval between images, 30 days, is longer of the annual hydroperiod of many ephemeral ponds, so it is difficult to obtain accurate estimates of annual hydroperiod duration for this kind of ponds. With our definition of water body, many water bodies are sets of smaller ponds that at our resolution appear as joined. In the Doñana National park another study by Gomez-Rodríguez et al. [
41] with higher spatial resolution images (5 m pixels) located twice as many temporary ponds as we did. Also, although the methods used to identify flooded areas have been validated in other papers [
27,
37] and we have performed a validation of our method to identify temporary water bodies by photo-interpreting a random sample, this validation is only partial. We cannot retrospectively test if a single pixel that we classified as temporarily flooded, or dry, has had water, or not, coincident with a Landsat overpass in the 30 years period. Our mean pixel hydroperiod values (
Table 1) are calculated including areas that flood only occasionally, and are values much lower than those provided by other works that estimate hydroperiod duration from initial flooding to complete dry-up of each pond [
33,
34,
41].
Even though, we think our methods provide a new synoptic approach to the study of temporary ponds on the Doñana’s aeolian sands, point out that surface water availability is created not only by natural ponds but also by a diverse gradient from natural to artificial water bodies. All this suggest that the hydrodynamic behavior detected by remote sensing could be also used to identify and monitor the natural or artificial flooding regime of water bodies in the area.
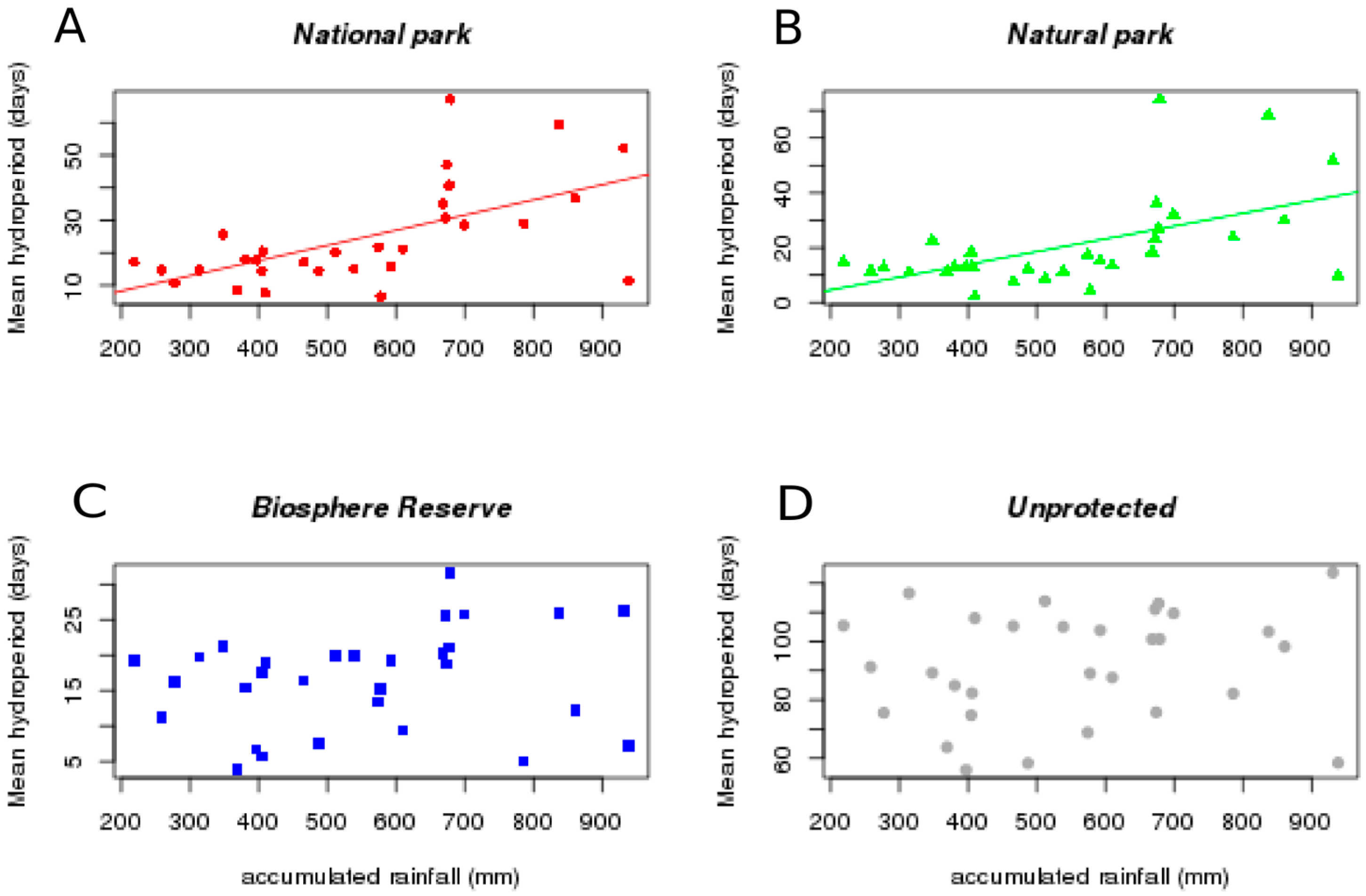
The main results of our study show that there is a higher density, extension, and variability of temporary water bodies in the areas of the Doñana’s aeolian sands that have received higher levels of environmental protection (
Table 1). As our analyses with Landsat images start in 1985, once the area was already protected, we cannot discriminate if it was that the area with a higher richness and diversity of temporary ponds was selected for protection, or if legal protection has prevented a stronger decline in the National park compared to the Natural park or the Biosphere reserve (that is the dryer one, with a lower extension and density of temporary water bodies).
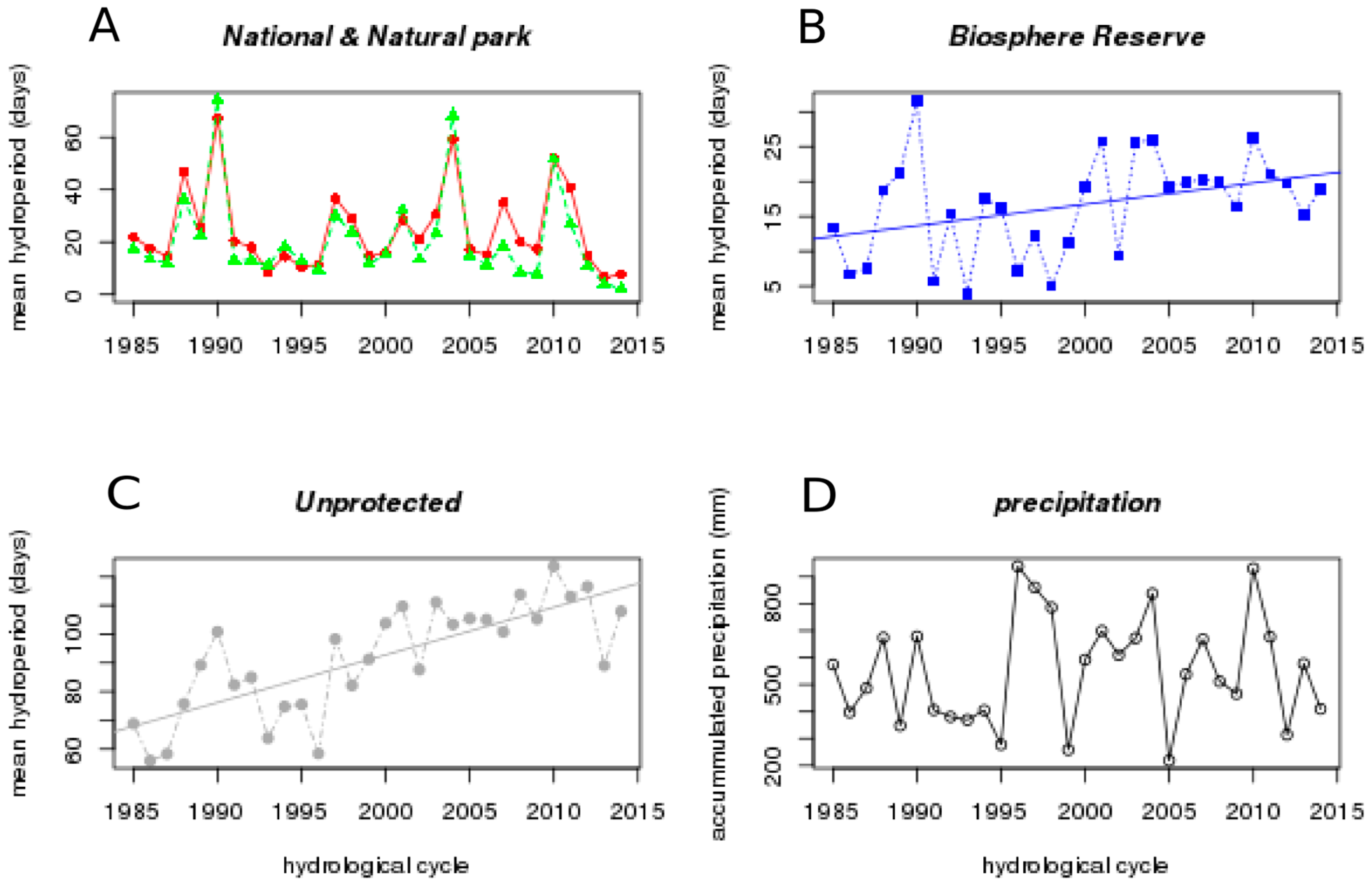
The Doñana protected areas (National and Natural park) have temporary water bodies with wider fluctuations in hydroperiod and more dependent on annual precipitation. Protected areas show a slight decline in mean hydroperiod while precipitation has been slightly increasing during the last 30 years, although neither trends are statistically significant (
Figure 3A,D).
Hydroperiod of temporary water bodies has increased in the areas with low or no protection (Biosphere reserve and unprotected area
Figure 3C,D), that are the areas receiving the greater impact of irrigated agriculture and residential use (
Figure 2), and there is no correlation between precipitation and mean hydroperiod (
Figure 5C,D) or annual flooded surface in these areas.
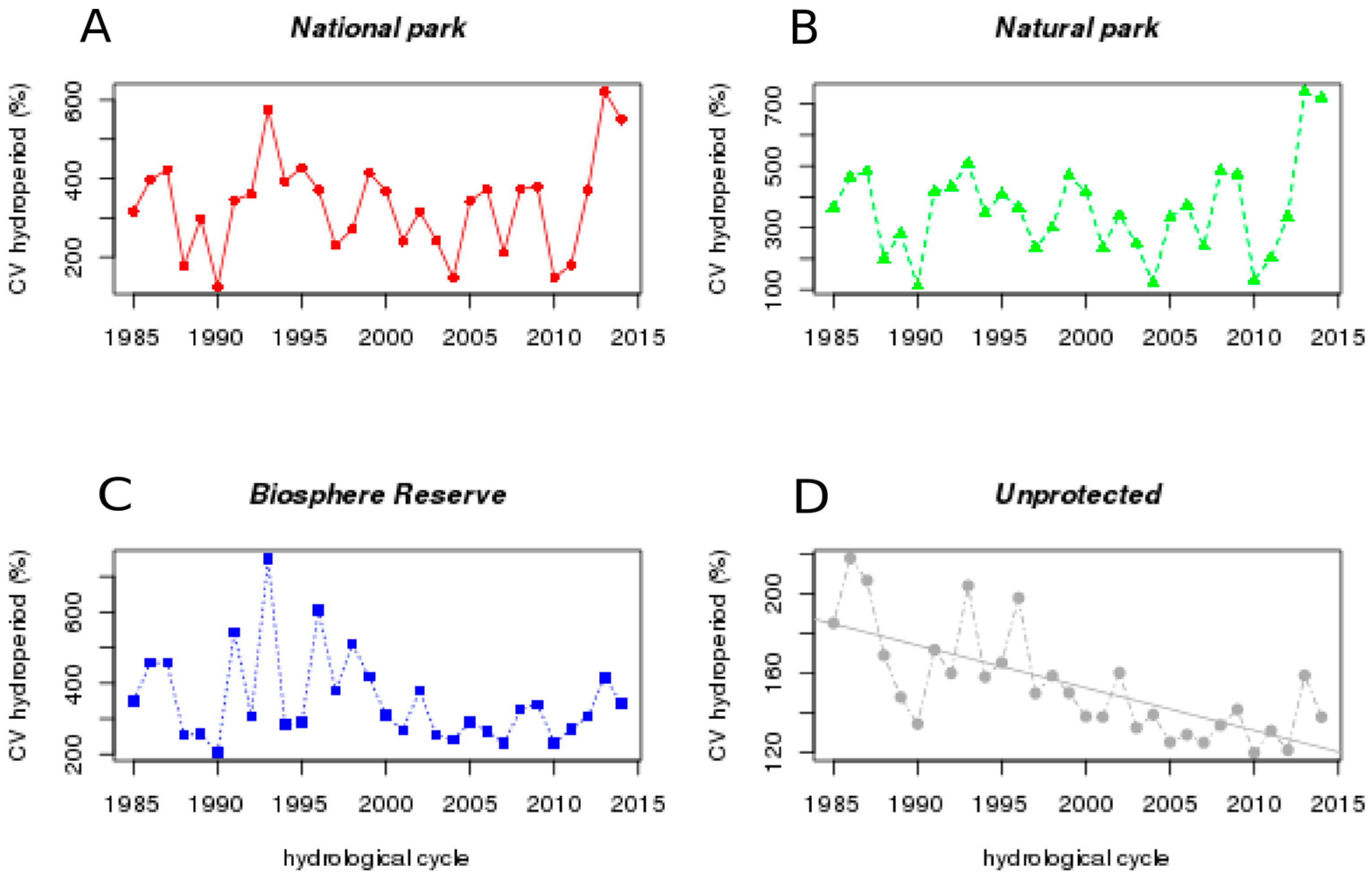
The coefficient of variation of the hydroperiod has significantly declined in the unprotected areas (water bodies showing less variability in hydrological regime,
Figure 4D) and the surface flooded has increased also (
Figure S1).
A random selection and photo-interpretation of water bodies suggest low commission errors (only less than 4% water bodies could be errors) and validates partially our approach to study this system of small temporary water bodies on the aeolian sands. It also shows that we are detecting different types of water bodies both according to their origin (natural ponds, artificial irrigation ponds, ponds transformed into water reservoirs for agriculture) and to their hydrodynamics (rain puddles, epigenetic and hypogenetic temporary ponds, water-table lakes, etc.). The photo-interpretation indicates that the contribution of the different typologies of water bodies to the sample is variable depending on protection level. In the aeolian sands out of the protected areas 22% of the water bodies that hold surface water are artificial irrigation ponds or ponds that have been modified for irrigation (pond that have been artificialized and show irrigation pumps and pipes). In the Biosphere reserve artificial ponds are 14% of the water bodies (
Table 2). These artificial water bodies have been increasing during the last 30 years, and, at least partially, explain the increase in surface flooded and in mean hydroperiod, and the decline in the coefficient of variation of the hydroperiod out of the protected area. We checked the 20 irrigation ponds identified in the random sample (
Table 2) in historical aerial photos and no one was visible in 1984 (one was a natural pond at that time) while 13 years later, in 1997, 17 of the irrigation ponds (85%) had already been built. Artificial ponds are no substitute for natural temporary ponds, but provide alternative habitats for certain aquatic organisms and can act, in certain situations, as complementary habitats of conservation value [
56]; but, in general, artificial water bodies have a reduced biodiversity value [
57].
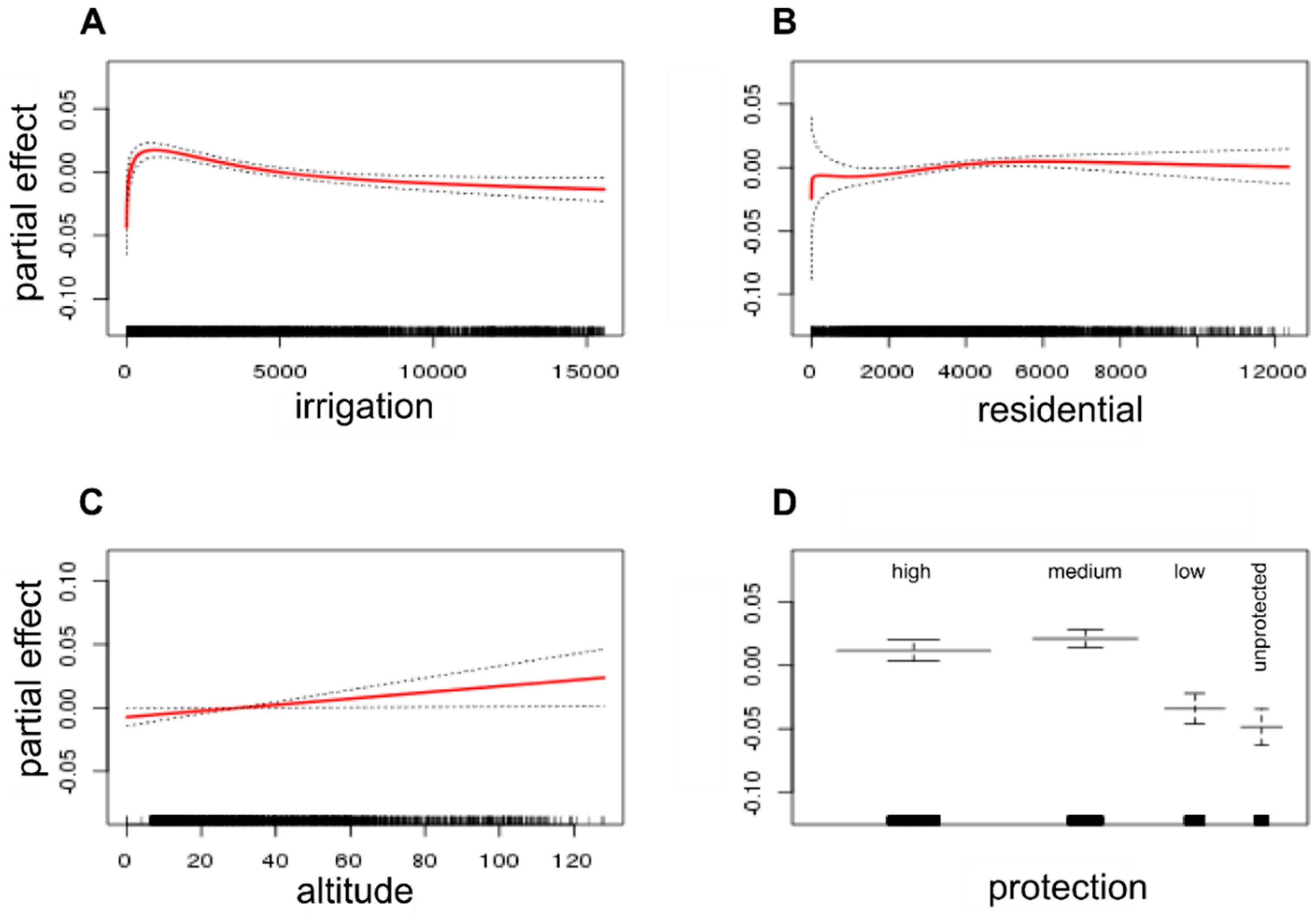
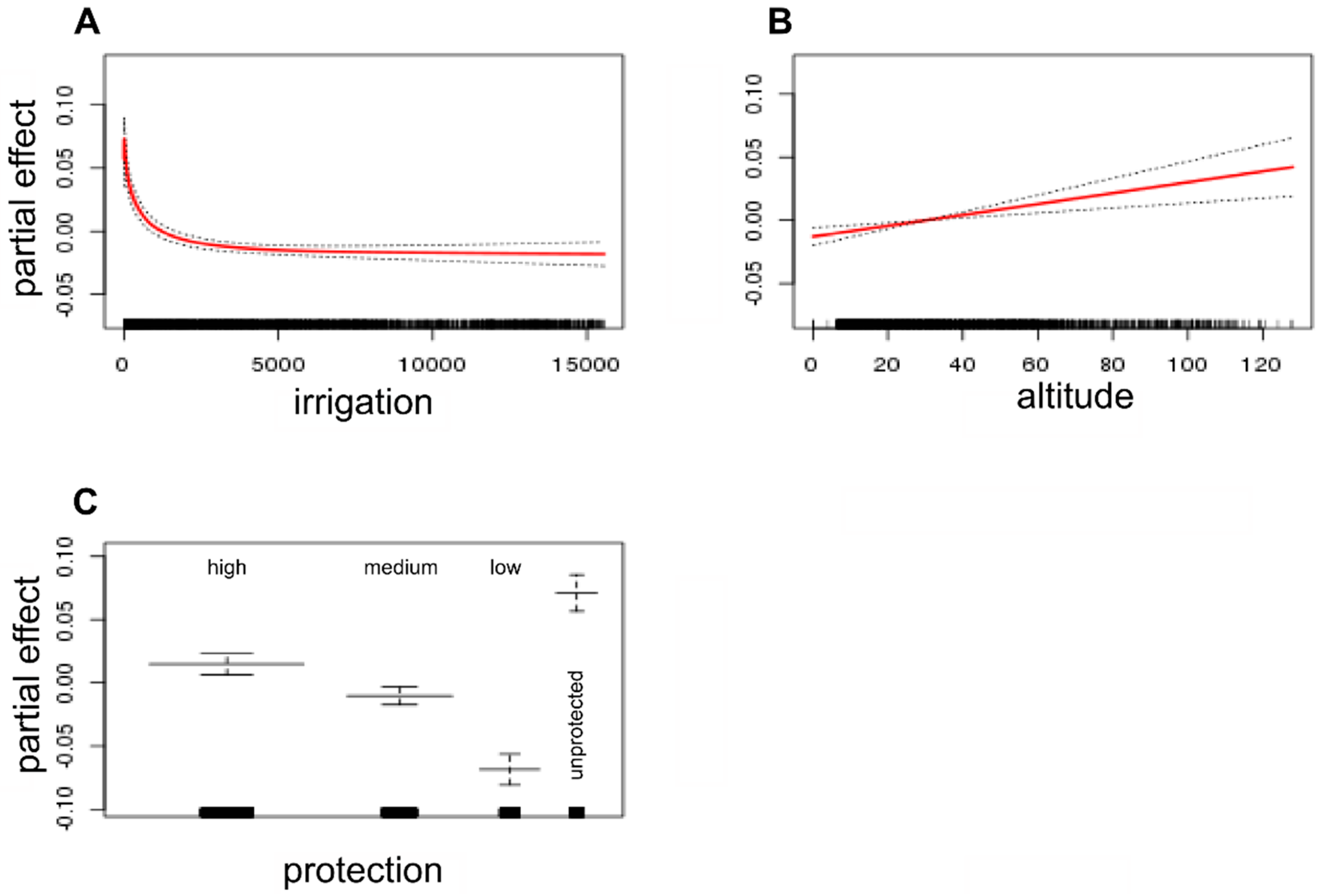
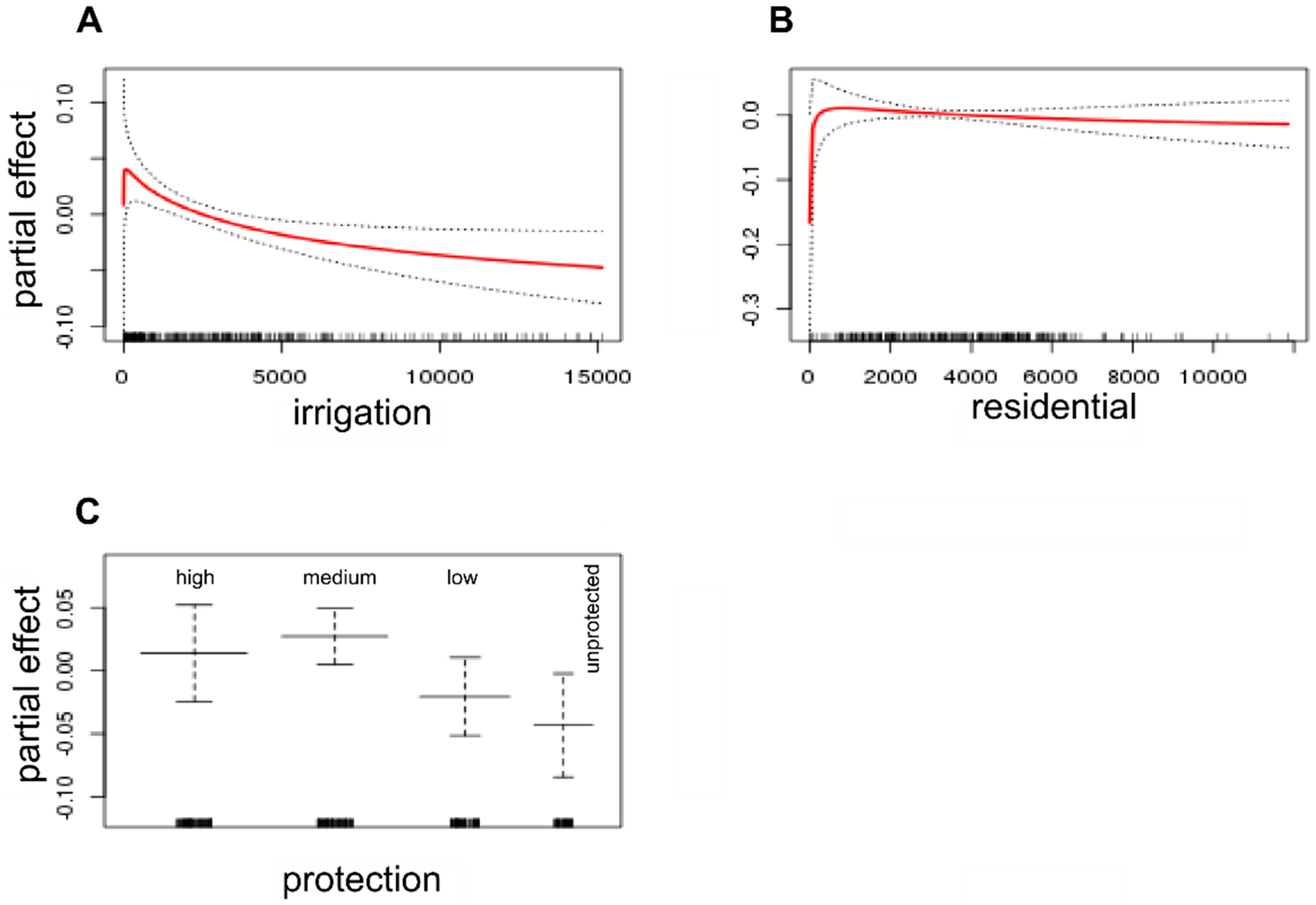
The models for correlation of hydroperiod with precipitation, and the temporal trends in hydroperiod once corrected for precipitation, indicate important effects of distance to water abstraction pressures (irrigated cultures and residential areas) and of protection level in the hydrological behavior of temporary water bodies. First of all, distance to irrigated cultures is an important driver but its overall effect is contrary to what we expected a priori. Water bodies close to irrigated cultures show an increasing trend in hydroperiod, mainly because of the construction of new irrigation ponds. But also because natural ponds outside the protected areas have a trend of increasing hydroperiod (
Figure 10 and
Figure 12B). This change has affected natural ponds in the unprotected area, but not in the Biosphere Reserve that show declining hydroperiods (
Figure 10). One possible explanation is that the excess of water for irrigation finally flows into natural ponds close to the fields and these ponds increase their hydroperiods, and show lower fluctuations with annual precipitation. In fact, a transfer of 4.99 hm
3 of surface water from other basins has been authorized for the irrigation cultures on the wester sector of the aeolian sands, in the unprotected area (Huelva province), to reduce the illegal use of groundwater [
58,
59,
60,
61]. Distance to residential areas has a smaller impact, but tends to affect negatively the trend in hydroperiod (
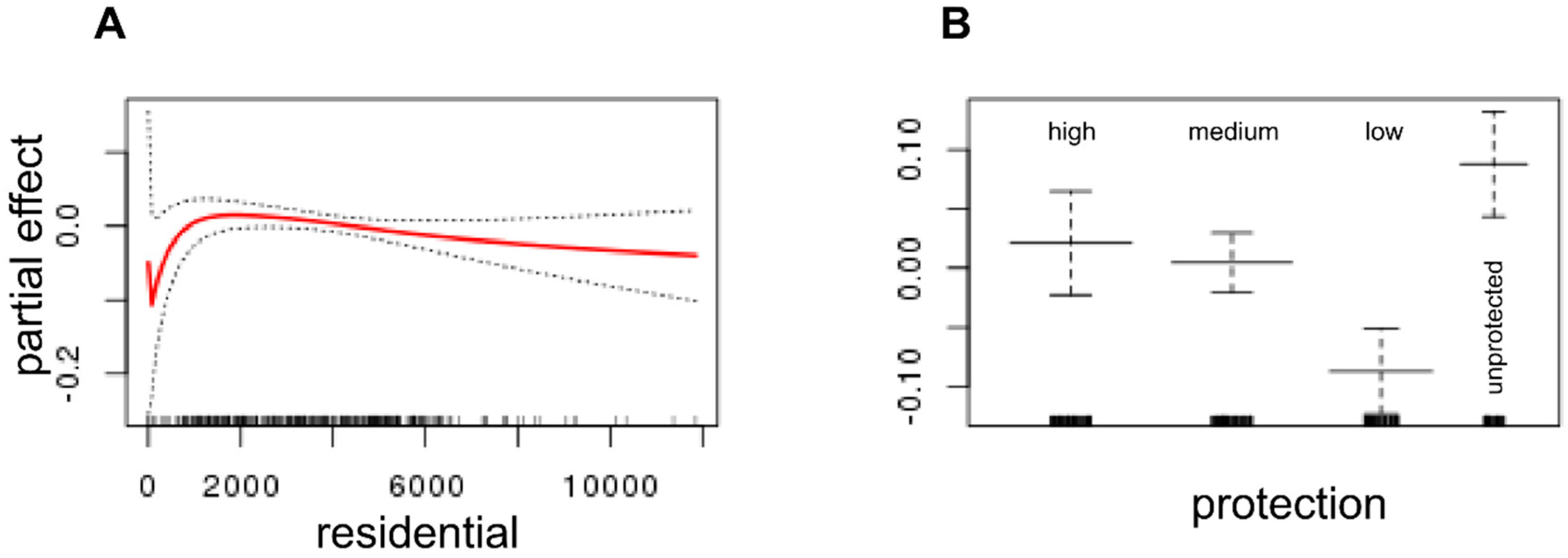
Figure 12A). In any case, the wide confidence intervals close to residential areas and irrigated cultures, mainly in relation to the correlation between hydroperiod and precipitation point to the existence of different types of water bodies that can be influenced in different ways. New artificial water bodies are created in gardens and golf courses that are artificially flooded and do not depend on annual precipitation, while water-table lakes close to extraction wells suffer stronger fluctuations with the water table and show a stronger correlation with annual precipitation [
34]. At the same time, other water-table lakes have hydroperiods that depend on the accumulated rainfall over several years [
33], and have a smaller correlation with annual precipitation.