1. Background and Rationale
Food security will become increasingly challenged over the upcoming decades by climate change [
1,
2], natural resource degradation [
3], and a burgeoning global population [
4]. Smallholder farming systems are of particular concern given that farmers often do not have access to the inputs and technologies necessary for high-production agriculture [
5], and many of these systems are distributed across the tropics, where negative climate change impacts are expected to be greatest [
2,
6]. One way to enhance food security is to examine production levels, and identify factors associated with existing yield gaps. Remote sensing offers a low-cost way to obtain crop production statistics across large spatial and temporal scales [
7,
8]. However, to date it has been difficult to map the production of smallholder farms, given that the size of an individual field (<2 ha) is typically smaller than the spatial resolution of most freely-available satellite imagery (e.g., 30 m Landsat, 250 m MODIS; [
9,
10]). While these satellite data can be used to map aggregate-level yield statistics, at the scale of multiple fields or coarser, having the ability to map individual smallholder farms is important given the large heterogeneity in production within and across fields. Generating field-level statistics would result in a better understanding of the causes of yield gaps, and the ability to identify low-performing fields that can be targeted with yield-enhancing strategies.
There are several challenges that exist for mapping field-level production of smallholder farms. First, while high-resolution satellite imagery (e.g., <5 m, IKONOS, WorldView 2, and Quickbird) overcomes the issue of mixed pixels, the use of these products to map production across large areas has been limited. This is because these high-resolution data are costly to acquire (typically $15–$50 per square kilometer), and thus are typically used at low temporal frequency (e.g., [
11,
12]). However, previous studies have shown that the accuracy of mapping yields can be improved by using multiple images throughout a growing season [
13,
14,
15,
16]. Over the last decade, new low-cost microsatellites (e.g., Terra Bella’s SkySat, Planet’s PlanetScope) have been developed and deployed that allow for the collection of both high spatial (<5 m) and temporal resolution (<2 weeks) imagery at lower cost. These microsatellites offer the opportunity to obtain multiple measures of the same field throughout a single growing season, which should increase the ability to accurately map field-level crop production statistics. Thus, we will examine how well field-level production data can be estimated using new, low cost, high spatio-temporal datasets.
A second challenge is that most existing methods to map crop production require field-level yield data to develop and calibrate models that translate satellite vegetation indices to yield. These production statistics are typically collected via crop cuts, where individual harvests are weighed, or social surveys, where farmers are interviewed about the amount of production from an individual field [
17]. While previous studies have accurately mapped field-level yield using on-the-ground data for calibration [
18,
19,
20], these data are very time and cost intensive to collect and often do not exist in many smallholder systems across the globe [
21]. Furthermore, even if they do exist, they are typically only collected over small spatial and temporal scales, making it difficult to extrapolate any calibrated algorithms to broader regions or across multiple years. To overcome these issues, a new method, SCYM (the scalable crop yield mapper), has been developed that uses crop models to simulate the necessary on-the-ground data used to train remote sensing algorithms that predict yield [
16]. In this study, we will develop and compare models that use typical on-the-ground training datasets (e.g., crop cuts and social surveys) and the new SCYM approach that requires no calibration data. Understanding how well these different sources of data can be used to parameterize and calibrate remote sensing algorithms would be beneficial as it would help identify possible data sources that are both low cost and provide high predictive accuracy.
3. Study Area
We obtained high-resolution SkySat imagery for an 8 × 16 km
2 region in Arrah district, Bihar, India (central coordinates: 25.47°N, 84.52°E) for the 2014–2015 and 2015–2016 winter growing seasons (
Figure 1). This region is predominantly composed of smallholder agriculture, with farms covering over 80% of land area. There are three agricultural growing seasons in this region: the monsoon (kharif) season when a majority of farmers plant rice, the winter (rabi) season when most farmers plant wheat, and the summer (garmi) season when most fields remain fallow. We specifically focused this study on the winter season, which spans from early November to early April. There is significant heterogeneity in management practices, which leads to large variation in wheat yields across fields. Most farmers apply phosphate and nitrogen fertilizers, like DAP and urea, yet the amount applied varies from 20 kg to over 100 kg. There is also variation in the number of irrigations applied (typically one to three times) since irrigation is costly due to expensive diesel pumps. There is also a wide range in sow dates, spanning from 1 November to early January. Sow date has large impacts on yield, as crops that are sown late (typically from December onwards) face heat stress during grain filling, which leads to large reductions in yield [
23,
24]. Previous studies have shown that higher yields are associated with optimum sow dates [
25,
26], higher fertilizer use [
27], and increased irrigation use [
28,
29]. Given the significant heterogeneity in yields across smallholder farms in this region, this site is ideal to examine how well micro-satellites can map field-level statistics. It is important to note that a large proportion of farmers intercrop mustard (varieties Rajendra Rye and RD 1002) with wheat (<10% of the total field), which potentially may lead to mixed spectral signatures within a given wheat field in our remote sensing analyses.
6. Methods
We calculated wheat yield from SkySat imagery using three different datasets to parameterize linear models. The first method used crop cut data, the second method used self-report data, and the third method used outputs from our crop model simulations. In the case of sow date, only two types of data were used, self-reports and outputs from crop models. However, since there was temporal variation in when the self-reports were collected, with self-report sow date collected close to the timing of planting in our crop cut survey but at the end of the growing season in the self-report survey, we parameterized two separate models using these two datasets. The difference in performance between these two datasets can help identify whether the timing of surveys has an effect on self-report accuracy. Model parameterization and validation are described below.
6.1. Model Parameterization
We developed and calibrated linear models because the relationship between our outcome variables of interest (sow date and yield) and GCVI for our crop cut plots was predominantly linear (
Figures S1 and S2). We also observed that GCVI and yield were not linearly related in fields that were heavily lodged, likely because these plots had low yields regardless of early season GCVI. We thus removed fields that were heavily lodged (lodging score > 6) from our analyses since we would not expect a relationship between early season GCVI and final yield. To reduce the chance of model overfitting, we examined the correlation between GCVI across all dates (
Table S3). Since 22 March and 23 March in the 2014–2015 imagery were highly correlated (R > 0.92), we omit 23 March from all analyses. We also examined the phenologies of GCVI through time for each of our crop cut fields (
Figure S3), and since early sown and higher yielding plots had higher maximum GCVI values than late sown and low yielding plots, we consider the maximum GCVI value attained across all SkySat image dates as a predictor in our models.
We developed linear models that used all possible image dates. This is because our analyses suggested that models that used all image dates had the highest R
2 for both yield and sow date predictions (see Results,
Section 7). However, for crop model parameterized models, we restricted our analysis to only include images before mid-March. This is because wheat phenologies in our crop model simulations matured and senesced one month earlier than observed phenologies, resulting in a mismatch between our observed and crop model phenologies after mid-March. This mismatch has been well documented in previous studies [
35], especially for late sown wheat in north-western India, and this has been identified as a weakness in the APSIM model and an important area for future research [
38].
6.2. Validation of Models
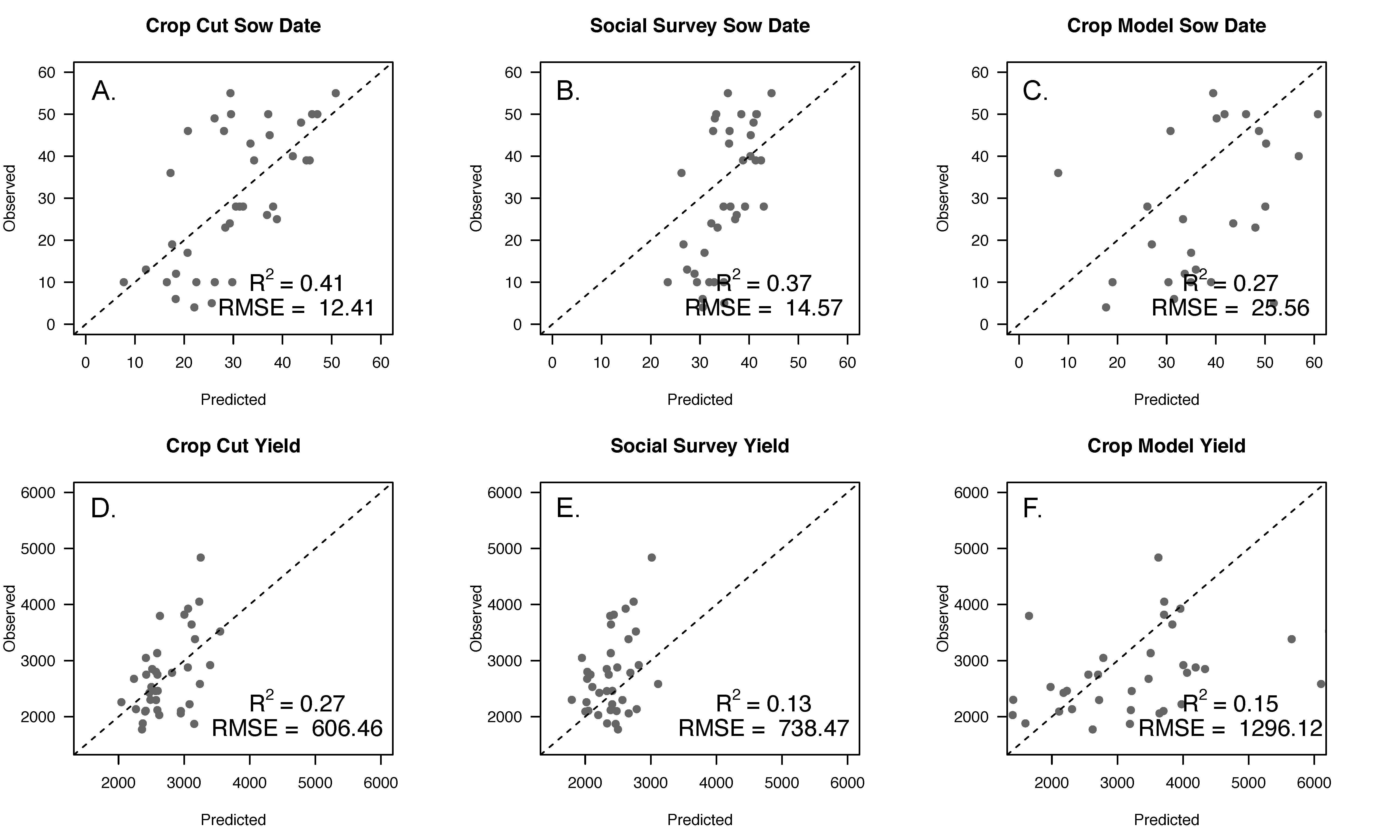
We validated sow date and yield estimates for the crop cut, self-report, and crop model parameterized models in two ways. First, we applied coefficient values derived from our linear models to the GCVIs associated with the crop cut polygons. We used the crop cut data for validation because we believe these data to be our most accurate measure for yields. We also used the sow date data collected in the crop cut survey as validation for sow dates, as we hypothesize that farmers will report sow date more accurately closer to the timing of planting. We then examined R2 and RMSE between predicted sow dates and yields from each of the best models and the observed sow dates and yields from our crop cut datasets.
Our second test examined whether these models could produce yield estimates that can detect known signals between management variables and yield. Specifically, we examined the relationship between predicted yields and reported sow date, amount of fertilizer used (urea fertilizers), and number of irrigations applied. The closer these relationships matched associations observed between our crop cut yields and management variables, the better the satellite yield estimates were thought to be. We were unable to examine the relationship between fertilizer and yield in the 2015–2016 dataset because fertilizer was applied equally to all farms due to our fertilizer experiment, and therefore there was no variation in fertilizer to examine.
6.3. Comparison of SkySat and Landsat Imagery
To better identify the additional information gained from SkySat imagery compared to freely-available, coarser Landsat data, we conducted two additional analyses. First, we resampled SkySat imagery to 30 m to match the resolution of Landsat imagery, and redeveloped coefficient values for linear models that translate satellite vegetation indices to sow date or yield. By resampling SkySat data to 30 m, we specifically examine the predictive ability that is lost with coarser scale imagery. Second, we redeveloped coefficient values for linear models using all available cloud-free Landsat images within the 2014–2015 and 2015–2016 growing seasons. This analysis both examines the effect of coarser scale imagery as well as the effect of having increased temporal frequency of imagery on our sow date and yield estimates. This is because we had seven images available for both the 2014–2015 and 2015–2016 growing seasons compared to only five images available for SkySat in each season. For these analyses, we only develop models that use crop cut data as calibration data since this dataset was shown to result in the highest prediction accuracies. We did not examine how well Sentinel-2, a new freely available satellite product at 10 m resolution, performed because no data were available for 2014–2015 as this was prior to the satellite’s launch and only two cloud-free images were available for the 2015–2016 growing season.
8. Discussion
This study adds to the growing body of literature that uses satellite imagery to monitor crop production of smallholder systems. This work is one of the first to examine how well new micro-satellite data can be used to map characteristics of individual fields, and assesses what types of calibration data can lead to the highest accuracies at low cost. Overall, we find that we were able to map sow date with high accuracies, particularly when using models that were parameterized with self-report sow dates collected close to the time of planting. While less accurate, we were able to capture the large range in sow dates across farms when using models parameterized with crop model simulations. We were also able to map yields fairly well, though the accuracy of yield predictions was not as high as that of sow date. When estimating yields, our models did best when parameterized with crop cut data. However, yields predicted using crop model simulations did almost as well in 2015–2016, when we had access to imagery throughout the growing season. These results suggest that new high-spatio temporal micro-satellite data can be used to map field-level characteristics of smallholder farms, but the accuracy of these estimates varies based on the type of data used to parameterize models that translate satellite vegetation indices to yield.
When deciding which data to use for calibration, it is important to consider not only prediction accuracy but also how easy it is to access training data given collection costs and data availability. While we find that models parameterized with crop cut data do best, it may be worth considering alternate lower-cost approaches to obtain training data. Considering sow date, models that were parameterized using crop models did almost as well as models that used self-reports (
Figure 4C and
Figure 5C). They were able to broadly capture the difference between early and late planted fields, and map the heterogeneity in sow date across farms. It may thus not be worth the cost and time needed to collect self-report sow date data since crop models that require no on-the-ground data do relatively well. Considering yield, while the crop cut parameterized model performed best, models parameterized with crop models were able to broadly distinguish between low versus high yielding plots (
Figure 4E and
Figure 5E) and did almost as well as crop cut calibrated models in 2015–2016 when we had imagery throughout the season. These models were able to capture the strongest associations between management factors, like sow date, and yield (
Figure 6 and
Figure 7). Interestingly, our social survey calibrated models performed worst on all measures of accuracy, though they were better in predicting sow date than yield. Our results suggest that models parameterized with lower cost data, like crop model simulations, may produce yield and sow date estimates that are accurate enough depending on the desired purpose of the study. For example, if one aims to distinguish between low versus high yielding plots, or to detect signals with large effect sizes, then yield estimates produced using lower-cost training data like crop models may do well.
While we were able to distinguish between low versus high yielding fields across all of our models, predictions were often biased. In the case of crop cut calibrated models, there is severe under-prediction of yields for high yielding fields (>3200 kg/ha) when we only had imagery towards the end of the growing season. This may have occurred because the linear relationship between GCVI and yield was weaker at the end of the growing season for fields with the highest yields (
Figures S1 and S2), potentially due to mixed spectral signatures caused by intercropping wheat with mustard. Having access to imagery throughout the growing season reduced this problem, likely because the relationship between GCVI and yield is more linear for early season imagery. Yields were over-estimated considering self-report data, averaging 2000 kg/ha greater than observed yields in 2015–2016. This may be because self-report data were collected over the phone in this year, and since most farmers in this region own multiple plots, it is possible that farmers were less precise in giving estimates of the specific field for which we had GPS boundaries. There was over-prediction of yields considering crop models in 2014–2015, with predicted yields that were often 1000 kg/ha greater than observed yields. This is likely because of a mismatch between observed phenologies in our SkySat imagery versus crop model phenologies; crops matured and senesced about one month earlier in crop model simulations. Because of this, the highest prediction accuracies were obtained when using early season imagery (before March), when the observed and simulated phenologies were more closely aligned. Not having access to early season imagery in 2014–2015 likely led to greater inaccuracies in our yield estimates for that year. Future work should identify ways to better match simulated phenologies with observed phenologies for wheat in this region. Overall, while all predictions had some biases, they may not be problematic if one is more interested in yield variability across plots than knowing the absolute yield of a field.
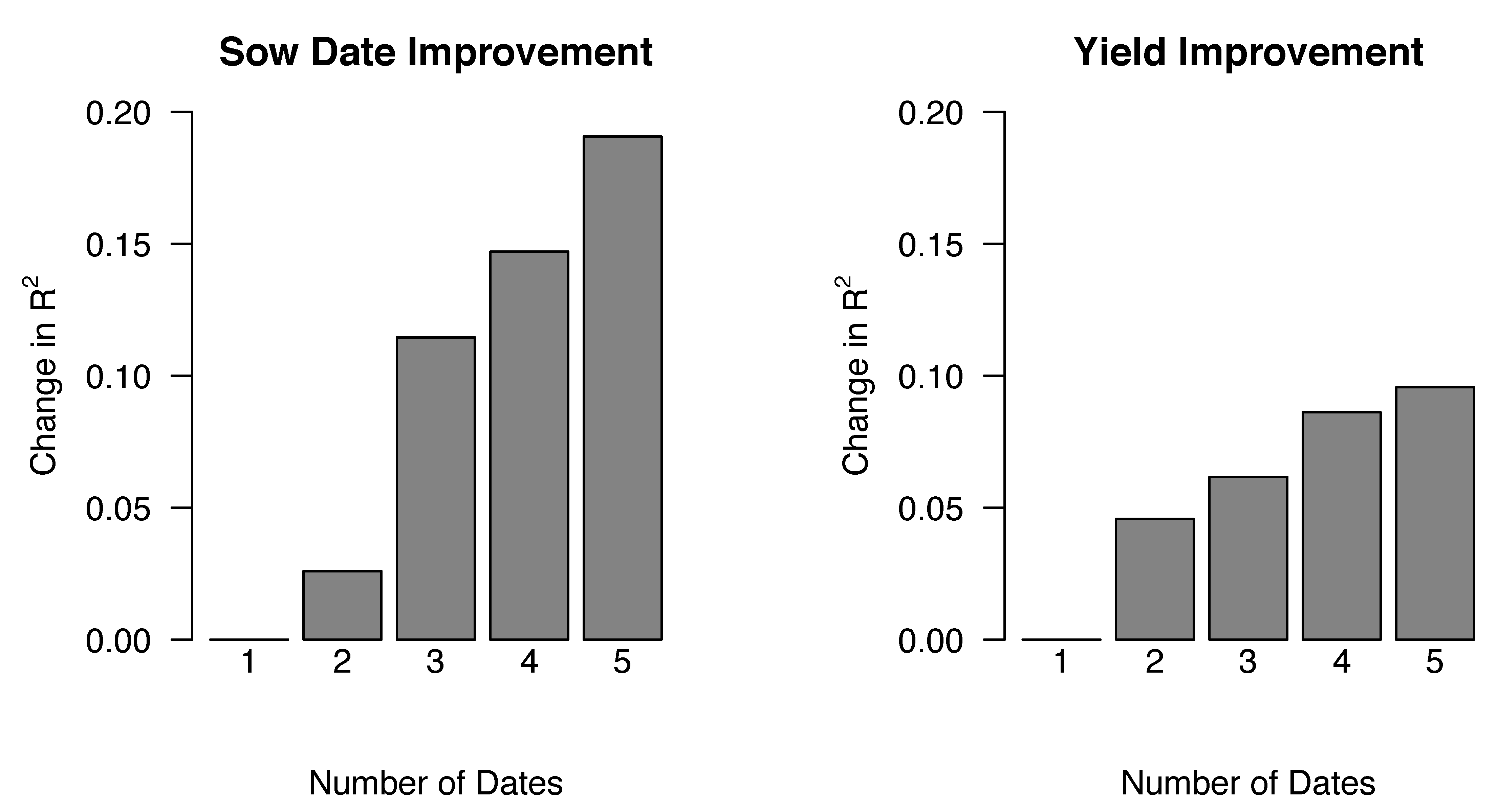
We were also interested in identifying whether our prediction accuracy improved with increased temporal frequency of imagery. We find that our models improve with access to satellite imagery throughout the growing season (
Figure 5). This is particularly true for sow date where R
2 improved from 0.41 to 0.62 when we had access to early season imagery. While yield estimates did not greatly improve with increased access to imagery, we were better able to capture the observed range in yields when we used early season imagery. Finally, our crop model calibrated algorithms performed significantly better when using early season imagery, with R
2 for both sow date and yield increasing by approximately 0.15. It is possible that our ability to predict both sow date and yield would improve even further if we had increased access to imagery throughout the growing season, with more than one image per month. This is suggested by previous studies that have found high accuracies in predicting yield with multi-temporal imagery that spans the length of the growing season [
14,
15,
16] as well as our Landsat analyses (
Figure 8). These previous studies were able to predict yields with R
2 ranging from 0.21 to 0.64 (e.g., [
14,
15,
16]), and our results are thus comparable to accuracies achieved in previous studies using other satellite data and on-the-ground calibration data. As more high-resolution satellite data become available, future work will examine how much prediction accuracies further improve with near weekly or bi-weekly imagery.
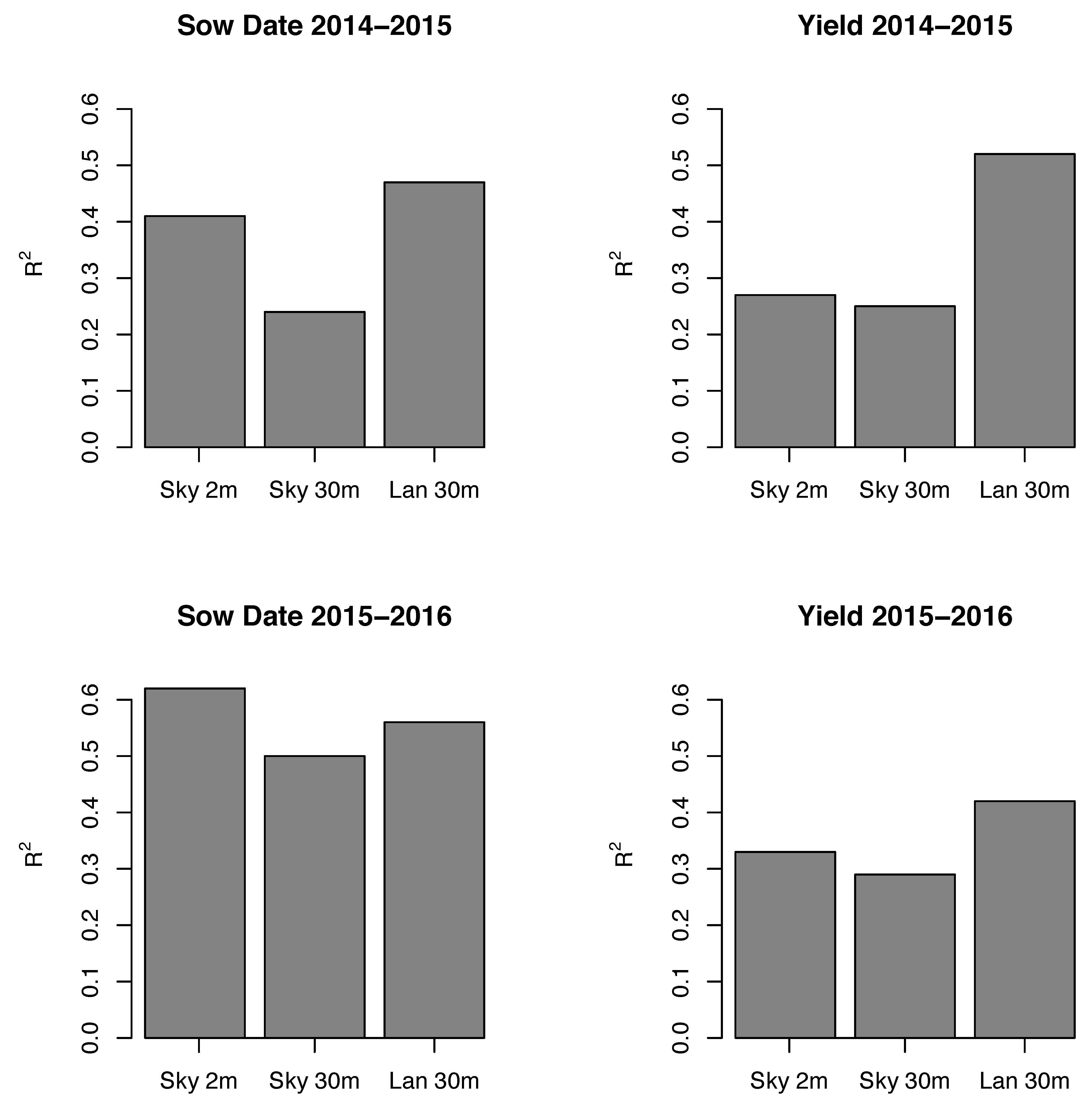
Considering the relative benefit of using high-resolution SkySat imagery compared to freely-available, coarser Landsat imagery, we find that accuracies for predicting sow date and yield decrease when SkySat imagery is resampled to match the spatial resolution of Landsat (
Figure 8). This suggests that high-resolution imagery results in more accurate field-level predictions, likely by reducing the effect of mixed pixels caused by small field sizes and heterogeneous management across farms. We find that we produce more accurate yield estimates but comparable sow date estimates to those produced using SkySat imagery when we use all-available Landsat imagery (
Figure 8). It is likely these improved accuracies are driven by the increased temporal frequency of Landsat, as seven Landat images were available versus five for SkySat. Despite these improved accuracies in mapping field-level yields, a significant amount of spatial information is lost when using coarser Landsat imagery. With high-resolution SkySat data, we captured within field heterogeneity, which is often as large as across field variation (
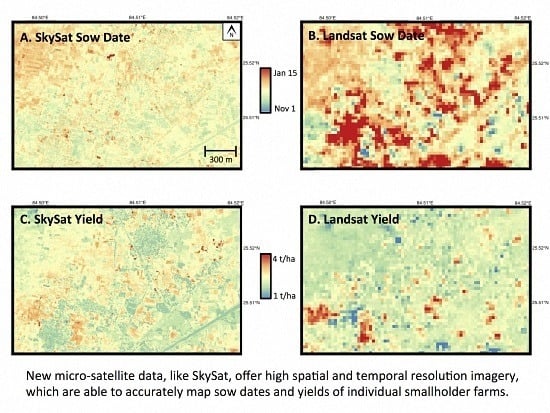
Figure 9). These tradeoffs suggest that whether one should use micro-satellite data or current, freely-available imagery depends on the goals of the study. Landsat currently offers better temporal coverage, and our results suggest that this increased temporal frequency is particularly important for mapping field-level yields. However, SkySat imagery offer the ability to examine within and across field yield variation that is not possible using coarser resolution Landsat data.
Future work should further explore several uncertainties in this study. First, it is unclear how widely the algorithms that we developed to map yield and sow date can be applied. For example, future work should examine whether the same models can be used across larger spatial scales and across multiple years. Furthermore, we were unable to partition the amount of predictive error that was due to radiometric correction issues with SkySat; it is possible that future studies may be able to achieve higher predictive accuracies once micro-satellite data are better radiometrically calibrated and mosaicked.