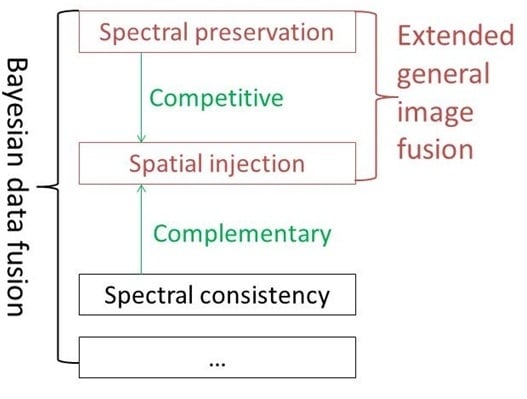
1. Introduction
With the development of science and technology, remote sensing data have exhibited explosive growth trends for multi-sensor, multi-temporal and multi-resolution characteristics. However, there are contradictions between the resolution limitations of current remote sensing systems and the increasing need for high-spatial, high-temporal and high-spectrum resolutions of satellite images [
1]. One limitation is the spectral and spatial resolution tradeoff, as more than 70% of current optical earth observation satellites simultaneously collect low-spatial resolution (LR) multispectral (MS) and high-spatial resolution (HR) panchromatic (Pan) images [
2]. This tradeoff will survive in forthcoming hyperspectral and MS sensors such as WorldView-3, EnMAP, PRISMA and HyspIRI [
3]. Based on information fusion theory, satellite image fusion has been proposed to handle these limitations [
4,
5]. Pansharpening, which is a spatial and spectral fusion method, focuses on enhancing LR MS images using the Pan image to obtain both high-spatial and high-spectral resolution images [
6]. Despite the variety of current pansharpening methods, they can generally be classified into component substitution (CS) and multi-resolution analysis (MRA) methods. Both the CS and MRA methods have been generalized into the extended general fusion framework (EGIF) [
7,
8].
Many studies have focused on comparing and reviewing these methods [
4,
5,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23] and had several common findings. First, among the CS methods, the Gram-Schmidt (GS) algorithm [
24] was found to be the best in terms of spectral preservation and spatial injection [
2,
7,
25]. Second, among the MRA methods, the generalized Laplacian pyramid (GLP) has been shown to present advantages, as it can adapt to the sensor point spread function (PSF) [
15,
26,
27,
28]. Finally, a current trend of pansharpening methods is to preserve the spectral information of the original MS images. This preservation is accomplished in two ways. First, CS methods are either adopted on their own to create an ideal intensity by accounting for the spectral response functions or using linear regression technology [
25,
29,
30,
31], or combined with MRA methods [
32,
33,
34]. Second, MRA methods are adopted to modulate high frequencies using global or local injection models [
23,
35] such as AABP (an acronym formed from its authors’ initials,
i.e., Aiazzi, Alparone, Baronti and Pippi [
36]), high-pass modulation (HPM) [
37], context-based decision (CBD) [
15,
28], enhanced CBD [
27], proportional additive wavelet LHS (intensity-hue-saturation) [
38] and Model 3 (M3) [
39]. Despite these findings, pansharpening remains a source of confusion and unaddressed questions, which are listed as follows.
Question 1: The relationship between the CS and MRA methods is not well understood. According to the EGIF, the only difference between CS and MRA methods is how to extract the spatial details. And the injection models to control the spatial detail injection amount utilized by the CS and MRA methods are similar [
7]. Thus the enhancement of CS methods should be comparable to that of MRA methods. However, there are some studies which observed that the spatial enhancement of CS methods is larger than that of MRA methods [
27,
40,
41,
42].
Question 2: There is a contradicting conclusion on the existence of the spatial enhancement and spectral preservation tradeoff in the fused images. Many CS method developers believed this tradeoff and tried to balance this tradeoff by introducing weight parameters to control the spatial injection [
41,
43,
44]. Some MRA method developers implicitly assumed this tradeoff as they used optimization technologies with competitive objectives,
i.e., to maximize the spatial similarity to the Pan image and the spectral similarity to the up-sampled MS images [
45] to determine the best injection model [
45,
46,
47]. Furthermore, in the MRA and CS comparison studies, researchers have found that although the spatial enhancement of CS methods is better than that of MRA methods [
40,
41,
42], the spectral preservation of the former is worse. This indeed enhances the fidelity of the tradeoff quality in fused images [
17,
48,
49]. However, Thomas
et al. [
10] challenged the existence of the tradeoff by stating that “
this tradeoff is a consequence of the use of certain tools and not an a priori compulsory”. They claimed that it cannot be reduced to the spatial information of its associated spectral information in an image. As such, the question remains: does the tradeoff really exist?
In fact, the question 2 originates from that the implicit spectral preservation definition in current pansharpening algorithms is improper. In pansharpening algorithms, the spectral preservation is defined to be as identical as possible to the up-sampled MS images. We will prove that from a Baysian perspective that all the EGIF methods have used the MS image as prior knowledge to preserve spectral information although only a few have explicitly stated that. For example, some intensity-hue-saturation-based (IHS-based) methods for spectral preservation have been developed by maintaining the saturation of the up-sampled MS images [
29,
41,
50]. Some MRA methods indicate that if the Pan and MS images exhibit a low correlation, the up-sampled images can be used as a fused product for preserving spectral information [
10,
28,
47]. In contrast, as observed by Wald
et al. [
51], spectral consistency infers that any synthetic image degraded to its original resolution with respect to the sensor PSF should be as identical as possible to the original image [
51,
52]. Recently, Chen
et al. [
53] have noticed the upsampled MS image (used in EGIF) is not as accurate as the original MS image (defined by Wald) for preserving the spectral information. The questions are how to guarantee spectral consistency with Wald’s definition with arbitrary sensor PSF and how much the methods can be improved if spectral consistency is achieved.
In this paper, we find that the CS and MRA methods are special cases of the Bayesian data fusion method. And all of the preceding questions can be answered by interpreting fusion from a Bayesian perspective. Bayesian data fusion methods are rooted in image formulation models and consider the fusion process as an inverse problem [
54,
55,
56,
57]. It includes two steps, the modeling step to build the equations and the inversion step to find the solution. Interpreting fusion from a Bayesian data fusion framework can answer these questions due to its explicit assumptions in modeling process and its flexibility in inverse process. The modeling step is easy to interpret with explicit assumptions and thus we can find out what are the assumptions used in EGIF. And the diversity of the optimization technology provides more flexibility to solve the complicated models which cannot be solved in EGIF,
i.e., to guarantee spectral consistency with regard to arbitrary sensor PSF.
1.1. Image Fusion from a Bayesian Perspective
We interpret the fusion from a Bayesian perspective with images in vector form and operations on images in matrix form. Although the deduction process may not be straightforward by the vector and matrix forms, the benefits lie in interpreting the fusion more easily. We assume that each LR image has M pixels and that each HR image has N pixels. As such, N = r2M, where r is the spatial resolution ratio. The desired HR MS images with Q spectral bands in band-interleaved-by-pixel lexicographical notation is denoted as a vector with NQ elements, Z = . The observed HR Pan image is denoted as a vector with N elements, X = [X1, X2, …, XN]T. Zn = is the spectra at the spatial location n (n = 1, 2, …, N). The corresponding LR versions of Z and X in lexicographical form are denoted as z and x, respectively, and comprise only M pixels.
In terms of notations of this paper we use boldface upper- and lowercase letters to differentiate matrices and vectors. However, in one exception, the HR MS and Pan image vectors are denoted as Z and X (in both italics and bold) to correspond with LR vectors z and x. z̃ and x̃ represent the up-sampled MS and Pan images, respectively, and have the same dimensions as the HR images. Denote Zq = as the spectra vector of the band q, for q = 1, 2, …, Q. z̃q and zq can be similarly defined. The superscript q indicates the qth band and the subscript n indicates the nth pixel in the following analysis.
Treating the observed vectors,
i.e.,
z and
X, and the vector to be estimated,
i.e.,
Z, as random vectors, the maximum
a posteriori (MAP) estimate is given by a vector
, which maximizes the conditional probability density function of
Z given
X and
z,
p(
Z|
z,
X). Applying the Bayes rule, we obtain.
1.2. Spectral Consistency, Spectral Preservation and Spatial Injection Models: Modeling Step
(1) Firstly, the observation model
h correlates the LR and HR MS images,
z and
Z, which mathematically describes the spectral consistency defined by Wald
et al. [
51]:
where
H is a matrix with (
QM) × (
QN) elements representing the low-pass filtering and down-sampling process, and
n is the random noise vector with
QM elements.
Z denotes the desirable HR MS images that are assumed to be the real scene without any blur. Thus, the specific sensor PSF, e.g., the blur effect, should be modeled in the
H matrix.
H usually comprises at least two parts: at least one image filtering matrix representing the blur PSF and at least one image down-sampling matrix to change the dimension of
Z to that of
z. For example, in a PSF case simulated by a two-level “
à trous” wavelet (ATW) transformation filter [
28] with a scale ratio of
r = 4, there are two filtering matrices and two down-sampling matrices, respectively:
where
F is the ATW filter (
F1 with (
QN) × (
QN) elements and
F2 with (
QN/2) × (
QN/2) elements) and
D is the down-sampling process by two (
D1 with (
QN/2) ×
QN elements and
D2 with
QM × (
QN/2) elements).
D and
F require a huge storage space,
i.e., more than
M times that required for storing the MS images
Z. In our final solution, we find that the
H matrix and
Z vectors do not have to be formed, and that the solution can be expressed in image form (see the discussion in
Section 1.5,
Section 1.6 and
Section 2.6).
(2) Secondly, the relationship between the observed Pan image
X and the MS images
Z is represented by
g(
Z):
where
e is a vector of random errors with
N elements. We usually assume that they are linearly correlated:
where
Β is a coefficient matrix with
N × (
QN) elements and
α is a coefficient vector with
N elements. We will prove later that this model mainly related to the spatial detail injection in EGIF.
(3) Finally, we assume that Z is a Gaussian vector with a mean vector z̃ and covariance matrix CZ,Z with QN × QN elements. This is a very important assumption as it can roughly satisfy the spectral preservation requirement using the up-sampled MS images as the mean value. It is simply referred to as the Gaussian assumption of the MS images.
Denoting the covariance matrices of
e and
n as
Ce with
N ×
N elements and
Cn with
QM ×
QM elements, respectively, we have:
1.3. Maximum A Posteriori (MAP) Estimation: Inversion Step
It is reasonable to assume that
n is a Gaussian random vector and independent of
z,
X and
e. Thus,
X and
z are independent conditional on the knowledge of
Z. This allows Equation (1) to change as follows:
Note that in Equation (9),
p(
X,
z) is a constant. Although this equation is different from Equation (10) in a study by Hardie
et al. (2004), they are equivalent. See
Appendix A for details.
We begin by deriving the MAP estimation by neglecting the spectral consistency term of
p(
z|
Z) in Equation (9):
Although neglecting the spectral consistency term is unreasonable, we will find that it is what EGIF does from the Bayesian perspective. And
Section 2.5 introduces the MAP solution with consideration of the spectral consistency term.
The MAP solution
can be found by minimizing the corresponding objective function [
12,
55] of Equation (10),
o(
Z), which can be formed by the exponent terms in Equations (7) and (8):
can be calculated as:
where
is the estimated covariance matrix with
QN ×
QN elements, measuring the uncertainty of the
estimation.
Ce and
CZ,Z can be interpreted as the relative contribution from the observed Pan and MS images. Similar to Fasbender
et al. [
54], we define a weight parameter
s to adjust their contributions, which we interpret as the weight given to the Pan information at the expense of the MS information. By introducing
s,
Ce and
CZ,Z are divided by 2
s and 2(1 −
s), respectively, as the final covariance matrix. In this way, the best estimation can be given by
with a generalized intensity vector,
ỹ =
Βz̃ +
α, defined as in a study by [
25], applying the matrix inversion lemma and simplifying the results yields the following equation:
s is in a range from 0 to 1. Setting s = 0.5 lends the same weight to both images. If s = 0, the results are = z̃, which are the blurred images obtained by up-sampling the LR MS images. The information from the Pan image is simply neglected in this case.
This solution unfortunately involves many unknown parameters, including a QN × QN covariance matrix CZ,Z, an N × N covariance matrix Ce, an N × QN coefficient matrix Β and an N element coefficient vector α. Thus assumptions must be made about the properties of these random vectors to lower the number of parameters to be estimated and make the problem manageable.
1.4. Extended General Image Fusion (EGIF) Framework
The detail injection methods can be expressed in an EGIF [
8,
11,
13]:
where
Ω represents the modulation coefficient matrix with
QN ×
N elements.
ỹ represents a vector with the same dimensions as the HR image
X, which can be calculated by low-pass filtering image
X according to an MRA method or by combining the LR MS images according to a CS method.
1.5. CS Methods from a Bayesian Perspective
One common assumption in some model-based and CS methods is that the Pan image
X is a linear combination of HR MS images
Z [
54,
58,
59,
60,
61,
62,
63,
64,
65,
66] as in Equation (5). Equation (16) solves for these methods.
To estimate the unknown parameters, we assume that the pixels are spatially independent (
Appendix B discusses spatial independence in detail) and share the same variance and regression coefficients,
i.e., stationary second-order statistics. The local and global modulation coefficients correspond with the local and global stationarity, respectively:
where
IN is an identity matrix with
N ×
N elements,
iN is an identity vector with
N elements,
β = [β
1, β
2, …, β
Q], α, β
1, β
2, …,β
Q are regression coefficients,
CQ is a covariance matrix with
Q ×
Q elements to measure the covariance between different spectral bands and σ
e is the variance of the regression residual in the relationship
g seen in Equation (5). These (
Q2 +
Q + 2) unknown parameters,
i.e.,
β, α,
CQ and σ
e, can be estimated from the observed MS images
z, the intensity image
y and the degraded Pan image
x. Define an modulation coefficient vector,
ω = [ω
1, ω
2, …, ω
Q]
T, with ω
q being the modulation coefficient for the
qth band:
The solution Equation (16) has the same formulation as Equation (17) (
Ω = diag(
ωT,
ωT, …,
ωT)
N with
ω as Equation (19) and follows the general scheme of a CS method [
25]. This indicates that all CS methods are special cases of this MAP solution that use different
s and covariance values in Equation (19). In IHS method,
ω =
iQ (with
Q elements) is a constant for all the pixels. In Brovey transformation method,
ωn =
z̃n/
ỹn (with
Q elements and the subscript
n indicating the corresponding vector for the
nth pixel) is pixel dependent (
Table 1). Setting
s = 1,
ω =
CQβT(
βCQβT)
−1. According to the covariance properties, σ
Y,Y =
βCQβT and
=
CQβT, where σ
Y,Y is the variance of the intensity variable
ỹ and
is the covariance between the intensity
ỹ and the
qth MS band
z̃q. Thus
ω =
with
being exactly the same modulation coefficient with the GS method (
Table 1). If
s is in the range of [0, 1] and
is positive, which is usually true, then ω
q is a monotonic increasing function of
s ranging in [0,
].
Table 1.
The corresponding modulation coefficients for the different component substitution (CS) and multi-resolution analysis (MRA) methods.
Table 1.
The corresponding modulation coefficients for the different component substitution (CS) and multi-resolution analysis (MRA) methods.
| CS | MRA | ω/ωn |
|---|
| GIHS and IHS | GLP | iQ |
| GS (s = 1) | GLP-M3 (s = 0.5) | (Y = X for MRA) |
| Brovey | HPM | z̃n/ỹn (ỹn = x̃ for MRA) |
We can interpret the IHS and Brovey transformation methods as special cases of the GS method. In the GS method (derived by setting
s = 1), the relationship between the modulation coefficient vector
ω =
=
CQβT(
βCQβT)
−1 and regression coefficient vector
β is:
Actually, we found that the IHS, generalized IHS (GIHS) and Brovey transform methods all satisfy this equation. Thus they can be interpreted as special cases of the GS method by neglecting the time-consuming covariance calculation process and redistributing the detail injection among different bands under Equation (20). This also explains why all the comparison studies of the IHS, GIHS, Brovey transform and GS methods have found the GS method to be the best in terms of spectral preservation and spatial injection [
2,
7,
25].
Previous studies have introduced similar weighting parameters
s to balance the contributions from different information sources [
41,
44,
54] but lack of detail explanation. With a parameter
t, Choi’s method [
41] can be rewritten into the general CS framework by setting
Tu
et al. [
44] introduced a parameter
l, which can be written into the general CS framework by setting
1.6. MRA Methods from a Bayesian Perspective
The MRA method formulations show that estimate of fused MS band
q,
, is independent of the other MS bands [
11,
27,
67]. Thus, we assume that
Z1,
Z2, …,
ZQ are all conditionally independent on
X, with a mean vector
z̃1,
z̃2, …,
z̃Q and a covariance matrix
. Furthermore,
Zq and
X are linearly correlated [
55,
56,
57,
67]:
where
αq and
eq have
N elements,
Βq has
N ×
N elements and
eq has a covariance matrix
. Thus, the MAP estimate is given by
where
ỹq =
Βqz̃q +
αq and
sq is the weight parameter for the
qth band.
X has a Gaussian distribution with an unknown mean E(
X) and a covariance
CX,X with
N ×
N elements as we assume that
Z and
X are linearly correlated and that
Z has a Gaussian distribution. We can similarly assume that
X has an expected value E(
X) =
x̃. Furthermore,
Βqz̃q +
αq =
x̃ =
ỹq, for
q = 1, 2, …,
Q. Thus,
where
Βq =
and
, with
being the covariance matrix between vectors
Zq and
X.
As with the CS methods, assumptions must be made to make the parameters easier to estimate:
where
, σ
X,X and
are the variance and covariance values for the corresponding covariance matrices. These matrices have only (2
Q + 1) unknown parameters and can be estimated from the observed MS images
z and degraded Pan image
x. Thus, the modulation coefficient for the
qth band, ω
q, is:
where ρ
q =
represents the correlation coefficient between bands
X and
Zq.
Thus the MRA methods, derived by setting
Ω =
diag(
ωT,
ωT, …,
ωT)
N in Equation (17) with
ω = [ω
1, ω
2,…, ω
Q] and ω
q as Equation (28), are special cases of the Bayesian fusion method that uses different
sq values to weigh the different information sources.
Table 1 lists some MRA modulation coefficients derived from different weights. Setting ω
q = 1 produces the high-pass filtering method or the simple GLP method depending on what filtering is used in MRA. Setting ω
q =
gives the HPM method [
37], which corresponds to the Brovey method in CS category as
x̃n corresponds to
ỹn deducted above. Setting
produces the M3 modulation coefficient [
11,
68] corresponding to the GS method in CS category (
Table 1).
We can derive the weight from the modulation coefficient,
From this equation we can derive
sq = 0.5 from the M3 modulation coefficient, which has the similar formulation with the GS method derived by setting
s = 1 in the CS method (
Table 1). Similarly, introducing a new variable, global correlation coefficient
ρq, we can derive
sq = (1 − (ρ
q)
2)/(
ρq + 1 − 2(ρ
q)
2) from the ECB coefficient [
27] and
sq = (1 − (ρ
q)
2)/(ρ + 1 − 2(ρ
q)
2) from the AABP coefficient [
36].
3. Experimental Confirmation
To experimentally confirm our previous analysis, we compared the GLP method coupled with two different injection models (
i.e., M3 and ECB) representing the MRA category and the GS method representing the CS category. There are many other MRA methods in the literatures [
80,
81,
82,
83], such as wavelet filter banks [
80,
81], which may have similar performance of the GLP method in terms of spectral preservation as opposed to Wald’s spectral consistency. The GLP-M3 method was implemented by setting different
s values to examine its spatial enhancement capability. To examine the relationship between the spatial enhancement and spectral preservation, we also incorporated the traditional detail injection methods with the spectral consistency constraint of Equation (2) as described in
Section 2.5. We named these methods GS-S, GLP-M3-S and GLP-ECB-S, respectively, with “
S” representing the spectral consistency. We omitted “
GLP” from the names in the following analysis without ambiguity, e.g., “
M3” refers to “
GLP-M3.”
We implemented GS by computing the simulated LR Pan image as the pixel average of the MS bands, and performed histogram matching using the linear transformation method. The slope of the linear function was the ratio of the standard variances between the LR image
x and the intensity image
y. The intercept of the linear function was set to make the line pass through the point (mean(
x), mean(
y)), where “
mean” refers to the average of all of the vector elements. Following [
28], in all of the cases involving the GS method,
z̃ and
x̃ were up-sampled using an expansion and a corresponding low-pass expansion filter,
i.e., a 23-taps filter. We also included the plain expansion of the MS dataset,
z̃, for comparison, which we referred to as “
EXP”. The conjugate gradient search was run for 5 iterations to secure a robust estimation. The ECB was the only local-adaptive injection model. Its coefficients were calculated on a square sliding window of 13 × 13 pixels in size, centered on the pixel in question in the up-sampled images
z̃ and
x̃ [
27] and clipped above 3 and below 0 to avoid numerical instabilities. In this study the 13 × 13 pixel window was used as sensitivity analysis undertaken using different window sizes on our test data did not reveal much difference for windows with 11 to 15 pixel side dimensions. Similar window size of 11 × 11 was utilized in Aiazzi
et al. [
7].
3.1. Experimental Data
We conducted experiments using two datasets acquired by the QuickBird and WorldView-2 satellites. The selected QuickBird data, with 0.6-m Pan and 2.4-m MS images, consisted of a forest landscape bisected by a broad road near Boulder City, Colorado, U.S. (
Figure 1). The MS image consisted of four bands, including R, G, B and NIR. The MS image was 600 × 600 pixels in size with a 2.4-m spatial resolution. The WorldView-2, which simultaneously collects Pan imagery at 0.46 m and MS imagery at 1.84 m, was the first commercial HR satellite to provide eight spectral sensors in the visible NIR range. Due to U.S. government licensing, the imagery information is made commercially available at 0.5 m and 2.0 m. In our dataset, the MS image was 800 × 800 pixels in size with a 2.0-m spatial resolution. We divided the eight MS bands into two groups for testing according to their bandwidth relationship with the Pan band (
Figure 2). The first group contained bands 3 (green), 4 (yellow), 5 (red) and 6 (red edge), which were all covered by the Pan band wavelength. For the second group, we selected bands 1 (coastal), 2 (blue), 7 (NIR1) and 8 (NIR2), which were either not covered or not fully covered by the Pan band wavelength. The WorldView-2 scene subset, which contained many complex urban buildings and vegetation across San Francisco, was observed on 9 October 2011 (
Figure 1). DigitalGlobe released the data through the 2012 IEEE GRSS Data Fusion Contest.
Figure 1.
Color compositions of (a) the original QuickBird MS image (2.4 m) at 600 × 600 pixels combined from red, green and blue bands and (b) the original WorldView-2 MS image (2.0 m) at 800 × 800 pixels combined from green, red and red edge bands. The degraded Pan images for (c) QuickBird at 2.4 m and (d) WorldView-2 at 2.0 m.
Figure 1.
Color compositions of (a) the original QuickBird MS image (2.4 m) at 600 × 600 pixels combined from red, green and blue bands and (b) the original WorldView-2 MS image (2.0 m) at 800 × 800 pixels combined from green, red and red edge bands. The degraded Pan images for (c) QuickBird at 2.4 m and (d) WorldView-2 at 2.0 m.
Figure 2.
Relative spectral radiance response of the WorldView-2 instrument. The bandwidths are Coastal: 400–450 nm, Blue: 450–510 nm, Green: 510–580 nm, Yellow: 585–625 nm, Red: 630–690 nm, Red Edge: 705–745 nm, NIR1: 770–895 nm and NIR2: 860–1040 nm. (Image credit: Digital Globe.)
Figure 2.
Relative spectral radiance response of the WorldView-2 instrument. The bandwidths are Coastal: 400–450 nm, Blue: 450–510 nm, Green: 510–580 nm, Yellow: 585–625 nm, Red: 630–690 nm, Red Edge: 705–745 nm, NIR1: 770–895 nm and NIR2: 860–1040 nm. (Image credit: Digital Globe.)
3.2. Validation Strategies
We conducted pan-sharpening at both reduced and full scales. At the reduced scale, we degraded the Pan and MS images by four before fusion so that we could use the original MS data as references for the fusion result evaluation. We applied a low-pass filter to the HR data, decimated the filtered images by two along both directions, reapplied the same filter and decimated the images again by two. We used 23-taps and ATW low-pass filters on the Pan and MS images, respectively [
27,
28] to match the MTF of the bands. At the full scale, we directly pansharpened the original MS images using the original Pan image and thus no MS reference images were used for the fusion results evaluation.
The consistency property of the Wald’s protocol, the synthesis property of the Wald’s protocol and Alparone’s protocol without reference were adopted as the validation strategies. To check the consistency property of the Wald’s protocol, we degraded all of the fused products to the original MS resolution by mimicking the sensor PSF [
52]. We then evaluated the degraded fused MS product against the original reference MS images. This validation can be applied to both the reduced and full scale experiments. To check the synthesis property of the Wald’s protocol, we need the reference HR MS images and thus can only be applied to the reduced scale experiments. To check the Alparone’s protocol, we do not need the reference HR MS images and thus can be applied to the full scale experiments. Obviously, with reference available, the validation procedure of the consistency and synthesis properties of the Wald’s protocol is very accurate. However, the consistency property is just a necessary condition but not a sufficient condition to guarantee the fused image quality. And the synthesis property is founded on the hypothesis of invariance between scales, which is not always fulfilled in practice [
51]. As such validation using Alparone’s protocol without reference is still necessary. Furthermore, a visual comparison is a mandatory step to appreciate the quality of the fused images.
If there are reference images in validation as in checking the consistency and synthesis properties of the Wald’s protocol, four quality indices can be adopted. (1) The first is the ERGAS index, from its French name “
relative dimensionless global error in synthesis,” which calculates the amount of spectral distortion [
84]. The best ERGAS value is zero; (2) The second is the Q4 index proposed by [
85], which is an extension of the universal quality index (
i.e.,
Q) suitable for four-band MS images. This index is sensitive to both correlation loss and spectral distortion between two MS images, and allows both spectral and spectral distortions to be combined in a unique parameter. The best value is one, with a range from zero to one. In our experiments, we calculated Q4 on 32 × 32 blocks; (3) The third is the spectral angle mapper (SAM), which calculates the angle between two spectral vectors to estimate the similarities between two different images. The best value is zero. (4) The last is signal to noise ratio (SNR, [
86]) in decibel (dB). It is used to measure the ratio between information and noise of the fused image.
If there are no reference images in validation as in checking Alparone’s protocol, three following different quality indices can be adopted. (1) A spectral distortion index,
Dλ, is derived from the difference of inter-band
Q values calculated from the fused MS bands and from the original LR MS bands; (2) A spatial distortion index,
DS, is derived from the difference of inter-band
Q values calculated between the fused MS bands and HR Pan band and between the original LR MS bands and the degraded Pan band; (3) QNR (
i.e.,
Quality with No Reference) is a combination of the preceding spectral/spatial distortion index [
87]. They all take values in [0, 1], with zero being the best value for
Dλ and
DS, and one being the best value for QNR.
3.3. Experimental Results
Figure 3,
Figure 4 and
Figure 5 show the fusion results of different pansharpening methods for the QuickBird and WorldView-2 datasets at the reduced scale. The quantitative evaluation indices are reported in
Table 2,
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13, which checked the synthesis property of the Wald’s protocol at the reduced scale (
Table 2,
Table 6 and
Table 10), the consistency property of the Wald’s protocol at both the reduced and full scale (
Table 3,
Table 5,
Table 7,
Table 9,
Table 11 and
Table 13) and Alparone’s protocol without reference at the full scale (
Table 4,
Table 8 and
Table 12).
Table 2.
Quantitative comparison of the fusion results to check the synthesis property of the Wald’s protocol for the QuickBird dataset at the reduced scale, i.e., at 2.4 m. The best result in each row is displayed in bold, and the second best is displayed in italics. The shaded gray cells are for alternative group columns with different categories.
Table 2.
Quantitative comparison of the fusion results to check the synthesis property of the Wald’s protocol for the QuickBird dataset at the reduced scale, i.e., at 2.4 m. The best result in each row is displayed in bold, and the second best is displayed in italics. The shaded gray cells are for alternative group columns with different categories.
| Category | No-Sharpening | CS | MRA-Local | MRA-Global |
|---|
| Method | EXP | GS | GS-S | ECB | ECB-S | M3, s = 0.5 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
| ERGAS | 5.132 | 4.690 | 3.515 | 5.122 | 4.303 | 3.942 | 3.312 | 4.790 | 4.086 | 5.699 | 4.815 |
| Q4 | 0.579 | 0.851 | 0.890 | 0.822 | 0.860 | 0.853 | 0.894 | 0.825 | 0.861 | 0.793 | 0.831 |
| SAM (◦) | 4.946 | 5.511 | 4.449 | 6.029 | 4.993 | 5.064 | 4.123 | 5.513 | 4.491 | 6.104 | 4.840 |
| SNR | 14.56 | 15.92 | 17.98 | 15.01 | 16.45 | 16.93 | 18.44 | 15.32 | 16.68 | 13.97 | 15.36 |
Table 3.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 9.6 m, to check the consistency property of the Wald’s protocol for the QuickBird dataset at the reduced scale.
Table 3.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 9.6 m, to check the consistency property of the Wald’s protocol for the QuickBird dataset at the reduced scale.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| ERGAS | 1.166 | 1.881 | 0.402 | 1.033 | 0.804 | 0.919 | 0.357 | 1.016 | 0.539 | 1.149 | 0.701 |
| Q4 | 0.983 | 0.986 | 0.999 | 0.990 | 0.999 | 0.991 | 0.999 | 0.989 | 0.999 | 0.986 | 0.998 |
| SAM (◦) | 1.098 | 1.330 | 0.235 | 1.140 | 0.282 | 1.118 | 0.214 | 1.148 | 0.256 | 1.188 | 0.314 |
| SNR | 27.26 | 23.93 | 36.79 | 28.65 | 31.89 | 29.46 | 37.50 | 28.61 | 34.21 | 27.65 | 32.23 |
Table 4.
Quantitative comparison of the fusion results to check Alparone’s protocol for the QuickBird dataset at full scale,
i.e., at 0.6 m. Time is measured in minutes. The font face indicators are identical to those in
Table 2.
Table 4.
Quantitative comparison of the fusion results to check Alparone’s protocol for the QuickBird dataset at full scale, i.e., at 0.6 m. Time is measured in minutes. The font face indicators are identical to those in Table 2.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| Dλ | 0.037 | 0.117 | 0.034 | 0.081 | 0.057 | 0.070 | 0.030 | 0.119 | 0.055 | 0.149 | 0.078 |
| Ds | 0.193 | 0.174 | 0.023 | 0.045 | 0.021 | 0.070 | 0.040 | 0.139 | 0.024 | 0.162 | 0.042 |
| QNR | 0.777 | 0.729 | 0.944 | 0.878 | 0.922 | 0.864 | 0.931 | 0.758 | 0.922 | 0.713 | 0.883 |
| Time | 0.02 | 0.28 | 6.30 | 3.10 | 9.12 | 0.27 | 6.29 | 0.29 | 6.42 | 0.28 | 6.44 |
Table 5.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 2.4 m, to check the consistency property of the Wald’s protocol for the QuickBird dataset at full scale.
Table 5.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 2.4 m, to check the consistency property of the Wald’s protocol for the QuickBird dataset at full scale.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| ERGAS | 0.815 | 2.490 | 0.303 | 1.170 | 0.620 | 0.845 | 0.232 | 1.232 | 0.349 | 1.552 | 0.429 |
| Q4 | 0.989 | 0.966 | 0.998 | 0.983 | 0.992 | 0.988 | 0.999 | 0.977 | 0.998 | 0.967 | 0.996 |
| SAM (◦) | 0.880 | 1.537 | 0.375 | 1.036 | 0.652 | 0.867 | 0.310 | 0.986 | 0.339 | 1.112 | 0.365 |
Table 6.
Quantitative comparison of the fusion results to check the synthesis property of the Wald’s protocol for the WorldView-2 group 1 dataset at the reduced scale,
i.e., at 2.0 m. The font face indicators are identical to those in
Table 2.
Table 6.
Quantitative comparison of the fusion results to check the synthesis property of the Wald’s protocol for the WorldView-2 group 1 dataset at the reduced scale, i.e., at 2.0 m. The font face indicators are identical to those in Table 2.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| ERGAS | 9.340 | 5.573 | 4.368 | 4.093 | 3.846 | 4.225 | 3.939 | 4.033 | 3.728 | 3.994 | 3.671 |
| Q4 | 0.542 | 0.875 | 0.906 | 0.923 | 0.931 | 0.912 | 0.924 | 0.923 | 0.933 | 0.926 | 0.936 |
| SAM (◦) | 6.106 | 6.184 | 5.400 | 5.820 | 5.290 | 6.019 | 5.317 | 5.950 | 5.282 | 5.935 | 5.275 |
| SNR | 9.92 | 14.92 | 16.52 | 17.13 | 17.64 | 16.83 | 17.42 | 17.24 | 17.90 | 17.33 | 18.03 |
Table 7.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 8.0 m, to check the consistency property of the Wald’s protocol for the WorldView-2 group 1 dataset at the reduced scale.
Table 7.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 8.0 m, to check the consistency property of the Wald’s protocol for the WorldView-2 group 1 dataset at the reduced scale.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| ERGAS | 1.908 | 2.439 | 0.168 | 0.646 | 0.190 | 0.644 | 0.136 | 0.663 | 0.139 | 0.685 | 0.143 |
| Q4 | 0.977 | 0.982 | 1.000 | 0.997 | 1.000 | 0.997 | 1.000 | 0.997 | 1.000 | 0.997 | 1.000 |
| SAM (◦) | 1.154 | 1.333 | 0.205 | 1.009 | 0.284 | 1.070 | 0.183 | 1.064 | 0.183 | 1.067 | 0.184 |
| SNR | 23.13 | 21.65 | 44.21 | 32.75 | 43.16 | 32.73 | 46.02 | 32.50 | 45.79 | 32.23 | 45.55 |
Table 8.
Quantitative comparison of the fusion results to check Alparone’s protocol for the WorldView-2 group 1 dataset at full scale,
i.e., at 0.5 m. Time is measured in minutes. The font face indicators are identical to those in
Table 2.
Table 8.
Quantitative comparison of the fusion results to check Alparone’s protocol for the WorldView-2 group 1 dataset at full scale, i.e., at 0.5 m. Time is measured in minutes. The font face indicators are identical to those in Table 2.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| Dλ | 0.046 | 0.013 | 0.015 | 0.021 | 0.012 | 0.030 | 0.013 | 0.035 | 0.018 | 0.036 | 0.020 |
| Ds | 0.197 | 0.023 | 0.024 | 0.010 | 0.023 | 0.015 | 0.019 | 0.018 | 0.009 | 0.019 | 0.007 |
| QNR | 0.766 | 0.964 | 0.962 | 0.969 | 0.965 | 0.955 | 0.969 | 0.948 | 0.974 | 0.945 | 0.974 |
| Time | 0.03 | 0.50 | 11.20 | 5.64 | 16.25 | 0.48 | 11.22 | 0.49 | 11.21 | 0.49 | 11.31 |
Table 9.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 2.0 m, to check the consistency property of the Wald’s protocol for the WorldView-2 group 1 dataset at full scale.
Table 9.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 2.0 m, to check the consistency property of the Wald’s protocol for the WorldView-2 group 1 dataset at full scale.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| ERGAS | 1.453 | 2.894 | 0.732 | 1.191 | 0.934 | 1.104 | 0.642 | 1.191 | 0.776 | 1.230 | 0.838 |
| Q4 | 0.990 | 0.965 | 0.997 | 0.993 | 0.996 | 0.994 | 0.998 | 0.993 | 0.997 | 0.993 | 0.997 |
| SAM (◦) | 0.927 | 1.433 | 0.420 | 0.860 | 0.523 | 0.925 | 0.353 | 0.931 | 0.417 | 0.936 | 0.448 |
Table 10.
Quantitative comparison of the fusion results to check the synthesis property of the Wald’s protocol for the WorldView-2 group 2 dataset at the reduced scale,
i.e., at 2.0 m. The font face indicators are identical to those in
Table 2.
Table 10.
Quantitative comparison of the fusion results to check the synthesis property of the Wald’s protocol for the WorldView-2 group 2 dataset at the reduced scale, i.e., at 2.0 m. The font face indicators are identical to those in Table 2.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| ERGAS | 8.098 | 11.01 | 5.404 | 6.289 | 5.474 | 6.129 | 5.423 | 5.988 | 5.130 | 7.206 | 5.676 |
| Q4 | 0.516 | 0.705 | 0.849 | 0.803 | 0.845 | 0.751 | 0.820 | 0.810 | 0.858 | 0.801 | 0.852 |
| SAM (◦) | 8.769 | 9.850 | 6.581 | 7.383 | 6.600 | 7.729 | 6.735 | 7.206 | 6.383 | 8.428 | 6.934 |
| SNR | 12.48 | 12.80 | 16.04 | 16.18 | 16.98 | 16.11 | 16.93 | 16.36 | 17.36 | 15.50 | 16.88 |
Table 11.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 8.0 m, to check the consistency property of the Wald’s protocol for the WorldView-2 group 2 dataset at the reduced scale.
Table 11.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 8.0 m, to check the consistency property of the Wald’s protocol for the WorldView-2 group 2 dataset at the reduced scale.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| ERGAS | 1.632 | 7.631 | 0.353 | 1.368 | 0.412 | 1.202 | 0.220 | 1.333 | 0.262 | 1.793 | 0.480 |
| Q4 | 0.974 | 0.826 | 0.999 | 0.985 | 0.999 | 0.987 | 1.000 | 0.986 | 0.999 | 0.976 | 0.998 |
| SAM (◦) | 1.726 | 6.976 | 0.388 | 1.587 | 0.487 | 1.484 | 0.263 | 1.547 | 0.283 | 1.989 | 0.480 |
| SNR | 25.97 | 17.64 | 40.60 | 30.16 | 38.13 | 30.65 | 42.69 | 29.95 | 41.36 | 28.40 | 38.15 |
Table 12.
Quantitative comparison of the fusion results to check Alparone’s protocol for the WorldView-2 group 2 dataset at full scale,
i.e., at 0.5 m. Time is measured in minutes. The font face indicators are identical to those in
Table 2.
Table 12.
Quantitative comparison of the fusion results to check Alparone’s protocol for the WorldView-2 group 2 dataset at full scale, i.e., at 0.5 m. Time is measured in minutes. The font face indicators are identical to those in Table 2.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| Dλ | 0.024 | 0.065 | 0.023 | 0.060 | 0.044 | 0.072 | 0.045 | 0.078 | 0.050 | 0.072 | 0.048 |
| Ds | 0.151 | 0.217 | 0.077 | 0.049 | 0.042 | 0.039 | 0.026 | 0.068 | 0.021 | 0.067 | 0.013 |
| QNR | 0.828 | 0.732 | 0.902 | 0.894 | 0.915 | 0.892 | 0.931 | 0.860 | 0.930 | 0.866 | 0.939 |
| Time | 0.03 | 0.50 | 11.29 | 5.67 | 16.32 | 0.52 | 11.15 | 0.49 | 11.10 | 0.50 | 11.26 |
Table 13.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 2.0 m, to check the consistency property of the Wald’s protocol for the WorldView-2 group 2 dataset at full scale.
Table 13.
Quantitative comparison of the fusion results after degrading the images into the LR resolution, i.e., at 2.0 m, to check the consistency property of the Wald’s protocol for the WorldView-2 group 2 dataset at full scale.
| Method | EXP | GS | GS-S | ECB | ECB-S | M3 | M3-S | s = 0.75 | s = 0.75, S | s = 0.9 | s = 0.9, S |
|---|
| ERGAS | 1.286 | 8.393 | 0.375 | 1.369 | 0.812 | 1.087 | 0.267 | 1.345 | 0.371 | 1.719 | 0.477 |
| Q4 | 0.989 | 0.804 | 0.999 | 0.988 | 0.995 | 0.992 | 1.000 | 0.989 | 0.999 | 0.982 | 0.999 |
| SAM (◦) | 1.365 | 6.644 | 0.381 | 1.364 | 0.738 | 1.202 | 0.217 | 1.336 | 0.271 | 1.612 | 0.348 |
3.3.1. Degree of Spatial Enhancement
The GLP-based methods (e.g., the GLP-M3 method) could exhibit better spatial enhancement than the GS method when the
s value was adjusted properly. In all of these figures, when
s is set to be larger than 0.75, the spatial enhancement of the MRA methods is larger than that of the GS method (
Figure 3,
Figure 4 and
Figure 5).
3.3.2. Are the Up-Sampled Images Spectrally Consistent?
None of the up-sampled images found to be strictly spectrally consistent from both the quantitative measurements and visual comparisons. The consistency quantitative matrices of the up-sampled images were shown in the first columns of
Table 3,
Table 5,
Table 7,
Table 9,
Table 11 and
Table 13 (3, 7 and 11 for the reduced scale, and 5, 9 and 13 for the full scale). The ERGAS values are around 1, which is not close to 0. In
Figure 3,
Figure 4 and
Figure 5, we can also see that that the up-sampled images have larger spectral distortions than the MRA fused images as opposed to the reference images, e.g., the roofs in
Figure 3 and
Figure 4 and the vegetation in
Figure 5.
None of the MRA methods actually satisfied the spectral consistency property (
Table 3,
Table 5,
Table 7,
Table 9,
Table 11 and
Table 13). However, the spectral consistency performance of the GLP-based methods was always better than that of the GS method even when the
s value increased from 0.5 to 0.75 and 0.9 for the M3 method to gain more spatial enhancement. This indicated that although the GLP-based methods were not spectrally consistent by design, their spectral inconsistency was not as obvious as that of the GS method. That is why so many studies have stated that GLP-based methods perform better in terms of spectral preservation.
3.3.3. Spectral Preservation is Complementary with Spatial Injection
All of the fused images at both the reduced and full scales were almost perfectly spectrally consistent with the LR MS images by adding the spectral consistency constraint (
Table 3,
Table 5,
Table 7,
Table 9,
Table 11 and
Table 13). They all had Q4 values close to 1, big SNR values, and very small ERGAS and SAM values when checking the consistency property at their LR resolutions [
52]. The fused products under the spectral consistency constraint also had better quantitative evaluation indices when checking the synthesis property (
Table 2,
Table 6 and
Table 10) and checking Alparone’s protocol (
Table 4,
Table 8 and
Table 12). This improvement was obvious given the respective one-unit decrease in ERGAS and SAM values for the GLP-based methods (
Table 2,
Table 6 and
Table 10). The improvement was even more obvious for the GS method, which made GS-S the second best performance for the QuickBird and WorldView-2 group 2 datasets. The performance increases were also obvious visually. For example, the tone in
Figure 3d (GS-S) is closer to the observed reference scene than that in
Figure 3c (GS). However, there is a case for the WorldView-2 group 1 dataset (
Table 8) that the ECB method with spectral consistency constraint showed no improvement in terms of QNR metric. This is possibly because that the QNR at the full scale is not as reliable as the other metrics used at the reduced scale [
88] or because that the spatial independence assumptions is violated in the HR dataset.
Furthermore, we found only a negligible decrease in spatial enhancement after making the fused products spectrally consistent (
Figure 3,
Figure 4 and
Figure 5). This indicated that spectral consistency, which is quite different from spectral preservation to the up-sampled MS images, is complementary with spatial enhancement rather than competitive. For example, comparing the GS-S and GS methods, the sharpness was only slightly weakened (
Figure 3,
Figure 4 and
Figure 5e and f). Moreover the GS-S method performed very closely to the M3-S method, which indicated that the proposed spectral consistency model was quite effective for making up for the spectral distortion caused by the fusion method.
Figure 3.
True color display of the fused results from different strategies for the QuickBird dataset at the reduced scale. (a): Observed at a 2.4-m spatial resolution; (b): EXP; (c): GS; (d): GS-spectrally consistent; (e): GLP-ECB; (f): GLP-ECB-spectrally consistent; (g): GLP-M3; (h): GLP-M3-spectrally consistent; (i): GLP with s = 0.75; (j): Spectrally consistent GLP with s = 0.75.
Figure 3.
True color display of the fused results from different strategies for the QuickBird dataset at the reduced scale. (a): Observed at a 2.4-m spatial resolution; (b): EXP; (c): GS; (d): GS-spectrally consistent; (e): GLP-ECB; (f): GLP-ECB-spectrally consistent; (g): GLP-M3; (h): GLP-M3-spectrally consistent; (i): GLP with s = 0.75; (j): Spectrally consistent GLP with s = 0.75.
Figure 4.
A subset, marked in the left white box in
Figure 1, of different fusion results at the reduced scale of the WorldView-2 group 1 dataset. Bands 3, 5 and 6 are combined for RGB display. (
a): Observed at a 2.0-m spatial resolution; (
b): EXP; (
c): GS; (
d): GS-spectrally consistent; (
e): GLP-ECB; (
f): GLP-ECB-spatially consistent; (
g): GLP-M3; (
h): GLP-M3-spectrally consistent;(
i): GLP with
s = 0.75; (
j): Spectrally consistent GLP with
s = 0.75.
Figure 4.
A subset, marked in the left white box in
Figure 1, of different fusion results at the reduced scale of the WorldView-2 group 1 dataset. Bands 3, 5 and 6 are combined for RGB display. (
a): Observed at a 2.0-m spatial resolution; (
b): EXP; (
c): GS; (
d): GS-spectrally consistent; (
e): GLP-ECB; (
f): GLP-ECB-spatially consistent; (
g): GLP-M3; (
h): GLP-M3-spectrally consistent;(
i): GLP with
s = 0.75; (
j): Spectrally consistent GLP with
s = 0.75.
Figure 5.
A subset, marked in the right white box in
Figure 1, of different fusion results at the reduced scale of the WorldView-2 group 2 dataset. Bands 1, 7 and 8 are combined for RGB display. (
a): Observed at a 2.0-m spatial resolution; (
b): EXP; (
c): GS; (
d): GS-spectrally consistent; (
e): GLP-ECB; (
f): GLP-ECB-spatially consistent; (
g): GLP-M3; (
h): GLP-M3-spectrally consistent;(
i): GLP with
s = 0.75; (
j): Spectrally consistent GLP with
s = 0.75.
Figure 5.
A subset, marked in the right white box in
Figure 1, of different fusion results at the reduced scale of the WorldView-2 group 2 dataset. Bands 1, 7 and 8 are combined for RGB display. (
a): Observed at a 2.0-m spatial resolution; (
b): EXP; (
c): GS; (
d): GS-spectrally consistent; (
e): GLP-ECB; (
f): GLP-ECB-spatially consistent; (
g): GLP-M3; (
h): GLP-M3-spectrally consistent;(
i): GLP with
s = 0.75; (
j): Spectrally consistent GLP with
s = 0.75.
3.4. Discussions
The Bayesian perspective of the pansharpening methods can be supported by the GS performance dependence of the linear fitness of Equation (5) in our experimental results,
i.e., the Pan approximation by the linear MS combination. As basic assumption of the GS method is the perfect linear relationship between the Pan band and MS bands, its performance may be largely affected by the fitness of this linear relationship. As shown in
Table 14, the residual variance of the linear regression in Equations (5) and (18) for the WorldView-2 group 2 dataset is much larger (indicating worse representation of Equation 5) than that for the QuickBird and WorldView-2 group 1 datasets. Thus the GS method performed much worse for the WorldView-2 group 2 dataset than the other two datasets. Researchers have tried to make the regression residual as small as possible, such as via histogram matching in the original CS methods and via injecting spatial details into the linear combination results
y in the combined CS/MRA method [
34].
Table 14.
The variance of the regression residual σe in Equation (18), the modulation coefficient ωq in Equation (19) for the GS method and the weight parameter sq in Equation (29) averaged over the image for the ECB method for the reduced scale experiments. Their average values over all the four bands are shown in the last column.
Table 14.
The variance of the regression residual σe in Equation (18), the modulation coefficient ωq in Equation (19) for the GS method and the weight parameter sq in Equation (29) averaged over the image for the ECB method for the reduced scale experiments. Their average values over all the four bands are shown in the last column.
| Band (q) | 1 | 2 | 3 | 4 | Average |
|---|
QuickBird
σe = 429 | ωq: GS | 0.589 | 1.086 | 0.940 | 1.384 | 1.00 |
| sq: ECB | 0.565 | 0.536 | 0.575 | 0.715 | 0.597 |
WorldView-2, group 1
σe = 154 | ω
q: GS | 0.948 | 1.183 | 0.849 | 1.020 | 1.00 |
| sq: ECB | 0.621 | 0.595 | 0.583 | 0.655 | 0.613 |
WorldView-2, group 2
σe = 4558 | ωq: GS | 0.237 | 0.318 | 1.806 | 1.639 | 1.00 |
| sq: ECB | 0.662 | 0.649 | 0.689 | 0.705 | 0.676 |
The Bayesian perspective of the pansharpening methods can also be supported by confirming the relationship between regression and modulation coefficients of the CS methods (
i.e., Equation (20)). For the GS method, because the regression coefficient in Equation (18), β
q, equals 1/4, the average modulation coefficient (ω
q) value shown in
Table 14 is actually Ʃβ
qω
q. They are all equal to 1, which satisfies Equation (20).
The s value is important as it controls the amount of modulation coefficient and thus the spatial enhancement degree. Theoretically setting s = 0.5 would get the best results as there is no prior information on the priority between the linear correlation assumption and the Gaussian distribution assumption. Thus when setting s = 0.5 the modulation coefficients were automatically and precisely controlled by the variance and covariance values in Equation (28). However, we could not estimate the variance and covariance properly due to the scale effect [
18,
87]. As such, the best s value should also compensate the scale effect which is hard to predict [
51] and thus requires further research. For example, in our experiments, the best s value was not 0.5. Increasing s from 0.5 to 0.75, i.e., from M3 (s = 0. 5) and ECB (s ≈ 0. 6) to M3 with s = 0.75, resulted in some increase in the algorithm performance for all of the WorldView-2 datasets (The s values for the ECB method were spatially adaptive, with averages around 0.6, as shown in
Table 14.)
The Bayesian perspective of the pansharpening methods can also be supported by that experimentally the best
s value is 0.5 when there is no scale effect in calculating variance and covariance.
Figure 6 shows ERGAS, SAM and Q4 as functions of the
s value in the GLP-based methods for the three datasets at the reduced scale. The coefficients were calculated based on the HR images to avoid the scale effect, which was not available in practice. Without exception, the best ERGAS, SAM and Q4 values were achieved by setting
s = 0.5.
Figure 6.
ERGAS, SAM (a) and Q4 (b) as functions of the s value in the GLP-based methods for all three datasets, including WorldView-2 (WV) and QuickBird (QB).
Figure 6.
ERGAS, SAM (a) and Q4 (b) as functions of the s value in the GLP-based methods for all three datasets, including WorldView-2 (WV) and QuickBird (QB).
3.5. Computational Complexity
The last rows of
Table 4,
Table 8 and
Table 12 show the computational times of each algorithm in the full scale experiments. We used an Intel
® Dual-Core™ i5 CPU with installed memory of 4.00 GB and a 32-bit Windows 7 operating system as the computer platform in the experiment. All of the codes were written in Matlab language.
The efficiency of the conjugate gradient search to guarantee the spectral consistency was acceptable in the computing environment for an LR MS image around 800 × 800 pixels in size. And it can be improved using recently developed parallel computing paradigm [
89]. The algorithm efficiency was proportional to the product of the LR MS pixel number and the spectral band number (
i.e.,
M ×
Q). This means that when the study area was increased, the computation time increased linearly along with the number of pixels. Compared with the ECB method, the main computational time of the ECB-S method was spent on the conjugate gradient search, as they required the same amount of time to calculate the modulation coefficients. Most of the time spent by the algorithms with the spectral consistency constraint was spent on the conjugate gradient search. The MRA methods with spatial varying modulation coefficients, e.g., ECB, required more time for calculation than the global modulation coefficients, e.g., M3.
4. Conclusions
Despite continuous improvements in the pansharpening algorithm performance, many questions have arisen over the last decade. For example, is the spatial enhancement of CS methods better than MRA methods? Is there a tradeoff between spectral preservation and spatial enhancement in the fused product? What is the difference between the spectral preservation of up-sampled MS images and the spectral consistency against original MS images?
By analyzing the solution of the Bayesian data fusion framework, we found that both CS and MRA methods are special cases of Bayesian data fusion by assuming/modeling (1) the Gaussian distribution of the desirable MS images with the up-sampled MS images comprising the mean value to preserve spectral information and (2) the linear correlation between the MS and Pan bands to inject spatial information. We derived the established EGIF with different injection models by setting different weight parameters to control the different assumption/model contributions.
The only difference between the CS and MRA methods is how the MS and Pan images are linearly correlated. By adjusting weight parameters to balance the spectral preservation and spatial injection, the MRA methods can perform better than the CS methods in terms of spatial injection. The experimental results related to two images captured by QuickBird and WorldView-2 satellites confirmed this conclusion.
It is widely believed that building these two assumptions/models into the detail injection pansharpening framework results in a tradeoff of spatial and spectral quality in the fused product. However, this conclusion comes from an implicit and improper assumption that the up-sampled MS images best preserve the spectral information. The spectral consistency should be defined as that any synthetic image should be as identical as possible to the original image once degraded to its original resolution with regard to sensor PSF. The up-sampled MS images are actually not spectral consistent. And the spectral consistency is guaranteed by incorporating a third model, the spectral consistency model, in the Bayesian data fusion framework. In this way, the spectral consistency constraint should be complementary with spatial injection rather than competitive. Spectrally consistent images with arbitrary sensor PSF can be estimated using the conjugate gradient search method at the expense of computational efficiency. The experimental results confirmed our analysis and found that the performance of the traditional EGIF methods improved significantly after adding the spectral consistency constraint.
The assumptions of the Gaussian distribution of the data and the spatial independence (
Appendix B) in the Bayesian method deduction might not be practical in some cases. Future research may attempt to segment the image into regions to make the assumptions more reasonable in each region rather than in the whole image. Alternative solutions are to make a non-Gaussian distribution assumption and to consider the spatial correlation as did in the co-kriging downscaling method [
90,
91], which may need more complicated optimization techniques to solve the models.