Segmentation-Based PolSAR Image Classification Using Visual Features: RHLBP and Color Features
Abstract
: A segmentation-based fully-polarimetric synthetic aperture radar (PolSAR) image classification method that incorporates texture features and color features is designed and implemented. This method is based on the framework that conjunctively uses statistical region merging (SRM) for segmentation and support vector machine (SVM) for classification. In the segmentation step, we propose an improved local binary pattern (LBP) operator named the regional homogeneity local binary pattern (RHLBP) to guarantee the regional homogeneity in PolSAR images. In the classification step, the color features extracted from false color images are applied to improve the classification accuracy. The RHLBP operator and color features can provide discriminative information to separate those pixels and regions with similar polarimetric features, which are from different classes. Extensive experimental comparison results with conventional methods on L-band PolSAR data demonstrate the effectiveness of our proposed method for PolSAR image classification.1. Introduction
Polarimetric synthetic aperture radar (PolSAR) has increasingly attracted researchers’ attention for its ability to capture images and the large variety of available data. PolSAR can obtain omnifarious properties of target by radar echoes of various combinations of transmitting and receiving polarizations from scattering media. For that reason, PolSAR data obtained from airborne or space-borne radar systems provide much more information than single polarization SAR [1]. One of the most challenging applications of polarimetry in remote sensing is land cover classification using fully PolSAR images [2–4].
Recently, many PolSAR image classification methods have been proposed. These methods mainly consist of two parts: (1) extracting features; and (2) designing a suitable classifier. For PolSAR data, the polarimetric features can be extracted by target decomposition methods [5–8], which aim at establishing a correspondence between the physical characteristics of the considered area and the observed scattering mechanism. Based on those polarimetric features, various classifier schemes, such as maximum likelihood (ML) [9–11], random forests (RF) [12,13] and support vector machine (SVM) [14,15], are introduced for PolSAR image classification. Lee and Grunes [10] proposed the method that used the maximum likelihood classifier based on the complex Wishart distribution. This method improved the result by the iterative classification, which also increased the complexity at the same time. Loosvelt and Peters [13] presented two different strategies to reduce the number of features in multi-date SAR datasets, but the experiments only used the polarimetric features. Fukuda and Hirosawa [14] applied SVM to PolSAR image classification, and the classification result was interrupted by the speckle noise. Moreover, Cloude and Pottier [16] proposed an unsupervised classification method based on the distribution of scattering entropy and scattering angle. However, this method only used the physical interpretation of the basic scattering mechanism to estimate the properties of targets, which leads to the consequence that targets belonging to different classes may have similar H and α values. Van Zyl and Burnette [17] proposed an iterative Bayesian classification method for PolSAR images using adaptive a priori probabilities, which can dramatically improve the classification accuracy with only a few iterations.
Most of the classification methods are pixel-based. Speckle noise inherent in PolSAR data has strong negative effects on image analysis and classification [4]. For pixel-based classification methods, filter processing can restrain the noise. Various filters are proposed, such as the Lee filter [18], the refined Lee filter [19], the intensity-driven adaptive-neighborhood (IDAN) filter [20], the scattering model-based (SMB) filter [21], and so on. However, these filters cannot filter out all of the speckle noise. They would even change the original image information, especially the texture and the shape with small surfaces. In order to better tackle the noise, segmentation-based classification methods are introduced, which are based on the concept of object-oriented classification [22,23], such as the classification method based on statistical region merging (SRM) [24], the classification method based on the joint use of the H/A/α polarimetric decomposition and multivariate annealed segmentation [25] and the region-based unsupervised segmentation and classification algorithm that incorporates region growing and a Markov random field (MRF) edge strength model [26]. These methods are efficient for PolSAR data without filtering preprocess and could achieve satisfactory results. Furthermore, more features, such as color features [27], can be adopted to provide useful information. In this paper, we propose a new segmentation-based classification method by introducing texture features and color features.
For segmentation-based classification approaches, the segmentation results play a foundational role. To achieve satisfactory PolSAR image segmentation results, we introduce texture features into the framework of SRM. There are many texture features that could be employed to analyze PolSAR images, such as local binary pattern (LBP) [28], edge histogram descriptor (EHD) [29], Gabor wavelets [30], gray level co-occurrence matrices (GLCM) [31], multilevel local pattern histogram (MLPH) [32] and local primitive pattern [33]. In this paper, we propose an improved LBP operator, named the regional homogeneity local binary pattern (RHLBP) operator, which makes those pixels in the same region share the homogeneous texture features. By the combination of SRM algorithm and RHLBP operator, we obtain segmentation results with exact region edges.
In the classification step, we introduce visual features in the form of color features [27]. Color features exacted from false color images are usually ignored in many applications of PolSAR data processing. Although color features cannot present the real color information of the target, Uhlmann’s research [27] shows that color features can provide useful information for PolSAR data understanding and analyses. Through a great deal of experimental analyses, we found that color features can also perform excellently in the field of segmentation-based PolSAR image classification. Combining color features with polarimetric features as the input of the SVM classifier could improve the classification accuracy.
Under our proposed segmentation-based classification framework, the polarimetric features, texture features and color features are effectively used to implement PolSAR image classification. Extensive experimental results show that our proposed approach outperforms the conventional PolSAR image classification methods.
This paper is organized as follows. In Section 2.1, we review some target decomposition methods used in our experiments, and the outline of the SRM algorithm is given in Section 2.2. Our proposed method is described in Section 3, mainly including the segmentation step and the classification step. The experimental comparison results and analyses are in Section 4. Section 5 is the conclusion.
2. Related Work
We briefly review three target decomposition methods, including Krogager decomposition [6], Cloude–Pottier decomposition [7], four-component decomposition [8] and the segmentation algorithm SRM [24].
2.1. Target Decomposition
To obtain a better interpretation of the underlying scattering from the measured radar data, various polarimetric target decomposition methods are developed by describing the obtained average backscattering as the sum of independent components. The three target decomposition methods introduced in this section will be used for our following experiments.
Krogager decomposition: As a coherent target decomposition method [6], it decomposes a complex symmetric radar target scattering matrix into the sum of three coherent components, sphere, diplane and helix components. Its advantages are present in the entire use of coherent properties of targets. Considering the scattering matrix [S] in the linear orthogonal basis (h, v), the Krogager decomposition has the formulation as follows,
Cloude–Pottier decomposition: As an incoherent target decomposition theorem [7], it is based on eigen analysis of the polarimetric coherency matrix 〈[T]〉, which leads to the following decomposition,
The Cloude–Pottier decomposition theorem contains all of the scattering mechanism. Angle α has a relationship with the physical mechanism of the scattering process. Entropy H expresses the randomness of scattering medium from isotropic scattering (H = 0) to completely random scattering (H = 1). The anisotropy parameter A provides more details about the distribution of the eigenvalues. The stability of the Cloude–Pottier decomposition theorem makes it superior to the other methods.
Four-component decomposition: This is another kind of incoherent target decomposition theorem based on covariance matrix 〈[C]〉 [8]. The four-component decomposition describes the covariance matrix 〈[C]〉 as a combination of four simple scattering mechanisms, single-bounce scatter, double-bounce scatter, volume scatter and helix scatter. The scattering power for single-bounce, Ps, the double-bounce, Pd, the volume scattering, Pv, and the helix scattering, Ph, are expressed as follows,
2.2. SRM Algorithm
The SRM algorithm exhibits good performance in solving significant noise corruption and does not depend on the data distribution. The original SRM algorithm is designed for RGB or gray images characterized by additive noise. For fully-PolSAR image segmentation, the SRM procedure is applied to the false color image, which is obtained from the PolSAR data. The SRM algorithm can be described as follows. Firstly, the pairs of adjacent pixels in the four-neighborhood are sorted in ascending order by a sorting function. Then, this order is traversed for any pair of pixels. If the regions that the two pixels belong to are not the same one, the merging test is made. If the test result is true, the two regions are merged.
The SRM algorithm has two key steps:
To define a sorting function, by which the adjacent regions are sorted;
To ascertain a merging predication, by which the adjacent regions are judged for whether they could be merged.
Nielsen and Nock [34] defined a sorting function f as follows,
From Nielsen and Nock’s model, the merging predication of regions R and R′ is defined as follows,
3. The Segmentation-Based PolSAR Image Classification
The proposed segmentation-based PolSAR image classification method mainly contains two parts, the segmentation step and the classification step. Compared to other applications of the SRM algorithm for PolSAR image segmentation or classification [24,36], the proposed method is mainly improved in two aspects, the introduction of the RHLBP operator for segmentation and the color features for classification.
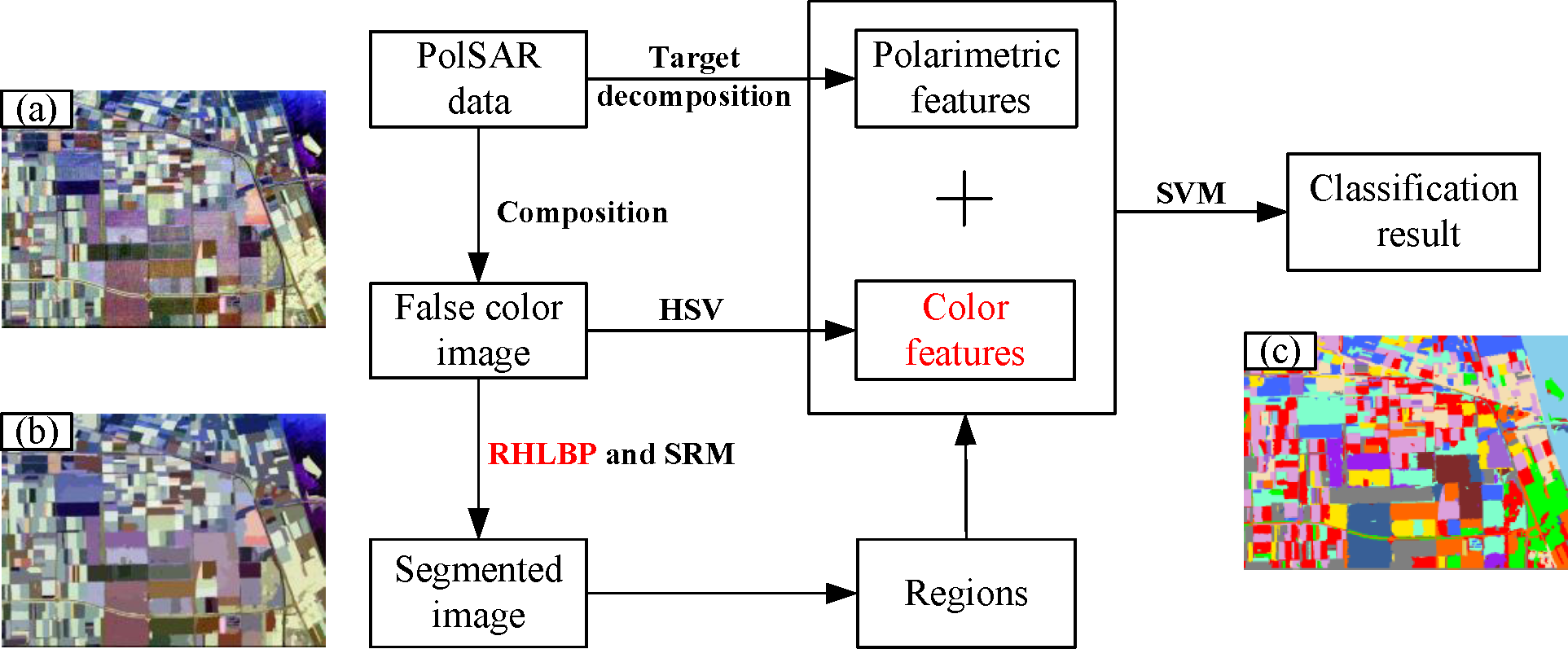
The procedure of the proposed PolSAR image classification algorithm is shown in Figure 1. We obtain the polarimetric features and false color images from the PolSAR data firstly. Figure 1a is a false color image of the PolSAR data that we will use in our experiments. In the segmentation step based on SRM, the RHLBP operator is introduced to provide texture information, and a segmented result is shown in Figure 1b. The HSV color space [29] is employed to extract color features from the false color images. Then, the average values of polarimetric features and color features are calculated according to the segmented regions. These features are taken as the input of the SVM classifier. A classification result is shown in Figure 1c.
3.1. Segmentation Based on SRM and RHLBP
For pixel-based PolSAR image classification methods, the process of the abundant PolSAR data needs extensive computation. Moreover, due to the interference of the significant noise inherent in the PolSAR data, the pixel-based methods might produce salt-and-pepper classification results.
To improve the classification result, the image segmentation technique has been adopted into the classification process. The segmentation technique can split the PolSAR image into disjoint and homogeneous regions with uniform or similar polarimetric backscatter characteristics. For PolSAR image classification, the segmentation process can significantly remove the disturbance of the speckle noise and reduce the computing complexity of classification.
The segmentation method in this paper conjunctively uses the SRM algorithm and our proposed RHLBP operator. The SRM algorithm has been introduced in Section 2.2. The segmentation results by the SRM algorithm are shown in Section 4.1.1. From these segmented results, we can find that the boundaries between regions are not good. The reason is that the original SRM algorithm cannot take enough information to separate the regions with similar polarimetric features. A possible solution is to explore new discriminative features. In this paper, we propose an improved operator RHLBP to extract the texture information among the PolSAR image.
3.1.1. RHLBP
The LBP operator, which works directly on pixels and their neighborhoods, can provide useful texture features. With extensive statistical analyses of the images processed by the LBP operator, Ojala et al. defined a rotation invariant uniform local binary pattern (RIU-LBP) operator [28,37] to treat those patterns with a strong regular form as ‘uniform’ patterns, which could reduce the number of binary patterns.
The following function is used to judge whether a local binary pattern is uniform,
However, during our experiments for PolSAR images, after the process of the false color image by the RIU-LBP operator, we noticed that even slight variation of intensity values in the neighborhood pixels will affect the value of , as shown in Figure 2a,c. To guarantee the regional homogeneity, we add a threshold T to make stable. The proposed operator RHLBP is defined as follows,
As the influence of speckle noise, the texture information of the PolSAR data presents great complexity. We introduce the RHLBP operator to control the slight variation, so as to restrain the influence of speckle noise. To demonstrate the advantage of our proposed RHLBP operator in presenting texture features compared to the RIU-LBP operator, we conducted three experiments on pixels and regions, respectively. Several images are used to demonstrate the improvement details of the RHLBP operator in the following. These images are tailored from the overall image used in our experiment. The information of the PolSAR data will be introduced in Section 4.1.
(1) Pixel-based illustration
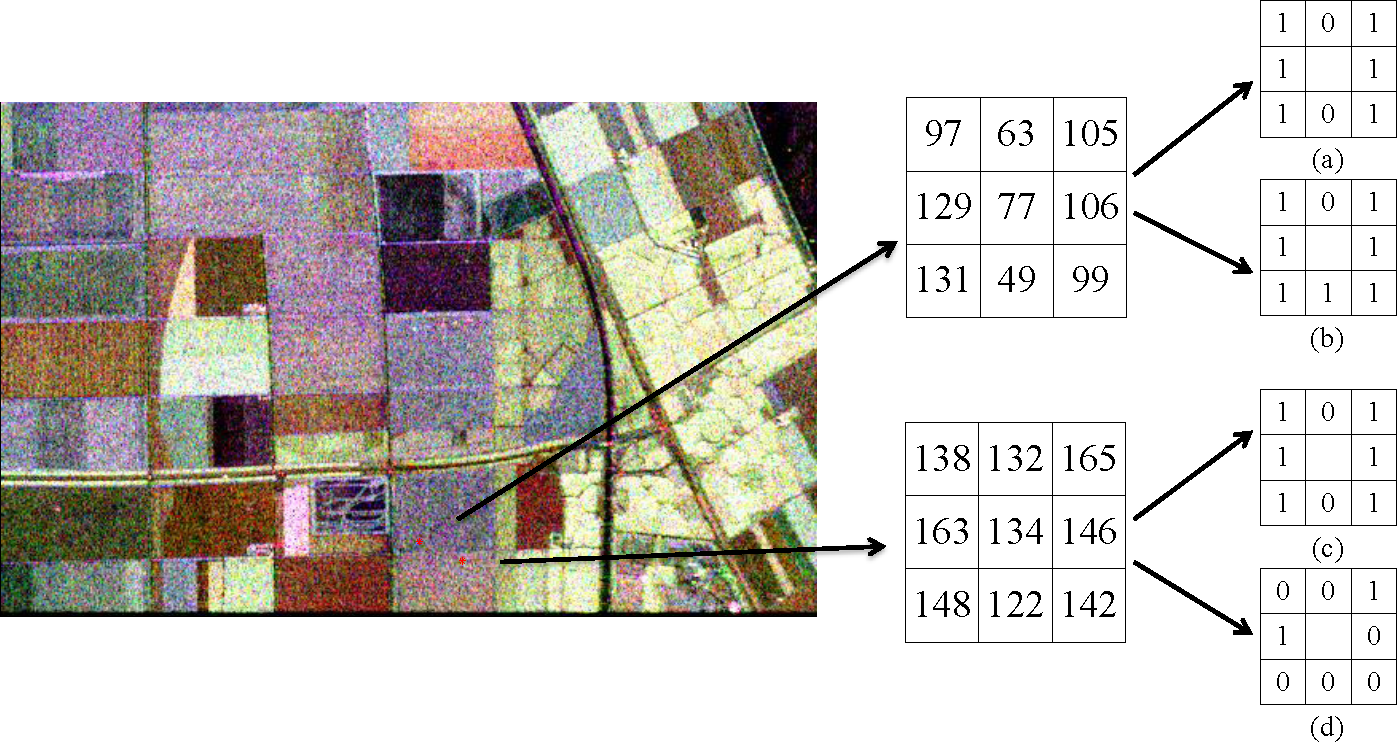
Figure 2 illustrates the effectiveness of RHLBP for representing two pixels (red dots) from the same class. The intensity values of the two pixels and their eight neighbor pixels show that they should share similar texture features (regional homogeneity). However, from Figure 2a,c, we can see that the value of the left pixel is two, while the value of the right pixel is nine. The values indicate that there is a great difference between the two pixels, even though they have similar texture features. Namely, RIU-LBP fails to extract the texture information in PolSAR images with speckle noise. In contrast, Figure 2b,d shows that their values are both four; this indicates that their texture features are similar. The effectiveness of RHLBP is demonstrated for the texture representation. Moreover, RHLBP can restrain the influence of speckle noise by introducing the threshold T.
Meanwhile, Figure 3 illustrates the effectiveness of RHLBP for representing two pixels (red dots) from two different classes. From the intensity values of the two pixels and their eight neighbor pixels, we can see that the texture information of the upper pixel is relatively rough, while the other pixel is relatively flat. However, their values are the same, as shown in Figure 3a,c, while their values are remarkably different, as shown in Figure 3b,d.
(2) Region-based illustration
The distribution of LBP values shows good regularity for image representation. Those areas with similar texture information are basically similar in the distributions of LBP values. For flat areas, the proportion of pixels whose patterns are uniform is large, while for areas with rough texture properties, the number of pixels whose patterns are uniform is small. To demonstrate the effectiveness of RHLBP for representing regions, the following experiments are implemented.
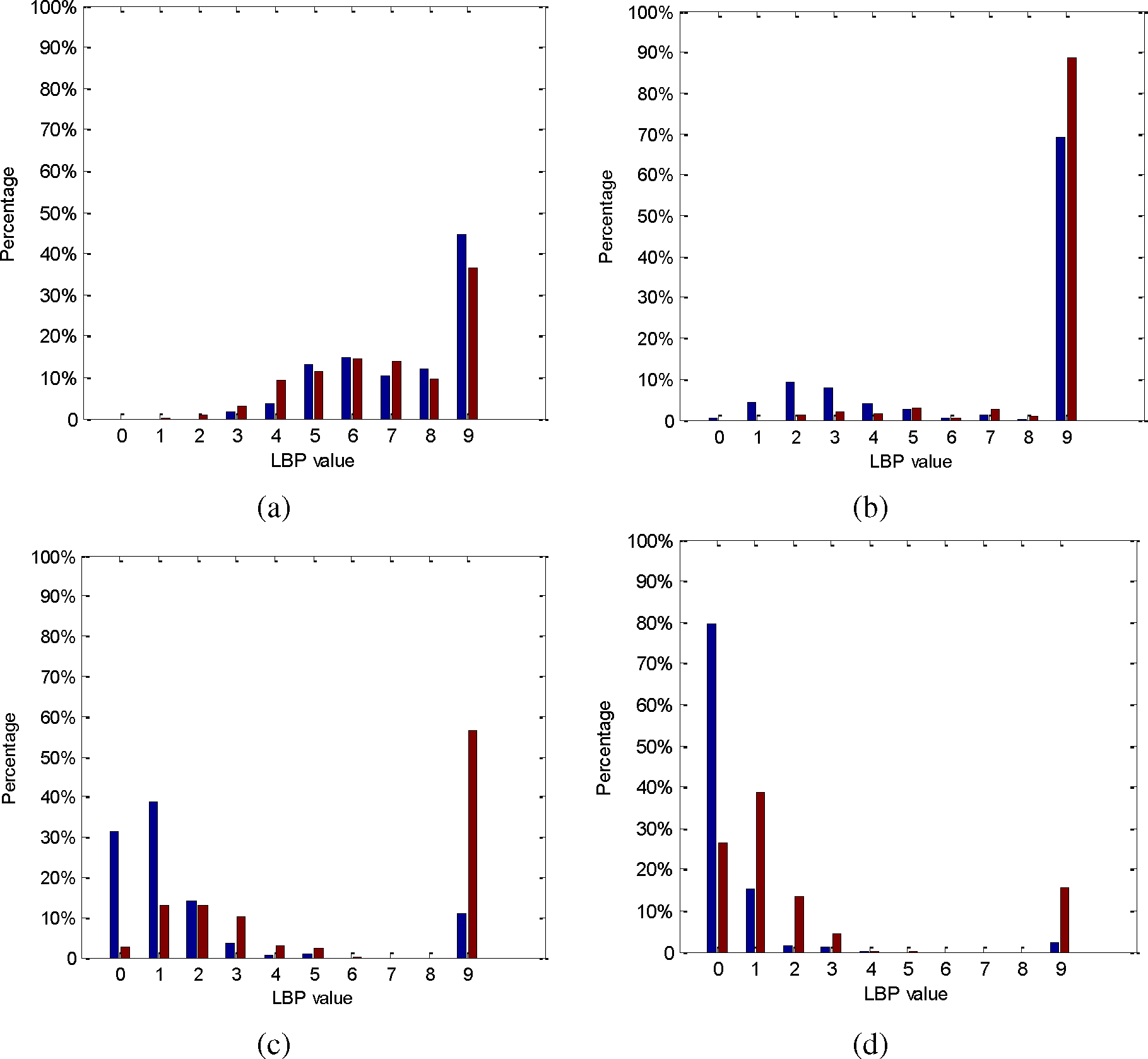
To compare the ability of the RIU-LBP operator and RHLBP operator to discriminate different texture information, we select two areas in Figure 4a that belong to two different classes. We process the two regions with the RIU-LBP operator and RHLBP operator, calculating the corresponding LBP value distributions (Figure 5). The threshold T is set to 10, 20 and 30, and the RHLBP value distributions are shown in Figure 5b–d. The blue bar reflects the area in the yellow rectangle, and the red bar reflects the other region. As shown in Figure 5, it is obvious that the distributions of values of heterogeneous regions are similar, while the distributions of values are different. RHLBP can better distinguish heterogeneous regions than RIU-LBP does, which demonstrates the discrimination of RHLBP. Moreover, we can see that with a bigger T value, the proportion of uniform pixels is higher.
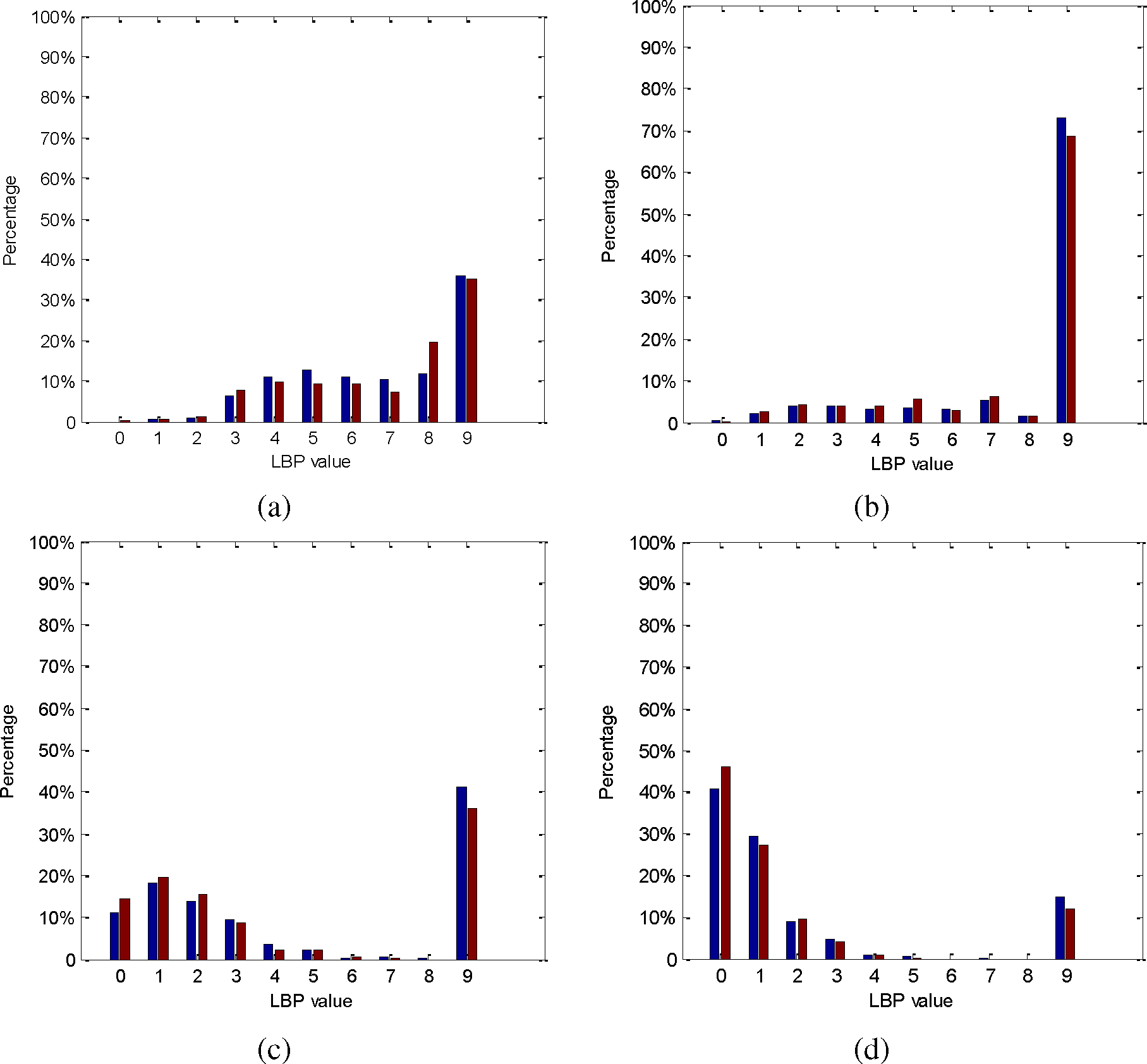
To compare the stability of the RIU-LBP operator and RHLBP operator to homogenous regions, two areas that belong to the same class are selected in Figure 4b. We process the two regions with similar procedures. The distributions of the two kinds of LBP values are presented in Figure 6. The blue bar represents the area in the yellow rectangle, and the red bar represents the other region. As we can see from Figure 6, the distributions of both the RIU-LBP values and RHLBP values are similar for homogenous regions.
The two experiments demonstrate the effectiveness of RHLBP, that is it has high discrimination for representing heterogeneous regions and good stability for representing homogenous regions.
(3) Analysis of threshold T
To quantitatively analyze the performance of the two operators and the influences of threshold T in RHLBP, we introduce the Bhattacharyya distance [38] to measure the similarity of the texture information between two regions. The Bhattacharyya distance of regions R and R′ is defined as follows,
Figure 7a shows the Bhattacharyya distances of the two regions from Figure 4a after computing their and values with different thresholds T. From Figure 7a, we can find that the Bhattacharyya distances of are greater than those of when 1 ≤ T ≤ 60. This indicates that the LBP value distributions of the two different regions are more dissimilar when using the RHLBP operator. Namely, the RHLBP operator is more discriminative to represent different texture regions.
To further verify the stability of RHLBP operator to describe homogenous regions, comparison results of the Bhattacharyya distances of the two regions from Figure 4b are shown in Figure 7b. The distances with RHLBP are smaller than those with RIU-LBP when 1 ≤ T ≤ 60. This denotes that the RHLBP operator’s representation ability for homogenous regions is more stable than that of the RIU-LBP operator.
According to the experimental analyses above, we can draw a conclusion that the texture representation ability of the RHLBP operator is better than the RIU-LBP operator for the stability for homogenous regions and the discrimination for heterogeneous regions. Moreover, we can find that the patterns of pixels will be influenced by the threshold T when using the RHLBP operator. With larger T, the proportion of pixels whose patterns are uniform is higher. When T increases to a certain degree, the texture representation ability of RHLBP will reduce, since too many uniform pixels are produced. Through the comparison of the RHLBP value distribution and Bhattacharyya distances of different pairs of regions, we set T = 20 for the experimented PolSAR data. When T is set as 20, the RHLBP operator presents good performance in discriminating heterogeneous regions and describing homogenous regions.
3.1.2. Merging Criteria
The merging criteria based on the Bhattacharyya distance is defined as follows,
The overall merging criteria for two regions R and R′ is defined by the combination of the SRM algorithm and the RHLBP operator,
3.2. Classification Using Polarimetric Features and Color Features
In this section, we introduce the classification step of our proposed method; the color features are introduced as important information to improve the classification accuracy.
3.2.1. Classification Procedure
After the segmentation step, we obtain regions with almost no speckle noise. The classification results are obtained by classifying those regions using the libsvm classifier with the RBF kernel [39]. The procedure mainly contains three steps:
To obtain segmented regions from the segmentation results;
To extract features of every region, such as polarimetric features and visual features, according to the segmented regions;
To classify regions using the SVM classifier. For Step (2), taking polarimetric feature ks from Krogager decomposition (introduced in Section 2.1) as an example, the formula to calculate the average feature for region j is as follows,
For Step (3), the features of every region serve as the input of the SVM classifier. The training samples are extracted from the regions whose information is provided by the ground truth image. Thus, we can obtain the classification results with nearly no speckle noise.
3.2.2. Features for Classification
Color features that are simple and useful usually are not considered as the information for PolSAR image classification, since the PolSAR data do not indeed provide the real color of the observed target. However, the false color images can provide useful information according to Uhlmann’s extensive experiments about the application of the color features [27]. To explore more information to improve the classification accuracy, we introduce the color features in this paper for segmentation-based classification.
Color features of PolSAR data are extracted from false color images. False color images of PolSAR data can present the information of targets for visualization. This can be obtained using the H, V polarization basis by assigning the backscattering matrices HH, VH and VV directly to the red, green and blue image components. In this paper, we assign the |HH − VV|, |HV| and |HH + VV| scatter matrices to red, green and blue image components, since this mapping produces more human-preferable, natural colors [27]. In Figure 8, the left image shows a false color image of the PolSAR data that we study. We employ the HSV color space [29] to obtain the hue (Hu), saturation (Sa) and value (Va) components of the false color image. The Hu, Sa and Va values are the color features. In this paper, we will verify the feasibility of the color features’ application in the framework of segmentation-based classification.
As the input vectors of SVM classifier, the polarimetric features of every region are the Krogager decomposition features, the Cloude–Pottier decomposition features or the four-component decomposition features. Moreover, we introduce the color features from the false color image in the HSV color space. The combination of feature vectors is shown in Table 1. Feature 1 to 3 are the polarimetric features, and color features are added into each polarimetric features to obtain Features 4 to 6.
4. Experimental Results and Analyses
Two NASA/JPL AirSAR L-band PolSAR data [40] are used to demonstrate the performance of the proposed algorithm, including the data of Flevoland and San Francisco.
4.1. Polarimetric SAR Data of Flevoland
Figure 8 (left) shows the false color image of the four-look fully-polarimetric L-band data, Flevoland. It is obtained by assigning the |HH − VV|, |HV| and |HH + VV| scatter matrices to the red, green and blue image components. The false color image has meaningful information, and pixels with a similar color have similar polarimetric features. The image has a size of, 1024 × 750 pixels. From the available ground truth data [27], we can know that there are about 15 classes, including water, buildings, forests, crops, and so on. Each region is in a regular shape. There is almost no aliasing among different classes. The ground truth image is also shown in Figure 8 (right).
4.1.1. Segmentation Results
Since our method is a kind of segmentation-based classification approach, segmentation will play a foundational role for the classification task. Our method incorporates the RHLBP operator into SRM to perform the segmentation. For the Flevoland PolSAR data, we empirically set Q = 250 (Equation (7)), M = 0.12 (Equation (13)), N = 20 (Equation (14)) and T = 20 in RHLBP. In our experiments, the determination of parameter M is similar to the analysis of threshold T in Section 3.1.1, and the determination of parameter N is similar to the case of parameter Q. In the following, we will take the parameter Q as an example to show how we decide to choose Q = 250. The parameter Q determines the quantification of the statistical complexity of a region. Different Q values will lead to different segmentation results, as shown in Figures 9 and 10. We will analyze them mainly from three aspects, over-merging, over-segmentation and the boundaries between regions.
Figure 9a is the result by SRM algorithm when Q = 100. Over-merging regions are easily observed, such as those areas in red ellipses. The lines and edges in the yellow circles also present obvious mistakes. Figure 9b is the result when Q = 500. There is nearly no over-merging. The boundaries between regions look more natural. However, a lot of over-segmentation regions appear as little holes in black ellipses. From the two figures, we can draw the conclusion that small Q will lead to over-merging, while big Q will lead to over-segmentation.
The experimental results show that Q = 250 seems to be a good choice. From Figure 10a, we can see that there are nearly no over-merging and few over-segmentation regions. However, the boundaries between regions in the red ellipses are not good results, which could not make the regions be in regular shapes. Through a lot of experiments with different Q values, we notice that we cannot obtain satisfactory results by just changing the parameter Q with the original SRM algorithm.
Figure 10b shows the result of the RHLBP operator method. The merging predication follows Equation (14). From the figure, we can see that the boundaries between regions are preserved very well, while there are nearly no over-merging and few over-segmentation regions, which is just the segmentation result we want. This demonstrates the effectiveness of introducing the texture information for segmentation and the capacity of the RHLBP operator for describing the texture information.
To demonstrate the effectiveness of RHLBP for segmentation compared to RIU-LBP, we conducted the following experiment, using SRM and the original RIU-LBP operator to perform the segmentation task. The parameters are the same as what we utilized in the above experiment, Q = 250, M = 0.12 and N = 20. Figure 11 is the segmentation result. Compared with Figure 10b, we can know that for the result by SRM and RIU-LBP, there exist many inaccurate segmentations. There are many over-segmented areas and bad boundaries between regions. It is obvious that our proposed RHLBP performs better than RIU-LBP for representing the texture information in the PolSAR image.
4.1.2. Classification Results and Analyses
We adopted different classification methods for PolSAR image classification including: (1) the proposed method, RHLBP + SRM + color + SVM (segmentation-based); (2) the proposed method without color features during the classification step, RHLBP + SRM + SVM (segmentation-based); (3) the SRM algorithm with color features, SRM + color + SVM (segmentation-based); (4) the original classification algorithm based on SRM, SRM + SVM (segmentation-based); (5) the SVM classification, color + SVM (pixel-based); and (6) the classical supervised Wishart classification (pixel-based). The features used for classification of Methods (1) to (5) are chosen from Table 1.
In all experiments, the classification accuracy values were obtained over multiple runs with different training samples for the reason that different training samples for the SVM classifier would influence the classification results. The classification accuracies were calculated according to those pixels’ labels provided by the ground truth image. We recorded the average values over 12 runs, leaving out the maximum and minimum values to reduce the effects of extreme outliers. The illustration for one of our training samples is shown as Figure 12.
(1) The comparison experiments for color features
We first verify the effectiveness of the introduction of color features. The six kinds of average features for every region utilized in our experiments are listed in Table 1. Figure 13a,c,e is the results of the proposed method without color features (RHLBP + SRM + SVM). Figure 13b,d,f is the results of the proposed method (RHLBP + SRM + color + SVM). The comparison of the six figures shows that with the introduction of color features, the number of those small misclassified regions is fewer compared to those without color features (in the black rectangles and circles), which could demonstrate the effectiveness of color features.
Polarimetric features extracted by target decomposition provide polarimetric information for classification. However, in the experiments only using polarimetric features, those regions belonging to different categories are misclassified into the same category, which we can see from the experimental results (Figure 13a,c,e) and the ground truth image (Figure 8 (right)). The reason may be that the information is not enough to figure out those regions with similar polarimetric features. Thus, the color features are introduced to provide more information for classification.
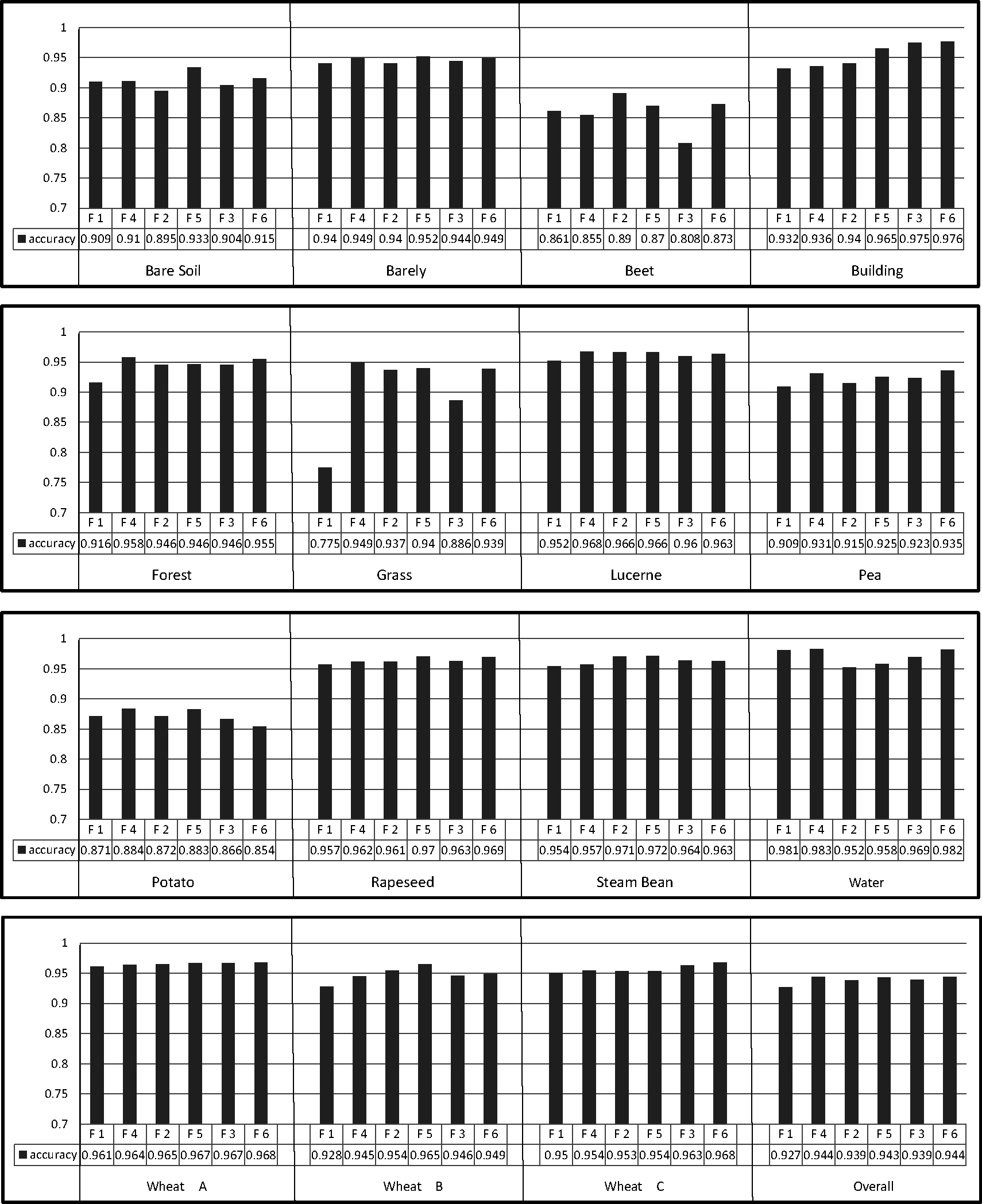
Figure 14 shows the classification accuracies for each class and the overall image, where F1, F2, F3, F4, F5 and F6 stand for the experiments using Feature 1, Feature 2, Feature 3, Feature 4, Feature 5 and Feature 6 from Table 1 as the input of the SVM classifier, respectively. From Figure 14, we can see that the color features truly can provide useful information for segmentation-based PolSAR image classification. For almost all of the classes and the overall image, the classification accuracies with color features are higher than those without color features. The improvement on classification accuracy values is not obvious, maybe due to the limited number of pixels provided by the ground truth image.
For different polarimetric features, the results of adding color features are different. Since the Krogager decomposition is relevant only for pure coherent targets (usually man-made targets), it leads to the worst performance for the natural scene among the three decomposition methods. However, the improvement of adding color features to Krogager decomposition features is the most obvious. For example, the accuracy for grass is improved from 77.5% to 94.9%, and for forest, the accuracy increases by 4.2%. We can see the effect from the comparison between Figure 13a,b. For the adding to Cloude–Pottier decomposition features, the improvement is not so obvious: the accuracy of bare soil increases by 3.8%; this is the largest improvement. The improvement can be seen from Figure 13c and Figure 13d. From the accuracy results of Feature 3 and Feature 6, we can know that the improvement of beet and grass is the most obvious, which we can also see from Figure 13e,f.
However, there are also the situations for which the classification accuracies of some classes, such as beet and potato, are lower than those without color features. The reason may be that the added color features of the two classes are useless with the polarimetric features used in our experiments. However, the classification accuracies of the other 13 classes present satisfactory results, which indicates that the color features can have a good performance for the task of segmentation-based PolSAR image classification.
(2) The comparison experiments for the RHLBP operator
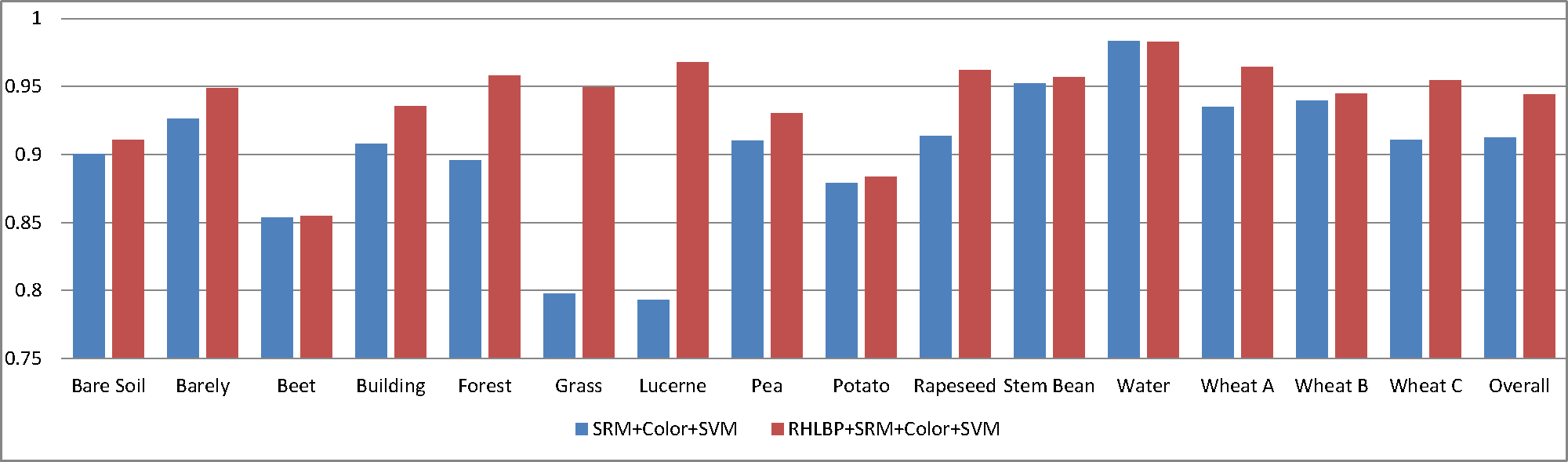
Section 4.1.1 has demonstrated the effectiveness of RHLBP operator for segmentation. In this section, we will statistically evaluate the RHLBP operator for PolSAR image classification. Our proposed method (RHLBP + SRM + color + SVM) is compared to the classification algorithm based on SRM algorithm adding color features for classification (SRM + color + SVM). For example, Feature 4 (in Table 1) is taken as the input. The classification accuracies for each class and the overall image by the two methods are shown in Figure 15. In the figure, the red bar is higher than the blue bar for every pair (one class), which indicates that our proposed method can obtain higher classification accuracies than the compared one. This also denotes that the texture information (RHLBP operator) can improve the classification performance for PolSAR image.
(3) The comparison experiments with the original SRM algorithm
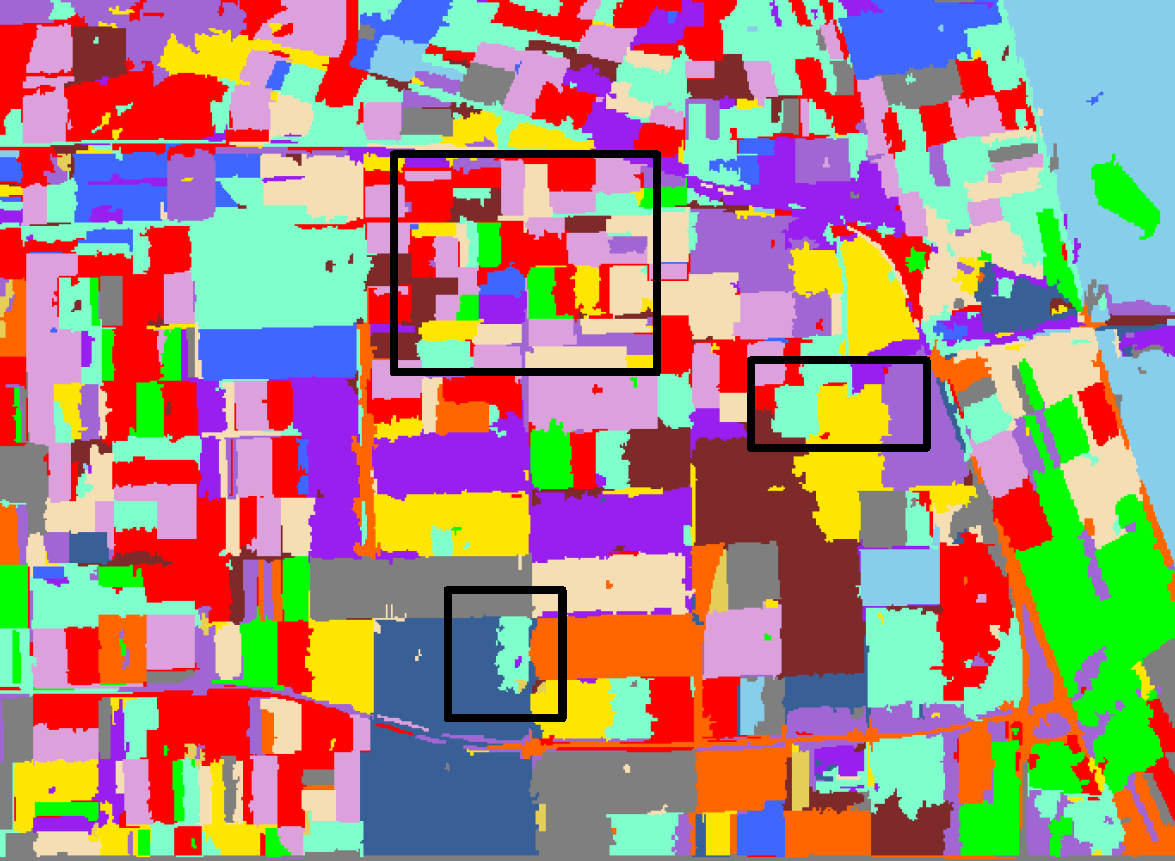
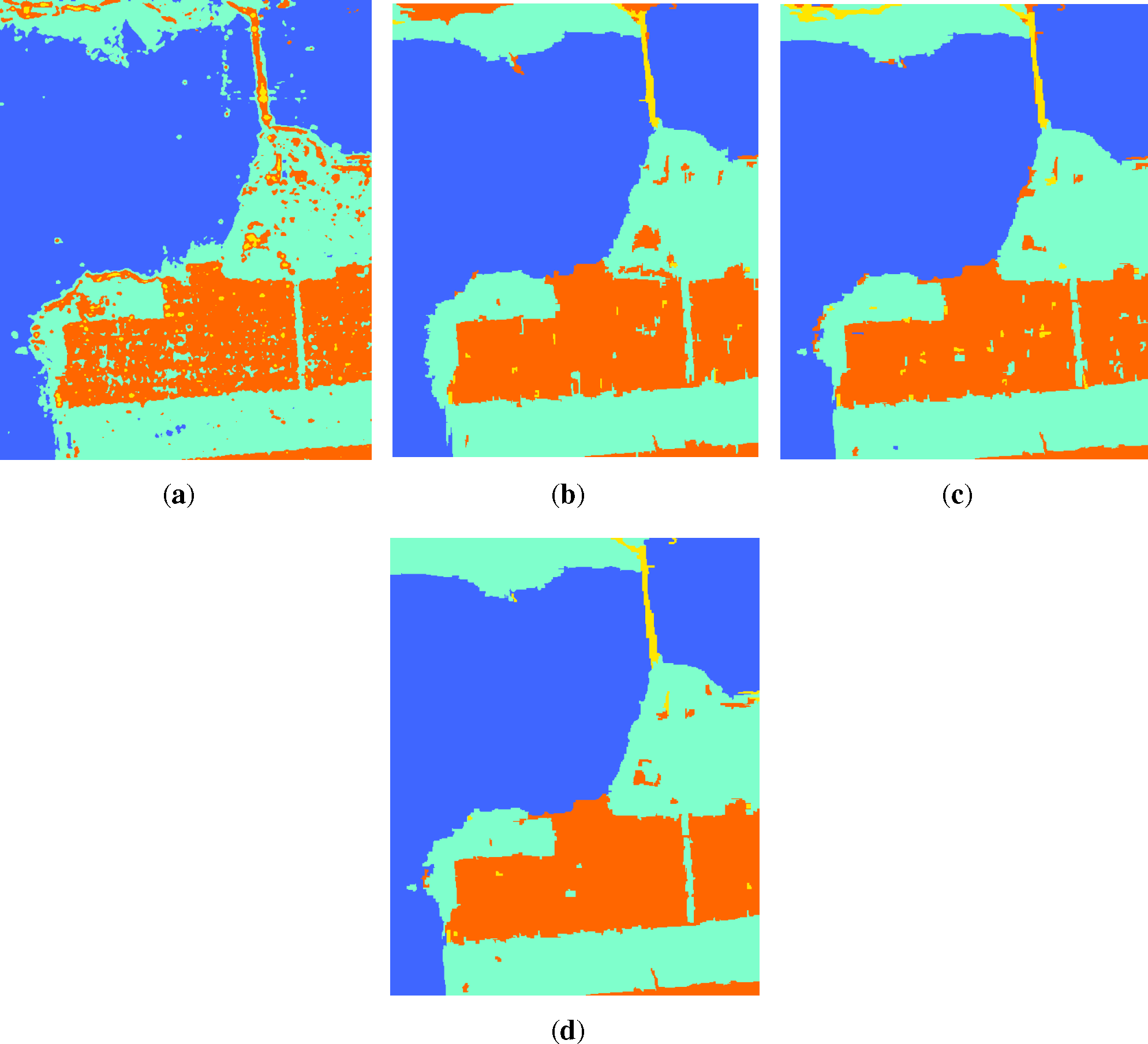
The experiment comparing the original SRM algorithm (SRM + SVM) [24] was also conducted. The classification result with Feature 3 is shown in Figure 16, compared with the result of our proposed method using Feature 6, which is shown in Figure 13f. Without the texture and color information, there exist many classification errors, especially the areas in the black rectangles. Regions belonging to wheat C are misclassified to rapeseed; the rapeseed areas are misclassified to pea; and the classes of beet and potato cannot be figured out. What is more, the edges of classified regions turn out to be bad results because of the segmentation errors. The overall accuracy of the original SRM algorithm is 89.3%, while that of our proposed method is 94.4%. From the comparison, we can know that our proposed method presents great advantages over the original SRM algorithm.
(4) The comparison with the SVM algorithm
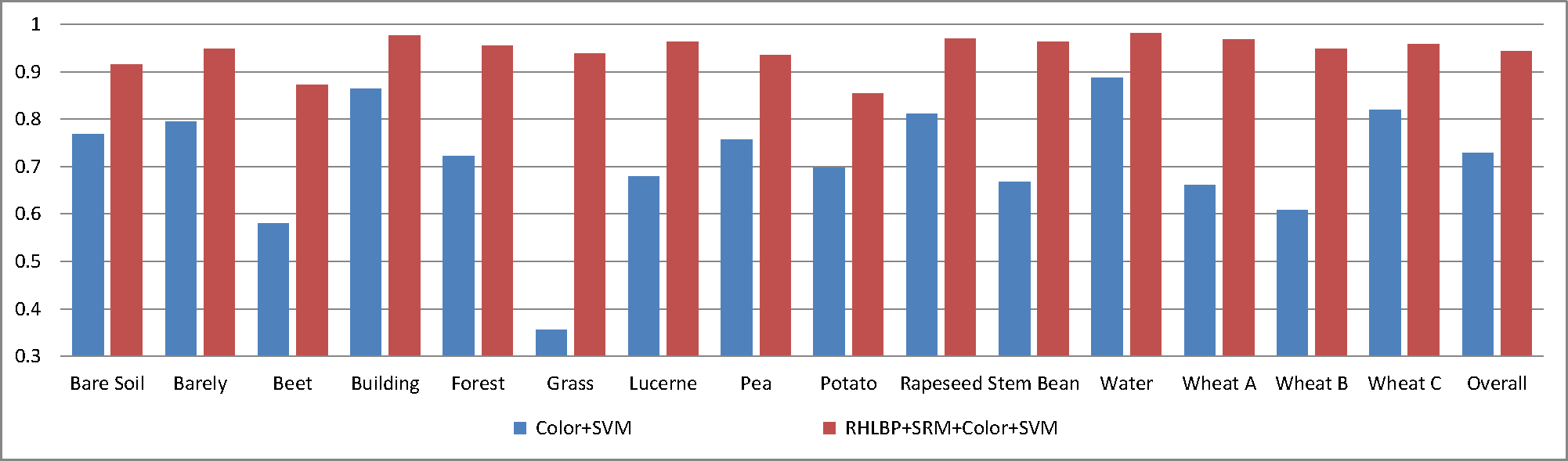
The pixel-based classification experiment by SVM was conducted to compare with the method that we proposed. The color features are used to provide more information, and Feature 6 (in Table 1) was taken as the input. The visual result by SVM (pixel-based) is shown in Figure 17; the result by our proposed method (segmentation-based) is shown in Figure 13f. The comparison between Figures 17 and 13f shows that, though the same features are adopted, the result by SVM classification has too many errors, because of the interruption of the speckle noise, while our proposed segmentation-based method classifies those regions more consistently with the ground truth image where each class is covering a regular region. The classification accuracies of the results by the two methods are shown in Figure 18, which statistically demonstrates that our proposed segmentation-based method is much better than the pixel-based SVM classification method.
(5) The comparison with the supervised Wishart classification algorithm
Another pixel-based classification experiment with the supervised Wishart classification algorithm was conducted. The PolSAR data were filtered by the Gaussian filter, and the training samples of the two methods were from the same set. The visual result by the supervised Wishart classification algorithm (pixel-based) is shown in Figure 19. Compared to the result by our proposed method (segmentation-based) shown in Figure 13f, which uses Feature 6, the pixel-based method also has too many classification errors caused by speckle noise. Compared with the SVM algorithm, the supervised Wishart classification algorithm obtains a better result for the step of filtering noise. However, there are also many misclassified pixels, while the result of our proposed method is better.
4.2. PolSAR Data of San Francisco
We adopted another PolSAR image to evaluate the effectiveness of our proposed method. Figure 20 (left) shows the false color image of the area around the bay of San Francisco with the golden gate bridge. The experiment image was selected from the original data with a size of 585 × 472 pixels. These data provide good coverage of both natural and man-made targets. The ground truth image is shown in Figure 20 (right) [27]; there are four classes, including water, urban, vegetation and bridge.
4.2.1. Segmentation Results
For the San Francisco PolSAR data, the segmentation results of the original SRM algorithm and our proposed algorithm (RHLBP + SRM) are shown in Figure 21. The parameter Q = 160 for both of the two methods, and for our proposed method, we also set M = 0.12, N = 20. The parameter threshold T = 35 in RHLBP is empirically set after some experiments. Compared with the PolSAR data of Flevoland, the data of San Francisco presents stronger textural properties.
The advantage of our proposed method is obvious through the comparison of the two segmentation results. Segmentation errors of the SRM algorithm exist, especially those areas in the black rectangle in Figure 21a, while the result of our proposed method keeps the detailed shapes of the ground objects well in Figure 21b. The boundaries between regions in the black circles in Figure 21b present better results than those in Figure 21a. Therefore, our proposed method obtains better results than the SRM algorithm.
4.2.2. Classification Results and Analyses
We compared our proposed method (RHLBP + SRM + color + SVM) with the other three classification methods, including the supervised Wishart classification algorithm, the original SRM algorithm (SRM + SVM) and the SRM algorithm with RHLBP (RHLBP + SRM + SVM). The illustration of the training samples is shown in Figure 22, and the classification results are shown in Figure 23. We used Feature 3 and Feature 6 to verify the effectiveness of our proposed method for the data of San Francisco. Feature 3 was used during the experiment of the original SRM algorithm and the RHLBP operator introduced in the SRM algorithm; Feature 6 was used in our proposed method.
From Figure 23, for the classification results of the four classification methods, we can see that the supervised Wishart algorithm performs worst. Although the PolSAR data are filtered by the Gaussian filter, there are still many misclassified pixels, e.g., the classes of bridge and urban are difficult to figure out. Although the result by the original SRM algorithm is improved compared with Figure 23a, many small over-segmented regions are misclassified. For example, the regions of urban are classified to vegetation. The boundaries of different regions are also not well processed. In Figure 23c, which is obtained by the RHLBP + SRM + SVM algorithm, the boundaries between different regions are improved for the adding of texture features. The classification result by our proposed method shown in Figure 23d is the best, where color features provide useful information to distinguish different classes. Together with the improvement of segmentation by the RHLBP operator, our proposed method presents excellent classification results.
5. Conclusions
In this paper, we propose an improved segmentation-based method for PolSAR image classification. An improved texture operator RHLBP is proposed to help the SRM algorithm obtain satisfactory segmentation results. Moreover, color features are introduced as the inputs of the SVM classifier to improve the classification accuracy. The method can process the speckle noise well in the PolSAR data. To evaluate the performance of our proposed approach, we conducted a series of experiments on the PolSAR dataset of Flevoland and San Francisco obtained by the airborne system. The experimental results demonstrate the effectiveness of our proposed method for PolSAR image classification.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (61201271), the Fundamental Research Funds for the Central Universities (ZYGX2013J019), the Science and Technology Support Program of Sichuan Province, China (co-operated with the Chinese Academy of Sciences) (2012JZ0001) and the State Key Laboratory of Synthetical Automation for Process Industries (PAL-N201401).
Author Contributions
Jian Cheng designed the algorithm and experiments; he also revised the paper. Yaqi Ji performed the experiments and wrote the paper. Haijun Liu suggested the experiments’ design and revised the paper in presenting the technical details.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, J.S.; Grunes, M.R.; Pottier, E. Quantitative comparison of classification capability: Fully polarimetric versus dual and single-polarization SAR. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2343–2351. [Google Scholar]
- Zyl, J.J.; Zebker, H.A.; Elachi, C. Imaging radar polarization signatures: Theory and observation. Radio Sci. 1987, 22, 529–543. [Google Scholar]
- Evans, D.L.; Farr, T.G.; van Zyl, J.J.; Zebker, H.A. Radar polarimetry: Analysis tools and applications. IEEE Trans. Geosci. Remote Sens. 1988, 26, 774–789. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar]
- Krogager, E. New decomposition of the radar target scattering matrix. Electron. Lett. 1990, 26, 1525–1527. [Google Scholar]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; Ainsworth, T.L.; Du, L.J.; Schuler, D.L.; Cloude, S.R. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2249–2258. [Google Scholar]
- Hoekman, D.H.; Vissers, M.A. A new polarimetric classification approach evaluated for agricultural crops. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2881–2889. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Loosvelt, L.; Peters, J.; Skriver, H.; De Baets, B.; Verhoest, N.E. Impact of reducing polarimetric SAR input on the uncertainty of crop classifications based on the random forests algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4185–4200. [Google Scholar]
- Fukuda, S.; Hirosawa, H. Support vector machine classification of land cover: Application to polarimetric SAR data. IGARS 2001, 1, 187–189. [Google Scholar] [CrossRef]
- Fukuda, S.; Katagiri, R.; Hirosawa, H. Unsupervised approach for polarimetric SAR image classification using support vector machines. IGARS 2002, 5, 2599–2601. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar]
- Van Zyl, J.; Burnette, C. Bayesian classification of polarimetric SAR images using adaptive a priori probabilities. Int. J. Remote Sens. 1992, 13, 835–840. [Google Scholar]
- Lee, J.S.; Grunes, M.; Mango, S.A. Speckle reduction in multipolarization, multifrequency SAR imagery. IEEE Trans. Geosci. Remote Sens. 1991, 29, 535–544. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; de Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar]
- Vasile, G.; Trouvé, E.; Lee, J.S.; Buzuloiu, V. Intensity-driven adaptive-neighborhood technique for polarimetric and interferometric SAR parameters estimation. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1609–1621. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; Schuler, D.L.; Pottier, E.; Ferro-Famil, L. Scattering-model-based speckle filtering of polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2006, 44, 176–187. [Google Scholar]
- Coad, P.; Yourdon, E. Object-Oriented Analysis; Yourdon Press: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Dabboor, M.; Karathanassi, V. A knowledge-based classification method for polarimetric SAR data. Proc. SPIE 2005. [Google Scholar] [CrossRef]
- Li, H.; Gu, H.; Han, Y.; Yang, J. Object-oriented classification of polarimetric SAR imagery based on statistical region merging and support vector machine, Proceedings of the International Workshop on Earth Observation and Remote Sensing Applications(EORSA), Beijing, China, 30 June–2 July 2008; pp. 1–6.
- Macrì Pellizzeri, T. Classification of polarimetric SAR images of suburban areas using joint annealed segmentation and “H/A/α” polarimetric decomposition. ISPRS J. Photogramm. Remote Sens. 2003, 58, 55–70. [Google Scholar]
- Yu, P.; Qin, A.; Clausi, D.A. Unsupervised polarimetric SAR image segmentation and classification using region growing with edge penalty. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1302–1317. [Google Scholar]
- Uhlmann, S.; Kiranyaz, S. Integrating color features in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2197–2216. [Google Scholar]
- Ojala, T.; Pietikäinen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar]
- Manjunath, B.S.; Ohm, J.R.; Vasudevan, V.V.; Yamada, A. Color and texture descriptors. IEEE Trans. Circuits Syst. Video Technol. 2001, 11, 703–715. [Google Scholar]
- Wu, P.; Manjunath, B.; Newsam, S.; Shin, H. A texture descriptor for browsing and similarity retrieval. Signal Process. Image Commun. 2000, 16, 33–43. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar]
- Dai, D.; Yang, W.; Sun, H. Multilevel local pattern histogram for SAR image classification. IEEE Geosci. Remote Sens. Lett. 2011, 8, 225–229. [Google Scholar]
- Aytekin, O.; Koc, M.; Ulusoy, I. Local primitive pattern for the classification of SAR images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2431–2441. [Google Scholar]
- Nock, R.; Nielsen, F. Statistical region merging. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1452–1458. [Google Scholar]
- Nock, R.; Nielsen, F. Semi-supervised statistical region refinement for color image segmentation. Pattern Recognit. 2005, 38, 835–846. [Google Scholar]
- Lang, F.; Yang, J.; Li, D.; Zhao, L.; Shi, L. Polarimetric SAR image segmentation using statistical region merging. IEEE Geosci. Remote Sens. Lett. 2014, 11, 509–513. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar]
- Kailath, T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2. [Google Scholar] [CrossRef]
- European Space Agency. Sample Datasets, Available online: http://earth.eo.esa.int/polsarpro/datasets.html accessed on 19 November 2014.








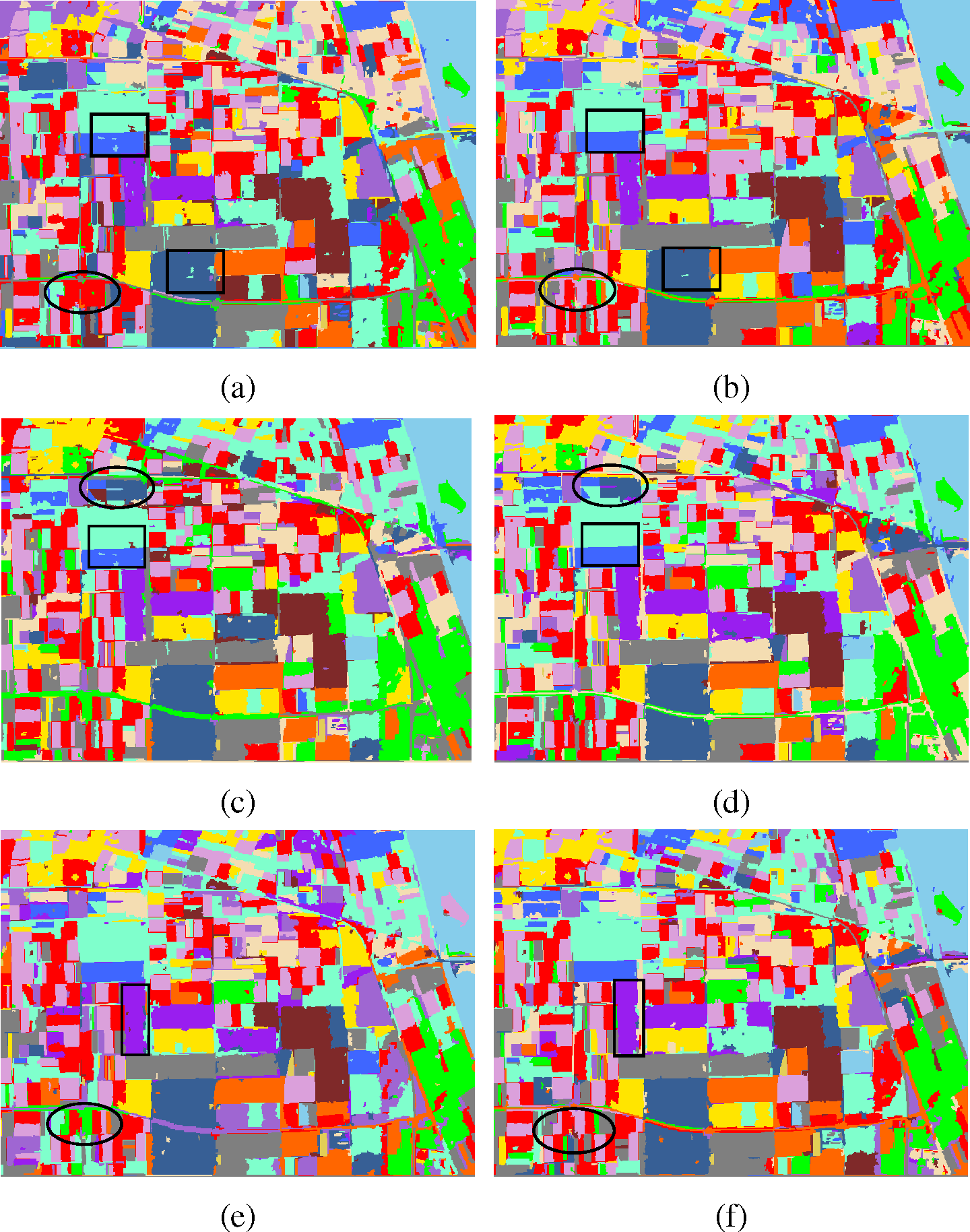





| Feature 1 | Krogager decomposition features | (ks, kd, kh) |
| Feature 2 | Cloude–Pottier decomposition features | (H, A, α) |
| Feature 3 | Four-component decomposition features | (Ps, Pd, Pv, Ph) |
| Feature 4 | Feature 1 and color features | (ks, kd, kh, Hu, Sa, Va) |
| Feature 5 | Feature 2 and color features | (H, A, α, Hu, Sa, Va) |
| Feature 6 | Feature 3 and color features | (Ps, Pd, Pv, Ph, Hu, Sa, Va) |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Ji, Y.; Liu, H. Segmentation-Based PolSAR Image Classification Using Visual Features: RHLBP and Color Features. Remote Sens. 2015, 7, 6079-6106. https://doi.org/10.3390/rs70506079
Cheng J, Ji Y, Liu H. Segmentation-Based PolSAR Image Classification Using Visual Features: RHLBP and Color Features. Remote Sensing. 2015; 7(5):6079-6106. https://doi.org/10.3390/rs70506079
Chicago/Turabian StyleCheng, Jian, Yaqi Ji, and Haijun Liu. 2015. "Segmentation-Based PolSAR Image Classification Using Visual Features: RHLBP and Color Features" Remote Sensing 7, no. 5: 6079-6106. https://doi.org/10.3390/rs70506079





