Inner FoV Stitching of Spaceborne TDI CCD Images Based on Sensor Geometry and Projection Plane in Object Space
Abstract
:1. Introduction
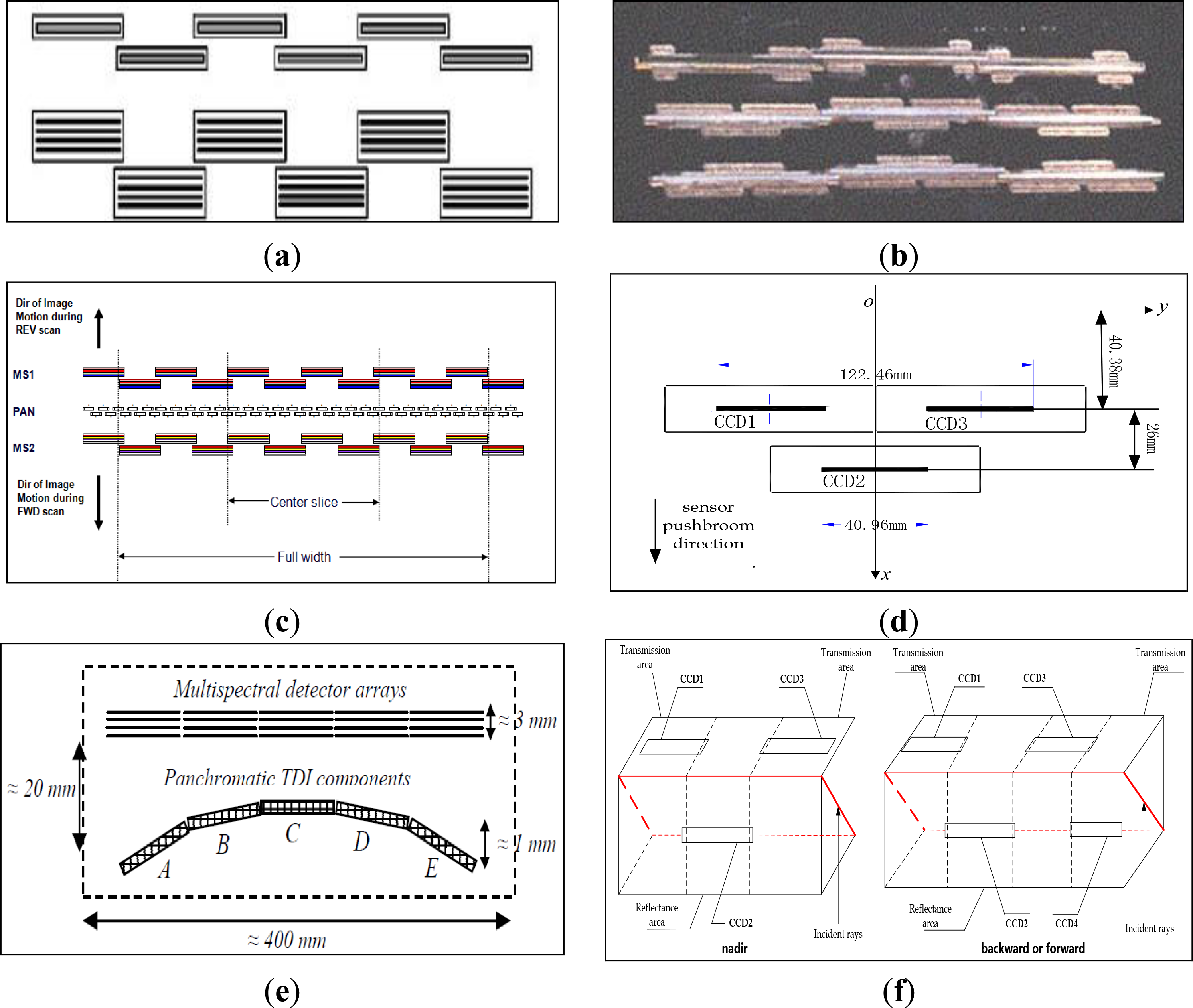
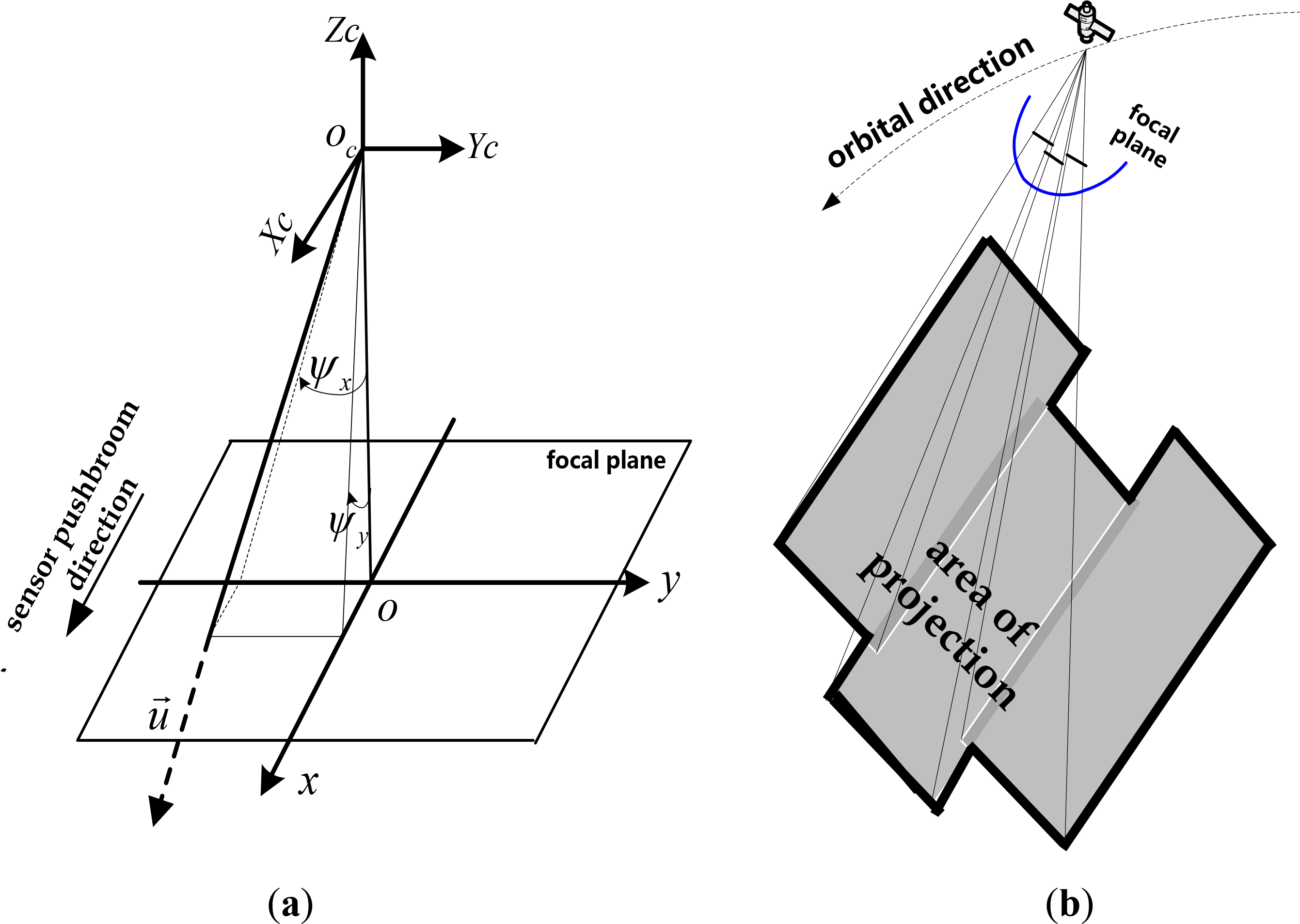
2. Geometric Sensor Model of Spaceborne TDI CCD Images
3. Inner FoV Stitching of TDI CCD Images Based on Sensor Geometry and Projection Plane in Object Space
3.1. Principle
3.2. Analysis of Error Sources
3.2.1. Inconsistent Geometric Accuracy of Adjacent Sub-Images
3.2.2. Height Difference between the Actual Ground Surface and the Projection Plane
3.3. Workflow
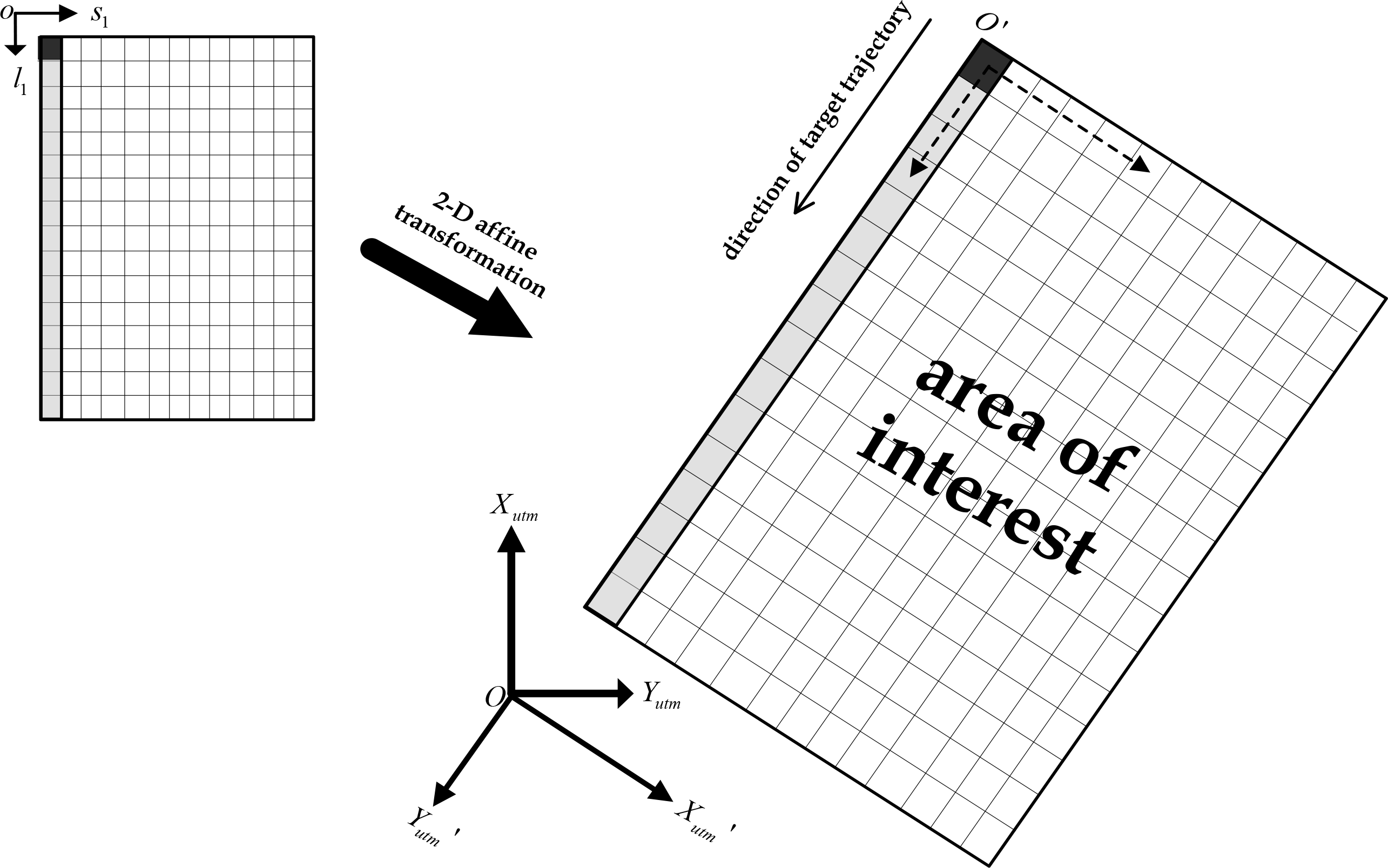
3.3.1. Deciding the Coverage of a Stitched Image on Projection Plane
- (1)
- Define the object-space projection plane in UTM coordinates system in average elevation H (an altitude value relative to the WGS84 ellipsoid). As illustrated in Figure 6, supposing O-XutmYutm represents the UTM coordinates system, which is a left-handed coordinate system whose Xutm axis coincides with the projection line of central meridian, and Yutm axis coincides with the projection line of equator and pointing in the due-east direction;
- (2)
- Choose the pixels at the two ends of the first column of the original image, and decide the positions of their ground points on projection plane by Equations (6), (9) and (10), and then the line connecting the two projective points thus could define the direction of target trajectory on projection plane;
- (3)
- Suppose O-Xutm′Yutm′ is a left-handed coordinate system sharing the same origin as that of, O-XutmYutm and with its Yutm′ axis pointing in the direction of target trajectory; if (Xutm Yutm)T denote the UTM coordinates of a certain point on projection plane, then the corresponding coordinates in O-Xutm′Yutm′ can be thus obtained by Equation (12), where R is the 2-D rotation matrix derived from direction of target trajectory;
- (4)
- Find the coverage of the original image, i.e., the area of projection (AOP), by Equations (6), (9) and (10), and then the ground cover of a stitched image, i.e., AOI, is decided by the minimum rectangular region enveloping AOP, in which the boundaries of AOI are parallel and perpendicular to the line direction of target trajectory.
3.3.2. Establishing the Relation between Pixels of a Stitched Image and Grid Units of AOI
- (1)
- Segment AOI into regular grid units with uniform size almost identical with ground sample distance (GSD) of the original image, and then the grid units are associated with pixels of stitched image one by one. That is, the number of image rows and columns are the same as the number of grid units along and across the direction of target trajectory, respectively;
- (2)
- Suppose (s1, l1)T are pixel coordinates of a stitched image, k is the size of each grid unit, i.e., the scaling parameter, O′ is the grid unit at the upper left corner of AOI, (dX, dY)T are the translation parameters which are equal to the coordinates of O′ in O-Xutm′Yutm′, and then there is
3.3.3. Perform Image Resampling to Generate a Stitched Image
3.3.4. Establishing the Geometric Model of a Stitched Image
- (1)
- Let (s1, l1)T be the pixel coordinates of the stitched image, the ground coordinates of corresponding gird unit that represented as (Xutm, Yutm)T can be determined by Equation (14);
- (2)
- Perform a back-projection calculation with Equations (7), (8) and (11), to find its position on the origial image, having pixel coordinates represented as so, lo)T;
- (3)
- In regard to (so, lo)T, when the altitude value is assigned as hei, the ground point coordinates expressed as (lat, lon, hei)T is determined using Equations (6) and (9).
- (4)
- Set up the virtual control points in object space by the strict geometric model, and calculate the coefficients of RFM by least-square adjustment [14,27,32]; hence, the RFM in the form of (s1, l1)T = F′(lat, lon, hei)T is established; F′ represents the RFM-based backward coordinates transformation, from the geodetic coordinates in object space to the pixel coordinates of a stitched image correspondingly.
4. Experiment Data and Result Analysis
4.1. Data Description
4.2. Experimental Results and Analysis
4.2.1. Evaluation of the Stitching Precision
4.2.2. Geometric Quality Assessment of the Stitched Images
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, B.X. Characteristics and main specifications of IKONOS and QuickBird2 satellite camera—Some points for developing such like satellite camera. Spacecr. Recover. Remote Sens 2002, 23, 14–16. [Google Scholar]
- Updike, T.; Comp, C. Radiometric Use of WorldView-2 Imagery, Technical Note (2010), DigitalGlobe, 1601 Dry Creek Drive Suite 260 Longmont, CO, USA, 80503. Available online: http://www.digitalglobe.com/resources/technical-information/ (accessed on 28 February 2014).
- Jacobsen, K. Calibration of Optical Satellite Sensors. Available online: http://www.isprs.org/proceedings/2006/euroCOW06/euroCOW06_files/papers/CalSatJac_Jacobsen.pdf (accessed on 28 February 2014).
- Materne, A.; Bardoux, A.; Geoffray, H.; Tournier, T.; Kubik, P.; Morris, D. Backthinned TDI CCD image sensor design and performance for the Pleiades high resolution earth observation satellites. Proceedings of the 6th International Conference on Space Optics, Noordwijk, The Netherlands, 27–30 June 2006.
- Feng, Z.K.; Shi, D.; Chen, W.X.; Luo, A.R. The progress of French remote sensing satellite—From SPOT toward Pleiades. Remote Sens. Inf 2007, 4, 89–92. [Google Scholar]
- Lussy, F.D.; Philippe, K.; Daniel, G.; Véronique, P. Pleiades-HR Image System Products and Quality Pleiades-HR Image System Products and Geometric Accuracy. Available Online: http://www.isprs.org/proceedings/2005/hannover05/paper/075-delussy.pdf (accessed on 28 February 2014).
- Li, D.R. China’s first civilian three-line-array stereo mapping satellite ZY-3. Acta Geod. Cartogr. Sin 2012, 41, 317–322. [Google Scholar]
- Tang, X.M.; Zhang, G.; Zhu, X.Y.; Pan, H.B.; Jiang, Y.H.; Zhou, P.; Wang, X. Triple linear-array imaging geometry model of ZIYuan-3 surveying satellite and its validation. Int. J. Image Data Fusion 2013, 41, 33–51. [Google Scholar]
- Hu, F.; Wang, M.; Jin, S.Y. An algorithm for mosaicking non-collinear TDI CCD images based on reference plane in object-space. Proceedings of the ISDE6, Beijing, China, 9 September 2009.
- Zhang, S.J.; Jin, S.Y. In-orbit calibration method based on empirical model for non-collinear TDI CCD camera. Int. J. Comput. Sci. Issues 2013, 10, 1694–0814. [Google Scholar]
- Yang, B.; Wang, M. On-orbit geometric calibration method of ZY1–02C panchromatic camera. J. Remote Sens 2013, 17, 1175–1190. [Google Scholar]
- Hu, F. Research on Inner FOV Stitching Theories and Algorithms for Sub-Images of Three Non-collinear TDI CCD Chips.
- Long, X.X.; Wang, X.Y.; Zhong, H.M. Analysis of image quality and processing method of a space-borne focal plane view splicing TDI CCD camera. Sci. China Inf. Sci 2011, 41, 19–31. [Google Scholar]
- Yang, X.H. Accuracy of rational function approximation in photogrammetry. Int. Arch. Photogramm. Remote Sens 2000, 33, 146–156. [Google Scholar]
- Zhang, G.; Liu, B; Jiang, W.S. Inner FOV stitching algorithm of spaceborne optical sensor based on the virtual CCD line. J. Image Graphics 2012, 17, 696–701. [Google Scholar]
- Pan, H.B.; Zhang, G.; Tang, X.M.; Zhou, P.; Jiang, Y.H.; Zhu, X.Y.; Jiang, W.S.; Xu, M.Z.; Li, D.R. The geometrical model of sensor corrected products for ZY-3 satellite. Acta Geod. Cartogr. Sin 2013, 42, 516–522. [Google Scholar]
- Li, S.W.; Liu, T.J.; Wang, H.Q. Image mosaic for TDI CCD push-broom camera image based on image matching. Remote Sens. Technol. Appl 2009, 24, 374–378. [Google Scholar]
- Lu, J.B. Automatic Mosaic Method of Large Field View and Multi-Channel Remote Sensing Images of TDICCD Cameras.
- Meng, W.C.; Zhu, S.L.; Zhu, B.S.; Bian, S.J. The research of TDI-CCDs imagery stitching using information mending algorithm. Proc. SPIE 2013, 89081C. [Google Scholar] [CrossRef]
- Poli, D.; Toutin, T. Review of developments in geometric modeling for high resolution satellite pushbroom sensors. Photogramm. Record Spec. Issue 2012, 27, 58–73. [Google Scholar]
- Toutin, T. Review article: Geometric processing of remote sensing images: Models, algorithms and methods. Int. J. Remote Sens 2004, 25, 1893–924. [Google Scholar]
- Wolf, P.R.; Dewitt, B.A. Principles of Photography and Imaging (Chapter2). In Elements of Photogrammetry with Applications in GIS, 3rd ed.; McGraw-Hill: Toronto, ON, Canada, 2000; p. 608. [Google Scholar]
- Weser, T.; Rottensteiner, F.; Willneff, J.; Fraser, C. A generic pushbroom sensor model for high-resolution satellite imagery applied to SPOT5, Quickbird and ALOS data sets. Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Hannover, Germany, 29 May–1 June 2007.
- Yamakawa, T.; Fraser, C.S. The Affine projection model for sensor orientation: Experiences with high-resolution satellite imagery. Int. Arch. Photogramm. Remote Sens 2004, 35, 142–147. [Google Scholar]
- Li, D.R; Wang, M. On-orbit geometric calibration and accuracy assessment of ZY-3. Spacecr. Recover. Remote Sens 2012, 33, 1–6. [Google Scholar]
- Wang, M.; Yang, B.; Hu, F.; Zang, Z. On-orbit geometric calibration model and its applications for high-resolution optical satellite imagery. Remote Sens. 2014, 6, 4391–4408. [Google Scholar]
- Zhang, G. Rectification for High Resolution Remote Sensing Image Under Lack of Ground Control Points.
- Zhang, C.S.; Fraser, C.S.; Liu, S.J. Interior orientation error modeling and correction for precise georeferencing of satellite imagery. Proceedings of the 2012 XXII ISPRS Congress International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, VIC, Australia, 25 August–1 September 2012.
- Mulawa, D. On-orbit geometric calibration of the orbview-3 high resolution imaging satellite. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2004, 35, 1–6. [Google Scholar]
- Kocaman, S.; Gruen, A. Orientation and self-calibration of ALOS PRISM imagery. Photogramm. Rec 2008, 23, 323–340. [Google Scholar]
- Delussy, F.; Greslou, D.; Dechoz, C.; Amberg, V.; Delvit, J.; Lebegue, L.; Blanchet, G.; Fourest, S. PLEIADES HR in-flight geometric calibration: Location and mapping of the focal plane. Proceedings of the 2012 XXII ISPRS Congress International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, VIC, Australia, 25 August–1 September 2012.
- Tao, C.V.; Hu, Y. A comprehensive study of the rational function model for photogrammetric processing. Photogramm. Eng. Remote Sens 2001, 67, 1347–1357. [Google Scholar]
- Fraser, C.S.; Hanley, H.B. Bias-compensated RFMs for sensor orientation of high resolution satellite imagery. Photogramm. Eng. Remote Sens 2005, 71, 909–915. [Google Scholar]




| Camera | ZY-3 Triple Linear-Array | ZY-1 02C HR1/HR2 |
|---|---|---|
| Pixel Size (μm) | Nadir: 7 | 10 |
| Forward: 10 | ||
| Backward: 10 | ||
| Focal Length (mm) | 1700 | 3300 |
| Ground Sample Distance (m) | Nadir: 2.1 | 2.36 |
| Forward: 3.5 | ||
| Backward: 3.5 | ||
| No. of CCD detectors | Nadir: 8192 × 3 | 4096 × 3 |
| Forward: 4096 × 4 | ||
| Backward: 4096 × 4 | ||
| Swath Width (km) | Nadir: 51 | 27 |
| Forward: 52 | ||
| Backward: 52 | ||
| Image Data 1 | Image Data 2 | Image Data 3 | Image Data 4 | ||
|---|---|---|---|---|---|
| Sensor Name | ZY-3 Triple linear-array | ZY-1 02C HR1/HR2 | |||
| Image Size (Pixels) | Nadir: 24,576 × 24,576 (8192 × 3) | 17,575 × 12,288 (4096 × 3) | |||
| Forward: 16,384 × 16,384 (4096 × 4) | |||||
| Backward: 16,384 × 16,384 (4096 × 4) | |||||
| Location | Dengfeng, Henan, China | Anyang, Henan, China | Dengfeng, Henan, China | Anyang, Henan, China | |
| Range | 51 km × 51 km | 51 km × 51 km | 27 km × 27 km | 27 km × 27 km | |
| Acquisition Date | 23 March 2012 | 4 June 2013 | 7 April 2013 | 15 March 2013 | |
| Terrain Type | Mountainous and hilly | Plain | Mountainous and hilly | Plain | |
| Mean altitude: 340 m | Mean altitude: 340 m | ||||
| Max. altitude: 1450 m | Max. altitude: 1450 m | ||||
| Reference Data | DOM | GSD: 1 m | GSD: 1 m | GSD: 1 m | GSD: 1 m |
| Planimetric accuracy | Planimetric accuracy | Planimetric accuracy | Planimetric accuracy | ||
| (RMSE): 1 m | (RMSE): 0.5 m | (RMSE): 1 m | (RMSE): 0.5 m | ||
| DEM | GSD: 5 m | GSD: 2 m | GSD: 5 m | GSD: 2 m | |
| Height accuracy | Height accuracy | Height accuracy | Height accuracy | ||
| (RMSE): 2 m | (RMSE):0.5 m | (RMSE): 2 m | (RMSE): 0.5 m | ||
| Row | Column | ||||
|---|---|---|---|---|---|
| Max. Error | StdDev. Error | Max. Error | StdDev. Error | ||
| Image Data 1 | ZY-3 Forward | 0.000311 | 0.000081 | 0.010009 | 0.001687 |
| ZY-3 Nadir | 0.000274 | 0.000128 | 0.000306 | 0.000151 | |
| ZY-3 Backward | 0.000323 | 0.000081 | 0.006011 | 0.001076 | |
| Image Data 3 | ZY-1 02C HR1 | 0.000255 | 0.000114 | 0.000285 | 0.000134 |
| Geometric Accuracy of Stitched Images Generated by Our Proposed Method | |||||
| Image Data | Sensor Name | No. of Control Points for RFM Error Compensation | No. of Check Points | StdDev. Error | |
| Cross-Track (Row) | Along-Track (Column) | ||||
| 1 | ZY-3 Forward | 0 | 165 | 0.54 | 1.87 |
| 85 | 80 | 0.53 | 0.48 | ||
| ZY-3 Nadir | 0 | 157 | 1.37 | 1.19 | |
| 74 | 83 | 1.39 | 0.68 | ||
| ZY-3 Backward | 0 | 170 | 0.49 | 0.46 | |
| 87 | 83 | 0.47 | 0.45 | ||
| 2 | ZY-3 Forward | 0 | 110 | 0.63 | 0.86 |
| 50 | 55 | 0.61 | 0.86 | ||
| ZY-3 Nadir | 0 | 83 | 1.54 | 1.40 | |
| 44 | 39 | 0.60 | 1.02 | ||
| ZY-3 Backward | 0 | 56 | 0.55 | 0.78 | |
| 32 | 24 | 0.52 | 0.80 | ||
| 3 | ZY1-02C HR1 | 0 | 209 | 3.75 | 2.17 |
| 102 | 107 | 3.71 | 2.09 | ||
| 4 | ZY1-02C HR2 | 0 | 52 | 1.46 | 2.56 |
| 27 | 25 | 0.85 | 0.78 | ||
| Geometric Accuracy of Stitched Images Generated by the Virtual CCD Line based Method | |||||
| Image Data | Sensor Name | No. of Control Points for RFM Error Compensation | No. of Check Points | StdDev. Error | |
| Cross-Track (Row) | Along-Track (Column) | ||||
| 1 | ZY-3 Forward | 0 | 146 | 0.56 | 0.50 |
| 70 | 76 | 0.55 | 0.50 | ||
| ZY-3 Nadir | 0 | 172 | 0.66 | 0.63 | |
| 90 | 82 | 0.59 | 0.62 | ||
| ZY-3 Backward | 0 | 142 | 0.49 | 0.58 | |
| 60 | 82 | 0.48 | 0.58 | ||
| 2 | ZY-3 Forward | 0 | 105 | 0.63 | 0.83 |
| 50 | 55 | 0.63 | 0.82 | ||
| ZY-3 Nadir | 0 | 89 | 0.76 | 1.07 | |
| 40 | 49 | 0.76 | 1.06 | ||
| ZY-3 Backward | 0 | 115 | 0.78 | 1.70 | |
| 60 | 55 | 0.71 | 1.19 | ||
| 3 | ZY1-02C HR1 | 0 | 197 | 3.84 | 2.02 |
| 90 | 107 | 3.84 | 1.99 | ||
| 4 | ZY1-02C HR2 | 0 | 41 | 3.52 | 2.91 |
| 20 | 21 | 1.71 | 1.27 | ||
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tang, X.; Hu, F.; Wang, M.; Pan, J.; Jin, S.; Lu, G. Inner FoV Stitching of Spaceborne TDI CCD Images Based on Sensor Geometry and Projection Plane in Object Space. Remote Sens. 2014, 6, 6386-6406. https://doi.org/10.3390/rs6076386
Tang X, Hu F, Wang M, Pan J, Jin S, Lu G. Inner FoV Stitching of Spaceborne TDI CCD Images Based on Sensor Geometry and Projection Plane in Object Space. Remote Sensing. 2014; 6(7):6386-6406. https://doi.org/10.3390/rs6076386
Chicago/Turabian StyleTang, Xinming, Fen Hu, Mi Wang, Jun Pan, Shuying Jin, and Gang Lu. 2014. "Inner FoV Stitching of Spaceborne TDI CCD Images Based on Sensor Geometry and Projection Plane in Object Space" Remote Sensing 6, no. 7: 6386-6406. https://doi.org/10.3390/rs6076386






