Numerical Simulation of Whitecaps and Foam Effects on Satellite Altimeter Response
Abstract
: The determination of wave height by active satellite remote sensing, be it Synthetic Aperture Radar (SAR) or altimeter, has been a common practice for many years and is now imbedded on many meteorological and oceanographic forecasting systems. Despite their differences, all active sensors are based on the measurement of the Normalized Radar Cross Section (NRCS) of the sea surface, i.e., of its backscattering properties, which in turn depend on the wind velocity. At small and moderate wind speeds, the main mechanism is the formation of ripples (small scale waves); at higher speeds, whitecaps appear, and foam starts playing an essential role in determining NRCS. In the past few years much research effort has gone into clarifying these effects, thus improving the general quality of the measurements. Little work, however, has been devoted so far to consider the vertical spatial variation of backscattering properties, and in particular of the floating foam, over the sea surface. As it is shown in the present paper, the shape of the backscattered electromagnetic impulse in radar altimeters depends on the spatial distribution of foam over the water height in the sea waves and therefore the performance of these instruments in determining Significant Wave Height (Hs) and Sea Surface Level (SSL) is strongly affected by this effect. This work tackles these problems by making use of specially implemented numerical algorithms to simulate both sea surface processes and radar altimeter techniques. Results show that some causes of errors can be better understood and eventually corrected: in particular, the paper deals with the reconstruction of the electromagnetic Sea State Bias (SSB), the well known altimeter ranging error due to the presence of ocean waves on the sea surface.1. Introduction
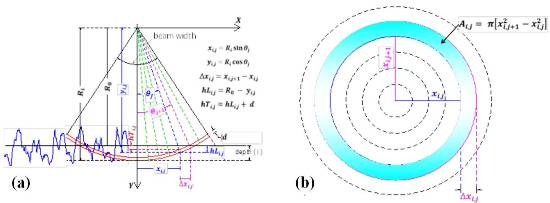
Radar altimeters such as fitted in many satellite constellations (i.e., TOPEX/Poseidon, Jason-1 and -2, ERS-1 and 2, Envisat, CryoSat-2, SARAL) have carried out systematic measurements of SSL (Sea Surface Level) and Hs (Significant Wave Height) over the oceans for many years. The theory, as well as the practice of radar altimeter is fully consolidated, and it is reported in many classical works. Briefly summarizing, an electromagnetic impulse of very short duration (typical effective pulse duration after pulse compression technique is about 3 n∙s) is sent from the antenna to the sea surface and the reflected signal (waveform) after preliminary processing to correct errors of electromagnetic origin, is analyzed to extract the required parameters. A schematic waveform is illustrated in Figure 1. The algorithms and the values of the gates follow Chelton et al. [1].
Total reflected energy (segment P), integrated over the whole radar footprint is strictly correlated to the NRCS (Normalized Radar Cross Section, in the following σ0) and it provides an estimate of the wind velocity, since both wind induced ripples and sea foam decrease the local surface reflectivity.
Calibration of the link between σ0 and wind speed has been carried out by many researchers with different techniques over many years of data so that various empirical or semi-empirical correlation functions are now available. A description of radar techniques is reported in [2].
Signal processing also provides the delay of the central point (epoch at middle height in Figure 1) and the curve slope: these two measures are related to two extremely important geophysical parameters, respectively the Mean Sea Level (MSL), i.e., the long term average of SSL, and Hs [3–5]. The retrieval of those parameters is far from trivial and implies many aspects of the physical processes of the sea surface and of its modeling techniques. Conceptually at least, most techniques to extract Hs from radar altimeters data originate from the so called Brown’s model and successive variants. According to such models, the only relevant information on the sea state is the statistical distribution P(η), i.e., the percentage of the area at height η where a free surface is present water, since the local backscattering coefficient σ is assumed to be uniformly distributed over the wave surface.
Under such assumptions, SSL derives immediately from the position of the P(η) mean, i.e., “epoch at mid-height” of the signal in Figure 1. A normal distribution is the most common hypothesis for P(η), but skewed distributions [6] have also been considered to account for the difference between crest and trough heights.
Things become more complicated if the effects of floating foam are taken into consideration. The mechanics of foam over the sea surface is still an active subject of research, and the terminology is not totally uniform. Following, for instance, Holthuijsen et al. [7], we define as “whitecap” the breaking crest of a wave (Monahan’s “A” stage), “floating foam” the bubble layer which keeps floating after the breaking has terminated (Monahan’s “B” stage) and “foam” for the two effects together. We do not take into account the ocean-atmosphere interface made up of foam, spray and bubble emulsion, sometimes called “spray and foam” or “foam”, which forms for very high winds (>30 m/s).
Foam backscatters electromagnetic waves very differently from blue water, and in particular the reflection at nearly-vertical incidence angle, as it occurs in altimeters, is much lower. Floating foam is far from being uniformly distributed over the wave height, and the shape of the waveform is no longer related in a simple way to P(η); a more accurate spatial description of the wave field processes is therefore needed. Neglecting this aspect necessarily implies that errors will arise in the estimation of both the Hs and the SSL; this latter, in particular is very important because the precision needed for the geophysical applications [8–10] of SSL—e.g., sea level rise monitoring—is very high. These effects have therefore been the object of intense research over the years: the subject was indeed considered early as by Zheng et al. [11]. Further studies were carried out more recently, to the point that the error on the altimeter Sea Level caused by the wave agitation (known as Sea State Bias, SSB) is now empirically well known.
At present, however, a full reconstruction of all the phenomena involved is still barred by the complexity of the hydrodynamic aspects which limits the applicability of analytical approaches.
2. Procedure
A numerical rather than analytical technique is certainly the best way to take into account the geometrically and physically complex problem of the spatial distribution of the backscattering coefficient over the sea surface; this comes, of course, at the price of a very heavy computational effort, which explains why only recently useful results have become available in this field. An early work along these lines was started by Pugliese Carratelli et al. [12,13]: even though the techniques were crude at the time, some results managed to reproduce a dependence of Hs on the peak spectrum period. More recent results for both altimeter and SAR data can be found in [14–16].
In the present work a more complete algorithm is used. By starting from a pseudo-random realization of the sea state water height and by adding appropriate hypotheses on the dynamics and the positions of whitecaps and foam, radio altimeter waveforms are simulated. A description is reported in Figures 2 and 3. The simulation follows in finite steps i = 1, ..., n the physical evolution in time and in elevation of the illuminated surface as the electromagnetic wave front proceeds over the altimeter footprint. Following the pseudo-code reported in Figure 3, the wave form is computed as a succession WFi of the total backscatter of single resolution steps d, at a range Ri along the nadir direction: each single WFi is the integral over the beam aperture β of the annuli defined by leading and trailing edge of each resolution step i; this requires a separate definition of σ(η, X), the average backscattering coefficient of the annulus of radius X at the local height η.
The computation of σ(η, X) function implies all the physical phenomena taking place on the surface and it is therefore critical. Assuming uniform average spatial properties, it becomes simply σ(η) and can be calculated from the description of sea surface and for each η as in Equation (1):
The example shown in this paper is an attempt to investigate into the effects of foam on such function. Fractional water covered surface P(η) as a function of local water height η can be taken to be purely Gaussian, as in Brown-like models; or it can be easily computed, as it will be shown in the following.
The evaluation of F(η) is more complex. A number of results do exist—even if they do not always agree—on the total percentage W of foam covered sea surface, from the classical work by Monahan to more recent work by Moat et al. [17]
Its distribution F(η) over the wave, however, is not known from any empirical analysis, and are estimated through an appropriate simulation procedures. In order to do so there are three aspects to consider:
the frequency and the location of foam birth (defined as “whitecaps” in the following);
the time decay of foam once it is generated (defined as “floating foam” in the following);
the movement of floating foam over the wave surface.
Ample research work has been carried out on these three aspects separately, and by appropriately making use of available results a solution can be found to the problem of defining the average F(η) position of foam for a given height over the sea level. No attempt however is made here to consider the effects of suspended water particles (“foam” or “spray”) which develops for very high wind speeds.
As for the formation of whitecaps, [18] provides a number of local parameters, and in particular it provides a “dynamic indicator” based on the value of the vertical acceleration of the surface particles. Negative (i.e., downward) values of the acceleration below a certain threshold are likely to induce wave breaking. Thus the “birth” of foam covered areas can be simulated for a given instantaneous realization of the sea surface. Pugliese Carratelli et al. [14] have successfully applied this technique to the simulation of SAR images of the sea.
After its birth, floating foam decays, and this process has also been the object of much research work; to our purposes the results are summarized as in [19] where it is assumed that foam thickness grows and then decays according to two characteristic times τ* and τ′ (Equation (2) and Figure 4). This approach recalls Monahan distinction between “A” and “B” foam.
For the purpose of present work the formation time of whitecaps τ* is negligible [20], so the only parameter left is the decay time τ′.
A connection between the thickness of the foam layer and the microwave properties is provided in [11,21]. According to these results, it can be assumed that σf is equal to a constant, and very low, backscattering value; as it is very well known for very strong winds, when the sea surface is entirely covered by foam, the vertical average backscattering coefficient reduces to a very low value, which obviously coincides with the local backscattering of the foam.
The next step is the calculation of the vertical distribution σf(η, X) of the local vertical backscattering coefficient; as stated above, σf(η, X) turns out to be a simple σf(η) if average horizontal uniformity is assumed.
The calculations are carried out through a pseudo-code outlined in Figure 5.
Sea surface realizations η(X, t) are generated by Inverse Fast Fourier Transform (IFFT) of directional JONSWAP sea spectra and random phase values; particle velocity and acceleration components are similarly computed according to a procedure which has been developed and tested in [13], and reported for example in [22].
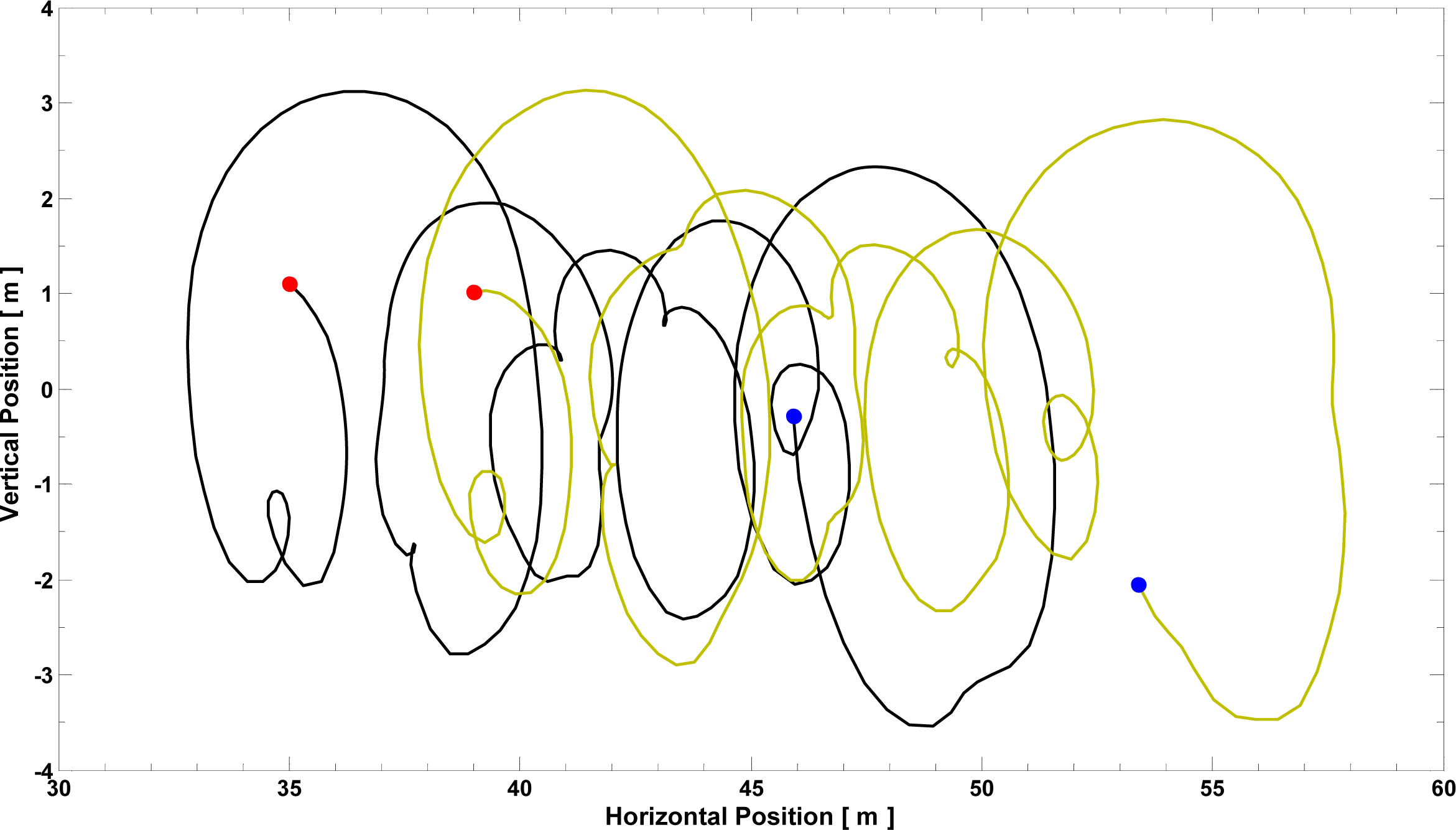
The trajectories of foam particles are then calculated from their birth to their disappearance by considering the surface velocity values and the time evolution laws described above. Figure 6 yields a graphical example.
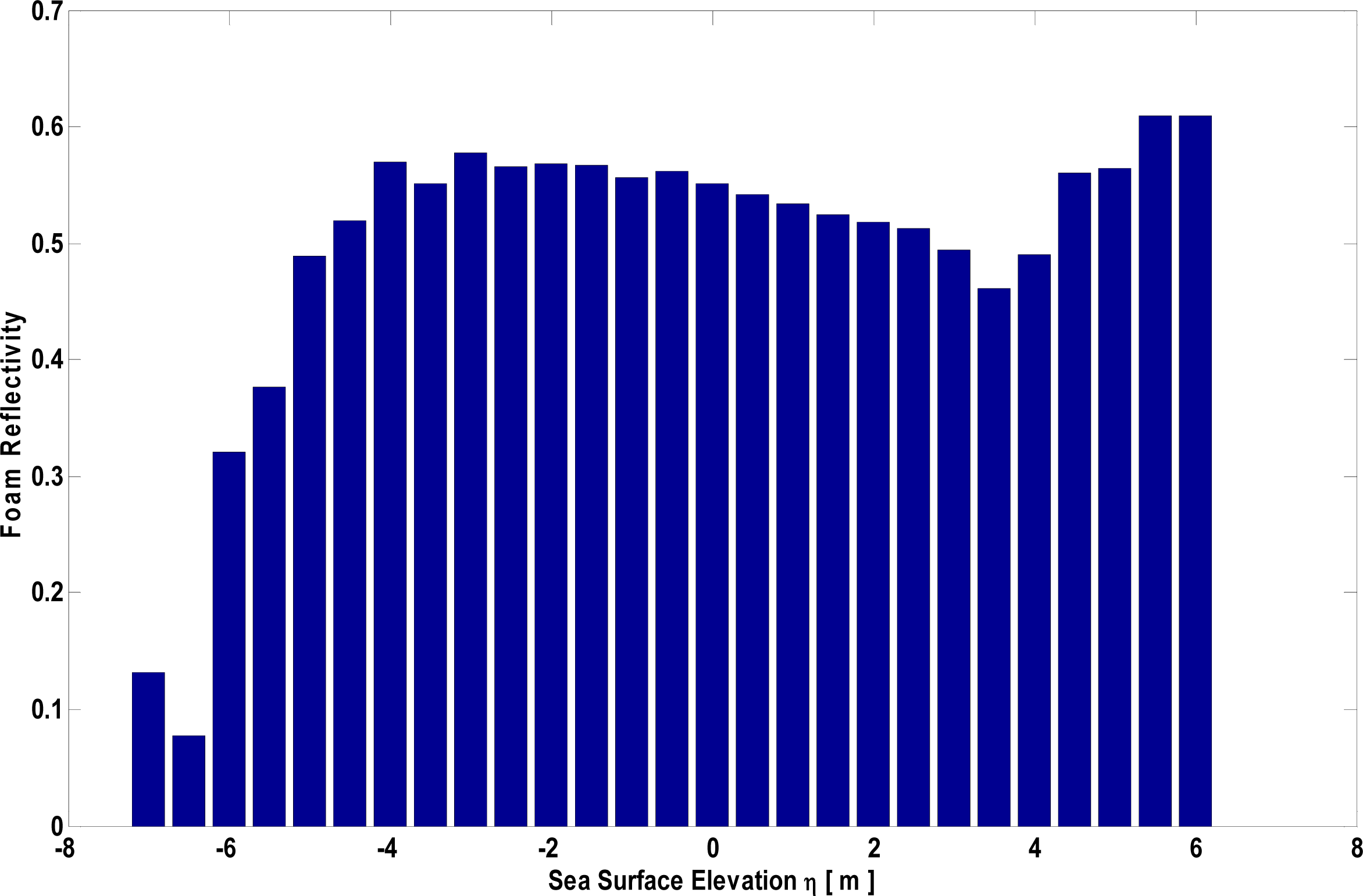
σf(η) is thus numerically computed for each η by making use of Equation (1); a typical result is shown in Figure 7.
Such functions are in turn used in the procedure outlined in Figure 2. The required parameters, i.e., Hs and SSL are then computed from the simulated waveform WFi through the standard algorithms.
3. Results
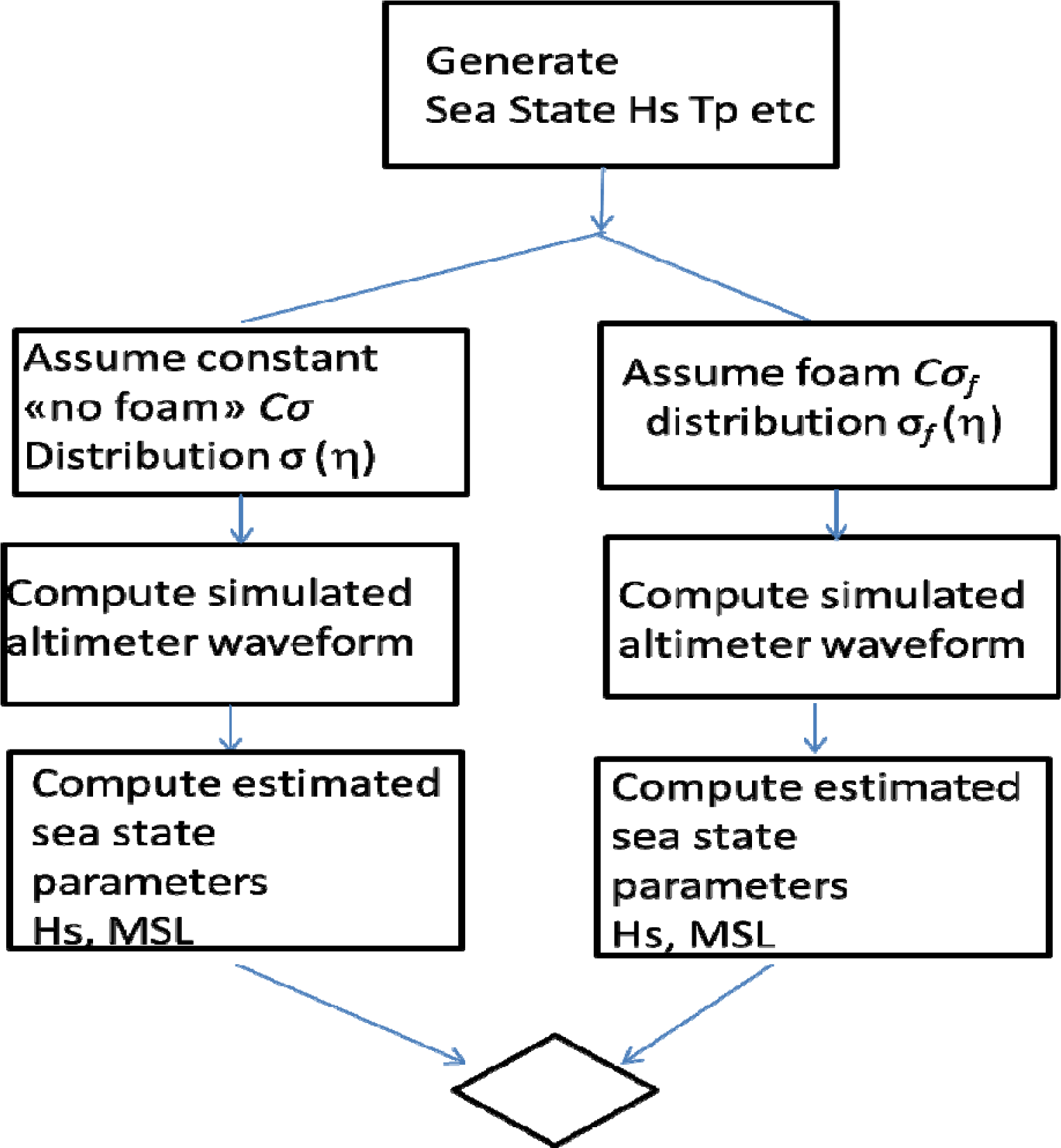
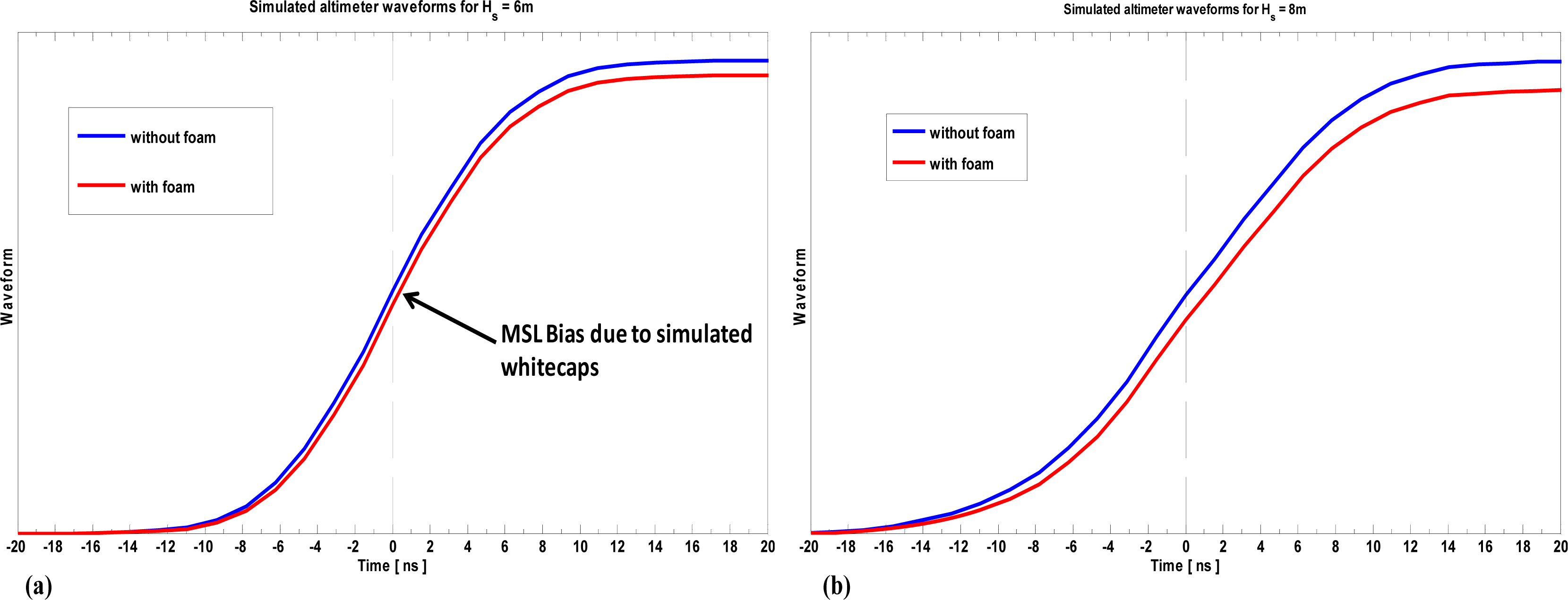
As shown above, it is possible to simulate the effects of foam spatial distribution on the sea state parameters. According to the diagram outlined in Figure 8, waveforms are calculated in two different ways: by taking the foam effect into account, or by neglecting it.
Applying the standard procedure to extract the sea parameters from the waveforms, two different set of values are thus obtained, one of which represents the conventional “constant backscattering” point of view, the other—presumably—more realistic. The best candidate for this kind of test is SSL, since the accuracy required for this parameter is very high: Figure 9 shows some results. The waveforms for a given sea state (Hs) is calculated by taking into account the presence of foam (red line) or by ignoring it (F(η) = 0 in Equation (1), blue line). Neglecting foam effect—as it is generally assumed—provides a SSL lower than the “real” one.
This difference is one of the components of the so-called Sea State Bias (SSB) [1,23], i.e., the error in the SSL evaluation induced by the wave agitation. The following Table 1 and Figure 10 illustrate the trend of Foam Induced Sea Surface Bias (FISSB) as function of Hs and wind speed U10.
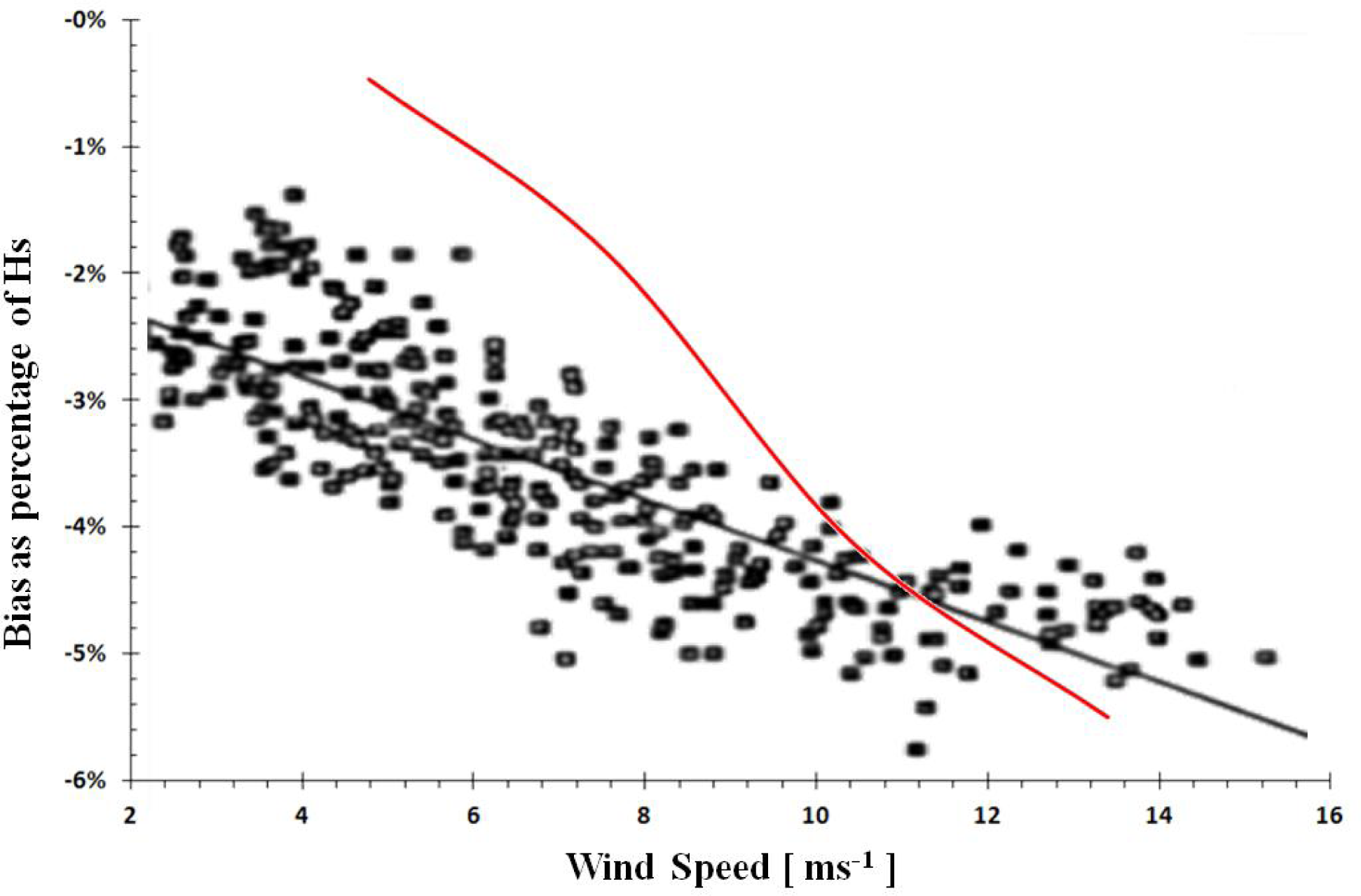
Even though a proper calibration of the procedure cannot be carried out since no universally valid procedure to model SSB exists to date, it makes however sense to compare the results against a classical set of experimental data such as those provided by Melville et al. [24] reported by Gomminger et al. [23]. Melville’s SSB percentage values are given as a function of wind speed for much longer fetches than those considered by us; his data were therefore transformed into SSW by assuming a 1000 km fetch and then compared with the previous results (Figure 11).
The order of magnitude is well reproduced, and what is more important FISSB is systematically lower—for low winds and wave heights—than the measured one, as it could be expected since other mechanisms which contribute to SSB and in particular the non-symmetry of water heights has not been taken onto account, since the surface model used here is inherently Gaussian. The difference tends to disappear for very strong seas and wind, but the dispersion of data and the various uncertainties of the procedure make the comparison arguable beyond a certain point. A consistent explanation of the effects of uneven distribution of foam over the wave has however been provided, and it has been shown to be a major effect.
4. Conclusions
A numerical flexible and comprehensive model has been presented to simulate the formation of the waveforms of satellite altimeters by taking into account the non-uniform distribution of the backscattering coefficient over the waves. The algorithm has been applied successfully to simulate the influence of whitecaps and floating foam, and results show that part of the SSB can be consistently attributed to these effects.
The flexible numerical model presented here is already useful to improve the understanding of SSB, and might eventually prove also a tool to investigate into the mechanism of whitecaps formation and floating foam movement. Future developments should involve the introduction of a non-linear sea surface model to correctly represent wave skewness. Simulated results should be compared with available altimeter wind speed calibration curves and—when available—with altimeter waveform data.
Acknowledgments
Work carried out within ESA-ESRIN Project CAT-1 No 1172: “Remote sensing of wave transformation”. The contribution of CUGRI (University Centre for Research on Major Hazard) is also gratefully acknowledged.
Author Contributions
The main ideas leading to this work were equally due to the three authors. F. Reale carried out most of the computations.
Conflicts of Interest
The Authors declare no conflict of interest.
References
- Chelton, D.B.; Ries, J.C.; Haines, B.J.; Fu, L.-L.; Callahan, P.S. Satellite Altimetry. In Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications; Fu, L.-L., Cazenave, A., Eds.; Academic Press: San Diego, CA, USA, 2001; pp. 1–131. [Google Scholar]
- Benveniste, J.; Rosmorduc, V.; Niemeijer, S.; Picot, N. Basic Radar Altimetry Toolbox. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 6–11 July 2008; III, pp. 895–898.
- Ocampo-Torres, F.J. On the homogeneity of the wave field in coastal areas as determined from ERS-2 and RADARSAT Synthetic Aperture Radar images of the ocean surface. Sci. Mar 2001, 65, 215–228. [Google Scholar]
- Reale, F.; Dentale, F.; Pugliese Carratelli, E.; Torrisi, L. Remote sensing of small-scale storm variations in coastal seas. J. Coastal. Res 2013. doi: http://dx.doi.org/10.2112/JCOASTRES-D-12-00239.1. [Google Scholar]
- Feng, X.; Tsimplis, M.N.; Quartly, G.D.; Yelland, M.J. Wave height analysis from 10 years of observations in the Norwegian Sea. Cont. Shelf Res 2014, 72, 47–56. [Google Scholar]
- Gómez-Enri, J.; Vignudelli, S.; Quartly, G.D.; Gommenginger, C.P.; Cipollini, P.; Challenor, P.G.; Benveniste, J. Modeling ENVISAT RA-2 waveforms in the coastal zone: Case study of calm water contamination. IEEE Geosci. Remote Sens 2010, 7, 474–478. [Google Scholar]
- Holthuijsen, L.H.; Powell, M.D.; Pietrzak, J.D. Wind and waves in extreme hurricanes. J. Geophys. Res 2012, 117, C09003, doi: 10.1029.2012JC007983. [Google Scholar]
- Klemas, V. Remote sensing of coastal and ocean currents: An overview. J. Coastal Res 2012, 28, 576–586. [Google Scholar]
- Klemas, V. The role of remote sensing in predicting and determining coastal storm impacts. J. Coastal Res 2009, 25, 1264–1275. [Google Scholar]
- Rémy, F.; Parouty, S. Antarctic ice sheet and radar altimetry: A review. Remote Sens 2009, 1, 1212–1239. [Google Scholar]
- Zheng, Q.A.; Klemas, V.; Hayne, G.S.; Huang, N.E. The effect of oceanic whitecaps and foams on pulse-limited radar altimeters. J. Geophys. Res 1983, 88, 2571–2578. [Google Scholar]
- Pugliese Carratelli, E.; Dentale, F.; Reale, F. Numerical Pseudo-Random Simulation of SAR Sea and Wind Response. In Advances in SAR Oceanography from ENVISAT and ERS Missions, Proceedings of the SEASAR 2006 (ESA SP-613), Frascati, Italy, 23–26 January 2006; Lacoste, H., Ed.; ESA Publications Division: Noordwijk, The Netherlands, 2006. [Google Scholar]
- Pugliese Carratelli, E.; Dentale, F.; Reale, F. Reconstruction of SAR Wave Image Effects through Pseudo Random Simulation. Proceedings of the Envisat Symposium 2007 (ESA SP-636), Montreux, Switzerland, 23–27 April 2007; Lacoste, H., Ouwehand, L., Eds.; ESA Communication Production Office: Noordwijk, The Netherlands, 2007. [Google Scholar]
- Pugliese Carratelli, E.; Chapron, B.; Dentale, F.; Reale, F. Simulating the Influence of Wave Whitecaps on SAR Images. Proceedings of the SeaSAR 2008 (ESA SP-656), Frascati Italy, 21–25 January 2008; Lacoste, H., Ouwehand, L., Eds.; ESA Communication Production Office: Noordwijk, The Netherlands, 2008. [Google Scholar]
- Clarizia, M.P.; Gommenginger, C.; Di Bisceglie, M.; Galdi, C.; Srokosz, M.A. Simulation of L-band bistatic returns from the ocean surface: A facet approach with application to ocean GNSS reflectometry. IEEE Trans. Geosci. Remote Sens 2012, 50, 960–971. [Google Scholar]
- Clarizia, M.P.; Di Bisceglie, M.; Galdi, C.; Gommenginger, C.; Srokosz, M. Simulation of GNSS-R Returns for Delay-Doppler Analysis of the Ocean Surface. Proceedings of IEEE International Geoscience and Remote Sensing Symposium(IGARSS 2009), Cape Town, South Africa, 12–17 July 2009.
- Moat, B.I.; Yelland, M.J.; Pascal, R.W. Oceanic Whitecap Coverage Measured during UK-SOLAS Cruises. Proceedings of 16th Conference on Air-Sea Interaction, Phoenix, AZ, USA, 11–15 January 2009.
- Oh, S.-H.; Mizutani, N.; Suh, K.-D.; Hashimoto, N. Experimental investigation of breaking criteria of deepwater wind waves under strong wind action. Appl. Ocean Res 2005, 27, 235–250. [Google Scholar]
- Reul, N.; Chapron, B. A model of sea-foam thickness distribution for passive microwave remote sensing applications. J. Geophys. Res 2003, 108, 3321. [Google Scholar] [CrossRef]
- Anguelova, M.D.; Gaiser, P.W. Dielectric and radiative properties of sea foam at microwave frequencies: Conceptual understanding of foam emissivity. Remote Sens 2012, 4, 1162–1189. [Google Scholar]
- Anguelova, M.D.; Gaiser, P.W. Skin depth at microwave frequencies of sea foam layers with vertical profile of void fraction. J. Geophys. Res 2011, 116, C11002. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Hu, C.; Zheng, L. Combining numerical ocean circulation models with satellite observations in a trajectory forecast system: A rapid response to the deepwater horizon oil spill. Proc. SPIE 2011, 8030. [Google Scholar] [CrossRef]
- Gommenginger, G.P.; Srokosz, M.A. Sea State Bias—20 Years on. Proceeding of the Symposium on 15 Years of Progress in Radar Altimetry (ESA SP-614), Venice Lido, Italy, 13–18 March 2006; Danesy, D., Ed.; ESA Publications Division: Noordwijk, The Netherlands, 2006. [Google Scholar]
- Melville, W.K.; Stewart, R.H.; Keller, W.C.; Kong, J.A.; Arnold, D.V.; Jessup, A.T.; Loewen, M.R.; Slinn, A.M. Measurements of electromagnetic bias in radar altimetry. J.Geophys. Res 1991, 96, 4915–4924. [Google Scholar]






| Hs (m) | Tp (s) | U10 (m∙s−1) | Fetch (km) | W (%) | SSB (cm) | SSB as % of Hs |
|---|---|---|---|---|---|---|
| 4 | 8.84 | 11.39 | 250 | 1.65 | 19 | 0.48% |
| 6 | 10.29 | 18.00 | 250 | 6.19 | 11 | 1.83% |
| 8 | 11.47 | 24.89 | 250 | 16.17 | 33 | 4.13% |
| 10 | 12.47 | 32.00 | 250 | 34.60 | 55 | 5.50% |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Reale, F.; Dentale, F.; Carratelli, E.P. Numerical Simulation of Whitecaps and Foam Effects on Satellite Altimeter Response. Remote Sens. 2014, 6, 3681-3692. https://doi.org/10.3390/rs6053681
Reale F, Dentale F, Carratelli EP. Numerical Simulation of Whitecaps and Foam Effects on Satellite Altimeter Response. Remote Sensing. 2014; 6(5):3681-3692. https://doi.org/10.3390/rs6053681
Chicago/Turabian StyleReale, Ferdinando, Fabio Dentale, and Eugenio Pugliese Carratelli. 2014. "Numerical Simulation of Whitecaps and Foam Effects on Satellite Altimeter Response" Remote Sensing 6, no. 5: 3681-3692. https://doi.org/10.3390/rs6053681