1. Introduction
Aerosols refer to solid or liquid particulates suspended in the atmosphere. As they strongly absorb and scatter solar radiation over the ultraviolet, visible light, and infrared spectrum, they exert a significant influence on global climate and weather processes [
1,
2]. A rise in the quantity of aerosols in the atmosphere worsens air quality, which in turn, has a detrimental impact on human health [
3–
5].
Of all the factors indicative of the physical characteristics of aerosols, aerosol optical depth (AOD, a measure of the columnar extinction of solar radiation by aerosols) is an important optical parameter in estimation of aerosol concentration, evaluation of the level of atmospheric pollution, and assessment of the climate effect of aerosols. AOD can be determined using two methods, ground-based monitoring and via satellite imagery. Ground-based determination involves direct measurement using different instruments, as the Multifilter Rotating Shadowband Radiometer (MFRSR), the Lambda Instruments Corporation (LICOR) spectroradiometer, the Microtops Sun photometer, Linke-Feussner actinometers and light detection and ranging (LIDAR). Nevertheless, Cienciae Investigación Médica Estudiantil Latinoamericana (CIMEL) sunphotometer is the most employed instrument for characterizing the column integrated AOD. This method is able to yield accurate readings of aerosol, but is constrained by data availability at certain fixed positions only. Such point-specific data are unable to yield a detailed pattern of aerosol spatiotemporal distribution. By comparison, the satellite remote sensing method is able to generate results over an extensive area in real-time. The gained results can be updated periodically at a relatively short span. Such advantages make this method a vital addition to supplement ground-based measurement so as to gather accurate aerosol information effectively and quickly.
Over recent years a large number of achievements have been accomplished in retrieving AOD from satellite imagery, with many kinds of retrieval algorithms developed, such as the dark-target method [
6], the structure function method [
7,
8], polarization measurements [
9,
10], the multi-angle method [
11,
12], and the deep blue algorithm [
13]. Common to all of these methods is the complex retrieval process, but each has its own special applicability. For instance, the dark-object method is more accurate in areas of dense vegetation cover. The structure function method requires information on a clear background, and its retrieval accuracy is higher in areas of a bright ground surface.
In remote sensing characteristic indexing has been a rather simple but highly effective method of extracting information from images as the ground object of interest is likely to exhibit different spectral characteristics over different wavebands. For instance, the distinctive reflectance and absorption of vegetation, water, and built-up areas in different wavelengths has been used to derive normalized difference vegetation index (NDVI) that is able to capture vegetation distribution effectively [
14], normalized difference water index (NDWI) that is indicative of water distribution [
15], and normalized difference built-up index (NDBI) indicating the distribution of built-up areas and barren ground [
16]. The construction of these indices is underpinned by the principle of locating the most sensitive and insensitive spectral bands among all multispectral bands available [
17]. Of these two bands, the most sensitive is treated as the numerator, and the most insensitive as the denominator. Ratioing of the two bands artificially enlarges the spectral dissimilarity among all ground features drastically. Consequently, information on the target of interest is maximally enhanced on the newly derived index image while information of other background objects in the same image is suppressed simultaneously.
Apparent reflectance as recorded on satellite imagery depends on both surface and atmospheric composition. Therefore, it is possible to retrieve the physical and chemical properties of aerosols from the variation in apparent reflectance caused by aerosol backscattering. Griggs [
18] found that the amount of solar radiation vertically reflected over the ocean surface increases almost linearly with AOD. The National Oceanic and Atmospheric Administration (NOAA) started to monitor AOD over oceans in 1977 using the first visible light channel (0.63 μm) of Advanced Very High Resolution Radiometer (AVHRR). Durkee
et al. [
19] demonstrated that radiation detected in the red and near infrared wavebands of satellite imagery is correlated positively with maritime AOD. Hsu
et al. [
20] reported that the Total Ozone Mapping Spectrometer (TOMS)-derived absorbing aerosol index (difference in reflectance between the violet 340 nm and 380 nm channels) is highly consistent with the spatiotemporal pattern of AOD after analyzing the AOD data collected with a sun photometer on the ground during the burning season of bio-substances in South America. After deriving difference vegetation index (DVI) from NOAA AVHRR data, Yu
et al. [
21] constructed a relationship between DVI and PM
10 so that the latter can be retrieved from the former via the established relationship quantitatively. Zha
et al. [
22] put forward a normalized difference haze index (NDHI) for studying atmospheric haze weather from winter Moderate Resolution Imaging Spectroradiometer (MODIS) imagery. These methods are common in that
in situ measured data were statistically analyzed to establish the relationship between apparent reflectance and the physical and chemical properties of aerosols. Such empirical statistical relationship faces limitations as it is subject to the influence of the underlying surface, atmospheric conditions, as well as the observation conditions.
In this study the response of apparent reflectance in each of the MODIS wavebands 1–7 to AOD that has been simulated using the Second Simulation of the Satellite Signal in the Solar Spectrum (6S) radiative transfer model is first assessed. A comparison among the seven responses reveals the most and least sensitive MODIS wavebands. These two bands were then used to construct three aerosol indices that can be easily derived from remotely sensed imagery, for the effective detection of atmospheric aerosol pollution with relative ease. The relationship between in situ measured AOD at the Lake Taihu, Beijing, and Xianghe stations in the Aerosol Robotic NETwork (AERONET) over one year with the proposed aerosol indices was analyzed to validate the applicability of the proposed aerosol indices in estimating atmospheric pollution caused by aerosols.
3. Results
3.1. AOD Variation
The CE-318 sun photometer measured AOD data were averaged, and the seasonal variations of AOD are given in
Table 2. An overview of the yearly observations shows that AOD in all four seasons is higher than 0.5, indicating that the atmosphere in the Taihu region is rather murky. Summer AOD is the highest while winter AOD is the lowest. Of the four seasons, both summer and autumn have a relatively large standard deviation in AOD, suggesting that AOD tends to change more in these two seasons. Summer and autumn are the rainy seasons in this region when the weather changes rather abruptly and drastically, triggering a huge change in AOD. In the winter and spring seasons, near surface air is relatively stable, causing little change in AOD during these seasons.
Shown in
Figure 1 is the frequency distribution of AOD values over September 2011–August 2012. It illustrates that the highest frequency of year-long AOT occurs within 0.6–0.8, accounting for 28% of the total. Those observations having a relatively high AOD (>0.8) comprise 41% of the total. Those extremely high AOD values (AOD > 1.6) make up only 4% of the total samples. The yearly average AOD stands at 0.59, lower than the mean averaged over multiple years (0.80) [
34].
It should be noted that the data statistics above are results from the ground-based data recorded within half an hour of the satellite overpass on cloud-free days. The statistics for all of the level 2.0 AOD retrieved from the direct solar radiation observed at the Lake Taihu station is shown in the
Appendix (
Table A1). The yearly average AOD stands at 0.55, and it is found that the seasonal change tendency of the AOD is also similar as showed in
Table 2.
3.2. Spectral Properties of the Study Site
MODIS nadir observed surface reflectance product (MCD43A4) is derived from 16 consecutive observations that have been calibrated using the surface BRDF model. Since the impact of atmosphere and observation angle has been removed from the data product, it can be treated as the surface reflectance. Illustrated in
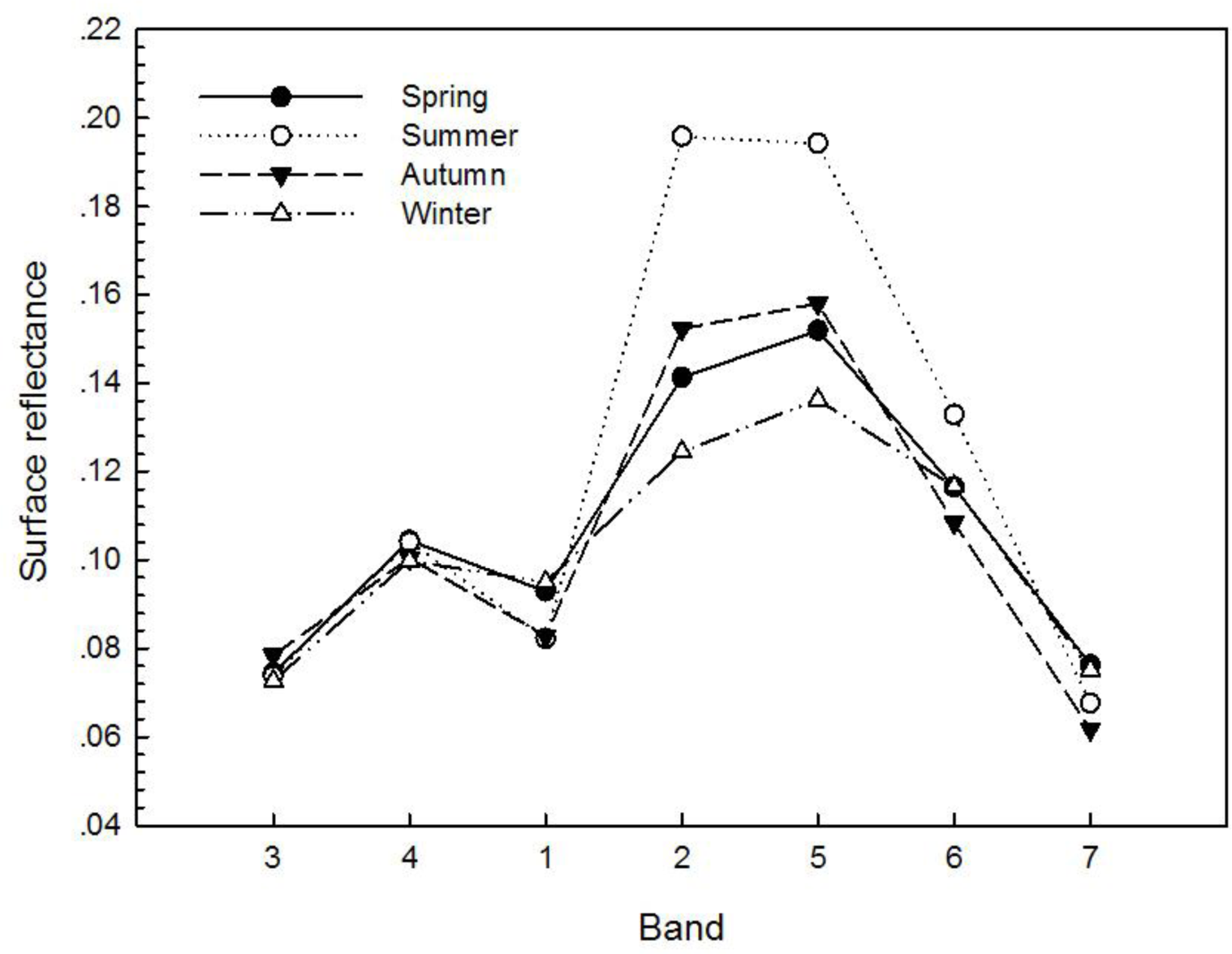
Figure 2 are the seasonal variations of retrieved surface reflectance from MODIS bands 1–7. In order to facilitate subsequent discussion, the horizontal axis has been arranged by wavelength in the ascending order. The general shape of the spectral response is highly reminiscent of vegetation spectral response with an apparent distinction among the four seasons. In the summer season, there is an obvious disparity in bands 1 (0.66 μm) and 2 (0.86 μm) used in vegetation index (NDVI). The surface reflectance curve in spring and autumn has a similar distribution. In winter the difference between different wavebands becomes noticeably less distinctive than in other seasons. In particular, those wavebands that are used in deriving vegetative index show a markedly subdued effect.
Shown in
Figure 3 is the variation of apparent reflectance with wavelength in four seasons. Its comparison with
Figure 2 reveals that apparent reflectance is markedly higher in every waveband, especially in those visible light wavebands. The increase is attributed to the stronger atmospheric effect in short wavelengths that has caused a rise of varying magnitude in apparent reflectance.
3.3. Variation of Simulated Apparent Reflectance
For the convenience of comparison, the difference between the apparent reflectance of each waveband simulated using the 6S model and apparent reflectance at AOD = 0.1 was used to reveal the variation of apparent reflectance of each waveband with AOD intuitively (
Figure 4).
As shown in
Figure 4, apparent reflectance simulated from the visible light channels of Band 3 (0.47 μm), Band 4 (0.55 μm), and Band 1 (0.66 μm) of MODIS is rather sensitive to AOD. Apparent reflectance increases with AOD. And the slope for the curve of Band 3 (0.47 μm) relating apparent reflectance to AOD is larger than that of other wavebands. The increase from the initial AOD of 0.1 is the largest in the blue light Band 3 at a magnitude of 0.104 (summer). In addition, a similar trend of increase with AOD is also found in the near infrared Band 2 (0.86 μm) in all other seasons. In contrast, apparent reflectance is related inversely to AOD in the infrared channels of Band 5 (1.24 μm) and Band 6 (1.64 μm) in all four seasons. Apparent reflectance simulated from the infrared Band 7 (2.13μm) is hardly subject to the influence of AOD. In other words, with the increase in AOD, apparent reflectance is almost the same as the surface reflectance. Both are true representation of the inherent optical properties of ground objects.
The influence of AOD on apparent reflectance is suppressed at a longer wavelength because the larger dimension of wavelength than aerosol diameter undermines backscattering. Strong scattering of blue light by aerosols (
Figure 3) and the low reflection of blue light by the Earth’s surface (
Figure 2) make the MODIS blue channel (Band 3) contain the most information on path radiation whereas band 7 is not subject to such an influence. Therefore, it is concluded that apparent reflectance is the most sensitive to AOD in Band 3 (0.47 μm), but least sensitive in Band 7 (2.13 μm). These two bands were thus used to construct three aerosol indices (AI). They are difference aerosol index (DAI), ratio aerosol index (RAI), as well as normalized difference aerosol index (NDAI) using the following equations, respectively:
Listed in
Table 3 are the correlation coefficients between the aforementioned indices and AOD in four seasons. These coefficient values demonstrate that under the simulation conditions, each of the indices bears a high linear relationship with AOD. In addition to aerosol, atmospheric absorption gas such as water vapor, ozone, and oxygen all have influence on satellite reflectance in the visible and near-infrared spectrums. By using the default values for the related parameters in the theoretical model, it disturbs the simulative apparent reflectance relatively less, and its calculating results for aerosol indices are more accurate relatively. Therefore, the seasonal variation of correlation coefficients is close. As shown in
Table 3, NDAI has the loosest correlationof the three indices. Even so, the minimum correlation coefficient is still as high as 0.9669 in autumn. These results suggest that the proposed aerosol indices can effectively indicate AOD under the simulation conditions. However, the digital images collected by image sensors are generally contaminated in the process of data acquisition, digitization, compression, and transmission. The influenced factors are various and much more complex. Therefore, errors will be inevitably introduced under the actual atmospheric conditions.
3.4. Correlation between in situ Measured AOD and Aerosol Indices
In order to assess the applicability of the proposed aerosol indices in estimating aerosol-induced atmospheric pollution, the
in situ measured AOD data at the Lake Taihu station were correlated with aerosol indices calculated from MODIS-derived apparent reflectance by seasons (
Table 4). The scatter plots are shown in the
Appendix (
Figure A1).
Given that the actual atmospheric conditions differ from the standard atmospheric conditions used in the 6S simulation, and that surface reflectance varies with time, errors will be inevitably introduced to the results if
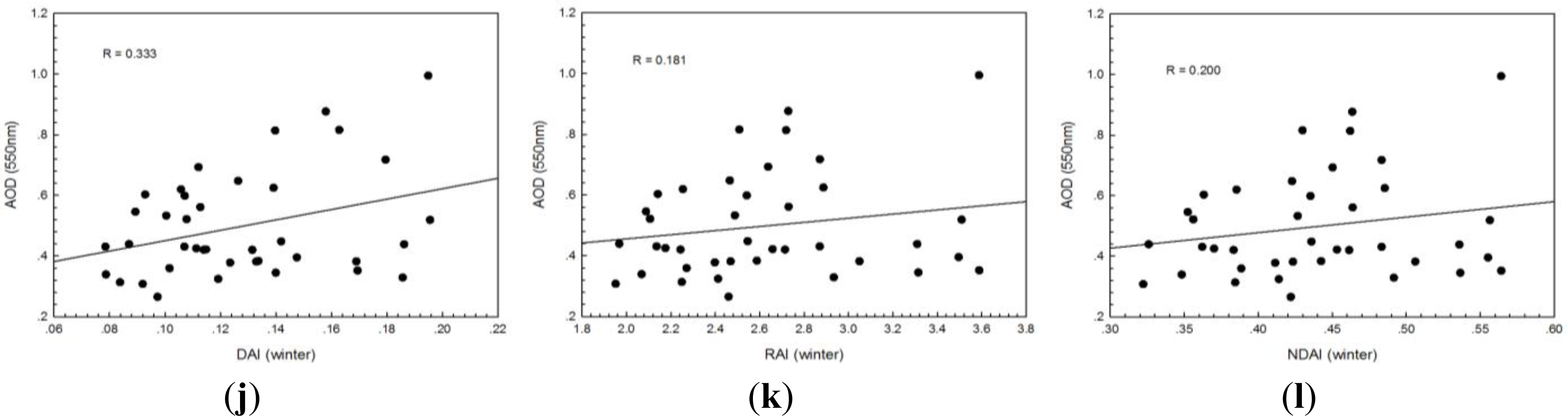
in situ measured data were used to construct the model. Judging from the year-long data statistically, the linear correlation between AOD and the three proposed aerosol indices is the closest in summer, but the loosest in winter. A plausible explanation is that AOD in winter over the study site hardly varied, causing a high degree of uncertainty in the retrieved results (
Table 2). Since AOD exhibits a relatively large pace of variation both temporally and spatially, and the
in situ measured results at the Lake Taihu station do not completely match the satellite imagery-derived counterparts. Such spatiotemporal disparity has also contributed to their deviation from the simulated results. Finally, the close proximity of the study site to the lake water means that a huge quantity of water vapor originating from the lake has also exerted an influence on the retrieved AOD for this region. In the literature it has been reported that relative humidity of a study area, to a large extent, is the lead factor influencing AOD [
35].
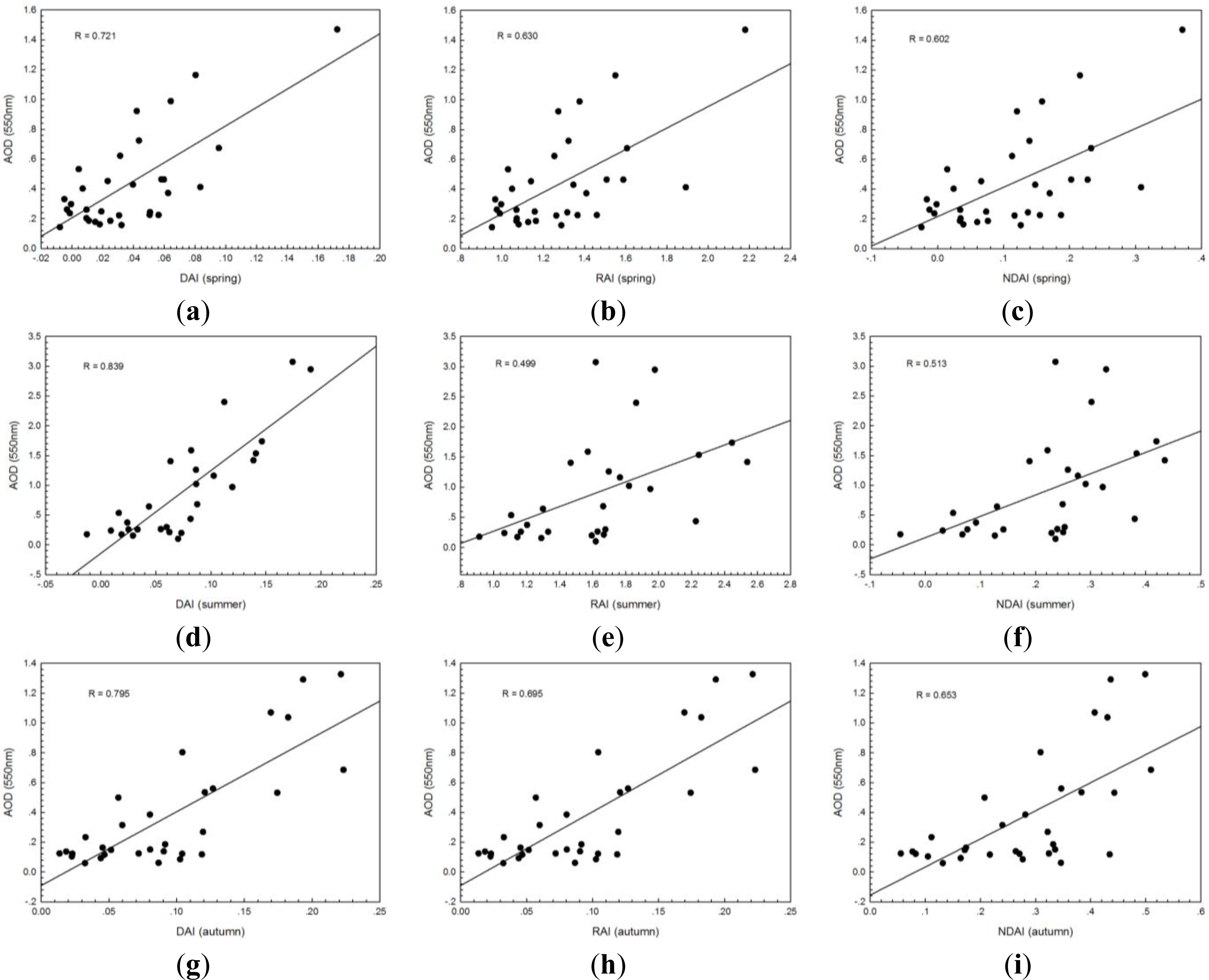
A comparison of the three indices in a given season demonstrates that difference aerosol index (DAI) has the highest correlation with AOD. This correlation is as high as 0.585 in spring, 0.860 in summer, 0.685 in autumn, and 0.333 in winter. These four correlation coefficients are all significant at the 0.05 significance level. Moreover, the correlation in summer, spring and autumn is still significant at the 0.01 significance level. The spectral index is designed to effectively synthesize the relevant spectral signal, enhance the information of target objects, and decrease the interference of the extra information. Thus far a number of indices, such as NDVI, NDWI, and NDBI, have been used routinely to depict ground objects quantitatively. Similarly, it is assumed that in a clear-sky (non-cloudy) scene, the solar radiation backscattered from aerosols have different spectral signatures with either the Earth’s surface or atmospheric molecules. By using multiple bands in the visible, near-IR, and IR wavelength regions, one can perform a retrieval to back out the aerosol signature, and infer the physical properties of the aerosols within the scene. However, dissimilar to ground objects, aerosols are solid or liquid substances suspended in the atmosphere. Their spectral properties are inevitably affected by the characteristics of underlying ground objects. Both RAI and DNAI involve ratioing, which makes them more effective than DAI in suppressing the contribution of weak signals of aerosols to observed apparent reflectance from the satellite to a large degree. Therefore, DAI is a more suitable indicator of aerosol-related atmospheric pollution than the other two indices.
In addition, to investigate if the proposed method can be applied to other places, the observational data at the AERONET Beijing and Xianghe stations over June 2011–May 2012 were also analyzed. The two stations are situated in Northern China, where the environment is different from Lake Taihu with the colder and drier climate.
The Beijing site (39.98°N, 116.38°E) is located on a terrace on the roof of the Institute of Atmospheric Physics building in Beijing. The main land-use types around this site are roads and residential areas. The Xianghe site (39.75°N, 116.96°E) is located on the roof of a four-floor building of Xianghe Observatory, Institute of Atmospheric Physics. This site is surrounded by a small town in the east and by agricultural fields in the remaining directions.
The analysis results also show that DAI bears a relatively high correlation with AOD measured with a CE-318 sun photometer in all four seasons (
Table 5). The summer and autumn AOD have much correlation with DAI calculated from MODIS-derived apparent reflectance. The scatter plots are also shown in the
Appendix (
Figures A2 and
A3).